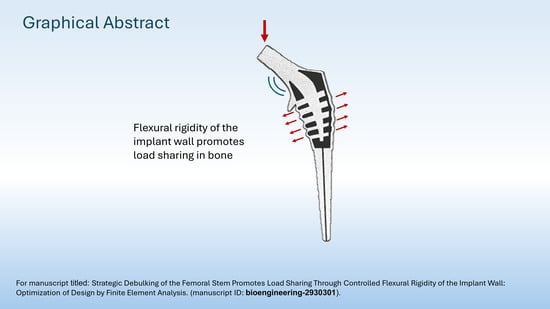
Debulking of the Femoral Stem in a Primary Total Hip Joint Replacement: A Novel Method to Reduce Stress Shielding
Abstract
1. Introduction
2. Materials and Methods
2.1. The Femur and Material Property Derivation
2.2. Femoral Implant Material Properties
2.3. FEA Setup
2.3.1. Meshing, Material Models, Part Tie-Constraints, and Part-to-Part Contact
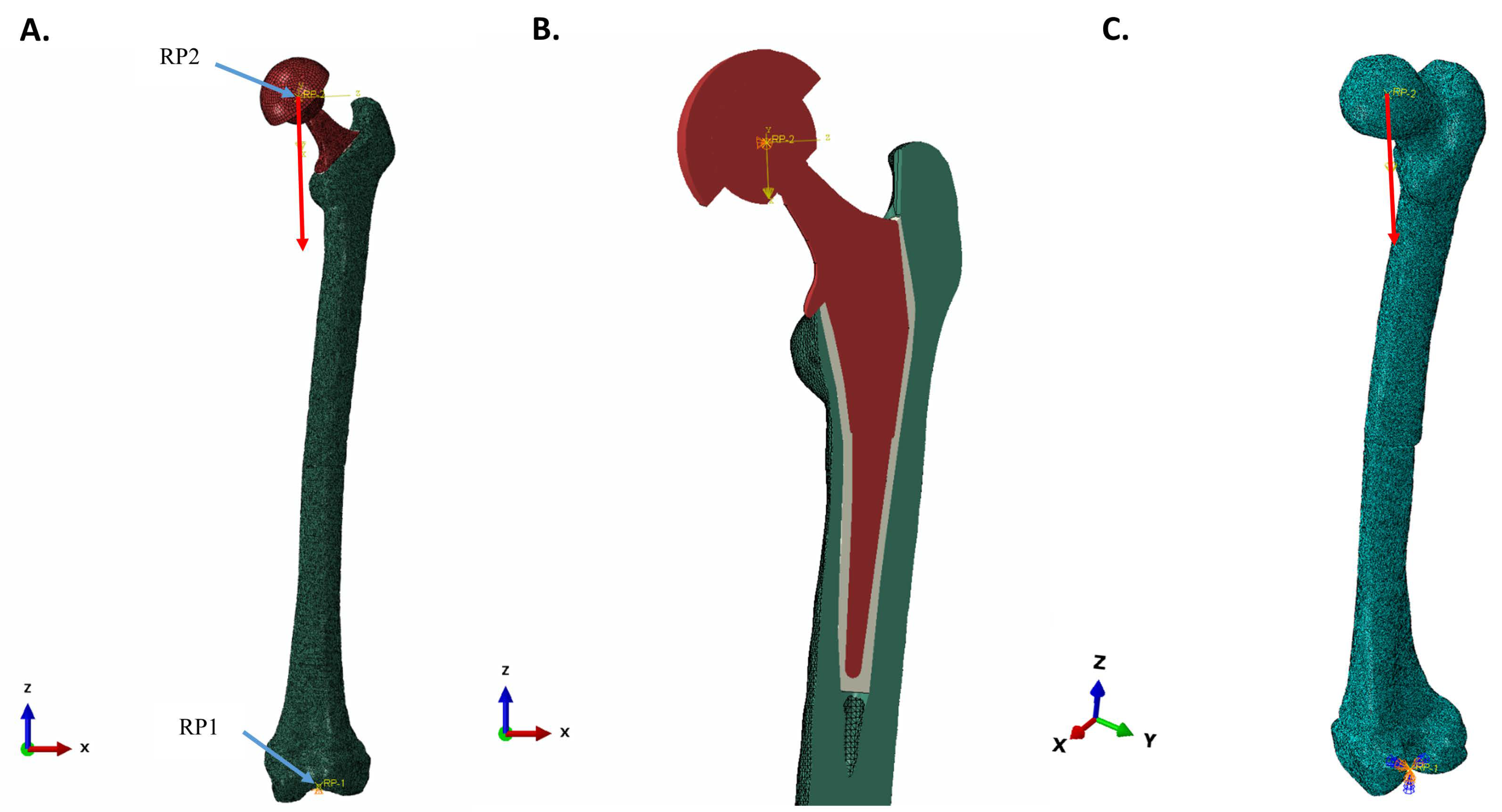
2.3.2. Boundary Conditions, Couplings, and Spatial Model Constraints
2.3.3. Loads and Creation of Load Direction in the Local Coordinate System
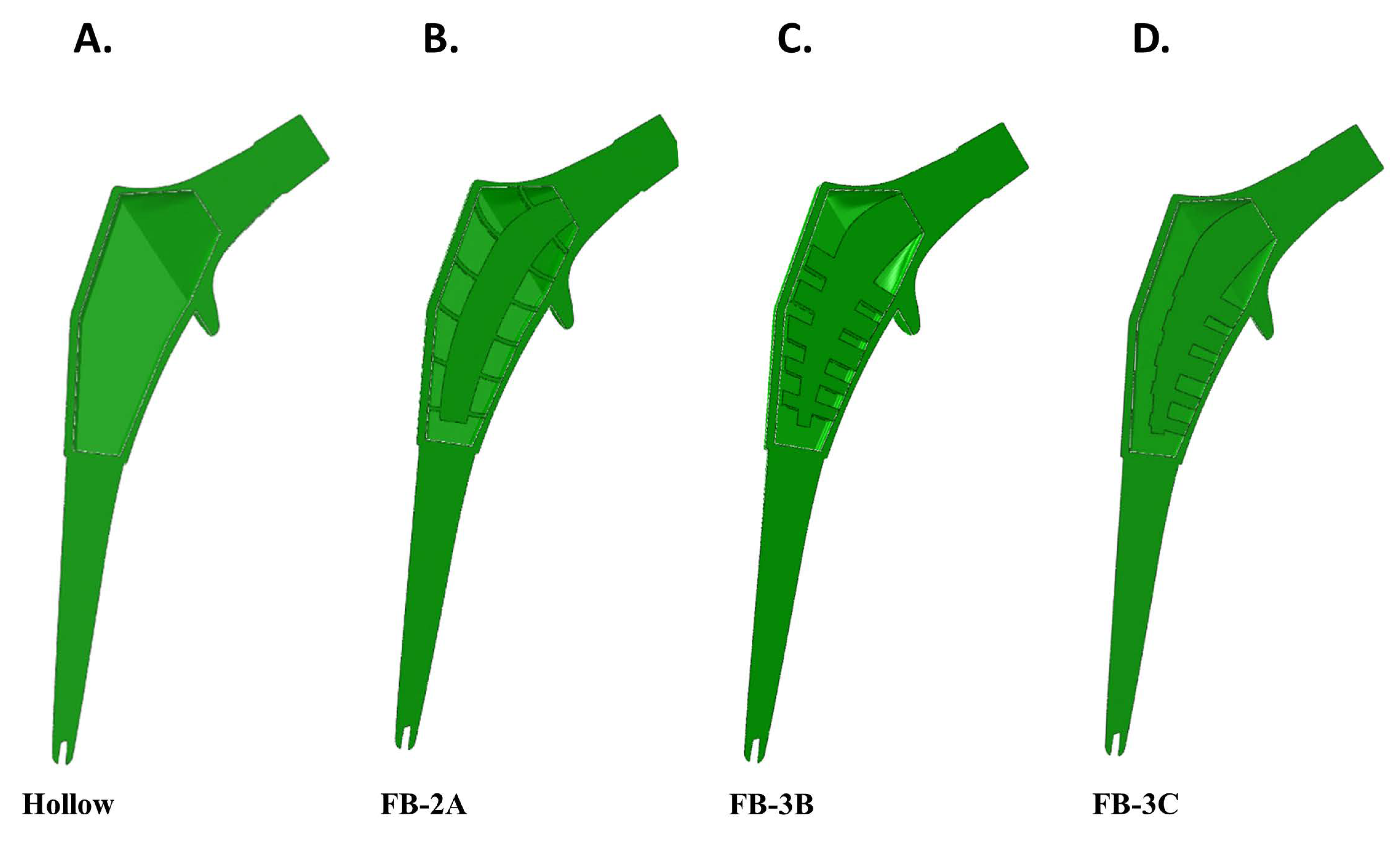
2.3.4. Solid, Hollow, and Truss Implant Model Descriptions
3. Results
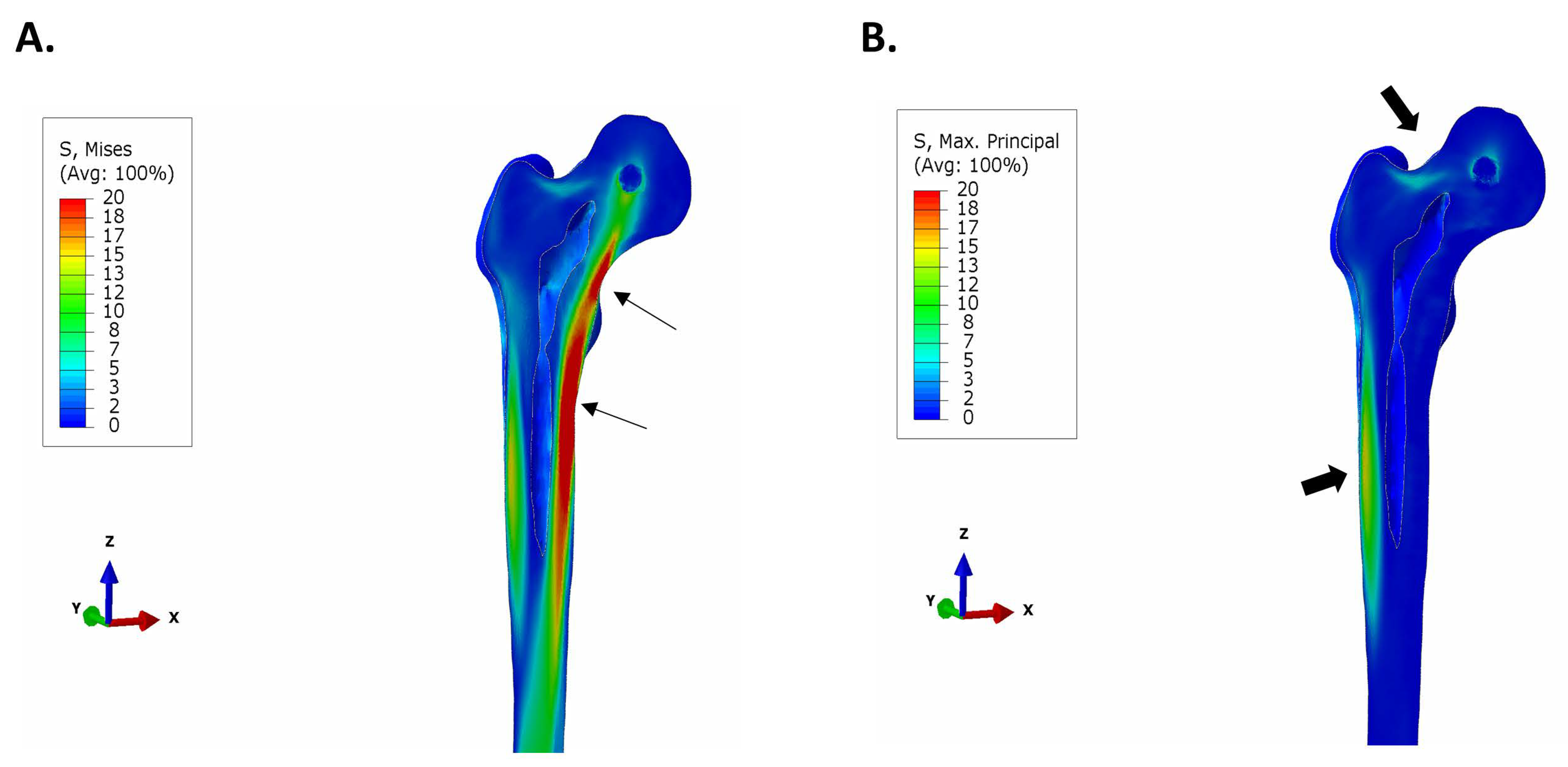
3.1. Stresses in Intact Femur
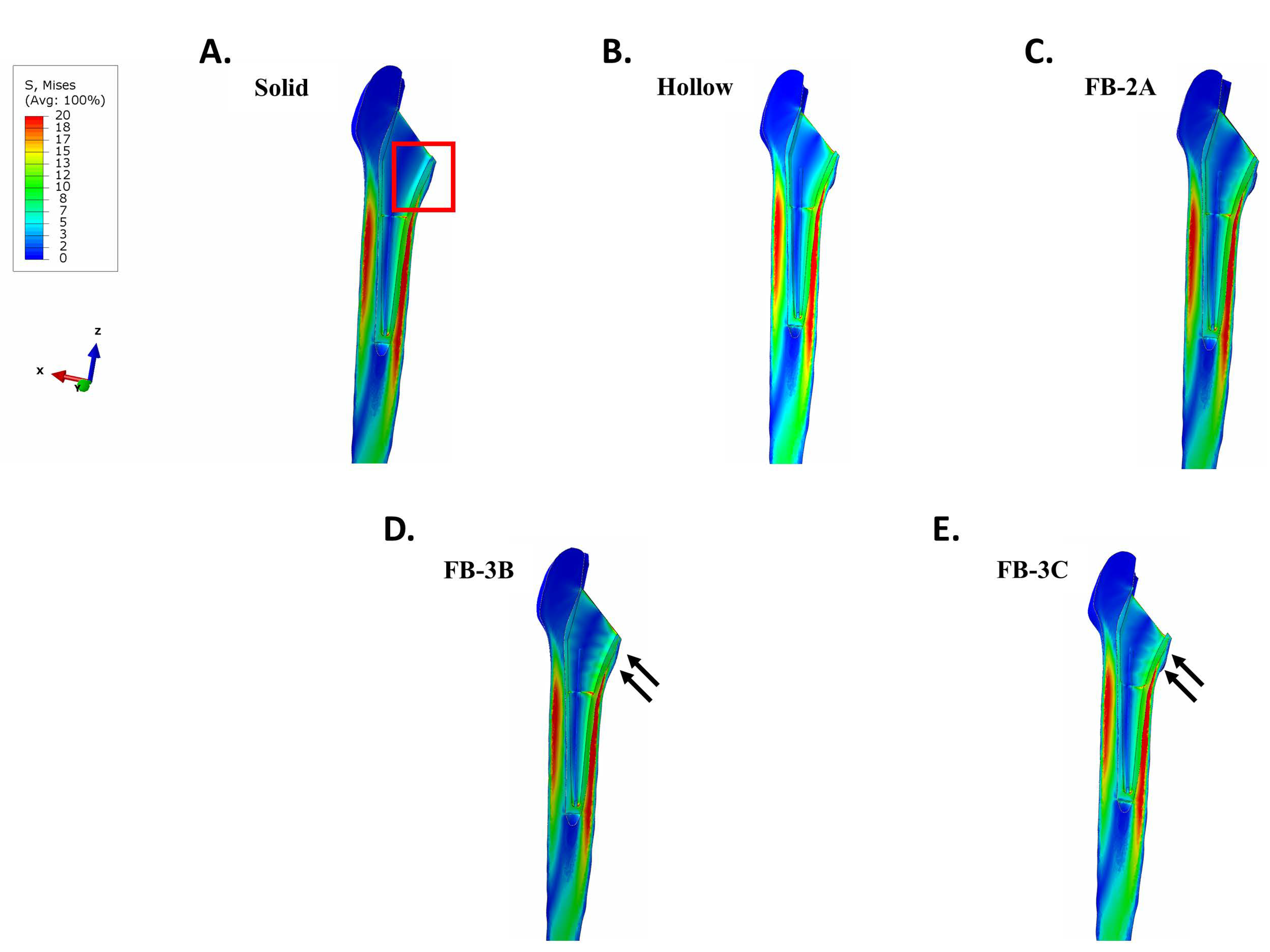
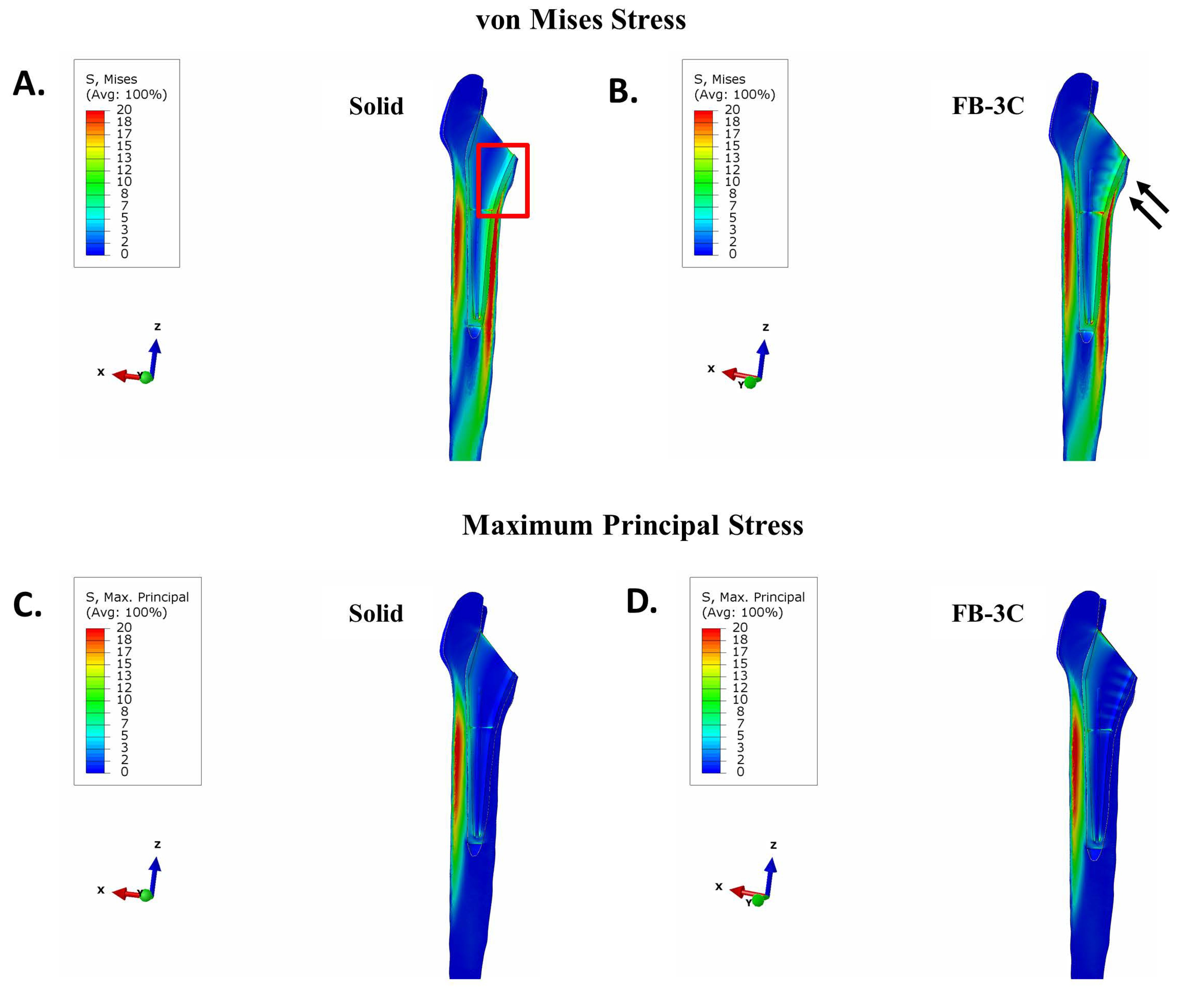
3.2. Stresses in Implanted Femur
3.2.1. Uncemented vs. Cemented Stems
3.2.2. Collared vs. Collarless Femoral Stem
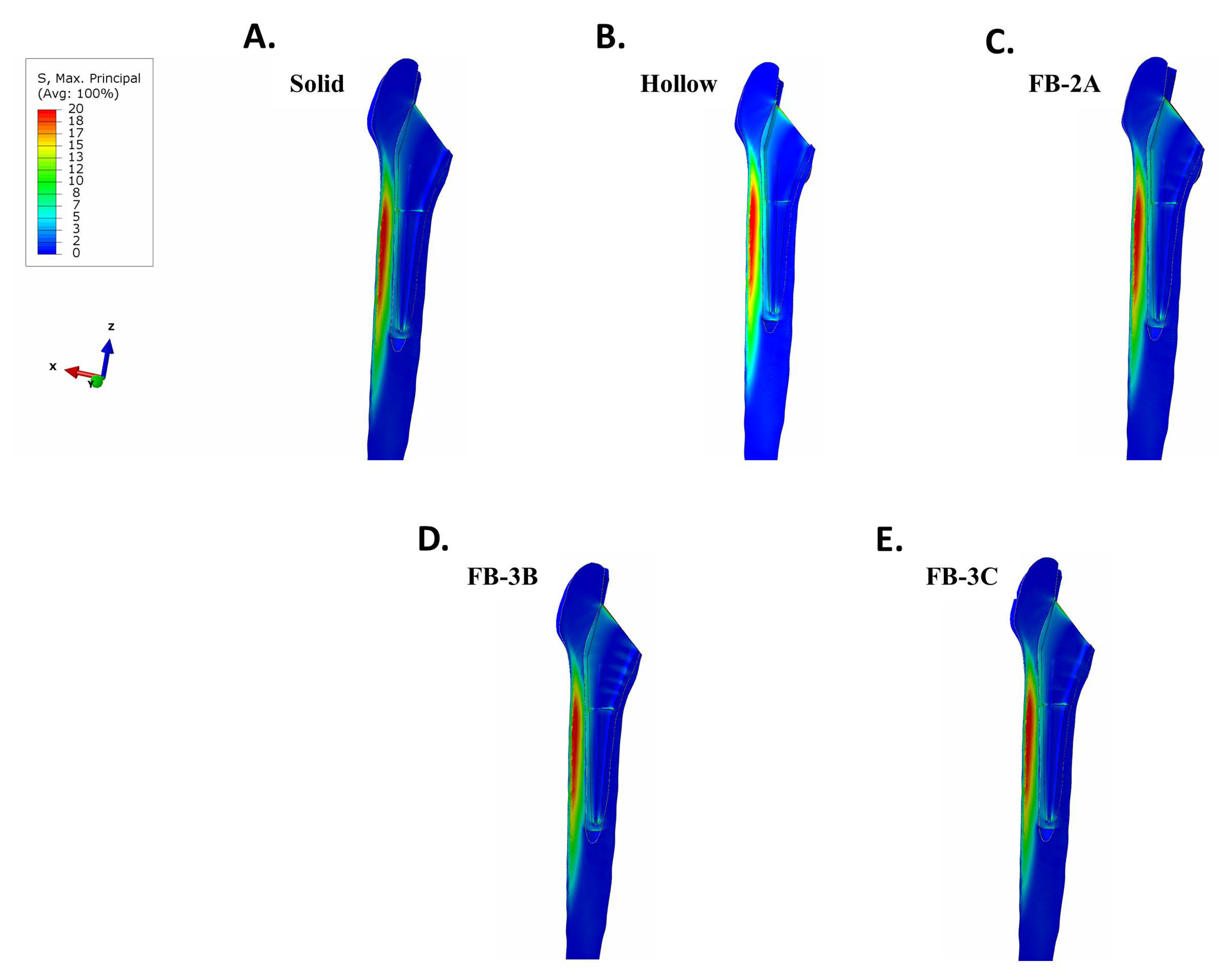
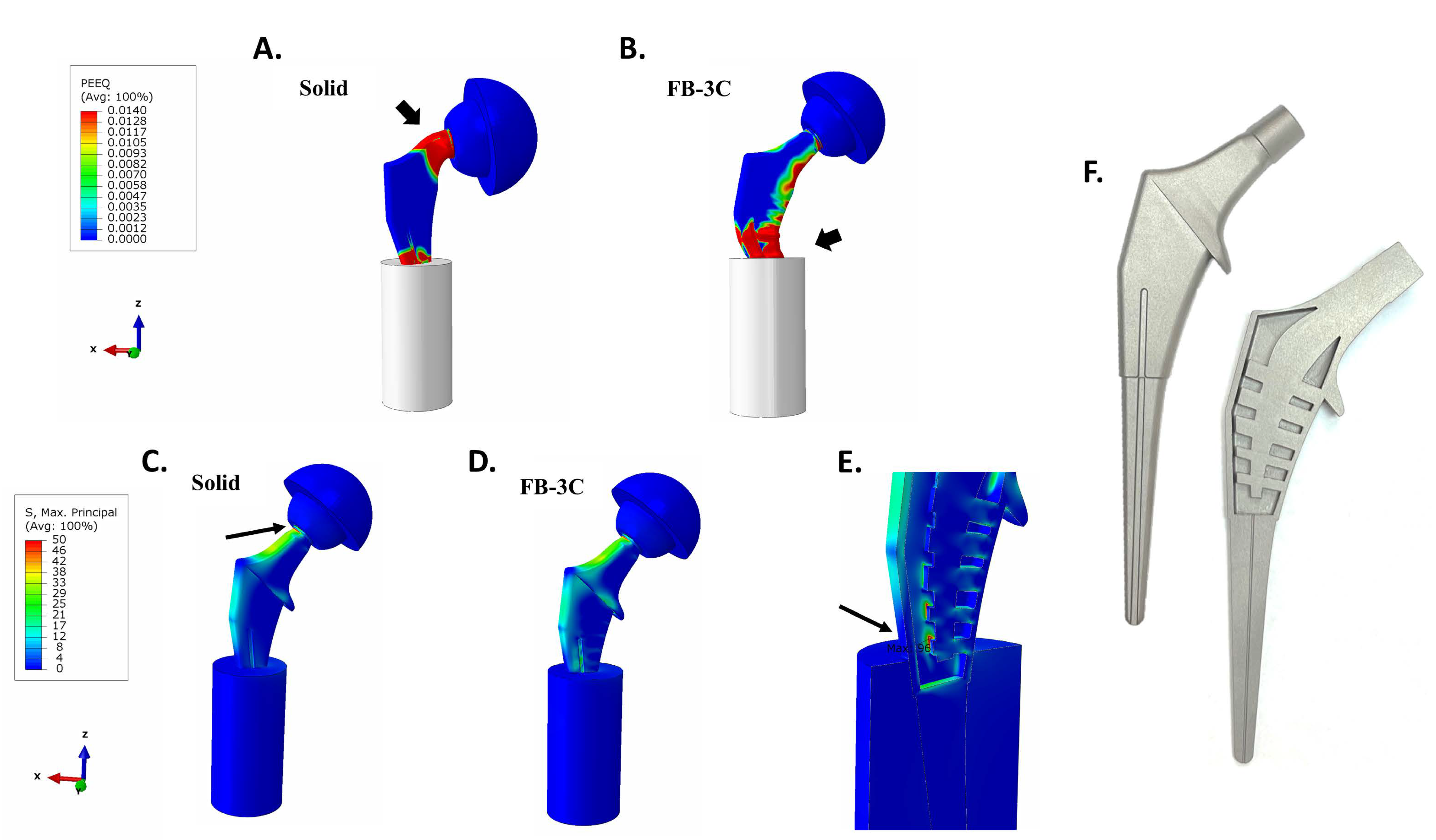
3.3. Maximum Principal (Tensile) Stress in Implant
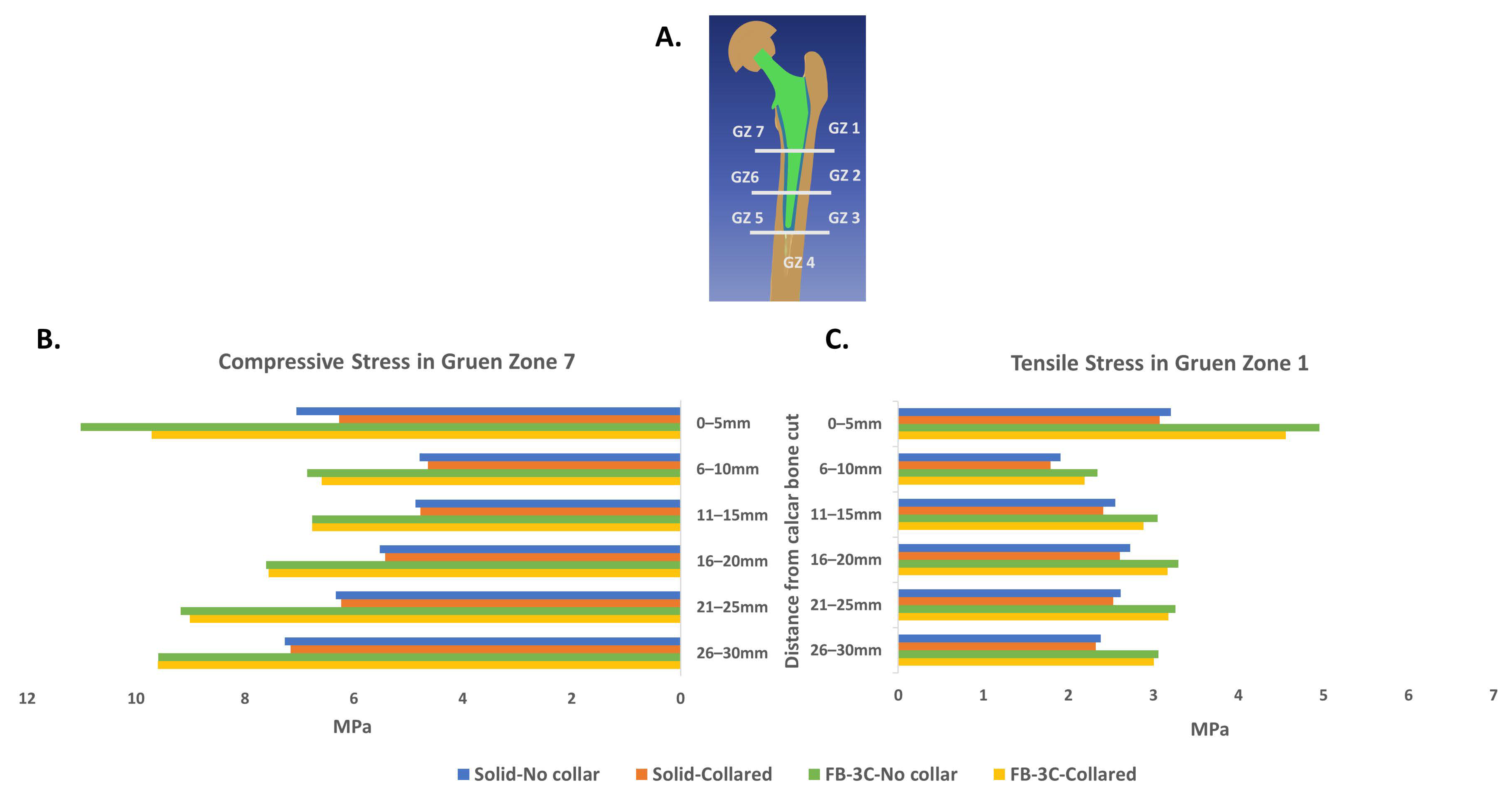
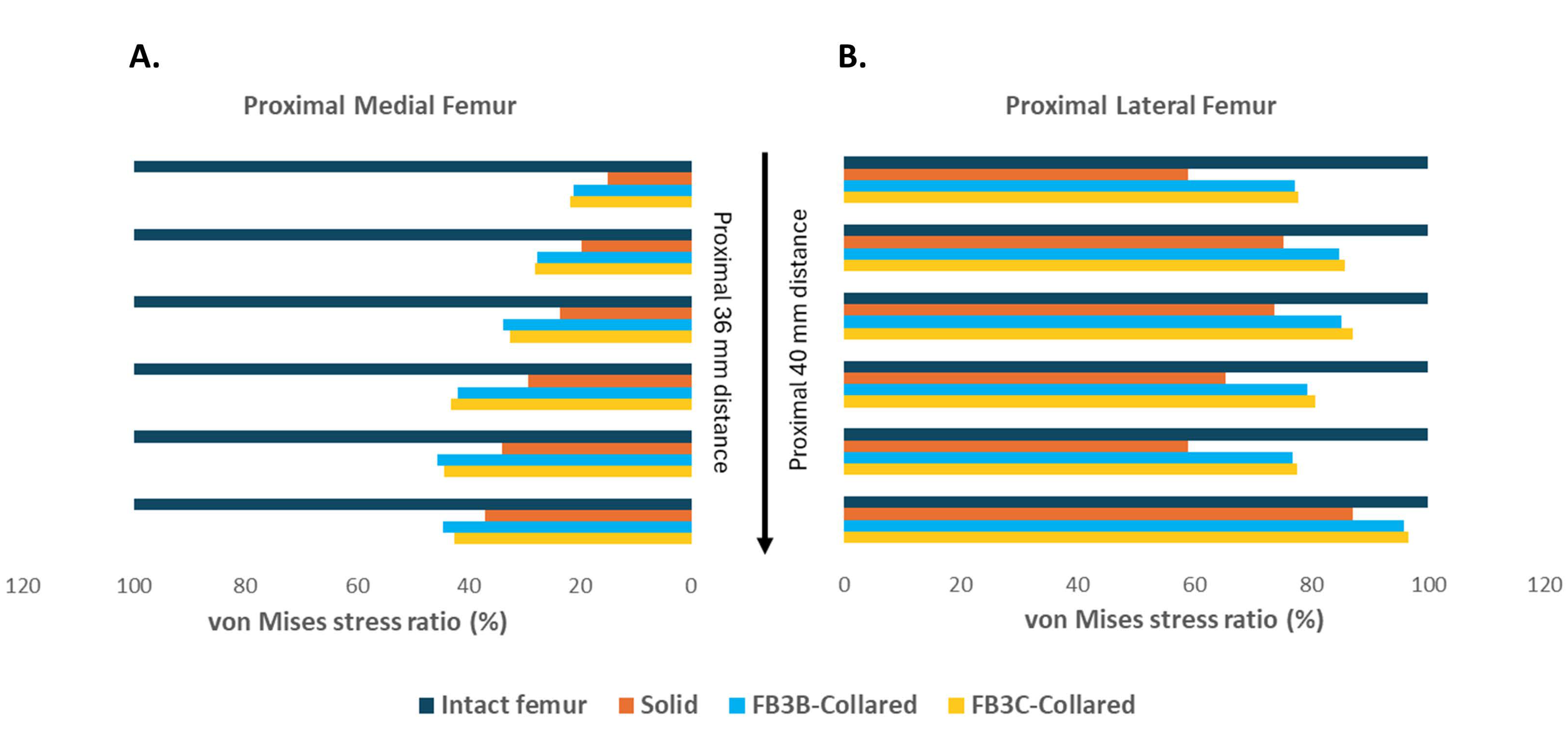
3.4. Quantification of Stress in Proximal Bone
3.5. Implant Static Load Tests to Failure
3.6. Implant Endurance Load Tests
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pivec, R.; Johnson, A.J.; Mears, S.C.; Mont, M.A. Hip arthroplasty. Lancet 2012, 380, 1768–1777. [Google Scholar] [CrossRef] [PubMed]
- Goldman, A.H.; Osmon, D.R.; Hanssen, A.D.; Pagnano, M.W.; Berry, D.J.; Abdel, M.P. The Lawrence D. Dorr Surgical Techniques & Technologies Award: Aseptic Reoperations Within One Year of Primary Total Hip Arthroplasty Markedly Increase the Risk of Later Periprosthetic Joint Infection. J. Arthroplast. 2020, 35, S10–S14. [Google Scholar]
- Ulrich, S.D.; Seyler, T.M.; Bennett, D.; Delanois, R.E.; Saleh, K.J.; Thongtrangan, I.; Kuskowski, M.; Cheng, E.Y.; Sharkey, P.F.; Parvizi, J.; et al. Total hip arthroplasties: What are the reasons for revision? Int. Orthop. 2008, 32, 597–604. [Google Scholar] [CrossRef] [PubMed]
- Arabnejad Khanoki, S.; Pasini, D. Multiscale design and multiobjective optimization of orthopedic hip implants with functionally graded cellular material. J. Biomech. Eng. 2012, 134, 031004. [Google Scholar] [CrossRef] [PubMed]
- Sumner, D.R.; Turner, T.M.; Igloria, R.; Urban, R.M.; Galante, J.O. Functional adaptation and ingrowth of bone vary as a function of hip implant stiffness. J. Biomech. 1998, 31, 909–917. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Gu, J.; Zhou, Y. Primary total hip arthroplasty failure: Aseptic loosening remains the most common cause of revision. Am. J. Transl. Res. 2022, 14, 7080–7089. [Google Scholar] [PubMed]
- Bieger, R.; Ignatius, A.; Decking, R.; Claes, L.; Reichel, H.; Durselen, L. Primary stability and strain distribution of cementless hip stems as a function of implant design. Clin. Biomech. 2012, 27, 158–164. [Google Scholar] [CrossRef] [PubMed]
- Hnat, W.P.; Conway, J.S.; Malkani, A.L.; Yakkanti, M.R.; Voor, M.J. The effect of modular tapered fluted stems on proximal stress shielding in the human femur. J. Arthroplast. 2009, 24, 957–962. [Google Scholar] [CrossRef] [PubMed]
- Jeon, I.; Bae, J.Y.; Park, J.H.; Yoon, T.R.; Todo, M.; Mawatari, M.; Hotokebuchi, T. The biomechanical effect of the collar of a femoral stem on total hip arthroplasty. Comput. Methods Biomech. Biomed. Engin 2011, 14, 103–112. [Google Scholar] [CrossRef]
- Heyland, M.; Checa, S.; Kendoff, D.; Duda, G.N. Anatomic grooved stem mitigates strain shielding compared to established total hip arthroplasty stem designs in finite-element models. Sci. Rep. 2019, 9, 482. [Google Scholar] [CrossRef]
- Arabnejad, S.; Johnston, B.; Tanzer, M.; Pasini, D. Fully porous 3D printed titanium femoral stem to reduce stress-shielding following total hip arthroplasty. J. Orthop. Res. 2017, 35, 1774–1783. [Google Scholar] [CrossRef] [PubMed]
- Limmahakhun, S.; Oloyede, A.; Chantarapanich, N.; Jiamwatthanachai, P.; Sitthiseripratip, K.; Xiao, Y.; Yan, C. Alternative designs of load-sharing cobalt chromium graded femoral stems. Mater. Today Commun. 2017, 12, 1–10. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, X.; Liu, L.; Shi, Z.; Hao, Y. On the design and properties of porous femoral stems with adjustable stiffness gradient. Med. Eng. Phys. 2020, 81, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Zhao, Y.; Wang, M.; Liu, Z.; Liu, C. Parametric Design of Hip Implant with Gradient Porous Structure. Front. Bioeng. Biotechnol. 2022, 10, 850184. [Google Scholar] [CrossRef] [PubMed]
- Naghavi, S.A.; Tamaddon, M.; Garcia-Souto, P.; Moazen, M.; Taylor, S.; Hua, J.; Liu, C. A novel hybrid design and modelling of a customised graded Ti-6Al-4V porous hip implant to reduce stress-shielding: An experimental and numerical analysis. Front. Bioeng. Biotechnol. 2023, 11, 1092361. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Wang, H.; Zhang, N.; Zhang, M.; Cheng, C.K. Femoral Stems with Porous Lattice Structures: A Review. Front. Bioeng. Biotechnol. 2021, 9, 772539. [Google Scholar] [CrossRef] [PubMed]
- Huiskes, R.I.K.; Weinans, H.; Rietbergen, B.V. The Relationship Between Stress Shielding and Bone Resorption Around Total Hip Stems and the Effects of Flexible Materials. Clin. Orthop. Relat. Res. 1992, 274, 124–134. [Google Scholar] [CrossRef]
- Adam, F.; Hammer, D.S.; Pfautsch, S.; Westermann, K. Early failure of a press-fit carbon fiber hip prosthesis with a smooth surface. J. Arthroplast. 2002, 17, 217–223. [Google Scholar] [CrossRef]
- Trebse, R.; Milosev, I.; Kovac, S.; Mikek, M.; Pisot, V. Poor results from the isoelastic total hip replacement: 14–17-year follow-up of 149 cementless prostheses. Acta Orthop. 2005, 76, 169–176. [Google Scholar] [CrossRef]
- Hanada, S.; Masahashi, N.; Jung, T.K.; Yamada, N.; Yamako, G.; Itoi, E. Fabrication of a high-performance hip prosthetic stem using beta Ti-33.6Nb-4Sn. J. Mech. Behav. Biomed. Mater. 2014, 30, 140–149. [Google Scholar] [CrossRef]
- Chiba, D.; Yamada, N.; Mori, Y.; Oyama, M.; Ohtsu, S.; Kuwahara, Y.; Baba, K.; Tanaka, H.; Aizawa, T.; Hanada, S.; et al. Mid-term results of a new femoral prosthesis using Ti-Nb-Sn alloy with low Young’s modulus. BMC Musculoskelet. Disord. 2021, 22, 987. [Google Scholar] [CrossRef] [PubMed]
- Yamako, G.; Janssen, D.; Hanada, S.; Anijs, T.; Ochiai, K.; Totoribe, K.; Chosa, E.; Verdonschot, N. Improving stress shielding following total hip arthroplasty by using a femoral stem made of beta type Ti-33.6Nb-4Sn with a Young’s modulus gradation. J. Biomech. 2017, 63, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Ni, S.; Ma, L.; Li, M. Porous construction and surface modification of titanium-based materials for osteogenesis: A review. Front. Bioeng. Biotechnol. 2022, 10, 973297. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical performance of additively manufactured meta-biomaterials. Acta Biomater. 2019, 85, 41–59. [Google Scholar] [CrossRef] [PubMed]
- Kolken, H.M.A.; de Jonge, C.P.; van der Sloten, T.; Garcia, A.F.; Pouran, B.; Willemsen, K.; Weinans, H.; Zadpoor, A.A. Additively manufactured space-filling meta-implants. Acta Biomater. 2021, 125, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Kolken, H.M.A.; Janbaz, S.; Leeflang, S.M.A.; Lietaert, K.; Weinans, H.H.; Zadpoor, A.A. Rationally designed meta-implants: A combination of auxetic and conventional meta-biomaterials. Mater. Horiz. 2018, 5, 28–35. [Google Scholar] [CrossRef]
- Liu, B.; Wang, H.; Zhang, M.; Li, J.; Zhang, N.; Luan, Y.; Fang, C.; Cheng, C.K. Capability of auxetic femoral stems to reduce stress shielding after total hip arthroplasty. J. Orthop. Translat 2023, 38, 220–228. [Google Scholar] [CrossRef] [PubMed]
- Rana, M.; Karmakar, S.; Bandyopadhyay, A.; Roychowdhury, A. Design and manufacturing of patient-specific Ti6Al4V implants with inhomogeneous porosity. J. Mech. Behav. Biomed. Mater. 2023, 143, 105925. [Google Scholar] [CrossRef] [PubMed]
- Morgan, E.F.; Bayraktar, H.H.; Keaveny, T.M. Trabecular bone modulus-density relationships depend on anatomic site. J. Biomech. 2003, 36, 897–904. [Google Scholar] [CrossRef]
- Javid, S. Optimized Evaluation of Bone Tissue Material Properties by Inverse Finite Element Analysis and Femur Fracture Testing. Ph.D. Dissertation, North Dakota State University of Agriculture and Applied Science, Fargo, ND, USA, October 2014. [Google Scholar]
- Lampman, S.R. ASM Handbook. Fatigue and Fracture; ASM International: Almere, The Netherlands, 1996; Volume 19, p. 842. [Google Scholar]
- ISO Standard No. 7206-4:2010; Implants for Surgery—Partial and Total Hip Joint Prostheses—Part 4: Determination of Endurance Properties and Performance of Stemmed Femoral Components. ISO, International Organization for Standardization: Geneva, Switzerland, 2010.
- ISO Standard No. 7206-6:2013; Implants for Surgery—Partial and Total Hip Joint Prostheses—Part 6: Endurance Properties Testing and Performance Requirements of Neck Region of Stemmed Femoral Components. ISO, International Organization for Standardization: Geneva, Switzerland, 2013.
- ISO Standard No. 7206-10:2018; Implants for Surgery—Partial and Total Hip Joint Prostheses—Part 10: Determination of Resistance to Static Load of Modular Femoral Heads. ISO, International Organization for Standardization: Geneva, Switzerland, 2018.
- Bergmann, G.; Bender, A.; Dymke, J.; Duda, G.; Damm, P. Standardized Loads Acting in Hip Implants. PLoS ONE 2016, 11, e0155612. [Google Scholar] [CrossRef]
- Beckmann, N.A.; Bitsch, R.G.; Seeger, J.B.; Klotz, M.C.; Kretzer, J.P.; Jaeger, S. Mechanical properties of a cemented porous implant interface. Acta Orthop. 2014, 85, 531–537. [Google Scholar] [CrossRef] [PubMed]
- Kundu, J.; Pati, F.; Shim, J.-H.; Cho, D.-W.; Narayan, R. (Eds.) Rapid Prototyping Technology for Bone Regeneration. In Rapid Prototyping of Biomaterials—Principles and Applications; Woodhead Publishing: Sawston, UK, 2014. [Google Scholar]
- AAOS. American Joint Replacement Registry (AJRR): 2022 Annual Report; AAOS: Rosemont, IL, USA, 2022. [Google Scholar]
- Deere, K.; Whitehouse, M.R.; Kunutsor, S.K.; Sayers, A.; Mason, J.; Blom, A.W. How long do revised and multiply revised hip replacements last? A retrospective observational study of the National Joint Registry. Lancet Rheumatol. 2022, 4, e468–e479. [Google Scholar] [CrossRef] [PubMed]
- Inaba, Y.; Kobayashi, N.; Oba, M.; Ike, H.; Kubota, S.; Saito, T. Difference in Postoperative Periprosthetic Bone Mineral Density Changes Between 3 Major Designs of Uncemented Stems: A 3-Year Follow-Up Study. J. Arthroplast. 2016, 31, 1836–1841. [Google Scholar] [CrossRef] [PubMed]
- Gross, S.; Abel, E.W. A finite element analysis of hollow stemmed hip prostheses as a means of reducing stress shielding of the femur. J. Biomech. 2001, 34, 995–1003. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.T.; Wei, H.W.; Kao, H.C.; Cheng, C.K. Design and test of hip stem for medullary revascularization. Med. Eng. Phys. 2009, 31, 994–1001. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.J.; Desai, S.; Zhang, C.Y.; Koh, K.; Zhang, L.Q.; Costales, T.; O’Toole, R.V.; Manson, T.T. A calcar collar is protective against early torsional/spiral periprosthetic femoral fracture: A paired cadaveric biomechanical analysis. J. Bone Joint Surg. Am. 2020, 102, 1427–1433. [Google Scholar] [CrossRef]
- Levadnyi, I.; Gubaua, J.E.; Dicati, G.W.O.; Awrejcewicz, J.; Gu, Y.D.; Pereira, J.T.; Loskutov, A. Comparative analysis of the biomechanical behavior of collar and collarless stems: Experimental testing and finite element modelling. J. Med. Biol. Eng. 2021, 41, 844–855. [Google Scholar] [CrossRef]
- Chang, Y.; Shao, Y.; Liu, Y.; Xia, R.; Tong, Z.; Zhang, J.; Zhai, Z.; Cheng, W.; Li, H. Mechanical strain promotes osteogenic differentiation of mesenchymal stem cells on TiO(2) nanotubes substrate. Biochem. Biophys. Res. Commun. 2019, 511, 840–846. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, W.; Zhao, Y.; Gao, L.; Chang, Y.; Tong, Z.; Li, H.; Jing, J. Cyclic Mechanical Strain Regulates Osteoblastic Differentiation of Mesenchymal Stem Cells on TiO(2) Nanotubes Through GCN5 and Wnt/beta-Catenin. Front. Bioeng. Biotechnol. 2021, 9, 735949. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.D.; Zhang, N.; Tong, W.X.; Zhang, Y.F.; Shan, S.Z.; Zhang, X.L.; Li, Q.F. Mechanical stimulation orchestrates the osteogenic differentiation of human bone marrow stromal cells by regulating HDAC1. Cell Death Dis. 2016, 7, e2221. [Google Scholar] [CrossRef]
- Boden, H.; Adolphson, P. No adverse effects of early weight bearing after uncemented total hip arthroplasty: A randomized study of 20 patients. Acta Orthop. Scand. 2004, 75, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Wolf, O.; Mattsson, P.; Milbrink, J.; Larsson, S.; Mallmin, H. Periprosthetic bone mineral density and fixation of the uncemented CLS stem related to different weight bearing regimes: A randomized study using DXA and RSA in 38 patients followed for 5 years. Acta Orthop. 2010, 81, 286–291. [Google Scholar] [CrossRef] [PubMed]
- Wolf, O.; Mattsson, P.; Milbrink, J.; Larsson, S.; Mallmin, H. Effects of postoperative weight-bearing on body composition and bone mineral density after uncemented total hip arthroplasty. J. Rehabil. Med. 2013, 45, 498–503. [Google Scholar] [CrossRef] [PubMed]
- Ran, Q.; Yang, W.; Hu, Y.; Shen, X.; Yu, Y.; Xiang, Y.; Cai, K. Osteogenesis of 3D printed porous Ti6Al4V implants with different pore sizes. J. Mech. Behav. Biomed. Mater. 2018, 84, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chang, B.; Song, W.; Han, T.; Yan, J.; Li, F.; Zhao, L.; Kou, H.; Zhang, Y. Influence of pore size of porous titanium fabricated by vacuum diffusion bonding of titanium meshes on cell penetration and bone ingrowth. Acta Biomater. 2016, 33, 311–321. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, N.; Zhu, M.; Qiu, Q.; Zhao, P.; Zheng, C.; Bai, Q.; Zeng, Q.; Lu, T. The contribution of pore size and porosity of 3D printed porous titanium scaffolds to osteogenesis. Biomater. Adv. 2022, 133, 112651. [Google Scholar] [CrossRef]
- Matsuyama, K.; Ishidou, Y.; Guo, Y.M.; Kakoi, H.; Setoguchi, T.; Nagano, S.; Kawamura, I.; Maeda, S.; Komiya, S. Finite element analysis of cementless femoral stems based on mid- and long-term radiological evaluation. BMC Musculoskelet. Disord. 2016, 17, 397. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zadpoor, A.A. Additively manufactured porous metallic biomaterials. J Mater Chem B. 2019, 7, 4088–4117. [Google Scholar] [CrossRef] [PubMed]
- Zerbst, U.; Madia, M.; Klinger, C.; Bettge, D.; Murakami, Y. Defects as a root cause of fatigue failure of metallic components. I: Basic aspects. Eng. Fail. Anal. 2019, 97, 777–792. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Garcia, A.F.; Du Plessis, A.; Rans, C.; Mirzaali, M.J.; Zadpoor, A.A. Fatigue performance of auxetic meta-biomaterials. Acta Biomater. 2021, 126, 511–523. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Garcia, A.F.; Plessis, A.D.; Meynen, A.; Rans, C.; Scheys, L.; Mirzaali, M.J.; Zadpoor, A.A. Mechanisms of fatigue crack initiation and propagation in auxetic meta-biomaterials. Acta Biomater. 2022, 138, 398–409. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, A.; Downing, D.; Tino, R.; Almalki, A.; Maconachie, T.; Lozanovski, B.; Brandt, M.; Qian, M.; Leary, M. Buckling phenomena in AM lattice strut elements: A design tool applied to Ti-6Al-4V LB-PBF. Mater. Des. 2021, 208, 109892. [Google Scholar] [CrossRef]
- Wauthle, R.; Vrancken, B.; Beynaerts, B.; Jorissen, K.; Schrooten, J.; Kruth, J.P.; Van Humbeeck, J. Effects of build orientation and heat treatment on the microstructure and mechanical properties of selective laser melted Ti6Al4V lattice structures. Addit. Manuf. 2015, 5, 77–84. [Google Scholar] [CrossRef]
- Afroz, L.; Das, R.; Qian, M.; Easton, M.; Brandt, M. Fatigue behaviour of laser powder bed fusion (L-PBF) Ti-6Al-4V, Al-Si-Mg and stainless steels: A brief overview. Int. J. Fract. 2022, 235, 3–46. [Google Scholar] [CrossRef]
- Segersall, M.; Kerwin, A.; Hardaker, A.; Kahlin, M.; Moverare, J. Fatigue response dependence of thickness measurement methods for additively manufactured E-PBF Ti-6Al-4 V. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 1931–1943. [Google Scholar] [CrossRef]
- Kahlin, M.; Ansell, H.; Basu, D.; Kerwin, A.; Newton, L.; Smith, B.; Moverare, J.J. Improved fatigue strength of additively manufactured Ti6Al4V by surface post processing. Int. J. Fatigue 2020, 134, 105497. [Google Scholar] [CrossRef]
- Kahlin, M.; Ansell, H.; Moverare, J. Fatigue crack growth for through and part-through cracks in additively manufactured Ti6Al4V. Int. J. Fatigue 2022, 155, 106608. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunavala-Dossabhoy, G.; Saba, B.M.; McCarthy, K.J. Debulking of the Femoral Stem in a Primary Total Hip Joint Replacement: A Novel Method to Reduce Stress Shielding. Bioengineering 2024, 11, 393. https://doi.org/10.3390/bioengineering11040393
Sunavala-Dossabhoy G, Saba BM, McCarthy KJ. Debulking of the Femoral Stem in a Primary Total Hip Joint Replacement: A Novel Method to Reduce Stress Shielding. Bioengineering. 2024; 11(4):393. https://doi.org/10.3390/bioengineering11040393
Chicago/Turabian StyleSunavala-Dossabhoy, Gulshan, Brent M. Saba, and Kevin J. McCarthy. 2024. "Debulking of the Femoral Stem in a Primary Total Hip Joint Replacement: A Novel Method to Reduce Stress Shielding" Bioengineering 11, no. 4: 393. https://doi.org/10.3390/bioengineering11040393
APA StyleSunavala-Dossabhoy, G., Saba, B. M., & McCarthy, K. J. (2024). Debulking of the Femoral Stem in a Primary Total Hip Joint Replacement: A Novel Method to Reduce Stress Shielding. Bioengineering, 11(4), 393. https://doi.org/10.3390/bioengineering11040393