Postmortem Digital Image Correlation and Finite Element Modeling Demonstrate Posterior Scleral Deformations during Optic Nerve Adduction Tethering
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overall Workflow (Figure 1)
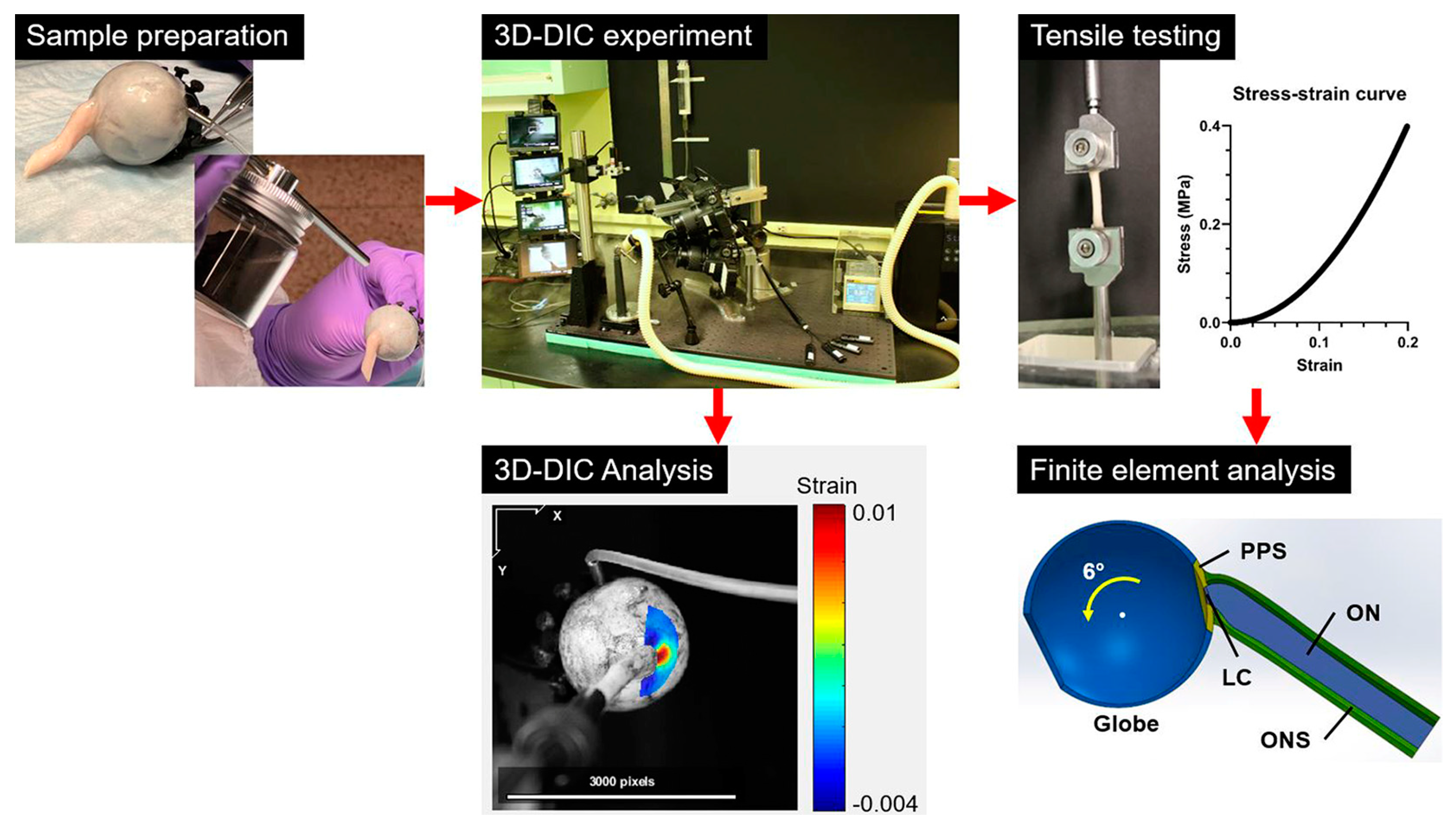
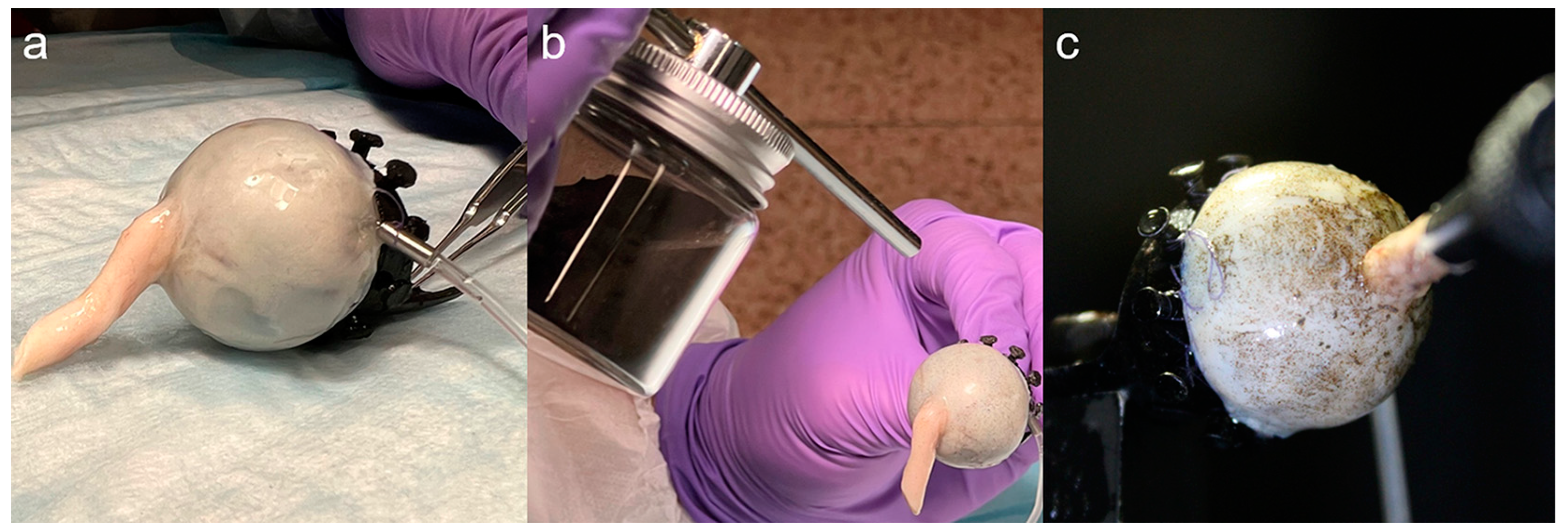
2.2. Specimen Preparation
2.3. Apparatus for 3D-DIC
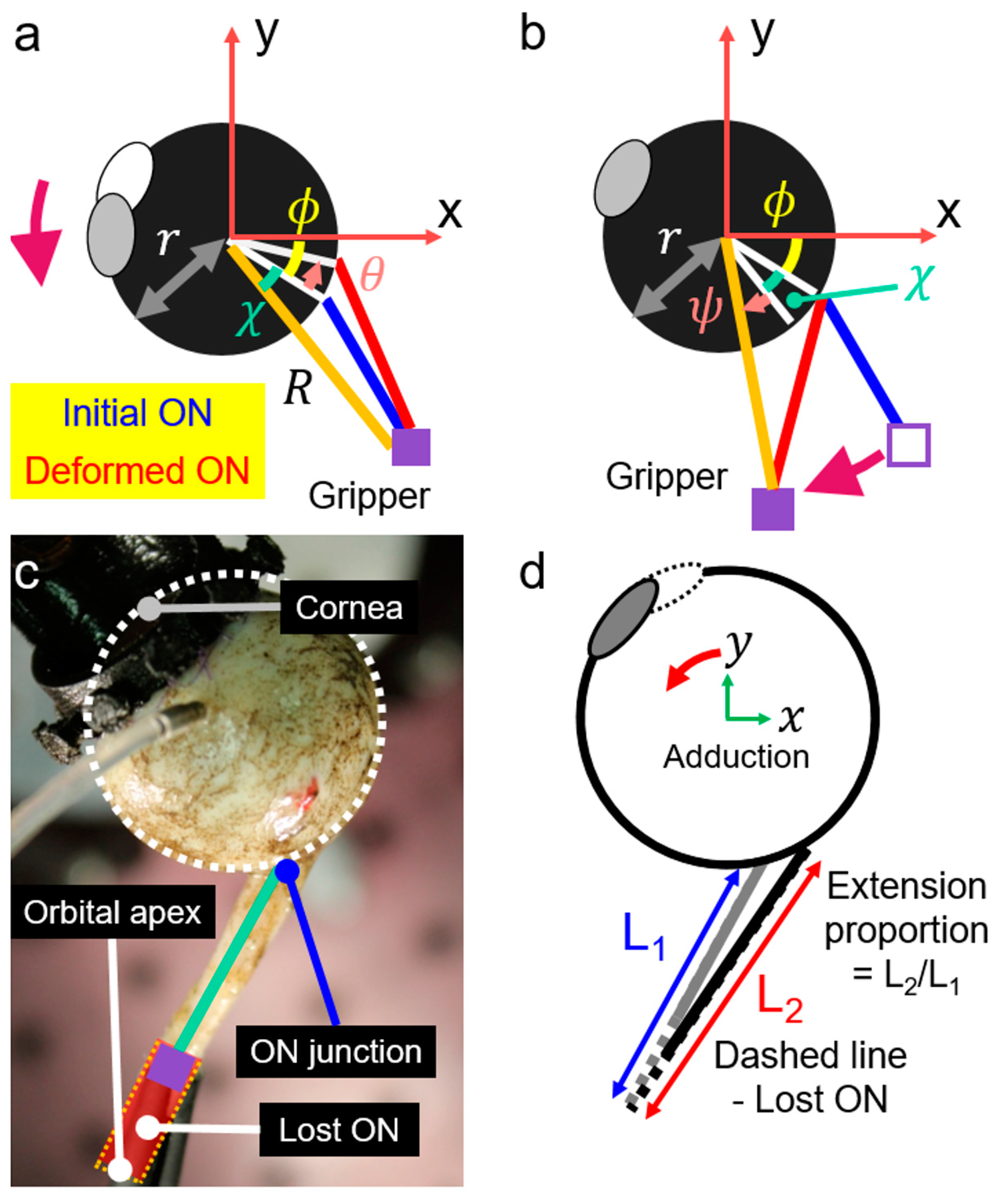
2.4. Geometric Consideration for Adduction Loading
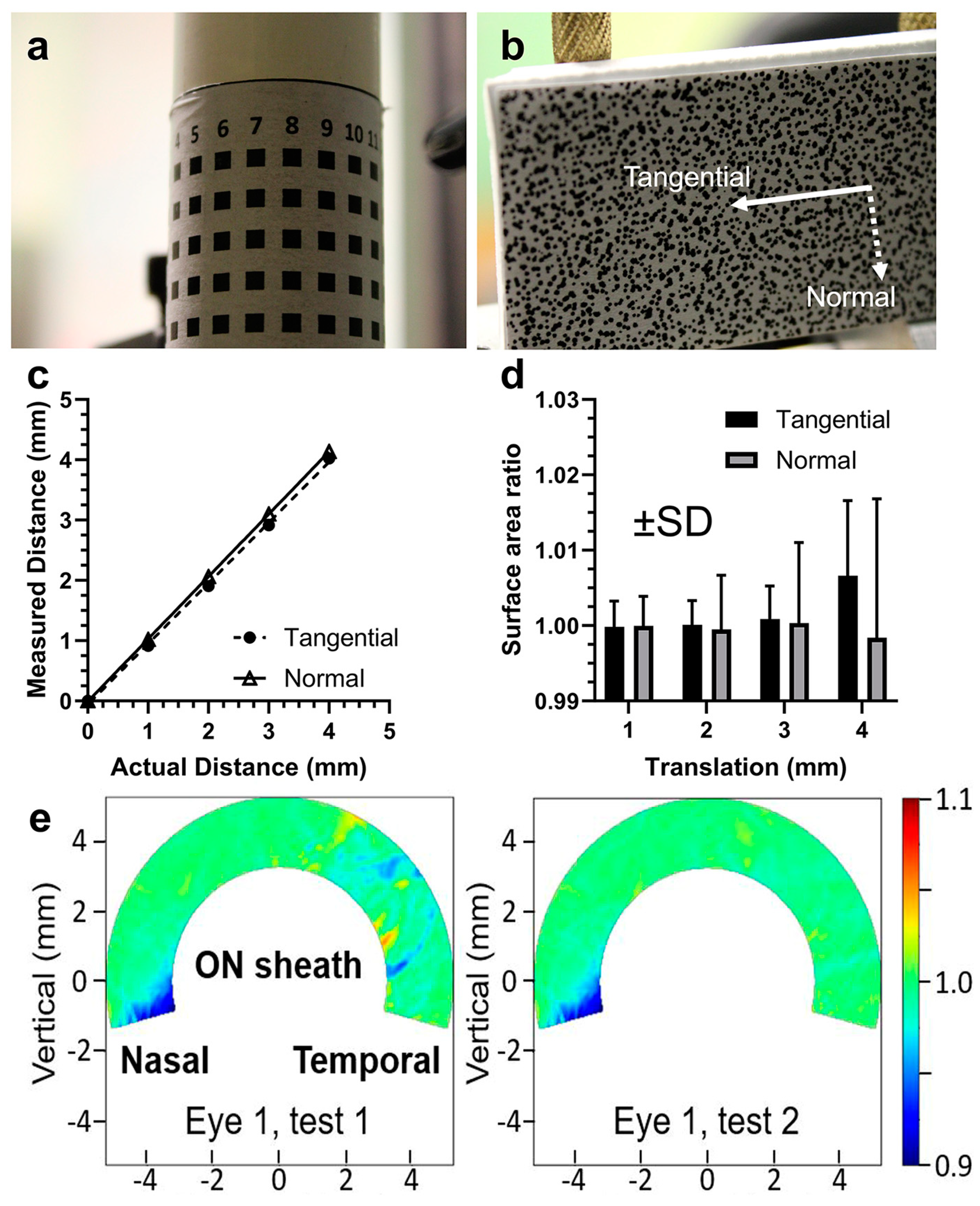
2.5. Validation of 3D-DIC
2.6. Measurements by 3D-DIC
2.7. Tensile Testing
2.8. Analysis of Tensile Results
2.9. Simulation by FEMs
2.10. Statistical Analysis
3. Results
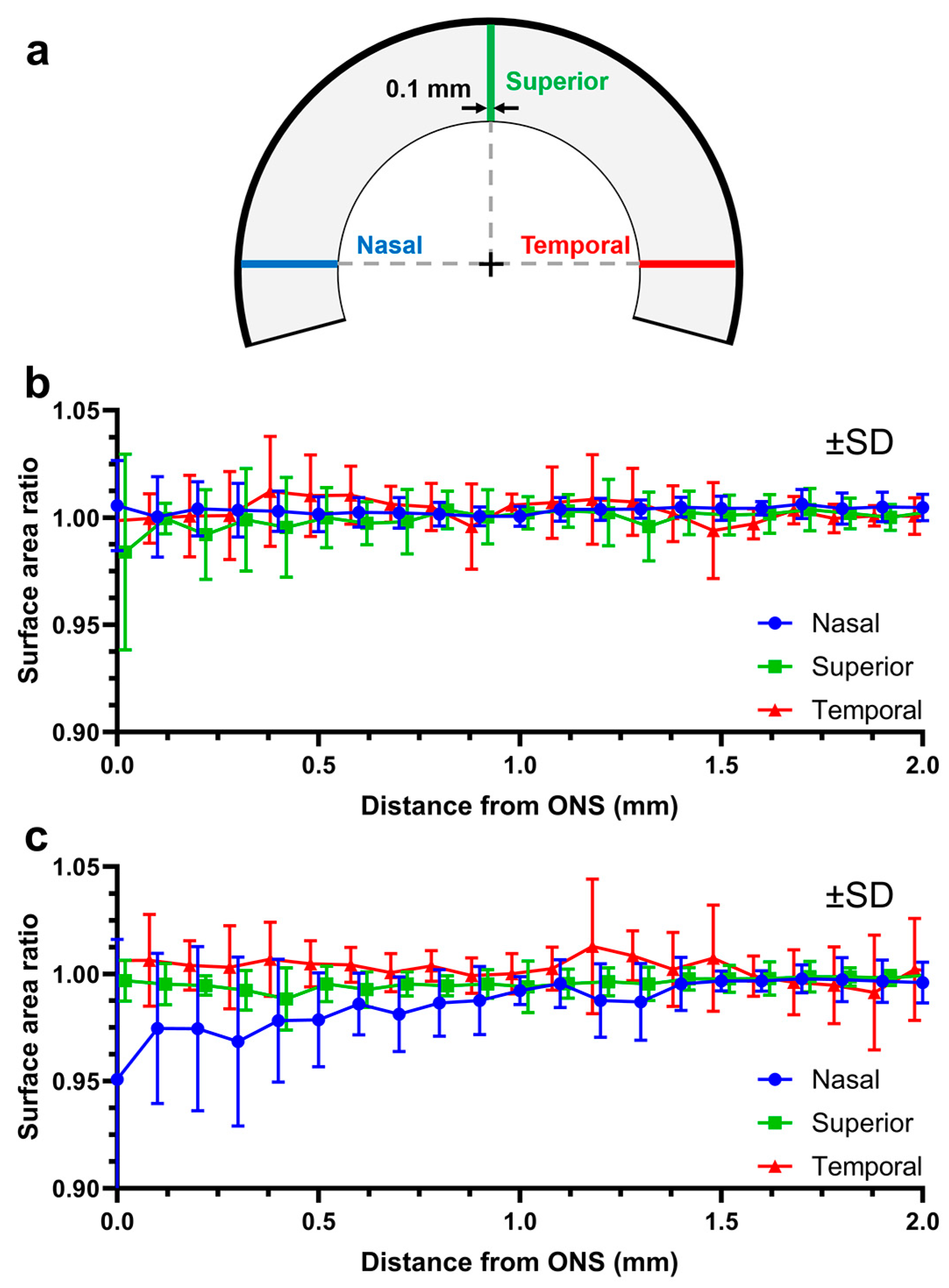
3.1. Reliability and Repeatability of DIC
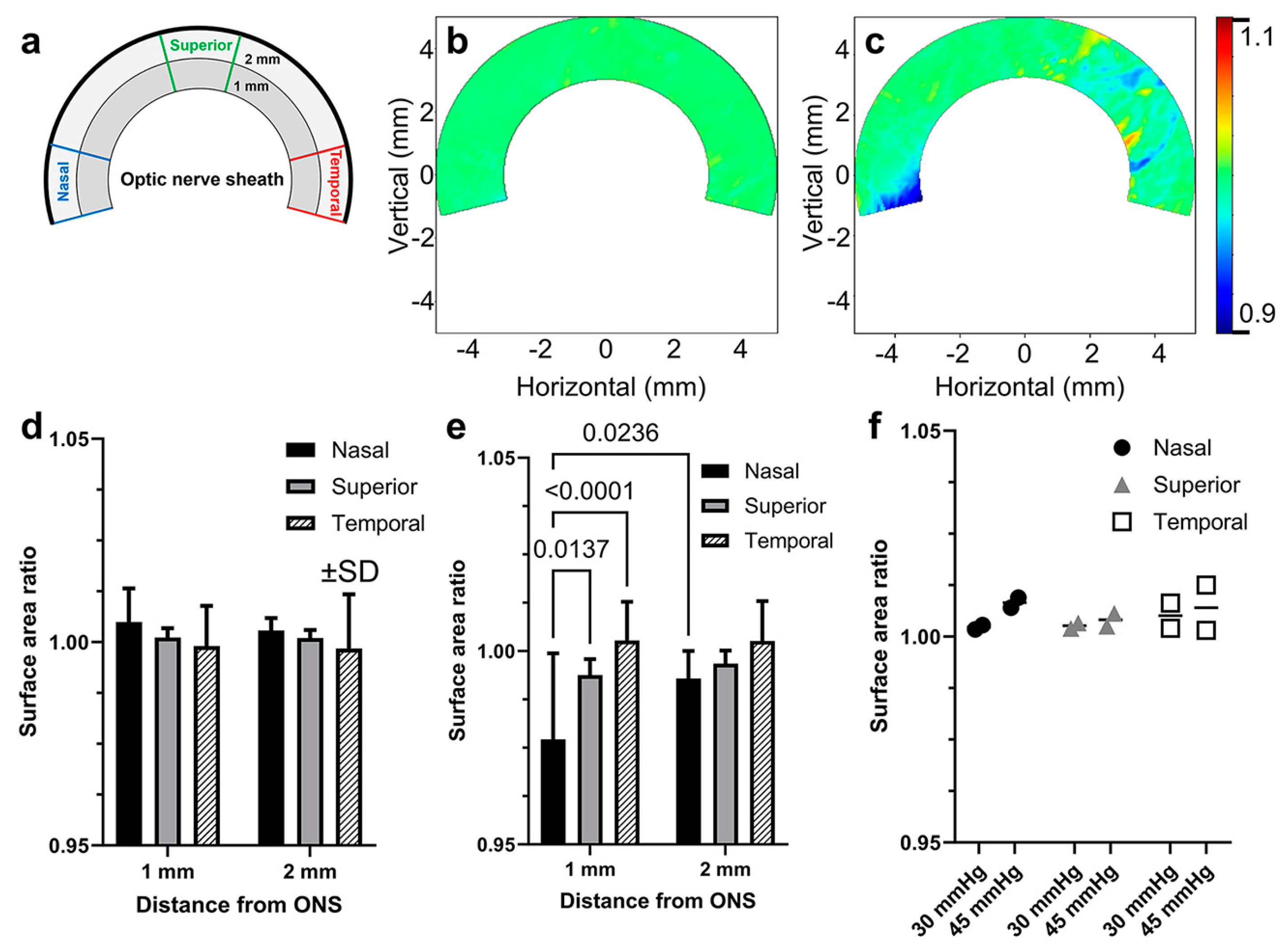
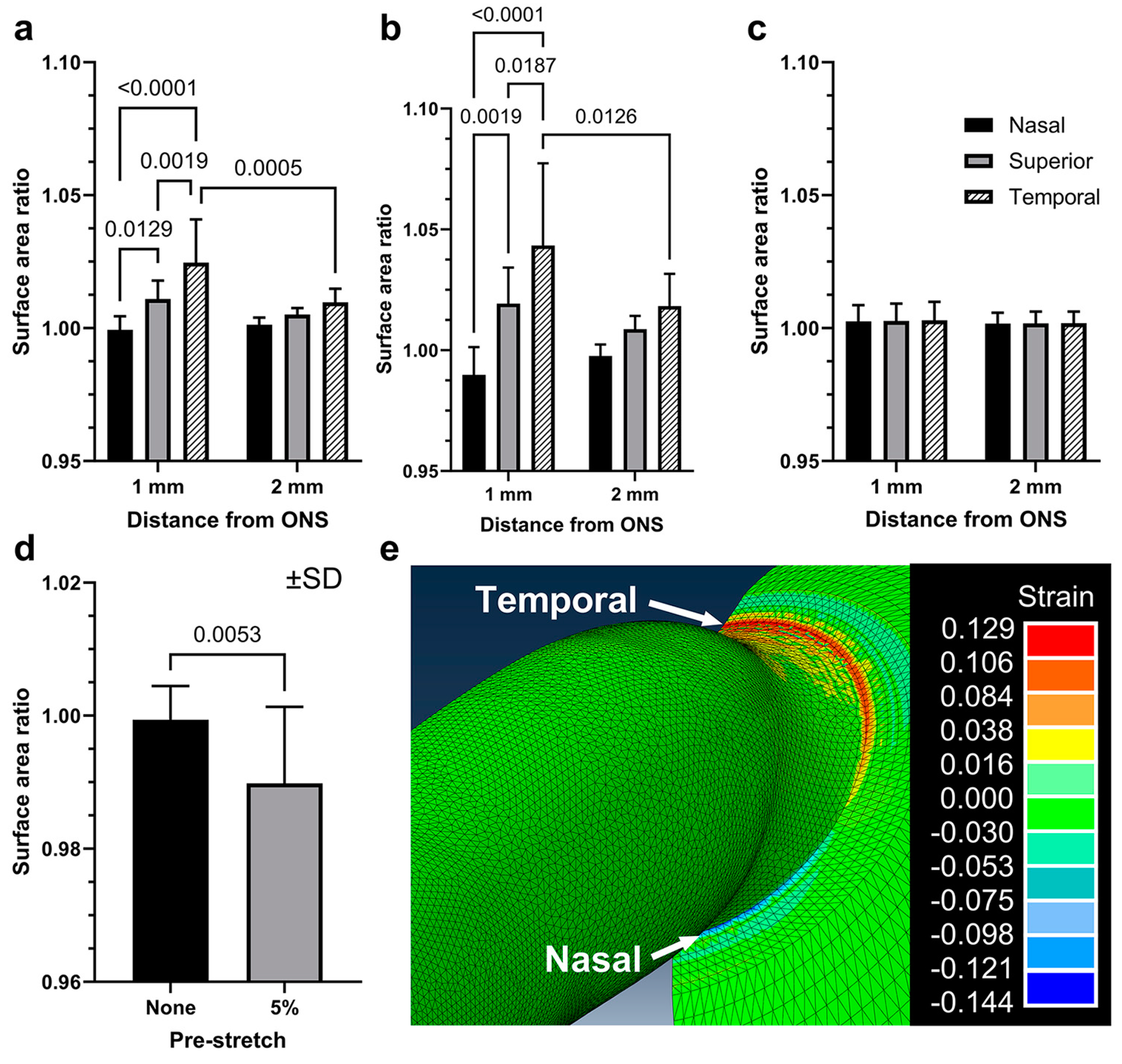
3.2. Scleral Deformations around the ON Sheath during Adduction
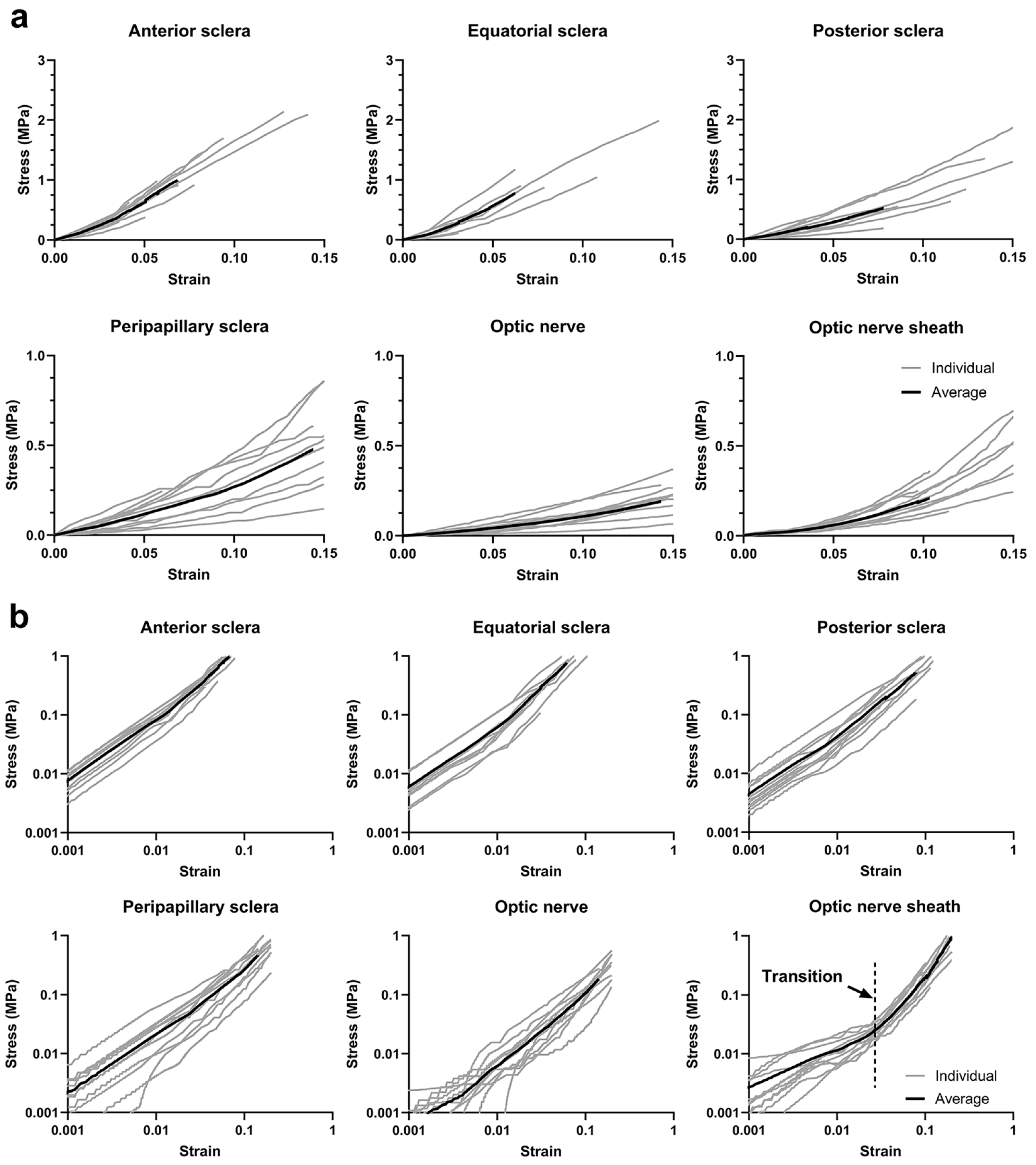
3.3. Uniaxial Tensile Behavior
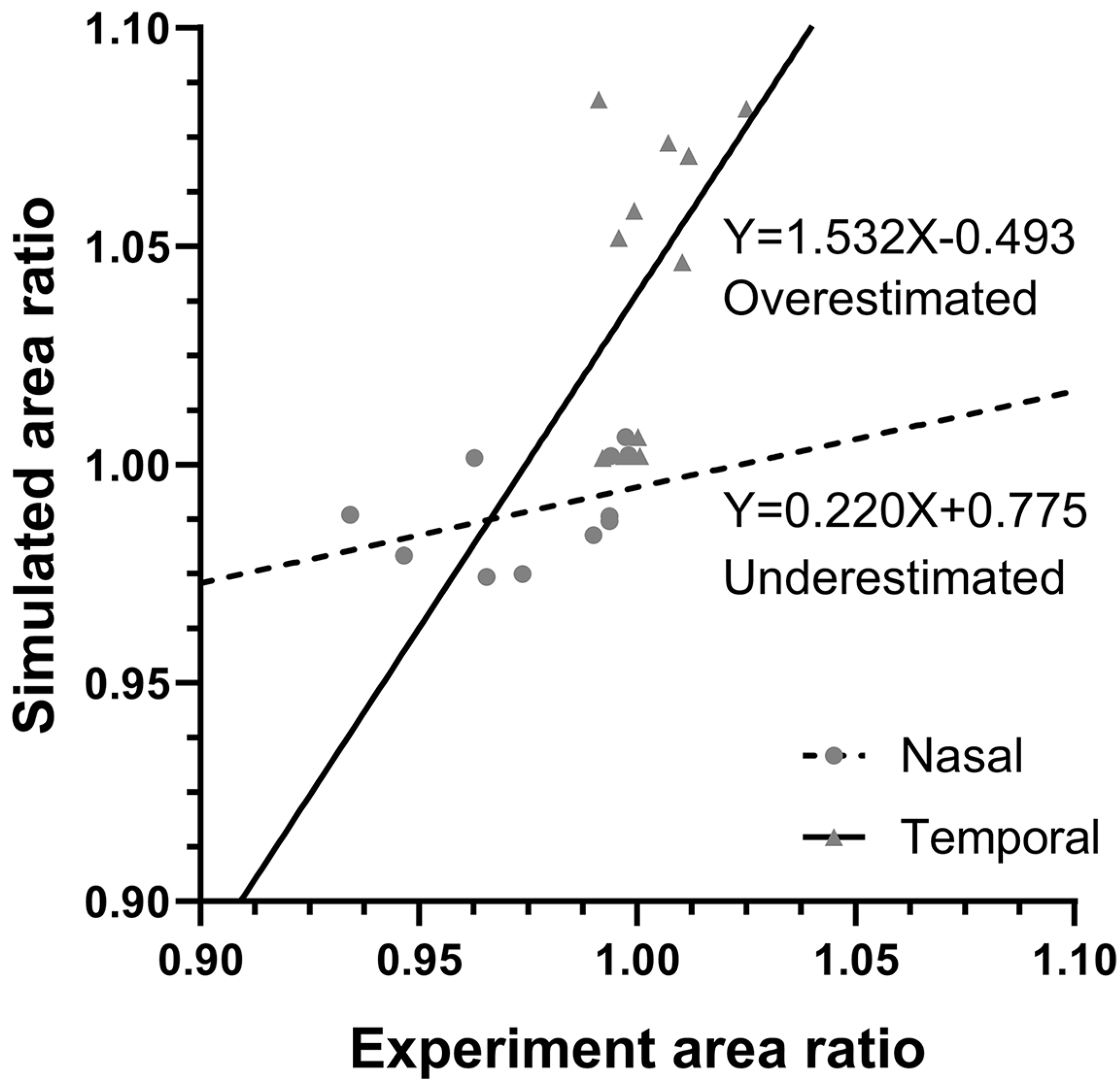
3.4. Finite Element Modeling
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guitton, D.; Volle, M. Gaze control in humans: Eye-head coordination during orienting movements to targets within and beyond the oculomotor range. J. Neurophysiol. 1987, 58, 427–459. [Google Scholar] [CrossRef]
- Demer, J.L. Optic nerve sheath as a novel mechanical load on the globe in ocular duction. Investig. Ophthalmol. Vis. Sci. 2016, 57, 1826–1838. [Google Scholar] [CrossRef]
- Sibony, P.A. Gaze evoked deformations of the peripapillary retina in papilledema and ischemic optic neuropathy. Investig. Ophthalmol. Vis. Sci. 2016, 57, 4979–4987. [Google Scholar] [CrossRef]
- Wang, X.; Beotra, M.R.; Tun, T.A.; Baskaran, M.; Perera, S.; Aung, T.; Strouthidis, N.G.; Milea, D.; Girard, M.J. In vivo 3-dimensional strain mapping confirms large optic nerve head deformations following horizontal eye movements. Investig. Ophthalmol. Vis. Sci. 2016, 57, 5825–5833. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.Y.; Shin, A.; Park, J.; Nagiel, A.; Lalane, R.A.; Schwartz, S.D.; Demer, J.L. Deformation of optic nerve head and peripapillary tissues by horizontal duction. Am. J. Ophthalmol. 2017, 174, 85–94. [Google Scholar] [CrossRef]
- Lee, W.J.; Kim, Y.J.; Kim, J.H.; Hwang, S.; Shin, S.H.; Lim, H.W. Changes in the optic nerve head induced by horizontal eye movements. PLoS ONE 2018, 13, e0204069. [Google Scholar] [CrossRef] [PubMed]
- Sibony, P.A.; Wei, J.; Sigal, I.A. Gaze-evoked deformations in optic nerve head drusen: Repetitive shearing as a potential factor in the visual and vascular complications. Ophthalmology 2018, 125, 929–937. [Google Scholar] [CrossRef]
- Le, A.; Chen, J.; Lesgart, M.; Gawargious, B.A.; Suh, S.Y.; Demer, J.L. Age-dependent deformation of the optic nerve head and peripapillary retina by horizontal duction. Am. J. Ophthalmol. 2020, 209, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Moon, S.; Lim, S.; Demer, J.L. Scanning laser ophthalmoscopy demonstrates disc and peripapillary strain during horizontal eye rotation in adults. Am. J. Ophthalmol. 2023, 254, 114–127. [Google Scholar] [CrossRef]
- Lim, S.; Tran, A.; Garcia, S.S.; Demer, J.L. Optical coherence tomography angiography demonstrates strain and volume effects on optic disk and peripapillary vasculature caused by horizontal duction. Curr. Eye Res. 2023, 48, 518–527. [Google Scholar] [CrossRef]
- Lim, S.; Demer, J.L. Empirical quantification of optic nerve strain due to horizontal duction. Bioengineering 2023, 10, 931. [Google Scholar] [CrossRef]
- Ayyalasomayajula, A.; Park, R.I.; Simon, B.R.; Vande Geest, J.P. A porohyperelastic finite element model of the eye: The influence of stiffness and permeability on intraocular pressure and optic nerve head biomechanics. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Schwaner, S.A.; Perry, R.N.; Kight, A.M.; Winder, E.; Yang, H.; Morrison, J.C.; Burgoyne, C.F.; Ross Ethier, C. Individual-specific modeling of rat optic nerve head biomechanics in glaucoma. J. Biomech. Eng. 2021, 143, 041004. [Google Scholar] [CrossRef] [PubMed]
- Jafari, S.; Lu, Y.; Park, J.; Demer, J.L. Finite element model of ocular adduction by active extraocular muscle contraction. Investig. Ophthalmol. Vis. Sci. 2021, 62, 1. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Rumpel, H.; Lim, W.E.H.; Baskaran, M.; Perera, S.A.; Nongpiur, M.E.; Aung, T.; Milea, D.; Girard, M.J. Finite element analysis predicts large optic nerve head strains during horizontal eye movements. Investig. Ophthalmol. Vis. Sci. 2016, 57, 2452–2462. [Google Scholar] [CrossRef]
- Wang, X.; Fisher, L.K.; Milea, D.; Jonas, J.B.; Girard, M.J. Predictions of optic nerve traction forces and peripapillary tissue stresses following horizontal eye movements. Investig. Ophthalmol. Vis. Sci. 2017, 58, 2044–2053. [Google Scholar] [CrossRef] [PubMed]
- Shin, A.; Yoo, L.; Park, J.; Demer, J.L. Finite element biomechanics of optic nerve sheath traction in adduction. J. Biomech. Eng. 2017, 139, 101010. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Shin, A.; Demer, J.L. Finite element modeling of effects of tissue property variation on human optic nerve tethering during adduction. Sci. Rep. 2022, 12, 18985. [Google Scholar] [CrossRef] [PubMed]
- Eilaghi, A.; Flanagan, J.G.; Simmons, C.A.; Ethier, C.R. Effects of scleral stiffness properties on optic nerve head biomechanics. Ann. Biomed. Eng. 2010, 38, 1586–1592. [Google Scholar] [CrossRef]
- Coudrillier, B.; Tian, J.; Alexander, S.; Myers, K.M.; Quigley, H.A.; Nguyen, T.D. Biomechanics of the human posterior sclera: Age-and glaucoma-related changes measured using inflation testing. Investig. Ophthalmol. Vis. Sci. 2012, 53, 1714–1728. [Google Scholar] [CrossRef]
- Grytz, R.; Fazio, M.A.; Girard, M.J.; Libertiaux, V.; Bruno, L.; Gardiner, S.; Girkin, C.A.; Downs, J.C. Material properties of the posterior human sclera. J. Mech. Behav. Biomed. Mater. 2014, 29, 602–617. [Google Scholar] [CrossRef] [PubMed]
- Demer, J.L.; Clark, R.A.; Suh, S.Y.; Giaconi, J.A.; Nouri-Mahdavi, K.; Law, S.K.; Bonelli, L.; Coleman, A.L.; Caprioli, J. Magnetic resonance imaging of optic nerve traction during adduction in primary open-angle glaucoma with normal intraocular pressure. Investig. Ophthalmol. Vis. Sci. 2017, 58, 4114–4125. [Google Scholar] [CrossRef] [PubMed]
- Demer, J.L.; Clark, R.A.; Suh, S.Y.; Giaconi, J.A.; Nouri-Mahdavi, K.; Law, S.K.; Bonelli, L.; Coleman, A.L.; Caprioli, J. Optic nerve traction during adduction in open angle glaucoma with normal versus elevated intraocular pressure. Curr. Eye Res. 2020, 45, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.A.; Suh, S.Y.; Caprioli, J.; Giaconi, J.A.; Nouri-Mahdavi, K.; Law, S.K.; Bonelli, L.; Coleman, A.L.; Demer, J.L. Adduction-induced strain on the optic nerve in primary open angle glaucoma at normal intraocular pressure. Curr. Eye Res. 2021, 46, 568–578. [Google Scholar] [CrossRef] [PubMed]
- Suh, S.Y.; Le, A.; Shin, A.; Park, J.; Demer, J.L. Progressive deformation of the optic nerve head and peripapillary structures by graded horizontal duction. Investig. Ophthalmol. Vis. Sci. 2017, 58, 5015–5021. [Google Scholar]
- Suh, S.Y.; Clark, R.A.; Demer, J.L. Optic nerve sheath tethering in adduction occurs in esotropia and hypertropia, but not in exotropia. Investig. Ophthalmol. Vis. Sci. 2018, 59, 2899–2904. [Google Scholar] [CrossRef] [PubMed]
- Spaide, R.F. Applications for OCT Enhanced depth imaging. Retin. Today Sept. 2011, 57–60. Available online: https://retinatoday.com/articles/2011-sept/applications-for-oct-enhanced-depth-imaging (accessed on 26 April 2024).
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Genovese, K.; Herr, H.M. MultiDIC: An open-source toolbox for multi-view 3D digital image correlation. IEEE Access 2018, 6, 30520–30535. [Google Scholar] [CrossRef]
- Girard, M.; Suh, J.K.; Hart, R.T.; Burgoyne, C.F.; Downs, J.C. Effects of storage time on the mechanical properties of rabbit peripapillary sclera after enucleation. Curr. Eye Res. 2007, 32, 465–470. [Google Scholar] [CrossRef] [PubMed]
- Morch, A.; Astruc, L.; Mayeur, O.; Witz, J.F.; Lecomte-Grosbras, P.; Brieu, M. Is there any objective and independent characterization and modeling of soft biological tissues? J. Mech. Behav. Biomed. Mater. 2020, 110, 103915. [Google Scholar] [CrossRef]
- Bianco, G.; Levy, A.M.; Grytz, R.; Fazio, M.A. Effect of different preconditioning protocols on the viscoelastic inflation response of the posterior sclera. Acta Biomater. 2021, 128, 332–345. [Google Scholar] [CrossRef]
- Tonge, T.K.; Murienne, B.J.; Coudrillier, B.; Alexander, S.; Rothkopf, W.; Nguyen, T.D. Minimal preconditioning effects observed for inflation tests of planar tissues. J. Biomech. Eng. 2013, 135, 114502. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Shin, A.; Jafari, S.; Demer, J.L. Material properties and effect of preconditioning of human sclera, optic nerve, and optic nerve sheath. Biomech. Model. Mechanobiol. 2021, 20, 1353–1363. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, R. Direct linear transformation method for three-dimensional cinematography. Res. Q. 1978, 49, 197–205. [Google Scholar] [CrossRef] [PubMed]
- Shin, A.; Yoo, L.; Demer, J.L. Biomechanics of superior oblique Z-tenotomy. J. AAPOS 2013, 17, 612–617. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; Hao, Z.; Wen, S.; Leng, H. A quantitative study of the relationship between the distribution of different types of collagen and the mechanical behavior of rabbit medial collateral ligaments. PLoS ONE 2014, 9, e103363. [Google Scholar] [CrossRef] [PubMed]
- Chuangsuwanich, T.; Tun, T.A.; Braeu, F.A.; Wang, X.; Chin, Z.Y.; Panda, S.K.; Buist, M.; Milea, D.; Strouthidis, N.; Perera, S.; et al. Adduction induces large optic nerve head deformations in subjects with normal-tension glaucoma. Br. J. Ophthalmol. 2024, 108, 522–529. [Google Scholar] [CrossRef] [PubMed]
- Geraghty, B.; Jones, S.W.; Rama, P.; Akhtar, R.; Elsheikh, A. Age-related variations in the biomechanical properties of human sclera. J. Mech. Behav. Biomed. Mater. 2012, 16, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Friberg, T.R.; Lace, J.W. A comparison of the elastic properties of human choroid and sclera. Exp. Eye Res. 1988, 47, 429–436. [Google Scholar] [CrossRef]
- Wollensak, G.; Spoerl, E. Collagen crosslinking of human and porcine sclera. J. Cataract. Refract. Surg. 2004, 30, 689–695. [Google Scholar] [CrossRef]
- Girard, M.J.; Downs, J.C.; Bottlang, M.; Burgoyne, C.F.; Suh, J.K.F. Peripapillary and posterior scleral mechanics—Part II: Experimental and inverse finite element characterization. ASME J. Biomech. Eng. 2009, 131, 051012. [Google Scholar] [CrossRef]
- Elsheikh, A.; Geraghty, B.; Alhasso, D.; Knappett, J.; Campanelli, M.; Rama, P. Regional variation in the biomechanical properties of the human sclera. Exp. Eye Res. 2010, 90, 624–633. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Argento, A.; Rozsa, F.W.; Mallett, K. Constitutive behavior of ocular tissues over a range of strain rates. ASME J. Biomech. Eng. 2012, 134, 061002. [Google Scholar] [CrossRef]
- Wale, M.E.; Nesbitt, D.Q.; Henderson, B.S.; Fitzpatrick, C.K.; Creechley, J.J.; Lujan, T.J. Applying ASTM standards to tensile tests of musculoskeletal soft tissue: Methods to reduce grip failures and promote reproducibility. J. Biomech. Eng. 2021, 143, 011011. [Google Scholar] [CrossRef] [PubMed]
- Bekerman, I.; Gottlieb, P.; Vaiman, M. Variations in eyeball diameters of the healthy adults. J. Ophthalmol. 2014, 2014, 503645–503649. [Google Scholar] [CrossRef] [PubMed]
- Demer, J.L.; Clark, R.A. Translation and eccentric rotation in ocular motor modeling. Prog. Brain Res. 2019, 248, 117–126. [Google Scholar]
- Kapetanakis, V.V.; Chan, M.P.; Foster, P.J.; Cook, D.G.; Owen, C.G.; Rudnicka, A.R. Global variations and time trends in the prevalence of primary open angle glaucoma (POAG): A systematic review and meta-analysis. Br. J. Ophthalmol. 2016, 100, 86–93. [Google Scholar] [CrossRef]
- Kingman, S. Glaucoma is second leading cause of blindness globally. Bull. World Health Organ. 2004, 82, 887–888. [Google Scholar]
- Shi, D.; Funayama, T.; Mashima, Y.; Takano, Y.; Shimizu, A.; Yamamoto, K.; Mengkegale, M.; Miyazawa, A.; Yasuda, N.; Fukuchi, T.; et al. Association of HK2 and NCK2 with normal tension glaucoma in the Japanese population. PLoS ONE 2013, 8, e54115. [Google Scholar] [CrossRef]
- Iwase, A.; Suzuki, Y.; Araie, M.; Yamamoto, T.; Abe, H.; Shirato, S.; Kuwayama, Y.; Mishima, H.K.; Shimizu, H.; Tomita, G.; et al. The prevalence of primary open-angle glaucoma in Japanese: The Tajimi Study. Ophthalmology 2004, 111, 1641–1648. [Google Scholar] [CrossRef]
- Kim, C.S.; Seong, G.J.; Lee, N.H.; Song, K.C.; Ahn, B.H.; Ahn, M.D.; Baek, N.H.; Choi, K.R.; Ha, S.J.; Han, G.H.; et al. Prevalence of primary open-angle glaucoma in central South Korea: The Namil study. Ophthalmology 2011, 118, 1024–1030. [Google Scholar] [CrossRef]
- Ha, A.; Kim, Y.K.; Jeoung, J.W.; Kim, D.M.; Park, K.H. Association of angle width with progression of normal-tension glaucoma: A minimum 7-year follow-up study. JAMA Ophthalmol. 2019, 137, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Solano, M.M.; Oldenburg, C.E.; Liu, T.; Wang, Y.; Wang, N.; Lin, S.C. Prevalence of normal-tension glaucoma in the Chinese population: A systematic review and meta-analysis. Am. J. Ophthalmol. 2019, 199, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.A.; Kim, T.W.; Lee, E.J.; Girard, M.J.; Mari, J.M. Lamina cribrosa morphology in glaucomatous eyes with hemifield defect in a Korean population. Ophthalmology 2019, 126, 692–701. [Google Scholar] [CrossRef] [PubMed]
- Killer, H.; Pircher, A. Normal tension glaucoma: Review of current understanding and mechanisms of the pathogenesis. Eye 2018, 32, 924–930. [Google Scholar] [CrossRef] [PubMed]
- Sommer, A.; Tielsch, J.M.; Katz, J.; Quigley, H.A.; Gottsch, J.D.; Javitt, J.C.; Martone, J.F.; Royall, R.M.; Witt, K.A.; Ezrine, S. Racial differences in the cause-specific prevalence of blindness in east Baltimore. N. Engl. J. Med. 1991, 325, 1412–1417. [Google Scholar] [CrossRef] [PubMed]
- Bonomi, L.; Marchini, G.; Marraffa, M.; Bernardi, P.; De Franco, I.; Perfetti, S.; Varotto, A.; Tenna, V. Prevalence of glaucoma and intraocular pressure distribution in a defined population: The Egna-Neumarkt Study. Ophthalmology 1998, 105, 209–215. [Google Scholar] [CrossRef]
- Klein, B.E.; Klein, R.; Sponsel, W.E.; Franke, T.; Cantor, L.B.; Martone, J.; Menage, M.J. Prevalence of glaucoma: The Beaver Dam eye study. Ophthalmology 1992, 99, 1499–1504. [Google Scholar] [CrossRef] [PubMed]
- Rotchford, A.P.; Johnson, G.J. Glaucoma in Zulus: A population-based cross-sectional survey in a rural district in South Africa. Arch. Ophthalmol. 2002, 120, 471–478. [Google Scholar] [CrossRef]
- Seol, B.R.; Kim, S.; Kim, D.M.; Park, K.H.; Jeoung, J.W.; Kim, S.H. Influence of intraocular pressure reduction on progression of normal-tension glaucoma with myopic tilted disc and associated risk factors. Jpn. J. Ophthalmol. 2017, 61, 230–236. [Google Scholar] [CrossRef]
- Tseng, V.L.; Kim, C.H.; Romero, P.T.; Yu, F.; Robertson-Brown, K.W.; Phung, L.; Raygoza, D.; Caprioli, J.; Coleman, A.L. Risk factors and long-term outcomes in patients with low intraocular pressure after trabeculectomy. Ophthalmology 2017, 124, 1457–1465. [Google Scholar] [CrossRef]
- Siaudvytyte, L.; Januleviciene, I.; Ragauskas, A.; Bartusis, L.; Siesky, B.; Harris, A. Update in intracranial pressure evaluation methods and translaminar pressure gradient role in glaucoma. Acta Ophthalmol. 2015, 93, 9–15. [Google Scholar] [CrossRef]
- Jonas, J.B.; Yang, D.; Wang, N. Intracranial pressure and glaucoma. J. Glaucoma 2013, 22, S13–S14. [Google Scholar] [CrossRef] [PubMed]
- Berdahl, J.P.; Fautsch, M.P.; Stinnett, S.S.; Allingham, R.R. Intracranial pressure in primary open angle glaucoma, normal tension glaucoma, and ocular hypertension: A case–control study. Investig. Ophthalmol. Vis. Sci. 2008, 49, 5412–5418. [Google Scholar] [CrossRef] [PubMed]
- Berdahl, J.P.; Allingham, R.R. Intracranial pressure and glaucoma. Curr. Opin. Ophthalmol. 2010, 21, 106–111. [Google Scholar] [CrossRef] [PubMed]
- Gramer, G.; Weber, B.H.; Gramer, E. Migraine and vasospasm in glaucoma: Age-related evaluation of 2027 patients with glaucoma or ocular hypertension. Investig. Ophthalmol. Vis. Sci. 2015, 56, 7999–8007. [Google Scholar] [CrossRef] [PubMed]
- Pircher, A.; Remonda, L.; Weinreb, R.N.; Killer, H.E. Translaminar pressure in Caucasian normal tension glaucoma patients. Acta Ophthalmol. 2017, 95, e524–e531. [Google Scholar] [CrossRef] [PubMed]
- Lindén, C.; Qvarlander, S.; Jóhannesson, G.; Johansson, E.; Östlund, F.; Malm, J.; Eklund, A. Normal-tension glaucoma has normal intracranial pressure: A prospective study of intracranial pressure and intraocular pressure in different body positions. Ophthalmology 2018, 125, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Fortune, B. Pulling and tugging on the retina: Mechanical impact of glaucoma beyond the optic nerve head. Investig. Ophthalmol. Vis. Sci. 2019, 60, 26–35. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Jiang, R.; Wang, N.L.; Xu, L.; Jonas, J.B. Acute peripapillary retinal pigment epithelium changes associated with acute intraocular pressure elevation. Ophthalmology 2015, 122, 2022–2028. [Google Scholar] [CrossRef]
- Hong, S.; Yang, H.; Gardiner, S.K.; Luo, H.; Sharpe, G.P.; Caprioli, J.; Demirel, S.; Girkin, C.A.; Mardin, C.Y.; Quigley, H.A.; et al. OCT optic nerve head morphology in myopia III: The exposed neural canal region in healthy eyes–implications for high myopia. Am. J. Ophthalmol. 2024, 258, 55–75. [Google Scholar] [CrossRef]
- Pijanka, J.K.; Spang, M.T.; Sorensen, T.; Liu, J.; Nguyen, T.D.; Quigley, H.A.; Boote, C. Depth-dependent changes in collagen organization in the human peripapillary sclera. PLoS ONE 2015, 10, e0118648. [Google Scholar] [CrossRef] [PubMed]
- Coudrillier, B.; Boote, C.; Quigley, H.A.; Nguyen, T.D. Scleral anisotropy and its effects on the mechanical response of the optic nerve head. Biomech. Model. Mechanobiol. 2013, 12, 941–963. [Google Scholar] [CrossRef] [PubMed]
- Eilaghi, A.; Flanagan, J.G.; Tertinegg, I.; Simmons, C.A.; Brodland, G.W.; Ethier, C.R. Biaxial mechanical testing of human sclera. J. Biomech. 2010, 43, 1696–1701. [Google Scholar] [CrossRef] [PubMed]
- Shin, A.; Park, J.; Le, A.; Poukens, V.; Demer, J.L. Bilaminar mechanics of the human optic nerve sheath. Curr. Eye Res. 2020, 45, 854–863. [Google Scholar] [CrossRef]
- Jafari, S.; Demer, J.L. Finite element model (FEM) of the effect of optic nerve (ON) sheath anisotropy on ocular loading during horizontal duction. In Proceedings of the ARVO 2024 Annual Meeting, Seattle, WA, USA, 5–9 May 2024. Abstract number 5173. [Google Scholar]
- Grytz, R.; Downs, J.C. A forward incremental prestressing method with application to inverse parameter estimations and eye-specific simulations of posterior scleral shells. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 768–780. [Google Scholar] [CrossRef]
- Schoemaker, I.; Hoefnagel, P.P.; Mastenbroek, T.J.; Kolff, C.F.; Schutte, S.; van der Helm, F.C.; Picken, S.J.; Gerritsen, A.F.; Wielopolski, P.A.; Spekreijse, H.; et al. Elasticity, viscosity, and deformation of orbital fat. Investig. Ophthalmol. Vis. Sci. 2006, 47, 4819–4826. [Google Scholar] [CrossRef]

| No. | Axial Length (mm) | Transverse Diameter (mm) | ON Length (mm) | ON Sheath Outer Radius (mm) | Enucleation to Delivery Time (h) |
|---|---|---|---|---|---|
| 1 | 23.7 | 23.2 | 14.4 | 3.65 | 38 |
| 2 | 25.9 | 24.3 | 22.0 | 3.12 | 28 |
| 3 | 25.7 | 24.5 | 17.2 | 2.85 | 28 |
| 4 | 24.2 | 23.9 | 15.1 | 3.05 | 65 |
| 5 | 24.5 | 24.2 | 13.4 | 3.12 | 65 |
| 6 | 24.5 | 23.1 | 19.9 | 3.25 | 31 |
| 7 | 24.5 | 23.0 | 18.1 | 2.81 | 31 |
| 8 | 25.0 | 25.6 | 23.5 | 3.21 | 31 |
| 9 | 25.1 | 24.7 | 16.0 | 3.03 | 42 |
| 10 | 25.9 | 25.9 | 17.4 | 2.86 | 32 |
| 11 | 25.8 | 25.8 | 17.7 | 3.51 | 32 |
| IOP Elevation 15 to 30 mmHg | Adduction 26° to 32° | |
|---|---|---|
| 1 mm nasal | 0.0057 | 0.0228 |
| 1 mm superior | 0.0019 | 0.0062 |
| 1 mm temporal | 0.0062 | 0.0072 |
| 2 mm nasal | 0.0032 | 0.0071 |
| 2 mm superior | 0.0019 | 0.0033 |
| 2 mm temporal | 0.0061 | 0.0064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, S.; Kim, C.; Jafari, S.; Park, J.; Garcia, S.S.; Demer, J.L. Postmortem Digital Image Correlation and Finite Element Modeling Demonstrate Posterior Scleral Deformations during Optic Nerve Adduction Tethering. Bioengineering 2024, 11, 452. https://doi.org/10.3390/bioengineering11050452
Lim S, Kim C, Jafari S, Park J, Garcia SS, Demer JL. Postmortem Digital Image Correlation and Finite Element Modeling Demonstrate Posterior Scleral Deformations during Optic Nerve Adduction Tethering. Bioengineering. 2024; 11(5):452. https://doi.org/10.3390/bioengineering11050452
Chicago/Turabian StyleLim, Seongjin, Changzoo Kim, Somaye Jafari, Joseph Park, Stephanie S. Garcia, and Joseph L. Demer. 2024. "Postmortem Digital Image Correlation and Finite Element Modeling Demonstrate Posterior Scleral Deformations during Optic Nerve Adduction Tethering" Bioengineering 11, no. 5: 452. https://doi.org/10.3390/bioengineering11050452
APA StyleLim, S., Kim, C., Jafari, S., Park, J., Garcia, S. S., & Demer, J. L. (2024). Postmortem Digital Image Correlation and Finite Element Modeling Demonstrate Posterior Scleral Deformations during Optic Nerve Adduction Tethering. Bioengineering, 11(5), 452. https://doi.org/10.3390/bioengineering11050452







