Improving the Generalizability of Deep Learning for T2-Lesion Segmentation of Gliomas in the Post-Treatment Setting
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Data
2.2. Network Architecture and Hyperparameters
2.3. Preprocessing and Augmentation
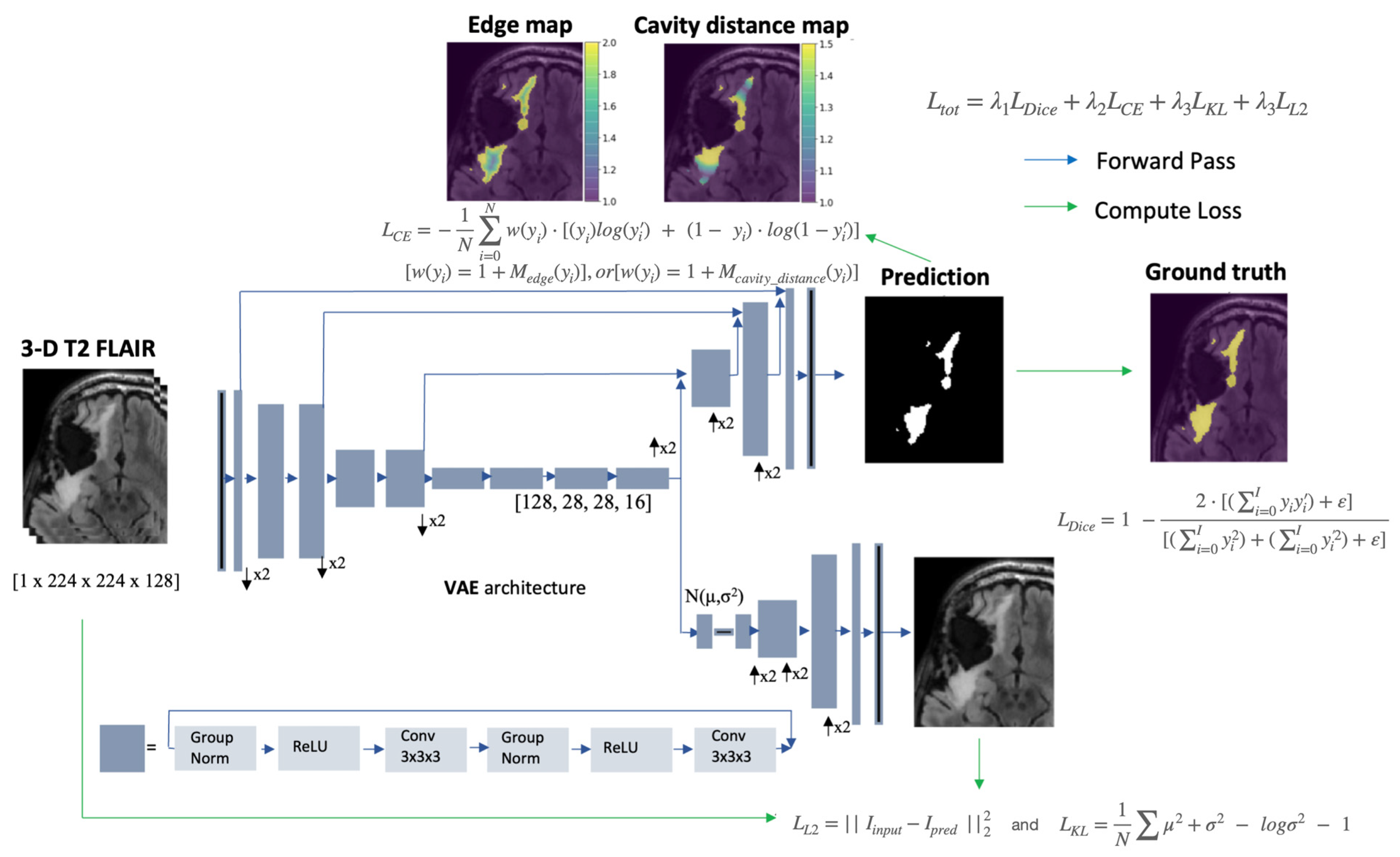
2.4. Loss Function
2.5. Training
2.6. Evaluation Metrics
3. Results
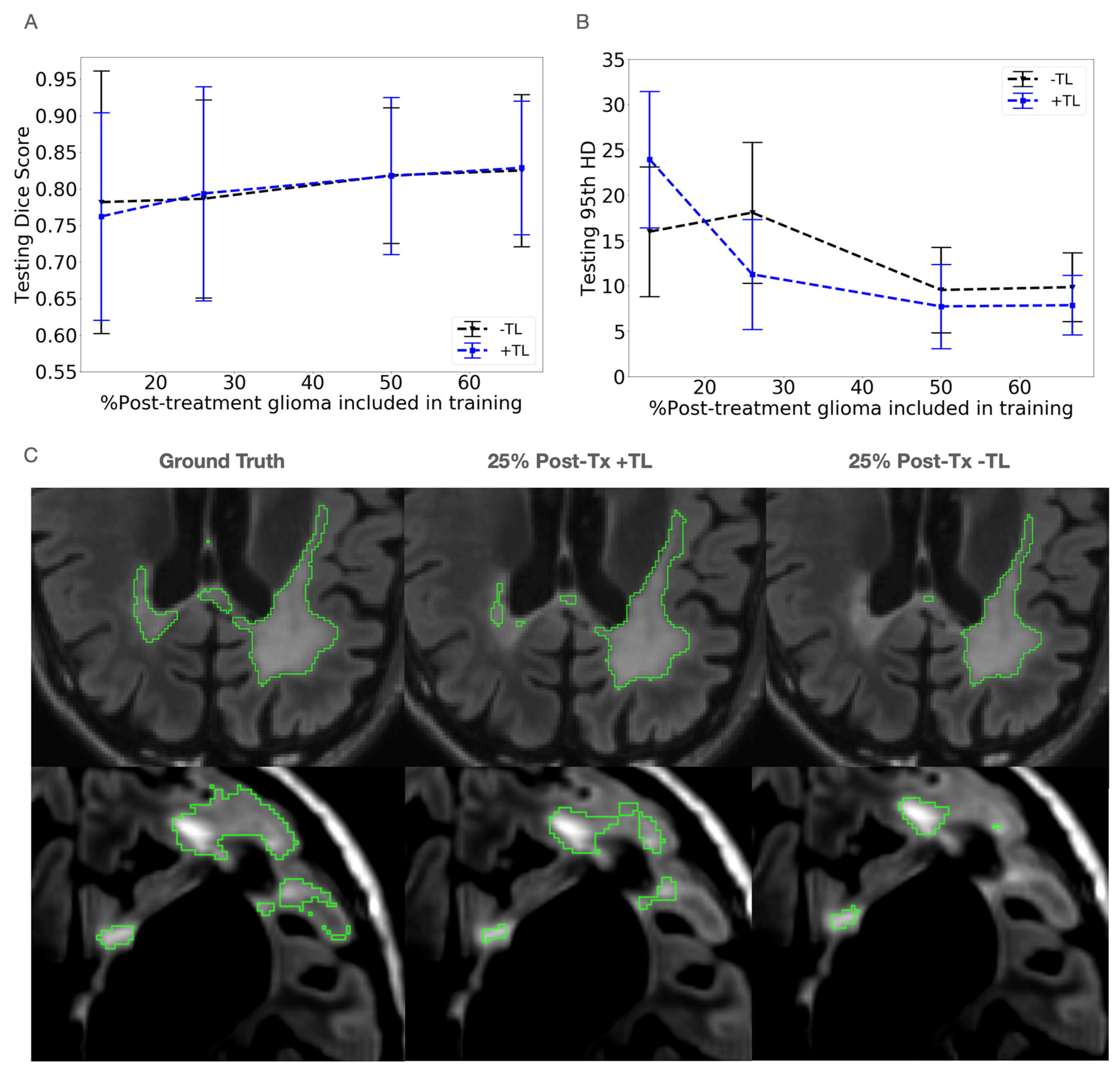
3.1. Data Mixing
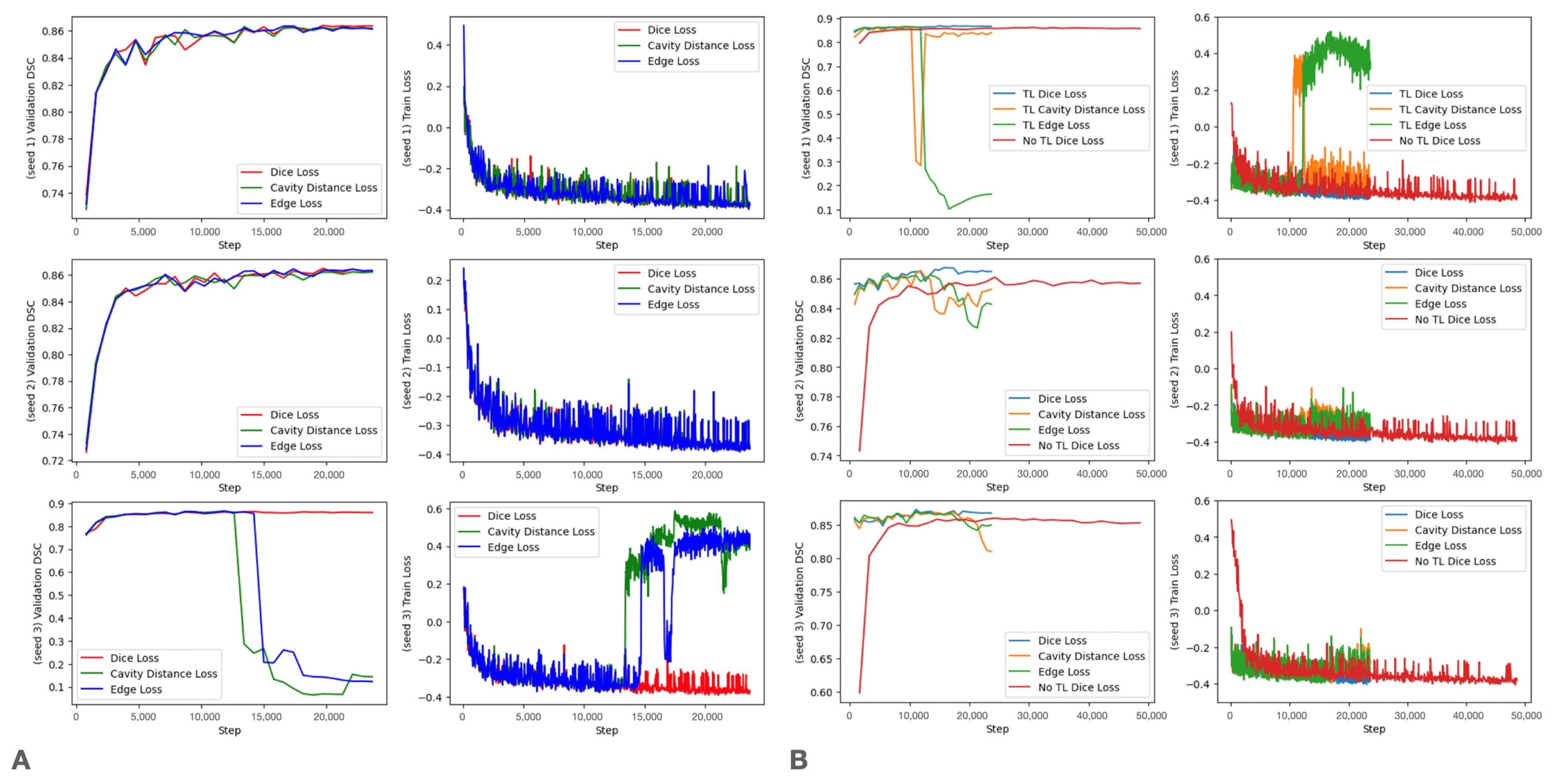
3.2. Transfer Learning
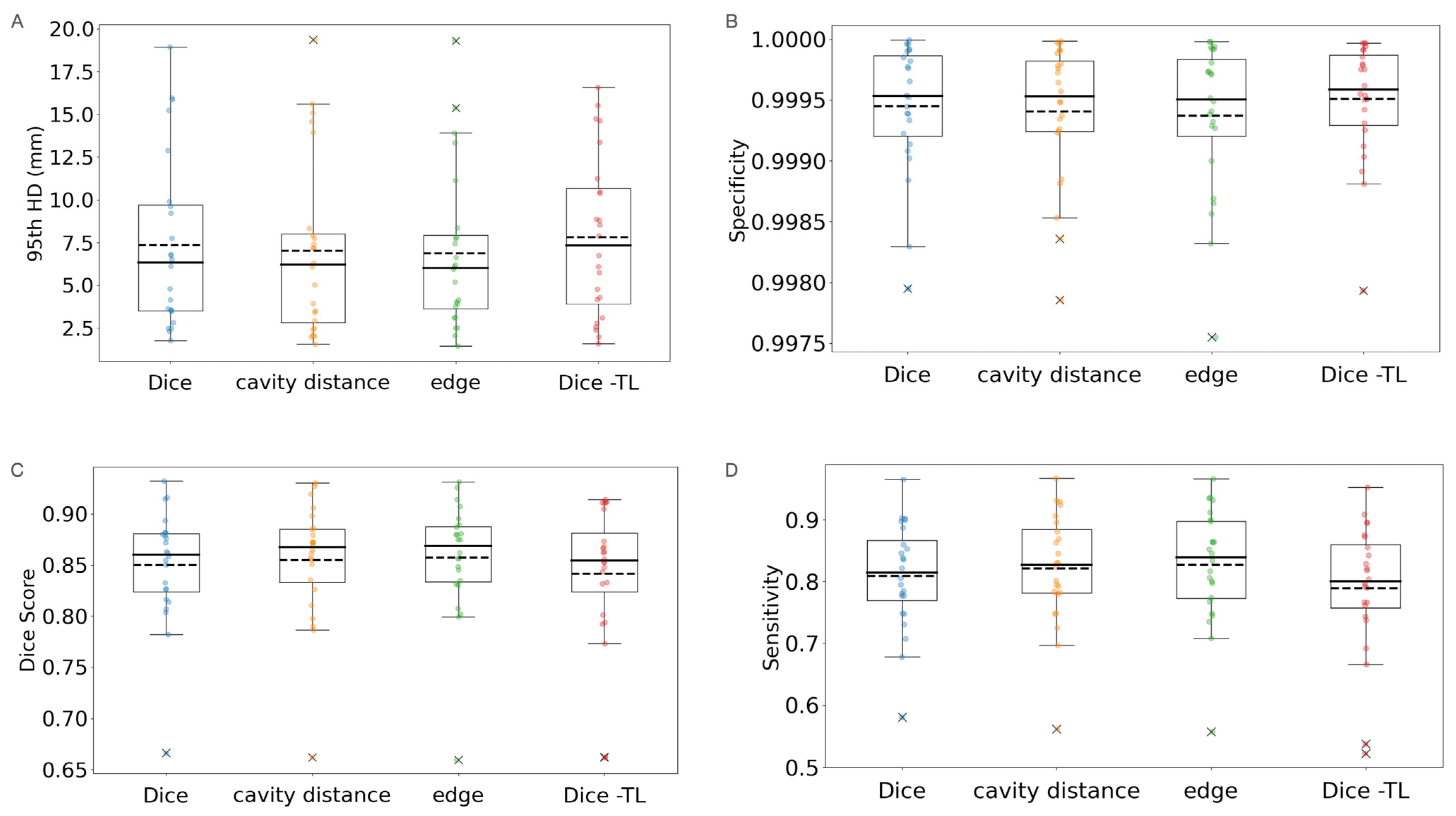
3.3. Loss Modification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Scan Parameters
| FOV | Number of Pixels | |
|---|---|---|
| Min resolution | [205,205,257] | [256,256,208] |
| Max resolution | [179,179,249] | [256,256,214] |
Appendix B
Generating Distance Maps for Weighting the Loss
Appendix C
Training Curves
References
- Louis, D.N.; Perry, A.; Wesseling, P.; Brat, D.J.; Cree, I.A.; Figarella-Branger, D.; Hawkins, C.; Ng, H.K.; Pfister, S.M.; Reifenberger, G. The 2021 WHO classification of tumors of the central nervous system: A summary. Neuro-Oncol. 2021, 23, 1231–1251. [Google Scholar] [CrossRef] [PubMed]
- Louis, D.N.; Perry, A.; Reifenberger, G.; Von Deimling, A.; Figarella-Branger, D.; Cavenee, W.K.; Ohgaki, H.; Wiestler, O.D.; Kleihues, P.; Ellison, D.W. The 2016 World Health Organization classification of tumors of the central nervous system: A summary. Acta Neuropathol. 2016, 131, 803–820. [Google Scholar] [CrossRef]
- Ostrom, Q.T.; Price, M.; Neff, C.; Cioffi, G.; Waite, K.A.; Kruchko, C.; Barnholtz-Sloan, J.S. CBTRUS Statistical Report: Primary brain and other central nervous system tumors diagnosed in the United States in 2016—2020. Neuro-Oncol. 2023, 25, iv1–iv99. [Google Scholar] [CrossRef]
- Bondy, M.L.; Scheurer, M.E.; Malmer, B.; Barnholtz-Sloan, J.S.; Davis, F.G.; Il’Yasova, D.; Kruchko, C.; McCarthy, B.J.; Rajaraman, P.; Schwartzbaum, J.A. Brain tumor epidemiology: Consensus from the Brain Tumor Epidemiology Consortium. Cancer 2008, 113, 1953–1968. [Google Scholar] [CrossRef] [PubMed]
- Ostrom, Q.T.; Cote, D.J.; Ascha, M.; Kruchko, C.; Barnholtz-Sloan, J.S. Adult glioma incidence and survival by race or ethnicity in the United States from 2000 to 2014. JAMA Oncol. 2018, 4, 1254–1262. [Google Scholar] [CrossRef]
- Ostrom, Q.T.; Gittleman, H.; Liao, P.; Vecchione-Koval, T.; Wolinsky, Y.; Kruchko, C.; Barnholtz-Sloan, J.S. CBTRUS statistical report: Primary brain and other central nervous system tumors diagnosed in the United States in 2010–2014. Neuro-Oncol. 2017, 19, v1–v88. [Google Scholar] [CrossRef] [PubMed]
- Wen, P.Y.; van den Bent, M.; Youssef, G.; Cloughesy, T.F.; Ellingson, B.M.; Weller, M.; Galanis, E.; Barboriak, D.P.; de Groot, J.; Gilbert, M.R. RANO 2.0: Update to the response assessment in neuro-oncology criteria for high-and low-grade gliomas in adults. J. Clin. Oncol. 2023, 41, 5187–5199. [Google Scholar] [CrossRef]
- Kickingereder, P.; Isensee, F.; Tursunova, I.; Petersen, J.; Neuberger, U.; Bonekamp, D.; Brugnara, G.; Schell, M.; Kessler, T.; Foltyn, M. Automated quantitative tumour response assessment of MRI in neuro-oncology with artificial neural networks: A multicentre, retrospective study. Lancet Oncol. 2019, 20, 728–740. [Google Scholar] [CrossRef]
- Chang, K.; Beers, A.L.; Bai, H.X.; Brown, J.M.; Ly, K.I.; Li, X.; Senders, J.T.; Kavouridis, V.K.; Boaro, A.; Su, C. Automatic assessment of glioma burden: A deep learning algorithm for fully automated volumetric and bidimensional measurement. Neuro-Oncology 2019, 21, 1412–1422. [Google Scholar] [CrossRef]
- Rudie, J.D.; Calabrese, E.; Saluja, R.; Weiss, D.; Colby, J.B.; Cha, S.; Hess, C.P.; Rauschecker, A.M.; Sugrue, L.P.; Villanueva-Meyer, J.E. Longitudinal assessment of posttreatment diffuse glioma tissue volumes with three-dimensional convolutional neural networks. Radiol. Artif. Intell. 2022, 4, e210243. [Google Scholar] [CrossRef]
- Vollmuth, P.; Foltyn, M.; Huang, R.Y.; Galldiks, N.; Petersen, J.; Isensee, F.; van den Bent, M.J.; Barkhof, F.; Park, J.E.; Park, Y.W. Artificial intelligence (AI)-based decision support improves reproducibility of tumor response assessment in neuro-oncology: An international multi-reader study. Neuro-Oncology 2023, 25, 533–543. [Google Scholar] [CrossRef]
- Lacroix, M.; Abi-Said, D.; Fourney, D.R.; Gokaslan, Z.L.; Shi, W.; DeMonte, F.; Lang, F.F.; McCutcheon, I.E.; Hassenbusch, S.J.; Holland, E. A multivariate analysis of 416 patients with glioblastoma multiforme: Prognosis, extent of resection, and survival. J. Neurosurg. 2001, 95, 190–198. [Google Scholar] [CrossRef]
- Grossman, R.; Shimony, N.; Shir, D.; Gonen, T.; Sitt, R.; Kimchi, T.J.; Harosh, C.B.; Ram, Z. Dynamics of FLAIR volume changes in glioblastoma and prediction of survival. Ann. Surg. Oncol. 2017, 24, 794–800. [Google Scholar] [CrossRef]
- Grabowski, M.M.; Recinos, P.F.; Nowacki, A.S.; Schroeder, J.L.; Angelov, L.; Barnett, G.H.; Vogelbaum, M.A. Residual tumor volume versus extent of resection: Predictors of survival after surgery for glioblastoma. J. Neurosurg. 2014, 121, 1115–1123. [Google Scholar] [CrossRef]
- Marko, N.F.; Weil, R.J.; Schroeder, J.L.; Lang, F.F.; Suki, D.; Sawaya, R.E. Extent of resection of glioblastoma revisited: Personalized survival modeling facilitates more accurate survival prediction and supports a maximum-safe-resection approach to surgery. J. Clin. Oncol. 2014, 32, 774. [Google Scholar] [CrossRef]
- Menze, B.H.; Jakab, A.; Bauer, S.; Kalpathy-Cramer, J.; Farahani, K.; Kirby, J.; Burren, Y.; Porz, N.; Slotboom, J.; Wiest, R. The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Trans. Med. Imaging 2014, 34, 1993–2024. [Google Scholar] [CrossRef]
- Havaei, M.; Davy, A.; Warde-Farley, D.; Biard, A.; Courville, A.; Bengio, Y.; Pal, C.; Jodoin, P.; Larochelle, H. Brain tumor segmentation with deep neural networks. Med. Image Anal. 2017, 35, 18–31. [Google Scholar] [CrossRef]
- Reddy, C.; Gopinath, K.; Lombaert, H. Brain tumor segmentation using topological loss in convolutional networks. In Proceedings of the 2019 Medical Imaging with Deep Learning Conference (MIDL 2019), London, UK, 8–10 July 2019. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention, Proceedings of the MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S. V-net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 4th International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 565–571. [Google Scholar]
- Myronenko, A. 3D MRI brain tumor segmentation using autoencoder regularization. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 16 September 2018; Revised Selected Papers, Part II; Springer: Berlin/Heidelberg, Germany, 2019; pp. 311–320. [Google Scholar]
- Ngo, D.; Tran, M.; Kim, S.; Yang, H.; Lee, G. Multi-task learning for small brain tumor segmentation from MRI. Appl. Sci. 2020, 10, 7790. [Google Scholar] [CrossRef]
- Cheng, G.; Cheng, J.; Luo, M.; He, L.; Tian, Y.; Wang, R. Effective and efficient multitask learning for brain tumor segmentation. J. Real-Time Image Process. 2020, 17, 1951–1960. [Google Scholar] [CrossRef]
- Weninger, L.; Liu, Q.; Merhof, D. Multi-task learning for brain tumor segmentation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 5th International Workshop, BrainLes 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, 17 October 2019; Revised Selected Papers Part I; Springer: Berlin/Heidelberg, Germany, 2020; pp. 327–337. [Google Scholar]
- Hatamizadeh, A.; Terzopoulos, D.; Myronenko, A. End-to-end boundary aware networks for medical image segmentation. In Machine Learning in Medical Imaging, Proceedings of the 10th International Workshop, MLMI 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, 13 October 2019; Proceedings 10; Springer: Berlin/Heidelberg, Germany, 2019; pp. 187–194. [Google Scholar]
- Mok, T.C.; Chung, A.C. Learning data augmentation for brain tumor segmentation with coarse-to-fine generative adversarial networks. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 16 September 2018; Revised Selected Papers, Part I 4; Springer: Berlin/Heidelberg, Germany, 2019; pp. 70–80. [Google Scholar]
- Pei, L.; Vidyaratne, L.; Rahman, M.M.; Iftekharuddin, K.M. Context aware deep learning for brain tumor segmentation, subtype classification, and survival prediction using radiology images. Sci. Rep. 2020, 10, 19726. [Google Scholar] [CrossRef]
- Baid, U.; Ghodasara, S.; Mohan, S.; Bilello, M.; Calabrese, E.; Colak, E.; Farahani, K.; Kalpathy-Cramer, J.; Kitamura, F.C.; Pati, S. The rsna-asnr-miccai brats 2021 benchmark on brain tumor segmentation and radiogenomic classification. arXiv 2021, arXiv:2107.02314. [Google Scholar]
- Eker, A.G.; Pehlivanoğlu, M.K.; İnce, İ.; Duru, N. Deep Learning and Transfer Learning Based Brain Tumor Segmentation. In Proceedings of the 2023 8th International Conference on Computer Science and Engineering (UBMK), Burdur, Turkiye, 13–15 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 163–168. [Google Scholar]
- Magadza, T.; Viriri, S. Deep learning for brain tumor segmentation: A survey of state-of-the-art. J. Imaging 2021, 7, 19. [Google Scholar] [CrossRef]
- Wang, P.; Chung, A.C. Relax and focus on brain tumor segmentation. Med. Image Anal. 2022, 75, 102259. [Google Scholar] [CrossRef]
- Liu, Z.; Tong, L.; Chen, L.; Jiang, Z.; Zhou, F.; Zhang, Q.; Zhang, X.; Jin, Y.; Zhou, H. Deep learning based brain tumor segmentation: A survey. Complex Intell. Syst. 2023, 9, 1001–1026. [Google Scholar] [CrossRef]
- Zhu, Z.; He, X.; Qi, G.; Li, Y.; Cong, B.; Liu, Y. Brain tumor segmentation based on the fusion of deep semantics and edge information in multimodal MRI. Inf. Fusion 2023, 91, 376–387. [Google Scholar] [CrossRef]
- Allah, A.M.G.; Sarhan, A.M.; Elshennawy, N.M. Edge U-Net: Brain tumor segmentation using MRI based on deep U-Net model with boundary information. Expert Syst. Appl. 2023, 213, 118833. [Google Scholar] [CrossRef]
- Ahamed, M.F.; Hossain, M.M.; Nahiduzzaman, M.; Islam, M.R.; Islam, M.R.; Ahsan, M.; Haider, J. A review on brain tumor segmentation based on deep learning methods with federated learning techniques. Comput. Med. Imaging Graph. 2023, 110, 102313. [Google Scholar] [CrossRef]
- Nalepa, J.; Marcinkiewicz, M.; Kawulok, M. Data augmentation for brain-tumor segmentation: A review. Front. Comput. Neurosci. 2019, 13, 83. [Google Scholar] [CrossRef]
- Zeng, K.; Bakas, S.; Sotiras, A.; Akbari, H.; Rozycki, M.; Rathore, S.; Pati, S.; Davatzikos, C. Segmentation of gliomas in pre-operative and post-operative multimodal magnetic resonance imaging volumes based on a hybrid generative-discriminative framework. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the Second International Workshop, BrainLes 2016, with the Challenges on BRATS, ISLES and mTOP 2016, Held in Conjunction with MICCAI 2016, Athens, Greece, 17 October 2016; Revised Selected Papers 2; Springer: Berlin/Heidelberg, Germany, 2016; pp. 184–194. [Google Scholar]
- Huang, L.; Zhu, E.; Chen, L.; Wang, Z.; Chai, S.; Zhang, B. A transformer-based generative adversarial network for brain tumor segmentation. Front. Neurosci. 2022, 16, 1054948. [Google Scholar] [CrossRef]
- Kalejahi, B.K.; Meshgini, S.; Danishvar, S. Segmentation of Brain Tumor Using a 3D Generative Adversarial Network. Diagnostics 2023, 13, 3344. [Google Scholar] [CrossRef]
- Sille, R.; Choudhury, T.; Sharma, A.; Chauhan, P.; Tomar, R.; Sharma, D. A novel generative adversarial network-based approach for automated brain tumour segmentation. Medicina 2023, 59, 119. [Google Scholar] [CrossRef]
- Akbar, M.U.; Larsson, M.; Eklund, A. Brain tumor segmentation using synthetic MR images—A comparison of GANs and diffusion models. Sci. Data 2024, 11, 259. [Google Scholar] [CrossRef]
- Haq, E.U.; Jianjun, H.; Huarong, X.; Li, K.; Weng, L. A hybrid approach based on deep cnn and machine learning classifiers for the tumor segmentation and classification in brain MRI. Comput. Math. Methods Med. 2022, 2022, 6446680. [Google Scholar] [CrossRef]
- He, K.; Ji, W.; Zhou, T.; Li, Z.; Huo, J.; Zhang, X.; Gao, Y.; Shen, D.; Zhang, B.; Zhang, J. Cross-modality brain tumor segmentation via bidirectional global-to-local unsupervised domain adaptation. arXiv 2021, arXiv:2105.07715. [Google Scholar]
- Dai, L.; Li, T.; Shu, H.; Zhong, L.; Shen, H.; Zhu, H. Automatic brain tumor segmentation with domain adaptation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 16 September 2018; Revised Selected Papers, Part II 4; Springer: Berlin/Heidelberg, Germany, 2019; pp. 380–392. [Google Scholar]
- Kushibar, K.; Salem, M.; Valverde, S.; Rovira, À.; Salvi, J.; Oliver, A.; Lladó, X. Transductive transfer learning for domain adaptation in brain magnetic resonance image segmentation. Front. Neurosci. 2021, 15, 608808. [Google Scholar] [CrossRef]
- Wacker, J.; Ladeira, M.; Nascimento, J.E.V. Transfer learning for brain tumor segmentation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 6th International Workshop, BrainLes 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, 4 October 2020; Revised Selected Papers, Part I 6; Springer: Berlin/Heidelberg, Germany, 2021; pp. 241–251. [Google Scholar]
- Amin, J.; Sharif, M.; Yasmin, M.; Saba, T.; Anjum, M.A.; Fernandes, S.L. A new approach for brain tumor segmentation and classification based on score level fusion using transfer learning. J. Med. Syst. 2019, 43, 326. [Google Scholar] [CrossRef]
- Pravitasari, A.A.; Iriawan, N.; Almuhayar, M.; Azmi, T.; Irhamah, I.; Fithriasari, K.; Purnami, S.W.; Ferriastuti, W. UNet-VGG16 with transfer learning for MRI-based brain tumor segmentation. TELKOMNIKA (Telecommun. Comput. Electron. Control.) 2020, 18, 1310–1318. [Google Scholar] [CrossRef]
- Ahuja, S.; Panigrahi, B.K.; Gandhi, T. Transfer learning based brain tumor detection and segmentation using superpixel technique. In Proceedings of the 2020 International Conference on Contemporary Computing and Applications (IC3A), Lucknow, India, 5–7 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 244–249. [Google Scholar]
- Ghafoorian, M.; Mehrtash, A.; Kapur, T.; Karssemeijer, N.; Marchiori, E.; Pesteie, M.; Guttmann, C.R.; de Leeuw, F.; Tempany, C.M.; Van Ginneken, B. Transfer learning for domain adaptation in MRI: Application in brain lesion segmentation. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017, Proceedings, Part III 20; Springer: Berlin/Heidelberg, Germany, 2017; pp. 516–524. [Google Scholar]
- Razzaghi, P.; Abbasi, K.; Shirazi, M.; Rashidi, S. Multimodal brain tumor detection using multimodal deep transfer learning. Appl. Soft Comput. 2022, 129, 109631. [Google Scholar] [CrossRef]
- Swaraja, K.; Meenakshi, K.; Valiveti, H.B.; Karuna, G. Segmentation and detection of brain tumor through optimal selection of integrated features using transfer learning. Multimed. Tools Appl. 2022, 81, 27363–27395. [Google Scholar] [CrossRef]
- Tataei Sarshar, N.; Ranjbarzadeh, R.; Jafarzadeh Ghoushchi, S.; de Oliveira, G.G.; Anari, S.; Parhizkar, M.; Bendechache, M. Glioma Brain Tumor Segmentation in Four MRI Modalities Using a Convolutional Neural Network and Based on a Transfer Learning Method. In Proceedings of the 7th Brazilian Technology Symposium (BTSym’21)—Emerging Trends in Human Smart and Sustainable Future of Cities, Campinas, Brazil, 19–21 October 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 386–402. [Google Scholar]
- Sugino, T.; Kawase, T.; Onogi, S.; Kin, T.; Saito, N.; Nakajima, Y. Loss weightings for improving imbalanced brain structure segmentation using fully convolutional networks. Healthcare 2021, 9, 938. [Google Scholar] [CrossRef]
- Rouzrokh, P.; Khosravi, B.; Faghani, S.; Moassefi, M.; Vahdati, S.; Erickson, B.J. Multitask brain tumor inpainting with diffusion models: A methodological report. arXiv 2022, arXiv:2210.12113. [Google Scholar]
- Wu, J.; Fu, R.; Fang, H.; Zhang, Y.; Yang, Y.; Xiong, H.; Liu, H.; Xu, Y. Medsegdiff: Medical image segmentation with diffusion probabilistic model. PLMR 2024, 227, 1623–1639. [Google Scholar]
- Wolleb, J.; Sandkühler, R.; Bieder, F.; Valmaggia, P.; Cattin, P.C. Diffusion models for implicit image segmentation ensembles. In Proceedings of the 5th International Conference on Medical Imaging with Deep Learning, Zurich, Switzerland, 6–8 July 2022; PMLR: Westminster, UK, 2022; pp. 1336–1348. [Google Scholar]
- Wang, W.; Chen, C.; Ding, M.; Yu, H.; Zha, S.; Li, J. Transbts: Multimodal brain tumor segmentation using transformer. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2021, Proceedings of the 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part I 24; Springer: Berlin/Heidelberg, Germany, 2021; pp. 109–119. [Google Scholar]
- Hatamizadeh, A.; Nath, V.; Tang, Y.; Yang, D.; Roth, H.R.; Xu, D. Swin unetr: Swin transformers for semantic segmentation of brain tumors in MRI images. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 7th International Workshop, BrainLes 2021, Held in Conjunction with MICCAI 2021, Virtual Event, 27 September 2021; Revised Selected Papers, Part I; Springer: Berlin/Heidelberg, Germany, 2021; pp. 272–284. [Google Scholar]
- Ranjbarzadeh, R.; Bagherian Kasgari, A.; Jafarzadeh Ghoushchi, S.; Anari, S.; Naseri, M.; Bendechache, M. Brain tumor segmentation based on deep learning and an attention mechanism using MRI multi-modalities brain images. Sci. Rep. 2021, 11, 10930. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Liu, T.; Lu, J.; Chen, X.; Yu, L.; Wu, J.; Chen, D.Z.; Cai, W. Influence of data distribution on federated learning performance in tumor segmentation. Radiol. Artif. Intell. 2023, 5, e220082. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Milletarì, F.; Xu, D.; Rieke, N.; Hancox, J.; Zhu, W.; Baust, M.; Cheng, Y.; Ourselin, S.; Cardoso, M.J. Privacy-preserving federated brain tumour segmentation. In Machine Learning in Medical Imaging, Proceedings of the 10th International Workshop, MLMI 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, 13 October 2019; Proceedings 10; Springer: Berlin/Heidelberg, Germany, 2019; pp. 133–141. [Google Scholar]
- Tedeschini, B.C.; Savazzi, S.; Stoklasa, R.; Barbieri, L.; Stathopoulos, I.; Nicoli, M.; Serio, L. Decentralized federated learning for healthcare networks: A case study on tumor segmentation. IEEE Access 2022, 10, 8693–8708. [Google Scholar] [CrossRef]
- Luu, H.M.; Park, S. Extending nn-UNet for brain tumor segmentation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 7th International Workshop, BrainLes 2021, Held in Conjunction with MICCAI 2021, Virtual Event, 27 September 2021; Revised Selected Papers, Part II; Springer: Berlin/Heidelberg, Germany, 2021; pp. 173–186. [Google Scholar]
- Kessler, A.T.; Bhatt, A.A. Brain tumour post-treatment imaging and treatment-related complications. Insights Into Imaging 2018, 9, 1057–1075. [Google Scholar] [CrossRef] [PubMed]
- Ramesh, K.K.; Xu, K.M.; Trivedi, A.G.; Huang, V.; Sharghi, V.K.; Kleinberg, L.R.; Mellon, E.A.; Shu, H.G.; Shim, H.; Weinberg, B.D. A Fully Automated Post-Surgical Brain Tumor Segmentation Model for Radiation Treatment Planning and Longitudinal Tracking. Cancers 2023, 15, 3956. [Google Scholar] [CrossRef] [PubMed]
- Helland, R.H.; Ferles, A.; Pedersen, A.; Kommers, I.; Ardon, H.; Barkhof, F.; Bello, L.; Berger, M.S.; Dunås, T.; Nibali, M.C. Segmentation of glioblastomas in early post-operative multi-modal MRI with deep neural networks. Sci. Rep. 2023, 13, 18897. [Google Scholar] [CrossRef]
- Holtzman Gazit, M.; Faran, R.; Stepovoy, K.; Peles, O.; Shamir, R.R. Post-operative glioblastoma multiforme segmentation with uncertainty estimation. Front. Hum. Neurosci. 2022, 16, 932441. [Google Scholar] [CrossRef]
- Ghaffari, M.; Samarasinghe, G.; Jameson, M.; Aly, F.; Holloway, L.; Chlap, P.; Koh, E.; Sowmya, A.; Oliver, R. Automated post-operative brain tumour segmentation: A deep learning model based on transfer learning from pre-operative images. Magn. Reson. Imaging 2022, 86, 28–36. [Google Scholar] [CrossRef]
- Calivá, F.; Kamat, S.; Morales Martinez, A.; Majumdar, S.; Pedoia, V. Surface spherical encoding and contrastive learning for virtual bone shape aging. Med Image Anal. 2022, 77, 102388. [Google Scholar] [CrossRef] [PubMed]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 1–28. [Google Scholar]
- Zhang, D.; Lu, G. Review of shape representation and description techniques. Pattern Recognit. 2004, 37, 1–19. [Google Scholar] [CrossRef]
- Gerig, G.; Jomier, M.; Chakos, M. Valmet: A new validation tool for assessing and improving 3D object segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2001, Proceedings of the 4th International Conference Utrecht, The Netherlands, 14–17 October 2001; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2001; pp. 516–523. [Google Scholar]
- Nikolov, S.; Blackwell, S.; Zverovitch, A.; Mendes, R.; Livne, M.; De Fauw, J.; Patel, Y.; Meyer, C.; Askham, H.; Romera-Paredes, B. Deep learning to achieve clinically applicable segmentation of head and neck anatomy for radiotherapy. arXiv 2018, arXiv:1809.04430. [Google Scholar]
- Ranjbar, S.; Singleton, K.W.; Curtin, L.; Paulson, L.; Clark-Swanson, K.; Hawkins-Daarud, A.; Mitchell, J.R.; Jackson, P.R.; Swanson, K.R. Towards Longitudinal Glioma Segmentation: Evaluating combined pre-and post-treatment MRI training data for automated tumor segmentation using nnU-Net. medRxiv 2023, in press. [Google Scholar]
- Breto, A.L.; Cullison, K.; Zacharaki, E.I.; Wallaengen, V.; Maziero, D.; Jones, K.; Valderrama, A.; de la Fuente, M.I.; Meshman, J.; Azzam, G.A. A Deep Learning Approach for Automatic Segmentation during Daily MRI-Linac Radiotherapy of Glioblastoma. Cancers 2023, 15, 5241. [Google Scholar] [CrossRef] [PubMed]
- Lotan, E.; Zhang, B.; Dogra, S.; Wang, W.D.; Carbone, D.; Fatterpekar, G.; Oermann, E.K.; Lui, Y.W. Development and practical implementation of a deep learning–based pipeline for automated pre-and postoperative glioma segmentation. Am. J. Neuroradiol. 2022, 43, 24–32. [Google Scholar] [CrossRef]
- Sheller, M.J.; Reina, G.A.; Edwards, B.; Martin, J.; Bakas, S. Multi-institutional deep learning modeling without sharing patient data: A feasibility study on brain tumor segmentation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 16 September 2018; Revised Selected Papers, Part I 4; Springer: Berlin/Heidelberg, Germany, 2019; pp. 92–104. [Google Scholar]
- Pati, S.; Baid, U.; Edwards, B.; Sheller, M.; Wang, S.; Reina, G.A.; Foley, P.; Gruzdev, A.; Karkada, D.; Davatzikos, C. Federated learning enables big data for rare cancer boundary detection. Nat. Commun. 2022, 13, 7346. [Google Scholar] [CrossRef]
- Islam, M.; Glocker, B. Spatially varying label smoothing: Capturing uncertainty from expert annotations. In Information Processing in Medical Imaging, Proceedings of the 27th International Conference, IPMI 2021, Virtual Event, 28–30 June 2021; Proceedings 27; Springer: Berlin/Heidelberg, Germany, 2021; pp. 677–688. [Google Scholar]




| Pre-Tx Training | Pre-Tx Validation | Post-Tx Training | Post-Tx Validation | Post-Tx/Total | Pre-Tx/Total | Training Total |
|---|---|---|---|---|---|---|
| 153 | 39 | 0 | 0 | 0 | -- | 192 |
| 134 | 33 | 20 | 5 | 0.13 | -- | 192 |
| 114 | 28 | 40 | 10 | 0.26 | -- | 192 |
| 77 | 19 | 77 | 19 | 0.5 | -- | 192 |
| 51 | 13 | 103 | 25 | 0.67 | -- | 192 |
| 0 | 0 | 153 | 39 | 1 | 0 | 192 |
| 40 | 10 | 153 | 39 | -- | 0.21 | 242 |
| 80 | 20 | 153 | 39 | -- | 0.34 | 292 |
| 120 | 30 | 153 | 39 | -- | 0.44 | 342 |
| 166 | 42 | 153 | 39 | -- | 0.52 | 400 |
| Pre-Tx Training | PreTx Validation | Post-Tx Training | Post-Tx Validation | Post-Tx/Total | Training Total | TL Pre-Train | TL Fine-Tune | |
|---|---|---|---|---|---|---|---|---|
| TL splits | 134 | 33 | 20 | 5 | 0.13 | 192 | 167 | 25 |
| 114 | 28 | 40 | 10 | 0.26 | 192 | 172 | 50 | |
| 77 | 19 | 77 | 19 | 0.5 | 192 | 96 | 96 | |
| 51 | 13 | 103 | 25 | 0.67 | 192 | 64 | 128 | |
| Loss splits | -- | -- | 158 | 39 | -- | -- | -- | -- |
| TL + Loss splits | 166 | 42 | 158 | 39 | 0.49 | 405 | 208 | 197 |
| Spatial Weighting Post-Treatment Only | Dice Loss | Cavity Loss | Edge Loss | |
| Dice score | 0.849 ± 0.011 | 0.837 ± 0.013 | 0.845 ± 0.012 | |
| 95th HD | 10.23 ± 1.81 | 8.97 ± 1.60 | 7.23 ± 0.98 | |
| Sensitivity | 0.811 ± 0.016 | 0.786 ± 0.020 | 0.802 ± 0.019 | |
| Specificity | 0.99940 ± 0.00010 | 0.99948 ± 0.00012 | 0.99945 ± 0.00012 | |
| Transfer Learning (TL) + Spatial Weighting | TL + Dice Loss | TL + Cavity Loss | TL + Edge Loss | no TL + Dice Loss |
| Dice score | 0.850 ± 0.010 | 0.855 ± 0.011 | 0.857 ± 0.011 | 0.842 ± 0.013 |
| 95th HD | 7.35 ± 0.96 | 7.00 ± 0.97 | 6.88 ± 0.88 | 7.81 ± 0.89 |
| Sensitivity | 0.809 ± 0.016 | 0.821 ± 0.017 | 0.827 ± 0.017 | 0.789 ± 0.02 |
| Specificity | 0.99945 ± 0.00010 | 0.9994 ± 0.00012 | 0.99937 ± 0.00012 | 0.9995 ± 0.00012 |
| Study | Tumor Component | Dice Score | HD (mm) | Year | Method | N | Imaging Modality | Preprocessing |
|---|---|---|---|---|---|---|---|---|
| Post-operative glioblastoma multiforme segmentation with uncertainty estimation [68] | T1 enhancement (Whole Tumor) * | 0.81 | 29.56 | 2022 | 3D nnUNet + manual uncertainty threshold | 340 post-treatment patients (270 train, 70 test) | T1 post gadolinium contrast enhancement | Bias field correction + skull stripping |
| Segmentation of glioblastomas in early post-operative multi-modal MRI with deep neural networks [67] | Residual Tumor Volume * | 0.5919 | 22.56 (95th HD) | 2023 | 3D nnUNet | 956 post-treatment patients (73 testing) | T1 + T1 post gadolinium contrast enhancement | Alignment |
| A Fully Automated Post-Surgical Brain Tumor Segmentation Model for Radiation Treatment Planning and Longitudinal Tracking [66] | Radiotherapy Targets (Gross Tumor Volume 1) | 0.72 | 12.77 | 2023 | 3D UNet | 255 patients (202 train, 23 validation, 30 test) | T1 post gadolinium contrast enhancement + T2 FLAIR | Skull stripping + alignment |
| Longitudinal Assessment of Posttreatment Diffuse Glioma Tissue Volumes with Three-dimensional Convolutional Neural Networks [10] | Whole Tumor Post-treatment | 0.86 | 6.9 (95th HD) | 2022 | 3D nnUNet | 298 patients post-treatment (198 train, 100 test) | T1 + T1 post gadolinium contrast enhancement + T2 + T2 FLAIR | Skull stripping + alignment |
| Development and Practical Implementation of a Deep Learning–Based Pipeline for Automated Pre- and Postoperative Glioma Segmentation [77] | Whole Tumor Post-treatment | 0.83 | N/A | 2022 | Autoencoder regularization–cascaded anisotropic CNN | 437 patients post-treatment (40 test, 397 training) | T1 + T1 post gadolinium contrast enhancement + T2 + T2-FLAIR | Skull stripping + alignment |
| A Deep Learning Approach for Automatic Segmentation during Daily MRI-Linac Radiotherapy of Glioblastoma [76] | Whole Tumor Post-treatment | 0.67 | N/A | 2023 | Mask R-CNN | 36 patients (imaging pre- and 30 times during treatment totaling 930 images; 9-fold cross validation with 80:10:10 train:val:test) | Predominantly T2-weighting low field (0.35T) bSSFP | None |
| Towards Longitudinal Glioma Segmentation: Evaluating combined pre- and post-treatment MRI training data for automated tumor segmentation using nnU-Net [75] | Whole Tumor Post-treatment | 0.8 | N/A | 2023 | 3D nnUNet | Pre-treatment training cases: (N = 502). Post-treatment training cases: (N = 588). Combined cases: (N = 1090). Test cases from pre-treatment: (N = 219); and post-treatment: (N = 254). | T1 post gadolinium contrast enhancement + T2 FLAIR | Alignment + denoting + N4 Bias correction + skull stripping |
| This manuscript | Whole Tumor Post-treatment | 0.86 | 6.88 (95th HD) | 2024 | Transfer learning 3D VAE with spatial regularization | Pre-treatment training cases: (N = 208). Post-treatment training cases: (N = 197). Post-treatment test cases: (N = 24). | T2 FLAIR | None |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellison, J.; Caliva, F.; Damasceno, P.; Luks, T.L.; LaFontaine, M.; Cluceru, J.; Kemisetti, A.; Li, Y.; Molinaro, A.M.; Pedoia, V.; et al. Improving the Generalizability of Deep Learning for T2-Lesion Segmentation of Gliomas in the Post-Treatment Setting. Bioengineering 2024, 11, 497. https://doi.org/10.3390/bioengineering11050497
Ellison J, Caliva F, Damasceno P, Luks TL, LaFontaine M, Cluceru J, Kemisetti A, Li Y, Molinaro AM, Pedoia V, et al. Improving the Generalizability of Deep Learning for T2-Lesion Segmentation of Gliomas in the Post-Treatment Setting. Bioengineering. 2024; 11(5):497. https://doi.org/10.3390/bioengineering11050497
Chicago/Turabian StyleEllison, Jacob, Francesco Caliva, Pablo Damasceno, Tracy L. Luks, Marisa LaFontaine, Julia Cluceru, Anil Kemisetti, Yan Li, Annette M. Molinaro, Valentina Pedoia, and et al. 2024. "Improving the Generalizability of Deep Learning for T2-Lesion Segmentation of Gliomas in the Post-Treatment Setting" Bioengineering 11, no. 5: 497. https://doi.org/10.3390/bioengineering11050497
APA StyleEllison, J., Caliva, F., Damasceno, P., Luks, T. L., LaFontaine, M., Cluceru, J., Kemisetti, A., Li, Y., Molinaro, A. M., Pedoia, V., Villanueva-Meyer, J. E., & Lupo, J. M. (2024). Improving the Generalizability of Deep Learning for T2-Lesion Segmentation of Gliomas in the Post-Treatment Setting. Bioengineering, 11(5), 497. https://doi.org/10.3390/bioengineering11050497








