Computational Modeling of Cardiac Electrophysiology with Human Realistic Heart–Torso Model
Abstract
:1. Introduction
2. Geometric Model Generation
3. Mathematical Modeling
3.1. Bidomain Model Incorporated with FHN Model
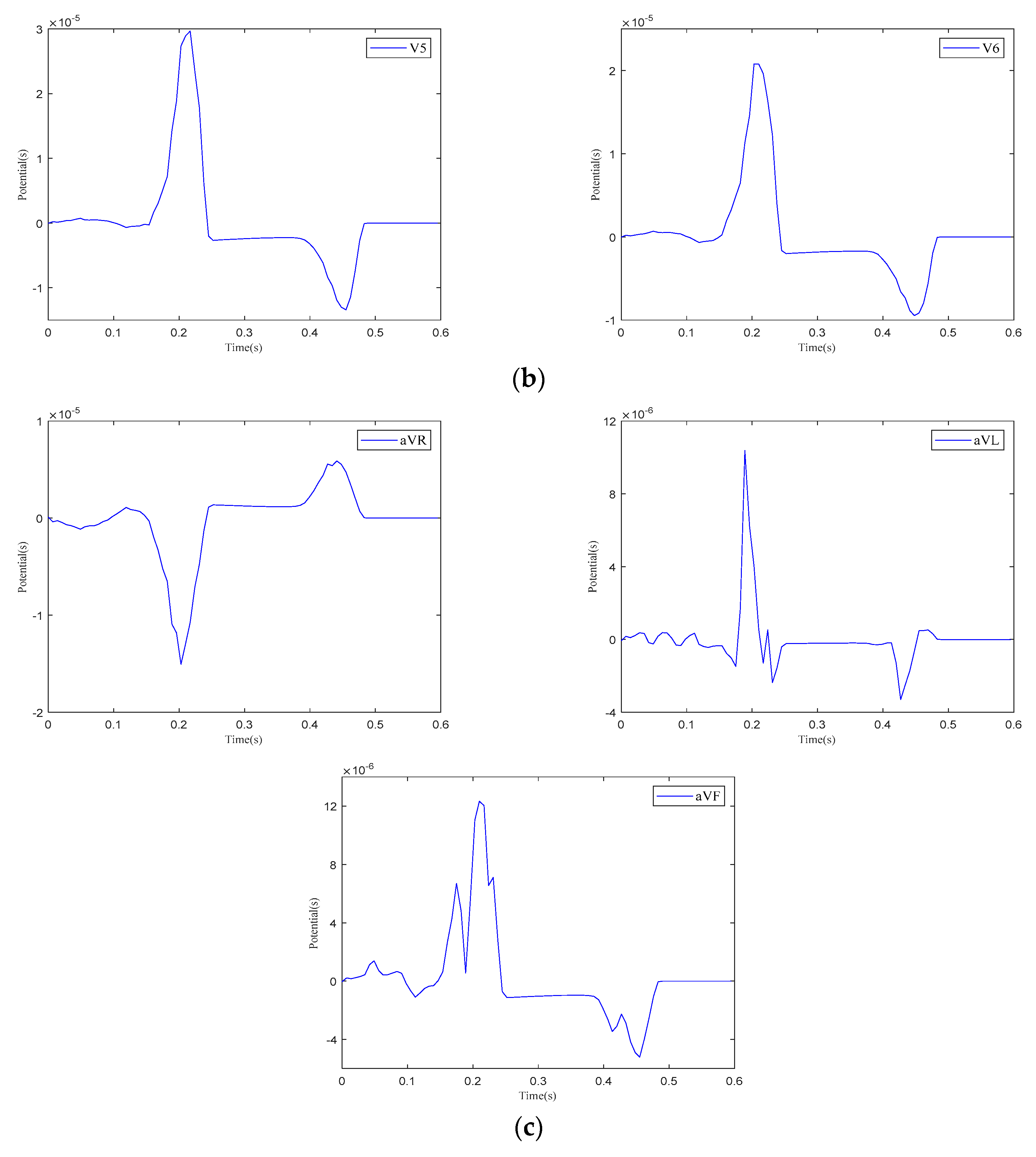
3.2. Simulation of Standard Twelve-Lead ECG
3.3. Model Boundary Conditions
3.4. Mesh Convergence Analysis
4. Results
4.1. Selection of Model Parameters
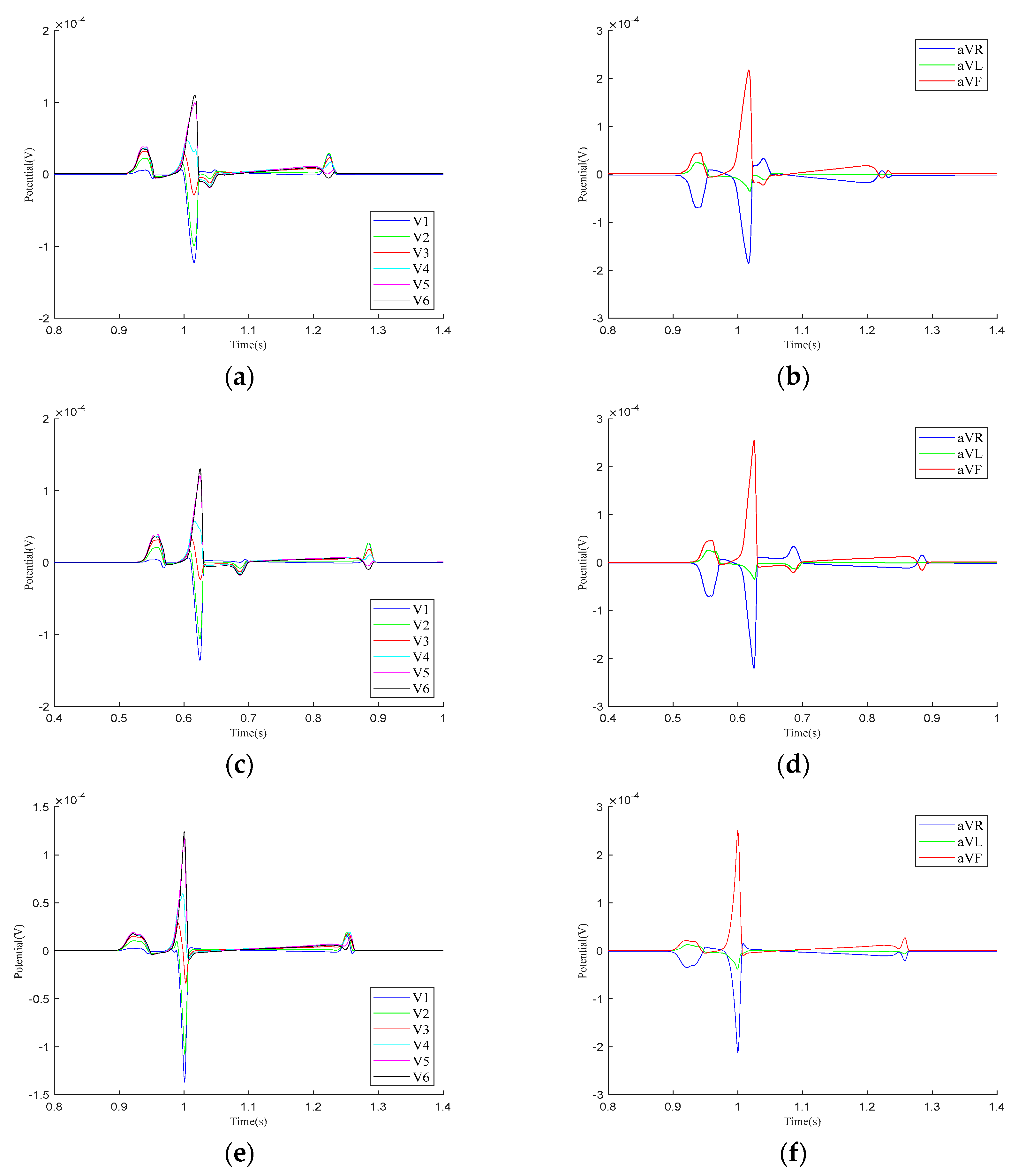
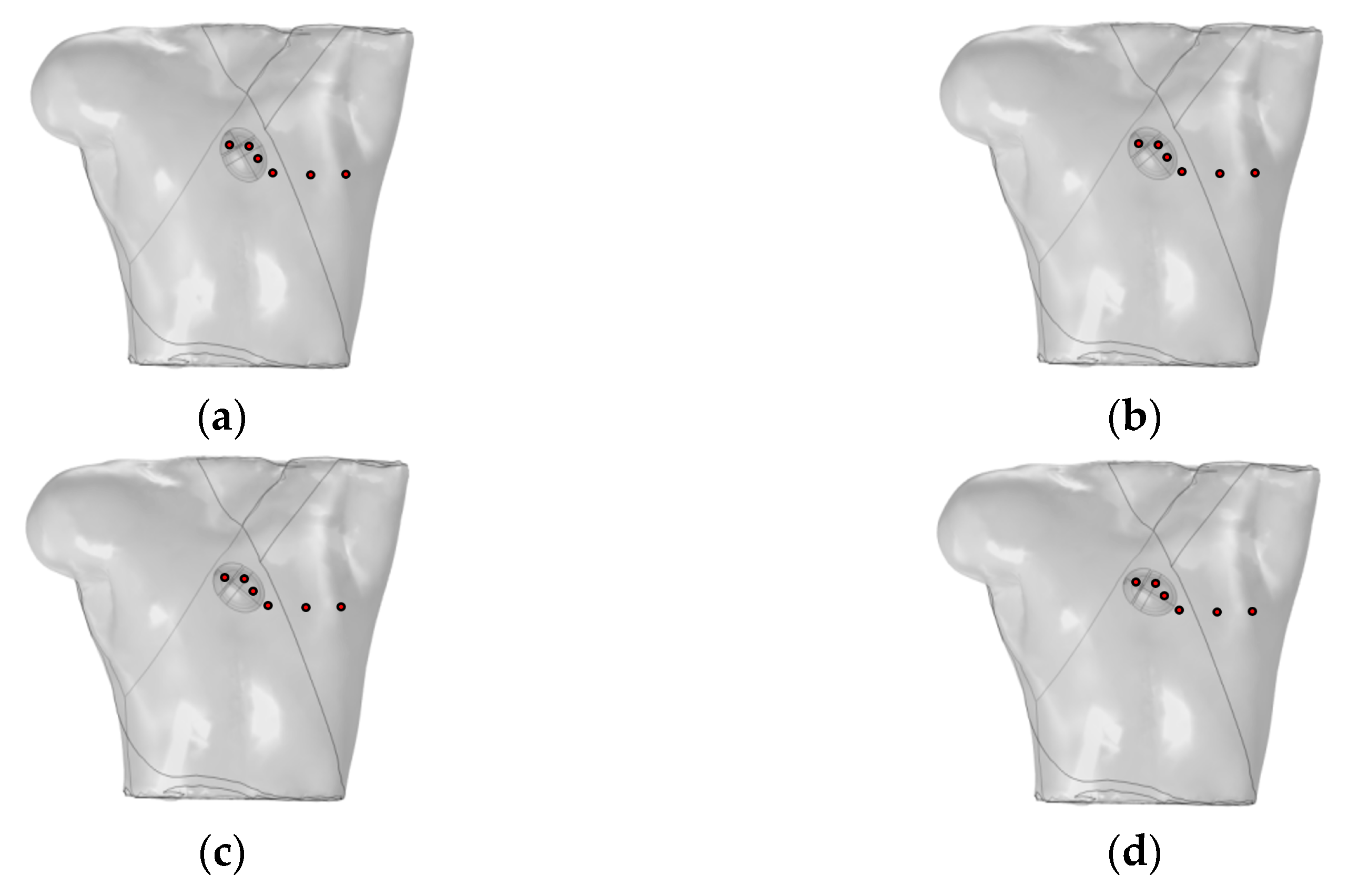
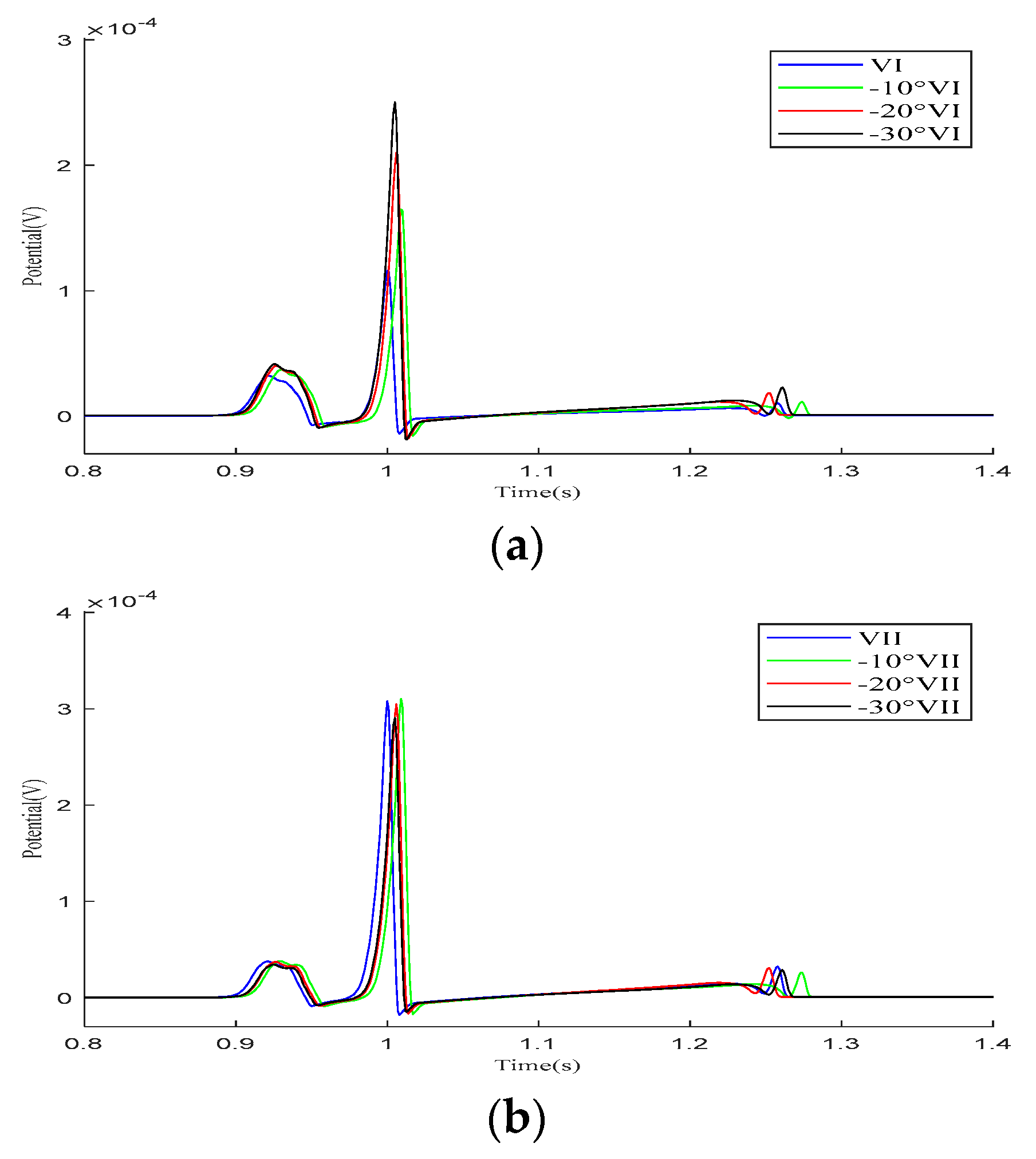
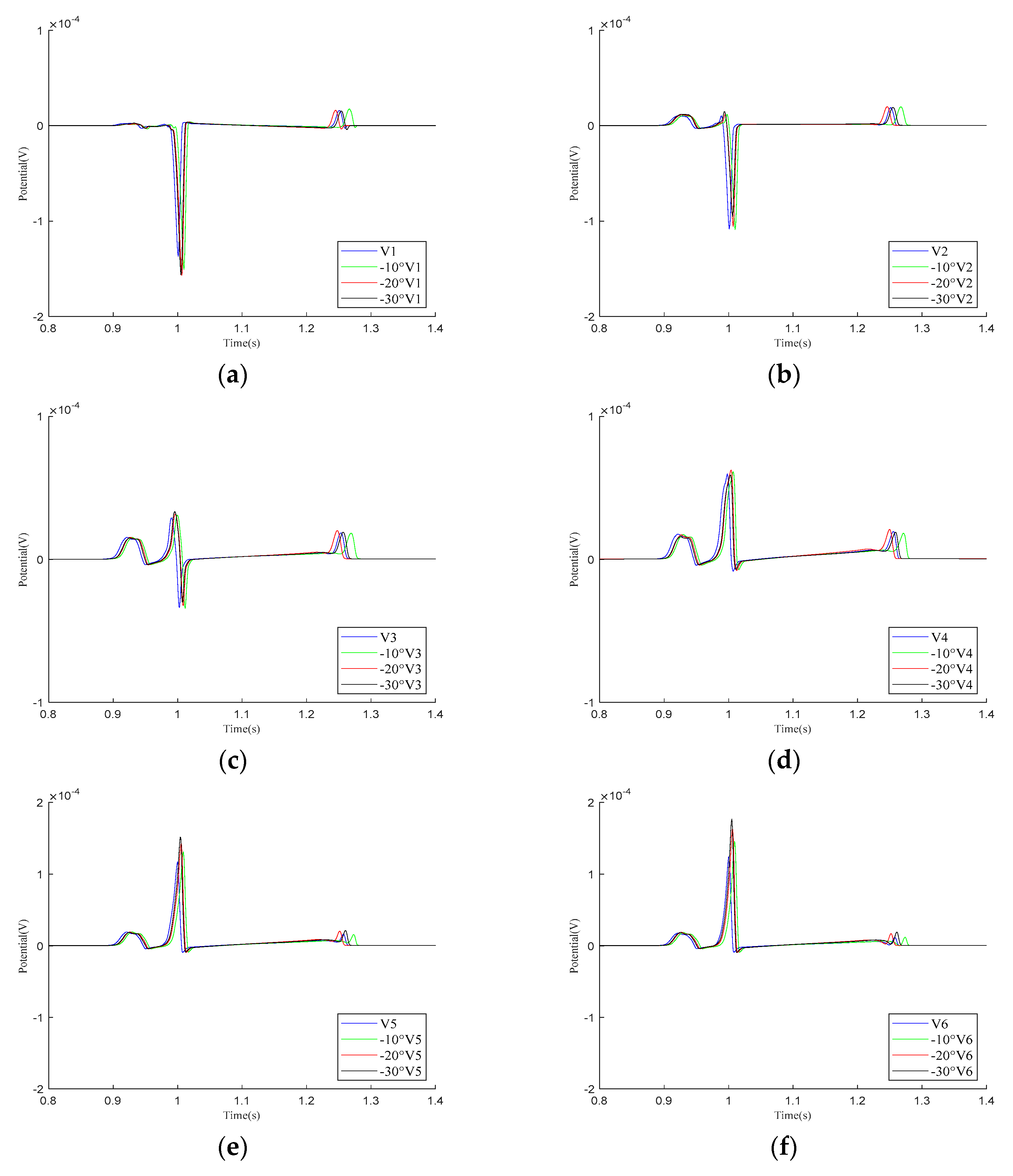
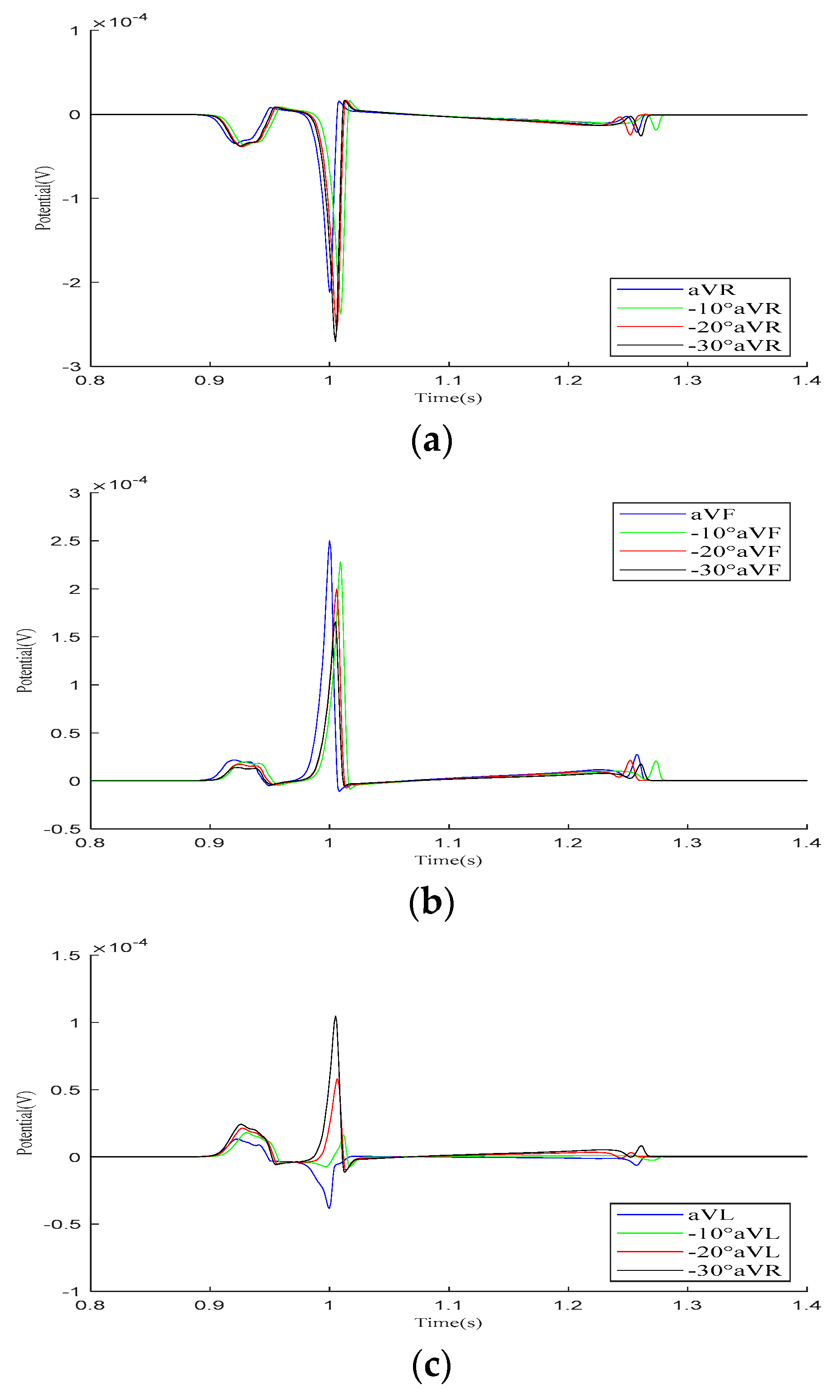
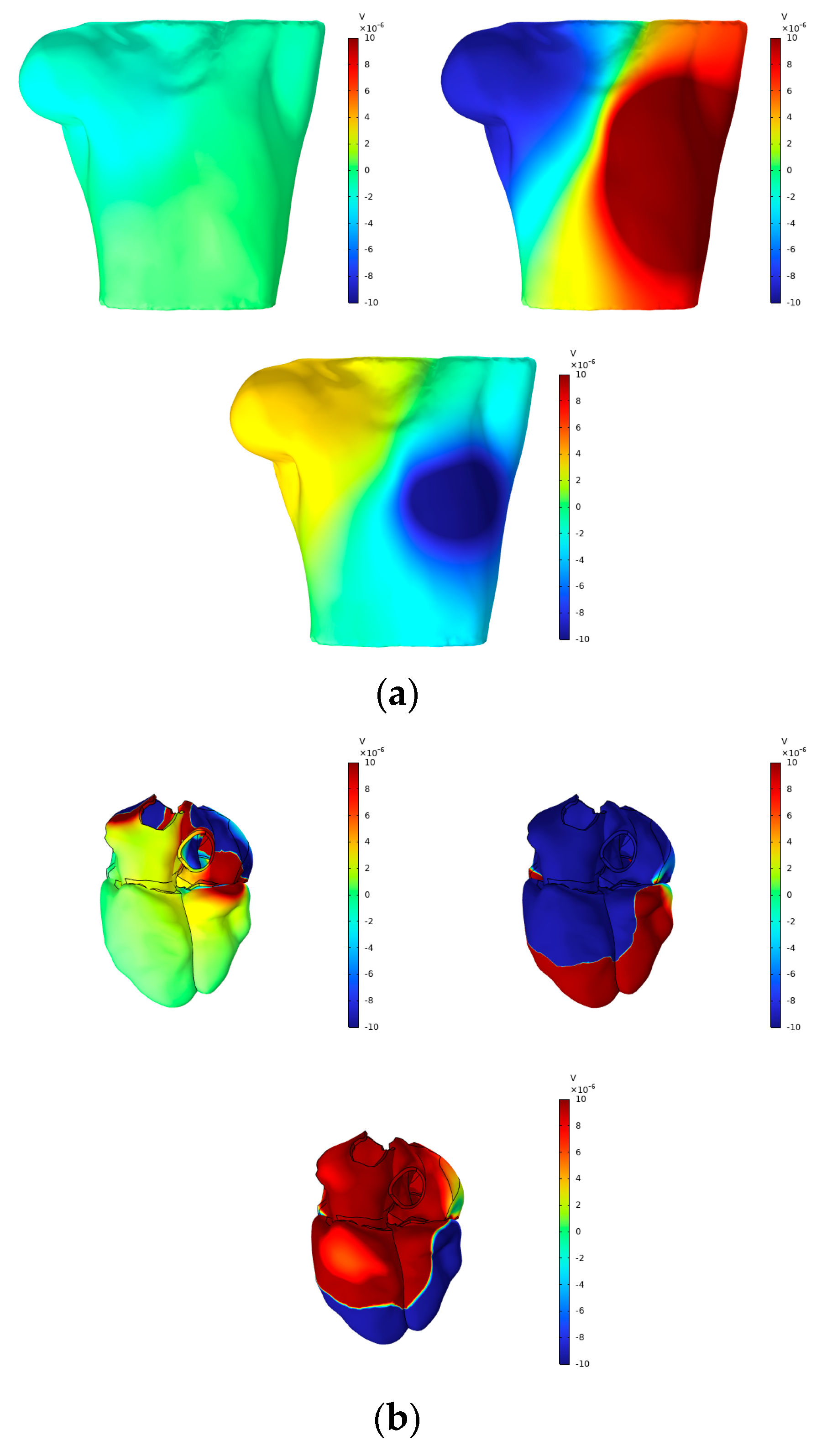
4.2. Impact of Heart–Torso Relative Position on Twelve-Lead ECG
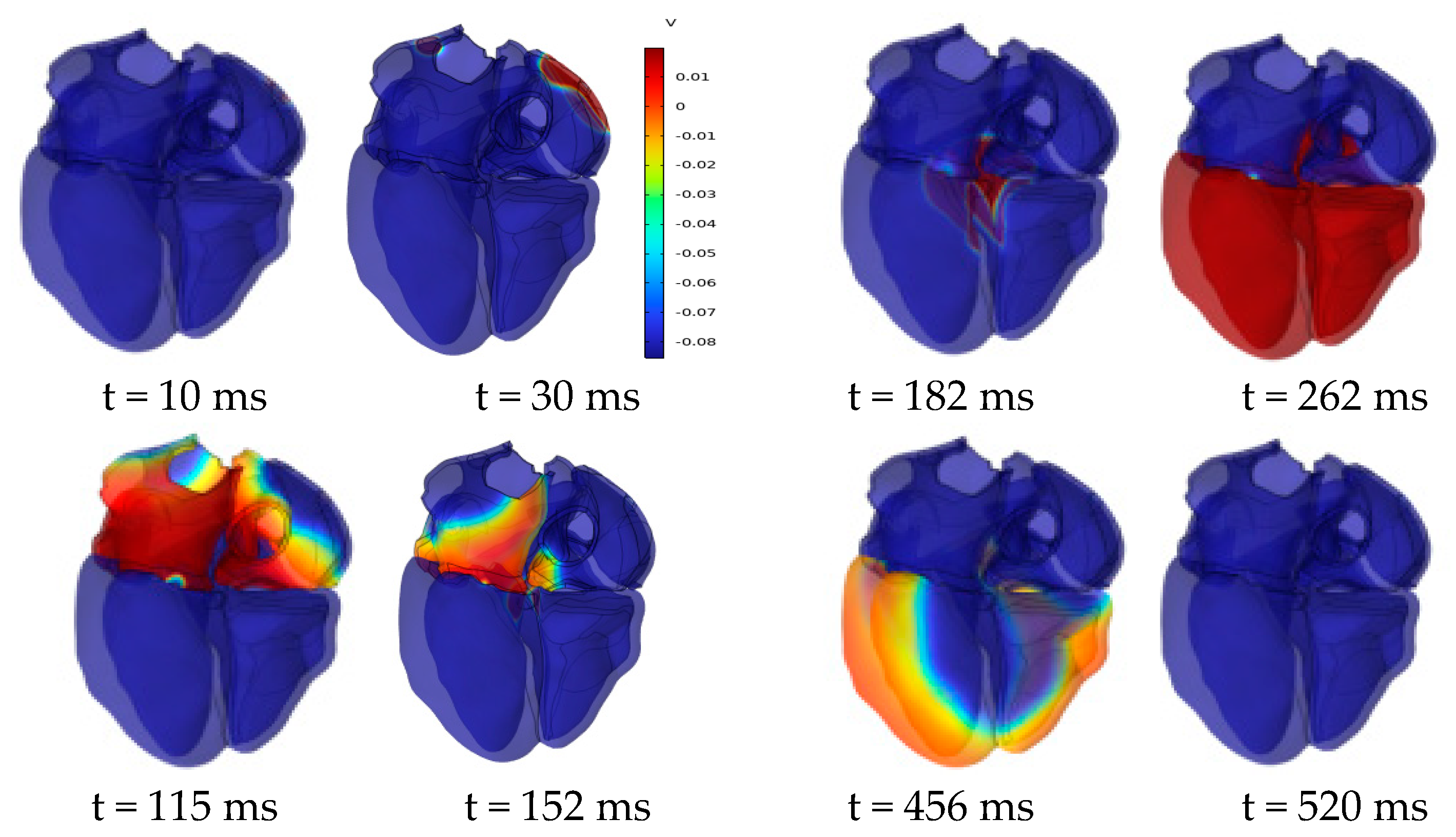
4.3. Electrophysiological Simulation Based on Realistic Heart–Torso Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ECG | Electrocardiogram |
| FHN | Fitzhugh–Nagumo |
| BSPMs | Body surface potential maps |
| SAN | Sinoatrial node |
| AVN | Atrioventricular node |
| His | His bundle |
| BNL | Bundle branches |
| PKJ | Purkinje network |
| CBIC | Centre for Integrative Biomedical Computing |
| BB | Bachmann’s Bundle |
| FEM | Finite element method |
| FDM | Finite difference method |
| FVM | Finite volume method |
| BEM | Boundary element method |
References
- Vieau, S.; Iaizzo, P.A. Basic ECG Theory, 12-Lead Recordings, and Their Interpretation. In Handbook of Cardiac Anatomy, Physiology, and Devices; Iaizzo, P.A., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 321–334. ISBN 978-3-319-19463-9. [Google Scholar]
- Potse, M. Scalable and Accurate ECG Simulation for Reaction-Diffusion Models of the Human Heart. Front. Physiol. 2018, 9, 370. [Google Scholar] [CrossRef] [PubMed]
- Loewe, A.; Wülfers, E.M.; Seemann, G. Cardiac Ischemia—Insights from Computational Models. Herzschr. Elektrophys. 2018, 29, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Amuzescu, B.; Airini, R.; Epureanu, F.B.; Mann, S.A.; Knott, T.; Radu, B.M. Evolution of Mathematical Models of Cardiomyocyte Electrophysiology. Math. Biosci. 2021, 334, 108567. [Google Scholar]
- Bazhutina, A.; Balakina-Vikulova, N.A.; Kursanov, A.; Solovyova, O.; Panfilov, A.; Katsnelson, L.B. Mathematical Modelling of the Mechano-Electric Coupling in the Human Cardiomyocyte Electrically Connected with Fibroblasts. Prog. Biophys. Mol. Biol. 2021, 159, 46–57. [Google Scholar] [CrossRef]
- Que, W.; Han, C.; Zhao, X.; Shi, L. An ECG Generative Model of Myocardial Infarction. Comput. Methods Programs Biomed. 2022, 225, 107062. [Google Scholar] [CrossRef]
- Bucelli, M.; Zingaro, A.; Africa, P.C.; Fumagalli, I.; Dede’, L.; Quarteroni, A. A Mathematical Model That Integrates Cardiac Electrophysiology, Mechanics, and Fluid Dynamics: Application to the Human Left Heart. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3678. [Google Scholar]
- Hodgkin, A.L.; Huxley, A.F. A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Ten Tusscher, K.H.W.J.; Panfilov, A.V. Alternans and Spiral Breakup in a Human Ventricular Tissue Model. Am. J. Physiol.-Heart Circ. Physiol. 2006, 291, H1088–H1100. [Google Scholar] [CrossRef]
- Ten Tusscher, K.H.W.J.; Noble, D.; Noble, P.J.; Panfilov, A.V. A Model for Human Ventricular Tissue. Am. J. Physiol.-Heart Circ. Physiol. 2004, 286, H1573–H1589. [Google Scholar] [CrossRef]
- Noble, D. A Modification of the Hodgkin—Huxley Equations Applicable to Purkinje Fibre Action and Pacemaker Potentials. J. Physiol. 1962, 160, 317–352. [Google Scholar] [CrossRef]
- Del Corso, G.; Verzicco, R.; Viola, F. A Fast Computational Model for the Electrophysiology of the Whole Human Heart. J. Comput. Phys. 2022, 457, 111084. [Google Scholar] [CrossRef]
- Nagel, C.; Espinosa, C.B.; Gillette, K.; Gsell, M.A.; Sánchez, J.; Plank, G.; Dössel, O.; Loewe, A. Comparison of Propagation Models and Forward Calculation Methods on Cellular, Tissue and Organ Scale Atrial Electrophysiology. IEEE Trans. Biomed. Eng. 2022, 70, 511–522. [Google Scholar]
- Sovilj, S.; Magjarević, R.; Lovell, N.H.; Dokos, S. A Simplified 3D Model of Whole Heart Electrical Activity and 12-Lead ECG Generation. Comput. Math. Methods Med. 2013, 2013, 134208. [Google Scholar] [CrossRef] [PubMed]
- Sovilj, S.; Magjarević, R.; Al Abed, A.; Lovell, N.H.; Dokos, S. Simplified 2D Bidomain Model of Whole Heart Electrical Activity and ECG Generation. Meas. Sci. Rev. 2014, 14, 136–143. [Google Scholar]
- Biasi, N.; Tognetti, A. Modelling Whole Heart Electrical Activity for Ischemia and Cardiac Pacing Simulation. Health Technol. 2020, 10, 837–850. [Google Scholar] [CrossRef]
- Hoogendoorn, C.; Duchateau, N.; Sanchez-Quintana, D.; Whitmarsh, T.; Sukno, F.M.; De Craene, M.; Lekadir, K.; Frangi, A.F. A High-Resolution Atlas and Statistical Model of the Human Heart from Multislice CT. IEEE Trans. Med. Imaging 2012, 32, 28–44. [Google Scholar]
- Sebastián Aguilar, R.; Ferrer Albero, A.; Saiz Rodríguez, F.J. Human Atria and Torso 3D Computational Models for Simulation of Atrial Arrhythmias. Ph.D. Thesis, Universitat Politècnica de València, València, Spain, 2015. [Google Scholar]
- MacLeod, R.S.; Johnson, C.R.; Ershler, P.R. Construction of an Inhomegeneous Model of the Human Torso for Use in Computational Electrocardiography. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 31 October–3 November 1991; IEEE: Piscataway, NJ, USA, 1991; Volume 13, pp. 688–689. [Google Scholar]
- Hua, Y.; Yeo, D.T.; Foo, T.K. With Human Body Models. In Brain and Human Body Modelling 2021: Selected Papers Presented at 2021 BHBM Conference at Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital; Springer Nature: Berlin/Heidelberg, Germany, 2022; p. 39. [Google Scholar]
- Tung, L. A Bi-Domain Model for Describing Ischemic Myocardial Dc Potentials. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1978. [Google Scholar]
- Khudhur, A.M.; Shano, A.M.; Abbas, A.S.H. A New Neuron Ion Channel Model Under Time Varying Input Currents. J. Phys. Conf. Ser. 2021, 1999, 012127. [Google Scholar] [CrossRef]
- Ivanovic, E.; Kucera, J.P. Localization of Na+ Channel Clusters in Narrowed Perinexi of Gap Junctions Enhances Cardiac Impulse Transmission via Ephaptic Coupling: A Model Study. J. Physiol. 2021, 599, 4779–4811. [Google Scholar] [CrossRef]
- Miller, L.; Penta, R. Homogenization of a Coupled Electrical and Mechanical Bidomain Model for the Myocardium. Math. Mech. Solids 2025, 30, 406–427. [Google Scholar] [CrossRef]
- Zirakashvili, N.; Zirakashvili, T. Study of Action Potential Propagation in Cardiac Tissues Using Cable Theory. Wseas Trans. Biol. Biomed. 2023, 20, 228–239. [Google Scholar]
- Jæger, K.H.; Tveito, A. Derivation of a Cell-Based Mathematical Model of Excitable Cells. In Modeling Excitable Tissue the EMI Framework; Springer: Cham, Switzerland, 2021; pp. 1–13. [Google Scholar]
- FitzHugh, R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.M.; McCulloch, A.D. A Collocation-Galerkin Finite Element Model of Cardiac Action Potential Propagation. IEEE Trans. Biomed. Eng. 1994, 41, 743–757. [Google Scholar] [PubMed]
- Mincholé, A.; Zacur, E.; Ariga, R.; Grau, V.; Rodriguez, B. MRI-Based Computational Torso/Biventricular Multiscale Models to Investigate the Impact of Anatomical Variability on the ECG QRS Complex. Front. Physiol. 2019, 10, 1103. [Google Scholar] [CrossRef] [PubMed]
- Piersanti, R.; Africa, P.C.; Fedele, M.; Vergara, C.; Dedè, L.; Corno, A.F.; Quarteroni, A. Modeling Cardiac Muscle Fibers in Ventricular and Atrial Electrophysiology Simulations. Comput. Methods Appl. Mech. Eng. 2021, 373, 113468. [Google Scholar]
- Berkaya, S.K.; Uysal, A.K.; Gunal, E.S.; Ergin, S.; Gunal, S.; Gulmezoglu, M.B. A Survey on ECG Analysis. Biomed. Signal Process. Control. 2018, 43, 216–235. [Google Scholar] [CrossRef]
- Harris, P.R. The Normal Electrocardiogram: Resting 12-Lead and Electrocardiogram Monitoring in the Hospital. Crit. Care Nurs. Clin. 2016, 28, 281–296. [Google Scholar]
- Corral-Acero, J.; Margara, F.; Marciniak, M.; Rodero, C.; Loncaric, F.; Feng, Y.; Gilbert, A.; Fernandes, J.F.; Bukhari, H.A.; Wajdan, A.; et al. The ‘Digital Twin’ to Enable the Vision of Precision Cardiology. Eur. Heart J. 2020, 41, 4556–4564. [Google Scholar] [CrossRef]
- Shou, G.; Xia, L.; Jiang, M.; Wei, Q.; Liu, F.; Crozier, S. Solving the ECG Forward Problem by Means of Standard H- and h-Hierarchical Adaptive Linear Boundary Element Method: Comparison with Two Refinement Schemes. IEEE Trans. Biomed. Eng. 2009, 56, 1454–1464. [Google Scholar] [CrossRef]
- Abdelazez, M.; Rajan, S.; Chan, A.D. Detection of Atrial Fibrillation in Compressively Sensed Electrocardiogram Measurements. IEEE Trans. Instrum. Meas. 2020, 70, 1–9. [Google Scholar] [CrossRef]
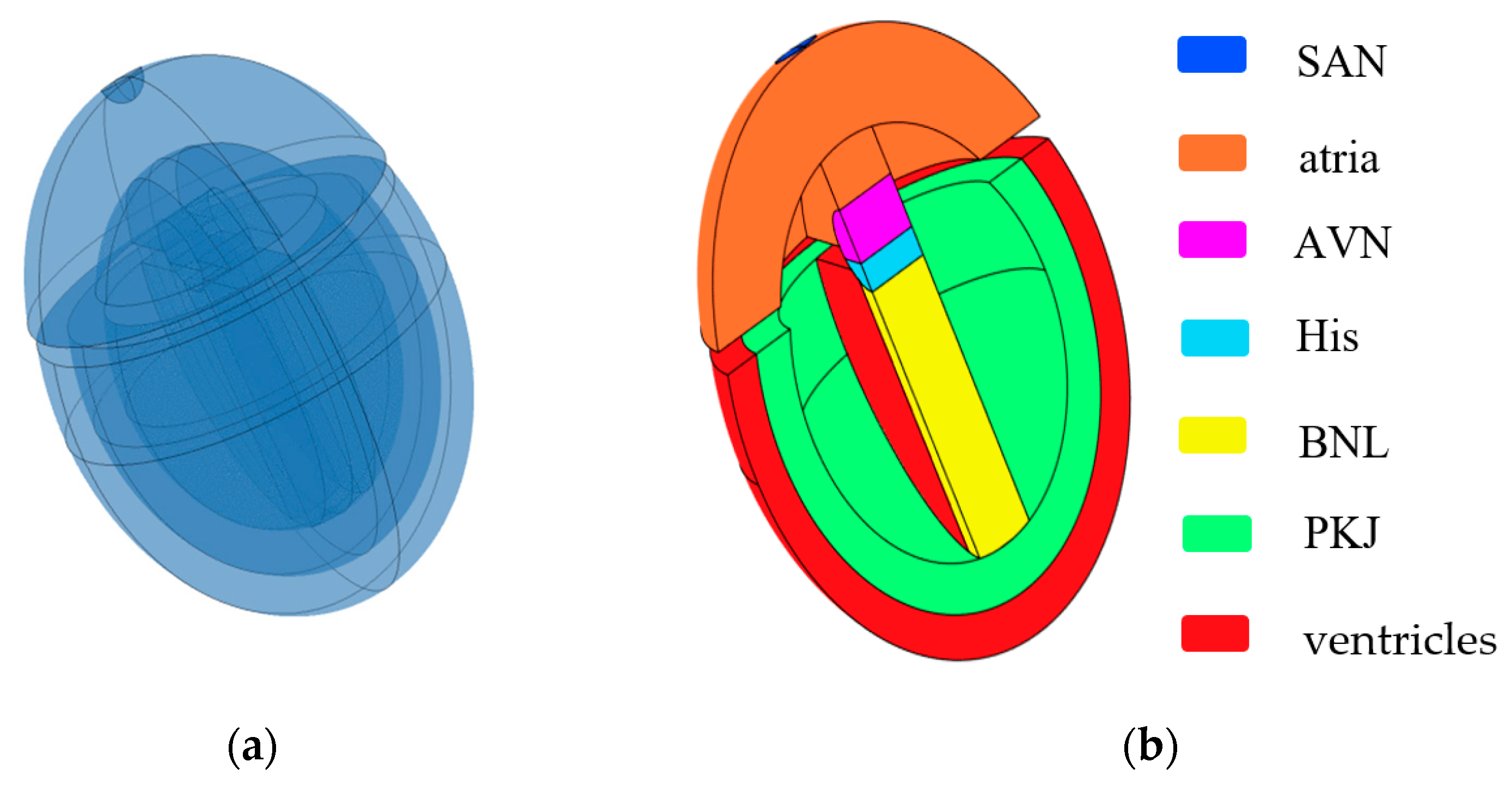
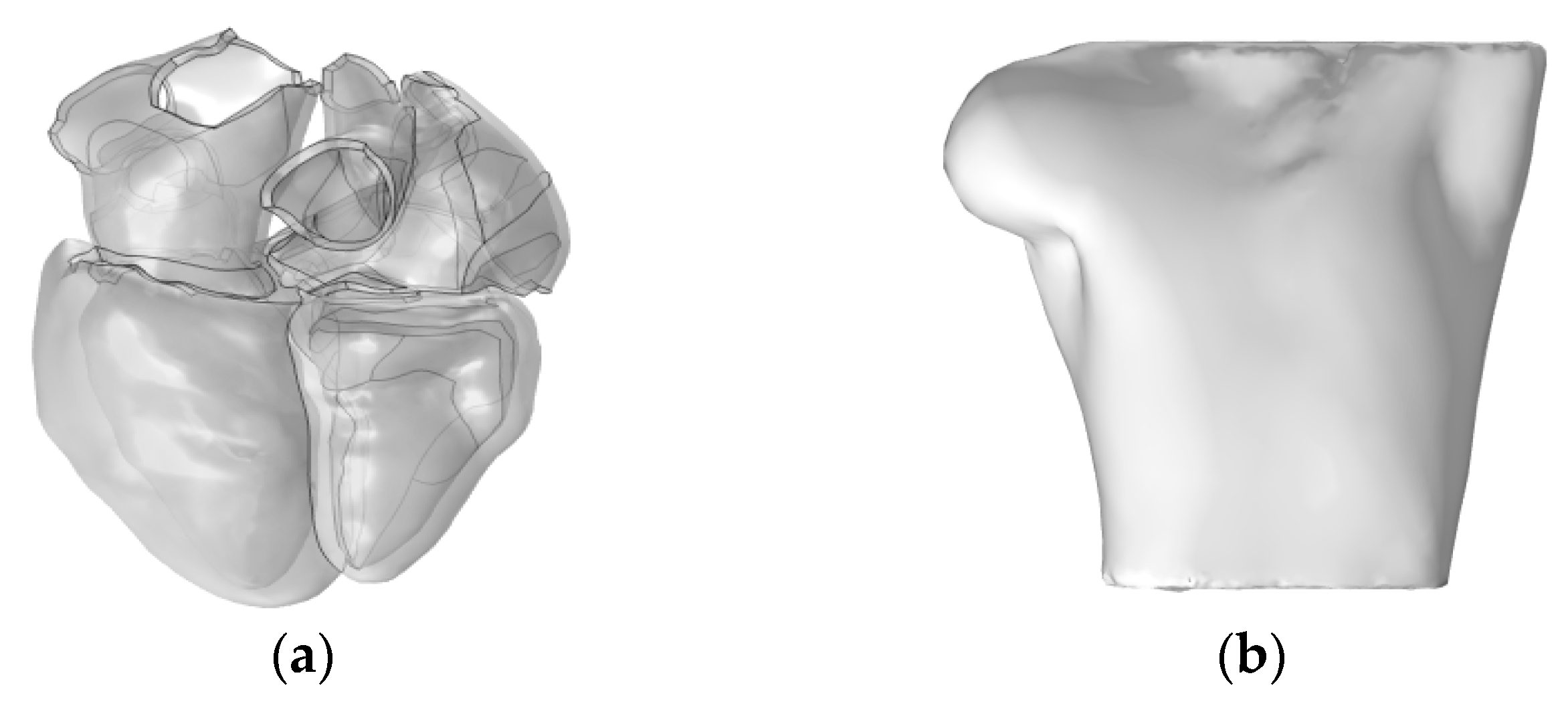




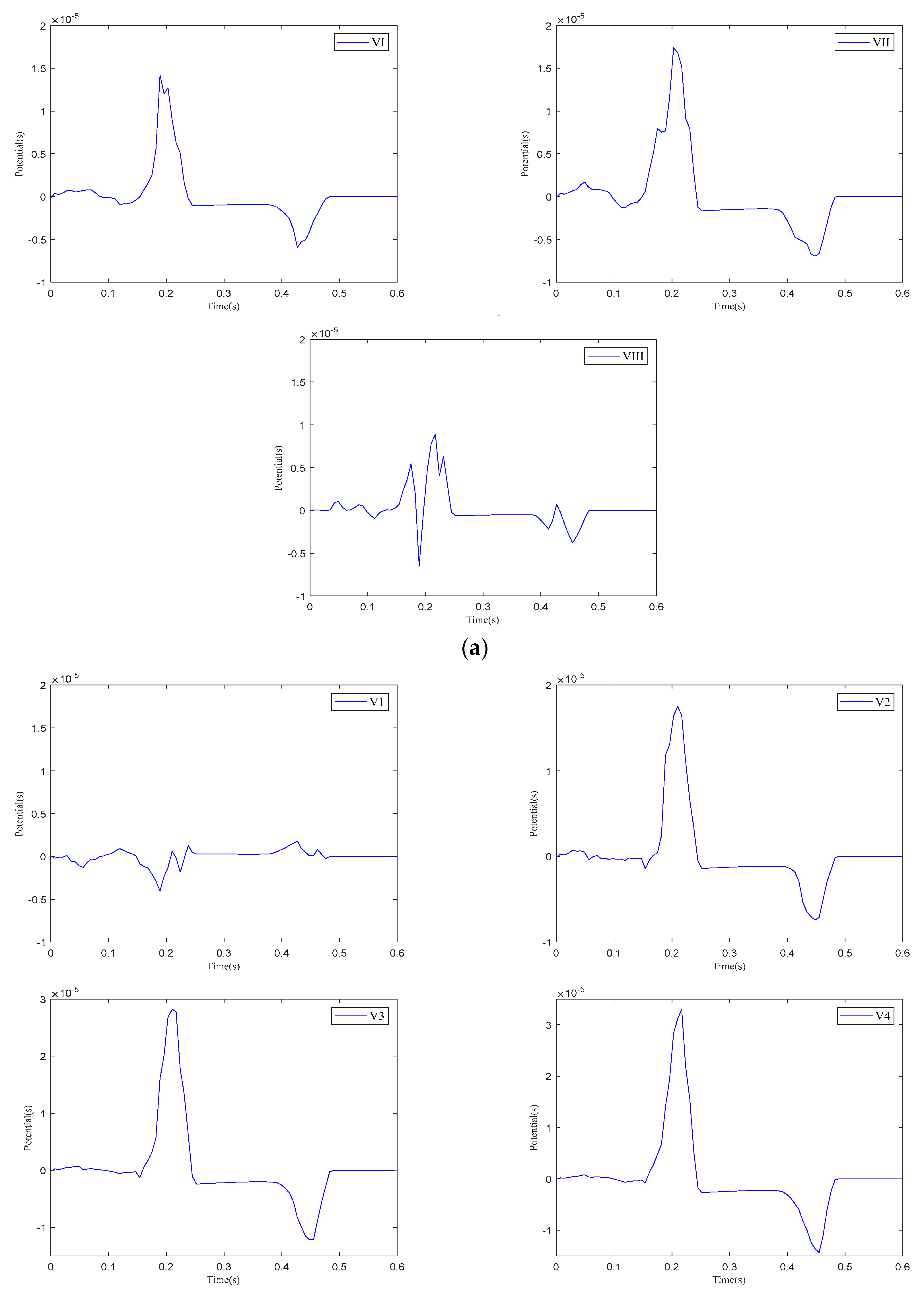


| Parameter | SAN | Atria | AVN | His | BNL | PKJ | Ventricles | Reference |
|---|---|---|---|---|---|---|---|---|
| −0.60 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | Model 1 [14] | |
| −0.30 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1000 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | ||
| 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | ||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0.0660 | 0.0132 | 0.0132 | 0.0050 | 0.0022 | 0.0047 | 0.0060 | ||
| (m V) | 33 | 140 | 140 | 140 | 140 | 140 | 140 | |
| (m V) | −22 | −85 | −85 | −85 | −85 | −85 | −85 | |
| (s−1) | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | |
| (m S·m−1) | 0.5 | 8 | 0.5 | 10 | 15 | 35 | 8 | |
| (m S·m−1) | 0.5 | 8 | 0.5 | 10 | 15 | 35 | 8 | |
| −1 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | Model 2 [15] | |
| −0.29 × 10−3 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1.9 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | ||
| 1 × 10−3 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | ||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0.060 | 0.010 | 0.010 | 0.0045 | 0.0028 | 0.0043 | 0.0050 | ||
| (m V) | 35 | 140 | 140 | 140 | 140 | 140 | 140 | |
| (m V) | −30 | −85 | −85 | −85 | −85 | −85 | −85 | |
| (s−1) | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | |
| (m S·m−1) | 0.5 | 8 | 0.5 | 10 | 15 | 35 | 8 | |
| (m S·m−1) | 0.5 | 8 | 0.5 | 10 | 15 | 35 | 8 | |
| −1 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | Model 3 [16] | |
| −0.29 × 10−3 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1.9 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | ||
| 1 × 10−3 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | ||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0.035 | 0.020 | 0.010 | 0.0045 | 0.0028 | 0.0043 | 0.0050 | ||
| (m V) | 35 | 140 | 140 | 140 | 140 | 140 | 140 | |
| (m V) | −30 | −85 | −85 | −85 | −85 | −85 | −85 | |
| (s−1) | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | |
| (m S·m−1) | 0.5 | 4 | 0.5 | 10 | 15 | 35 | 4 | |
| (m S·m−1) | 0.5 | 4 | 0.5 | 10 | 15 | 35 | 4 |
| Test Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Heart domain mesh setting | Fine | Finer | Finer | Fine |
| Torso domain mesh setting | Normal | Normal | Fine | Fine |
| Left ventricular epicardial transmembrane potential (V) | 0.053 | 0.0531 | 0.053 | 0.053 |
| Relative error (%) | - | 0.2 | 0.2 | 0 |
| Left ventricular endocardial transmembrane potential (V) | 0.0526 | 0.0526 | 0.0526 | 0.0526 |
| Relative error (%) | - | 0 | 0 | 0 |
| P-wave amplitude (10−5 V) | 0.0713 | 0.0716 | 0.0903 | 0.0903 |
| Relative error (%) | - | 0.4 | 20.71 | 21.04 |
| QRS-wave amplitude (10−5 V) | 3.1229 | 3.1104 | 3.7194 | 3.7194 |
| Relative error (%) | - | 0.4 | 16.37 | 16.04 |
| T-wave amplitude (10−5 V) | −1.3451 | −1.3462 | −1.5295 | −1.5295 |
| Relative error (%) | - | 0.08 | 11.98 | 12.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Cao, Y.; Li, P.; Yang, Y.; Xiang, M. Computational Modeling of Cardiac Electrophysiology with Human Realistic Heart–Torso Model. Bioengineering 2025, 12, 392. https://doi.org/10.3390/bioengineering12040392
Yang C, Cao Y, Li P, Yang Y, Xiang M. Computational Modeling of Cardiac Electrophysiology with Human Realistic Heart–Torso Model. Bioengineering. 2025; 12(4):392. https://doi.org/10.3390/bioengineering12040392
Chicago/Turabian StyleYang, Chen, Yidi Cao, Peilun Li, Yanfei Yang, and Min Xiang. 2025. "Computational Modeling of Cardiac Electrophysiology with Human Realistic Heart–Torso Model" Bioengineering 12, no. 4: 392. https://doi.org/10.3390/bioengineering12040392
APA StyleYang, C., Cao, Y., Li, P., Yang, Y., & Xiang, M. (2025). Computational Modeling of Cardiac Electrophysiology with Human Realistic Heart–Torso Model. Bioengineering, 12(4), 392. https://doi.org/10.3390/bioengineering12040392







