Simulation of the Diffusion Characteristics of Multifunctional Nanocarriers in Tumor Tissues Using Lattice Gas Automata and the Lattice Boltzmann Method
Abstract
1. Introduction
2. Modeling and Methods
2.1. Coupled Double-Distribution Function Model for Flow and Temperature Fields
2.2. Modeling of NP Movement
2.3. Model Validation
3. Results and Analysis
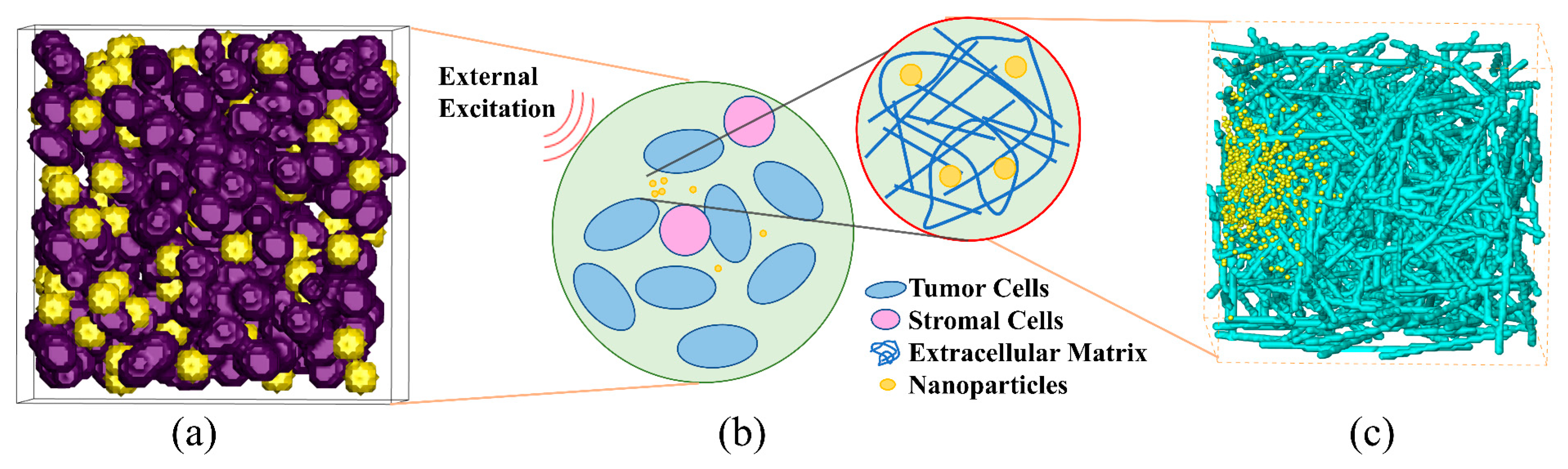
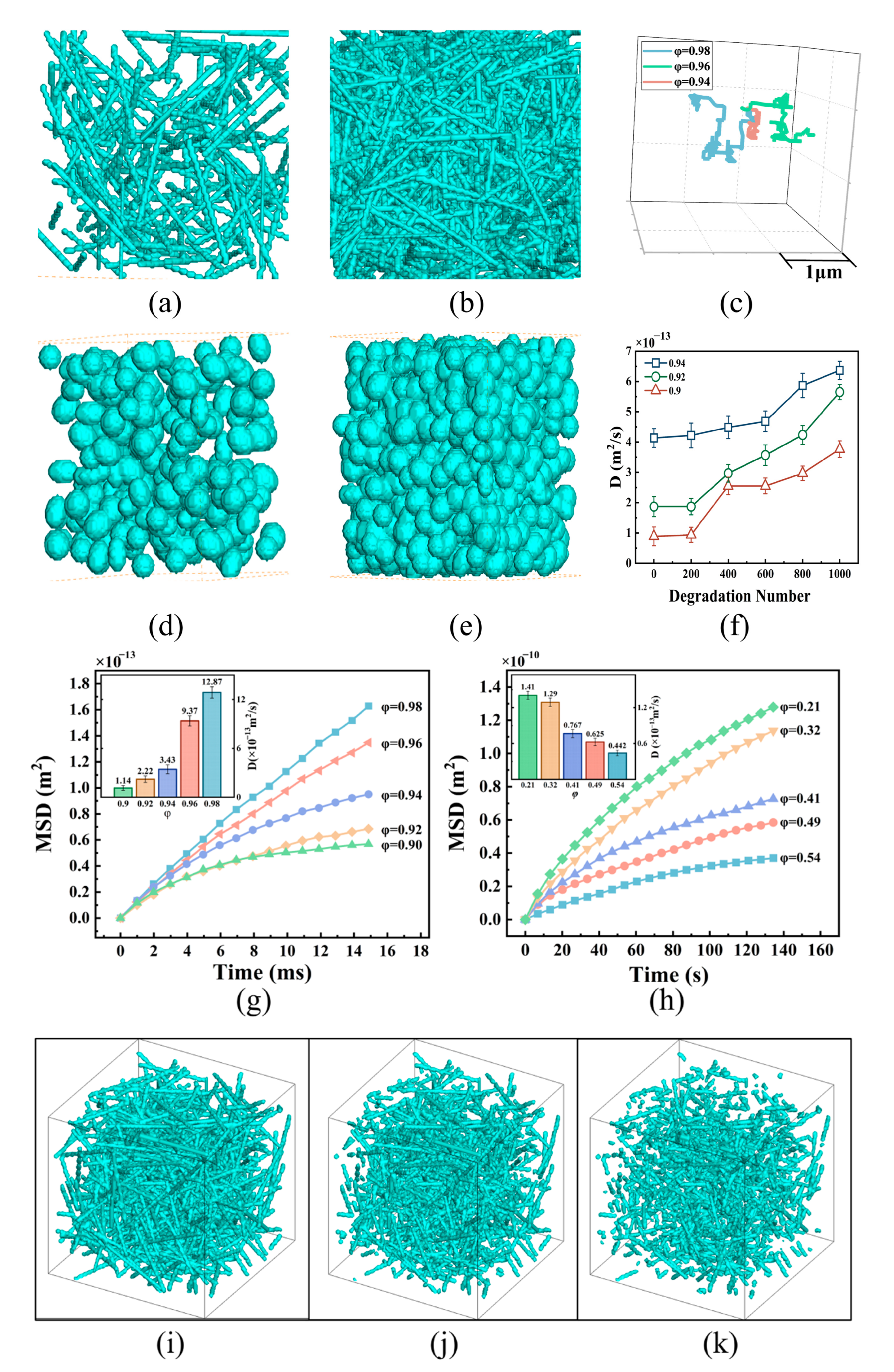
3.1. NP Diffusion in Tumor Tissues with Different Structures
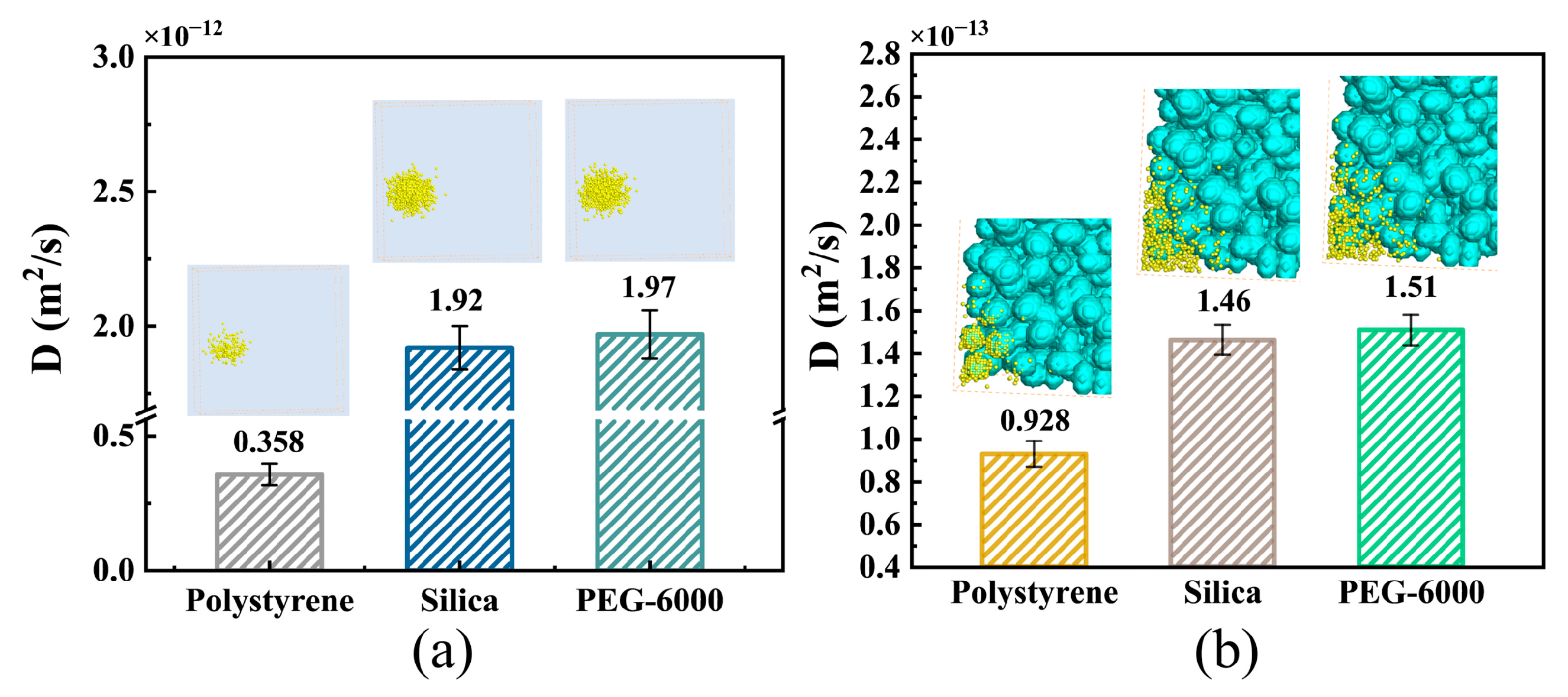
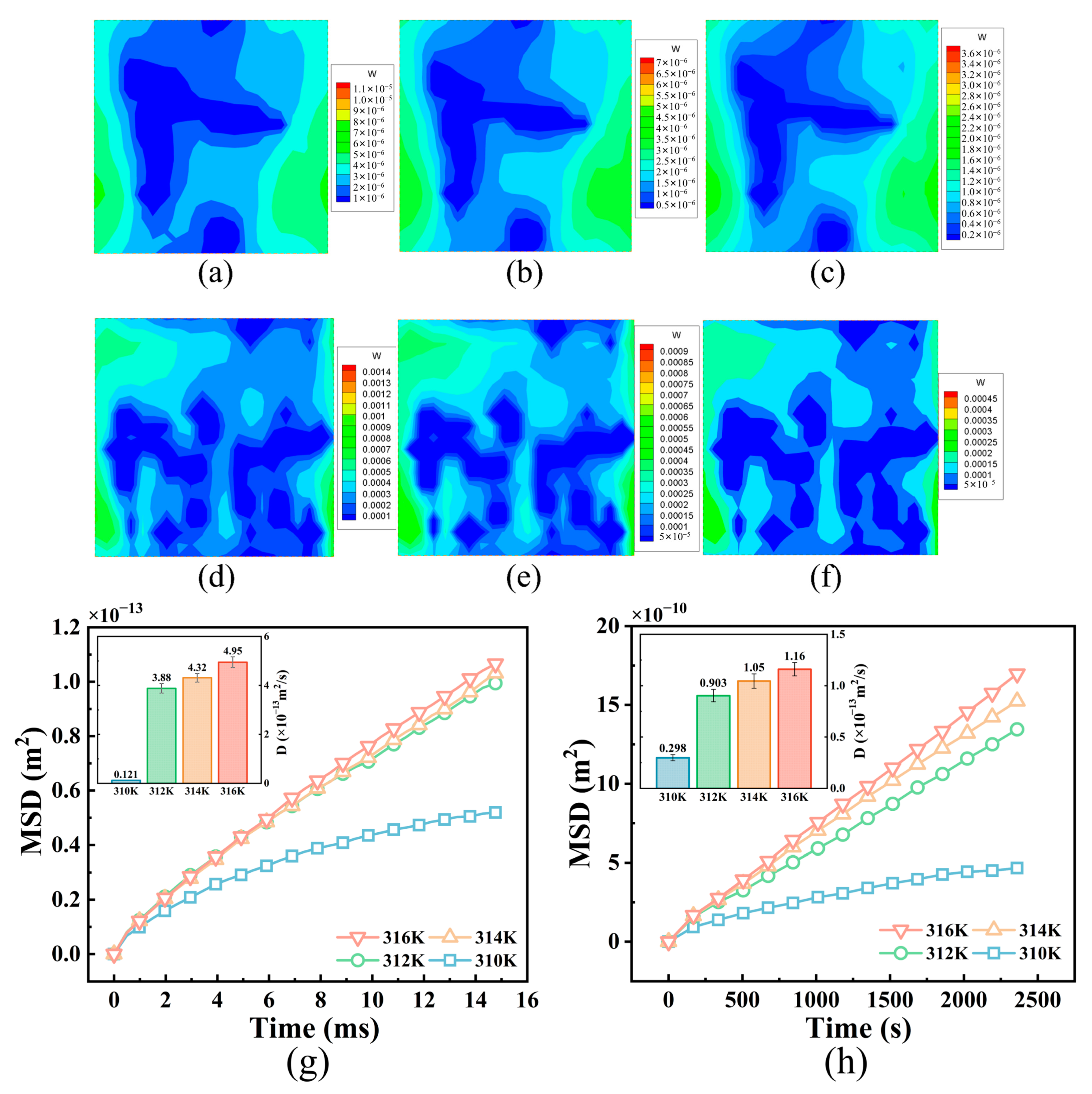
3.2. Effects of NP Surface Properties
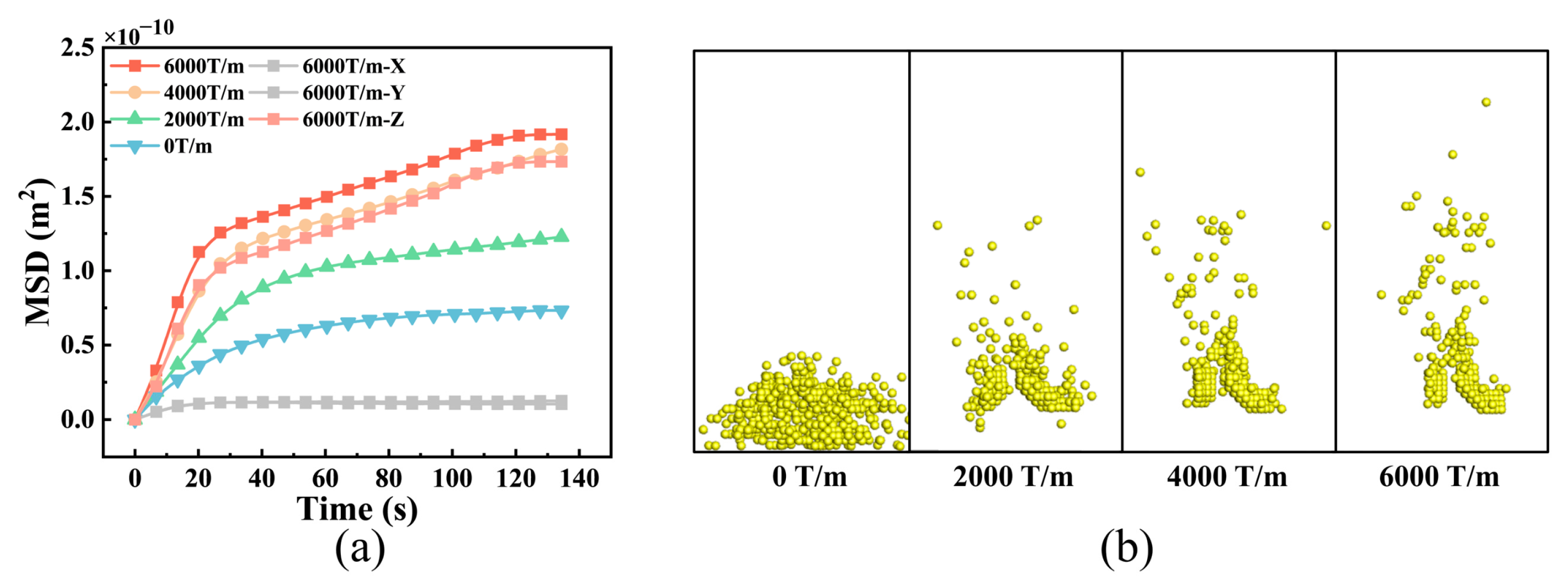
3.3. Changes in NP Diffusion Caused by External Fields
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NP | nanoparticle |
| ECM | extracellular matrix |
| LBM | lattice Boltzmann method |
| LGA | lattice gas automata |
| MSD | mean-square displacement |
References
- Chauvierre, C.; Labarre, D.; Couvreur, P.; Vauthier, C. Novel polysaccharide-decorated poly (isobutyl cyanoacrylate) nanoparticles. Pharm. Res. 2003, 20, 1786–1793. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.; Han, Y.; Gao, S.; Yan, H.; Cao, L.; Li, Z.; Liang, X.-J.; Zhang, J. Ultrasmall gold nanoparticles in cancer diagnosis and therapy. Theranostics 2020, 10, 4944. [Google Scholar] [CrossRef]
- Pallares, R.M.; Mottaghy, F.M.; Schulz, V.; Kiessling, F.; Lammers, T. Nanoparticle diagnostics and theranostics in the clinic. J. Nucl. Med. 2022, 63, 1802–1808. [Google Scholar] [CrossRef] [PubMed]
- Siddique, S.; Chow, J.C. Recent advances in functionalized nanoparticles in cancer theranostics. Nanomaterials 2022, 12, 2826. [Google Scholar] [CrossRef]
- Siddique, S.; Chow, J.C. Application of nanomaterials in biomedical imaging and cancer therapy. Nanomaterials 2020, 10, 1700. [Google Scholar] [CrossRef]
- Mitragotri, S.; Lahann, J. Physical approaches to biomaterial design. Nat. Mater. 2009, 8, 15–23. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Wang, X.; Nie, S.; Chen, Z.; Shin, D.M. Therapeutic nanoparticles for drug delivery in cancer. Clin. Cancer Res. 2008, 14, 1310–1316. [Google Scholar] [CrossRef] [PubMed]
- Farokhzad, O.C.; Langer, R. Nanomedicine: Developing smarter therapeutic and diagnostic modalities. Adv. Drug Deliv. Rev. 2006, 58, 1456–1459. [Google Scholar] [CrossRef]
- Golovin, Y.I.; Gribanovsky, S.L.; Golovin, D.Y.; Klyachko, N.L.; Majouga, A.G.; Master, A.M.; Sokolsky, M.; Kabanov, A.V. Towards nanomedicines of the future: Remote magneto-mechanical actuation of nanomedicines by alternating magnetic fields. J. Control. Release 2015, 219, 43–60. [Google Scholar] [CrossRef]
- Chow, J.C. Biophysical insights into nanomaterial-induced DNA damage: Mechanisms, challenges, and future directions. AIMS Biophys. 2024, 11, 340–369. [Google Scholar] [CrossRef]
- McGuire, S.; Yuan, F. Improving interstitial transport of macromolecules through reduction in cell volume fraction in tumor tissues. Nanomed. Nanotechnol. Biol. Med. 2012, 8, 1088–1095. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, X.; Yuan, H.; Yang, Z.; von Roemeling, C.A.; Qie, Y.; Zhao, H.; Wang, Y.; Jiang, W.; Kim, B.Y. Therapeutic remodeling of the tumor microenvironment enhances nanoparticle delivery. Adv. Sci. 2019, 6, 1802070. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Han, H.; Koo, H.; Na, J.H.; Yoon, H.Y.; Lee, K.E.; Lee, H.; Kim, H.; Kwon, I.C.; Kim, K. Extracellular matrix remodeling in vivo for enhancing tumor-targeting efficiency of nanoparticle drug carriers using the pulsed high intensity focused ultrasound. J. Control. Release 2017, 263, 68–78. [Google Scholar] [CrossRef]
- Le Goas, M.; Testard, F.; Taché, O.; Debou, N.; Cambien, B.; Carrot, G.; Renault, J.-P. How do surface properties of nanoparticles influence their diffusion in the extracellular matrix? A model study in Matrigel using polymer-grafted nanoparticles. Langmuir 2020, 36, 10460–10470. [Google Scholar] [CrossRef]
- Mohanty, R.P.; Liu, X.; Ghosh, D. Electrostatic driven transport enhances penetration of positively charged peptide surfaces through tumor extracellular matrix. Acta Biomater. 2020, 113, 240–251. [Google Scholar] [CrossRef]
- Gu, Q.; Dockery, L.; Daniel, M.-C.; Bieberich, C.J.; Ma, R.; Zhu, L. Nanoparticle delivery in prostate tumors implanted in mice facilitated by either local or whole-body heating. Fluids 2021, 6, 272. [Google Scholar] [CrossRef]
- Wan, M.; Wang, Q.; Li, X.; Xu, B.; Fang, D.; Li, T.; Yu, Y.; Fang, L.; Wang, Y.; Wang, M. Systematic research and evaluation models of nanomotors for cancer combined therapy. Angew. Chem. Int. Ed. 2020, 59, 14458–14465. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-X.; Zuo, Z.-Q.; Du, J.-Z.; Wang, Y.-C.; Sun, R.; Cao, Z.-T.; Ye, X.-D.; Wang, J.-L.; Leong, K.W.; Wang, J. Surface charge critically affects tumor penetration and therapeutic efficacy of cancer nanomedicines. Nano Today 2016, 11, 133–144. [Google Scholar] [CrossRef]
- Jin, S.; Ma, X.; Ma, H.; Zheng, K.; Liu, J.; Hou, S.; Meng, J.; Wang, P.C.; Wu, X.; Liang, X.-J. Surface chemistry-mediated penetration and gold nanorod thermotherapy in multicellular tumor spheroids. Nanoscale 2013, 5, 143–146. [Google Scholar] [CrossRef]
- White, B.E.; White, M.K.; Adhvaryu, H.; Makhoul, I.; Nima, Z.A.; Biris, A.S.; Ali, N. Nanotechnology approaches to addressing HER2-positive breast cancer. Cancer Nanotechnol. 2020, 11, 12. [Google Scholar] [CrossRef]
- Munir, M.U. Nanomedicine penetration to tumor: Challenges, and advanced strategies to tackle this issue. Cancers 2022, 14, 2904. [Google Scholar] [CrossRef]
- Priwitaningrum, D.L.; Blondé, J.-B.G.; Sridhar, A.; van Baarlen, J.; Hennink, W.E.; Storm, G.; Le Gac, S.; Prakash, J. Tumor stroma-containing 3D spheroid arrays: A tool to study nanoparticle penetration. J. Control. Release 2016, 244, 257–268. [Google Scholar] [CrossRef]
- Pratiwi, F.W.; Peng, C.-C.; Wu, S.-H.; Kuo, C.W.; Mou, C.-Y.; Tung, Y.-C.; Chen, P. Evaluation of nanoparticle penetration in the tumor spheroid using two-photon microscopy. Biomedicines 2020, 9, 10. [Google Scholar] [CrossRef] [PubMed]
- Golneshan, A.A.; Lahonian, M. Diffusion of magnetic nanoparticles in a multi-site injection process within a biological tissue during magnetic fluid hyperthermia using lattice Boltzmann method. Mech. Res. Commun. 2011, 38, 425–430. [Google Scholar] [CrossRef]
- Fatemi, B.; Halcrow, J.; Jaqaman, K. Geometric deep learning of particle motion by magik. Nat. Mach. Intell. 2023, 5, 483–484. [Google Scholar] [CrossRef]
- Sego, T.; Sluka, J.P.; Sauro, H.M.; Glazier, J.A. Tissue forge: Interactive biological and biophysics simulation environment. PLOS Comput. Biol. 2023, 19, e1010768. [Google Scholar] [CrossRef]
- Kutumova, E.; Akberdin, I.; Kiselev, I.; Sharipov, R.; Kolpakov, F. Modular representation of physiologically based pharmacokinetic models: Nanoparticle delivery to solid tumors in mice as an example. Mathematics 2022, 10, 1176. [Google Scholar] [CrossRef]
- Yuan, T.; Gao, L.; Zhan, W.; Dini, D. Effect of particle size and surface charge on nanoparticles diffusion in the brain white matter. Pharm. Res. 2022, 39, 767–781. [Google Scholar] [CrossRef]
- Corbetta, A.; Gabbana, A.; Gyrya, V.; Livescu, D.; Prins, J.; Toschi, F. Toward learning Lattice Boltzmann collision operators. Eur. Phys. J. E 2023, 46, 10. [Google Scholar] [CrossRef]
- Coreixas, C.; Wissocq, G.; Chopard, B.; Latt, J. Impact of collision models on the physical properties and the stability of lattice Boltzmann methods. Philos. Trans. R. Soc. A 2020, 378, 20190397. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Its Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Li, R.; Wang, Z.; Dong, H.; Yang, M.; Sun, X.; Zong, Q.; Xu, Z. Lattice Boltzmann modeling of the effective thermal conductivity in plant fiber porous media generated by Quartet Structure Generation Set. Mater. Des. 2023, 234, 112303. [Google Scholar] [CrossRef]
- Jiang, D.; Zhao, P.; Lu, Y.; Yi, Y.; Wu, B.; Tang, W. Numerical study on elliptical pillars with different angles-of-inclination in deterministic lateral displacement microfluidic channel based on lattice Boltzmann method. Microchem. J. 2025, 211, 113056. [Google Scholar] [CrossRef]
- Jannati, K.; Rahimian, M.-H.; Raisee, M.; Jafari, A. Investigating Cell-Induced Mixing Dynamics in Microfluidic Droplets Using the Lattice Boltzmann Method. Langmuir 2025, 41, 2386–2399. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Luo, L.-S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811. [Google Scholar] [CrossRef]
- Masselot, A.; Chopard, B. A lattice Boltzmann model for particle transport and deposition. Europhys. Lett. 1998, 42, 259. [Google Scholar] [CrossRef]
- Tian, X.; Yue, K.; You, Y.; Niu, Y.; Zhang, X. Lattice Boltzmann Simulation of Nanoparticle Transport and Attachment in a Microchannel Heat Sink. Fluid Dyn. Mater. Process. 2021, 17, 301–317. [Google Scholar] [CrossRef]
- Gaber, M.; Ribeiro, R.H.; Kozicki, J. From flow to jamming: Lattice Gas Automaton simulations in granular materials. Powder Technol. 2024, 433, 119283. [Google Scholar] [CrossRef]
- Cherry, E.M.; Maxim, P.G.; Eaton, J.K. Particle size, magnetic field, and blood velocity effects on particle retention in magnetic drug targeting. Med. Phys. 2010, 37, 175–182. [Google Scholar] [CrossRef]
- Pick, C.M. Electrical Double Layer Interactions with Surface Charge Heterogeneities. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2015. [Google Scholar]
- van der Hoef, M.A.; Beetstra, R.; Kuipers, J. Lattice-Boltzmann simulations of low-Reynolds-number flow past mono-and bidisperse arrays of spheres: Results for the permeability and drag force. J. Fluid Mech. 2005, 528, 233–254. [Google Scholar] [CrossRef]
- Nakayama, A.; Ando, K.; Yang, C.; Sano, Y.; Kuwahara, F.; Liu, J. A study on interstitial heat transfer in consolidated and unconsolidated porous media. Heat Mass Transf. 2009, 45, 1365–1372. [Google Scholar] [CrossRef]
- Cahn, D.; Stern, A.; Buckenmeyer, M.; Wolf, M.; Duncan, G.A. Extracellular Matrix Limits Nanoparticle Diffusion and Cellular Uptake in a Tissue-Specific Manner. ACS Nano 2024, 18, 32045–32055. [Google Scholar] [CrossRef]
- Kwak, B.; Ozcelikkale, A.; Shin, C.S.; Park, K.; Han, B. Simulation of complex transport of nanoparticles around a tumor using tumor-microenvironment-on-chip. J. Control. Release 2014, 194, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Raeesi, V.; Chan, W.C.W. Improving nanoparticle diffusion through tumor collagen matrix by photo-thermal gold nanorods. Nanoscale 2016, 8, 12524–12530. [Google Scholar] [CrossRef] [PubMed]
- Vasudevan, J.; Jiang, K.; Fernandez, J.G.; Lim, C.T. Extracellular matrix mechanobiology in cancer cell migration. Acta Biomater. 2023, 163, 351–364. [Google Scholar] [CrossRef]
- Marangio, A.; Biccari, A.; D’Angelo, E.; Sensi, F.; Spolverato, G.; Pucciarelli, S.; Agostini, M. The study of the extracellular matrix in chronic inflammation: A way to prevent cancer initiation? Cancers 2022, 14, 5903. [Google Scholar] [CrossRef]
- Zhou, Q.; Shao, S.; Wang, J.; Xu, C.; Xiang, J.; Piao, Y.; Zhou, Z.; Yu, Q.; Tang, J.; Liu, X. Enzyme-activatable polymer–drug conjugate augments tumour penetration and treatment efficacy. Nat. Nanotechnol. 2019, 14, 799–809. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Peng, F.; Shi, X.; Leong, D.T. Targeting endothelial cell junctions with negatively charged gold nanoparticles. Chem. Mater. 2018, 30, 3759–3767. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Yue, K.; Yan, X.; Zhang, X.; Yuan, C.; Wang, L.; Wang, H. Enhancement and characterization of nanoparticle diffusion in biological tissues by magnetic heating and oscillation. J. Control. Release 2025, 380, 725–735. [Google Scholar] [CrossRef]
- Klumpp, S.; Lefèvre, C.T.; Bennet, M.; Faivre, D. Swimming with magnets: From biological organisms to synthetic devices. Phys. Rep. 2019, 789, 1–54. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Yue, K.; Yu, X.; You, Y.; Yang, C.; Zhang, X. Simulation of the Diffusion Characteristics of Multifunctional Nanocarriers in Tumor Tissues Using Lattice Gas Automata and the Lattice Boltzmann Method. Bioengineering 2025, 12, 429. https://doi.org/10.3390/bioengineering12040429
Qin Y, Yue K, Yu X, You Y, Yang C, Zhang X. Simulation of the Diffusion Characteristics of Multifunctional Nanocarriers in Tumor Tissues Using Lattice Gas Automata and the Lattice Boltzmann Method. Bioengineering. 2025; 12(4):429. https://doi.org/10.3390/bioengineering12040429
Chicago/Turabian StyleQin, Yuming, Kai Yue, Xiaoling Yu, Yu You, Chao Yang, and Xinxin Zhang. 2025. "Simulation of the Diffusion Characteristics of Multifunctional Nanocarriers in Tumor Tissues Using Lattice Gas Automata and the Lattice Boltzmann Method" Bioengineering 12, no. 4: 429. https://doi.org/10.3390/bioengineering12040429
APA StyleQin, Y., Yue, K., Yu, X., You, Y., Yang, C., & Zhang, X. (2025). Simulation of the Diffusion Characteristics of Multifunctional Nanocarriers in Tumor Tissues Using Lattice Gas Automata and the Lattice Boltzmann Method. Bioengineering, 12(4), 429. https://doi.org/10.3390/bioengineering12040429







