An Improved Cole–Cole Model for Characterizing In Vivo Dielectric Properties of Lung Tissue at Different Tide Volumes: An Animal Study
Abstract
:1. Introduction
2. Methods
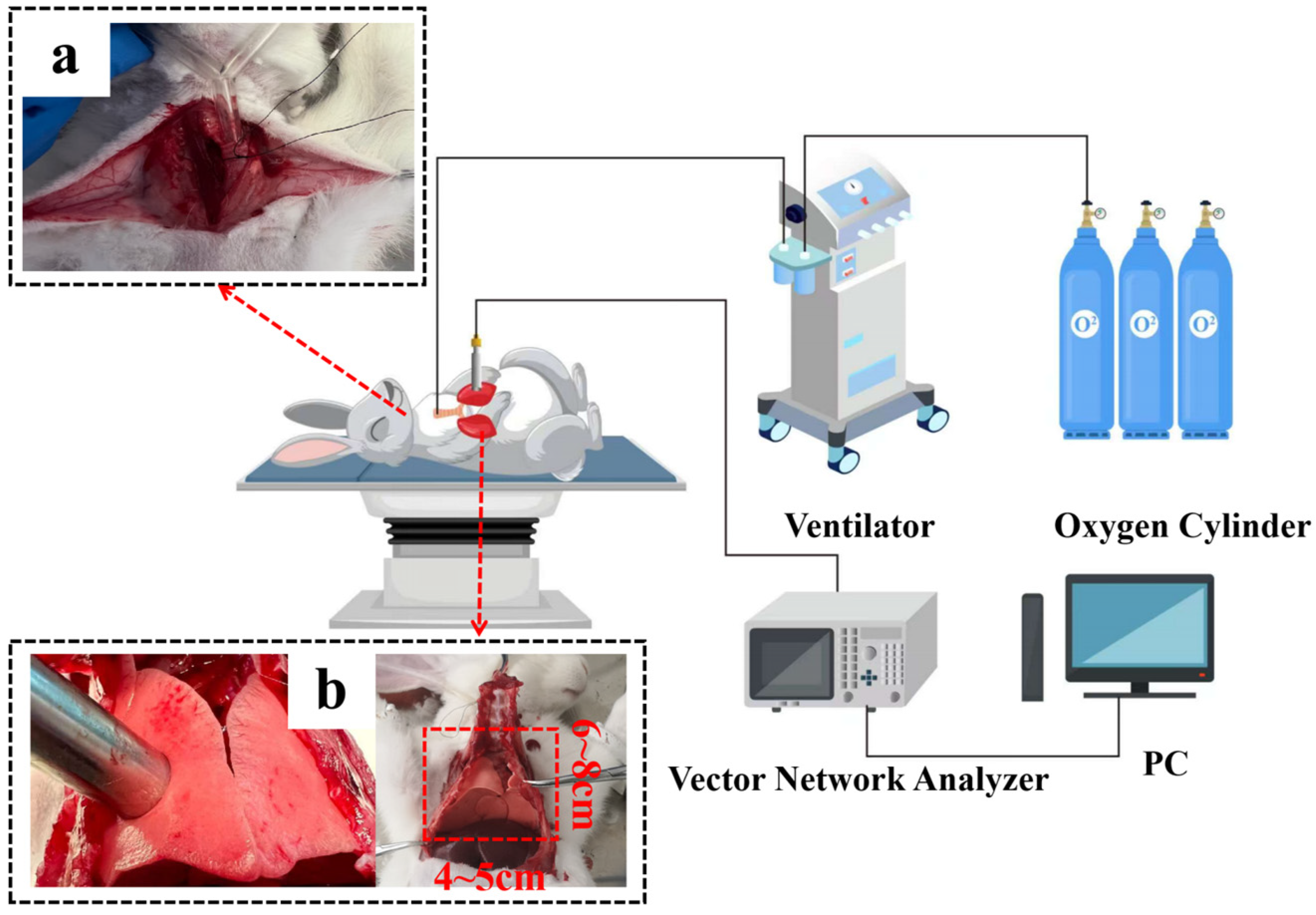
2.1. Measurement System and Accuracy Verification
2.1.1. Setup of the Measurement System
2.1.2. Methods of System Accuracy Verification
- (1)
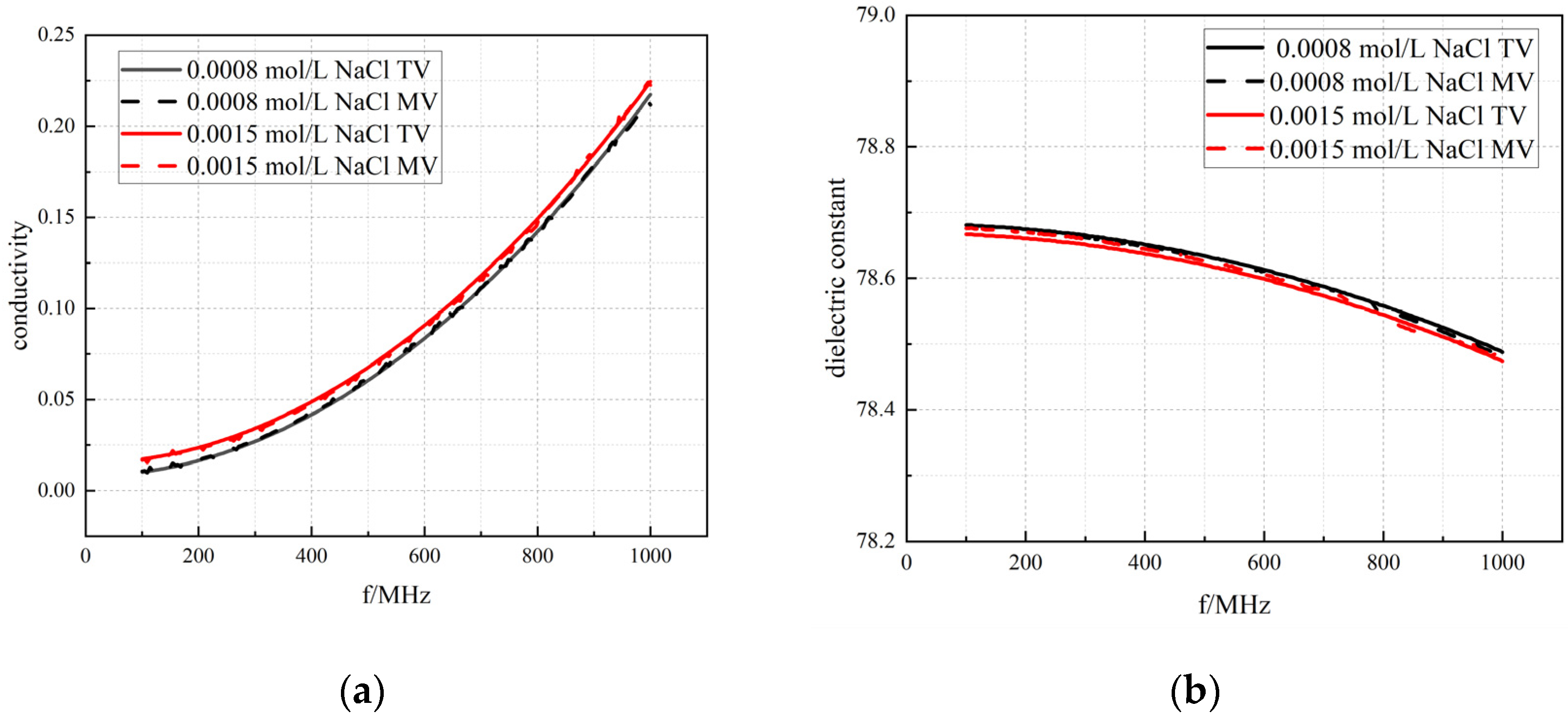
- The accuracy of the measurement system is verified using a standard sample of NaCl (sodium chloride) solution with known properties, which provides a reliable reference for calibrating the measurement equipment due to its stable conductivity and permittivity at different concentrations [27]. By comparing experimental data with theoretical values, the accuracy of the measurement system can be evaluated. Since the closer the calibration solution is to the dielectric properties of the tissue, the better the calibration effect is, three NaCl solutions with concentrations of 0.001, 0.0015, and 0.0008 mol/L were selected for the measurement.
- (2)
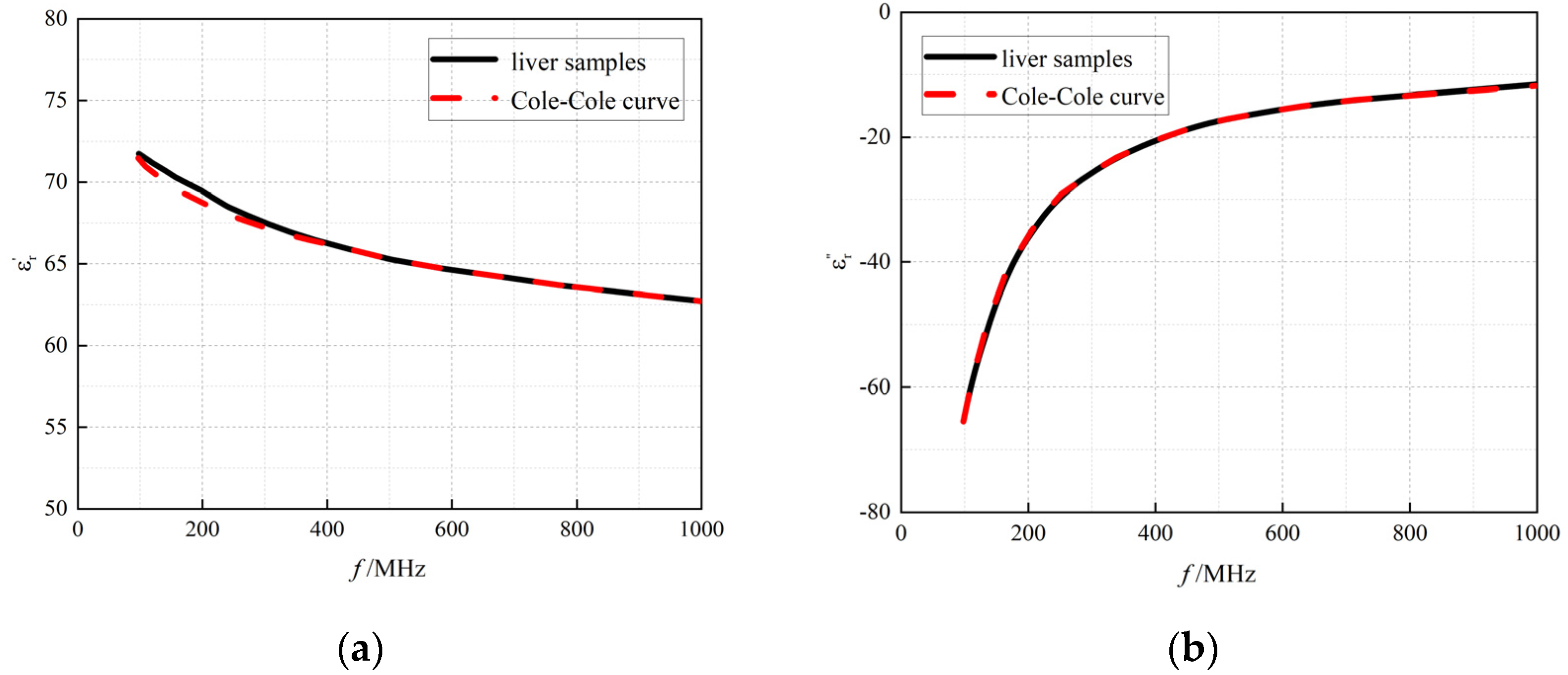
- Ex vivo porcine liver was selected to verify the reliability of the measurement system. This is because porcine liver tissue has stable dielectric properties and is often used as a reference standard in biological tissue studies [28], and its tissue structure and physiological properties are different from those of lung tissue, so that the influence of the air on the measurement results can be excluded. The same experimental set-up and procedures were maintained, and 10 replicates of the experiment were performed using isolated porcine liver tissue.
2.2. The Procedures of Rabbit Lung Measurement
2.3. Data Analysis
2.3.1. Cole–Cole Model
2.3.2. An Improved Cole–Cole Model Considering Air Content
2.3.3. Fitting Effect of the Models
2.3.4. Statistical Analysis
3. Results
3.1. Results of System Accuracy Verification
3.1.1. Measurement of Standard Solutions
3.1.2. Measurement of Ex Vivo Porcine Liver
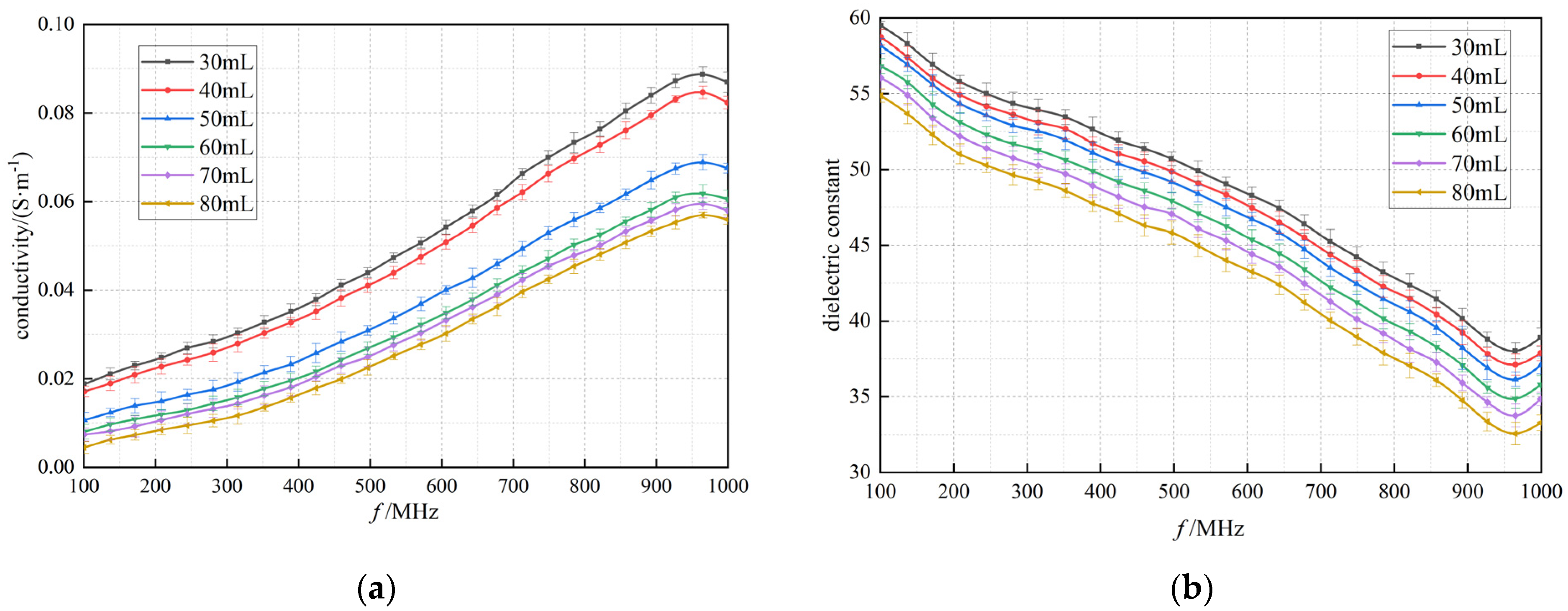
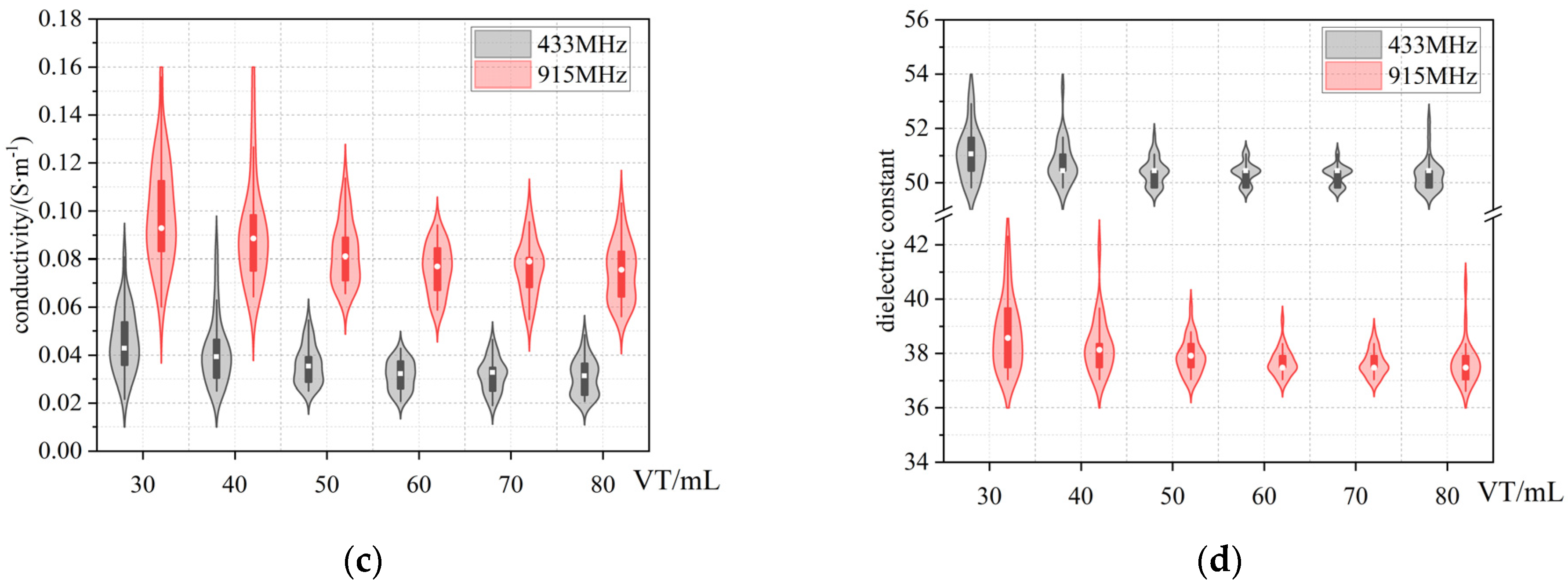
3.2. Dielectric Properties of Lung Tissue with Changing Air Volume
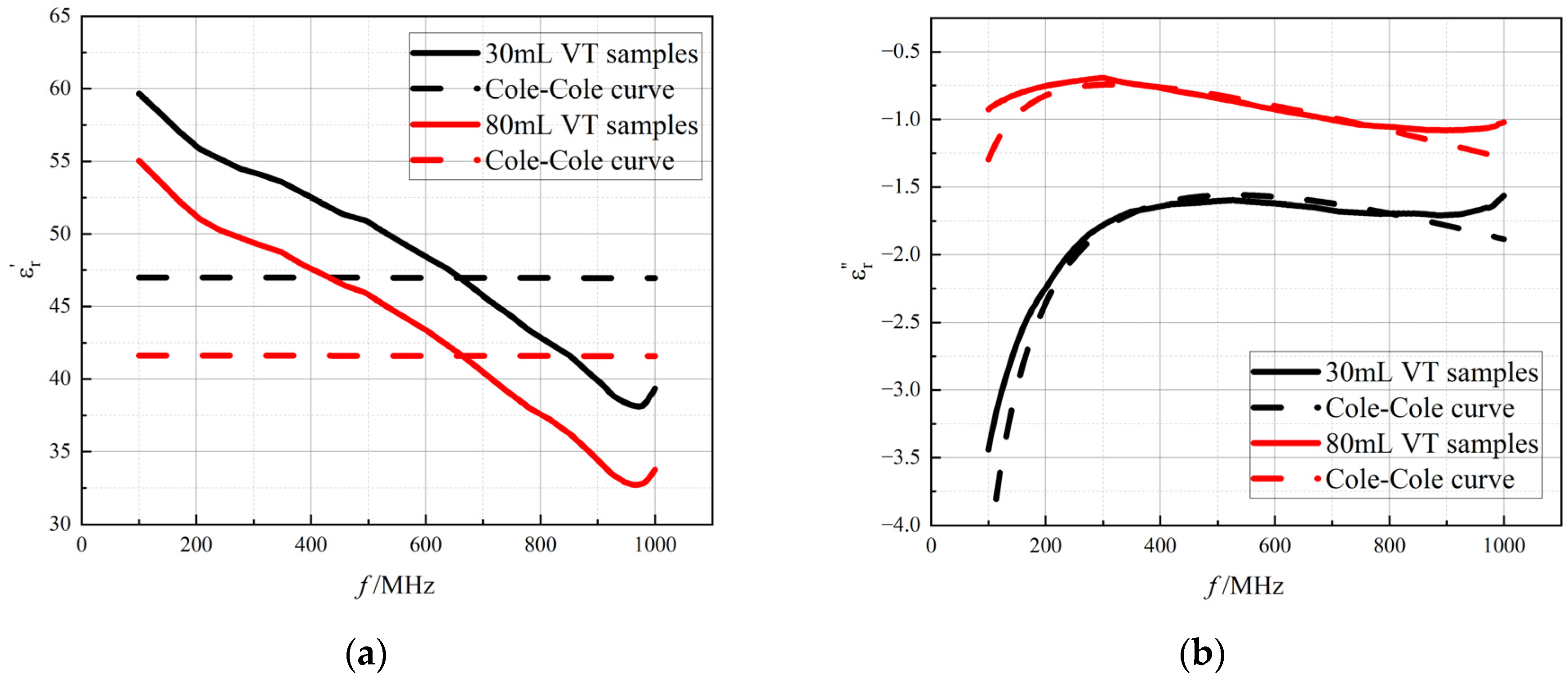
3.3. Cole−Cole Model Fitting
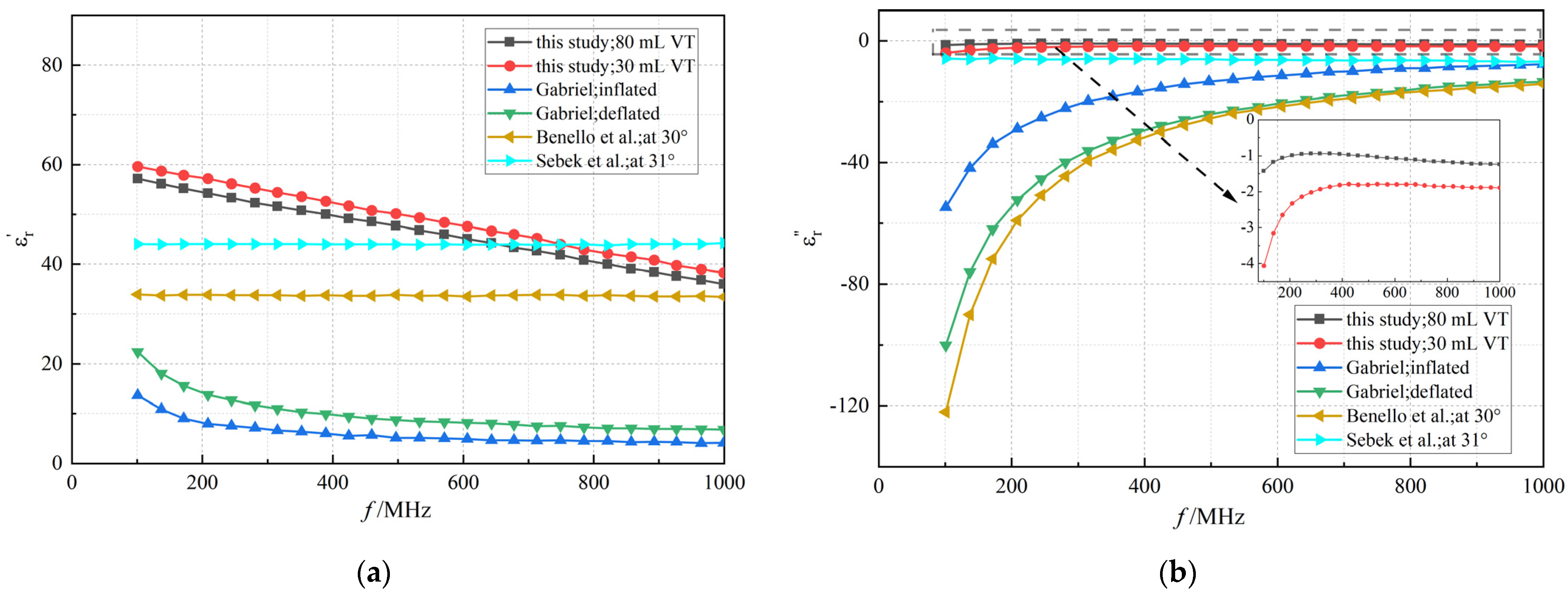
3.4. The Improved Cole–Cole Model Considering Air Content
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matković, A.; Kordić, A.; Jakovčević, A.; Šarolić, A. Complex Permittivity of Ex-Vivo Human, Bovine and Porcine Brain Tissues in the Microwave Frequency Range. Diagnostics 2022, 12, 2580. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Jiang, L.; Xiang, N.; Ni, Z. Discrimination of tumor cell type based on cytometric detection of dielectric properties. Talanta 2022, 246, 123524. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Cai, Z.; Han, S.; Lin, S.; He, L.; Chen, M.; Pan, D.; Deng, G.; Duan, S.; et al. Variation in the dielectric properties of freshly excised colorectal cancerous tissues at different tumor stages. Bioelectromagnetics 2017, 38, 522–532. [Google Scholar] [CrossRef] [PubMed]
- Chaudhry, R.; Omole, A.E.; Bordoni, B. Anatomy, Thorax, Lungs. In StatPearls; StatPearls Publishing LLC: Tampa, FL, USA, 2025. [Google Scholar]
- Nopp, P.; Rapp, E.; Pfützner, H.; Nakesch, H.; Ruhsam, C. Dielectric properties of lung tissue as a function of air content. Phys. Med. Biol. 1993, 38, 699–716. [Google Scholar] [CrossRef]
- Lymperopoulos, G.; Lymperopoulos, P.; Alikari, V.; Dafogianni, C.; Zyga, S.; Margari, N. Applications for Electrical Impedance Tomography (EIT) and Electrical Properties of the Human Body. Adv. Exp. Med. Biol. 2017, 989, 109–117. [Google Scholar] [PubMed]
- Yu, X.; Sun, Y.; Cai, K.; Yu, H.; Zhou, D.; Lu, D.; Xin, S.X. Dielectric Properties of Normal and Metastatic Lymph Nodes Ex Vivo From Lung Cancer Surgeries. Bioelectromagnetics 2020, 41, 148–155. [Google Scholar] [CrossRef]
- Wang, J. Experimental Study of Dielectric Properties on Human Lung Tissue. Chin. J. Biomed. Eng. 2013, 47, 1793–1803. [Google Scholar]
- Sebek, J.; Bortel, R.; Prakash, P. Broadband lung dielectric properties over the ablative temperature range: Experimental measurements and parametric models. Med. Phys. 2019, 46, 4291–4303. [Google Scholar] [CrossRef]
- Colebeck, E.; Asili, M.; Green, R.; Topsakal, E. The Effect of Temperature on the Microwave Dielectric Properties of Porcine Liver, Lung, and Heart. In Proceedings of the USNC-URSI NRSM 2013, Boulder, CO, USA, 9–12 January 2013. [Google Scholar]
- Nopp, P.; Harris, N.D.; Zhao, T.X.; Brown, B.H. Model for the dielectric properties of human lung tissue against frequency and air content. Med. Biol. Eng. Comput. 1997, 35, 695–702. [Google Scholar] [CrossRef]
- Fornes-Leal, A.; Cardona, N.; Frasson, M.; Castello-Palacios, S.; Nevarez, A.; Beltran, V.P.; Garcia-Pardo, C. Dielectric Characterization of In Vivo Abdominal and Thoracic Tissues in the 0.5–26.5 GHz Frequency Band for Wireless Body Area Networks. IEEE Access 2019, 7, 31854–31864. [Google Scholar] [CrossRef]
- Witsoe, D.A.; Kinnen, E. Electrical resistivity of lung at 100 kHz. Med. Biol. Eng. 1967, 5, 239–248. [Google Scholar] [CrossRef]
- Grant, E.H.; Sheppard, R.J. The measurement of permittivity of high-loss liquids at microwave frequencies using an unmatched phase changer. J. Phys. D Appl. Phys. 1970, 3, 84–90. [Google Scholar] [CrossRef]
- Buckmaster, H.A.; Hansen, C.H. Design optimization of a high precision microwave complex permittivity instrumentation system for use with high loss liquids. IEEE Trans. Instrum. Meas. 1990, 39, 964–968. [Google Scholar] [CrossRef]
- Stuchly, S.S.; Bassey, C. Microwave coplanar sensors for dielectric measurements. Meas. Sci. Technol. 1999, 9, 1324–1329. [Google Scholar] [CrossRef]
- Jordan, B.P.; Grant, E.H. Permittivity measurements on low and medium loss liquids using a terminated coaxial line. J. Phys. D Appl. Phys. 1970, 3, 1068. [Google Scholar] [CrossRef]
- Bahl, I.J.; Gupta, M.H. Microwave Measurement of Dielectric Constant of Liquids and Solids Using Partially Loaded Slotted Waveguide (Short Papers). IEEE Trans. Microw. Theory Tech. 1974, 22, 52–54. [Google Scholar] [CrossRef]
- Mclaughlin, B.L.; Robertson, P.A. Miniature open-ended coaxial probes for dielectric spectroscopy applications. J. Phys. D Appl. Phys. 2006, 40, 45. [Google Scholar] [CrossRef]
- Birnbaum, G.; Kryder, S.J.; Lyons, H. Microwave Measurements of the Dielectric Properties of Gases. J. Appl. Phys. 1951, 22, 95–102. [Google Scholar] [CrossRef]
- Works, C.N. Resonant Cavities for Dielectric Measurements. J. Appl. Phys. 1947, 18, 605–612. [Google Scholar] [CrossRef]
- Hamelin, J.; Mehl, J.B.; Moldover, M.R. Resonators for accurate dielectric measurements in conducting liquids. Rev. Sci. Instrum. 1998, 69, 255–260. [Google Scholar] [CrossRef]
- Vidjak, K.; Farina, L.; Ruvio, G.; Halloran, M.O.; Cavagnaro, M. Dielectric Properties of Healthy Ex Vivo Ovine Lung Tissue at Microwave Frequencies. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1162–1169. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, L.; Liu, Y.; Fu, F.; Yang, B.; Yang, L.; Liu, X.; Dai, M. Dielectric properties of tidal volume changes in rabbit lung tissue in the 100 MHz~1 GHz band. J. Biomed. Eng. 2024, 41, 447–454. [Google Scholar]
- Qin, Y.; Yang, L.; Fu, F.; Dai, M.; Zhang, L. Study on the difference of high frequency dielectric properties of biological tissues measured by air and packed coaxial probe. J. Biomed. Eng. 2023, 40, 886–893. [Google Scholar] [CrossRef]
- Cook, H.F. The dielectric behaviour of some types of human tissues at microwave frequencies. Br. J. Appl. Phys. 1951, 2, 295. [Google Scholar] [CrossRef]
- Stogryn, A. Equations for Calculating the Dielectric constant of saline water. IEEE Trans. Microw. Theory Tech. 1971, 19, 733–736. [Google Scholar] [CrossRef]
- Brace, C.L. Temperature-dependent dielectric properties of liver tissue measured during thermal ablation: Toward an improved numerical model. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008. [Google Scholar]
- Cole, K.S. Dispersion and absorption in dielectrics. Chem. Phys. 1941, 6, 42–52. [Google Scholar]
- Etoz, S.; Brace, C.L. Development of Water Content Dependent Tissue Dielectric Property Models. IEEE J. Electromagn. RF Microw. Med. Biol. 2019, 3, 105–110. [Google Scholar] [CrossRef] [PubMed]
- Schwan, H.P.; Foster, K.R. RF-field interactions with biological systems: Electrical properties and biophysical mechanisms. Proc. IEEE 1980, 68, 104–113. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Gabriel, C.; Corthout, E.; Gabriel, S. The Dielectric Properties of Biological Tissues. I. Literature Survey. Phys. Med. Biol. 1996, 41, 2231. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef] [PubMed]
- Bonello, J.; Elahi, M.A.; Porter, E.; O’Halloran, M.; Farrugia, L.; Sammut, C.V. An investigation of the variation of dielectric properties of ovine lung tissue with temperature. Biomed. Phys. Eng. Express 2018, 5, 045024. [Google Scholar] [CrossRef]
- Andreuccetti, D.; Fossi, R.; Petrucci, C. An Internet Resource for the Calculation of the Dielectric Properties of Body Tissues in the Frequency Range 10 Hz–100 GHz; IFAC-CNR: Florence, Italy, 1997; Available online: http://niremf.ifac.cnr.it/tissprop/ (accessed on 1 December 2024).


| VT (mL) | (Real Part) | (Imaginary Part) | |
|---|---|---|---|
| 30 | 12.85% | 0.084 | 0.801 |
| 40 | 13.78% | 0.084 | 0.631 |
| 50 | 16.73% | 0.079 | 0.302 |
| 60 | 15.10% | 0.062 | 0.398 |
| 70 | 16.31% | 0.083 | 0.720 |
| 80 | 15.57% | 0.107 | 0.491 |
| VT (mL) | (Real Part) | (Imaginary Part) | |
|---|---|---|---|
| 30 | 2.16% | 0.983 | 0.976 |
| 40 | 2.95% | 0.989 | 0.974 |
| 50 | 2.18% | 0.984 | 0.948 |
| 60 | 2.87% | 0.988 | 0.932 |
| 70 | 3.18% | 0.976 | 0.932 |
| 80 | 3.18% | 0.982 | 0.963 |
| VT (mL) | 30 | 40 | 50 | 60 | 70 | 80 | |
|---|---|---|---|---|---|---|---|
| Parameter | |||||||
| ε∞ | 3.48 | 3.22 | 3.63 | 2.28 | 3.81 | 2.13 | |
| ∆ε | 58.52 | 57.81 | 58.59 | 56.43 | 55.07 | 54.01 | |
| Τ (ps) | 6.04 | 5.91 | 5.15 | 4.93 | 5.31 | 5.02 | |
| α | 0 | 0 | 0 | 0 | 0 | 0 | |
| σs (×10−3 S/m) | 19.96 | 17.56 | 10.48 | 7.90 | 6.61 | 4.55 | |
| A (×10−9) | −3.66 | −3.74 | −3.74 | −3.68 | −3.82 | −3.53 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Zhang, L.; Han, T.; Liu, Y.; Liu, X.; Fu, F.; Wang, H.; Qu, S.; Zhao, Z.; Yang, L.; et al. An Improved Cole–Cole Model for Characterizing In Vivo Dielectric Properties of Lung Tissue at Different Tide Volumes: An Animal Study. Bioengineering 2025, 12, 445. https://doi.org/10.3390/bioengineering12050445
Qin Y, Zhang L, Han T, Liu Y, Liu X, Fu F, Wang H, Qu S, Zhao Z, Yang L, et al. An Improved Cole–Cole Model for Characterizing In Vivo Dielectric Properties of Lung Tissue at Different Tide Volumes: An Animal Study. Bioengineering. 2025; 12(5):445. https://doi.org/10.3390/bioengineering12050445
Chicago/Turabian StyleQin, Yangchun, Liang Zhang, Tixin Han, Yifan Liu, Xuechao Liu, Feng Fu, Hang Wang, Shuoyao Qu, Zhanqi Zhao, Lin Yang, and et al. 2025. "An Improved Cole–Cole Model for Characterizing In Vivo Dielectric Properties of Lung Tissue at Different Tide Volumes: An Animal Study" Bioengineering 12, no. 5: 445. https://doi.org/10.3390/bioengineering12050445
APA StyleQin, Y., Zhang, L., Han, T., Liu, Y., Liu, X., Fu, F., Wang, H., Qu, S., Zhao, Z., Yang, L., & Dai, M. (2025). An Improved Cole–Cole Model for Characterizing In Vivo Dielectric Properties of Lung Tissue at Different Tide Volumes: An Animal Study. Bioengineering, 12(5), 445. https://doi.org/10.3390/bioengineering12050445








