Integrated Process Modeling—A Process Validation Life Cycle Companion
Abstract
:1. Introduction
- Risk assessment using knowledge of process experts, which leads to a candidate set of potential critical PPs for each unit operation.
- Experimental investigation of the impact of potentially critical PPs onto CQAs. This is usually performed in DoE approaches and statistical regression modeling is used to describe the relationship between significantly impacting critical PPs and CQAs mathematically.
- Comparison of the output of statistical model predictions within normal operating ranges or a design space to pre-defined acceptance limits for each unit operation.
- The risk of not meeting acceptance limits is mitigated by applying an appropriate control strategy, such as a reduction of the normal operating range.
- Prove process robustness of an existing design space: Prove that under normal manufacturing conditions it is unlikely to miss drug substance specification for defined CQAs
- Test process robustness under accelerated variance of process parameters and increased impurity burden
- Establish a platform that leverages process knowledge from PV stage 1 for further usage within PPQ and CPV (Stage 2 and 3 of process validation)
2. Materials and Methods
- Description of the process, order of unit operations, and variance of PPs under normal operating conditions (see Section 2.1). It is assumed that estimation of variance of PPs is representative for routine manufacturing.
- Optional: If initial unit operation of the process is not modeled by the IPM the starting distribution of each CQA needs to be estimated at the starting unit operation of the IPM. It is assumed that the estimation of starting distribution is representative for the real CQA distribution under routine manufacturing (see Section 2.2).
- Statistical regression models that describe significant relationships between PPs and CQAs for each unit operation (see Section 2.3.1). It is assumed that scientifically sound analytical methods (high accuracy, precision, robustness, selectivity, etc.) have been used to record the data that led to formation of those regression models. Moreover, it is assumed that no critical effect has been overlooked, which can be tested using power analysis approaches [9]. This ensures that residual variance in the regression models can be attributed to normal analytical- and process variance.
- Optional: Statistical spiking models of each unit operation describing the dependency between varied impurity load and specific impurity clearance (see Section 2.3.2). Identical assumptions as for the regression models must be met.
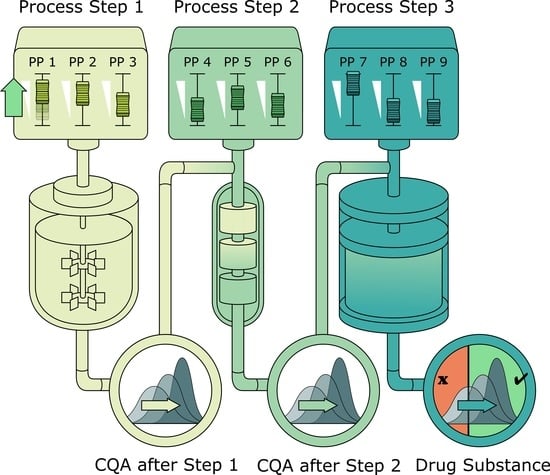
2.1. Description of Biopharmaceutical Manufacturing Process
2.2. Scope of IPM and Sampling Distribution of PPs
2.3. Impurity Clearance Models
2.3.1. Clearance and Yield as a Function of Process Parameters (DoE Models)
2.3.2. Increased Clearance Due to Varied Spiking of Impurities
3. Results
3.1. Monte Carlo Approach for Integrated Process Modeling
- 1000 simulations were performed, each having a different set of PPs () for the three modeled unit operations (chromatography column 1/2/3) and different initial specific CQA concentrations () at the load of chromatography column 1, sampled from distributions which were estimated from LS runs. Also the variance in PPs was estimated from LS runs and is indicated by a schematic distribution on the x-axis in Figure 2A,B. Additional increase in simulations did not increase model accuracy and 1000 simulations are a common standard for Monte Carlo simulations [7]. A more detailed description of this step and a list of used process parameters are provided in Section 2.2.
- For each unit operation, we modeled the specific clearance (SC) of each CQA as a function of the critical PPs and the ILD by multiple linear regression. Each model is associated with a prediction error, which is indicated by the blue shaded area around the found regression line Figure 2A,B. The ILD can be derived from of each unit operation, which equals for the first modeled unit operation and for all subsequent modeled unit operations (u).
- Since can be calculated from SC and , on the whole, can be seen as a function of as well as or , as indicated in the formula of Figure 2A,B, respectively. Thereby the model outputs from multiple unit operations can be stacked together, which is indicated by black arrows in Figure 2A, more thorough description of which models could be found on which CQA and unit operation is depicted in Section 2.3.
3.2. Validation of the IPM Using Observed CQA Distribution in Drug Substance
3.3. Impact of Accelerated Variation in Process Parameters on Drug Substance
4. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Process Validation: General Principles and Practices; U.S. Department of Health and Human Services: Washington, DC, USA, 2011.
- Guideline, I.H.T. Pharmaceutical Development Q8 (R2). Curr. Step 2009, 4, 1–24. [Google Scholar]
- Guideline, I.H.T. Quality risk management, Q9. Curr. Step 2005, 4, 408. [Google Scholar]
- Katz, P.; Campbell, C. FDA 2011 process validation guidance: Process validation revisited. J. GXP Compliance 2012, 16, 18. [Google Scholar]
- Peterson, J.J.; Lief, K. The ICH Q8 definition of design space: A comparison of the overlapping means and the bayesian predictive approaches. Stat. Biopharm. Res. 2010, 2, 249–259. [Google Scholar] [CrossRef]
- Herwig, C.; Wölbeling, C.; Zimmer, T. A holistic approach to production control. Pharm. Eng. 2017, 37, 44–46. [Google Scholar]
- Bonate, P.L. A brief introduction to Monte Carlo simulation. Clin. Pharmacokinet. 2001, 40, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Goudar, C.T.; Biener, R.; Konstantinov, K.B.; Piret, J.M. Error propagation from prime variables into specific rates and metabolic fluxes for mammalian cells in perfusion culture. Biotechnol. Prog. 2009, 25, 986–998. [Google Scholar] [CrossRef] [PubMed]
- Iman, R.L. Latin hypercube sampling. Encycl. Quant. Risk Anal. Assess. 2008. [Google Scholar] [CrossRef]
- Singhee, A.; Rutenbar, R.A. Why quasi-monte carlo is better than monte carlo or latin hypercube sampling for statistical circuit analysis. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2010, 29, 1763–1776. [Google Scholar] [CrossRef]
- Zahel, T.; Marschall, L.; Abad, S.; Vasilieva, E.; Maurer, D.; Mueller, E.M.; Murphy, P.; Natschläger, T.; Brocard, C.; Reinisch, D.; et al. Workflow for Criticality Assessment Applied in Biopharmaceutical Process Validation Stage 1. Bioengineering 2017, 4, 85. [Google Scholar] [CrossRef] [PubMed]







| UO | Available Data Sets | PPs Varied in DoEs | Rel. Std. of PPs between LS [%] 1 | Std/NOR [%] 2 | Monitored CQAs |
|---|---|---|---|---|---|
| CC 1 | pH [–] | 1.61 | 46 | PCI 1, PCI 2, PRI 1, PRI 2 | |
| Column loading density [g/L] | 12.05 | 50 | |||
| 9 manufacturing runs | Wash Strength [mM] | 5.00 | 62 | ||
| 13 DoE runs with definitive screening design | Elution strength [mM] | 5.00 | 44 | ||
| End pooling [CV] | 1.36 | 40 | |||
| CC 2 | 9 manufacturing runs | pH [–] | 0.79 | 30 | |
| 11 DoE runs using full factorial design | Column loading density [g/L] | 4.84 | 20 | ||
| 1 spiking run with increased PRI 1 concentration in load | Gradient slope [% of Buffer] | 5.00 | - | ||
| 1 spiking run with increased PCI 1 concentration in load | |||||
| CC 3 | pH [–] | 0.92 | 35 | ||
| 9 manufacturing runs | Column loading density [g/L] | 12.78 | 30 | ||
| 9 DoE runs using definitive screening design | Gradient slope [% of Buffer] | 5.00 | - | ||
| Wash Strength [mM] | 5.00 | 50 |
| CQA/Unit Operation | CC 1 | CC 2 | CC 3 |
|---|---|---|---|
| PRI 1 | DoE | LS clearance + Spiking | DoE |
| (linear, p = 0.09) | (p = 0.00) | (quadratic, p = 0.01) | |
| PRI 2 | DoE | LS clearance | LS clearance |
| (linear, p = 0.01) | |||
| PCI 1 | DoE | LS clearance + Spiking | DoE |
| (quadratic, p = 0.00) | (p = 0.04) | (quadratic, p = 0.00) | |
| PCI 2 | LS clearance + Spiking | LS clearance | LS clearance + Spiking |
| (linear, p = 0.00) | (linear, p = 0.00) | ||
| Yield | DoE | LS clearance | DoE |
| (linear, p = 0.00) | (quadratic, p = 0.00) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahel, T.; Hauer, S.; Mueller, E.M.; Murphy, P.; Abad, S.; Vasilieva, E.; Maurer, D.; Brocard, C.; Reinisch, D.; Sagmeister, P.; et al. Integrated Process Modeling—A Process Validation Life Cycle Companion. Bioengineering 2017, 4, 86. https://doi.org/10.3390/bioengineering4040086
Zahel T, Hauer S, Mueller EM, Murphy P, Abad S, Vasilieva E, Maurer D, Brocard C, Reinisch D, Sagmeister P, et al. Integrated Process Modeling—A Process Validation Life Cycle Companion. Bioengineering. 2017; 4(4):86. https://doi.org/10.3390/bioengineering4040086
Chicago/Turabian StyleZahel, Thomas, Stefan Hauer, Eric M. Mueller, Patrick Murphy, Sandra Abad, Elena Vasilieva, Daniel Maurer, Cécile Brocard, Daniela Reinisch, Patrick Sagmeister, and et al. 2017. "Integrated Process Modeling—A Process Validation Life Cycle Companion" Bioengineering 4, no. 4: 86. https://doi.org/10.3390/bioengineering4040086
APA StyleZahel, T., Hauer, S., Mueller, E. M., Murphy, P., Abad, S., Vasilieva, E., Maurer, D., Brocard, C., Reinisch, D., Sagmeister, P., & Herwig, C. (2017). Integrated Process Modeling—A Process Validation Life Cycle Companion. Bioengineering, 4(4), 86. https://doi.org/10.3390/bioengineering4040086