Breast Cancer Estimate Modeling via PDE Thermal Analysis Algorithms
Abstract
:1. Introduction
2. Test Materials and Methods
2.1. Theoretical PDE Thermal Analysis
2.2. PDE Analysis and Breast Cancer Research Flow
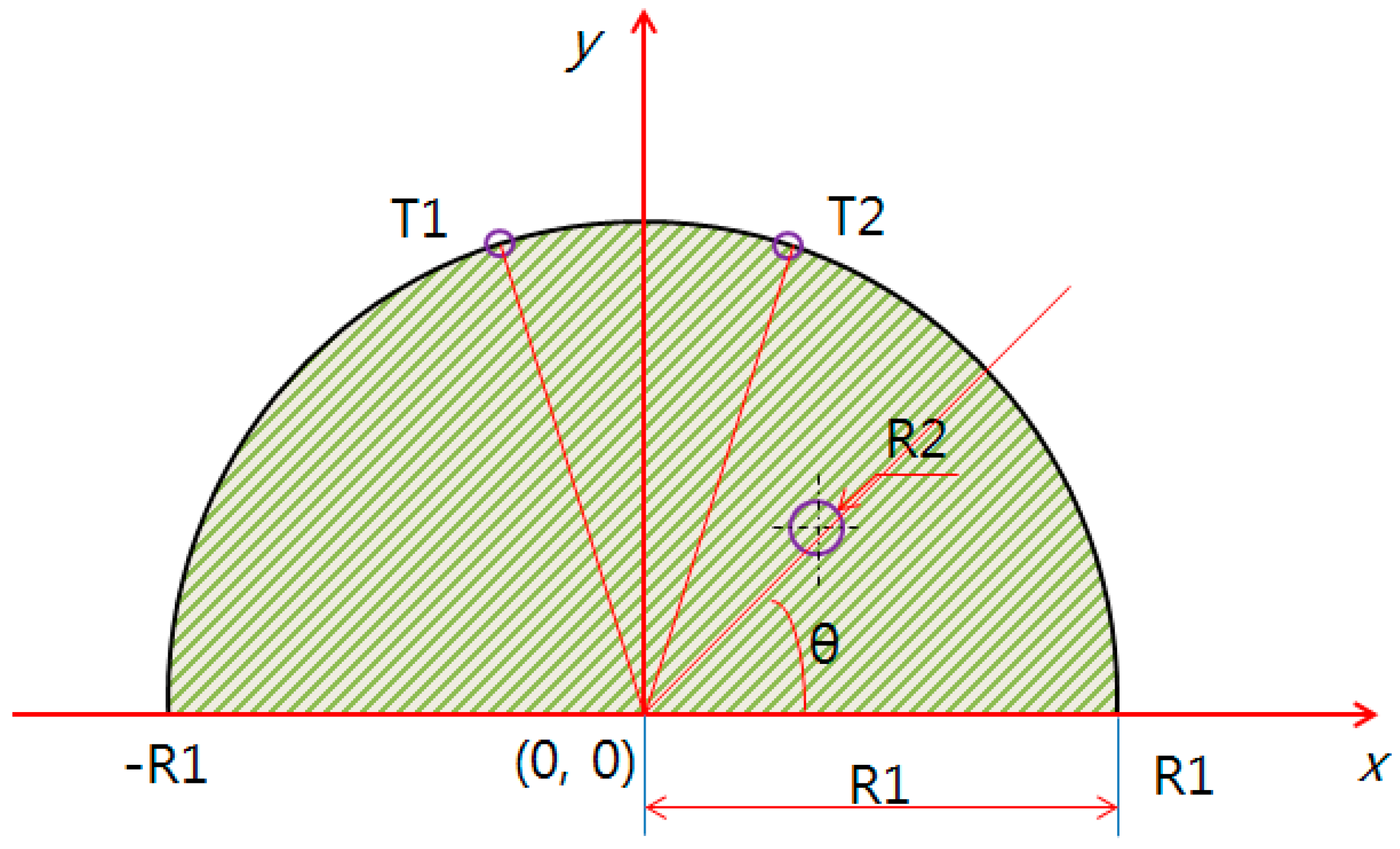
2.3. Modeling 1 (X = 10, Y = 0)
2.4. Modeling 2 (X = 10, Y = 10) and 3 (X = 0, Y = 10)
3. Results and Discussion
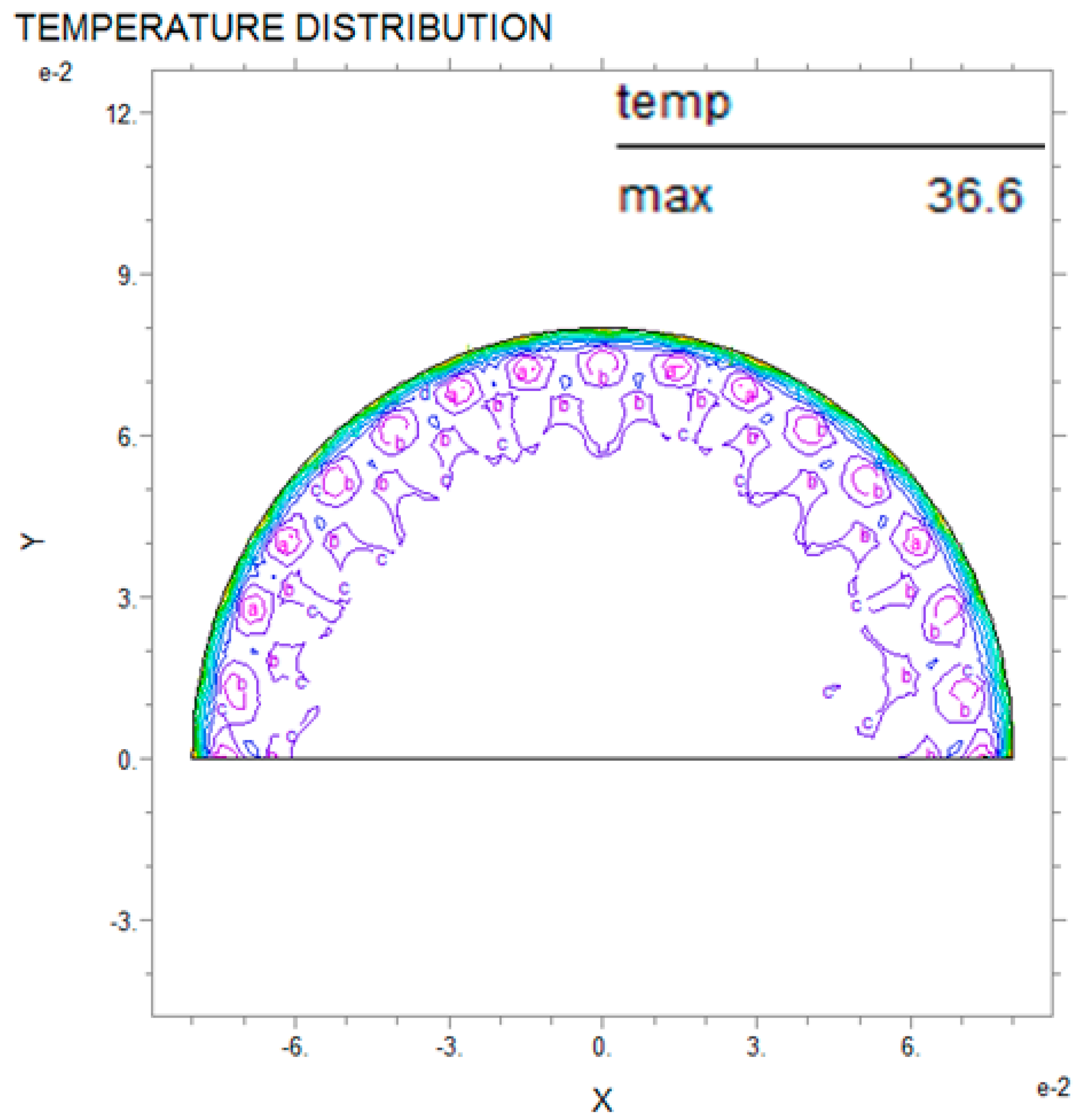
3.1. Application of PDE Thermal Analysis
3.2. Relationship of R1 (Breast Test Model) and R2 (Breast Cancer)
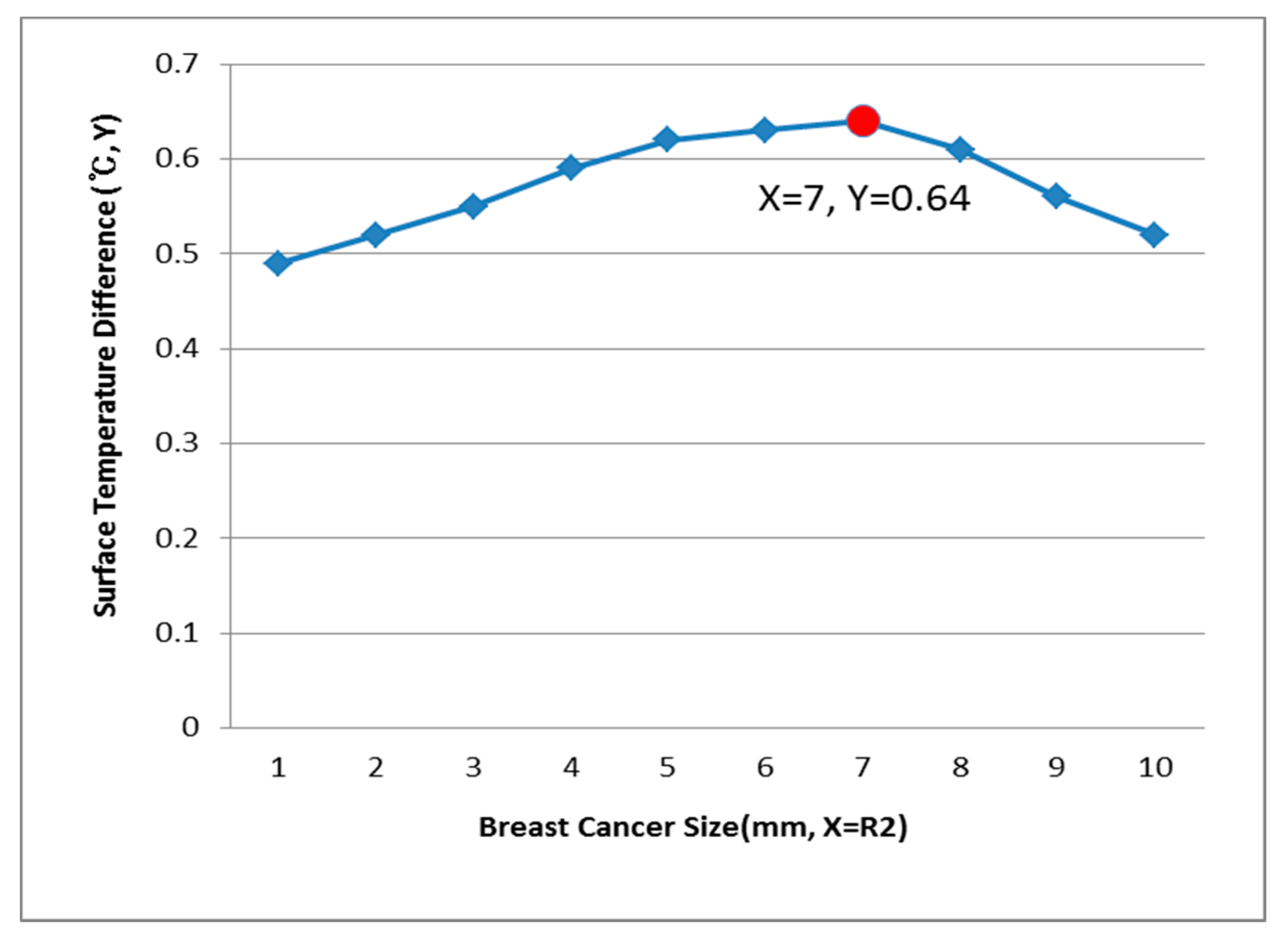
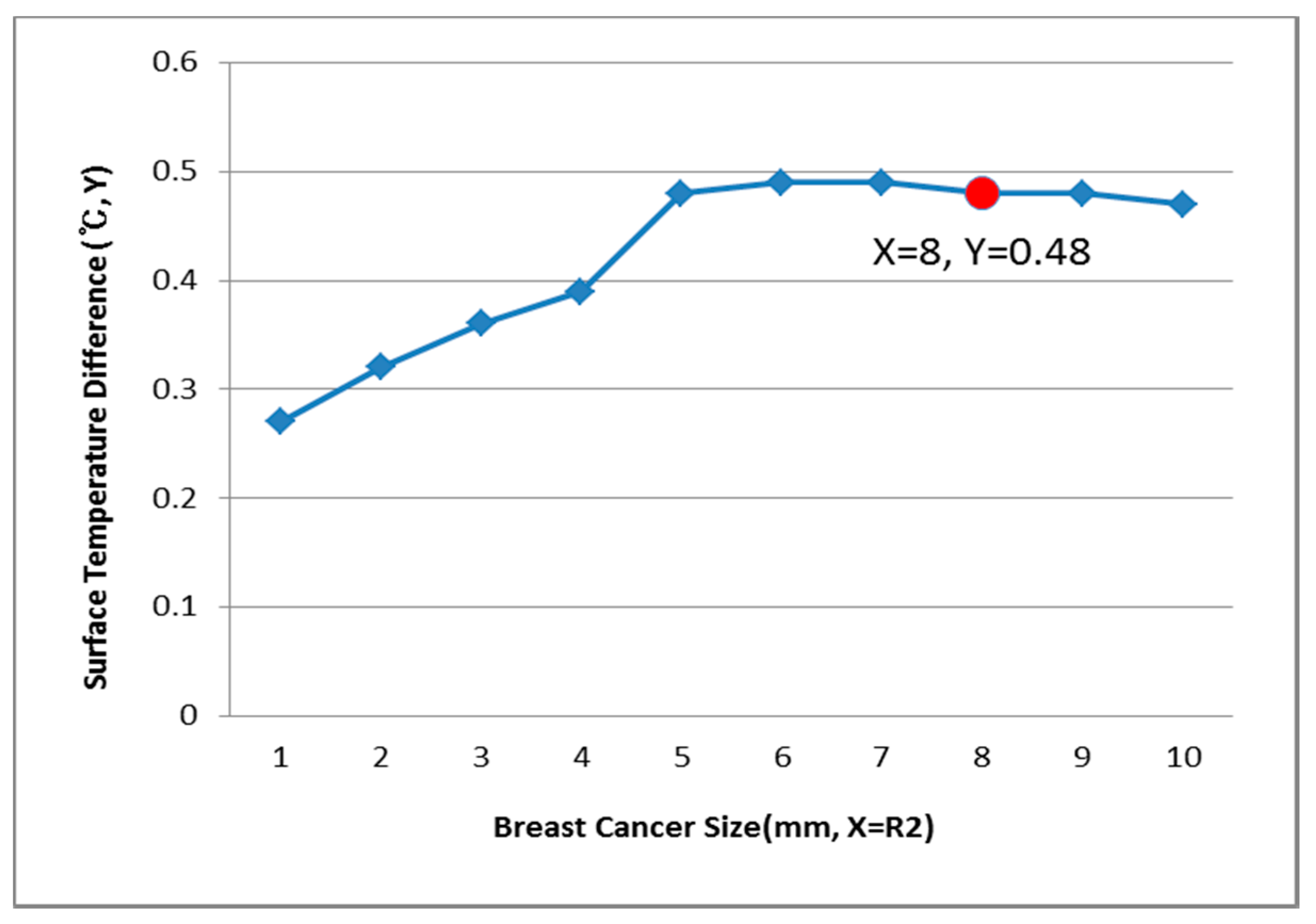
3.3. Relationship of R2 (Breast Cancer) and the Surface Temperature Difference
- If skin material and breast cancer data can be accumulated, the defects can be predicted without wounding the material.
- By using pure heat, it is possible to harmlessly predict flaws in the human body.
- Main arteries and blood flow intensity are important agenda items for our next thermal analysis study.
- In future studies, we should obtain the help of electronic engineers, and the digital work and the clinical experiment regarding the size of the breast cancer, which were observed immediately after the thermal analysis, should be conducted concurrently.
4. Conclusions
- It is possible to estimate the presence, position, and size of breast cancer in a two-dimensional model through PDE thermal analysis.
- Applied PDE analysis can be used to predict the presence, position, and size of breast cancer, specifically taking into account the surface temperature difference, and if the breast cancer position exhibits bilateral symmetry on the left- and right-hand sides, the analysis is the same.
- As the diameter of the breast model increased, heat transfer decreased, the surface temperature decreased, and the surface temperature difference increased generally.
- If the breast cancer (R2) position was (X = 10, Y = 0), the test model size (R1) was 50 mm, and the surface temperature difference was 0.60 °C, then the breast cancer at R2 was estimated as 3 mm, and the rest of the data were listed in the breast cancer estimation charts.
- If the relationship between the test material and the defect is varied and data are accumulated, then this model can be used for various different structures, including tumors and various cancers.
Author Contributions
Funding
Conflicts of Interest
References
- Inagaki, T. On the NDT and E for the diagnosis of defects using infrared thermography. NDT E Int. 1999, 32, 247–257. [Google Scholar] [CrossRef]
- Park, Y.H.; Yang, S.M. STS defect structure diagonis through the Infrared thermography mechanism and Flex-PDE thermal analysis. Trans. KSAE 2014, 22, 20–29. [Google Scholar] [CrossRef]
- Amri, A. Thermal analysis of a three-dimensional breast model with embedded tumour using the transmission line matrix (TLM) method. Comput. Biol. Med. 2011, 41, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.H. Diagnosis Method of Breast Cancer. Korea Patent 10-2013-0131018, 3 December 2013. [Google Scholar]
- Park, Y.H. Diagnosis System of Breast Cancer and Diagnosis Method of Breast Cancer. Korea Patent 10-2016-0017927, 17 February 2016. [Google Scholar]
- Park, Y.H. Breast Cancer Diagnosis System and Breast Cancer Diagnosis Method. PCT/KR2014/011860. 4 December 2014. [Google Scholar]
- Park, Y.H.; Yang, S.M. Defect depth hybrid study by IR IMAGE and PDE analysis. J. Korea Soc. Mech. Technol. 2015, 17, 665–674. [Google Scholar]
- Chala, T.F.; Wu, C.M.; Chou, M.H.; Gebeyehu, M.B.; Cheng, K.B. Highly Efficient Near Infrared Photothermal Conversion Properties of Reduced Tungsten Oxide/Polyurethane Nanocomposites. Nanomaterials 2017, 7, 191. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.S.; Ko, M.J. Comparison of Various Analysis Methods Based on Heat Flowmeters and Infrared Thermography Measurements for the Evaluation of the In Situ Thermal Transmittance of Opaque Exterior Walls. Energies 2017, 10, 1019. [Google Scholar] [CrossRef]
- Arena, F. USE OF Digital Infrared Imaging in Enhanced Breast Cancer Detection and Monitoring of the Clinical Response to Treatmen. In Proceedings of the 25th Annual International Conference of the IEEE EMBS, Cancun, Mexico, 17–21 September 2003. [Google Scholar]
- Agnelli, J.P.; Barrea, A.A.; Turner, C.V. Tumor location and parameter estimation by thermography. Math. Comput. Model. 2011, 53, 1527–1534. [Google Scholar] [CrossRef]
- Saniei, E.; Setayeshi, S.; Akbari, M.E.; Navid, M. Parameter estimation of breast tumour using dynamic neural network from thermal patten. J. Adv. Res. 2016, 7, 1045–1055. [Google Scholar] [CrossRef] [PubMed]
- Head, F.J.; Wang, F.; Lipari, C.A.; Elliott, R.L. The important role of infrared imaging in breast cancer. IEEE Eng. Med. Biol. Mag. 2000, 19, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Electronics and Telecommunications Research Institute. Breast Cancer Diagnosis Apparatus. Korea Patent 10-2009-0099687, 23 September 2009.
- Seoul National University. Apparatus of Detecting Cancer. Korea Patent 10-2006-0111154, 26 October 2006.
- Jung, M.G. Radiometric Breast Cancer Self-Detector Using the USB Interface and Apparatus and Method for Self-Detecting Breast Cancer. Korea Patent 10-2010-0112421, 19 October 2010. [Google Scholar]
- Holman, J.P. Heat Transfer, 9th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2011; pp. 1–23. [Google Scholar]
- Toh, Y.C.; Raja, A.; Yu, H.; van Noort, D. A 3D Microfluidic Model to Recapitulate Cancer Cell Migration and Invasion. Bioengineering 2018, 5, 29. [Google Scholar] [CrossRef] [PubMed]
- Priyadarshini, B.M.; Selvan, S.T.; Narayanan, K.; Fawzy, A.S. Characterization of Chlorhexidine-Loaded Calcium-Hydroxide Microparticles as a Potential Dental Pulp-Capping Material. Bioengineering 2017, 4, 59. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Z.; Yang, L.; Deng, G.; Huang, X.; Li, X.; Xie, X.; Wang, J.; Shuang, Z.; Wang, X. Patterns of Occurrence and Outcomes of Contralateral Breast Cancer: Analysis of SEER Data. J. Clin. Med. 2018, 7, 133. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.K. Appliction of Nondestructive Evaluation on Thermal Shock Damage Ceramics. J. KSMT 2015, 17, 183–188. [Google Scholar]
- Mortarotti, G.; Morganti, M.; Cecere, C. Thermal Analysis and Energy-Efficient Solutions to Preserve Listed Building Façades: The INA-Casa Building Heritage. Buildings 2017, 7, 56. [Google Scholar] [CrossRef]
- Kim, S.H. Computed Tomography useful Automotive parts Nondestructive analysis. Trans. KSAE 2004, 12, 143–150. [Google Scholar]
- Abukhshim, N.A. Heat generation and temperature prediction in metal cutting: A review and implications for high speed machining. Int. J. Mach. Tools Manuf. 2006, 46, 782–800. [Google Scholar] [CrossRef]
- Cui, Y.; Li, Y.; Xing, Y.; Yang, T.; Song, J. One-Dimensional Thermal Analysis of the Flexible Electronic Devices Integrated with Human Skin. Micromachines 2016, 7, 210. [Google Scholar] [CrossRef]
- Fernández, V.M.G.; Viejo, C.B.; González, D.A.M.; Vega, G.; Pulido, Y.F.; Antón, J.C.A. Thermal Analysis of a Fast Charging Technique for a High Power Lithium-Ion Cell. Batteries 2016, 2, 32. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, W.; Gong, M.; Meng, Y.; Wang, Y.; Fu, X. Four-Dimensional Thermal Analysis of 888 nm Pumped Nd: YVO4 Dual-Rod Acousto-Optic Q-Switched Laser. Appl. Sci. 2017, 7, 470. [Google Scholar] [CrossRef]
- Ulloa, C.; Arce, M.E.; Rey, G.; Míguez, J.L.; Hernández, J. Recycling COR-TEN® Sea Containers into Service Modules for Military Applications: Thermal Analysis. Energies 2017, 10, 820. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q.; Zhang, C.; Wu, L. High-Speed Visual Analysis of Fluid Flow and Heat Transfer in Oscillating Heat Pipes with Different Diameters. Appl. Sci. 2016, 6, 321. [Google Scholar] [CrossRef]
- Weinberger, C.; Roggenbuck, J.; Hanss, J.; Tiemann, M. Synthesis of Mesoporous Metal Oxides by Structure Replication: Thermal Analysis of Metal Nitrates in Porous Carbon Matrices. Nanomaterials 2015, 5, 1431–1441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, D.K. A Study on the Working Condition Effecting on the Maximum Working Temperature and Surface Roughness in Side Wall End Milling Using Design of Experiment. J. Korean Soc. Manuf. Process Eng. 2009, 8, 46–53. [Google Scholar]













| R1 | 40 mm | 50 mm | 60 mm | 70 mm | 80 mm | |
|---|---|---|---|---|---|---|
| R2 | ||||||
| 1 mm | 0.50 | 0.58 | 0.66 | 0.71 | 0.77 | |
| 2 mm | 0.42 | 0.51 | 0.69 | 0.65 | 0.71 | |
| 3 mm | 0.52 | 0.60 ℃ | 0.67 | 0.73 | 0.80 | |
| 4 mm | 0.34 | 0.51 | 0.59 | 0.66 | 0.71 | |
| 5 mm | 0.48 | 0.50 | 0.57 | 0.63 | 0.68 | |
| 6 mm | 0.35 | 0.48 | 0.55 | 0.63 | 0.68 | |
| 7 mm | 0.40 | 0.46 | 0.53 | 0.60 | 0.66 | |
| 8 mm | 0.34 | 0.40 | 0.52 | 0.60 | 0.65 | |
| 9 mm | 0.47 | 0.32 | 0.41 | 0.47 | 0.51 | |
| 10 mm | 0.32 | 0.47 | 0.47 | 0.52 | 0.58 | |
| R1 | 40 mm | 50 mm | 60 mm | 70 mm | 80 mm | |
|---|---|---|---|---|---|---|
| R2 | ||||||
| 1 mm | 0.35 | 0.42 | 0.46 | 0.49 | 0.51 | |
| 2 mm | 0.37 | 0.44 | 0.49 | 0.52 | 0.56 | |
| 3 mm | 0.40 | 0.46 | 0.51 | 0.55 | 0.60 | |
| 4 mm | 0.42 | 0.48 | 0.54 ℃ | 0.59 | 0.63 | |
| 5 mm | 0.43 | 0.52 | 0.56 | 0.62 | 0.67 | |
| 6 mm | 0.44 | 0.52 | 0.57 | 0.63 | 0.68 | |
| 7 mm | 0.41 | 0.50 | 0.56 | 0.64 | 0.66 | |
| 8 mm | 0.48 | 0.47 | 0.54 | 0.61 | 0.56 | |
| 9 mm | 0.31 | 0.48 | 0.51 | 0.56 | 0.63 | |
| 10 mm | 0.32 | 0.49 | 0.46 | 0.52 | 0.58 | |
| R1 | 40 mm | 50 mm | 60 mm | 70 mm | 80 mm | |
|---|---|---|---|---|---|---|
| R2 | ||||||
| 1 mm | 0.22 | 0.25 | 0.27 | 0.31 | 0.33 | |
| 2 mm | 0.27 | 0.28 | 0.32 | 0.36 | 0.38 | |
| 3 mm | 0.23 | 0.31 | 0.36 | 0.40 | 0.42 | |
| 4 mm | 0.24 | 0.33 | 0.39 | 0.43 | 0.47 | |
| 5 mm | 0.29 | 0.41 | 0.48 | 0.54 | 0.57 | |
| 6 mm | 0.30 | 0.42 | 0.49 | 0.55 °C | 0.61 | |
| 7 mm | 0.31 | 0.42 | 0.49 | 0.55 | 0.61 | |
| 8 mm | 0.35 | 0.49 | 0.48 | 0.55 | 0.60 | |
| 9 mm | 0.33 | 0.53 | 0.48 | 0.55 | 0.62 | |
| 10 mm | 0.32 | 0.48 | 0.47 | 0.53 | 0.58 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.H.; Yang, S.M. Breast Cancer Estimate Modeling via PDE Thermal Analysis Algorithms. Bioengineering 2018, 5, 98. https://doi.org/10.3390/bioengineering5040098
Park YH, Yang SM. Breast Cancer Estimate Modeling via PDE Thermal Analysis Algorithms. Bioengineering. 2018; 5(4):98. https://doi.org/10.3390/bioengineering5040098
Chicago/Turabian StylePark, Young Hoon, and Sung Mo Yang. 2018. "Breast Cancer Estimate Modeling via PDE Thermal Analysis Algorithms" Bioengineering 5, no. 4: 98. https://doi.org/10.3390/bioengineering5040098
APA StylePark, Y. H., & Yang, S. M. (2018). Breast Cancer Estimate Modeling via PDE Thermal Analysis Algorithms. Bioengineering, 5(4), 98. https://doi.org/10.3390/bioengineering5040098




