Monte Carlo-Based Error Propagation for a More Reliable Regression Analysis across Specific Rates in Bioprocesses
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data and Measurements
2.2. Measurement Errors
2.3. Rate Calculation
2.4. Linear Least Squares with Errors in Both Variables
2.5. Monte Carlo Sampling for Error Propagation and Regression Analysis
| Algorithm 1 Monte Carlo sampling for error propagation chain. |
|
| Algorithm 2 Monte Carlo sampling for regression analysis. |
|
3. Results
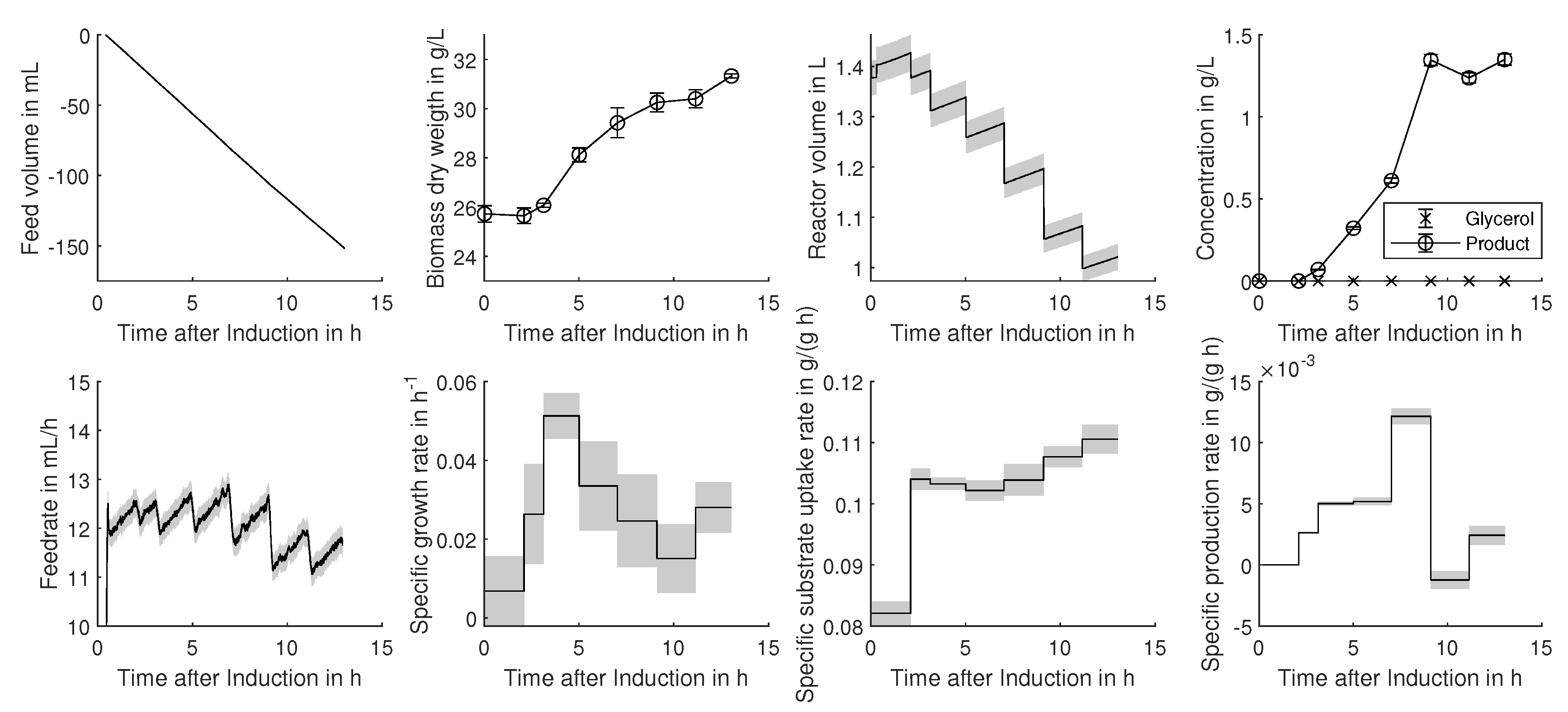
3.1. Propagation of the Analytical Uncertainties in the Data Evaluation Procedures
3.2. Regression Analysis Based on Uncertain Data
3.2.1. E. coli
3.2.2. CHO Cells
3.3. Determination of Confidence Bounds for Control
3.3.1. E. coli
3.3.2. CHO Cells
3.4. Prediction of Harvest Time Point Probability
4. Discussion
4.1. Realistic Quantification of Errors on Determined Specific Rates
4.2. Error Weighting for a Better Identification of the Regression Parameters
4.3. Achievable Control Limits
4.4. Probabilistic Rather Than Case-by-Case Decisions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HPLC | High Pressure Liquid Chromatography |
| CHO | Chinese Hamster Ovary |
| MC | Monte Carlo |
| FA | Functional Analysis |
| Gln | Glutamine |
| Lac | Lactate |
| biomass-specific growth rate | |
| biomass-specific product formation rate | |
| biomass-specific substrate uptake rate | |
| biomass-specific rate of component i | |
| concentration of component i | |
| X | biomass |
| S | substrate |
| P | product |
| D | dilution rate |
| substrate concentration in the feed | |
| feed rate | |
| t of sample k | |
| measured concentration at t | |
| true input | |
| reconstructed input by regression | |
| measured output | |
| predicted regression output | |
| weighting matrix of predictions | |
| weighting matrix of input variables | |
| S | weighted sum of squared error |
| standard deviation of measured output or true input | |
| N | number of Monte Carlo iterations |
| f | arbitrary function converting input to output |
| sampled input from Gaussian-distributed error | |
| calculation result of sampled input | |
| sampled input from output i | |
| standard deviation after calculation step i | |
| regression parameter for N Monte Carlo evaluations | |
| parameter covariance | |
| parameter standard deviation | |
| standard deviation of regression output |
References
- Chhatre, S.; Farid, S.S.; Coffman, J.; Bird, P.; Newcombe, A.R.; Titchener-Hooker, N.J. How implementation of quality by design and advances in biochemical engineering are enabling efficient bioprocess development and manufacture. J. Chem. Technol. Biotechnol. 2011, 86, 1125–1129. [Google Scholar] [CrossRef]
- Suarez-Zuluaga, D.A.; Borchert, D.; Driessen, N.N.; Bakker, W.A.M.; Thomassen, Y.E. Accelerating bioprocess development by analysis of all available data: A USP case study. Vaccine 2019, 37, 7081–7089. [Google Scholar] [CrossRef] [PubMed]
- Sagmeister, P.; Wechselberger, P.; Herwig, C. Information processing: Rate-based investigation of cell physiological changes along design space development. PDA J. Pharm. Sci. Technol. 2012, 66, 526–541. [Google Scholar] [CrossRef]
- Spadiut, O.; Rittmann, S.; Dietzsch, C.; Herwig, C. Dynamic process conditions in bioprocess development. Eng. Life Sci. 2013, 13, 88–101. [Google Scholar] [CrossRef]
- Posch, A.E.; Herwig, C. Physiological description of multivariate interdependencies between process parameters, morphology and physiology during fed-batch penicillin production. Biotechnol. Prog. 2014, 30, 689–699. [Google Scholar] [CrossRef] [PubMed]
- Le, H.; Kabbur, S.; Pollastrini, L.; Sun, Z.; Mills, K.; Johnson, K.; Karypis, G.; Hu, W.S. Multivariate analysis of cell culture bioprocess data—lactate consumption as process indicator. J. Biotechnol. 2012, 162, 210–223. [Google Scholar] [CrossRef]
- Bayer, B.; Sissolak, B.; Duerkop, M.; von Stosch, M.; Striedner, G. The shortcomings of accurate rate estimations in cultivation processes and a solution for precise and robust process modeling. Bioprocess Biosyst. Eng. 2020, 43, 169–178. [Google Scholar] [CrossRef] [Green Version]
- Oner, M.; Erickson, L.; Yang, S. Utilization of spline functions for smoothing fermentation data and for estimation of specific rates. Biotechnol. Bioeng. 1986, 28, 902–918. [Google Scholar] [CrossRef] [PubMed]
- Wechselberger, P.; Sagmeister, P.; Herwig, C. Model-based analysis on the extractability of information from data in dynamic fed-batch experiments. Biotechnol. Prog. 2013, 29, 285–296. [Google Scholar] [CrossRef] [Green Version]
- Anane, E.; García, Á.C.; Haby, B.; Hans, S.; Krausch, N.; Krewinkel, M.; Hauptmann, P.; Neubauer, P.; Cruz Bournazou, M.N. A model-based framework for parallel scale-down fed-batch cultivations in mini-bioreactors for accelerated phenotyping. Biotechnol. Bioeng. 2019, 116, 2906–2918. [Google Scholar] [CrossRef] [Green Version]
- Daume, S.; Kofler, S.; Kager, J.; Kroll, P.; Herwig, C. Generic workflow for the setup of mechanistic process models. In Animal Cell Biotechnology; Springer: Berlin, Germany, 2020; pp. 189–211. [Google Scholar]
- Zampieri, M.; Hörl, M.; Hotz, F.; Müller, N.F.; Sauer, U. Regulatory mechanisms underlying coordination of amino acid and glucose catabolism in Escherichia coli. Nat. Commun. 2019, 10, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Sinner, P.; Stiegler, M.; Herwig, C.; Kager, J. Noninvasive online monitoring of Corynebacterium glutamicum fed-batch bioprocesses subject to spent sulfite liquor raw material uncertainty. Bioresour. Technol. 2021, 321, 124395. [Google Scholar] [CrossRef]
- Jenzsch, M.; Simutis, R.; Luebbert, A. Generic model control of the specific growth rate in recombinant Escherichia coli cultivations. J. Biotechnol. 2006, 122, 483–493. [Google Scholar] [CrossRef] [PubMed]
- Kroll, P.; Hofer, A.; Stelzer, I.V.; Herwig, C. Workflow to set up substantial target-oriented mechanistic process models in bioprocess engineering. Process Biochem. 2017, 62, 24–36. [Google Scholar] [CrossRef]
- Farrance, I.; Frenkel, R. Uncertainty of Measurement: A Review of the Rules for Calculating Uncertainty Components through Functional Relationships. Clin. Biochem. Rev. 2012, 33, 49–75. [Google Scholar]
- Hughes, I.; Hase, T. Measurements and Their Uncertainties: A Practical Guide to Modern Error Analysis; Oxford University Press: Oxford, UK, 2010; p. 153. [Google Scholar]
- Gardenier, G.H.; Gui, F.; Demas, J.N. Error Propagation Made Easy Or at Least Easier. J. Chem. Educ. 2011, 88, 916–920. [Google Scholar] [CrossRef]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today: Why the MCM is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Anderson, G. Error propagation by the Monte Carlo method in geochemical calculations. Geochim. Et Cosmochim. Acta 1976, 40, 1533–1538. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Hobbs, R.; Caiado, C.; Sproson, A.D.; Selby, D.; Rooney, A.D. Monte Carlo sampling for error propagation in linear regression and applications in isochron geochronology. Sci. Bull. 2019, 64, 189–197. [Google Scholar] [CrossRef] [Green Version]
- Krausch, N.; Barz, T.; Sawatzki, A.; Gruber, M.; Kamel, S.; Neubauer, P.; Cruz Bournazou, M.N. Monte Carlo simulations for the analysis of nonlinear parameter confidence intervals in optimal experimental design. Front. Bioeng. Biotechnol. 2019, 7, 122. [Google Scholar] [CrossRef]
- Spann, R.; Lantz, A.E.; Roca, C.; Gernaey, K.V.; Sin, G. Model-based process development for a continuous lactic acid bacteria fermentation. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2018; Volume 43, pp. 1601–1606. [Google Scholar]
- Dabros, M.; Schuler, M.M.; Marison, I.W. Simple control of specific growth rate in biotechnological fed-batch processes based on enhanced online measurements of biomass. Bioprocess Biosyst. Eng. 2010, 33, 1109–1118. [Google Scholar] [CrossRef]
- Macdonald, J.R.; Thompson, W.J. Least-squares fitting when both variables contain errors: Pitfalls and possibilities. Am. J. Phys. 1992, 60, 66–73. [Google Scholar] [CrossRef]
- York, D. Least-Squares Fitting of a Straight Line. Can. J. Phys. 1966, 44, 1079–1086. [Google Scholar] [CrossRef] [Green Version]
- Alper, J.S.; Gelb, R.I. Standard errors and confidence intervals in nonlinear regression: Comparison of Monte Carlo and parametric statistics. J. Phys. Chem. 1990, 94, 4747–4751. [Google Scholar] [CrossRef]
- DeLisa, M.P.; Li, J.; Rao, G.; Weigand, W.A.; Bentley, W.E. Monitoring GFP-operon fusion protein expression during high cell density cultivation of Escherichia coli using an on-line optical sensor. Biotechnol. Bioeng. 1999, 65, 54–64. [Google Scholar] [CrossRef]
- Slouka, C.; Kopp, J.; Hutwimmer, S.; Strahammer, M.; Strohmer, D.; Eitenberger, E.; Schwaighofer, A.; Herwig, C. Custom made inclusion bodies: Impact of classical process parameters and physiological parameters on inclusion body quality attributes. Microb. Cell Factories 2018, 17, 148. [Google Scholar] [CrossRef] [PubMed]
- Paul, K.; Rajamanickam, V.; Herwig, C. Model-based optimization of temperature and pH shift to increase volumetric productivity of a Chinese hamster ovary fed-batch process. J. Biosci. Bioeng. 2019, 128, 710–715. [Google Scholar] [CrossRef] [PubMed]
- Frahm, B.; Lane, P.; Märkl, H.; Pörtner, R. Improvement of a mammalian cell culture process by adaptive, model-based dialysis fed-batch cultivation and suppression of apoptosis. Bioprocess Biosyst. Eng. 2003, 26, 1–10. [Google Scholar] [CrossRef]
- Borchert, D.; Suarez-Zuluaga, D.A.; Sagmeister, P.; Thomassen, Y.E.; Herwig, C. Comparison of data science workflows for root cause analysis of bioprocesses. Bioprocess Biosyst. Eng. 2019, 42, 245–256. [Google Scholar] [CrossRef] [Green Version]
- Douma, R.D.; Verheijen, P.J.; de Laat, W.T.; Heijnen, J.J.; van Gulik, W.M. Dynamic gene expression regulation model for growth and penicillin production in Penicillium chrysogenum. Biotechnol. Bioeng. 2010, 106, 608–618. [Google Scholar] [CrossRef]
- Kager, J.; Tuveri, A.; Ulonska, S.; Kroll, P.; Herwig, C. Experimental verification and comparison of model predictive, PID and model inversion control in a Penicillium chrysogenum fed-batch process. Process Biochem. 2019, 90, 1–11. [Google Scholar] [CrossRef]
- Oliveira, A.L. Biotechnology, big data and artificial intelligence. Biotechnol. J. 2019, 14, 1800613. [Google Scholar] [CrossRef] [Green Version]
- Mitra, A.; Munir, K. Big Data Application in Manufacturing Industry. In Encyclopedia of Big Data Technologies; Sakr, S., Zomaya, A.Y., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Mercier, S.M.; Diepenbroek, B.; Dalm, M.C.; Wijffels, R.H.; Streefland, M. Multivariate data analysis as a PAT tool for early bioprocess development data. J. Biotechnol. 2013, 167, 262–270. [Google Scholar] [CrossRef]
- Doherty, S.J.; Lange, A.J. Avoiding pitfalls with chemometrics and PAT in the pharmaceutical and biotech industries. TrAC Trends Anal. Chem. 2006, 25, 1097–1102. [Google Scholar] [CrossRef]
- Wang, X.; Germansderfer, A.; Harms, J.; Rathore, A.S. Using statistical analysis for setting process validation acceptance criteria for biotech products. Biotechnol. Prog. 2007, 23, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Nikzad-Langerodi, R.; Lughofer, E.; Saminger-Platz, S.; Zahel, T.; Sagmeister, P.; Herwig, C. Automatic feed phase identification in multivariate bioprocess profiles by sequential binary classification. Anal. Chim. Acta 2017, 982, 48–61. [Google Scholar] [CrossRef] [PubMed]
- Kroll, P.; Stelzer, I.V.; Herwig, C. Soft sensor for monitoring biomass subpopulations in mammalian cell culture processes. Biotechnol. Lett. 2017, 39, 1667–1673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cannizzaro, C.; Gügerli, R.; Marison, I.; von Stockar, U. On-line biomass monitoring of CHO perfusion culture with scanning dielectric spectroscopy. Biotechnol. Bioeng. 2003, 84, 597–610. [Google Scholar] [CrossRef]
- Hofer, A.; Kroll, P.; Barmettler, M.; Herwig, C. A Reliable Automated Sampling System for On-Line and Real-Time Monitoring of CHO Cultures. Processes 2020, 8, 637. [Google Scholar] [CrossRef]







| Raw Signal | Unit | Analytical Device | Error | Error Source |
|---|---|---|---|---|
| Weight substrate feed | g | Balance | ±0.1 g | manufacturer |
| Weight acid/feed feed | g | Balance | ±0.1 g | manufacturer |
| Sampling | mL | Graduated syringe | ±3 mL | manufacturer |
| Cell dry mass | g/L | Drying oven + balance | individual | triplicates |
| Total cell count | cells/mL | Cedex hi res | individual | duplicates |
| Viable cell count | cells/mL | Cedex hi res | individual | duplicates |
| Glycerol | g/L | HPLC (RI) | ±3% | triplicates |
| Glutamine | g/L | Cedex BioHT | ±3% | manufacturer |
| Lactate | g/L | Cedex BioHT | ±3% | manufacturer |
| Product E. coli | g/L | HPLC (UV) | ±2.5% | repeated measurements |
| Methodology | y-Intercept (g/(gh)) | Slope (-) |
|---|---|---|
| Ls | 0.0003 | 0.1321 |
| Ls MC | 0.0005 ± 0.0021 | 0.1319 ± 0.0117 |
| York | −0.0038 ± 0.0006 | 0.1567 ± 0.0036 |
| York MC | −0.0038 ± 0.0006 | 0.1566 ± 0.0038 |
| Methodology | y-Intercept (g/(108 Cells ∗ h)) | Slope (-) |
|---|---|---|
| Ls | −0.0046 | 1.9518 |
| Ls MC | −0.0028 ± 0.0016 | 1.6480 ± 0.4016 |
| York | −0.0040 ± 0.0005 | 1.8652 ± 0.2028 |
| York MC | −0.0043 ± 0.0006 | 1.8965 ± 0.2582 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kager, J.; Herwig, C. Monte Carlo-Based Error Propagation for a More Reliable Regression Analysis across Specific Rates in Bioprocesses. Bioengineering 2021, 8, 160. https://doi.org/10.3390/bioengineering8110160
Kager J, Herwig C. Monte Carlo-Based Error Propagation for a More Reliable Regression Analysis across Specific Rates in Bioprocesses. Bioengineering. 2021; 8(11):160. https://doi.org/10.3390/bioengineering8110160
Chicago/Turabian StyleKager, Julian, and Christoph Herwig. 2021. "Monte Carlo-Based Error Propagation for a More Reliable Regression Analysis across Specific Rates in Bioprocesses" Bioengineering 8, no. 11: 160. https://doi.org/10.3390/bioengineering8110160
APA StyleKager, J., & Herwig, C. (2021). Monte Carlo-Based Error Propagation for a More Reliable Regression Analysis across Specific Rates in Bioprocesses. Bioengineering, 8(11), 160. https://doi.org/10.3390/bioengineering8110160







