Preoperative Planning of Spiral Intestinal Lengthening and Tailoring: A Geometrical Approach
Abstract
:1. Introduction
2. Materials and Methods
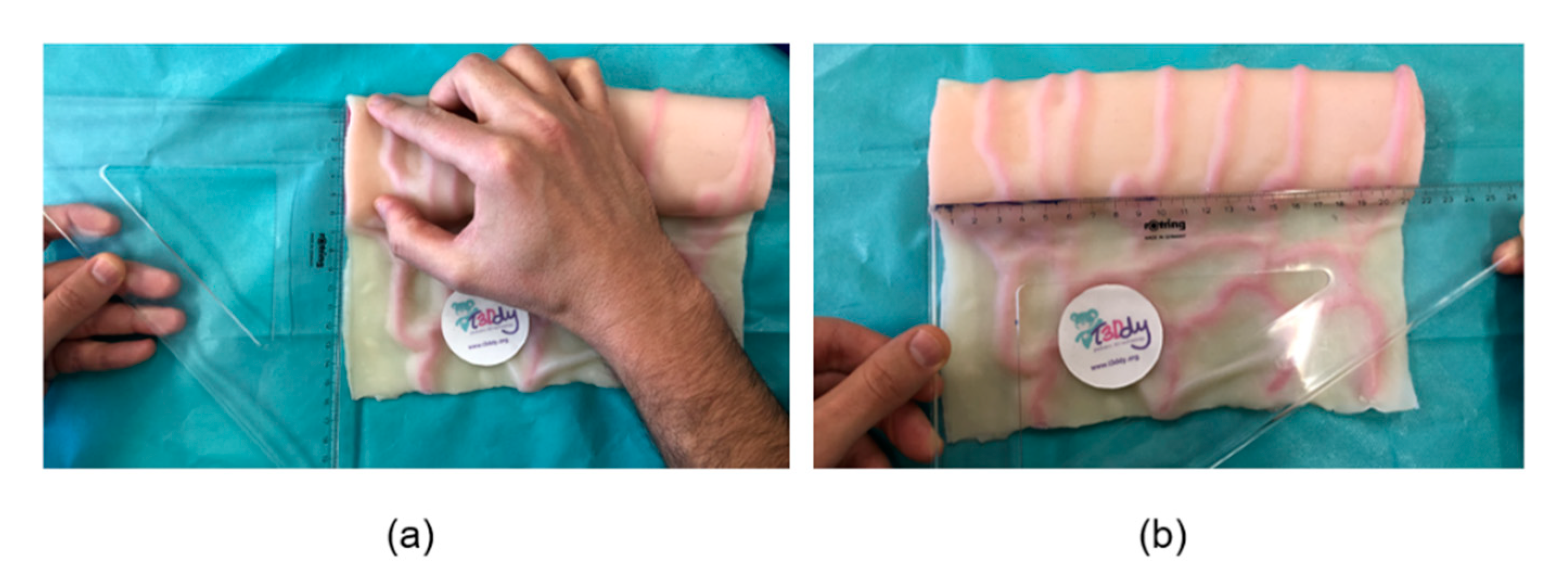
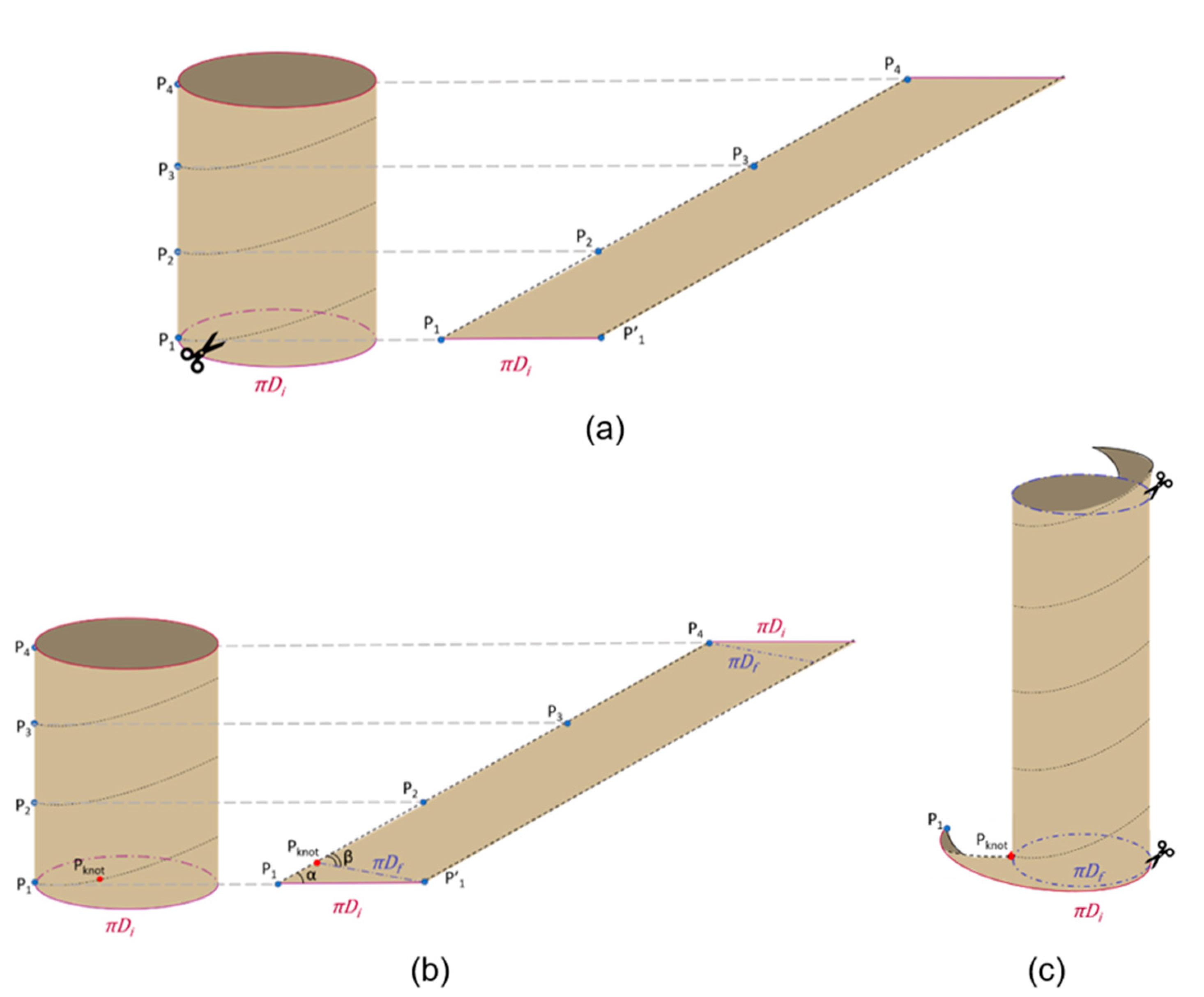
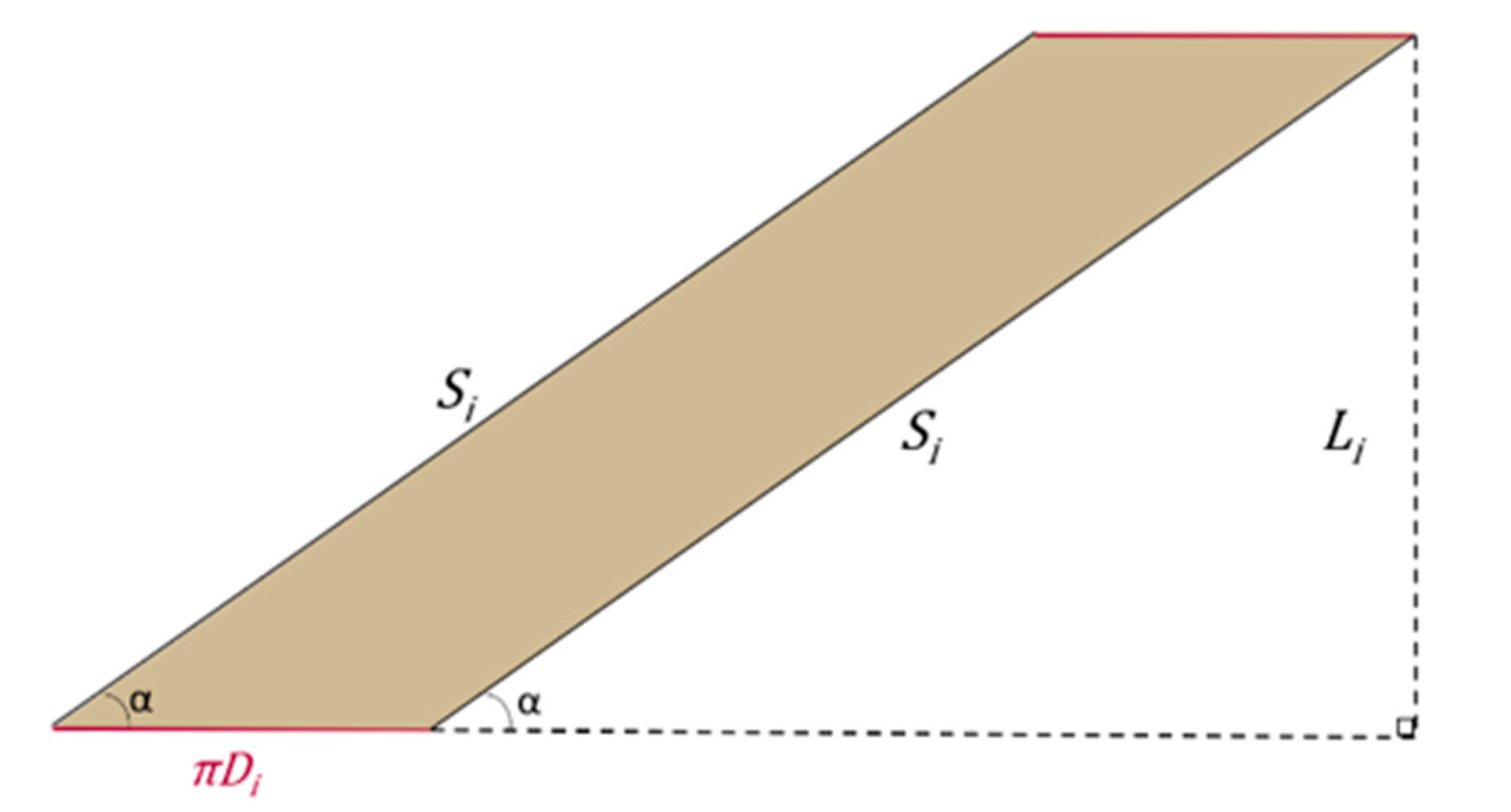
2.1. The Geometry of the SILT Procedure
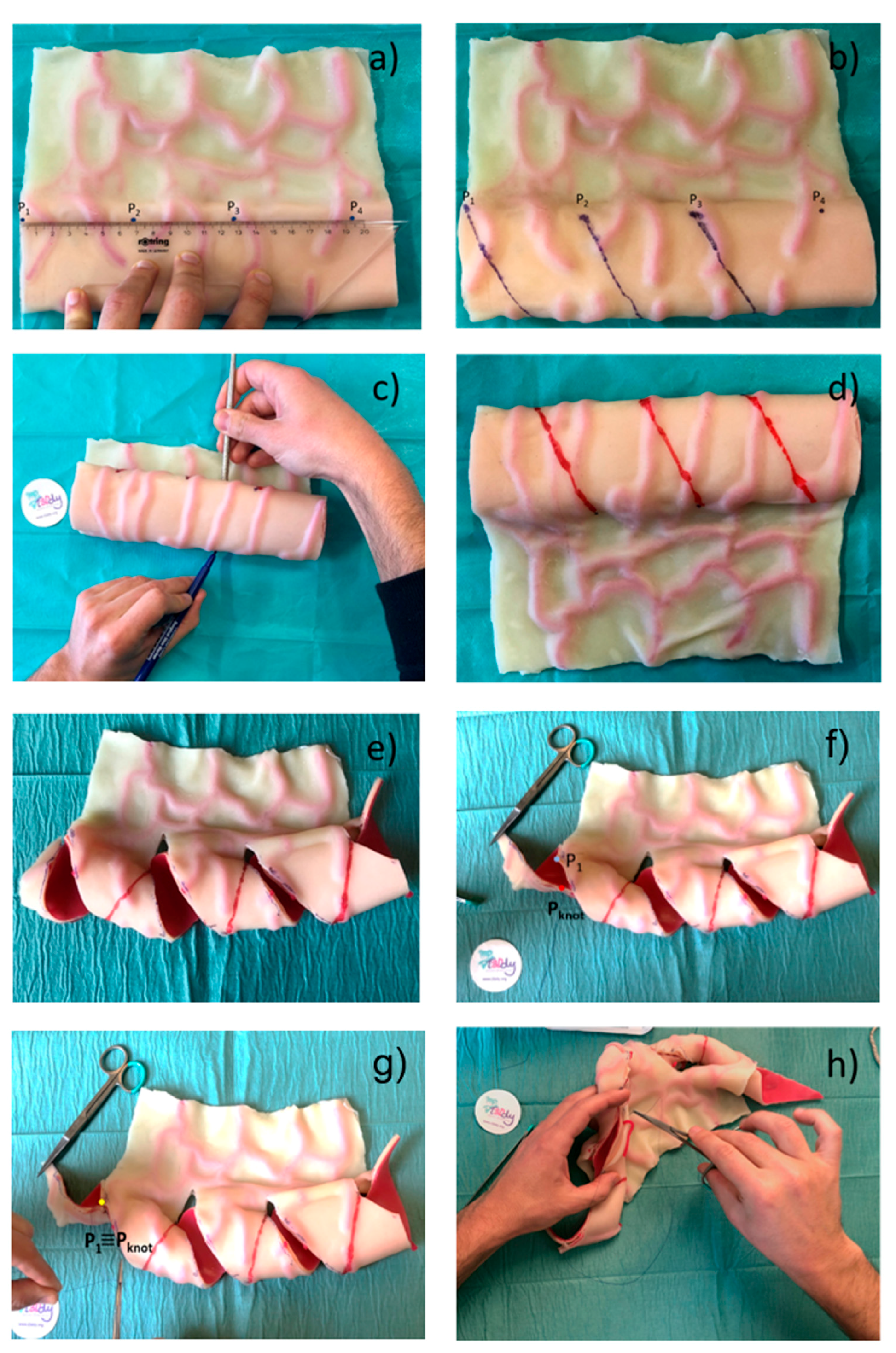
2.2. Surgical Feasibility
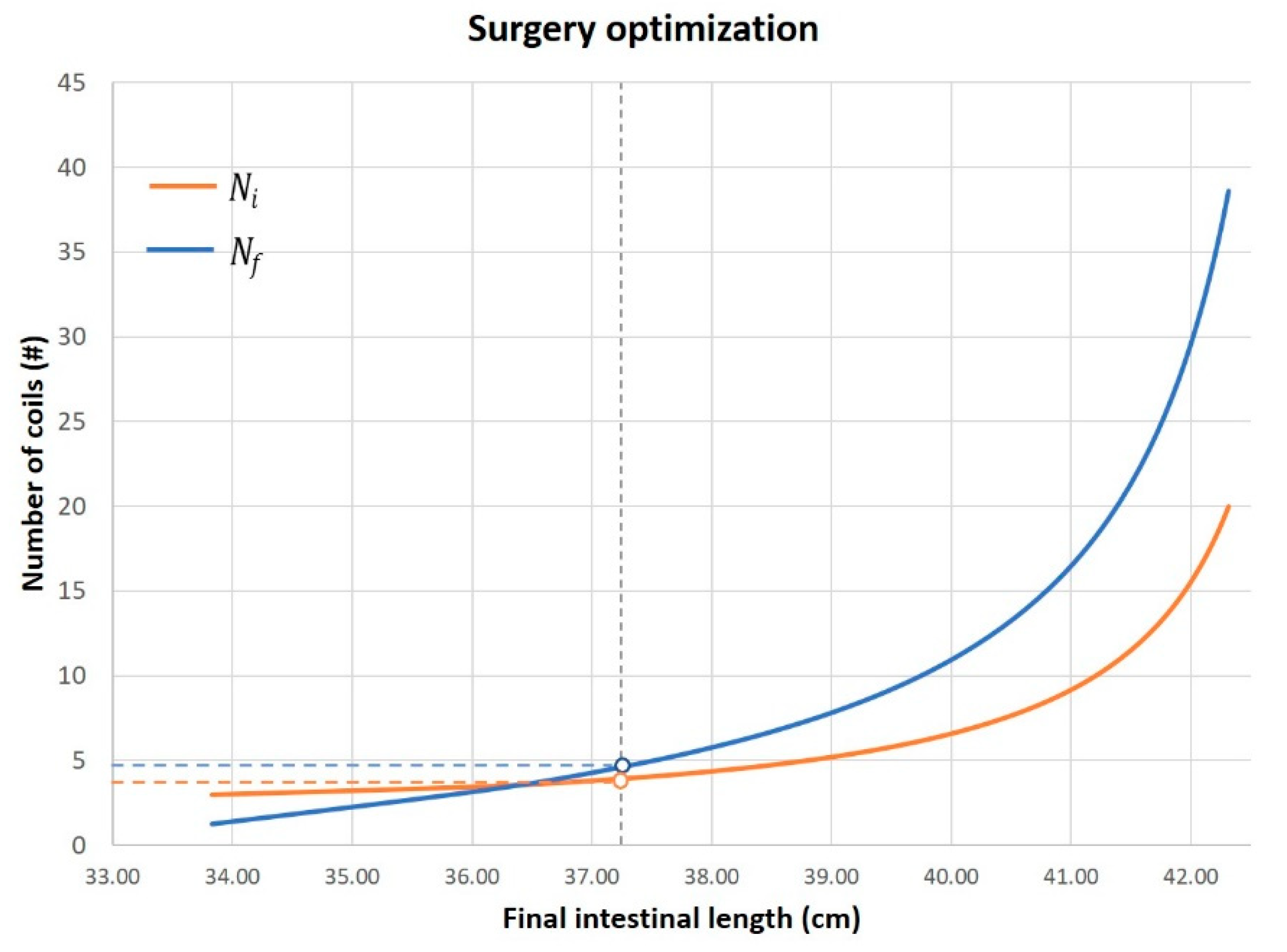
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- O’Keefe, S.J.; Buchman, A.L.; Fishbein, T.M.; Jeejeebhoy, K.N.; Jeppesen, P.B.; Shaffer, J. Short bowel syndrome and intestinal failure: Consensus definitions and overview. Clin. Gastroenterol. Hepatol. 2006, 4, 6–10. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, E.; Bosaeus, I.; Nordgren, S. Quality of life and concerns in patients with short bowel syndrome. Clin. Nutr. 2003, 22, 445–452. [Google Scholar] [CrossRef]
- Spencer, A.U.; Kovacevich, D.; McKinney-Barnett, M.; Hair, D.; Canham, J.; Maksym, C.; Teitelbaum, D.H. Pediatric short-bowel syndrome: The cost of comprehensive care. Am. J. Clin. Nutr. 2008, 88, 1552–1559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schalamon, J.; Mayr, J.M.; Höllwarth, M.E. Mortality and economics in short bowel syndrome. Bailliere’s Best Pract. Res. Clin. Gastroenterol. 2003, 17, 931–942. [Google Scholar] [CrossRef]
- Wales, P.W.; de Silva, N.; Kim, J.H.; Lecce, L.; Sandhu, A.; Moore, A.M. Neonatal short bowel syndrome: A cohort study. J. Pediatr. Surg. 2005, 40, 755–762. [Google Scholar] [CrossRef] [PubMed]
- Khalil, B.A.; Ba’ath, M.E.; Aziz, A.; Forsythe, L.; Gozzini, S.; Murphy, F.; Carlson, G.; Bianchi, A.; Morabito, A. Intestinal rehabilitation and bowel reconstructive surgery: Improved outcomes in children with short bowel syndrome. J. Pediatr. Gastroenterol. Nutr. 2012, 54, 505–509. [Google Scholar] [CrossRef] [PubMed]
- Coletta, R.; Khalil, B.A.; Morabito, A. Short bowel syndrome in children: Surgical and medical perspectives. Semin. Pediatr. Surg. 2014, 23, 291–297. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, A. Intestinal loop lengthening-A technique for increasing small intestinal length. J. Pediatr. Surg. 1980, 15, 145–151. [Google Scholar] [CrossRef]
- Kim, H.B.; Fauza, D.; Garza, J.; Oh, J.T.; Nurko, S.; Jaksic, T. Serial transverse enteroplasty (STEP): A novel bowel lengthening procedure. J. Pediatr. Surg. 2003, 38, 425–429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cserni, T.; Varga, G.; Erces, D.; Kaszaki, J.; Boros, M.; Laszlo, A.; Murphy, F.; Földvari, A.; Morabito, A.; Bianchi, A.; et al. Spiral intestinal lengthening and tailoring - First in vivo study. J. Pediatr. Surg. 2013, 48, 1907–1913. [Google Scholar] [CrossRef] [PubMed]
- Materialise Mimics|3D Medical Image Processing Software. Available online: https://www.materialise.com/en/medical/mimics-innovation-suite/mimics (accessed on 28 December 2020).
- Cserni, T.; Takayasu, H.; Muzsnay, Z.; Varga, G.; Murphy, F.; Folaranmi, S.E.; Rakoczy, G. New idea of intestinal lengthening and tailoring. Pediatr. Surg. Int. 2011, 27, 1009–1013. [Google Scholar] [CrossRef] [PubMed]
- Mehrabi, V.; Mehrabi, A.; Jamshidi, S.H.; Pedram, M.S.; Sabagh, M.S.; Jaberansari, N.; Fonouni, H.R.; Sharifi, A.H.; Malekzadeh, R.; Frongia, G. Modified spiral intestinal lengthening and tailoring for short bowel syndrome. Surg. Innov. 2016, 23, 30–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coletta, R.; Mussi, E.; Uccheddu, F.; Volpe, Y.; Morabito, A. Preoperative Planning of Spiral Intestinal Lengthening and Tailoring: A Geometrical Approach. Bioengineering 2021, 8, 20. https://doi.org/10.3390/bioengineering8020020
Coletta R, Mussi E, Uccheddu F, Volpe Y, Morabito A. Preoperative Planning of Spiral Intestinal Lengthening and Tailoring: A Geometrical Approach. Bioengineering. 2021; 8(2):20. https://doi.org/10.3390/bioengineering8020020
Chicago/Turabian StyleColetta, Riccardo, Elisa Mussi, Francesca Uccheddu, Yary Volpe, and Antonino Morabito. 2021. "Preoperative Planning of Spiral Intestinal Lengthening and Tailoring: A Geometrical Approach" Bioengineering 8, no. 2: 20. https://doi.org/10.3390/bioengineering8020020
APA StyleColetta, R., Mussi, E., Uccheddu, F., Volpe, Y., & Morabito, A. (2021). Preoperative Planning of Spiral Intestinal Lengthening and Tailoring: A Geometrical Approach. Bioengineering, 8(2), 20. https://doi.org/10.3390/bioengineering8020020






