CFD-Based and Experimental Hydrodynamic Characterization of the Single-Use Bioreactor XcellerexTM XDR-10
Abstract
:1. Introduction
2. Material and Methods
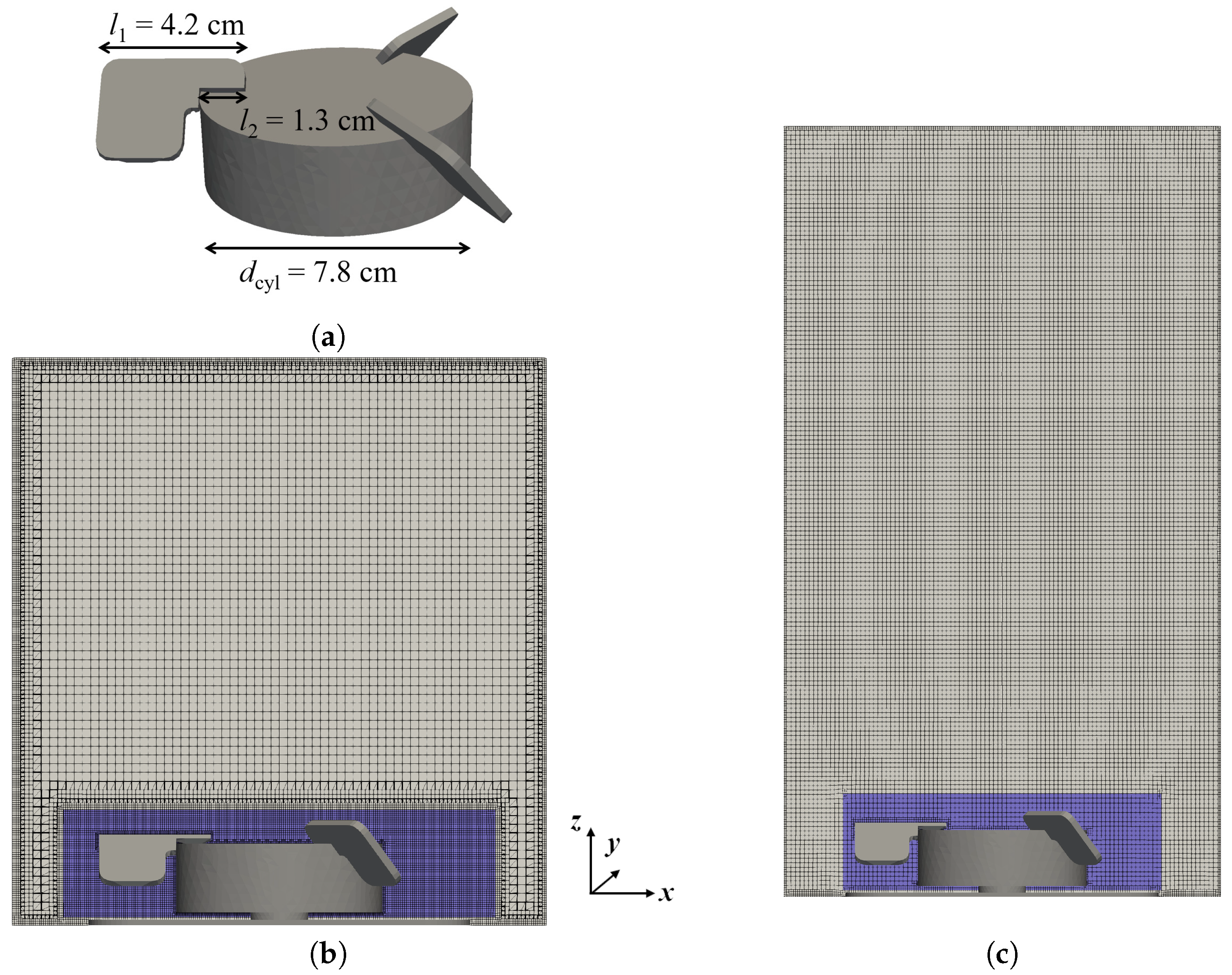
2.1. Configuration of the Bioreactor and Test Conditions
2.2. Experimental Methods
2.3. Mathematical Models
3. Results and Discussion
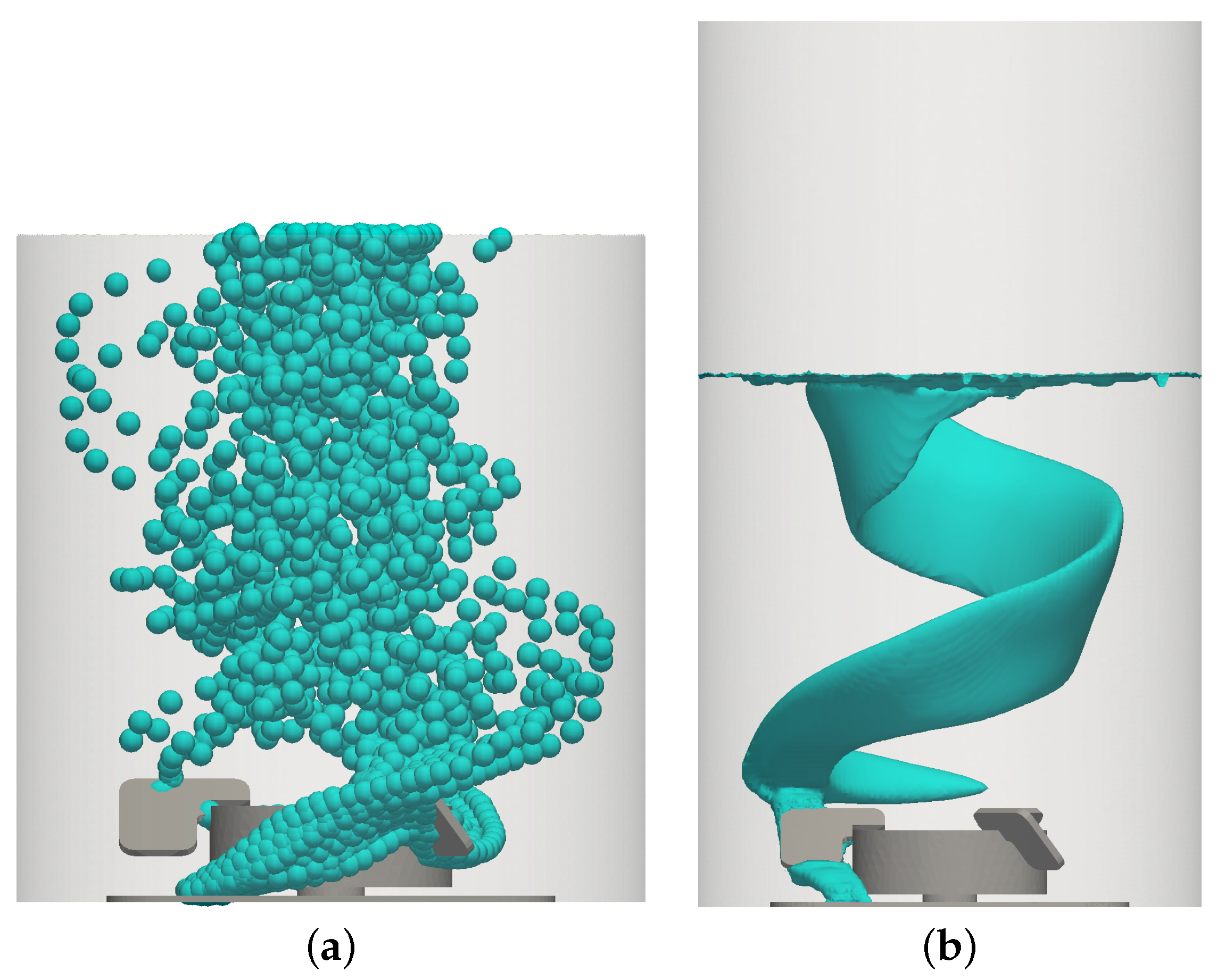
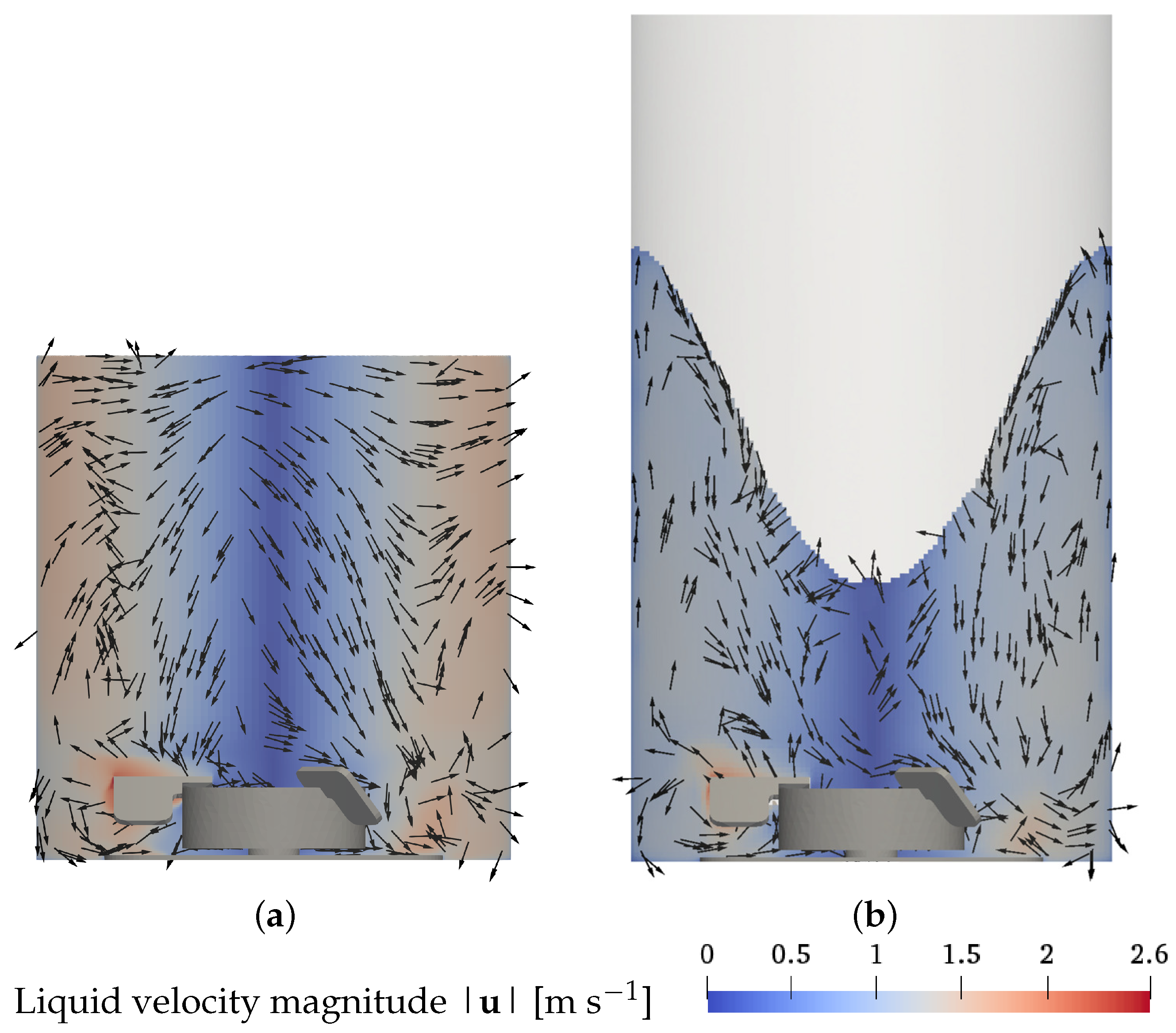
3.1. Liquid Velocity and Bubble Dispersion
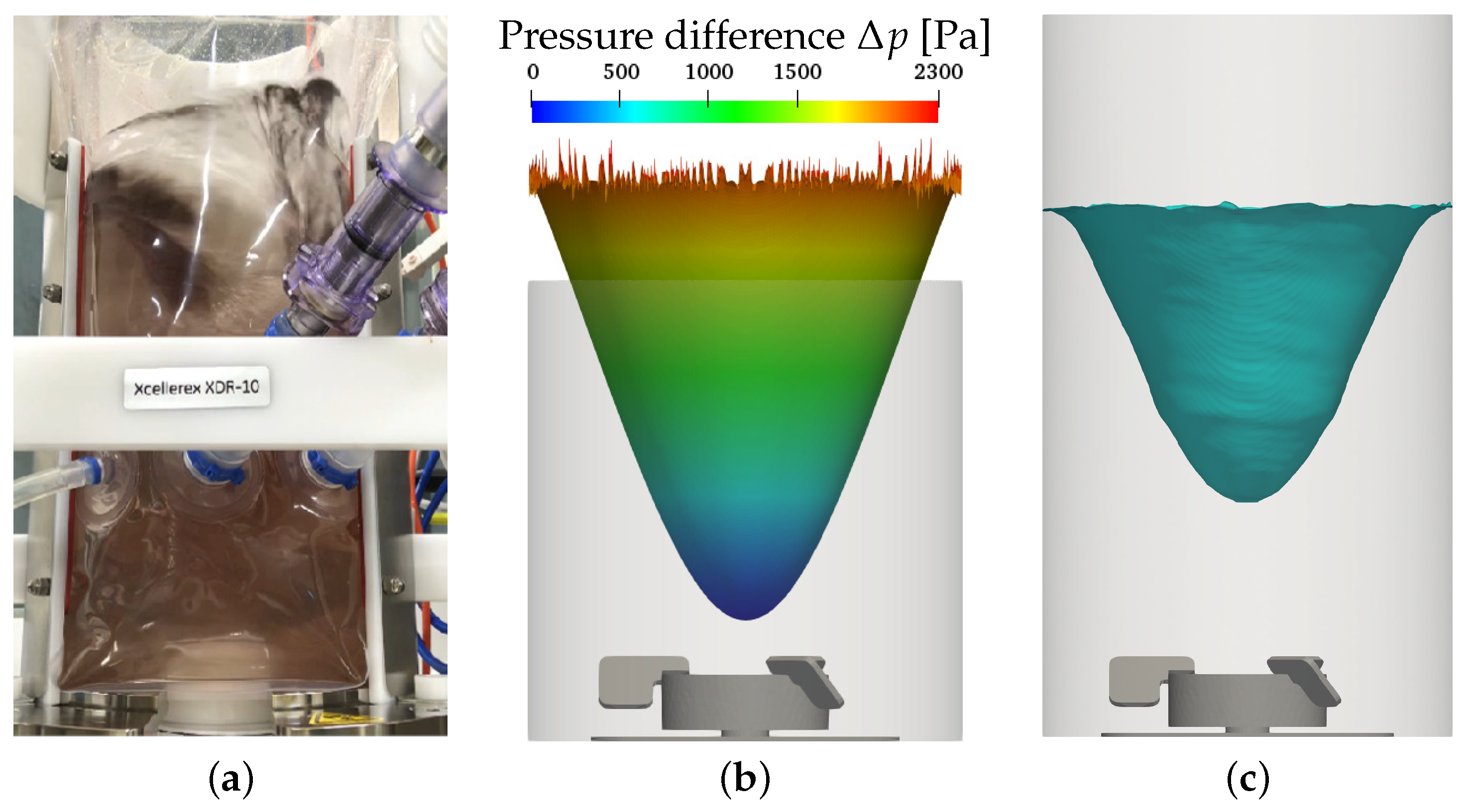
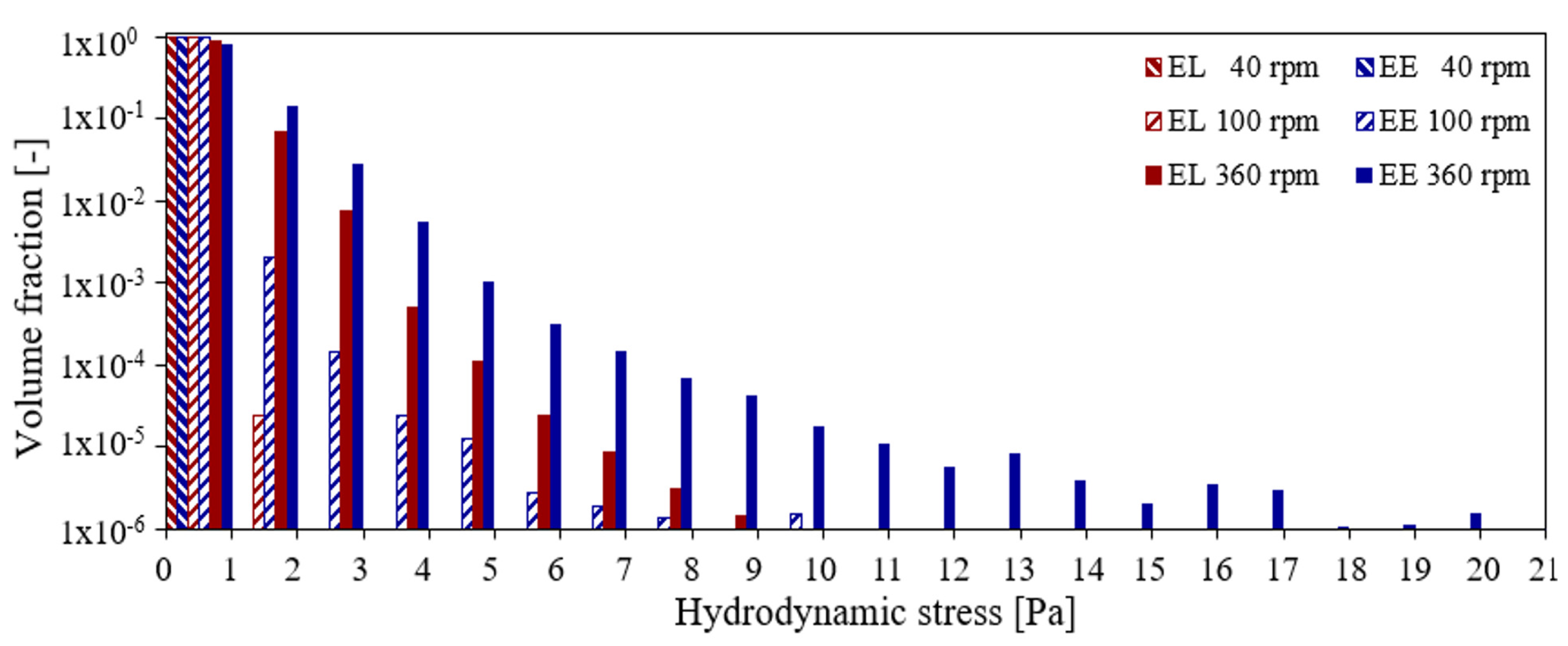
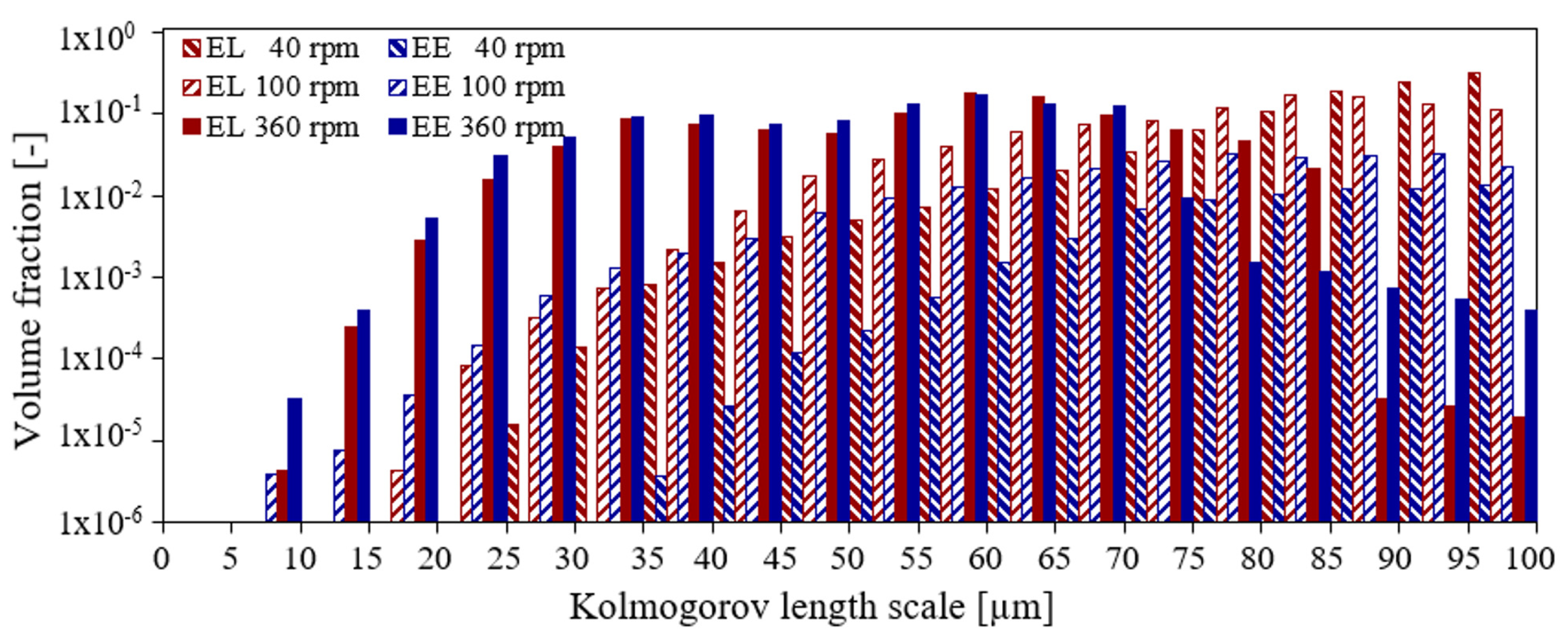
3.2. Liquid Height, Surface Vortex Formation, and Risk of Cell Damage
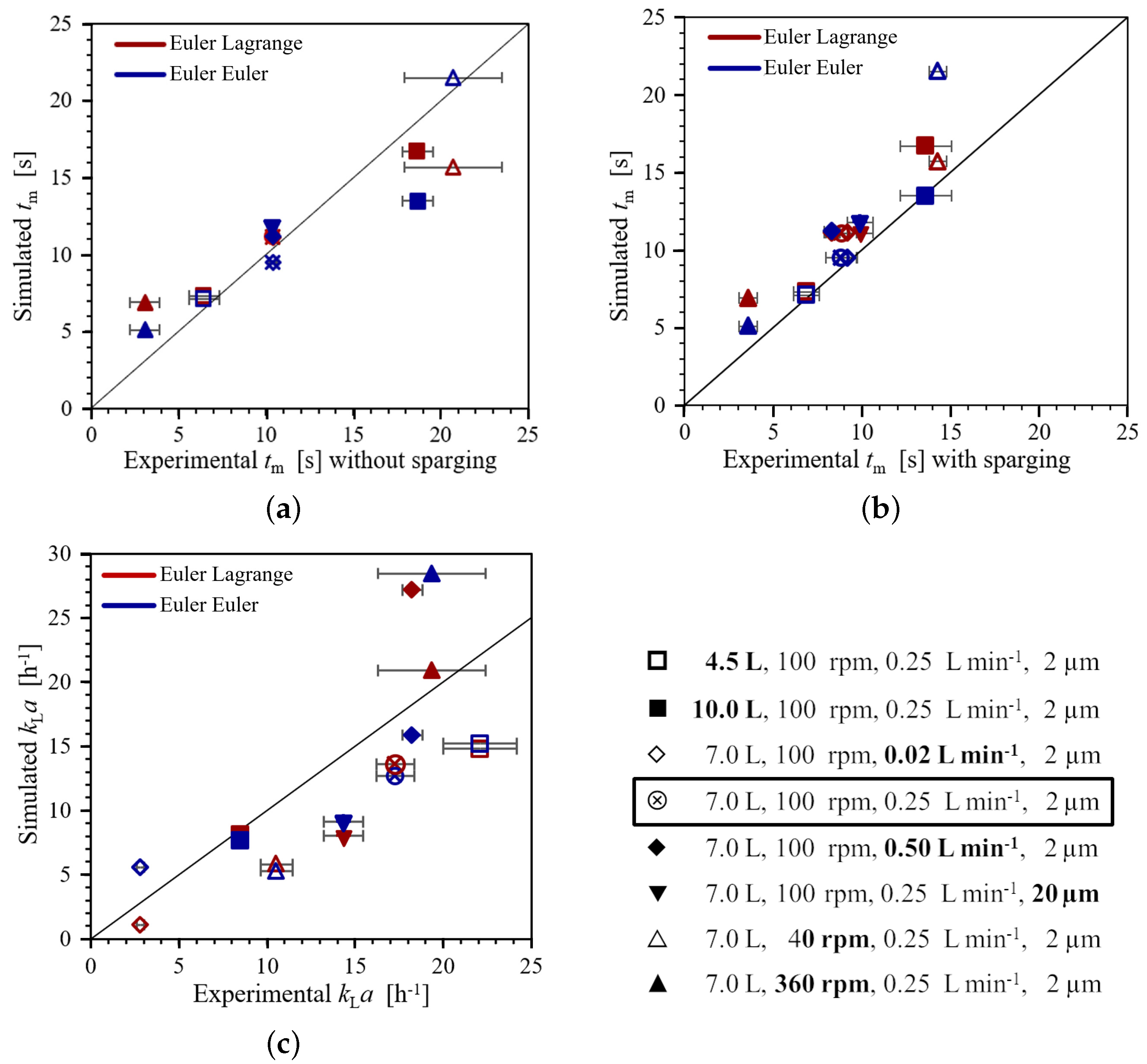
3.3. Experimental and Numerical Mixing Time and Volumetric Oxygen Mass Transfer Coefficient
3.3.1. Mixing Time
3.3.2. Volumetric Oxygen Mass Transfer Coefficient
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Eibl, R.; Kaiser, S.; Lombriser, R.; Eibl, D. Disposable bioreactors: The current state-of-the-art and recommended applications in biotechnology. Appl. Microbiol. Biotechnol. 2010, 86, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Paul, E.L.; Atiemo-Obeng, V.A.; Kresta, S.M. Handbook of Industrial Mixing: Science and Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Werner, S.; Kaiser, S.; Kraume, M.; Eibl, D. Computational fluid dynamics as a modern tool for engineering characterization of bioreactors. Pharm. Bioprocess. 2014, 2, 85–99. [Google Scholar] [CrossRef]
- Kaiser, S.C.; Löffelholz, C.; Werner, S.; Eibl, D. CFD for characterizing standard and single-use stirred cell culture bioreactors. In Computational Fluid Dynamics Technologies and Applications; Minin, I., Ed.; IntechOpen: Croatia, Balkans, 2011; Chapter 4; pp. 97–122. [Google Scholar]
- Cytiva. Xcellerex XDR Cell Culture Bioreactor Systems. Available online: https://cdn.cytivalifesciences.com/dmm3bwsv3/AssetStream.aspx?mediaformatid=10061&destinationid=10016&assetid=23694 (accessed on 9 March 2021).
- Seidel, S.; Maschke, R.W.; Werner, S.; Jossen, V.; Eibl, D. Oxygen mass transfer in biopharmaceutical processes: Numerical and experimental approaches. Chem. Ing. Tech. 2021, 93, 42–61. [Google Scholar] [CrossRef]
- Weber, A.; Bart, H. Flow simulation in a 2D bubble column with the Euler-Lagrange and Euler-Euler method. Open Chem. Eng. J. 2018, 12, 1–13. [Google Scholar] [CrossRef]
- Böhm, L.; Hohl, L.; Bliatsiou, C.; Kraume, M. Multiphase stirred tank bioreactors—New geometrical concepts and scale-up approaches. Chem. Ing. Tech. 2019, 91, 1724–1746. [Google Scholar] [CrossRef]
- Wutz, J.; Lapin, A.; Siebler, F.; Schäfer, J.E.; Wucherpfennig, T.; Berger, M.; Takors, R. Predictability of kLa in stirred tank reactors under multiple operating conditions using an Euler-Lagrange approach. Eng. Life Sci. 2016, 16, 633–642. [Google Scholar] [CrossRef]
- Mishra, S.; Kumar, V.; Sarkar, J.; Rathore, A.S. CFD based mass transfer modeling of a single use bioreactor for production of monoclonal antibody biotherapeutics. Chem. Eng. J. 2021, 412, 128592. [Google Scholar] [CrossRef]
- MixIT. Tridiagonal® Solutions. 2019. Available online: https://tridiagonal.com/mixit/ (accessed on 16 March 2020).
- OpenFOAM. The OpenFOAM Foundation. 2019. Available online: www.openfoam.org (accessed on 12 February 2020).
- Nienow, A.W. Reactor engineering in large scale animal cell culture. Cytotechnology 2006, 50, 9–33. [Google Scholar] [CrossRef] [Green Version]
- Chisti, Y. Hydrodynamic damage to animal cells. Crit. Rev. Biotechnol. 2001, 21, 67–110. [Google Scholar] [CrossRef]
- Hu, W.; Berdugo, C.; Chalmers, J.J. The potential of hydrodynamic damage to animal cells of industrial relevance: Current understanding. Cytotechnology 2011, 63, 445–460. [Google Scholar] [CrossRef] [Green Version]
- Sieck, J.B.; Cordes, T.; Budach, W.E.; Rhiel, M.H.; Suemeghy, Z.; Leist, C.; Villiger, T.K.; Morbidelli, M.; Soos, M. Development of a scale-down model of hydrodynamic stress to study the performance of an industrial CHO cell line under simulated production scale bioreactor conditions. J. Biotechnol. 2013, 164, 41–49. [Google Scholar] [CrossRef]
- Soos, M.; Kaufmann, R.; Winteler, R.; Kroupa, M.; Lüthi, B. Determination of maximum turbulent energy dissipation rate generated by a Rushton impeller through large eddy simulation. AIChE J. 2013, 59, 3642–3658. [Google Scholar] [CrossRef]
- Neunstoecklin, B.; Stettler, M.; Solacroup, T.; Broly, H.; Morbidelli, M.; Soos, M. Determination of the maximum operating range of hydrodynamic stress in mammalian cell culture. J. Biotechnol. 2015, 194, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Jamialahmadi, M.; Zehtaban, M.R.; Müller-Steinhagen, H.; Sarrafi, A.; Smith, J.M. Study of bubble formation under constant flow conditions. Chem. Eng. Res. Des. 2001, 79, 523–532. [Google Scholar] [CrossRef]
- Kazakis, N.; Mouza, A.; Paras, S. Experimental study of bubble formation at metal porous spargers: Effect of liquid properties and sparger characteristics on the initial bubble size distribution. Chem. Eng. J. 2008, 137, 265–281. [Google Scholar] [CrossRef]
- Löffelholz, C.; Husemann, U.; Greller, G.; Meusel, W.; Kauling, J.; Ay, P.; Kraume, M.; Eibl, R.; Eibl, D. Bioengineering parameters for single-use bioreactors: Overview and evaluation of suitable methods. Chem. Ing. Tech. 2013, 85, 40–56. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef] [PubMed]
- Kreitmayer, D.; Gopireddy, S.G.; Matsuura, T.; Aki, Y.; Katayama, Y.; Kakihara, H.; Nonaka, K.; Profitlich, T.; Urbanetz, N.A.; Gutheil, E. Numerical and experimental characterization of the single-use bioreactor XcellerexTM XDR-200. Biochem. Eng. J. 2022, 177, 108237. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Amsden, A.A.; Butler, T.D.; O’Rourke, P.J. KIVA-II: A Computer Program for Transient Multidimensional Chemically Reactive Flows with Sprays; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 1989. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W. Perry’s Chemical Engineers’ Handbook; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Behzadi, A.; Issa, R.I.; Rusche, H. Modelling of dispersed bubble and droplet flow at high phase fractions. Chem. Eng. Sci. 2004, 59, 759–770. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A.Z. A drag coefficient correlation. Z. Ver. Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Lamont, J.C.; Scott, D.S. An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J. 1970, 16, 513–519. [Google Scholar] [CrossRef]
- Han, P.; Bartels, D.M. Temperature dependence of oxygen diffusion in H2O and D2O. J. Phys. Chem. 1996, 100, 5597–5602. [Google Scholar] [CrossRef]
- Sieck, J.B.; Budach, W.E.; Suemeghy, Z.; Leist, C.; Villiger, T.K.; Morbidelli, M.; Soos, M. Adaption for survival: Phenotypic and transcriptome responses of CHO cells to elevated stress induced by agitation and sparging. J. Biotechnol. 2014, 189, 94–103. [Google Scholar] [CrossRef]
- Montante, G.; Paglianti, A. Gas hold-up distribution and mixing time in gas-liquid stirred tanks. Chem. Eng. J. 2015, 279, 648–658. [Google Scholar] [CrossRef]
- Kim, T.K. T test as a parametric statistic. Korean J. Anesthesiol. 2015, 68, 540–546. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, S.C.; Eibl, R.; Eibl, D. Engineering characteristics of a single-use stirred bioreactor at bench-scale: The Mobius CellReady 3L bioreactor as a case study. Eng. Life Sci. 2011, 11, 359–368. [Google Scholar] [CrossRef]
- Bach, C.; Yang, J.; Larsson, H.; Stocks, S.M.; Grenaey, K.V.; Albaek, M.O.; Kühne, U. Evaluation of mixing and mass transfer in a stirred pilot scale bioreactor utilizing CFD. Chem. Eng. Sci. 2017, 171, 19–26. [Google Scholar] [CrossRef]
- Gakingo, G.K.; Clarke, K.G.; Louw, T.M. A numerical investigation of the hydrodynamics and mass transfer in a three-phase gas-liquid-liquid stirred tank reactor. Biochem. Eng. J. 2020, 157, 107522. [Google Scholar] [CrossRef]
- Sarkar, J.; Shekhawat, L.K.; Loomba, V.; Rathore, A.S. CFD of mixing of multi-phase flow in a bioreactor using population balance model. Biotechnol. Prog. 2016, 32, 613–628. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Scott, K.; Kelly, W.J.; Huang, Z. Development of a Computational Fluid Dynamics Model for Scaling-up Ambr Bioreactors. Biotechnol. Bioprocess Eng. 2018, 23, 710–725. [Google Scholar] [CrossRef]



| Condition | Working Volume | Impeller Speed | Sparging Rate | Sparger Pore Size |
|---|---|---|---|---|
| # | (L) | (rpm) | (L min) | (m) |
| 1 | 4.5 | 100 | 0.25 | 2 |
| 2 | 10.0 | 100 | 0.25 | 2 |
| 3 | 7.0 | 100 | 0.02 | 2 |
| 4 | 7.0 | 100 | 0.25 | 2 |
| 5 | 7.0 | 100 | 0.50 | 2 |
| 6 | 7.0 | 100 | 0.25 | 20 |
| 7 | 7.0 | 40 | 0.25 | 2 |
| 8 | 7.0 | 350/360 | 0.25 | 2 |
| # | Condition | Change in Liquid Height | Vortex Depth | ||
|---|---|---|---|---|---|
| (mm) | (mm) | ||||
| Exp. | EE | EE | EL | ||
| 1 | 4.5 L, 100 rpm, 0.25 L min, 2 m | 4 | 2 | 10 | 15 |
| 2 | 10.0 L, 100 rpm, 0.25 L min, 2 m | 0 | 0 | 1 | 1 |
| 3 | 7.0 L, 100 rpm, 0.02 L min, 2 m | 3 | 1 | 8 | 12 |
| 4 | 7.0 L, 100 rpm, 0.25 L min, 2 m | 3 | 1 | 8 | 12 |
| 5 | 7.0 L, 100 rpm, 0.50 L min, 2 m | 3 | 1 | 8 | 12 |
| 6 | 7.0 L, 100 rpm, 0.25 L min, 20 m | 3 | 1 | 8 | 12 |
| 7 | 7.0 L, 40 rpm, 0.25 L min, 2 m | 0 | 0 | 0 | 1 |
| 8 | 7.0 L, 360 * rpm, 0.25 L min, 2 m | 28 | 44 | 145 | 229 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kreitmayer, D.; Gopireddy, S.R.; Matsuura, T.; Aki, Y.; Katayama, Y.; Nakano, T.; Eguchi, T.; Kakihara, H.; Nonaka, K.; Profitlich, T.; et al. CFD-Based and Experimental Hydrodynamic Characterization of the Single-Use Bioreactor XcellerexTM XDR-10. Bioengineering 2022, 9, 22. https://doi.org/10.3390/bioengineering9010022
Kreitmayer D, Gopireddy SR, Matsuura T, Aki Y, Katayama Y, Nakano T, Eguchi T, Kakihara H, Nonaka K, Profitlich T, et al. CFD-Based and Experimental Hydrodynamic Characterization of the Single-Use Bioreactor XcellerexTM XDR-10. Bioengineering. 2022; 9(1):22. https://doi.org/10.3390/bioengineering9010022
Chicago/Turabian StyleKreitmayer, Diana, Srikanth R. Gopireddy, Tomomi Matsuura, Yuichi Aki, Yuta Katayama, Takuya Nakano, Takuma Eguchi, Hirofumi Kakihara, Koichi Nonaka, Thomas Profitlich, and et al. 2022. "CFD-Based and Experimental Hydrodynamic Characterization of the Single-Use Bioreactor XcellerexTM XDR-10" Bioengineering 9, no. 1: 22. https://doi.org/10.3390/bioengineering9010022
APA StyleKreitmayer, D., Gopireddy, S. R., Matsuura, T., Aki, Y., Katayama, Y., Nakano, T., Eguchi, T., Kakihara, H., Nonaka, K., Profitlich, T., Urbanetz, N. A., & Gutheil, E. (2022). CFD-Based and Experimental Hydrodynamic Characterization of the Single-Use Bioreactor XcellerexTM XDR-10. Bioengineering, 9(1), 22. https://doi.org/10.3390/bioengineering9010022





