Improvement of a Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Steady State Mass Balance of Carbon Dioxide
2.2. Steady State Mass Balance of Oxygen
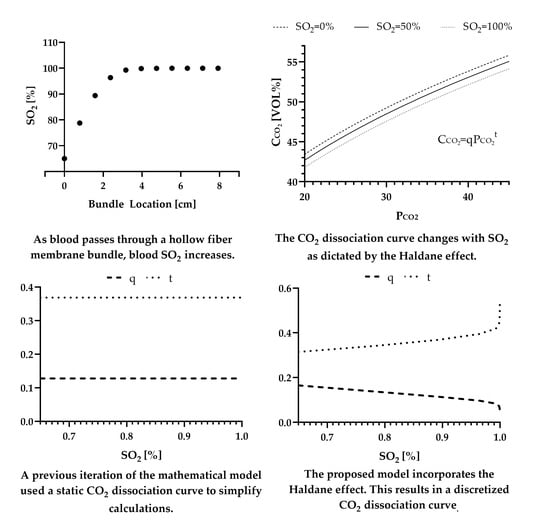
2.3. Incorporating the Haldane Effect
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Center for Health Statistics; Heron, M. Deaths: Leading Causes for 2018; National Center for Health Statistics: Hyattsville, MD, USA, 2021. [Google Scholar]
- Mockros, L.; Leonard, R.J. Compact Cross-Flow Tubular Oxygenators. Trans. Am. Soc. Artif. Intern. Organs 1985, 31, 628–633. [Google Scholar] [PubMed]
- Fournier, R.L. Oxygen Transport in Biological Systems. In Basic Transport Phenomena in Biomedical Engineering; Taylor & Francis: Philidelpha, PA, USA, 1999; p. 89. ISBN 1-56032-708-1. [Google Scholar]
- Svitek, R.G.; Federspiel, W.J. A Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators. Ann. Biomed. Eng. 2008, 36, 992–1003. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.E. Transport of Oxygen and Carbon Dioxide in Blood and Tissue Fluids. In Guyton and Hall Textbook of Medical Physiology; Elsevier, Inc.: Philidelpha, PA, USA, 2016; pp. 527–537. ISBN 978-1-4557-7005-2. [Google Scholar]
- West, J.B.; Luks, A.M. Gas Exchange. In West’s Pulmonary Pathophysiology: The Essentials; Wolters Kluwer: Philidelpha, PA, USA, 2017; pp. 20–43. ISBN 978-1-4963-3944-7. [Google Scholar]
- Jensen, F.B. Red Blood Cell PH, the Bohr Effect, and Other Oxygenation-Linked Phenomena in Blood O2 and CO2 Transport. Acta Physiol. Scand. 2004, 182, 215–227. [Google Scholar] [CrossRef] [PubMed]
- Teboul, J.-L.; Scheeren, T. Understanding the Haldane Effect. Intensive Care Med. 2017, 43, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Arthurs, G.J.; Sudhakar, M. Carbon Dioxide Transport. Contin. Educ. Anaesth. Crit. Care Pain 2005, 5, 207–210. [Google Scholar] [CrossRef] [Green Version]
- Loeppky, J.A.; Luft, U.C.; Fletcher, E.R. Quantitative Description of Whole Blood CO2 Dissociation Curve and Haldane Effect. Respir. Physiol. 1983, 51, 167–181. [Google Scholar] [CrossRef]
- Hines, A.L.; Maddox, R.N. Mass Transfer: Fundamentals and Apllications; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1985; ISBN 0-13-559609-2. [Google Scholar]
- Truskey, G.A.; Yuan, F.; Katz, D.F. Transport Phenomena in Biological Systems, 2nd ed.; Pearson Education Ltd.: Upper Saddle River, NJ, USA, 2009; ISBN 0-13-156988-0. [Google Scholar]
- Cardiovascular Implants and Artificial Organs-Blood-Gas Exchangers (Oxygenators); International Organization for Standards: Geneva, Switzerland, 2016.
- Hewitt, T.J.; Hattler, B.G.; Federspiel, W.J. A Mathematical Model of Gas Exchange in an Intravenous Membrane Oxygenator. Ann. Biomed. Eng. 1998, 26, 166–178. [Google Scholar] [CrossRef] [PubMed]
- Vaslef, S.N.; Mockros, L.F.; Anderson, R.W.; Leonard, R.J. Use of a Mathematical Model to Predict Oxygen Transfer Rates in Hollow Fiber Membrane Oxygenators. ASAIO J. 1994, 40, 990. [Google Scholar] [CrossRef] [PubMed]
- Pittman, R.N. Regulation of Tissue Oxygenation. In Regulation of Tissue Oxygenation; Colloquium Series on Integrated Systems Physiology: From Molecule to Function to Disease; Morgan & Claypool Life Sciences: San Rafael, CA, USA, 2011. [Google Scholar]
- Habler, O.P.; Messmer, K.F.W. The Physiology of Oxygen Transport. Transfus. Sci. 1997, 18, 425–435. [Google Scholar] [CrossRef]
- May, A.G.; Jeffries, R.G.; Frankowski, B.J.; Burgreen, G.W.; Federspiel, W.J. Bench Validation of a Compact Low-Flow CO2 Removal Device. Intensive Care Med. Exp. 2018, 6, 34. [Google Scholar] [CrossRef] [PubMed]
- Katoh, S.; Yoshida, F. Carbon Dioxide Transfer in a Membrane Blood Oxygenator. Ann. Biomed. Eng. 1978, 6, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.V. The Possible Effects of the Aggregation of the Molecules of Haemoglobin on Its Dissociation Curves. J. Physiol. 1910, 40, iv–vii. [Google Scholar] [CrossRef]
- Dash, R.K.; Bassingthwaighte, J.B. Erratum to: Blood HbO2 and HbCO2 Dissociation Curves at Varied O2, CO2, PH, 2,3-DPG and Temperature Levels. Ann. Biomed. Eng. 2010, 38, 1683–1701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peters, J.P.; Bulger, H.A.; Eisenman, A.J. Studies of the carbon dioxide absorption curve of human blood. J. Biol. Chem. 1924, 58, 747–768. [Google Scholar] [CrossRef]
- Lenfant, C. Gas Transport and Gas Exchange. In Circulation, Respiration, and Fluid Balance; Ruch, T.C., Patton, H.D., Eds.; Physiology and Biophysics; W.B. Saunders: Philidelpha, PA, USA, 1974; Volume 2, p. 330. [Google Scholar]
- O’Connor, T.M.; Barry, P.J.; Jahangir, A.; Finn, C.; Buckley, B.M.; El-Gammal, A. Comparison of Arterial and Venous Blood Gases and the Effects of Analysis Delay and Air Contamination on Arterial Samples in Patients with Chronic Obstructive Pulmonary Disease and Healthy Controls. Respiration 2011, 81, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Van Slyke, D.D.; Sendroy, J., Jr. Studies of Gas and Electrolyte Equilibria in Blood. XV. Line Charts for Graphic Calculations by the Henderson-Hasselbach Equation, and for Calculating Plasma Carbon Dioxide Content from Whole Blood Content. J. Biol. Chem. 1928, 79, 781–798. [Google Scholar] [CrossRef]
- Roselli, R.J.; Diller, K.R. Blood CO2 Transport and PH. In Biotransport: Principles and Applications; Springer Science+Buisness Media: New York, NY, USA, 2011; pp. 864–866. [Google Scholar]
- Greenberg, M.D. Chapter 6. Quantative Methods: Numerical Solution of Differential Equatons. In Advanced Engineering Mathematics; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1998; pp. 292–336. ISBN 0-13-321431-1. [Google Scholar]
- 3M Membrana OXYPLUS, Capillary Membrane, Type PMP 90/200; 3M Separation and Purification Sciences Division: Charlotte, NC, USA, 2019.
- Madhani, S.P.; D’Aloiso, B.D.; Frankowski, B.; Federspiel, W.J. Darcy Permeability of Hollow Fiber Membrane Bundles Made from Membrana Polymethylpentene Fibers Used in Respiratory Assist Devices. ASAIO J. 2016, 62, 329–331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Madhani, S.P.; Frankowski, B.J.; Federspiel, W.J. Fiber Bundle Design for an Integrated Wearable Artificial Lung. ASAIO J. 2017, 63, 631–636. [Google Scholar] [CrossRef] [PubMed]
- May, A.G.; Omecinski, K.S.; Frankowski, B.J.; Federspiel, W.J. Effect of Hematocrit on the CO2 Removal Rate of Artificial Lungs. ASAIO J. 2020, 66, 1161–1165. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Description | Value |
|---|---|---|
| Value of in the blood entering the HFM bundle | 45 mmHg [13] | |
| Initial value of in the blood entering the HFM bundle | 65% [13] | |
| Average value of in the sweep gas | 4 mmHg [4] | |
| Average value of in the sweep gas | 700 mmHg [4,14] | |
| Hemoglobin of blood | 12 g (dL blood)−1 [13] | |
| pH of blood entering the HFM bundle | 7.4 [5] | |
| at 50% Hb saturation for adult bovine blood | 29 mmHg [15] | |
| Hill parameter for adult bovine blood | 2.85 [15] | |
| Kinematic viscosity of blood | 0.023 cm2s−1 [4] | |
| Solubility of CO2 in blood | 6.62 × 10−4 (mL CO2) (mmHg) (mL blood)−1 [4] | |
| Solubility of O2 in blood | 3 × 10−2 (mL O2) (mmHg) (mL blood)−1 [4,14] | |
| Diffusivity of CO2 in blood | 7.39 × 10−6 cm2s−1 [4] | |
| Diffusivity of bicarbonate in blood | 4.62 × 10−6 cm2s−1 [4] | |
| Diffusivity of O2 in blood | 1.8 × 10−5 cm2s−1 [4,14] | |
| Binding capacity of hemoglobin | 1.34 mL O2 (g Hb)−1 [5,16,17] | |
| Blood flowrate | 0–600 (mL blood) min−1 [18] | |
| Measured coefficient for Equations (4), (12), and (18) | 0.54 [4] | |
| Measured coefficient for Equations (4), (12), and (18) | 0.42 [4] |
| Parameter | Description | Value |
|---|---|---|
| Cross sectional area of ModELAS HFM bundle | 16 cm2 | |
| Surface area to volume ratio of ModELAS HFM bundle | 55 cm−1 | |
| Active fiber surface area of ModELAS HFM bundle | 6700 cm2 | |
| Outer diameter of a single OXPLUS™, Membrana™ PMP fiber | 0.038 cm | |
| Porosity of ModELAS HFM bundle | 0.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omecinski, K.S.; Federspiel, W.J. Improvement of a Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators. Bioengineering 2022, 9, 568. https://doi.org/10.3390/bioengineering9100568
Omecinski KS, Federspiel WJ. Improvement of a Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators. Bioengineering. 2022; 9(10):568. https://doi.org/10.3390/bioengineering9100568
Chicago/Turabian StyleOmecinski, Katelin S., and William J. Federspiel. 2022. "Improvement of a Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators" Bioengineering 9, no. 10: 568. https://doi.org/10.3390/bioengineering9100568
APA StyleOmecinski, K. S., & Federspiel, W. J. (2022). Improvement of a Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators. Bioengineering, 9(10), 568. https://doi.org/10.3390/bioengineering9100568