Haemodynamic Analysis of Branched Endografts for Complex Aortic Arch Repair
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometric Model
2.2. Mathematical Model and Boundary Conditions
2.3. Haemodynamic Metrics
3. Results
3.1. Flow Patterns and Pressure
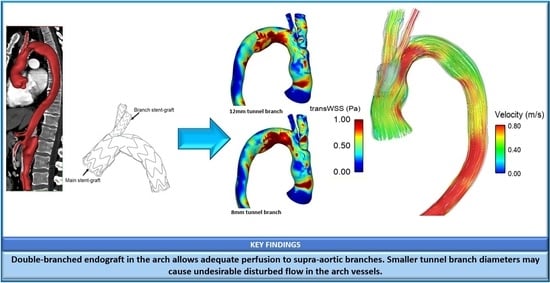
3.2. Wall Shear Stress
3.3. Vortical and Helical Flow
4. Discussion
4.1. Patient Comparison
4.2. Effect of Tunnel Branch Diameter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, Z.; Tan, F.P.P.; Riga, C.V.; Bicknell, C.D.; Hamady, M.S.; Gibbs, R.G.J.; Wood, N.B.; Xu, X.Y. Analysis of flow patterns in a patient-specific aortic dissection model. J. Biomech. Eng. 2010, 132, 051007. [Google Scholar] [CrossRef]
- Cheng, S. Aortic arch pathologies-incidence and natural history. Gefässchirurgie 2016, 21, 212–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nienaber, C.A.; Fattori, R.; Lund, G.; Dieckmann, C.; Wolf, W.; von Kodolitsch, Y.; Nicolas, V.; Pierangeli, A. Nonsurgical reconstruction of thoracic aortic dissection by stent–graft placement. N. Engl. J. Med. 1999, 340, 1539–1545. [Google Scholar] [CrossRef] [PubMed]
- Bodell, B.D.; Taylor, A.C.; Patel, P.J. Thoracic endovascular aortic repair: Review of current devices and treatments options. Tech. Vasc. Interv. Radiol. 2018, 21, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Kuratani, T. Best surgical option for arch extension of type B dissection: The endovascular approach. Ann. Cardiothorac. Surg. 2014, 3, 292. [Google Scholar]
- van Bakel, T.M.; Arthurs, C.J.; van Herwaarden, J.A.; Moll, F.L.; Eagle, K.A.; Patel, H.J.; Trimarchi, S.; Figueroa, C.A. A computational analysis of different endograft designs for Zone 0 aortic arch repair. Eur. J. Cardio-Thorac. Surg. 2018, 54, 389–396. [Google Scholar] [CrossRef] [Green Version]
- van Bakel, T.M.; de Beaufort, H.W.; Trimarchi, S.; Marrocco-Trischitta, M.M.; Bismuth, J.; Moll, F.L.; Patel, H.J.; van Herwaarden, J.A. Status of branched endovascular aortic arch repair. Ann. Cardiothorac. Surg. 2018, 7, 406–413. [Google Scholar] [CrossRef] [Green Version]
- Abraham, C.Z.; Rodriguez, V.M. Upcoming Technology for Aortic Arch Aneurysms. Endovasc. Today 2015, 46–52. Available online: https://evtoday.com/articles/2015-nov/upcoming-technology-for-aortic-arch-aneurysms (accessed on 10 August 2021).
- Rylski, B.; Czerny, M. Relay®Branch: A Review of the Technology and Early Results. Suppl. Endovasc. Today Eur. 2002, 6. Available online: https://vasculartube.com/2018/02/supplement2/relaybranch-a-review-of-the-technology-and-early-results/ (accessed on 10 August 2021).
- Ferrer, C.; Cao, P. Endovascular arch replacement with a dual branched endoprosthesis. Ann. Cardiothorac. Surg. 2018, 7, 366–371. [Google Scholar] [CrossRef] [Green Version]
- Heaton, D.H. The Next Generation of Aortic Endografts. Endovasc. Today 2009, 49–52. Available online: https://evtoday.com/articles/2009-jan/EVT0109_03-php (accessed on 21 August 2021).
- Santos, I.C.; Rodrigues, A.; Figueiredo, L.; Rocha, L.A.; Tavares, J.M.R. Mechanical properties of stent–graft materials. J. Mater. Des. Appl. 2012, 226, 330–341. [Google Scholar] [CrossRef] [Green Version]
- Prasad, A.; Xiao, N.; Gong, X.; Zarins, C.; Figueroa, C. A computational framework for investigating the positional stability of aortic endografts. Biomech. Model. Mechanobiol. 2013, 12, 869–887. [Google Scholar] [CrossRef] [PubMed]
- Figueroa, C.A.; Zarins, C. Computational analysis of displacement forces acting on endografts used to treat aortic aneurysms. In Biomechanics and Mechanobiology of Aneurysms; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7, pp. 221–246. [Google Scholar]
- Benard, N.; Coisne, D.; Donal, E.; Perrault, R. Experimental study of laminar blood flow through an artery treated by a stent implantation: Characterisation of intra- stent wall shear stress. J. Biomech. 2003, 36, 991–998. [Google Scholar] [CrossRef]
- Kandail, H.; Hamady, M.; Xu, X.Y. Patient-specific analysis of displacement forces acting on fenestrated stent grafts for endovascular aneurysm repair. J. Biomech. 2014, 47, 3546–3554. [Google Scholar] [CrossRef] [PubMed]
- Ong, C.; Xiong, F.; Kabinejadian, F.; Praveen Kumar, G.; Cui, F.; Chen, G.; Ho, P.; Leo, H. Hemodynamic analysis of a novel stent graft design with slit perforations in thoracic aortic aneurysm. J. Biomech. 2019, 85, 210–217. [Google Scholar] [CrossRef] [PubMed]
- Raptis, A.; Xenos, M.; Kouvelos, G.; Giannoukas, A.; Matsagkas, M. Haemodynamic performance of AFX and Nellix endografts: A computational fluid dynamics study. Interact. Cardiovasc. Thorac. Surg. 2018, 26, 826–833. [Google Scholar] [CrossRef] [PubMed]
- Tan, F.P.P.; Soloperto, G.; Bashford, S.; Wood, N.B.; Thom, S.; Hughes, A.; Xu, X.Y. Analysis of flow disturbance in a stenosed carotid artery bifurcation using two-equation transitional and turbulence models. J. Biomech. Eng. 2008, 130, 061008. [Google Scholar] [CrossRef]
- Kousera, C.A.; Wood, N.B.; Seed, W.A.; Torii, R.; O’Regan, D.; Xu, X.Y. A numerical study of aortic flow stability and comparison with in vivo flow measurements. J. Biomech. Eng. 2013, 135, 011003. [Google Scholar] [CrossRef]
- Tan, F.P.P.; Borghi, A.; Mohiaddin, R.H.; Wood, N.B.; Thom, S.; Xu, X.Y. Analysis of flow patterns in a patient-specific thoracic aortic aneurysm model. Comput. Struct. 2009, 87, 680–690. [Google Scholar] [CrossRef]
- Khanafer, K.; Berguer, R. Fluid–structure interaction analysis of turbulent pulsatile flow within a layered aortic wall as related to aortic dissection. J. Biomech. 2009, 42, 2642–2648. [Google Scholar] [CrossRef]
- Pirola, S.; Cheng, Z.; Jarral, O.A.; O’Regan, D.P.; Pepper, J.R.; Athanasiou, T.; Xu, X.Y. On the choice of outlet boundary conditions for patient-specific analysis of aortic flow using computational fluid dynamics. J. Biomech. 2017, 60, 15–21. [Google Scholar] [CrossRef]
- Vignon-Clementel, I.E.; Figueroa, C.A.; Jansen, K.E.; Taylor, C.A. Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 625–640. [Google Scholar] [CrossRef] [Green Version]
- Mohamied, Y.; Rowland, E.; Bailey, E.; Sherwin, S.; Schwartz, M.; Weinberg, P. Change of direction in the biomechanics of atherosclerosis. Ann. Biomed. Eng. 2015, 43, 16–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazakidi, A.; Plata, A.M.; Sherwin, S.J.; Weinberg, P.D. Effect of reverse flow on the pattern of wall shear stress near arterial branches. J. R. Soc. Interface 2011, 8, 1594–1603. [Google Scholar] [CrossRef] [PubMed]
- Mohamied, Y.; Sherwin, S.J.; Weinberg, P.D. Understanding the fluid mechanics behind transverse wall shear stress. J. Biomech. 2017, 50, 102–109. [Google Scholar] [CrossRef] [Green Version]
- Peiffer, V.; Sherwin, S.J.; Weinberg, P.D. Computation in the rabbit aorta of a new metric—the transverse wall shear stress—to quantify the multidirectional character of disturbed blood flow. J. Biomech. 2013, 46, 2651–2658. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersson, M.; Lantz, J.; Ebbers, T.; Karlsson, M. Multidirectional WSS disturbances in stenotic turbulent flows: A pre- and post-intervention study in an aortic coarctation. J. Biomech. 2016, 51, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Yan, Y.; Liu, C. New visualization method for vortex structure in turbulence by lambda2 and vortex filaments. Appl. Math. Model. 2016, 40, 500–509. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Chong, M.Y.; Gu, B.; Chan, B.T.; Ong, Z.C.; Xu, X.Y.; Lim, E. Effect of intimal flap motion on flow in acute type B aortic dissection by using fluid-structure interaction. Int. J. Numer. Meth. Biomed. Engng. 2020, 36, e3399. [Google Scholar] [CrossRef]
- Tasso, P.; Lodi Rizzini, M.; Raptis, A.; Matsagkas, M.; de Nisco, G.; Gallo, D.; Xenos, M.; Morbiducci, U. In-stent graft helical flow intensity reduces the risk of migration after endovascular aortic repair. J. Biomech. 2019, 94, 170–179. [Google Scholar] [CrossRef]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; de Cobelli, F.; del Maschio, A.; Montevecchi, F.; Redaelli, A. In vivo quantification of helical blood flow in human aorta by time-resolved three-dimensional cine phase contrast magnetic resonance imaging. Ann. Biomed. Eng. 2009, 37, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Ponzini, R.; Rizzo, G.; Cadioli, M.; Esposito, A.; Montevecchi, F.; Redaelli, A. Mechanistic insight into the physiological relevance of helical blood flow in the human aorta: An in vivo study. Biomech. Model. Mechanobiol. 2011, 10, 339–355. [Google Scholar] [CrossRef]
- Grigioni, M.; Daniele, C.; Morbiducci, U.; del Gaudio, C.; D’Avenio, G.; Balducci, A.; Barbaro, V. A mathematical description of blood spiral flow in vessels: Application to a numerical study of flow in arterial bending. J. Biomech. 2005, 38, 1375–1386. [Google Scholar] [CrossRef]
- Qiao, Y.; Fan, J.; Ding, Y.; Zhu, T.; Luo, K. A primary computational fluid dynamics study of pre- and post-TEVAR with intentional left subclavian artery coverage in a type B aortic dissection. J. Biomech. Eng. 2019, 141, 111002. [Google Scholar] [CrossRef]
- Zhu, G.; Yuan, Q.; Yang, J.; Yeo, J.H. The role of the circle of Willis in internal carotid artery stenosis and anatomical variations: A computational study based on a patient-specific three-dimensional model. Biomed. Eng. Online 2015, 14, 107. [Google Scholar] [CrossRef] [Green Version]
- DeVault, K.; Gremaud, P.A.; Novak, V.; Olufsen, M.S.; Vernières, G.; Zhao, P. Blood flow in the circle of willis: Modeling and calibration. Multiscale Modeling Simul. 2008, 7, 888–909. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Mao, L.; Ding, Y.; Fan, J.; Luo, K.; Zhu, T. Effects of in situ fenestration stent-graft of left subclavian artery on the hemodynamics after thoracic endovascular aortic repair. Vascular 2019, 27, 369–377. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Mao, L.; Ding, Y.; Fan, J.; Zhu, T.; Luo, K. Hemodynamic consequences of TEVAR with in situ double fenestrations of left carotid artery and left subclavian artery. Med. Eng. Phys. 2020, 76, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Kandail, H.; Hamady, M.; Xu, X.Y. Comparison of blood flow in branched and fenestrated stent-grafts for endovascular repair of abdominal aortic aneurysms. J. Endovasc. Ther. 2015, 22, 578–590. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Mao, L.; Zhu, T.; Fan, J.; Luo, K. Biomechanical implications of the fenestration structure after thoracic endovascular aortic repair. J. Biomech. 2020, 99, 109478. [Google Scholar] [CrossRef]
- Liu, X.; Pu, F.; Fan, Y.; Deng, X.; Li, D.; Li, S. A numerical study on the flow of blood and the transport of LDL in the human aorta: The physiological significance of the helical flow in the aortic arch. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Mazzi, V.; Morbiducci, U.; Calò, K.; De Nisco, G.; Lodi Rizzini, M.; Torta, E.; Caridi, G.C.A.; Chiastra, C.; Gallo, D. Wall shear stress topological skeleton analysis in cardiovascular flows: Methods and applications. Mathematics 2021, 9, 720. [Google Scholar] [CrossRef]
- Liu, X.; Fan, Y.; Deng, X. Effect of spiral flow on the transport of oxygen in the Aorta: A numerical study. Ann. Biomed. Eng. 2010, 38, 917–926. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zhan, W.; Hamady, M.; Xu, X.Y. A pilot study of aortic hemodynamics before and after thoracic endovascular repair with a double-branched endograft. Med. Nov. Technol. Devices 2019, 4, 100027. [Google Scholar] [CrossRef]











| Model | Tunnel Branch Diameter (mm) | Δ Pressure (mmHg) |
|---|---|---|
| Patient 1 | 12 | 10.45 |
| 1A | 10 | 9.95 |
| 1B | 8 | 9.53 |
| Model | Tunnel Branch Diameter (mm) | Lumen C.S. Area at Tunnel Branch Mouth (mm2) | % of Lumen C.S. Area Taken up by Tunnel Branches | HFI |
|---|---|---|---|---|
| Patient 1 | 12 | 706 | 32.03 | 0.391 |
| Model 1A | 10 | 706 | 22.25 | 0.380 |
| Model 1B | 8 | 706 | 14.24 | 0.397 |
| Patient 2 | 12 | 1219 | 18.55 | 0.476 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sengupta, S.; Hamady, M.; Xu, X.-Y. Haemodynamic Analysis of Branched Endografts for Complex Aortic Arch Repair. Bioengineering 2022, 9, 45. https://doi.org/10.3390/bioengineering9020045
Sengupta S, Hamady M, Xu X-Y. Haemodynamic Analysis of Branched Endografts for Complex Aortic Arch Repair. Bioengineering. 2022; 9(2):45. https://doi.org/10.3390/bioengineering9020045
Chicago/Turabian StyleSengupta, Sampad, Mohamad Hamady, and Xiao-Yun Xu. 2022. "Haemodynamic Analysis of Branched Endografts for Complex Aortic Arch Repair" Bioengineering 9, no. 2: 45. https://doi.org/10.3390/bioengineering9020045