Machine Learning for Shape Memory Graphene Nanoribbons and Applications in Biomedical Engineering
Abstract
:1. Introduction
2. Methods
2.1. Moment Tensor Potentials (MTP)
2.2. ML Implementation for a GO Layer
2.3. ML Implementation for GO Nanoribbons
3. Results and Discussion
3.1. ML Results for a GO Layer
3.2. ML Results for GO Nanoribbons
3.3. Effect of Oxygen Defects in GO Nanoribbons
3.4. Effect of Boron and Nitrogen Substitutions
4. Data-Driven Approaches for Studying Materials with Shape Memory Effects in Biomedical and Other Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Cui, L.; Li, Z.; Lu, H.H.; Qi, X.M.; Wang, W.J.; Jin, X.X.; Dong, Y.B.; Fu, Y.Q.; Jiang, W.B.; et al. Thermodynamic coupling behavior and energy harvesting of vapor grown carbon fiber/graphene oxide/epoxy shape memory composites. Compos. Sci. Technol. 2021, 203, 108583. [Google Scholar] [CrossRef]
- Shende, P.; Augustine, S.; Prabhakar, B. A review on graphene nanoribbons for advanced biomedical applications. Carbon Lett. 2020, 30, 465–475. [Google Scholar] [CrossRef]
- Stutzel, E.U.; Burghard, M.; Kern, K.; Traversi, F.; Nichele, F.; Sordan, R. A Graphene Nanoribbon Memory Cell. Small 2010, 6, 2822–2825. [Google Scholar] [CrossRef] [PubMed]
- Puster, M.; Rodriguez-Manzo, J.A.; Balan, A.; Drndic, M. Toward sensitive graphene nanoribbon-nanopore devices by preventing electron beam-induced damage. ACS Nano 2013, 7, 11283–11289. [Google Scholar] [CrossRef]
- Aissa, B.; Memon, N.K.; Ali, A.; Khraishehl, M.K. Recent progress in the growth and applications of graphene as a smart material: A review. Front. Mater. 2015, 2, 58. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.W.; Cheng, H.H.; Zhang, M.; Zhao, Y.; Qu, L.T.; Shi, G.Q. Graphene-based smart materials. Nat. Rev. Mater. 2017, 2, 17046. [Google Scholar] [CrossRef]
- Badu, S.; Melnik, R.; Singh, S. Mathematical and computational models of RNA nanoclusters and their applications in data-driven environments. Mol. Simul. 2020, 46, 1094–1115. [Google Scholar] [CrossRef]
- Sytnyk, D.; Melnik, R. Mathematical Models with Nonlocal Initial Conditions. Math. Comput. Appl. 2021, 26, 73. [Google Scholar]
- The rise of data-driven modelling. Nat. Rev. Phys. 2021, 3, 383. [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating Scientific Knowledge with Machine Learning for Engineering and Environmental Systems. arXiv 2021, arXiv:2003.04919. [Google Scholar]
- Ranjan, P.; Agrawal, S.; Sinha, A.; Rao, T.R.; Balakrishnan, J.; Thakur, A.D. A Low-Cost Non-explosive Synthesis of Graphene Oxide for Scalable Applications. Sci. Rep. 2018, 8, 12007. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Jia, J.; Yousefi, N.; Shen, X.; Kim, J.K. Excellent optoelectrical properties of graphene oxide thin films deposited on a flexible substrate by Langmuir–Blodgett assembly. J. Mater. Chem. C 2013, 1, 6869–6877. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. Synthesis of large scale graphene oxide using plasma enhanced chemical vapor deposition method and its application in humidity sensing. J. Appl. Phys. 2016, 119, 103301. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Raza, M.A.; Ghauri, F.A.; Kanwal, R.; Ahmad, A.; Inam, A. Graphene Oxide Coatings Deposited on Steel Substrate Using Electrophoretic Deposition and Electrochemical Evaluation of Coatings in Saline Media. In Key Engineering Materials; Advanced Materials—XV; Trans Tech Publications Ltd.: Baech, Switzerland, 2018; Volume 778, pp. 111–117. [Google Scholar]
- Smith, A.T.; LaChance, A.M.; Zeng, S.; Liu, B.; Sun, L. Synthesis, properties, and applications of graphene oxide/reduced graphene oxide and their nanocomposites. Nano Mater. Sci. 2019, 1, 31–47. [Google Scholar] [CrossRef]
- Mei, Q.; Liu, B.; Han, G.; Liu, R.; Han, M.Y.; Zhang, Z. Graphene Oxide: From Tunable Structures to Diverse Luminescence Behaviors. Adv. Sci. 2019, 6, 1900855. [Google Scholar] [CrossRef] [Green Version]
- Zheng, P.; Wu, N. Fluorescence and Sensing Applications of Graphene Oxide and Graphene Quantum Dots: A Review. Chem. Asian J. 2017, 12, 2343–2353. [Google Scholar] [CrossRef]
- Yogesh, G.K.; Shuaib, E.; Roopmani, P.; Gumpu, M.B.; Krishnan, U.M.; Sastikumar, D. Synthesis, characterization and bioimaging application of laser-ablated graphene-oxide nanoparticles (nGOs). Diam. Relat. Mater. 2020, 104, 107733. [Google Scholar] [CrossRef]
- Samad, A.; Kim, H.J.; Shin, Y.H. Structure stability and high Li storage capacity of the unzipped graphene oxide monolayer. Appl. Surf. Sci. 2019, 475, 151–157. [Google Scholar] [CrossRef]
- Jain, V.; Kandasubramanian, B. Functionalized graphene materials for hydrogen storage. J. Mater. Sci. 2020, 55, 1865–1903. [Google Scholar] [CrossRef]
- Jindal, H.; Oberoi, A.S.; Sandhu, I.S.; Chitkara, M.; Singh, B. Graphene for hydrogen energy storage—A comparative study on GO and rGO employed in a modified reversible PEM fuel cell. Int. J. Energy Res. 2021, 45, 5815–5826. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, L.J.; Wang, Y.X.; Tang, J.G.; Wang, Y.; Cheng, M.M.; Du, Y.C.; Yang, K.; Kipper, M.J.; Hedayati, M. The Preparation and Study of Ethylene Glycol-Modified Graphene Oxide Membranes for Water Purification. Polymers 2019, 11, 188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alnoor, O.; Laoui, T.; Ibrahim, A.; Kafiah, F.; Nadhreen, G.; Akhtar, S.; Khan, Z. Graphene Oxide-Based Membranes for Water Purification Applications: Effect of Plasma Treatment on the Adhesion and Stability of the Synthesized Membranes. Membranes 2020, 10, 292. [Google Scholar] [CrossRef] [PubMed]
- Morales-Zamudio, L.; Lozano, T.; Caballero-Briones, F.; Zamudio, M.A.M.; Angeles-San Martin, M.E.; de Lira-Gomez, P.; Martinez-Colunga, G.; Rodriguez-Gonzalez, F.; Neira, G.; Sanchez-Valdes, S. Structure and mechanical properties of graphene oxide-reinforced polycarbonate. Mater. Chem. Phys. 2021, 261, 124180. [Google Scholar] [CrossRef]
- Wan, S.; Peng, J.; Li, Y.; Hu, H.; Jiang, L.; Cheng, Q. Use of Synergistic Interactions to Fabricate Strong, Tough, and Conductive Artificial Nacre Based on Graphene Oxide and Chitosan. ACS Nano 2015, 9, 9830–9836. [Google Scholar] [CrossRef] [PubMed]
- Nath, J.; Shekhar, S.; Dolui, S.K. Artificial Nacre-based Chitosan/Graphene Oxide-Mg Hydrogel with Significant Mechanical Strength and Shape Memory Effect. Polym. Gels Ser. A 2021, 63, 123–132. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Liu, W.; Liu, Z. Graphene Nanoarchitectonics: A New Material Horizon for Reinforcement of Sustainable Polymers. Front. Mater. 2020, 7, 276. [Google Scholar] [CrossRef]
- Zhang, X.J.; Yang, Q.S.; Leng, J.S. How graphene oxide affects shape memory properties and strength of poly(l-lactide-co-ϵ-aprolactone)). J. Intell. Mater. Syst. Struct. 2020, 31, 2152–2164. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, J. Isocyanate Modified GO Shape-Memory Polyurethane Composite. Polymers 2020, 12, 118. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.; Sisodiya, M.; Khobragade, P.; Von Gratowski, S. Fast Triggered Controllable Electrically Actuated Shape Memory Epoxy: Graphene oxide Nanocomposites. Acad. J. Polym. Sci. 2020, 4, 555627. [Google Scholar]
- Chang, Z.; Deng, J.; Chandrakumara, G.G.; Yan, W.; Liu, J.Z. Two-dimensional shape memory graphene oxide. Nat. Commun. 2016, 7, 11972. [Google Scholar] [CrossRef] [Green Version]
- Chang, Z.; Deng, J.; Chandrakumara, G.G.; Yan, W.; Liu, J.Z. Two-way actuation of graphene oxide arising from quantum mechanical effects. Appl. Phys. Lett. 2016, 109, 143902. [Google Scholar] [CrossRef]
- Liu, J.Z.; Hughes, J. Electromechanical actuation of pristine graphene and graphene oxide: Origin, optimization, and comparison. arXiv 2019, arXiv:1903.02729. [Google Scholar]
- León, C.; Melnik, R. Studies of Shape Memory Graphene Nanostructures via Integration of Physics-based Modelling and Machine Learning. In Proceedings of the 9th Edition of the International Conference on Computational Methods for Coupled Problems in Science and Engineering (COUPLED PROBLEMS 2021), CIMNE, Barcelona, Spain, 13–16 June 2021; IS25–Physics Informed Machine Learning for Scientific Computing. pp. 1–12. [Google Scholar] [CrossRef]
- Bertolazzi, S.; Bondavalli, P.; Roche, S.; San, T.; Choi, S.Y.; Colombo, L.; Bonaccorso, F.; Samori, P. Nonvolatile memories based on graphene and related 2D materials. Adv. Mater. 2019, 31, 1806663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Novikov, I.S.; Gubaev, K.; Podryabinkin, E.V.; Shapeev, A.V. The MLIP package: Moment Tensor Potentials with MPI and active learning. Mach. Learn. Sci. Technol. 2021, 2, 025002. [Google Scholar] [CrossRef]
- Shapeev, A.V. Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simul. 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
- Prabhakar, S.; Melnik, R.; Bonilla, L.L.; Raynolds, J.E. Spin echo dynamics under an applied drift field in graphene nanoribbon superlattices. Appl. Phys. Lett. 2013, 103, 233112. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, S.; Melnik, R. Relaxation of electron–hole spins in strained graphene nanoribbons. J. Phys. Condens. Matter. 2015, 27, 435801. [Google Scholar] [CrossRef]
- Prabhakar, S.; Melnik, R.; Bonilla, L. Pseudospin lifetime in relaxed-shape armchair graphene nanoribbons due to in-plane phonon modes. Phys. Rev. B 2016, 93, 115417. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, S.; Melnik, R.; Bonilla, L. Strain engineering of graphene nanoribbons: Pseudomagnetic versus external magnetic fields. Eur. Phys. J. B 2017, 90, 92. [Google Scholar] [CrossRef]
- Prabhakar, S.; Melnik, R. Ab-initio calculations of strain induced relaxed shape armchair graphene nanoribbon. Phys. E Low-Dimens. Syst. Nanostructure 2019, 114, 113648. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.M.; Wang, H.S.; Ma, C.X.; Chen, L.X.; Jiang, C.X.; Chen, C.; Xie, X.M.; Li, A.P.; Wang, X.R. Graphene nanoribbons for quantum electronics. Nat. Rev. Phys. 2021, 3, 791–802. [Google Scholar] [CrossRef]
- Zakharova, O.V.; Mastalygina, E.E.; Golokhvast, K.S.; Gusev, A.A. Graphene nanoribbons: Prospects of application in biomedicine and toxicity. Nanomaterials 2021, 11, 2425. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.Y.; Chen, X.; He, Y.H.; Gu, Y.Q.; Zhu, C.Z.; Yang, G.H.; Qu, L.L. Recent advances in graphene nanoribbons for biosensing and biomedicine. J. Mater. Chem. B 2021, 9, 6129–6143. [Google Scholar] [CrossRef]
- Seki, K.; Kura, H.; Sato, T.; Taniyama, T. Size dependence of martensite transformation temperature in ferromagnetic shape memory alloy FePd. J. Appl. Phys. 2008, 103, 063910. [Google Scholar] [CrossRef]
- Dhote, R.; Melnik, R.; Zu, J. Dynamic thermo-mechanical coupling and size effects in finite shape memory alloy nanostructures. Comput. Mater. Sci. 2012, 63, 105–117. [Google Scholar] [CrossRef]
- Friedrich, N.; Brandimarte, P.; Li, J.C.; Saito, S.; Yamaguchi, S.; Pozo, I.; Pena, D.; Frederiksen, T.; Garcia-Lekue, A.; Sanchez-Portal, D.; et al. Magnetism of Topological Boundary States Induced by Boron Substitution in Graphene Nanoribbons. Phys. Rev. Lett. 2020, 125, 146801. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Zhang, Z.H.; Zhao, Y.J. Shape memory graphene and cutting-edge achievements. APL Mater. 2020, 8, 050903. [Google Scholar] [CrossRef]
- Kausar, A. Graphene to Polymer/Graphene Nanocomposites: Emerging Research and Opportunities; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Langer, R.; Tirrell, D. Designing materials for biology and medicine. Nature 2004, 428, 487–492. [Google Scholar] [CrossRef]
- Gebeshuber, I.C. Biotribology inspires new technologies. Nano Today 2007, 2, 30–37. [Google Scholar] [CrossRef]
- Siddaiah, A.; Menezes, P.L. Advances in bio-inspired tribology for engineering applications. J. Bio- Tribo-Corros. 2016, 2, 23. [Google Scholar] [CrossRef] [Green Version]
- Kujala, S.; Pajala, A.; Kallioinen, M.; Pramila, A.; Tuukkanen, J.; Ryhanen, J. Biocompatibility and strength properties of nitinol shape memory alloy suture in rabbit tendon. Biomaterials 2004, 25, 353–358. [Google Scholar] [CrossRef]
- Rocher, P.; El Medawar, L.; Hornez, J.C.; Traisnel, M.; Breme, J.; Hildebrand, H.F. Biocorrosion and cytocompatibility assessment of NiTi shape memory alloys. Scr. Mater. 2004, 50, 255–260. [Google Scholar] [CrossRef]
- Idelsohn, S.; Pena, J.; Lacroix, D.; Planell, J.A.; Gil, F.J.; Arcas, A. Continuous mandibular distraction osteogenesis using superelastic shape memory alloy (SMA). J. Mater. Sci. Mater. Med. 2004, 15, 541–546. [Google Scholar] [CrossRef] [PubMed]
- Florio, G.; Puglisi, G. Unveiling the influence of device stiffness in single macromolecule unfolding. Sci. Rep. 2019, 9, 4997. [Google Scholar] [CrossRef]
- Dhote, R.; Gomez, H.; Melnik, R.; Zu, J. 3D coupled thermo-mechanical phase-field modeling of shape memory alloy dynamics via isogeometric analysis. Comput. Struct. 2015, 154, 48–58. [Google Scholar] [CrossRef] [Green Version]
- Melnik, R.; Roberts, A.; Thomas, K. Computing dynamics of copper-based SMA via centre manifold reduction of 3D models. Comput. Mater. Sci. 2000, 18, 255–268. [Google Scholar] [CrossRef]
- Melnik, R.; Roberts, A. Thermomechanical behaviour of thermoelectric SMA actuators. J. Phys. IV 2001, 11, 515–520. [Google Scholar] [CrossRef] [Green Version]
- Melnik, R.; Roberts, A.; Thomas, K. Coupled thermomechanical dynamics of phase transitions in shape memory alloys and related hysteresis phenomena. Mech. Res. Commun. 2001, 28, 637–651. [Google Scholar] [CrossRef]
- Melnik, R.; Roberts, A.; Thomas, K. Phase transitions in shape memory alloys with hyperbolic heat conduction and differential-algebraic models. Comput. Mech. 2002, 29, 16–26. [Google Scholar] [CrossRef]
- Melnik, R.; Roberts, A. Computational models for multi-scale coupled dynamic problems. Future Gener. Comput. Syst. 2004, 20, 453–464. [Google Scholar] [CrossRef]
- Peng, G.; Alber, M.; Tepole, A.B.; Cannon, W.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; et al. Multiscale Modeling Meets Machine Learning: What Can We Learn? Arch. Comput. Methods Eng. 2021, 28, 1017–1037. [Google Scholar] [CrossRef] [Green Version]
- Quesada-Molina, J.; Mariani, S. A Deep Learning Approach for Polycrystalline Microstructure-Statistical Property Prediction; Paszynski, M., Kranzlmüller, D., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M., Eds.; LNCS: 12746, ICCS 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 549–561. [Google Scholar]
- Zong, H.; Pilania, G.; Ding, X.D.; Ackland, G.J.; Lookman, T. Developing an interatomic potential for martensitic phase transformations in zirconium by machine learning. npj Comput. Mater. 2018, 4, 48. [Google Scholar] [CrossRef]
- Onat, B.; Ortner, C.; Kermode, J.R. Sensitivity and dimensionality of atomic environment representations used for machine learning interatomic potentials. J. Chem. Phys. 2020, 153, 144106. [Google Scholar] [CrossRef]
- Cui, J.; Chu, Y.S.; Famodu, O.O.; Furuya, Y.; Hattrick-Simpers, J.; James, R.D.; Ludwig, A.; Thienhaus, S.; Wuttig, M.; Zhang, Z.Y. Combinatorial search of thermoelastic shape-memory alloys with extremely small hysteresis width. Nat. Mater. 2006, 5, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Larock, R. Novel polymeric materials from biological oils. J. Polym. Environ. 2002, 10, 59–67. [Google Scholar] [CrossRef]
- Jian, W.; Wang, X.D.; Lu, H.B.; Lau, D. Molecular dynamics simulations of thermodynamics and shape memory effect in CNT-epoxy nanocomposites. Compos. Sci. Technol. 2021, 211, 108849. [Google Scholar] [CrossRef]
- Boudjella, A.; Trache, D.; Khimeche, K.; Hafsaoui, S.L.; Bougamra, A.; Tcharkhtchi, A.; Durastanti, J.F. Stimulation and reinforcement of shape-memory polymers and their composites: A review. J. Thermoplast. Compos. Mater. 2020. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, J.; Weng, C.X.; Wang, T.; Liu, Y.Y.; Han, Z.P.; Zhang, Z. Three-dimensional graphene coated shape memory polyurethane foam with fast responsive performance. J. Mater. Chem. C 2021, 9, 7444–7451. [Google Scholar] [CrossRef]
- Gopinath, S.; Adarsh, N.N.; Nair, P.R.; Mathew, S. Shape-memory polymer nanocomposites of poly(e-caprolactone) with the polystyrene-block-polybutadiene-block-polystyrene-tri-block copolymer encapsulated with metal oxides. ACS Omega 2021, 6, 6261–6273. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Auxeticity in biosystems: An exemplification of its effects on the mechanobiology of heterogeneous living cells. In Computer Methods in Biomechanics and Biomechanical Engineering; Taylor & Francis: Abingdon, UK, 2021. [Google Scholar] [CrossRef]
- Tripathi, S.; Titus, M.; Strachana, A. Martensitic transformation in superlattices of two non-transforming metals. J. Appl. Phys. 2021, 130, 165105. [Google Scholar] [CrossRef]
- D’Elia, E.; Ahmed, H.S.; Feilden, E.; Saiz, E. Electrically-responsive graphene-based shape-memory composites. Appl. Mater. Today 2019, 15, 185–191. [Google Scholar] [CrossRef]
- Espinha, A.; Domínguez-Bajo, A.; González-Mayorga, A.; Concepción Serrano, M. Graphene-Based Composites with Shape Memory Effect—Properties, Applications, and Future Perspectives. In Handbook of Graphene Set, I–VIII; Celasco, E., Chaika, A.N., Stauber, T., Zhang, M., Ozkan, C., Ozkan, C., Ozkan, U., Palys, B., Harun, S.W., Eds.; Wiley: Hoboken, NJ, USA, 2019; Volume 4. [Google Scholar]
- Ferreira, W.; Andrade, C. The role of graphene on thermally induced shape memory properties of poly(lactic acid) extruded composites. J. Therm. Anal. Calorim. 2021, 143, 3107–3115. [Google Scholar] [CrossRef]
- Lin, Z.; Jiang, W.Z.; Chen, Z.H.; Zhong, L.X.; Liu, C.A.F. Shape-memory and anisotropic carbon aerogel from biomass and graphene oxide. Molecules 2021, 26, 5715. [Google Scholar] [CrossRef] [PubMed]
- Garces, I.; Ayranci, C. Active control of 4D prints: Towards 4D printed reliable actuators and sensors. Sens. Actuators A 2020, 301, 111717. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, F.H.; Sun, Y.; Sun, B.Z.; Gu, B.H.; Leng, J.S.; Zhang, W. Electrothermal shape memory behavior and recovery force of four-dimensional printed continuous carbon fiber/polylactic acid composite. Smart Mater. Struct. 2021, 30, 025040. [Google Scholar] [CrossRef]
- Liu, B.; Niu, M.Q.; Fu, J.; Xi, Z.Y.; Lei, M.; Quhe, R.G. Negative Poisson’s ratio in puckered two-dimensional materials. Phys. Rev. Mater. 2019, 3, 054002. [Google Scholar] [CrossRef]
- He, X.; Tong, Z.; Du, H.Y.; Wang, D.; Wang, L.X.; Melnik, R. Modeling microstructure evolution in shape memory alloy rods via Legendre wavelets collocation method. J. Mater. Sci. 2019, 54, 14400–14413. [Google Scholar] [CrossRef] [Green Version]
- Panahi-Sarmad, M.; Abrisham, M.; Noroozi, M.; Amirkiai, A.; Dehghan, P.; Goodarzi, V.; Zahiri, B. Deep focusing on the role of microstructures in shape memory properties of polymer composites: A critical review. Eur. Polym. J. 2019, 117, 280–303. [Google Scholar] [CrossRef]
- Cui, X.; Chen, J.W.; Zhu, Y.T.; Jiang, W. Natural sunlight-actuated shape memory materials with reversible shape change and self-healing abilities based on carbon nanotubes filled conductive polymer composites. Chem. Eng. J. 2020, 382, 122823. [Google Scholar] [CrossRef]
- Wang, J.; Sun, L.Y.; Zou, M.H.; Gao, W.; Liu, C.H.; Shang, L.R.; Gu, Z.Z.; Zhao, Y.J. Bioinspired shape-memory graphene film with tunable wettability. Sci. Adv. 2017, 3, e1700004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Wu, Y.Q.; Hong, Y.; Zhang, Z.T.; Yue, Y.A.; Zhang, J.C. Applications of machine learning in computational nanotechnology. Nanotechnology 2022, 33, 162501. [Google Scholar] [CrossRef] [PubMed]
- Vita, J.A.; Trinkle, D.R. Exploring the necessary complexity of interatomic potentials. Comput. Mater. Sci. 2021, 200, 110752. [Google Scholar] [CrossRef]
- Goryaeva, A.M.; Deres, J.; Lapointe, C.; Grigorev, P.; Swinburne, T.D.; Kermode, J.R.; Ventelon, L.; Baima, J.; Marinica, M.C. Efficient and transferable machine learning potentials for the simulation of crystal defects in bcc Fe and W. Phys. Rev. Mater. 2021, 5, 103803. [Google Scholar] [CrossRef]
- Hodapp, M.; Shapeev, A. Machine-learning potentials enable predictive and tractable high-throughput screening of random alloys. Phys. Rev. Mater. 2021, 5, 113802. [Google Scholar] [CrossRef]
- Zuo, Y.; Chen, C.; Li, X.G.; Deng, Z.; Chen, Y.M.; Behler, J.; Csanyi, G.; Shapeev, A.V.; Thompson, A.P.; Wood, M.A.; et al. Performance and cost assessment of machine learning interatomic potentials. J. Phys. Chem. A 2020, 124, 731–745. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, J.B.; Li, J.H.; Mei, J.N.; Li, Z.C.; Lai, W.S.; Xue, F. Machine-learning interatomic potential for radiation damage effects in bcc-iron. Comput. Mater. Sci. 2022, 202, 110960. [Google Scholar] [CrossRef]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltaysky, I.; Schutt, K.T.; Tkatchenko, A.; Muller, K.R. Machine learning force fields. Chem. Rev. 2021, 121, 10142–10186. [Google Scholar] [CrossRef]
- Yeo, B.C.; Kim, D.; Kim, C.; Han, S.S. Pattern learning electronic density of states. Sci. Rep. 2019, 9, 5879. [Google Scholar] [CrossRef] [PubMed]
- Hirn, M.; Mallat, S.; Poilvert, N. Wavelet scattering regression of quantum chemical energies. Multiscale Model. Simul. 2017, 15, 827–863. [Google Scholar] [CrossRef] [Green Version]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.F.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Bruneval, F.; Maliyov, I.; Lapointe, C.; Marinica, M.C. Extrapolating unconverged GW energies up to the complete basis set limit with linear regression. Chem. Theory Comput. 2020, 16, 4399–4407. [Google Scholar] [CrossRef] [PubMed]
- Staake, C.G.; Heenen, H.H.; Scheurer, C.; Csanyi, G.; Reuter, K.; Margraf, J.T. On the role of long-range electrostatics in machine-learned interatomic potentials for complex battery materials. ACS Appl. Energy Mater. 2021, 4, 12562–12569. [Google Scholar] [CrossRef]
- Leitherer, A.; Ziletti, A.; Ghiringhelli, L.M. Robust recognition and exploratory analysis of crystal structures via Bayesian deep learning. Nat. Commun. 2021, 12, 6234. [Google Scholar] [CrossRef] [PubMed]
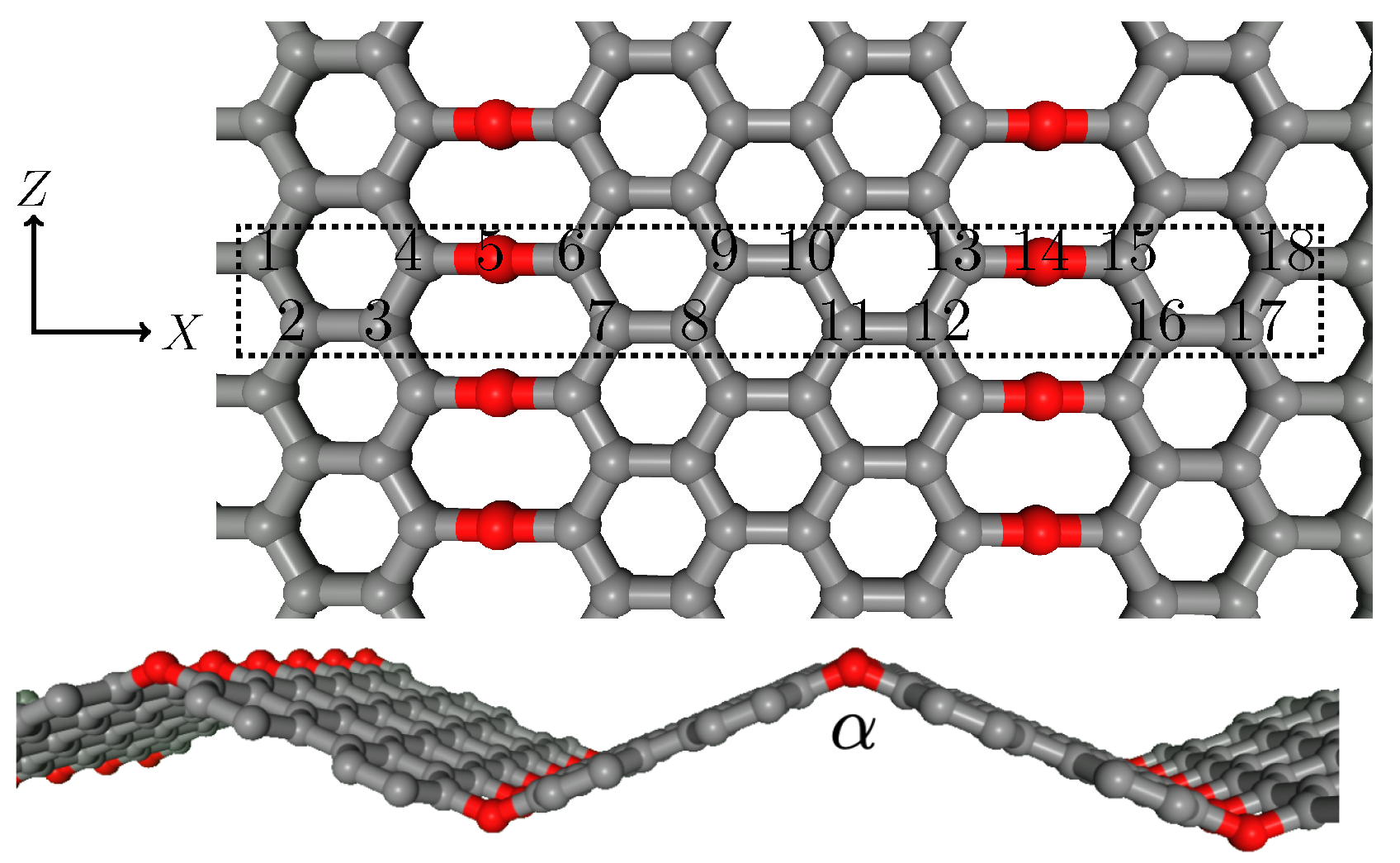
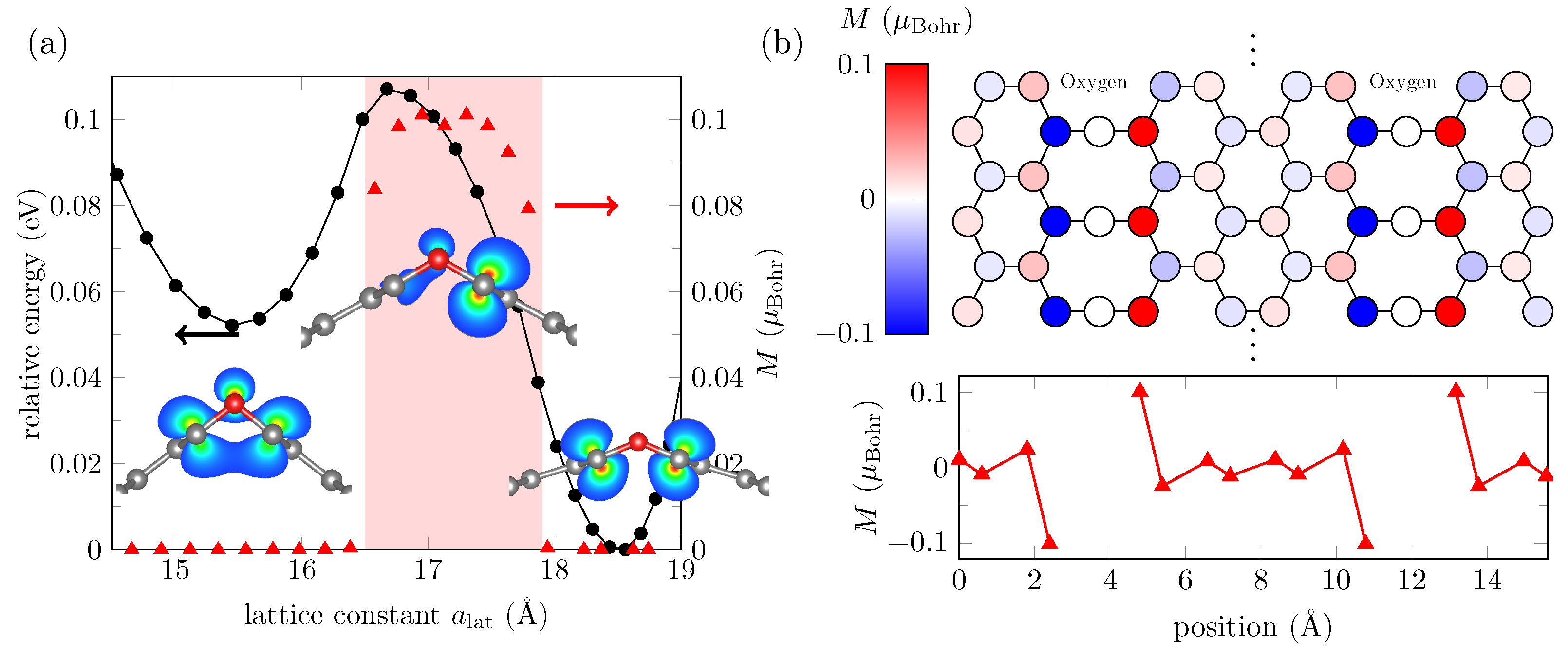

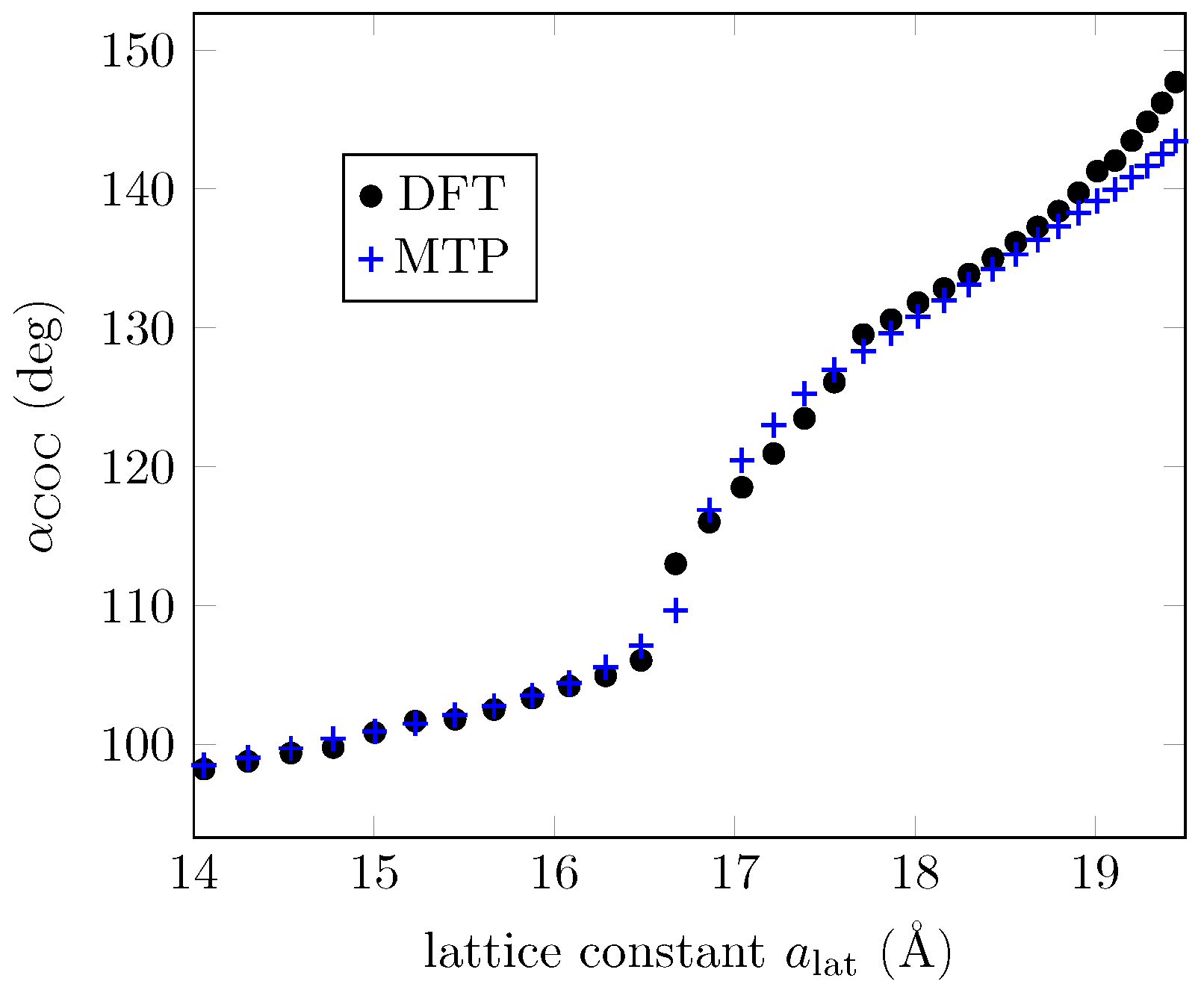
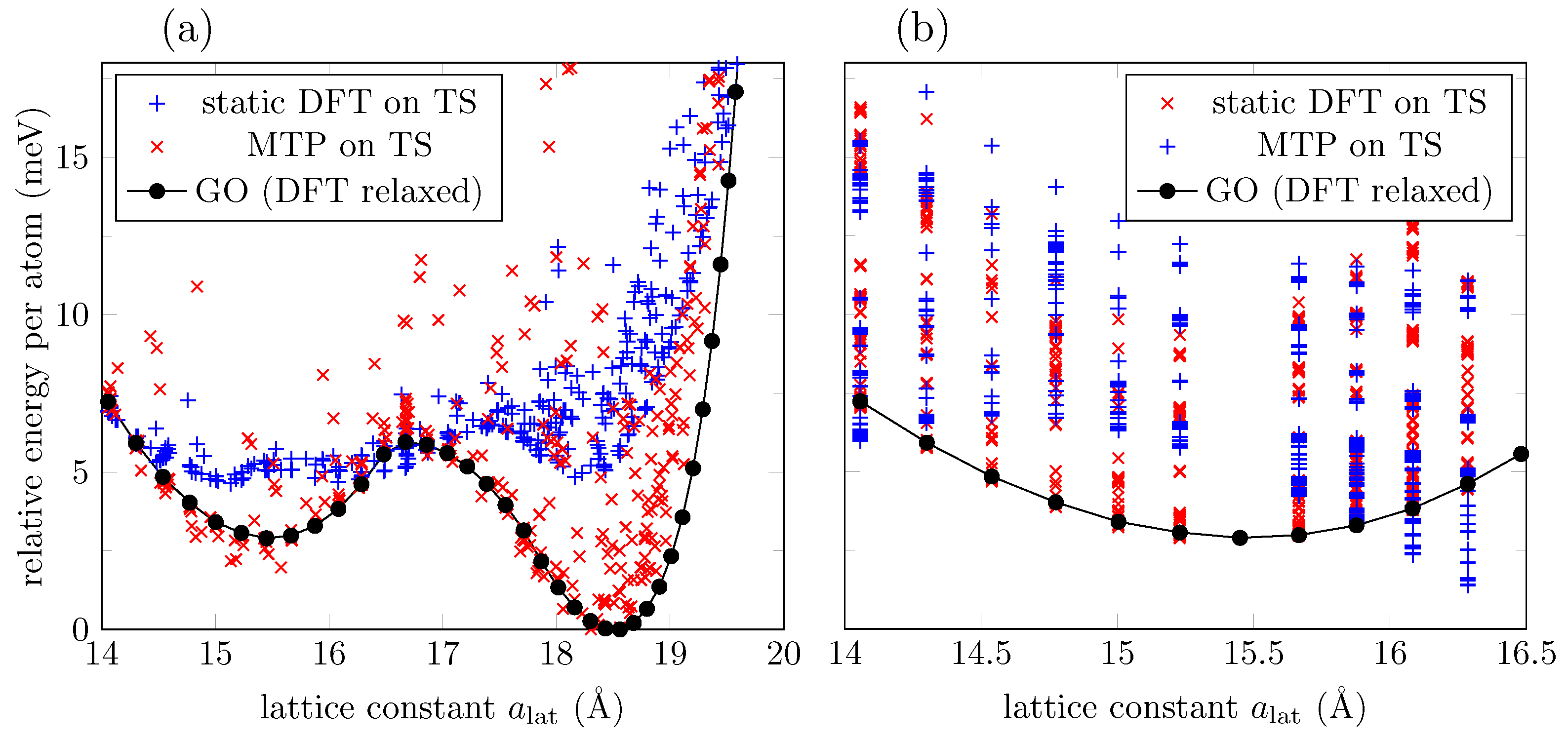

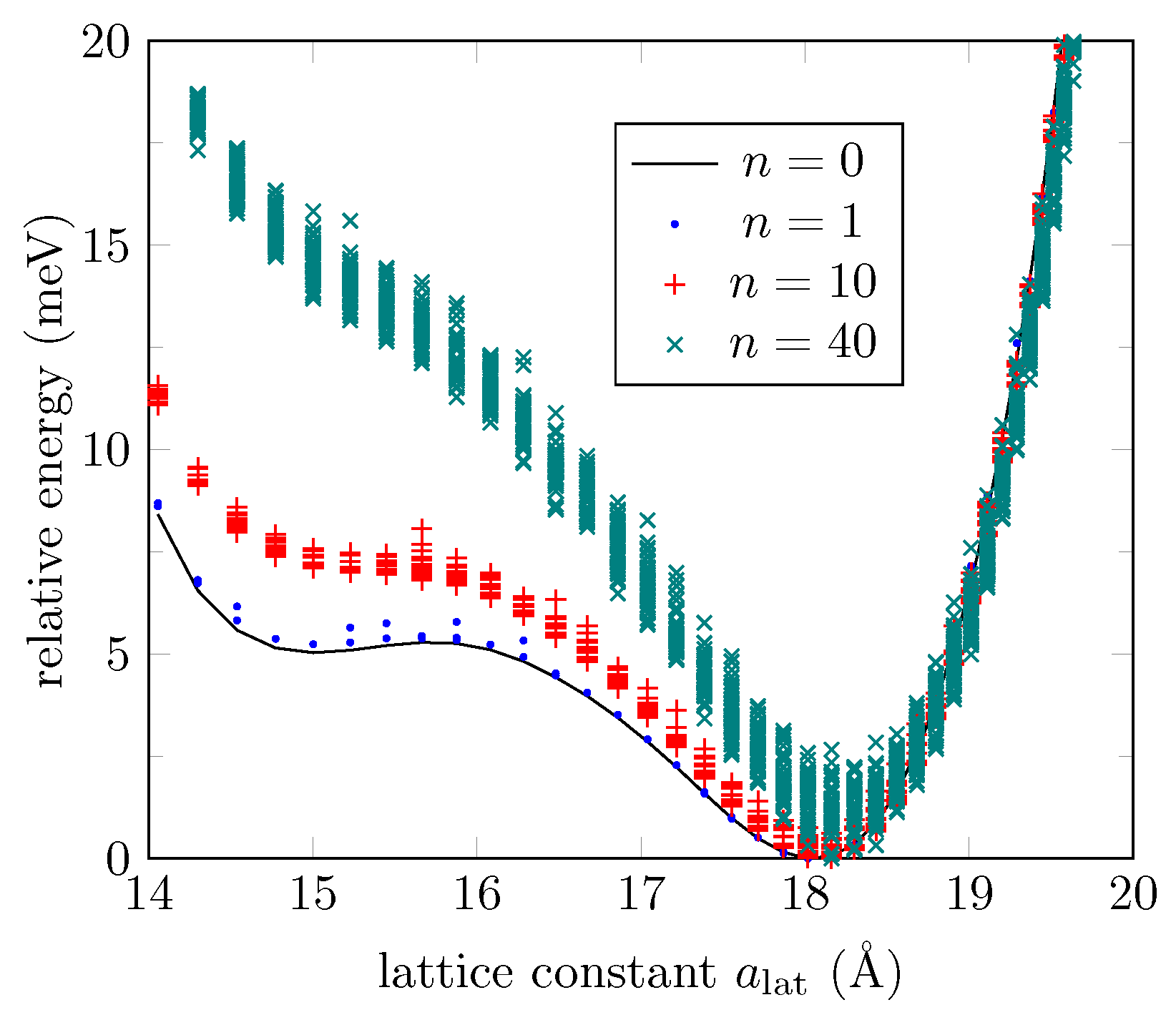

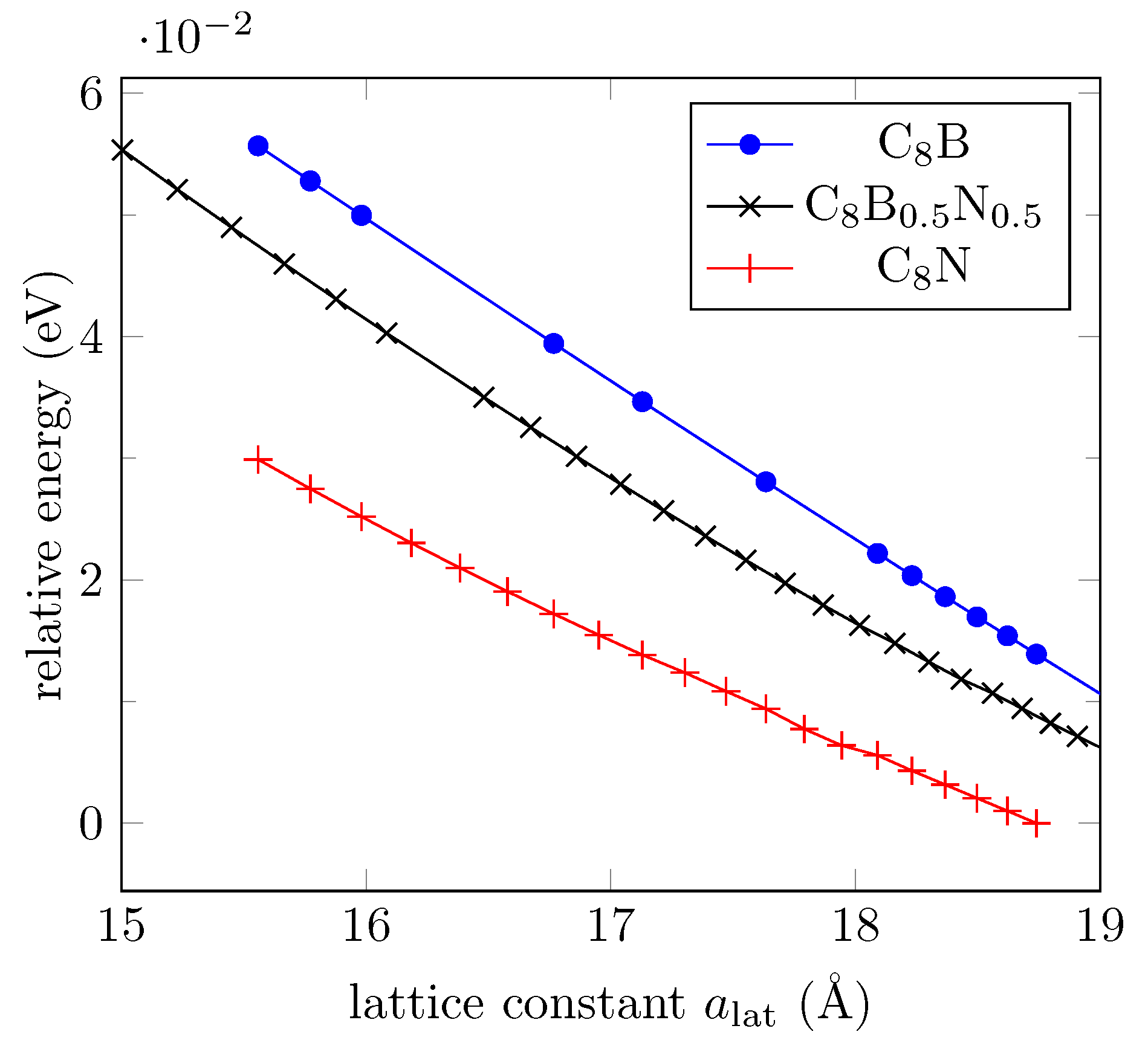
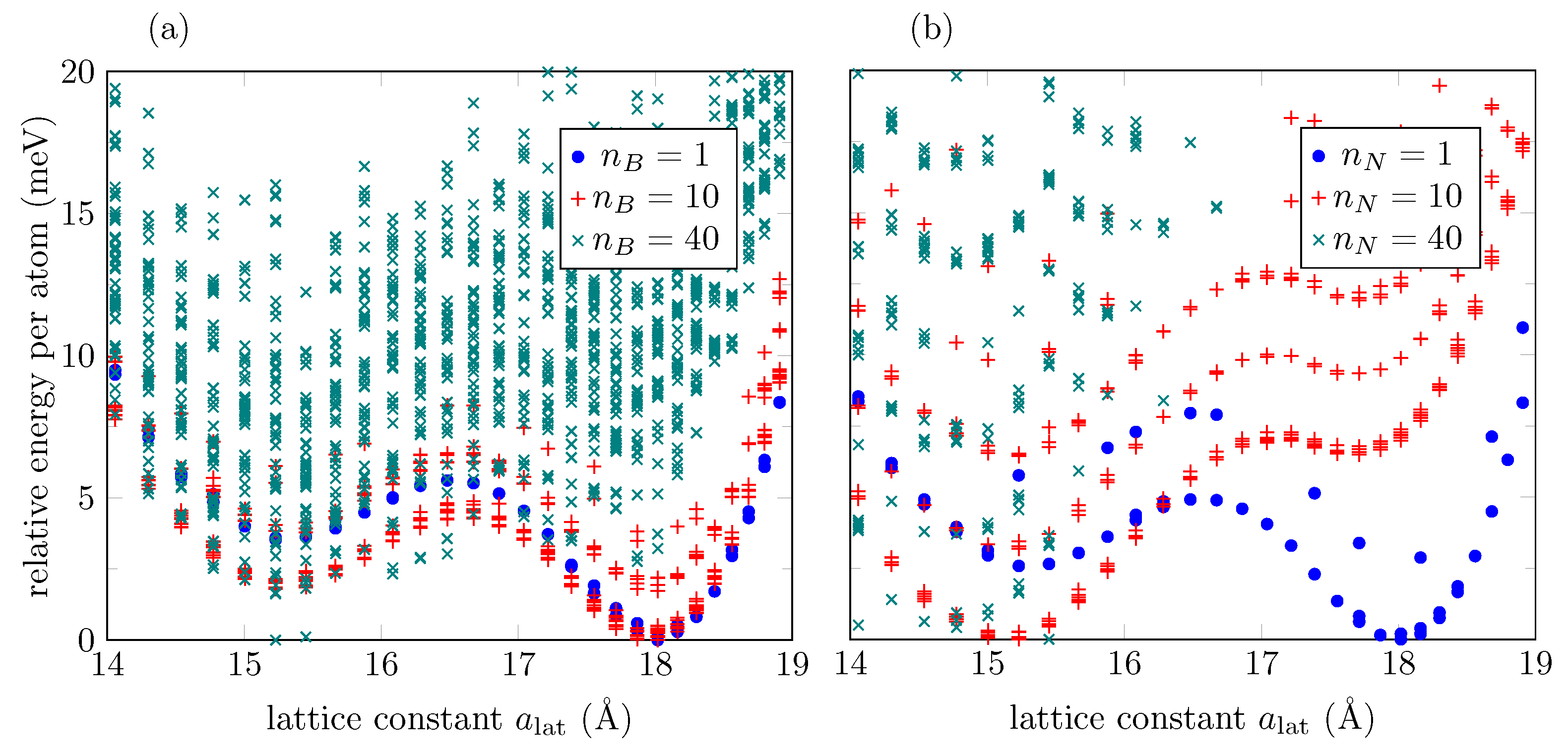
| MTP (Å) | MTP Energy (meV) | MTP C-O-C Angle (deg) |
|---|---|---|
| 15.45 | 101.86 | 102.1 |
| 18.02 | 101.20 | 130.8 |
| DFT (Å) | DFT Energy (meV) | DFT C-O-C Angle (deg) |
| 15.45 | 52.1 | 101.8 |
| 18.56 | 0.0 | 136.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
León, C.; Melnik, R. Machine Learning for Shape Memory Graphene Nanoribbons and Applications in Biomedical Engineering. Bioengineering 2022, 9, 90. https://doi.org/10.3390/bioengineering9030090
León C, Melnik R. Machine Learning for Shape Memory Graphene Nanoribbons and Applications in Biomedical Engineering. Bioengineering. 2022; 9(3):90. https://doi.org/10.3390/bioengineering9030090
Chicago/Turabian StyleLeón, Carlos, and Roderick Melnik. 2022. "Machine Learning for Shape Memory Graphene Nanoribbons and Applications in Biomedical Engineering" Bioengineering 9, no. 3: 90. https://doi.org/10.3390/bioengineering9030090
APA StyleLeón, C., & Melnik, R. (2022). Machine Learning for Shape Memory Graphene Nanoribbons and Applications in Biomedical Engineering. Bioengineering, 9(3), 90. https://doi.org/10.3390/bioengineering9030090






