Abstract
This article presents a dataset containing messages from the Digital Teaching Assistant (DTA) system, which records the results from the automatic verification of students’ solutions to unique programming exercises of 11 various types. These results are automatically generated by the system, which automates a massive Python programming course at MIREA—Russian Technological University (RTU MIREA). The DTA system is trained to distinguish between approaches to solve programming exercises, as well as to identify correct and incorrect solutions, using intelligent algorithms responsible for analyzing the source code in the DTA system using vector representations of programs based on Markov chains, calculating pairwise Jensen–Shannon distances for programs and using a hierarchical clustering algorithm to detect high-level approaches used by students in solving unique programming exercises. In the process of learning, each student must correctly solve 11 unique exercises in order to receive admission to the intermediate certification in the form of a test. In addition, a motivated student may try to find additional approaches to solve exercises they have already solved. At the same time, not all students are able or willing to solve the 11 unique exercises proposed to them; some will resort to outside help in solving all or part of the exercises. Since all information about the interactions of the students with the DTA system is recorded, it is possible to identify different types of students. First of all, the students can be classified into 2 classes: those who failed to solve 11 exercises and those who received admission to the intermediate certification in the form of a test, having solved the 11 unique exercises correctly. However, it is possible to identify classes of typical, motivated and suspicious students among the latter group based on the proposed dataset. The proposed dataset can be used to develop regression models that will predict outbursts of student activity when interacting with the DTA system, to solve clustering problems, to identify groups of students with a similar behavior model in the learning process and to develop intelligent data classifiers that predict the students’ behavior model and draw appropriate conclusions, not only at the end of the learning process but also during the course of it in order to motivate all students, even those who are classified as suspicious, to visualize the results of the learning process using various tools.
Dataset: doi: 10.5281/zenodo.8092417.
Dataset License: CC-BY-4.0
1. Introduction
In recent years, educational data mining (EDM) has become increasingly important due to its impressive results in the analysis and prediction of the academic performance of students, both in general and in individual disciplines [1]. Nowadays, EDM methods are successfully combined with various advanced machine learning tools that are used to solve problems of classification, clustering and prediction in the educational field. In particular, we should mention the random forest (RF) algorithm, support vector machine (SVM) algorithm, k-nearest neighbors (KNN) algorithm, logistic regression (LR) and deep artificial neural networks (ANN), which use features extracted from educational data [1,2,3,4] to help higher education institutions to form strategies, providing an increase in the academic performance of the students and a decrease in the proportion of students who are expelled.
With the increase in the number of tasks in the IT sector of the economy, there is a need for the large-scale training of IT specialists in higher educational institutions. This need arises due to the expansion of the range of tasks that need to be addressed in the IT sector, which can be related to various areas, such as software development, data analysis, cybersecurity and others. In order to meet this need, appropriate study programs should be available in higher education institutions that allow students to acquire the necessary knowledge and skills to work in the IT sector. At the same time, special attention should be paid to the issues of data management of the program of the academic discipline for the educational environment management information system, which will, among other things, increase the level of awareness of the participants in the educational process [5].
The automatic generation of tasks of certain types is an example of the effective use of IT technologies in the educational process. From the teachers’ point of view, automatic task generation makes it possible to reduce the time required to develop new teaching materials, which reduces the teachers’ working load and allows them to focus on individual work with students. In addition, it also helps to stimulate students’ interest by presenting each student with unique, individual tasks. Thus, automatic task generation is a valuable addition to the learning process.
Automatic task generation can be used in computer programming courses. In particular, such tools are discussed in [6,7,8,9,10]. To prevent fraud in such systems, plagiarism checks are carried out using various methods of analyzing program texts [10]. Such methods use an abstract syntax tree based on code clone detection algorithms [11,12,13], clustering algorithms based on pairwise comparisons of weighted keywords extracted from program source texts [14], as well as algorithms based on the preliminary conversion of program source texts into vectors [15]. It should be noted that students can deceive plagiarism detection software by making changes to the program source texts.
This article deals with a dataset containing information about the activities of second year students of MIREA—Russian Technological University (RTU MIREA) in the discipline “Programming in Python” in the spring semester of 2023. During the semester, students had to solve mandatory unique exercises on the 11 tasks automatically generated by the Digital Teaching Assistant (DTA) system [16,17] in order to receive admission to the intermediate certification in the form of a test. The generators of unique exercises for programming tasks used in the DTA system solve the problem of plagiarism of solutions and are useful, first of all, in mass training courses [18].
The dataset under consideration contains anonymous information about students, their groups, variants, the times for successful and unsuccessful attempts to send the solutions of exercises for 11 tasks to the DTA system, as well as the number of methods with which a particular student solved a particular unique exercise. The most common approaches to solving exercises on the 11 tasks can be identified at the end of the semester using intelligent algorithms [19,20] and added to the knowledge base of the DTA system.
During the analysis of the texts of the programs, it becomes possible to identify gaps in the knowledge of the students before the intermediate certification in the form of a test. In addition, a program text analysis is also useful for the quality control of the exercise generator in order to exclude tasks that allow typical or similar solutions. In order to find similar approaches to solving unique programming exercises in a dataset containing a large number of unique source texts verified and accepted by the DTA system, code vectorization methods based on Markov chains [20,21] with Jensen–Shannon pairwise discrepancies [22,23], as well as an agglomerative hierarchical clustering algorithm [24,25], were applied. The construction of Markov chains is based on the representation of the text of programs in the form of an abstract syntax tree, which allows for saving information about the hierarchy with a compact, limited size in the embedding process, which does not depend on the size of the original program.
The purpose of the analysis of the proposed dataset is to identify and study the hidden information about the behavior patterns of students in the process of interacting with the DTA system in the course of studying the discipline “Programming in Python”.
The analysis of statistical information collected by the DTA system makes it possible to identify general patterns in the course of the educational process. In particular, this information can be used to detect anomalies in the structure of a multidimensional time series formed from the messages sent to the DTA system as a whole, as well as in the behavior models of groups of students and individual students when working with the DTA system. An examination of the dataset may reveal:
- Models that describe typical students who perform the exact amount of work that is necessary for admission to the intermediate certification in the form of a test;
- Models that describe motivated students who are looking for alternative ways to solve exercises that have already been solved. Increased activity provides students with points that allow them to count on some preferences when passing an intermediate certification in the form of a test;
- Models that describe students who failed to submit correct solutions to all 11 exercises;
- Models that describe suspicious students, who although they successfully submitted all the tasks, did it extremely quickly, started working with the DTA system only at the very end of the semester.
The identification of various models of student behavior allows for developing and applying various motivating techniques in accordance with the nature of the students’ activity in the DTA system. If such information is available during the semester, it is possible to make adjustments to the interactions between students and teachers, as well as between students and the DTA system.
The proposed dataset can be used to:
- Develop regression models that will allow one to predict outbursts of student activity when interacting with the DTA system;
- Develop classification models that will allow one to identify different models of student behavior, both on the basis of the results of training in the semester as a whole and at earlier stages (for example, based on the results of training during the week);
- Perform a cluster analysis that allows one to group students with similar behaviors;
- Visualize the results of the learning process using various tools.
This article is structured as follows. Section 2 contains information about the DTA system and the tasks presented in it. Section 3 describes the content of the dataset under consideration. Section 4 presents the results of the analysis of the activity of the students of various categories, the entry criteria for which were formulated on the basis of a dataset. Section 5 is devoted to a discussion of the obtained results.
2. Digital Teaching Assistant
A detailed description of the DTA system that automates the Python programming course at RTU MIREA is presented in [26].
The types of tasks offered to students are presented in Table 1.

Table 1.
Types of tasks presented in the DTA.
All tasks can be divided into 2 blocks: the first block includes tasks with numbers 1, 2, 3, 4, and 5, and the second block includes tasks with numbers 6, 7, 8, 9, 10, and 11. The tasks from the first block are fairly simple and can be easily solved by most students. The tasks from the second block are more complex, and they require much more time to solve. At the same time, task 10 also involves the implementation of 100% code coverage by tests, meaning it is the most time-consuming.
3. Data Description
This article presents a dataset containing anonymous statistics from checking the texts of programs that solve programming exercises of the 11 different types generated by the DTA system. The dataset is represented by the “messages2023.csv” file, which describes the history of the students’ interactions with the DTA web application.
The “messages2023.csv” file contains a table with 7 columns, which are described in Table 2.

Table 2.
Structure of the “messages2023.csv” file.
The table in the “messages2023.csv” file contains 100,691 rows of data, as well as a header row. Each line of data represents the characteristics of a message sent to the DTA web application.
The first, second and third columns contain integers encoding the group number, task number and variant number, respectively; the fourth column contains timestamps indicating when the message was sent. Each timestamp is represented in the format ‘%Y-%m-%d %H:%M:%S.%f’. For example, a timestamp might look like ‘2023-02-08 22:09:13.821983’. The fifth column contains the status for checking the solution of the task by the student. The state transition diagram describing the transitions among different task statuses is shown in Figure 1.
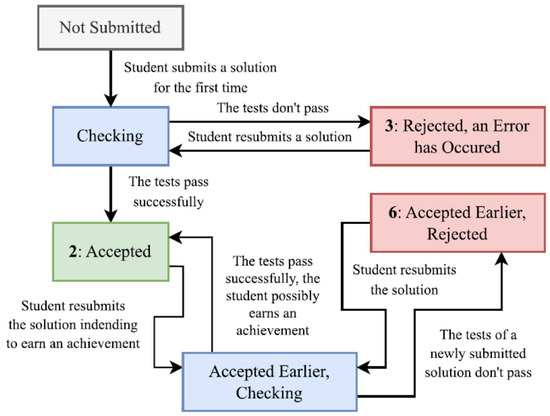
Figure 1.
State transition diagram describing how the task statuses change in the DTA system.
As shown in Figure 1, “2” means that the message was checked and accepted by the DTA system, “3” means that some error was detected during the check and “6” means that some correct solution for the exercise was previously accepted by the DTA system and one or another error was found in the new solution.
The sixth column contains the unique ID number assigned to the student upon registration in the DTA. It should be noted that generally speaking, a student who has been assigned a certain ID can submit solutions not only to the exercises of their own variant of their group but also to exercises of any additional variants, if they have a desire to practice solving tasks, because the exercises corresponding to the same task are unique for different students. Since there are usually no more than 30 students on the list in a group, options 30 to 39 are free and can be used to acquire additional programming skills. Unfortunately, a student may mistakenly or deliberately submit a solution to an exercise that is not their own, although this can be easily detected by analyzing the messages recorded in the DTA system. In addition, in 2023, students were given the opportunity to search extra solutions to exercises on writing programs for all variants of all tasks. In case of successful completion of the exercise for any task by any method known to the DTA system, the number of solution methods is fixed. The seventh column records the presence or absence of achievement in solving the exercise. If an error is found in the solution of an exercise sent to the DTA system, then there is no value in this column. If the solution to a certain exercise sent to the DTA system is recognized as correct during the verification, then the value in this column determines the method for solving the exercise (for example, “2” means that a particular exercise was solved by the second method known to the DTA system). The DTA system knows a specific number of distinct methods for each exercise. At the same time, the number of attempts to upload solutions to the same exercise by a student is not limited; even after successfully solving it in some way, the student can try to find solutions to the same exercise in other ways. If a student, by their own initiative, tries to find several ways to solve the same exercise, then all of their actions are also recorded in the form of messages. If the method proposed by the student for solving the exercise of a particular group and a particular variant repeats the method of solution already accepted by the DTA system as correct, then this solution is set to the status value equal to “2” (in the fifth column of the dataset), and the achievement value (in the seventh column of the dataset) is the number of methods with which the exercise was solved. If the method proposed by the student is correct and new, then this solution is set to the status value equal to “2” (in the fifth column of the dataset), and the achievement value (in the seventh column of the dataset) is set equal to the method number known to the DTA system. If the new method proposed by the student for solving the exercise of a specific group of a specific variant is determined by the DTA system as containing one or another error, then the fifth column of the dataset is set to the status value equal to “6” (and not “3”, as it is in the absence of any correct submitted solutions). This means that the correct solution to the task has already been obtained in some way but the new solution still contains certain errors.
The numbers of solution methods corresponding to each task given in Table 1 were determined experimentally using the author’s algorithms for clustering program codes represented by Markov chains. Table 3 lists the numbers of solution ways that the DTA system “knows”. In order to find the number of ways to solve unique programming exercises for each of the 11 tasks in the dataset [27], which contains a large number of unique source codes of programs tested and accepted by the DTA system, code vectorization methods based on Markov chains [20,21] with Jensen–Shannon pairwise discrepancies [22,23], as well as an agglomerative hierarchical clustering algorithm [24,25], were applied. The found number of clusters for each task determines the number of methods.

Table 3.
Number of solution methods for each task in the DTA system.
More detailed information on determining the number of ways to solve tasks can be found in [27]. The programs contained in the files of the dataset [28] were used in the development of classifiers that form the basis of the achievement assessment system [19,20]. In accordance with the number of methods to solve each task, the possible number of achievements for the exercise was determined.
The main difference between the considered dataset with messages and the set proposed in [26,28] is the use of additional characteristics responsible for the student ID and student achievements. For the characteristic responsible for the status of the solution of the exercise, an additional value equal to “6” is used, which is set in case of repeated unsuccessful attempts to solve a previously solved exercise using another method. At the same time, the characteristic responsible for the verification time of the sent message to the DTA system was excluded from consideration (since the difference between the sending time and verification time is minimal and does not play a significant role because the verification delay does not exceed a few seconds).
The presence of achievements allows students to count on some preferences when passing an intermediate certification in the form of a test.
The proposed changes in organizing a dataset with messages open up new opportunities for analyzing student activity; in particular, anomalous examples of student behavior can be identified, which can be referred to as examples formed with the participation of motivated students searching for various methods to solve tasks, as well as examples formed by suspicious students, which include students who started solving tasks late, students uploading solutions provided by other people, etc.
It should be noted that the unique exercises for 11 tasks were not published simultaneously at the beginning of the semester but instead with some changes in dates. Information on the publication dates is presented in Table 4.

Table 4.
Dates of publication of exercises for 11 tasks in the DTA system.
During the spring semester of 2023, the DTA system received 100,691 messages, and 82,008 solutions for writing programs for various tasks were automatically rejected as incorrect, while 18,683 solutions were automatically accepted as correct. Since in 2023 students could search for additional methods for solving the exercises they had already completed correctly in writing programs for various tasks, incorrect solutions submitted before and after the first correct solution were distinguished in the dataset. These options correspond to the status values “3” and “6” in the fifth column of the dataset. In this case, the total number of incorrect messages is the sum of the number of messages with status “3” and the number of messages with status “6”, i.e., 76,885 and 5123, respectively.
It should be noted that compared to 2022, in 2023 the DTA system received more solutions represented by program texts (100,691 in 2023 and 66,553 in 2022) [26,28], which can be explained by a slight complication of some tasks from the second block but also the excitement of motivated students who tried to discover new ways of solving the exercises they had already successfully completed in writing programs for various tasks.
Figure 2 shows the ratio of the numbers of accepted and rejected (before the first correct answer or after the first correct answer) solutions to exercises in writing programs for various tasks. The rejected (up to the first correct answer) solution to an exercise for a specific task is a solution in which the DTA system has detected a particular error, while the correct solution to the exercise for this task has not yet been obtained. Such a solution has a status of “3”. A rejected (after the first correct answer) solution to an exercise for a specific task is a solution in which the DTA system detected one or another error, while the correct solution of the exercise for this task was already obtained earlier. That means that the student tried to find another way to solve the exercise. Such a solution has a status of “6”.
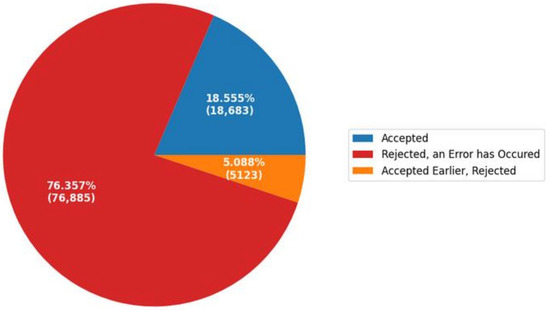
Figure 2.
Diagram describing the ratio of the numbers of accepted and rejected (before the first correct answer or after the first correct answer) solutions to exercises.
The solution accepted by the DTA system as correct has a status of “2”. The student can repeatedly submit the solution to the exercise using the same method or find new methods to solve the exercise. When evaluating a student’s achievements, unique ways of solving an exercise will be of interest.
As can be seen from Figure 2, a large proportion of messages in the DTA system are messages with errors.
Figure 3 shows the total number of program texts rejected due to errors (divided by status values “3” and “6”) and accepted by the DTA system, grouped by exercise numbers (see Table 1). In this case, the numbering of tasks starts from 0 and not from 1, as in Table 1, which can be explained by the fact that the numbering in Python starts from 0 by default.
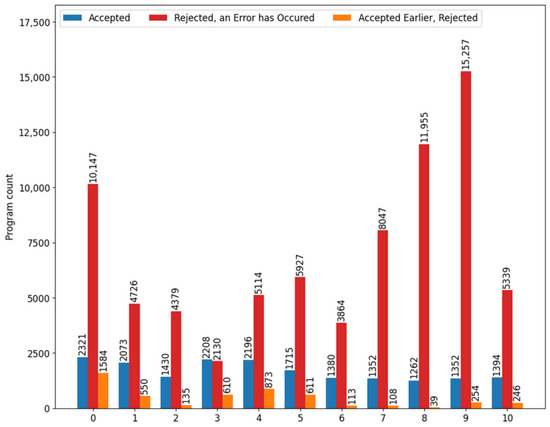
Figure 3.
The total numbers of program texts rejected due to errors (divided by status values “3” and “6”) and accepted by the DTA system, grouped by task numbers.
As can be seen from Figure 3, the largest number of unsuccessful attempts is associated with tasks 1, 9 and 10. For task 1, this can be explained by the fact that students who have never interacted with the DTA system before experience some difficulties when working with it, submitting solutions and observing the system’s reaction. The large number of unsuccessful attempts for tasks 9 and 10 is due to their complexity.
Solutions to problem-based programming exercises submitted to the DTA system may be rejected for various reasons. For example, a Python program may be rejected if it is not formatted according to the PEP8 standard [29], if the cyclomatic complexity of the program is too high [30], if the submitted program text does not contain a function named ‘main’, if there is a syntax error or if an exception occurs while testing the submitted exercise solution in a containerized environment. If the result returned by the program is incorrect, the solution is also rejected.
4. Intelligent Analysis of Dataset
The search for hidden information contained in a dataset that characterizes the activity of students in their interactions with the DTA system is of significant interest.
The preliminary mining of a dataset was performed in Google Collab using the Python programming language.
Ideally, each student interacting with the DTA system should come up with at least one method for each exercise when writing programs for 11 tasks, and all of these solutions should be evaluated in the DTA system as correct. In such cases it is considered that the student has successfully completed the discipline and is admitted to the intermediate certification in the form of a test. It should be noted that all exercises for all tasks are unique.
In the course of an analysis of the dataset under consideration, one may be primarily interested in the following questions.
How can one characterize the interactions of students with the DTA system as a whole?
How do typical students behave when they strive to gain admission to the test and solve unique exercises when writing programs for 11 exercises during the semester?
Are there any motivated students looking to find additional methods for solving the task exercises they have already solved? How do motivated students behave?
Are there any suspicious students who are trying to submit the solutions to the exercises for writing programs for 11 tasks completed not by themselves (entirely or partially)?
Of course, when answering this last question, we may be subjective. However, no one will argue that it is practically impossible to successfully submitted the solution of exercises for all 11 tasks in 3.5 min (after assessing their complexity and scale) without making a single mistake. Yes, there probably are some talented students who can do programming exercises very quickly. However, even they need time to get familiar with the DTA system (even at the PEP8 level). It can, of course, be assumed that the student will write the solutions to all the exercises for 11 tasks and then upload them into the DTA system all at once. However, would they really never want to check the written program (especially such a complex one) for the correctness of the solution? Or are they so confident in their abilities? It is obvious that an objective answer to this question can only be obtained in the test, when the student will be given the opportunity to interact with the DTA system in person for 50 min, during which time they must correctly complete the exercises on 2 tasks from 2 groups of tasks, the numbers of which are selected randomly from the sets {5, 6, 7} and {8, 10} (Table 1). If a student was able to successfully submit solutions for all 11 tasks in 3.5 min (or even an hour), then solving exercises for two tasks on the test should not be a problem for them. In the meantime, it is more logical to classify such students as very suspicious students. In addition, students can be considered suspicious if they start solving their unique exercises for the 11 tasks too late but in the end submit them successfully (of course not in 3.5 min and not in 1 h but perhaps in one day). It is possible that they are very talented but their attitude towards learning (their strategy of behavior) does not serve them well (preventing them from achieving full professional development).
For now, we are only interested in identifying typical, motivated and suspicious students in the proposed dataset. What are the proportions of first, second and third groups in this dataset?
Is it possible to identify the second and third groups as early as possible in order to offer interesting tasks to the second group, motivate the third group to study regularly (not occasionally) and at the same time spark the interest of typical students and help them?
4.1. Analysis of Student Activity by Weeks of the Spring Semester
The spring semester lasts 16 weeks, with classes starting on 9 February 2023. The first interaction with the DTA system was recorded on 8 February (‘2023-02-08, 22:09:13.821983’) but it should be noted that the first user registered during the semester was one of the teachers of the academic discipline. Initially, the DTA system was supposed to accept solutions for 11 tasks until the end of the day on 31 May 2023 but then their work was extended (at the request of students who did not have time to turn in the solutions for exercises for the last tasks) until 00:30 on 7 June 2023. The timestamp of the last submitted message was ‘2023-06-07, 00:20:25.250057’. It should be noted that the students had the opportunity to upload solutions to their unique exercises on tasks around the clock, writing program texts at any time convenient for them.
Figure 4 shows a visualization of the students’ activity in general when working with the DTA system, expressed in uploads of exercise solutions for 11 tasks by week during the semester.
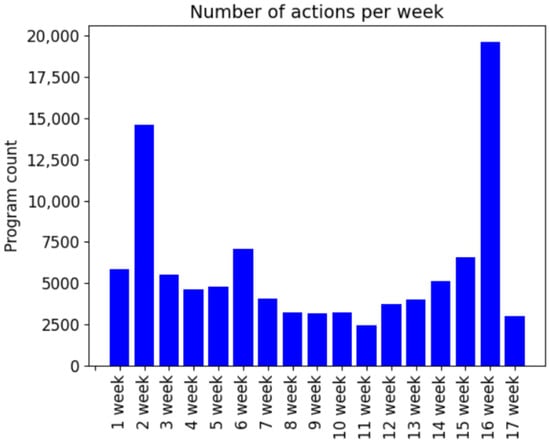
Figure 4.
Solution upload activity for all exercises by weeks.
We can see that in the 2nd week of the semester, the students uploaded a lot of exercise solutions, which is explained by them familiarizing themselves with this system. A slight jump in student activity in the 6th week was due to attempts to upload solutions to exercises on rather simple tasks from the first block (tasks numbered 1–5). Explosive growth of the student activity can be seen in the 16th week; it was then that the work on the DTA system for accepting solutions to exercises on the 11 tasks for verification should have been stopped. Such an increase in activity, of course, could not go unnoticed. Who was so active in solving exercises on tasks in the DTA? Students who worked in the classroom and completed exercises on tasks throughout the semester or suspicious students from the point of view of the educational process?
Answering this question requires a detailed study of the dataset in order to identify hidden patterns.
4.2. Development of Rules for Classifying Students as Typical, Motivated and Suspicious
Let us form the following set of rules, some of which may seem subjective.
- We will consider a student as typical if they successfully submitted all exercises on the 11 tasks to the DTA system (having solved each one in any one way known to the DTA system), while not being classified as suspicious by any rule given below.
- We will consider a student as motivated if they successfully submitted the exercises on the 11 tasks to the DTA system (and at the same time completed at least one exercise correctly in two different ways), while not being classified as suspicious by any rule given below. Each motivated student can be assigned a so-called number of achievements. This is defined as the number of additional unique ways of solving exercises for 11 tasks, not counting the ways in which the student completed these exercises earlier (to obtain admission to the intermediate certification in the form of a test). Thus, the number of achievements of a motivated student is at least 1. At the same time, motivated students, by scaling the values of the numbers of their achievements in the range [0, 1], can be divided into groups:
- A “slightly motivated student” is identified if the scaled number of achievements belongs to the range of (0, 1/3];
- A “moderately motivated student” is identified if the scaled number of achievements belongs to the range of (1/3, 2/3];
- A “highly motivated student” is identified if the scaled number of achievements is in the range of (2/3, 1].
- We will consider a student suspicious if they successfully submitted all exercises on the 11 tasks to the DTA system in the shortest possible time. At the same time, we define the “shortest timeframes” into 2 types: for exercises on all 11 tasks and for exercises on tasks 6–11. The emphasis on the “shortest timeframes” for exercises on tasks 6–11 can be explained by the higher complexity of these tasks, due to which the students were not able to deal with them (while students were able to find or hope to find the right solutions for tasks 1–5, which are easier). Suspicious students can be divided into the following groups:
- “Highly suspicious students” who successfully submitted solutions to the exercises for all 11 tasks in 1 h or less;
- “Highly suspicious students” who successfully submitted solutions to the exercises for tasks 6–11 in 1 h or less;
- “Moderately suspicious students” who successfully submitted solutions to the exercises for all 11 tasks within the time range of (1 h, 24 h];
- “Moderately suspicious students” who successfully submitted solutions to the exercises for tasks 6–11 within the time range of (1 h, 24 h];
- “Slightly suspicious students” who successfully submitted solutions to the exercises on all 11 tasks within the time range of (24 h, 48 h];
- “Slightly suspicious students” who successfully submitted solutions to the exercises for tasks 6–11 within the time range of (24 h, 48 h).
- We will consider a student to have failed the academic discipline if they did not solve all exercises for the 11 tasks during the semester.
Of course, we can divide the students into classes based on our rules, some of which can be called subjective. The question arises of whether it is possible to somehow visualize classification decisions according to our rules? Is it possible to cluster the data on the interactions of students with the DTA system?
Obviously, it is necessary to describe the interactions of students with the DTA system based on a certain set of features that will describe the activity of the students.
4.3. Feature Selection
4.3.1. Description of Student Activity Based on Two Features
In the simplest case, each student will be described by two features characterizing the minimum and maximum times for successfully sending the solutions of the exercises of all 11 tasks to the DTA system.
The student can send the exercise solutions for the 11 tasks to the DTA system in any order. At the same time, sending solutions can be either successful or unsuccessful. For example, a student can successfully submit the exercise solution for the 5th task before the exercise solution for the 1st one. It may be that the first successful submission for a student is the submission of the exercise solution for the 11th task, while the last successful submission is the submission of the exercise solution for the 1st task. Due to the fact that the student can look for additional ways to solve the exercise for each task, in the course of the formation of two features, we choose exactly the minimum time for the first successful submission of the exercise solutions for all 11 tasks and the maximum time for the first successful submission of the exercise solutions for all 11 tasks. As a result, we can determine the boundaries of the time range within which the first successful attempts are found for all 11 tasks.
Therefore, the minimum time is the minimum time for the first successful submission of the solutions of the exercises for all 11 tasks. The maximum time is the maximum time for first successful submission of the solutions of the exercises for all 11 tasks to the DTA system.
In addition, let us recalculate the time in seconds starting from 1 January 1970 (using Python language functions), followed by scaling to the range of [0, 1] for each coordinate (for each feature).
Figure 5 shows an example visualization of the students’ activity in a two-dimensional space in coordinates (minimum time, maximum time).
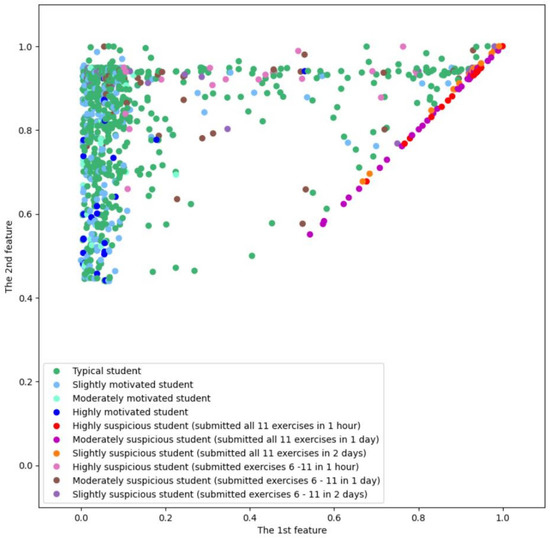
Figure 5.
An example visualization of the students’ activities in a two-dimensional space in coordinates (minimum time, maximum time).
It should be noted that most of the suspicious students (especially those who spent no more than 1 h sending the solutions to the exercises on all 11 tasks to the DTA system) are grouped close to the diagonal and began to interact with the DTA system towards the end of the semester. Most of highly motivated students started interacting with the DTA system at the beginning of the semester, reached their maximum fairly quickly (in terms of the number of successfully completed exercises on the 11 tasks) and then stopped interacting with the DTA system. The moderately motivated students started interacting with the DTA system at the beginning of the semester and continued to interact with it throughout the semester. Most of typical students also started interacting with the DTA system at the beginning of the semester and continued to interact with it throughout the semester. Obviously, such a two-dimensional dataset will be problematic to process with any clustering algorithm in order to obtain compact and well-separated clusters.
4.3.2. Description of Student Activity Based on Eleven Features
In order to describe each student, we will use eleven features, each of which determines the time when the first correct solution to the exercise was submitted to the DTA system. At the same time, we will preliminarily recalculate the time into seconds, starting from 1 January 1970, with subsequent scaling to the range of [0, 1] for each coordinate (for each feature).
Let us use the UMAP algorithm [31,32,33] to embed 11-dimensional objects (data points) characterizing student activity into a two-dimensional space and perform data visualization.
The UMAP algorithm allows us to perform a non-linear reduction in the dimension of a dataset, using the concepts of the fuzzy set theory and graph theory [31].
We used a software implementation of the UMAP algorithm with default parameter values [34].
Figure 6 presents the results of the visualization of 11-dimensional objects characterizing the activity of the students in a two-dimensional space based on the UMAP algorithm.
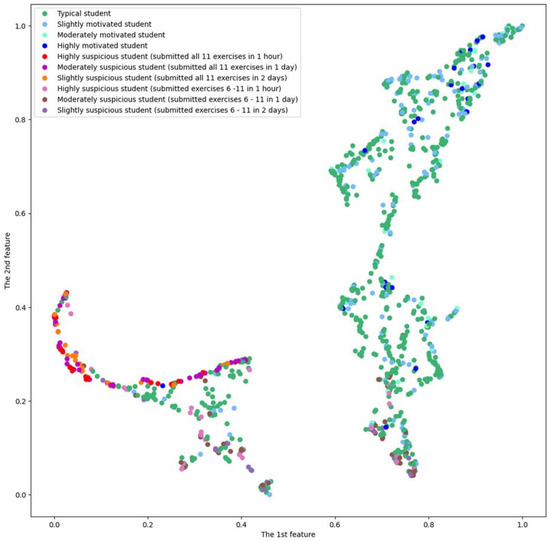
Figure 6.
Results of the visualization of 11-dimensional objects characterizing the activity of the students in a two-dimensional space based on the UMAP algorithm.
Two clusters are already clearly visible in this figure. Obviously, they correspond to students who began to interact with the DTA system at the beginning of the semester (the right cluster of points) and students who began to interact with the DTA system towards the end of the semester. It should be noted that there is a chain of data points corresponding to suspicious students (primarily those who successfully sent the solutions to exercises for all 11 tasks to the DTA system) in the upper left part of the data cloud. One can also see a number of suspicious data points at the bottom of the right cloud (these points describe prudent suspicious students who bothered to submit solutions to the tasks in the DTA system in April and did it successfully).
Can visualization results be improved by adding new features? Let’s try to get an answer to this question in the following sections of the article.
4.3.3. Description of Student Activity Based on Twelve Features
Let us append the list of 11 features from Section 4.3.2 with one more feature that characterizes the numbers of the students’ achievements in their interactions with the DTA system. We will assume that a student has a certain number of achievements if the DTA system has registered more than 11 successful unique submissions for exercise solutions for the 11 tasks. The difference between the total number of unique submissions (i.e., the number of different methods for the solutions to exercises for all 11 tasks) and the number 11 (i.e., the number that determines that the exercises for all 11 tasks are solved successfully) will be used as the number of achievements. At the same time, let us start with the scaling of the values by this attribute in the range of [0, 1].
Figure 7 presents the results of the visualization of 12-dimensional objects characterizing the activity of the students in a two-dimensional space based on the UMAP algorithm.
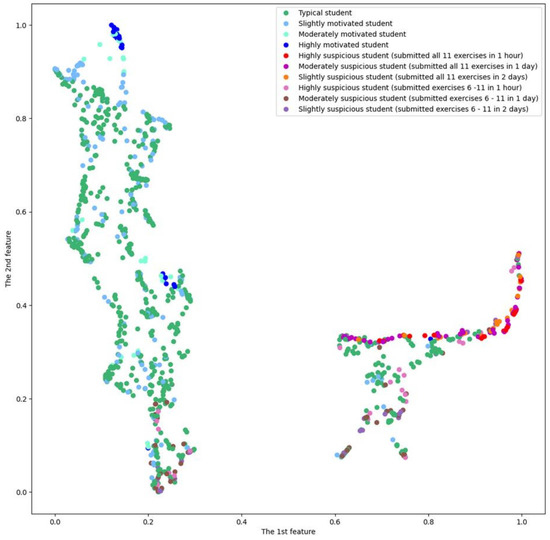
Figure 7.
Results of the visualization of 12-dimensional objects characterizing the activity of the students in a two-dimensional space based on the UMAP algorithm.
In this figure, as in Figure 6, 2 clusters are clearly visible. At the same time, thanks to the introduction of a feature that is responsible for the number of students’ achievements, students who showed motivation and students who were classified as highly suspicious were very well grouped; the motivated students made achievements and the suspicious students (who spent no more than 1 h on interactions with the DTA system during the successful submission of solutions to exercises for all 11 tasks or for tasks 6–11) did not (they simply would not even have time to send them to the DTA system, let alone perform any exercises on tasks in new ways due to the time limitations).
4.3.4. Description of Student Activity Based on Twenty-Three Features
Let us add 11 more features to the 12 features from Section 4.3.3 that characterize the number of unsuccessful submissions for exercise solutions for each task before the first successful submission.
Figure 8 presents the results of the visualization of 23-dimensional objects characterizing the activity of the students in a two-dimensional space based on the UMAP algorithm.
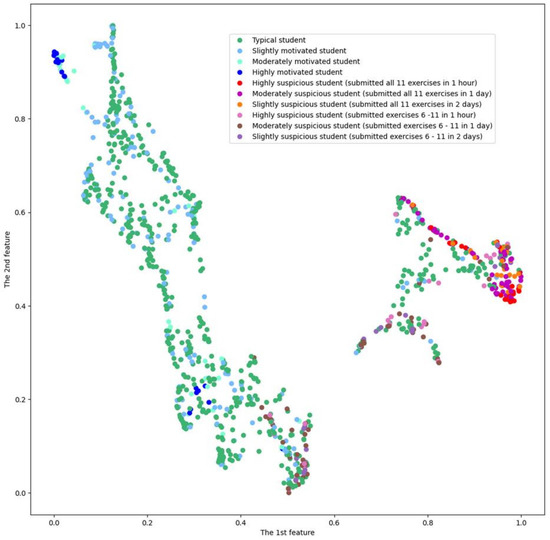
Figure 8.
Results of the visualization of 23-dimensional objects characterizing the activity of the students in a two-dimensional space based on the UMAP algorithm.
In this figure, as in Figure 6 and Figure 7, 2 clusters are clearly visible. At the same time, denser groups are visible for highly suspicious students in the data cloud on the left and for highly motivated students in the data cloud on the right.
The purpose of further research may be to search for new features that would make it possible to separate one group of students from the others even better.
4.4. Cluster Analysis
Let us study the results of the cluster analysis in the form of dividing students into groups with similar behavior models in the process of interacting with the DTA system. The division of students into groups was performed using clustering algorithms such as k-means [35,36,37] and DBSCAN [38,39,40]. Clustering was performed for the 11-, 12- and 23-dimensional datasets obtained in Section 4.3.2, Section 4.3.3 and Section 4.3.4 and for the corresponding two-dimensional sets obtained using the nonlinear dimensionality reduction algorithm, namely the UMAP algorithm.
The k-means algorithm is based on minimizing the total square deviation of objects belonging to clusters from the centroids of these clusters. This is the simplest and most commonly used clustering algorithm. It usually works well if the clusters are well separable from each other and have a hyperspherical shape. The main problem is finding the optimal number of clusters. However, this problem can be solved by enumerating the number of clusters in order to choose such a number for which the value of the cluster silhouette index [41] reaches its maximum value (ideally a value equal to 1).
DBSCAN (density-based spatial clustering of applications with noise) implements density-based spatial clustering with noise object extraction. It forms clusters of arbitrary shapes but it may experience difficulties in identifying clusters due to the peculiarities of their formation, taking into account their density; it is possible that a significant part of the objects will be classified as noise. By varying the values of the parameters of this algorithm, one can try to find the optimal number of clusters by maximizing the value of the cluster silhouette index.
When working with clustering algorithms, their software implementations in the Python language from the scikit-learn library [42,43] were used. In the case of the k-means algorithm, the values of only one parameter responsible for the number of clusters (the n_clusters parameter in the software implementation) varied, and for the DBSCAN algorithm, the varying parameters were responsible for the maximum distance between two samples for one to be considered as in the neighborhood of the other and the number of samples (or total weight) in a neighborhood for a point to be considered as a core point. This included the point itself (parameters eps and min_samples in the software implementation). For the remaining parameters of these algorithms, the default values in their software Implementation were used.
Table 5 summarizes the results of the application of the k-means and DBSCAN clustering algorithms for the 11-, 12-, and 23-dimensional datasets, as well as for their corresponding two-dimensional ones.

Table 5.
Summary table of the cluster analysis results.
Figure 9, Figure 10 and Figure 11 (right) show the best clustering results for the 2D datasets obtained using the UMAP algorithm for the 11-, 12- and 23-dimensional datasets generated in Section 4.3.2, Section 4.3.3 and Section 4.3.4. At the same time, Figure 9, Figure 10 and Figure 11 (left) show the cluster silhouettes of the selected clusters [44].
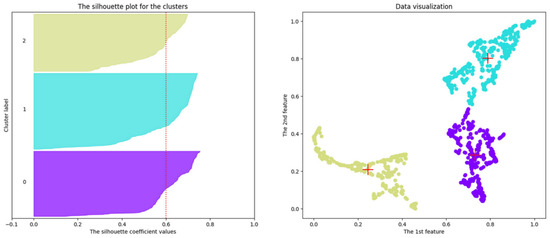
Figure 9.
Results of clustering using the k-means algorithm on a two-dimensional dataset obtained using the UMAP algorithm on the 11-dimensional dataset mentioned in Section 4.3.2.
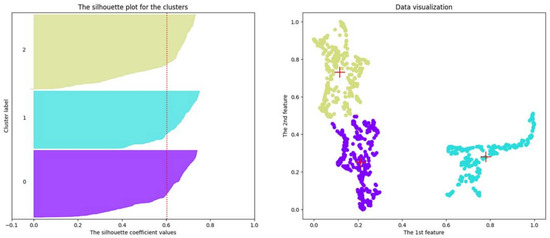
Figure 10.
Results of clustering using the k-means algorithm on a two-dimensional dataset obtained using the UMAP algorithm on the 12-dimensional dataset mentioned in Section 4.3.3.
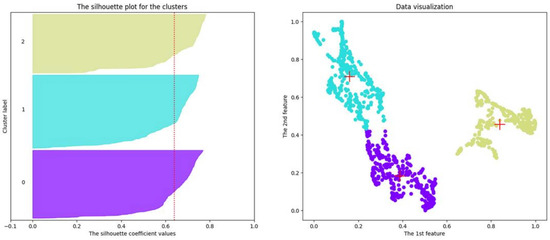
Figure 11.
Clustering results using the k-means algorithm on a two-dimensional dataset obtained using the UMAP algorithm on the 23-dimensional dataset mentioned in Section 4.3.4.
The red markers of the “+” type in the figures on the right show the locations of the cluster centroids. The red dotted vertical lines in the figures on the left show the average silhouette scores for all values. Different colors of cluster silhouettes in the left figures and dots in the right figures correspond to different clusters.
We can see 2 clusters that are well separated from each other. However, the k-means algorithm splits the data into 3 clusters.
Table 5 indicates the optimal number of clusters and the corresponding value of the cluster silhouette index, calculated as a result of applying the k-means algorithm to the corresponding dataset for each case. In all cases, the number of clusters is 3, while the maximum value of the cluster silhouette index is 0.639, which is obtained for a two-dimensional dataset built on the basis of a 23-dimensional one.
Figure 12, Figure 13 and Figure 14 (right) show the best clustering results using the DBSCAN algorithm for two-dimensional datasets obtained using the UMAP algorithm for the 11-, 12- and 23-dimensional datasets mentioned in Section 4.3.2, Section 4.3.3 and Section 4.3.4. At the same time, Figure 12, Figure 13 and Figure 14 (left) show the cluster silhouettes of the selected clusters. One can see by analyzing the cluster silhouettes of individual clusters that the number of objects that could be erroneously assigned to the cluster with the number “0” is greater in the case of a 23-dimensional dataset than in the case of an 11-dimensional dataset (while in the results clustering based on the k-means algorithm, the doubtful cluster membership of objects was not revealed at all). Noise objects in the results for the clustering based on the DBSCAN algorithm were not identified.
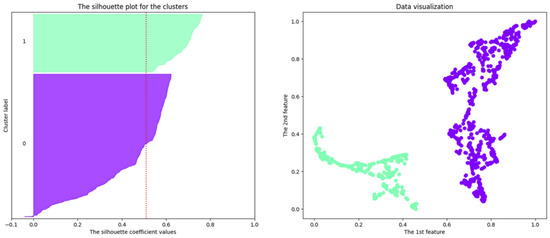
Figure 12.
Clustering results using the DBSCAN algorithm on a two-dimensional dataset obtained using the UMAP algorithm on the 11-dimensional dataset mentioned in Section 4.3.2.
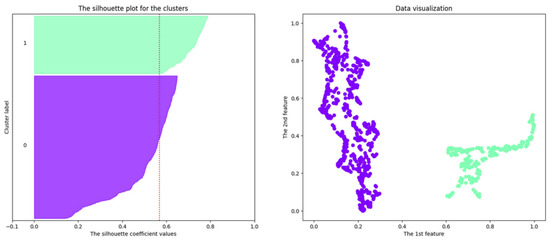
Figure 13.
Clustering results using the DBSCAN algorithm on a two-dimensional dataset obtained using the UMAP algorithm on the 12-dimensional dataset mentioned in Section 4.3.3.
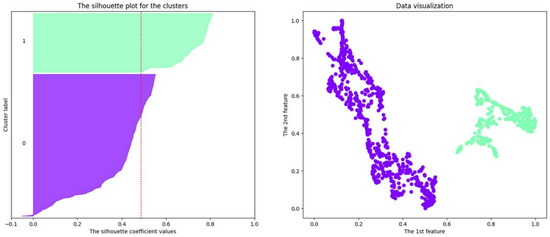
Figure 14.
Clustering results using the DBSCAN algorithm on a two-dimensional dataset obtained using the UMAP algorithm on the 23-dimensional dataset mentioned in Section 4.3.4.
Table 5 shows the optimal number of clusters and the corresponding value of the cluster silhouette index in the case of using the DBSCAN algorithm for each case. In all cases, the number of clusters is 2, while the maximum value of the cluster silhouette index is 0.568, which is obtained for a two-dimensional dataset built on the basis of a 12-dimensional one.
As noted above, Table 5 provides information on the results of a cluster analysis for the original 11-, 12-, and 23-dimensional datasets. However, these results are difficult to consider satisfactory in the case of working with the DBSCAN algorithm. At the same time, the k-means algorithm for the initial 11-, 12-, and 23-dimensional datasets determined the splitting into 2 clusters as the best, while in the two-dimensional space it revealed 3 clusters in all cases. Obviously, in multidimensional spaces there is a lot of noise in the data, which is leveled when moving to the two-dimensional space. It should be noted that clusters in multidimensional spaces with the numbers of clusters equal to 2 and 3 have similar values for the cluster silhouette index, although at the same time the results are more preferable with the number of clusters equal to 2 (in terms of maximizing the value of the cluster silhouette index).
Table 5 for the k-means algorithm shows the values of the n_clusters parameter, which is responsible for the number of clusters, with the value of the cluster silhouette index separated by a colon; for the DBSCAN algorithm, the number of clusters is indicated and separated by a colon, the values of the eps and min_samples parameters in parentheses are separated by a slash and the number of noise objects and the value of the cluster silhouette index are shown.
In general, the clustering takes into account the time of the first successful submission of the exercise solutions to the DTA system for each of the 11 tasks (Section 4.3.2), the time of the first successful submission of the exercise solutions to the DTA system for each of the 11 tasks and the number of student achievements (Section 4.3.3), the number of student achievements and the number of unsuccessful submissions (before the first successful one) of the exercise solutions for each of the 11 tasks (Section 4.3.4). Therefore, when grouping data points into clusters, they are first grouped by taking into account the time of the interaction of the students with the DTA system.
Therefore, the students who successfully submitted all exercise solutions for the 11 tasks towards the end of the semester, according to the k-means algorithm in Figure 9, Figure 10 and Figure 11, are shown in clusters with numbers 2, 1 and 2, respectively (see the colors of the markers of these clusters in the figures on the left). Most of the suspicious students marked with the corresponding markers in Figure 6, Figure 7 and Figure 8, respectively, fell into these clusters. The clusters with numbers 0, 0 and 0 according to the k-means algorithm in Figure 9, Figure 10 and Figure 11 include students who successfully submitted all exercise solutions for the 11 tasks in the second half of the semester. At the same time, the first suspicious students appear in these clusters. In addition, in these clusters one can see the presence of motivated students (Figure 6, Figure 7 and Figure 8, respectively). The students who quickly submitted all the exercise solutions for 11 tasks, according to the k-means algorithm in Figure 9, Figure 10 and Figure 11, are shown respectively in the clusters with numbers 1, 2 and 1. We can see that only typical and motivated students are present in these clusters (Figure 6, Figure 7 and Figure 8, respectively).
The addition of new features allows us to group data points corresponding to highly suspicious and moderately suspicious students (who submitted exercise solutions for all 11 tasks or for tasks 6–11 in less than 1 h or 1 day) more densely; they practically cannot have any number of achievements, and the number of failed submissions (before the first successful one) to the DTA system is low because of the extremely short duration of the interaction with the DTA system (Figure 8). Data points corresponding to highly and moderately motivated students will also be grouped more densely: such students have a large number of achievements and make fewer mistakes when performing exercises on the 11 tasks (Figure 8).
4.5. Motivated Students against Suspicious Ones
Despite the relative subjectivity of the rules for identifying motivated and suspicious students (perhaps we classified too many students as suspicious according to these rules, underestimating their intellectual potential), we can draw the following conclusions.
Motivated students prevail over suspicious ones with a ratio of 241:219.
In total, the number of students who successfully submitted the exercise solutions for all 11 tasks in the DTA system was 1056 (if some tasks for students with a specific ID were submitted by other authors then they were not included in this list, although they were admitted to the intermediate certification in the form of a test). At the same time, the total number of users registered in the DTA system was 1736.
The percentage of typical students who solved exercises for all 11 tasks was 56.439%. The percentage of motivated students who solved exercises for all 11 tasks was 22.822%. The percentage of suspicious students who solved exercises for all 11 tasks was 20.739%.
The overall percentage of typical and motivated students who solved exercises for all 11 tasks was 79.261%, which was not too bad. It is possible that we were mistaken in our subjectivity, and in fact the percentage of good students was even higher. This may be later discovered after the intermediate certification in the form of a test.
5. Discussion
The dataset presented and described in this article contains the DTA system messages generated by checking the solutions of unique exercises in the form of program texts for 11 tasks of various types, offered to students during the spring semester of 2023 in the process of learning to program in the Python language at RTU MIREA. Each message contains information on such parameters (features) as the group number, task number, variant number, solution loading time, solution status, student identifier and achievement number (method of solving the task), if there is one.
The DTA system automates a massive Python programming course at RTU MIREA starting from the spring semester of 2021. The architecture of the system is described in [26].
All program texts uploaded by students to the DTA system were checked and accepted by DTA. The result of the check firstly determines the status of the check (the solution to the exercise is accepted as correct, the solution of the exercise is accepted as incorrect or the solution of the exercise (in a new way) is accepted as incorrect but the correct decision was previously submitted).
The proposed dataset can be viewed as an event log that provides a complete picture of how students interacted with the DTA system throughout the semester while learning to program in Python. Such an event log can be the subject of an exploratory analysis in terms of detecting various anomalies and outbursts both in the structure of a multidimensional time series formed from the messages sent to the DTA system as a whole and in the behavioral models of student groups (for example, in order to identify stronger and weaker students for the formation of individual learning trajectories) and individual students when working with the DTA system.
The analysis of the proposed dataset should make it possible to reveal the patterns hidden in it by extracting features that describe various characteristics that give an idea of the peculiarities of students’ interactions with the DTA system during the semester when solving unique exercises on the 11 tasks.
The proposed dataset can be used, in particular to analyze the activity of all students in general, individual study groups of students and students separately, including during the day, by days of the week, by week, by month, by specific tasks (taking status values into account), according to the achievements of students in specific tasks and in general.
The study of the dataset in order to identify different patterns of student behavior throughout the semester in the process of learning to program in the Python language is of particular interest. In particular, it is possible to identify models of so-called typical students who diligently complete all required exercises on tasks during the semester (and not one more), motivated students who not only diligently perform all required exercises on tasks during the semester but also try to find additional ways to solve the same exercises and receiving points for such educational achievements (allowing them to count on some preferences when passing an intermediate assessment in the form of a test), students who did not cope with solving all required exercises on the tasks, as well as suspicious students who completed all obligatory exercises on the tasks during the semester but acted suspiciously (for example, because they were able to successfully submit all solutions to the exercises on the 11 tasks to the DTA system extremely quickly or started interacting with the DTA system only at the end of the semester).
It is obvious that for students implementing different models of interaction with the DTA system, it is advisable to apply different methods that encourage further learning, which will allow some to intensify their professional development and others to change the model of interaction with the DTA system to a more progressive one. It would be useful to receive information about student behavior patterns not at the end of the semester but during it in order to make adjustments to the interactions between students and teachers, and then the interactions between students and the DTA system.
Therefore, if the student is classified as motivated during the semester, then they may be offered additional tasks that contribute to their professional development, including a variety of so-called creative projects that allow a more in-depth study of certain topics in practice. If a student is classified as suspicious, then additional attention will be paid to their activity both during the semester and when they pass the intermediate certification in the form of a test. At the same time, attempts can be made to remove the student from the group of suspicious students. It is possible that face-to-face communication with a suspicious student will confirm their extraordinary abilities in the discipline. In this case, it may be possible to involve them in the professional development process, as well as motivated students. Otherwise, confirmation will be received that the student is not interested in gaining knowledge (at the moment), and then it will already be necessary to develop and implement strategies to change such a destructive (professional) behavior model (however, this should already be the subject of additional research and activities by educational institutions). It should be noted that the analysis of the proposed dataset may help in identifying students who experience difficulties while solving exercises on tasks. For example, if a student performs more submissions of exercise solutions for a particular task to the DTA system than the average student does, then we can assume that the student has difficulties and offer them timely help by explaining the material that they find difficult.
In the future, it is advisable to supplement the dataset under consideration with information about the results of students passing intermediate certifications in the form of a test, which will confirm or refute the assumptions about the probability of the successful study of the discipline. In addition, the dataset could be expanded with information about the types of errors that are diagnosed by the DTA system in case of an unsuccessful submission of the exercise solution for verification.
The proposed dataset can be used as follows:
- To develop regression models that will allow one to predict outbursts of student activity when interacting with the DTA system;
- To develop classification models that will allow one to identify different models of student behavior both based on the results of studying in the semester as a whole and at earlier stages (for example, based on the results of studying during the week);
- To perform a cluster analysis that groups students with similar behaviors;
- To visualize the results of the learning process using various tools.
In the course of further research, it is planned to explore various approaches to extracting features from the proposed dataset with their subsequent combinations in order to form models that provide a comprehensive description of student activity. In addition, it is planned to study the proposed dataset for the presence of outliers in it, as well as to test the hypothesis about the possibility of identifying elements of novelty of various types in the constantly updated dataset during the semester, formed on the basis of the event log, in order to provide timely responses from teachers.
Author Contributions
Conceptualization, methodology, L.A.D. and P.N.S.; software, L.A.D. and A.A.D.; validation, L.A.D. and E.G.A.; formal analysis, L.A.D., P.N.S. and A.A.D.; investigation, L.A.D., P.N.S. and A.A.D.; resources, P.N.S. and E.G.A.; writing—original draft preparation, A.A.D.; writing—review and editing, L.A.D., E.G.A. and P.N.S.; visualization, A.A.D.; supervision, project administration, E.G.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study is openly available in Zenodo at https://doi.org/10.5281/zenodo.8092417 (accessed on 3 August 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.L.; Dai, J.; Xu, L.J. Big Data and Data Mining in Education: A Bibliometrics Study from 2010 to 2022. In Proceedings of the 2022 7th International Conference on Cloud Computing and Big Data Analytics, ICCCBDA, Chengdu, China, 22–24 April 2022; pp. 507–512. [Google Scholar] [CrossRef]
- Baashar, Y.; Alkawsi, G.; Mustafa, A.; Alkahtani, A.A.; Alsariera, Y.A.; Ali, A.Q.; Hashim, W.; Tiong, S.K. Toward Predicting Student’s Academic Performance Using Artificial Neural Networks (ANNs). Appl. Sci. 2022, 12, 1289. [Google Scholar] [CrossRef]
- Alsariera, Y.A.; Baashar, Y.; Alkawsi, G.; Mustafa, A.; Alkahtani, A.A.; Ali, N. Assessment and Evaluation of Different Machine Learning Algorithms for Predicting Student Performance. Comput. Intell. Neurosci. 2022, 2022, 11. [Google Scholar] [CrossRef] [PubMed]
- Ordoñez-Avila, R.; Salgado Reyes, N.; Meza, J.; Ventura, S. Data mining techniques for predicting teacher evaluation in higher education: A systematic literature review. Heliyon 2023, 9, e13939. [Google Scholar] [CrossRef] [PubMed]
- Starichkova, J.V.; Rogov, I.E.; Tomashevskaya, V.S. Developing the data management component of an academic discipline program for an educational management information system. Russ. Technol. J. 2023, 11, 7–17. [Google Scholar] [CrossRef]
- Queirós, R.A.P.; Leal, J.P. PETCHA: A Programming Exercises Teaching Assistant. In Proceedings of the 17th ACM Annual Conference on Innovation and Technology in Computer Science Education, Haifa, Israel, 3–5 July 2012; pp. 192–197. [Google Scholar]
- Sadigh, D.; Seshia, S.A.; Gupta, M. Automating exercise generation: A step towards meeting the MOOC challenge for embedded systems. In Proceedings of the Workshop on Embedded and Cyber-Physical Systems Education—WESE ’12, New York, NY, USA, 17–18 October 2019; Association for Computing Machinery: New York, NY, USA, 2013. [Google Scholar]
- Tiam-Lee, T.J.; Sumi, K. Procedural generation of programming exercises with guides based on the student’s emotion. In Proceedings of the 2018 IEEE International Conference on Systems Man and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 1465–1470. [Google Scholar]
- Mekterović, I.; Brkić, L.; Milašinović, B.; Baranović, M. Building a Comprehensive Automated Programming Assessment System. IEEE Access 2020, 8, 81154–81172. [Google Scholar] [CrossRef]
- Combéfis, S. Automated Code Assessment for Education: Review, Classification and Perspectives on Techniques and Tools. Software 2022, 1, 3–30. [Google Scholar] [CrossRef]
- Baxter, I.D.; Yahin, A.; Moura, L.; Sant’Anna, M.; Bier, L. Clone detection using abstract syntax trees. In Proceedings of the International Conference on Software Maintenance (Cat. No. 98CB36272), Bethesda, MD, USA, 16–19 March 1998; pp. 368–377. [Google Scholar] [CrossRef]
- Jiang, L.; Misherghi, G.; Su, Z.; Glondu, S. Deckard: Scalable and Accurate Tree-Based Detection of Code Clones. In Proceedings of the 29th International Conference on Software Engineering (ICSE’07), Minneapolis, MN, USA, 20–26 May 2007; IEEE: Pistacaway, NJ, USA, 2007; pp. 96–105. [Google Scholar]
- Kustanto, C.; Liem, I. Automatic Source Code Plagiarism Detection. In Proceedings of the 2009 10th ACIS International Conference on Software Engineering, Artificial Intelligences, Networking and Parallel/Distributed Computing, Daegu, Republic of Korea, 27–29 May 2009; IEEE: Pistacaway, NJ, USA, 2009; pp. 481–486. [Google Scholar]
- Moussiades, L.; Vakali, A. PDetect: A Clustering Approach for Detecting Plagiarism in Source Code Datasets. Comput. J. 2005, 48, 651–661. [Google Scholar] [CrossRef]
- Yasaswi, J.; Kailash, S.; Chilupuri, A.; Purini, S.; Jawahar, C.V. Unsupervised Learning-Based Approach for Plagiarism Detection in Programming Assignments. In Proceedings of the 10th Innovations in Software Engineering Conference, Jaipur, India, 5–7 February 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 117–121. [Google Scholar]
- Sovietov, P.N.; Gorchakov, A.V. Digital Teaching Assistant for the Python Programming Course. In Proceedings of the 2022 2nd International Conference on Technology Enhanced Learning in Higher Education (TELE), Lipetsk, Russia, 26–27 May 2022; pp. 272–276. [Google Scholar]
- Andrianova, E.G.; Demidova, L.A.; Sovetov, P.N. Pedagogical Design of a Digital Teaching Assistant in Massive Professional Training for the Digital Economy. Russ. Technol. J. 2022, 10, 7–23. [Google Scholar] [CrossRef]
- Sovietov, P. Automatic Generation of Programming Exercises. In Proceedings of the 2021 1st International Conference on Technology Enhanced Learning in Higher Education (TELE), Lipetsk, Russia, 24–25 June 2021; pp. 111–114. [Google Scholar] [CrossRef]
- Demidova, L.A.; Sovietov, P.N.; Gorchakov, A.V. Clustering of Program Source Text Representations Based on Markov Chains. Vestn. Ryazan State Radio Eng. Univ. 2022, 81, 51–64. [Google Scholar]
- Demidova, L.A.; Gorchakov, A.V. Classification of Program Texts Represented as Markov Chains with Biology-Inspired Algorithms-Enhanced Extreme Learning Machines. Algorithms 2022, 15, 329. [Google Scholar] [CrossRef]
- Berthiaux, H.; Mizonov, V. Applications of Markov chains in particulate process engineering: A review. Can. J. Chem. Eng. 2004, 82, 1143–1168. [Google Scholar] [CrossRef]
- Lin, J. Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Nielsen, F. On the Jensen–Shannon Symmetrization of Distances Relying on Abstract Means. Entropy 2019, 21, 485. [Google Scholar] [CrossRef] [PubMed]
- Sokal, R.R.; Michener, C.D. A Statistical Method for Evaluating Systematic Relationships. Evolution 1957, 11, 130–162. [Google Scholar]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Demidova, L.A.; Andrianova, E.G.; Sovietov, P.N.; Gorchakov, A.V. Dataset of Program Source Codes Solving Unique Programming Exercises Generated by Digital Teaching Assistant. Data 2023, 8, 109. [Google Scholar] [CrossRef]
- Gorchakov, A.V.; Demidova, L.A.; Sovietov, P.N. Automated Program Text Analysis Using Representations Based on Markov Chains and Extreme Learning Machines. Vestn. Ryazan State Radio Eng. Univ. 2022, 82, 89–103. [Google Scholar]
- Dataset of Program Source Codes Solving Unique Programming Exercises Generated by Digital Teaching Assistant. Available online: https://zenodo.org/record/7799972 (accessed on 28 June 2023).
- PEP 8—Style Guide for Python Code. Available online: https://peps.python.org/pep-0008/ (accessed on 28 June 2023).
- Ebert, C.; Cain, J.; Antoniol, G.; Counsell, S.; Laplante, P. Cyclomatic complexity. IEEE Softw. 2016, 33, 27–29. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Wang, Y.; Huang, H.; Rudin, C.; Shaposhnik, Y. Understanding How Dimension Reduction Tools Work: An Empirical Approach to Deciphering t-SNE, UMAP, TriMAP, and PaCMAP for Data Visualization. J. Mach. Learn. Res. 2021, 22, 9129–9201. [Google Scholar]
- Demidova, L.A.; Gorchakov, A.V. Fuzzy Information Discrimination Measures and Their Application to Low Dimensional Embedding Construction in the UMAP Algorithm. J. Imaging 2022, 8, 113. [Google Scholar] [CrossRef] [PubMed]
- UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. Available online: https://umap-learn.readthedocs.io/en/latest/_modules/umap/umap_html (accessed on 28 June 2023).
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Yang, M.-S. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. KDD 1996, 96, 226–231. [Google Scholar]
- Khan, K.; Rehman, S.U.; Aziz, K.; Fong, S.; Sarasvady, S. DBSCAN: Past, present and future. In Proceedings of the Fifth International Conference on the Applications of Digital Information and Web Technologies (ICADIWT 2014), Bangalore, India, 17–19 February 2014; pp. 232–238. [Google Scholar] [CrossRef]
- Deng, D. DBSCAN Clustering Algorithm Based on Density. In Proceedings of the 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 949–953. [Google Scholar] [CrossRef]
- Shahapure, K.R.; Nicholas, C. Cluster Quality Analysis Using Silhouette Score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, Australia, 6–9 October 2020; IEEE: Pistacaway, NJ, USA, 2020; pp. 747–748. [Google Scholar]
- Scikit-Learn. Available online: https://scikit-learn.org/stable/ (accessed on 28 June 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Selecting the Number of Clusters with Silhouette Analysis on KMeans Clustering. Available online: https://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html#sphx-glr-auto-examples-cluster-plot-kmeans-silhouette-analysis-py (accessed on 28 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).