Leveraging Return Prediction Approaches for Improved Value-at-Risk Estimation
Abstract
:1. Introduction
2. Related Works
2.1. Machine Learning Approaches
2.2. Deep Learning Approaches
2.3. Differences with Respect to State-of-the-Art Approaches
- We leverage machine learning methods to predict the return for the day (d) for which VaR is being estimated, then integrate the obtained information with past returns to find the VaR estimate for d using univariate strategies and GARCH;
- To predict returns for the day for which the VaR is being estimated, we use two approaches: ARIMA and an ensemble of regressors successfully employed for statistical arbitrage [4];
- We also developed a Python package called PanelTime, which implements a GARCH model that can integrate the predicted return for the underlying day (d) with the returns of past days. PanelTime can simultaneously estimate panels with fixed/random effects and time series with GARCH/ARIMA. As far as we know, it is the only package that does this simultaneously. Unlike alternative Python packages, Paneltime also allows for the specification of additional regressors in the GARCH model and calculates the Hessian matrix analytically, which makes it more likely to obtain estimates close to the true parameters.
3. Background
3.1. VAR Prediction
3.2. ARIMA
- Autoregressive (AR) model: An Autoregressive model [27] with p, which represents the number of lagged observations, can be defined as:where Y represents the current value of the time series that we are attempting to predict, c is the constant term or the intercept, are the coefficients for the autoregressive terms, and are the lagged values of the time series. Here, the model relies on past values, and the objective is to derive estimates for the coefficients (). In other words, the current observation depends on past observations, as it is assumed that the current value of a variable is related to its previous values.
- Integrated (I) model: To deal with non-stationary time series data, an integrated part of ARIMA called differencing is used to transform the data to remove trends or cycles that change over time, thereby making them stationary. In a stationary time series, the mean and variance are constant over time. It is easier to predict values when the time series is stationary. Differencing is denoted by d in the ARIMA model and illustrates the number of differencing iterations needed to make the time series stationary. According to [28], if we define our original time series as , where Y is the observation at time t, for general differencing of order d, the operation is defined as:
- Moving average (MA) model: The moving average is expressed in [29] as:where represents the current value of the time series to be predicted, is the mean value of the time series, refers to the error term (or residual) at time t, and represents the coefficients for the moving average terms. The forecasting process of the moving average model involves estimating the coefficients () through the utilization of past errors, as evident in Equation (5). It assumes that the current value of a variable is related to the errors made in previous forecasts, and it captures the influence of past forecast errors on the current observation. The order of the moving average component, as denoted by the parameter q, represents the number of considered lagged forecast errors.
3.3. Walk-Forward Mechanism
- Obtain all relevant data;
- Divide the data into several parts;
- Run an optimization on the first dataset (first in-sample) to determine the best settings;
- Apply those criteria to the second dataset (first out-of-sample);
- Run an optimization on the upcoming in-sample data to obtain the optimum settings;
- Apply those criteria to the following out-of-sample data;
- Continue until all the data parts have been covered;
- Merge the results of all out-of-sample data.
4. The Used Datasets
4.1. Standard and Poor’s 500
4.2. Crude Oil
4.3. Silver
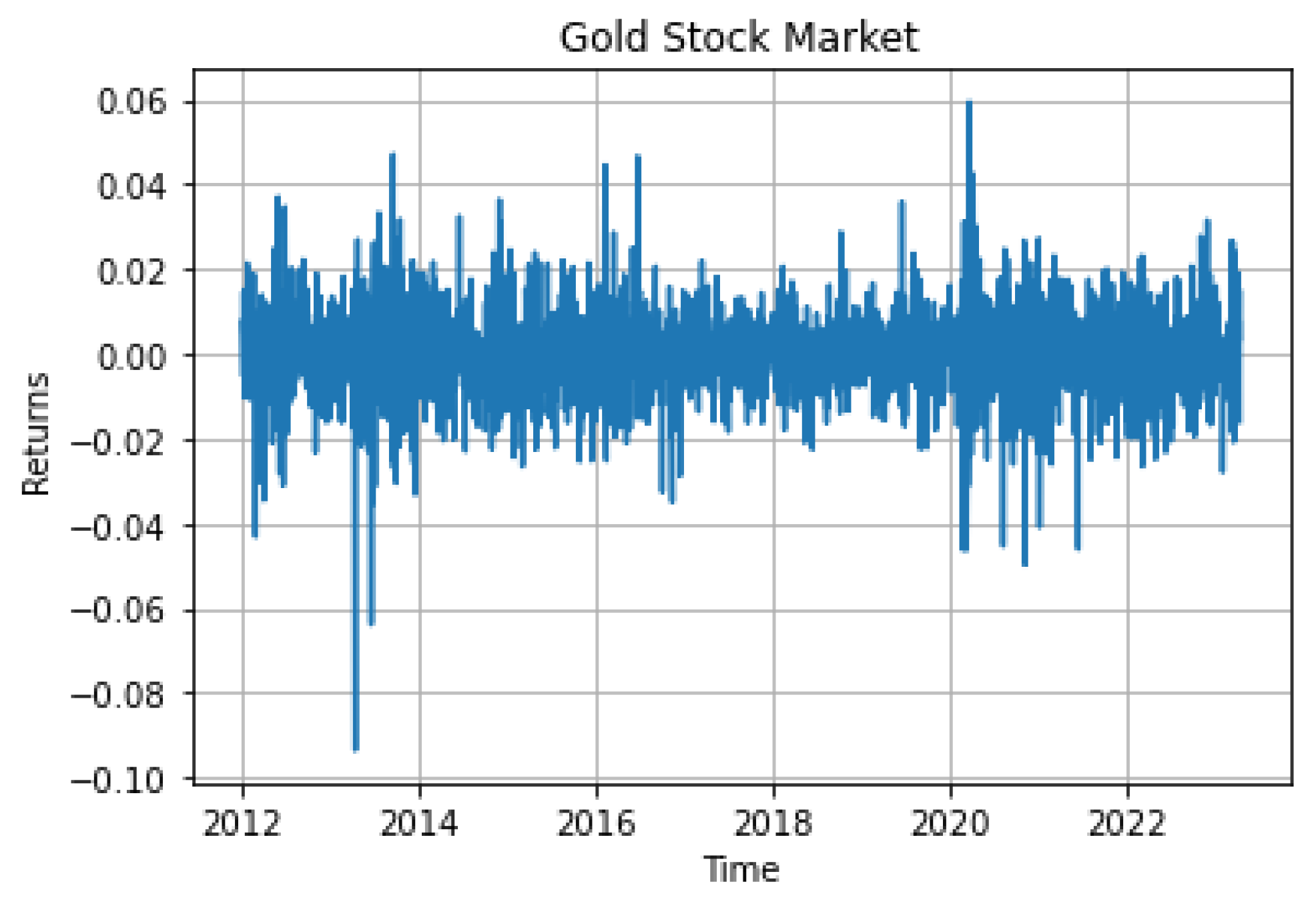
4.4. Gold
5. The Proposed Ensemble for Stock Return Prediction
6. Performance Evaluation
6.1. Baselines
6.1.1. Normal Distribution
6.1.2. Historical Simulation
6.1.3. EWMA
6.2. Used Metrics
6.3. VaR Estimation
6.4. Results
7. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | https://finance.yahoo.com/, accessed on 2 July 2023. |
| 2 | https://finance.yahoo.com/quote/%5EGSPC, accessed on 2 July 2023. |
| 3 | https://finance.yahoo.com/quote/CL=F?p=CL=F&.tsrc=fin-srch, accessed on 2 July 2023. |
| 4 | https://finance.yahoo.com/quote/SI=F?p=SI=F&.tsrc=fin-srch, accessed on 2 July 2023. |
| 5 | https://finance.yahoo.com/quote/GC=F?p=GC=F&.tsrc=fin-srch, accessed on 2 July 2023. |
| 6 | https://www.cmegroup.com/company/nymex.html, accessed on 2 July 2023. |
| 7 | https://www.cmegroup.com/, accessed on 2 July 2023. |
| 8 | https://en.wikipedia.org/wiki/Basel_Accords, accessed on 2 July 2023. |
| 9 | https://scikit-learn.org, accessed on 2 July 2023. |
| 10 | https://numpy.org, accessed on 2 July 2023. |
| 11 | https://pandas.pydata.org/, accessed on 2 July 2023. |
| 12 | https://www.statsmodels.org/stable/index.html, accessed on 2 July 2023. |
| 13 | https://scipy.org/, accessed on 2 July 2023. |
| 14 | https://matplotlib.org, accessed on 2 July 2023. |
| 15 | https://it.mathworks.com/help/risk/, accessed on 2 July 2023. |
References
- Gallati, R.R. (Ed.) Risk Management and Capital Adequacy; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Sharma, M. Evaluation of Basel III revision of quantitative standards for implementation of internal models for market risk. IIMB Manag. Rev. 2012, 24, 234–244. [Google Scholar] [CrossRef]
- Engle, R. GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics. J. Econ. Perspect. 2001, 15, 157–168. [Google Scholar] [CrossRef]
- Carta, S.M.; Consoli, S.; Podda, A.S.; Recupero, D.R.; Stanciu, M.M. Ensembling and Dynamic Asset Selection for Risk-Controlled Statistical Arbitrage. IEEE Access 2021, 9, 29942–29959. [Google Scholar] [CrossRef]
- Xu, Q.; Jiang, C.; He, Y. An exponentially weighted quantile regression via SVM with application to estimating multiperiod VaR. Stat. Methods Appl. 2016, 25, 285–320. [Google Scholar] [CrossRef]
- Khan, M.A.I. Modelling daily value-at-risk using realized volatility, non-linear support vector machine and ARCH type models. J. Econ. Int. Financ. 2011, 3, 305. [Google Scholar]
- Takeda, A.; Fujiwara, S.; Kanamori, T. Extended robust support vector machine based on financial risk minimization. Neural Comput. 2014, 26, 2541–2569. [Google Scholar] [CrossRef]
- Radović, O.; Stanković, J. Tail risk assessment using support vector machine. J. Eng. Sci. Technol. Rev. 2015, 8, 61–64. [Google Scholar] [CrossRef]
- Lux, M.; Härdle, W.K.; Lessmann, S. Data driven value-at-risk forecasting using a SVR-GARCH-KDE hybrid. Comput. Stat. 2020, 35, 947–981. [Google Scholar] [CrossRef]
- Wara, S.S.M.; Prastyo, D.D.; Kuswanto, H. Value at risk estimation with hybrid-SVR-GARCH-KDE model for LQ45 portfolio optimization. AIP Conf. Proc. 2023, 2540, 080013. [Google Scholar]
- Dunis, C.L.; Laws, J.; Sermpinis, G. Modelling commodity value at risk with higher order neural networks. Appl. Financ. Econ. 2010, 20, 585–600. [Google Scholar] [CrossRef]
- Sermpinis, G.; Laws, J.; Dunis, C.L. Modelling commodity value at risk with Psi Sigma neural networks using open–high–low–close data. Eur. J. Financ. 2015, 21, 316–336. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, X.; Jiang, C.; Yu, K. Quantile autoregression neural network model with applications to evaluating value at risk. Appl. Soft Comput. 2016, 49, 1–12. [Google Scholar] [CrossRef]
- Zhang, H.G.; Su, C.W.; Song, Y.; Qiu, S.; Xiao, R.; Su, F. Calculating Value-at-Risk for high-dimensional time series using a nonlinear random mapping model. Econ. Model. 2017, 67, 355–367. [Google Scholar] [CrossRef]
- He, K.; Ji, L.; Tso, G.K.; Zhu, B.; Zou, Y. Forecasting exchange rate value at risk using deep belief network ensemble based approach. Procedia Comput. Sci. 2018, 139, 25–32. [Google Scholar] [CrossRef]
- Banhudo, G.S.F.D. Adaptive Value-at-Risk Policy Optimization: A Deep Reinforcement Learning Approach for Minimizing the Capital Charge. PhD Thesis, ISCTE Business School, Lisbon, Portugal, 2019. [Google Scholar]
- Yu, P.; Lee, J.S.; Kulyatin, I.; Shi, Z.; Dasgupta, S. Model-based deep reinforcement learning for dynamic portfolio optimization. arXiv 2019, arXiv:1901.08740. [Google Scholar]
- Jin, B. A Mean-VaR Based Deep Reinforcement Learning Framework for Practical Algorithmic Trading. IEEE Access 2023, 11, 28920–28933. [Google Scholar] [CrossRef]
- Li, Z.; Tran, M.N.; Wang, C.; Gerlach, R.; Gao, J. A bayesian long short-term memory model for value at risk and expected shortfall joint forecasting. arXiv 2020, arXiv:2001.08374. [Google Scholar]
- Arian, H.; Moghimi, M.; Tabatabaei, E.; Zamani, S. Encoded Value-at-Risk: A machine learning approach for portfolio risk measurement. Math. Comput. Simul. 2022, 202, 500–525. [Google Scholar] [CrossRef]
- Zhao, L.; Gao, Y.; Kang, D. Construction and simulation of market risk warning model based on deep learning. Sci. Program. 2022, 2022, 3863107. [Google Scholar] [CrossRef]
- Blom, H.M.; de Lange, P.E.; Risstad, M. Estimating Value-at-Risk in the EURUSD Currency Cross from Implied Volatilities Using Machine Learning Methods and Quantile Regression. J. Risk Financ. Manag. 2023, 16, 312. [Google Scholar] [CrossRef]
- Linsmeier, T.J.; Pearson, N.D. Value at risk. Financ. Anal. J. 2000, 56, 47–67. [Google Scholar] [CrossRef]
- Alexander, C. Market Risk Analysis, Value at Risk Models; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Jorion, P. Risk2: Measuring the risk in value at risk. Financ. Anal. J. 1996, 52, 47–56. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Yoo, J.; Maddala, G. Risk premia and price volatility in futures markets. J. Futur. Mark. 1991, 11, 165–177. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Slutzky, E. The summation of random causes as the source of cyclic processes. Econom. J. Econom. Soc. 1937, 5, 105–146. [Google Scholar] [CrossRef]
- Carta, S.; Corriga, A.; Ferreira, A.; Recupero, D.R.; Saia, R. A Holistic Auto-Configurable Ensemble Machine Learning Strategy for Financial Trading. Computation 2019, 7, 67. [Google Scholar] [CrossRef]
- Sharkey, A. On Combining Artificial Neural Nets. Connect. Sci. 1996, 8, 299–314. [Google Scholar] [CrossRef]
- Tsymbal, A.; Pechenizkiy, M.; Cunningham, P. Diversity in search strategies for ensemble feature selection. Inf. Fusion 2005, 6, 83–98. [Google Scholar] [CrossRef]
- van Wezel, M.; Potharst, R. Improved customer choice predictions using ensemble methods. Eur. J. Oper. Res. 2007, 181, 436–452. [Google Scholar] [CrossRef]
- Davis, J.; Devos, L.; Reyners, S.; Schoutens, W. Gradient Boosting for Quantitative Finance. J. Comput. Financ. 2020, 24, 1–40. [Google Scholar] [CrossRef]
- jae Kim, K. Financial time series forecasting using support vector machines. Neurocomputing 2003, 55, 307–319. [Google Scholar] [CrossRef]
- Sadorsky, P. A Random Forests Approach to Predicting Clean Energy Stock Prices. J. Risk Financ. Manag. 2021, 14, 48. [Google Scholar] [CrossRef]
- Ammann, M.; Reich, C. VaR for nonlinear financial instruments-linear approximation or full Monte Carlo? Financ. Mark. Portf. Manag. 2001, 15, 363–378. [Google Scholar] [CrossRef]
- Hendricks, D. Evaluation of value-at-risk models using historical data. Econ. Policy Rev. 1996, 2, 39–69. [Google Scholar] [CrossRef]
- Damodaran, A. Strategic Risk Taking: A Framework for Risk Management, 1st ed.; Wharton School Publishing: Philadelphia, PA, USA, 2007. [Google Scholar]
- Wiener, Z. Introduction to VaR (value-at-risk). In Risk Management and Regulation in Banking: Proceedings of the International Conference on Risk Management and Regulation in Banking (1997); Springer: Berlin/Heidelberg, Germany, 1999; pp. 47–63. [Google Scholar]
- Dowd, K. Beyond Value at Risk: The New Science of Risk Management; John Wiley & Son Limited: Hoboken, NJ, USA, 1999; Volume 96. [Google Scholar]
- Cabedo, J.D.; Moya, I. Estimating oil price ‘Value at Risk’ using the historical simulation approach. Energy Econ. 2003, 25, 239–253. [Google Scholar] [CrossRef]
- Seyfi, S.M.S.; Sharifi, A.; Arian, H. Portfolio Value-at-Risk and expected-shortfall using an efficient simulation approach based on Gaussian Mixture Model. Math. Comput. Simul. 2021, 190, 1056–1079. [Google Scholar] [CrossRef]
- Morgan, J.P. RiskMetrics—Technical Document; J.P. Morgan/Reuters: New York, NY, USA, 1996. [Google Scholar]
- Alexander, C.O.; Leigh, C.T. On the covariance matrices used in value at risk models. J. Deriv. 1997, 4, 50–62. [Google Scholar] [CrossRef]
- Boudoukh, J.; Richardson, M.; Whitelaw, R.F. Investigation of a class of volatility estimators. J. Deriv. 1997, 4, 63–71. [Google Scholar] [CrossRef]
- Ding, J.; Meade, N. Forecasting accuracy of stochastic volatility, GARCH and EWMA models under different volatility scenarios. Appl. Financ. Econ. 2010, 20, 771–783. [Google Scholar] [CrossRef]
- Kupiec, P.H. Techniques for verifying the accuracy of risk measurement models. J. Deriv. 1995, 3, 73–84. [Google Scholar] [CrossRef]
- Haas, M. New Methods in Backtesting; Financial Engineering Research Center: Bonn, Germany, 2001. [Google Scholar]
- Christoffersen, P.F. Evaluating interval forecasts. Int. Econ. Rev. 1998, 39, 841–862. [Google Scholar] [CrossRef]
- Shaik, M.; Padmakumari, L. Value-at-risk (VAR) estimation and backtesting during COVID-19: Empirical analysis based on BRICS and US stock markets. Invest. Manag. Financ. Innov. 2022, 19, 51–63. [Google Scholar] [CrossRef]
- Nieppola, O. Backtesting Value-at-Risk Models. Master Thesis, Helsinki School of Economics, Espoo, Finland, 2009. [Google Scholar]




| Algorithm | Parameter | Values | Description |
|---|---|---|---|
| Gradient boosting | n_estimators learning_rate max_depth | 10, 25, 50, 100 0.0001, 0.001, 0.01, 0.1 2, 4, 6, 8, 10 | Boosting stages to perform Contribution of each tree Maximum depth of each estimator |
| Support vector machines | max_iter tol C gamma | 20, 50, 100 0.0001, 0.001, 0.01, 0.1 1, 10, 20, 50 0.0001, 0.001, 0.01, 0.1 | Hard limit of iterations within solver Tolerance for stopping criterion Penalty of the error term Coefficient for the used kernel |
| Random forests | n_estimators max_depth min_samples_split | 20, 50, 100 1, 5, 10, 50 0.2, 0.4, 0.8, 1.0 | Trees in the forest Max depth of the tree Min samples to split a node |
| Parameter | Values | Description |
|---|---|---|
| window_size | 100, 150, 200, 250, 300 | Days used for the training set |
| train_size | 60, 65, 70, 75, 80 | Percentage of window_size used for the training set |
| lags | 1, 3, 5, 7, 9 | Previous days to use in order to predict the return |
| Market | ARIMA | Ensemble |
|---|---|---|
| S&P stock market | 0.00653 | 0.00589 |
| Oil stock market | 0.00712 | 0.00601 |
| Silver stock market | 0.00815 | 0.00612 |
| Gold stock market | 0.01247 | 0.00901 |
| Used Method | LRatioTBFI | Failures | TBFMin | TBFQ1 | TBFQ2 | TBFQ3 | TBFMax |
|---|---|---|---|---|---|---|---|
| Paneltime_99_ENSEMBLE | 40.120 | 21 | 1 | 1 | 7 | 31 | 164 |
| Paneltime_99_ARIMA | 41.813 | 23 | 1 | 1 | 8 | 32 | 170 |
| Historical_99_ENSEMBLE | 149.932 | 43 | 1 | 2 | 17 | 68 | 430 |
| Historical_99_ARIMA | 149.932 | 43 | 1 | 2 | 17 | 68 | 430 |
| Historical_99 | 197.898 | 53 | 1 | 2 | 7 | 48 | 547 |
| Paneltime_95_ENSEMBLE | 222.193 | 63 | 1 | 2 | 6 | 39 | 316 |
| Paneltime_95_ARIMA | 244.809 | 65 | 1 | 2 | 7 | 40 | 320 |
| Normal_99_ENSEMBLE | 277.689 | 72 | 1 | 2 | 7 | 43 | 324 |
| Normal_99_ARIMA | 280.258 | 76 | 1 | 2 | 8 | 45 | 327 |
| Normal_99 | 343.423 | 90 | 1 | 2 | 7 | 35 | 351 |
| Historical_95_ENSEMBLE | 344.921 | 119 | 1 | 2 | 4 | 23 | 133 |
| Historical_95_ARIMA | 344.109 | 139 | 1 | 2 | 5 | 25 | 134 |
| Normal_95_ENSEMBLE | 350.790 | 143 | 1 | 2 | 5 | 17 | 166 |
| Normal_95_ARIMA | 355.022 | 150 | 1 | 2 | 5 | 18 | 172 |
| Historical_95 | 419.061 | 176 | 1 | 2 | 5 | 14 | 169 |
| Normal_95 | 420.112 | 175 | 1 | 2 | 5 | 14 | 169 |
| EWMA_99_0.94 | 530.177 | 157 | 1 | 4 | 10 | 25 | 66 |
| EWMA_95_0.94 | 565.432 | 282 | 1 | 2 | 6 | 13 | 61 |
| EWMA_99_0.3 | 968.365 | 268 | 1 | 4 | 8 | 13 | 39 |
| EWMA_99_0.2 | 1088.338 | 289 | 1 | 4 | 7 | 12 | 39 |
| EWMA_99_0.1 | 1198.688 | 308 | 1 | 4 | 7 | 11 | 31 |
| EWMA_95_ENSEMBLE_0.94 | 1306.871 | 440 | 1 | 1 | 3 | 6 | 110 |
| EWMA_95_ARIMA_0.94 | 1316.012 | 452 | 1 | 1 | 3 | 6 | 114 |
| EWMA_99_ENSEMBLE_0.94 | 1615.671 | 340 | 1 | 2 | 3 | 7 | 116 |
| EWMA_99_ARIMA_0.94 | 1900.344 | 342 | 1 | 2 | 3 | 7 | 118 |
| Used Method | LRatioTBFI | Failures | TBFMin | TBFQ1 | TBFQ2 | TBFQ3 | TBFMax |
|---|---|---|---|---|---|---|---|
| Paneltime_99_ENSEMBLE | 45.310 | 2 | 1 | 1 | 3 | 50 | 430 |
| Paneltime_99_ARIMA | 47.663 | 3 | 1 | 2 | 4 | 52 | 429 |
| Historical_99_ENSEMBLE | 145.110 | 43 | 1 | 3 | 8 | 56 | 367 |
| Historical_99_ARIMA | 151.813 | 46 | 1 | 4 | 11 | 63 | 379 |
| Normal_99_ARIMA | 208.652 | 57 | 1 | 3 | 9 | 34 | 442 |
| Normal_99_ENSEMBLE | 209.167 | 55 | 1 | 3 | 8 | 35 | 448 |
| Paneltime_95_ENSEMBLE | 209.259 | 3 | 1 | 2 | 3 | 61 | 390 |
| Paneltime_95_ARIMA | 209.578 | 3 | 1 | 2 | 4 | 43 | 378 |
| Historical_99 | 295.018 | 68 | 1 | 2 | 5 | 16 | 693 |
| Normal_95_ENSEMBLE | 303.610 | 113 | 1 | 3 | 5 | 11 | 309 |
| Normal_95_ARIMA | 310.868 | 140 | 1 | 3 | 6 | 15 | 312 |
| Historical_95_ENSEMBLE | 319.671 | 142 | 1 | 3 | 5 | 17 | 275 |
| Historical_95_ARIMA | 324.145 | 148 | 1 | 3 | 5 | 16 | 269 |
| Normal_99 | 363.302 | 81 | 1 | 2 | 5 | 12 | 419 |
| Normal_95 | 386.712 | 151 | 1 | 2 | 5 | 10 | 367 |
| Historical_95 | 465.254 | 205 | 1 | 2 | 5 | 11 | 223 |
| EWMA_99_0.94 | 516.944 | 159 | 1 | 4 | 11 | 20 | 99 |
| EWMA_95_0.94 | 550.936 | 308 | 1 | 3 | 6 | 11 | 75 |
| EWMA_99_0.3 | 1209.963 | 300 | 1 | 4 | 6 | 11 | 65 |
| EWMA_95_ENSEMBLE_0.94 | 1268.127 | 309 | 1 | 5 | 6 | 11 | 78 |
| EWMA_99_0.2 | 1274.892 | 313 | 1 | 4 | 6 | 10 | 65 |
| EWMA_95_ARIMA_0.94 | 1395.281 | 446 | 1 | 1 | 3 | 5 | 147 |
| EWMA_99_ENSEMBLE_0.94 | 1399.112 | 301 | 1 | 1 | 3 | 5 | 157 |
| EWMA_99_0.1 | 1405.215 | 333 | 1 | 3 | 6 | 9 | 65 |
| EWMA_99_ARIMA_0.94 | 1822.801 | 316 | 1 | 1 | 3 | 5 | 163 |
| Used Method | LRatioTBFI | Failures | TBFMin | TBFQ1 | TBFQ2 | TBFQ3 | TBFMax |
|---|---|---|---|---|---|---|---|
| Paneltime_99_ENSEMBLE | 38.750 | 26 | 1 | 2 | 14 | 60 | 395 |
| Paneltime_99_ARIMA | 41.813 | 30 | 1 | 2 | 15 | 65 | 410 |
| Historical_99 | 149.932 | 43 | 1 | 2 | 17 | 68 | 430 |
| Historical_99_ARIMA | 156.359 | 44 | 1 | 2 | 14 | 67 | 428 |
| Historical_99_ENSEMBLE | 167.119 | 49 | 1 | 2 | 17 | 68 | 431 |
| Normal_99_ENSEMBLE | 237.014 | 52 | 1 | 2 | 5 | 32 | 297 |
| Normal_99_ARIMA | 244.809 | 59 | 1 | 2 | 6 | 39 | 301 |
| Normal_99 | 304.284 | 81 | 1 | 2 | 7 | 43 | 327 |
| Normal_95_ENSEMBLE | 335.097 | 86 | 1 | 2 | 5 | 30 | 248 |
| Normal_95_ARIMA | 343.423 | 90 | 1 | 2 | 7 | 35 | 351 |
| Normal_95 | 355.022 | 150 | 1 | 2 | 5 | 18 | 172 |
| Historical_95_ENSEMBLE | 359.230 | 135 | 1 | 2 | 4 | 20 | 130 |
| Historical_95_ARIMA | 362.303 | 144 | 1 | 2 | 5 | 21 | 134 |
| Historical_95 | 419.061 | 176 | 1 | 2 | 5 | 14 | 169 |
| Paneltime_95_ENSEMBLE | 420.010 | 174 | 1 | 2 | 5 | 13 | 169 |
| Paneltime_95_ARIMA | 420.112 | 175 | 1 | 2 | 5 | 14 | 169 |
| EWMA_95 | 530.177 | 157 | 1 | 4 | 10 | 26 | 66 |
| EWMA_99 | 565.432 | 282 | 1 | 2 | 6 | 13 | 61 |
| EWMA_95_ENSEMBLE_0.94 | 798.012 | 243 | 1 | 3 | 6 | 11 | 41 |
| EWMA_99_0.3 | 968.365 | 268 | 1 | 4 | 8 | 13 | 39 |
| EWMA_99_ENSEMBLE_0.94 | 1043.797 | 276 | 1 | 3 | 4 | 10 | 43 |
| EWMA_99_0.2 | 1088.338 | 289 | 1 | 4 | 7 | 12 | 39 |
| EWMA_95_ARIMA_0.94 | 1198.688 | 308 | 1 | 4 | 7 | 11 | 31 |
| EWMA_99_0.1 | 1346.119 | 457 | 1 | 1 | 3 | 6 | 114 |
| EWMA_99_ARIMA_0.94 | 1900.344 | 342 | 1 | 2 | 3 | 7 | 118 |
| Used Method | LRatioTBFI | Failures | TBFMin | TBFQ1 | TBFQ2 | TBFQ3 | TBFMax |
|---|---|---|---|---|---|---|---|
| Paneltime_99_ENSEMBLE | 30.091 | 24 | 1 | 7 | 30 | 87 | 312 |
| Paneltime_99_ARIMA | 41.813 | 28 | 1 | 13 | 40 | 94 | 389 |
| Historical_99_ENSEMBLE | 54.185 | 30 | 1 | 13 | 40 | 97 | 397 |
| Historical_99_ARIMA | 61.681 | 31 | 1 | 15 | 45 | 101 | 401 |
| Historical_99 | 64.585 | 21 | 1 | 8 | 35 | 70 | 817 |
| Normal_99 | 81.221 | 33 | 1 | 9 | 34 | 59 | 700 |
| Normal_99_ENSEMBLE | 82.917 | 38 | 1 | 12 | 37 | 68 | 209 |
| Normal_99_ARIMA | 83.000 | 46 | 1 | 14 | 40 | 73 | 217 |
| Normal_95_ENSEMBLE | 139.290 | 117 | 1 | 6 | 14 | 29 | 101 |
| Normal_95_ARIMA | 158.421 | 129 | 1 | 6 | 14 | 30 | 107 |
| Historical_95_ENSEMBLE | 160.109 | 131 | 1 | 5 | 13 | 28 | 91 |
| Historical_95_ARIMA | 162.279 | 138 | 1 | 5 | 14 | 29 | 95 |
| Historical_95 | 181.480 | 130 | 1 | 5 | 13 | 29 | 156 |
| Normal_95 | 185.255 | 103 | 1 | 5 | 12 | 32 | 261 |
| Paneltime_95_ENSEMBLE | 212.475 | 98 | 1 | 4 | 8 | 13 | 82 |
| Paneltime_95_ARIMA | 244.809 | 103 | 1 | 4 | 8 | 13 | 87 |
| EWMA_95 | 394.123 | 274 | 1 | 4 | 7 | 14 | 45 |
| EWMA_99 | 428.975 | 147 | 1 | 6 | 14 | 26 | 80 |
| EWMA_99_0.3 | 1352.436 | 327 | 1 | 3 | 6 | 11 | 36 |
| EWMA_99_0.2 | 1484.849 | 351 | 1 | 3 | 6 | 10 | 34 |
| EWMA_95_ENSEMBLE_0.94 | 1509.104 | 513 | 1 | 2 | 3 | 5 | 71 |
| EWMA_95_ARIMA_0.94 | 1587.327 | 555 | 1 | 2 | 3 | 5 | 76 |
| EWMA_99_0.1 | 1657.845 | 375 | 1 | 3 | 5 | 10 | 31 |
| EWMA_99_ENSEMBLE_0.94 | 2168.110 | 409 | 1 | 2 | 3 | 7 | 95 |
| EWMA_99_ARIMA_0.94 | 2200.140 | 415 | 1 | 2 | 3 | 7 | 97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagheri, F.; Reforgiato Recupero, D.; Sirnes, E. Leveraging Return Prediction Approaches for Improved Value-at-Risk Estimation. Data 2023, 8, 133. https://doi.org/10.3390/data8080133
Bagheri F, Reforgiato Recupero D, Sirnes E. Leveraging Return Prediction Approaches for Improved Value-at-Risk Estimation. Data. 2023; 8(8):133. https://doi.org/10.3390/data8080133
Chicago/Turabian StyleBagheri, Farid, Diego Reforgiato Recupero, and Espen Sirnes. 2023. "Leveraging Return Prediction Approaches for Improved Value-at-Risk Estimation" Data 8, no. 8: 133. https://doi.org/10.3390/data8080133
APA StyleBagheri, F., Reforgiato Recupero, D., & Sirnes, E. (2023). Leveraging Return Prediction Approaches for Improved Value-at-Risk Estimation. Data, 8(8), 133. https://doi.org/10.3390/data8080133









