Degradation-Dependent Stress Relaxing Semi-Interpenetrating Networks of Hydroxyethyl Cellulose in Gelatin-PEG Hydrogel with Good Mechanical Stability and Reversibility
Abstract
:1. Introduction
2. Results and Discussions
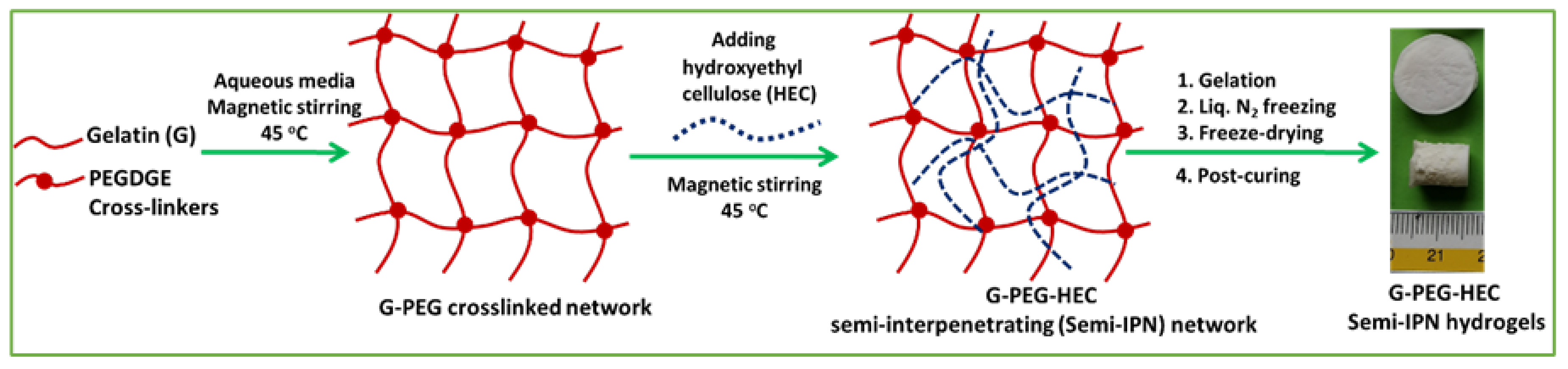
2.1. Preparation of Hydrogel and Physical Properties
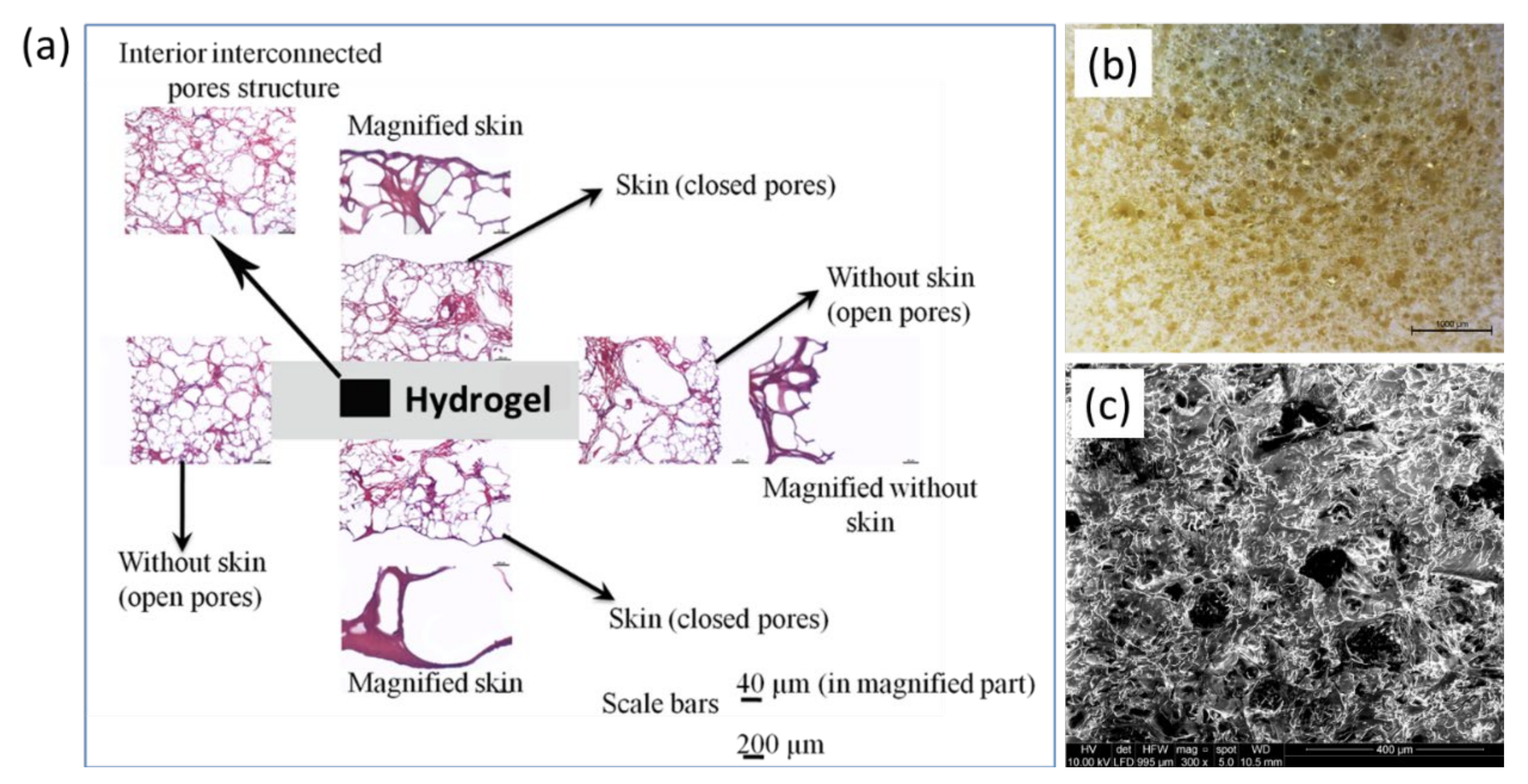
2.2. Morphology of Hydrogel
2.3. Mechanical Properties of Semi-IPN Hydrogel
2.3.1. Tensile Mechanical Properties
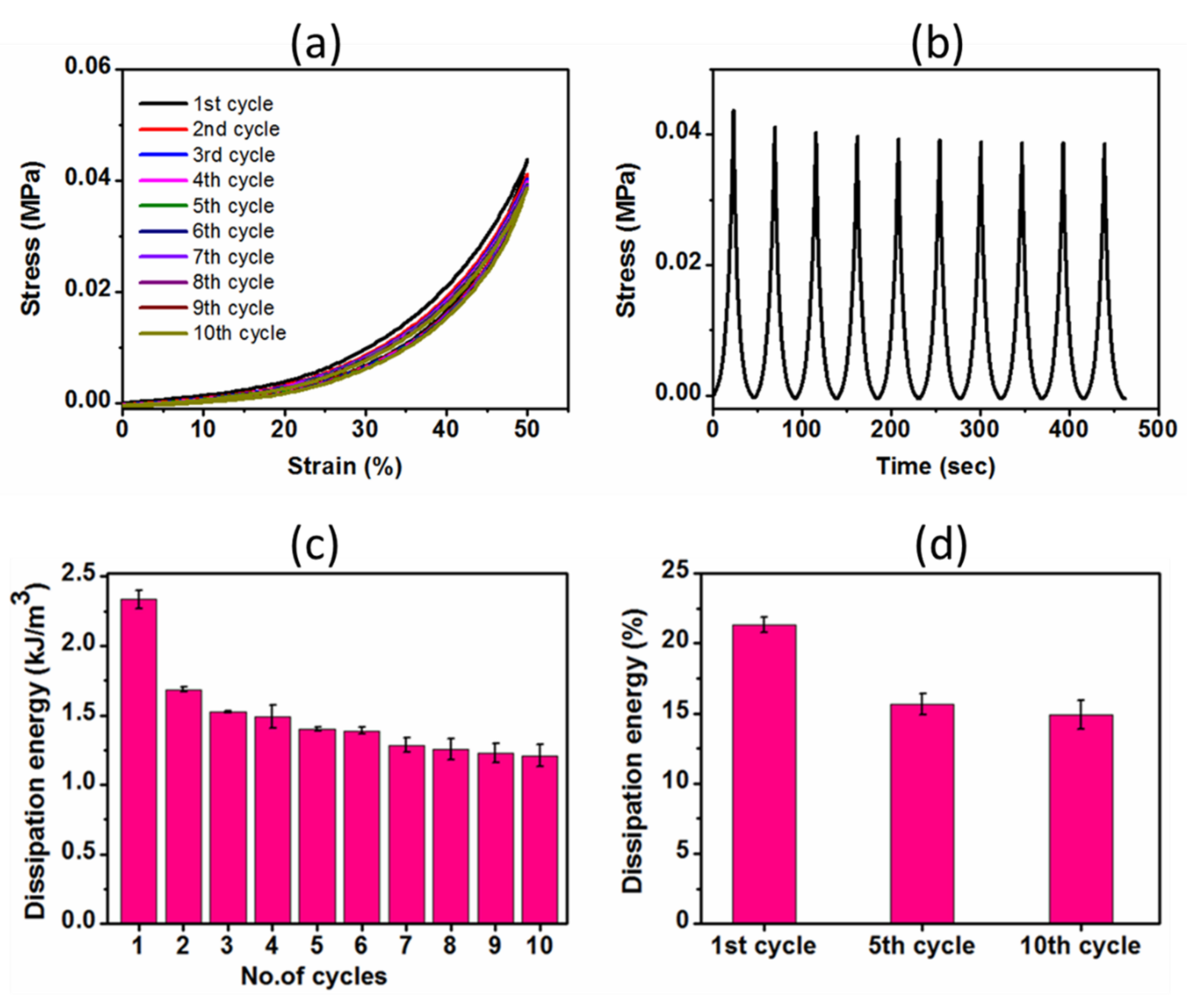
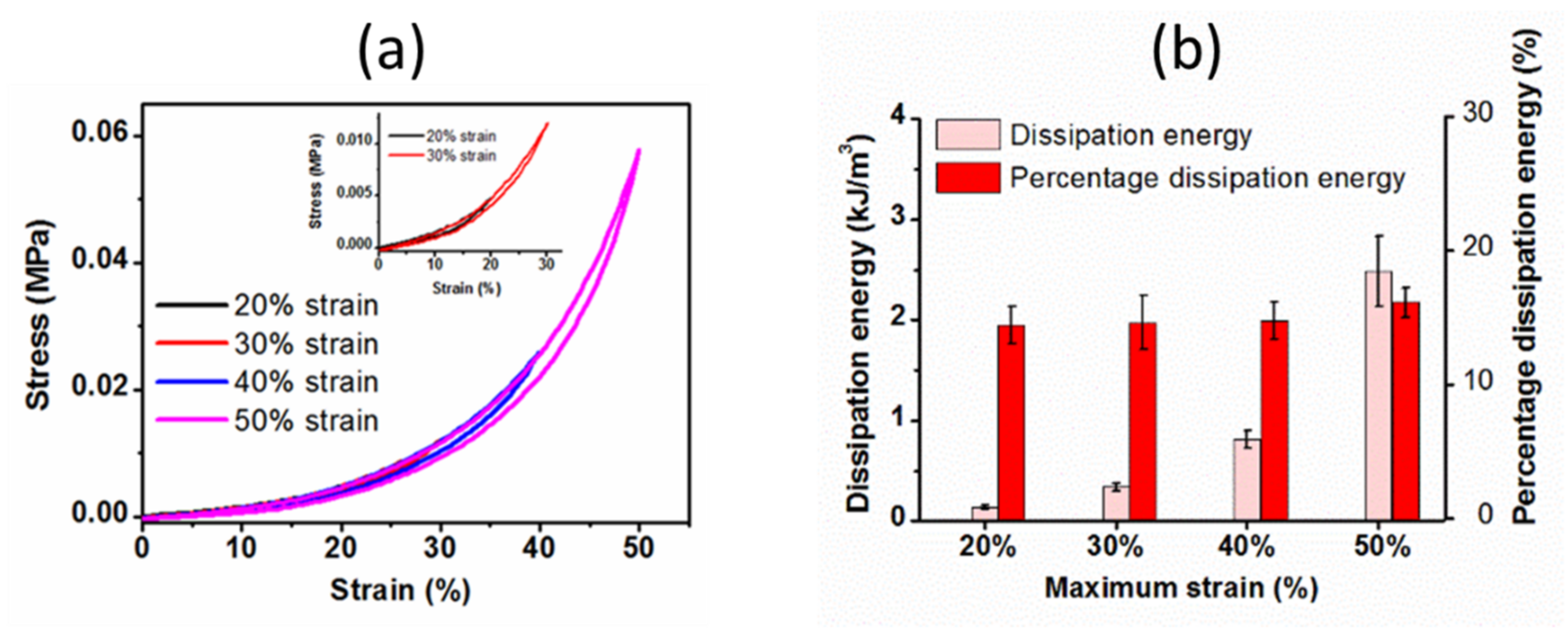
2.3.2. Cyclic Compressive Properties
2.3.3. Monitoring Mass Loss and Mechanical Properties during Hydrolytic Degradation
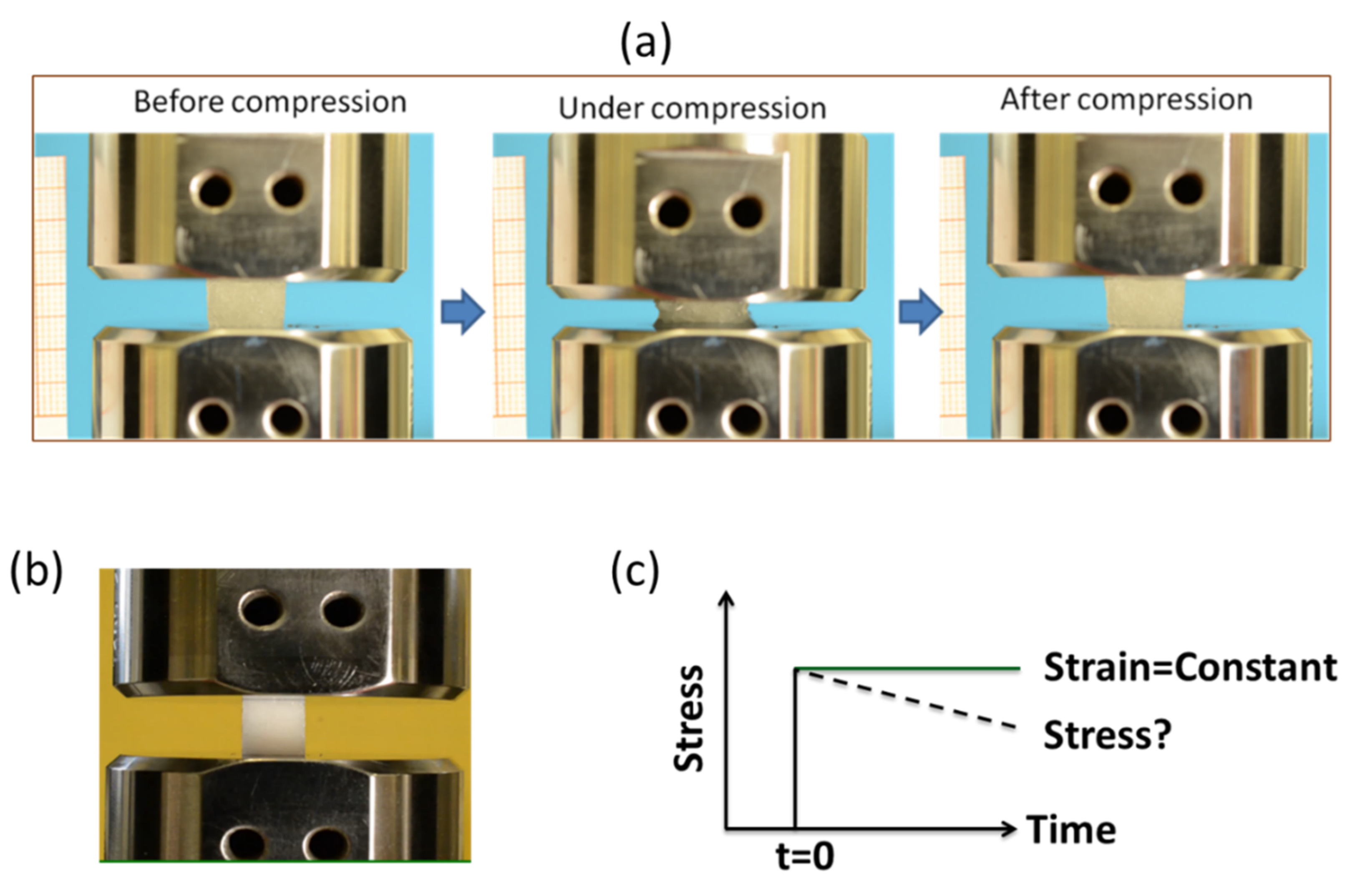
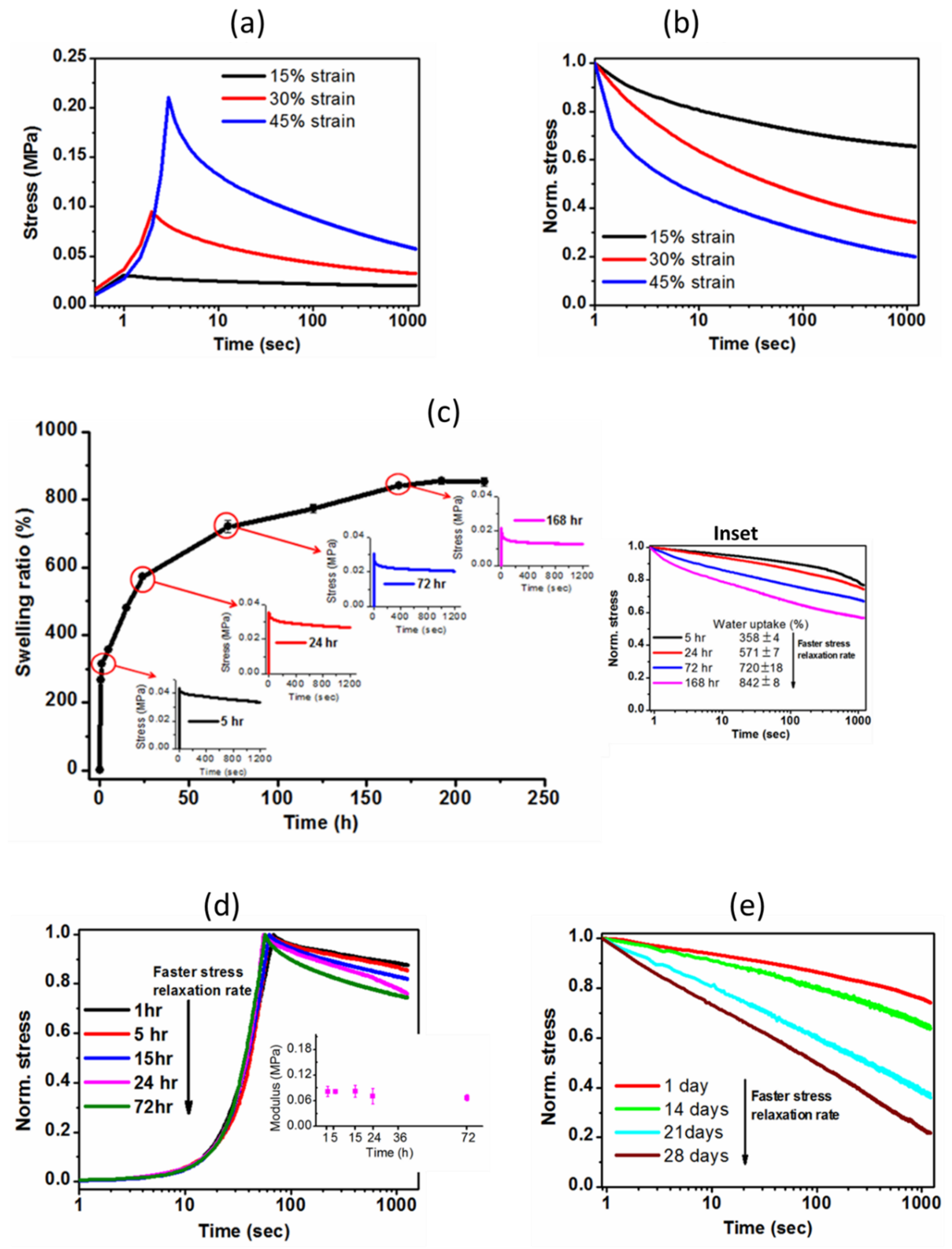
2.3.4. Stress Relaxation Behavior of Hydrogel
3. Conclusions
4. Materials and Methods
4.1. Materials
4.2. Synthesis of Semi-IPN G-PEG-HEC Hybrid Hydrogel
4.3. Gel Fraction
4.4. Apparent Density and Porosity Measurement
4.5. Equilibrium Swelling Ratio (%) of the Hydrogel
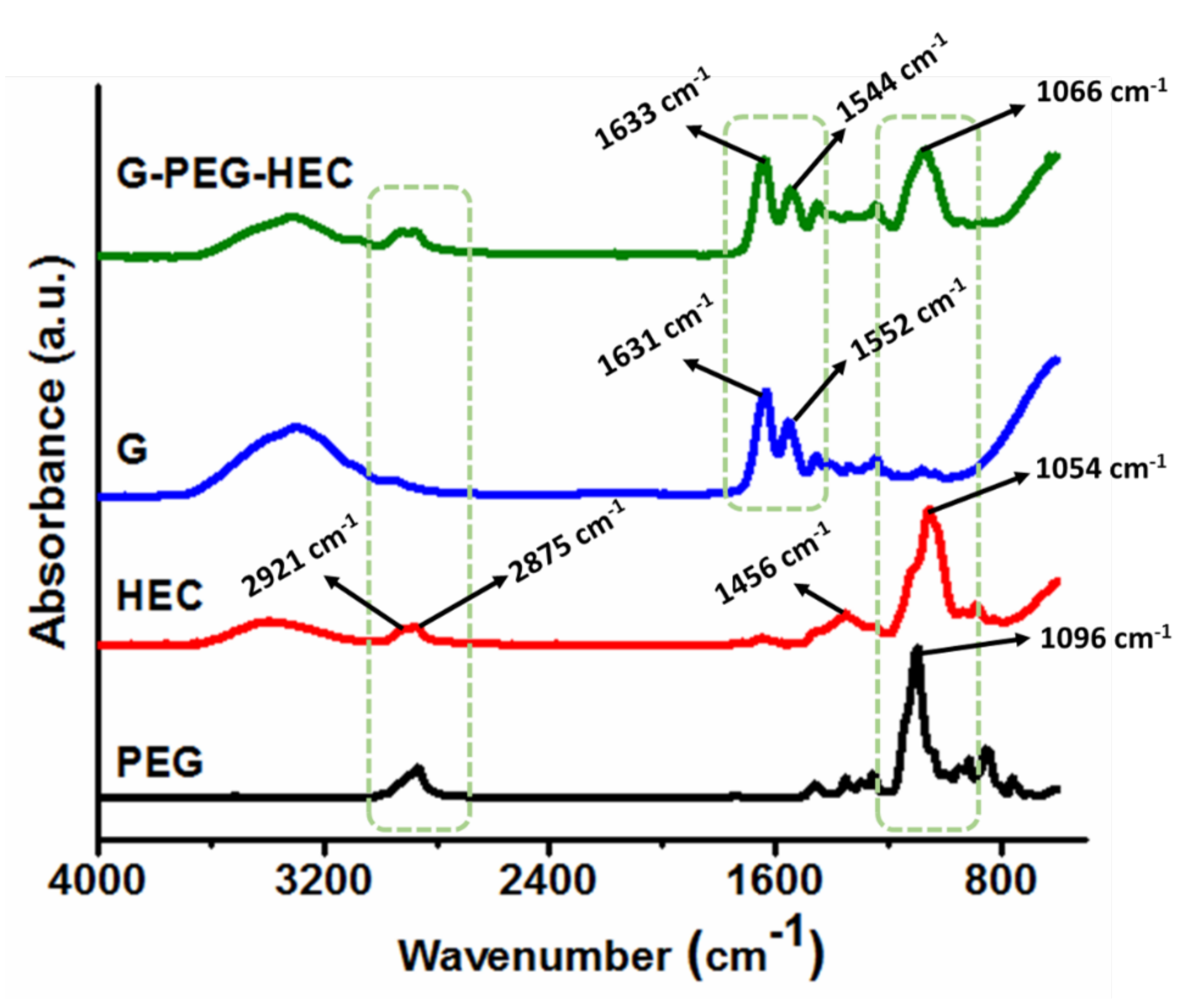
4.6. Structural Characterization
4.7. Morphological Analysis
4.8. Tensile Test
4.9. Compression and Cyclic Compression Tests
4.10. Hydrolytic Mass Loss Evaluation and Monitoring Mechanical Properties
4.11. Evaluation of Stress Relaxation Response
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, F.M.; Liu, X.H. Advancing biomaterials of human origin for tissue engineering. Prog. Polym. Sci. 2016, 53, 86–168. [Google Scholar] [CrossRef] [Green Version]
- Atala, A.; Kasper, F.K.; Mikos, A.G. Engineering Complex Tissues. Sci. Transl. Med. 2012, 4, 160rv12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khademhosseini, A.; Langer, R. A decade of progress in tissue engineering. Nat. Protoc. 2016, 11, 1775–1781. [Google Scholar] [CrossRef] [PubMed]
- Khademhosseini, A.; Vacanti, J.P.; Langer, R. Progress in Tissue Engineering. Sci. Am. 2009, 300, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Dey, K.; Roca, E.; Ramorino, G.; Sartore, L. Progress in the mechanical modulation of cell functions in tissue engineering. Biomater. Sci. 2020, 8, 7033–7081. [Google Scholar] [CrossRef]
- Huey, D.J.; Hu, J.C.; Athanasiou, K.A. Unlike Bone, Cartilage Regeneration Remains Elusive. Science 2012, 338, 917–921. [Google Scholar] [CrossRef] [Green Version]
- Armiento, A.; Stoddart, M.; Alini, M.; Eglin, D. Biomaterials for articular cartilage tissue engineering: Learning from biology. Acta Biomater. 2018, 65, 1–20. [Google Scholar] [CrossRef]
- Valot, L.; Maumus, M.; Brunel, L.; Martinez, J.; Amblard, M.; Noël, D.; Mehdi, A.; Subra, G. A Collagen-Mimetic Organic-Inorganic Hydrogel for Cartilage Engineering. Gels 2021, 7, 73. [Google Scholar] [CrossRef]
- Skaalure, S.; Dimson, S.O.; Pennington, A.; Bryant, S.J. Semi-interpenetrating networks of hyaluronic acid in degradable PEG hydrogels for cartilage tissue engineering. Acta Biomater. 2014, 10, 3409–3420. [Google Scholar] [CrossRef]
- Buxton, A.N.; Zhu, J.; Marchant, R.; West, J.L.; Yoo, J.U.; Johnstone, B. Design and Characterization of Poly(Ethylene Glycol) Photopolymerizable Semi-Interpenetrating Networks for Chondrogenesis of Human Mesenchymal Stem Cells. Tissue Eng. 2007, 13, 2549–2560. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Cao, X.; Zeng, L.; Zhang, Q.; Chen, X. An interpenetrating HA/G/CS biomimic hydrogel via Diels–Alder click chemistry for cartilage tissue engineering. Carbohydr. Polym. 2013, 97, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Junior, E.M.D.; Dias, D.d.R.C.; Rodrigues, A.P.D.; Dias, C.G.B.T.; Bastos, G.D.N.T.; de Oliveira, J.A.R.; Filho, R.M.; Passos, M.F. SIPNs polymeric scaffold for use in cartilaginous tissue engineering: Physical-chemical evaluation and biological behavior. Mater. Today Commun. 2021, 26, 102111. [Google Scholar] [CrossRef]
- Shi, Z.; Gao, X.; Ullah, M.W.; Li, S.; Wang, Q.; Yang, G. Electroconductive natural polymer-based hydrogels. Biomaterials 2016, 111, 40–54. [Google Scholar] [CrossRef]
- Jia, X.; Kiick, K.L. Hybrid Multicomponent Hydrogels for Tissue Engineering. Macromol. Biosci. 2009, 9, 140–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorgieva, S.; Kokol, V. Collagen- vs. Gelatine-Based Biomaterials and Their Biocompatibility: Review and Perspectives. In Biomaterials Applications for Nanomedicine; Pignatello, R., Ed.; Intechopen: Ljubljana, Slovenia, 2011; pp. 17–52. [Google Scholar]
- Klotz, B.J.; Gawlitta, D.; Rosenberg, A.J.; Malda, J.; Melchels, F.P. Gelatin-Methacryloyl Hydrogels: Towards Biofabrication-Based Tissue Repair. Trends Biotechnol. 2016, 34, 394–407. [Google Scholar] [CrossRef] [Green Version]
- Alizadehaghdam, M.; Abbasi, F.; Khoshfetrat, A.; Ghaleh, H. Microstructure and characteristic properties of gelatin/chitosan scaffold prepared by a combined freeze-drying/leaching method. Mater. Sci. Eng. C 2013, 33, 3958–3967. [Google Scholar] [CrossRef]
- Zulkifli, F.H.; Hussain, F.S.J.; Rasad, M.S.B.A.; Yusoff, M. Nanostructured materials from hydroxyethyl cellulose for skin tissue engineering. Carbohydr. Polym. 2014, 114, 238–245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyamoto, T.; Takahashi, S.-I.; Ito, H.; Inagaki, H.; Noishiki, Y. Tissue biocompatibility of cellulose and its derivatives. J. Biomed. Mater. Res. 1989, 23, 125–133. [Google Scholar] [CrossRef] [PubMed]
- Dey, K.; Agnelli, S.; Serzanti, M.; Ginestra, P.; Scarì, G.; Dell’Era, P.; Sartore, L. Preparation and properties of high performance gelatin-based hydrogels with chitosan or hydroxyethyl cellulose for tissue engineering applications. Int. J. Pol. Mat. Pol. Biom. 2018, 68, 183–192. [Google Scholar] [CrossRef]
- Stahl, P.J.; Romano, N.; Wirtz, D.; Yu, S.M. PEG-Based Hydrogels with Collagen Mimetic Peptide-Mediated and Tunable Physical Cross-Links. Biomacromolecules 2010, 11, 2336–2344. [Google Scholar] [CrossRef] [PubMed]
- Dey, K.; Agnelli, S.; Sartore, L. Effects of gamma sterilization on the physicomechanical and thermal properties of gelatin-based novel hydrogels. Polym. Eng. Sci. 2019, 59, 2533–2540. [Google Scholar] [CrossRef]
- Chaudhuri, O.; Gu, L.; Klumpers, D.; Darnell, M.; Bencherif, S.A.; Weaver, J.C.; Huebsch, N.; Lee, H.-P.; Lippens, E.; Duda, G.N.; et al. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat. Mater. 2016, 15, 326–334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dey, K.; Agnelli, S.; Sartore, L. Dynamic freedom: Substrate stress relaxation stimulates cell responses. Biomater. Sci. 2019, 7, 836–842. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, O.; Gu, L.; Darnell, M.; Klumpers, D.D.; Bencherif, S.A.; Weaver, J.C.; Huebsch, N.; Mooney, D.J. Substrate stress relaxation regulates cell spreading. Nat. Commun. 2015, 6, 6364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lou, J.; Stowers, R.; Nam, S.; Xia, Y.; Chaudhuri, O. Stress relaxing hyaluronic acid-collagen hydrogels promote cell spreading, fiber remodeling, and focal adhesion formation in 3D cell culture. Biomaterials 2018, 154, 213–222. [Google Scholar] [CrossRef]
- McKinnon, D.D.; Domaille, D.W.; Cha, J.N.; Anseth, K.S. Biophysically Defined and Cytocompatible Covalently Adaptable Networks as Viscoelastic 3D Cell Culture Systems. Adv. Mater. 2014, 26, 865–872. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wu, D.; Hu, D.; Zhu, S.; Pan, C.; Jiao, Y.; Li, L.; Luo, B.; Zhou, C.; Lu, L. Stress-relaxing double-network hydrogel for chondrogenic differentiation of stem cells. Mater. Sci. Eng. C 2020, 107, 110333. [Google Scholar] [CrossRef] [PubMed]
- Sartore, L.; Manferdini, C.; Saleh, Y.; Dey, K.; Gabusi, E.; Ramorino, G.; Zini, N.; Almici, C.; Re, F.; Russo, D.; et al. Polysaccharides on gelatin-based hydrogels differently affect chondrogenic differentiation of human mesenchymal stromal cells. Mater. Sci. Eng. C 2021, 126, 112175. [Google Scholar] [CrossRef]
- Dey, K.; Agnelli, S.; Re, F.; Russo, D.; Lisignoli, G.; Manferdini, C.; Bernardi, S.; Gabusi, E.; Sartore, L. Rational Design and Development of Anisotropic and Mechanically Strong Gelatin-Based Stress Relaxing Hydrogels for Osteogenic/Chondrogenic Differentiation. Macromol. Biosci. 2019, 19, 1900099. [Google Scholar] [CrossRef] [PubMed]
- Kajjari, P.B.; Manjeshwar, L.S.; Aminabhavi, T.M. Semi-Interpenetrating Polymer Network Hydrogel Blend Microspheres of Gelatin and Hydroxyethyl Cellulose for Controlled Release of Theophylline. Ind. Eng. Chem. Res. 2011, 50, 7833–7840. [Google Scholar] [CrossRef]
- Hutson, C.B.; Nichol, J.W.; Aubin, H.; Bae, H.; Yamanlar, S.; Al-Haque, M.S.; Koshy, S.; Khademhosseini, A. Synthesis and Characterization of Tunable Poly(Ethylene Glycol): Gelatin Methacrylate Composite Hydrogels. Tissue Eng. Part A 2011, 17, 1713–1723. [Google Scholar] [CrossRef] [PubMed]
- Khetan, S.; Guvendiren, M.; Legant, W.R.; Cohen, D.; Chen, C.; Burdick, J.A. Degradation-mediated cellular traction directs stem cell fate in covalently crosslinked three-dimensional hydrogels. Nat. Mater. 2013, 12, 458–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suhr, J.; Victor, P.J.; Ci, L.; Sreekala, S.; Zhang, X.; Nalamasu, O.; Ajayan, P.M. Fatigue resistance of aligned carbon nanotube arrays under cyclic compression. Nat. Nanotechnol. 2007, 2, 417–421. [Google Scholar] [CrossRef]
- Chaudhuri, O. Viscoelastic hydrogels for 3D cell culture. Biomater. Sci. 2017, 5, 1480–1490. [Google Scholar] [CrossRef] [PubMed]
- Nam, S.; Hu, K.H.; Butte, M.J.; Chaudhuri, O. Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels. Proc. Natl. Acad. Sci. USA 2016, 113, 5492–5497. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Huebsch, N.; Mooney, D.; Suo, Z. Stress-relaxation behavior in gels with ionic and covalent crosslinks. J. Appl. Phys. 2010, 107, 063509. [Google Scholar] [CrossRef] [Green Version]


| Dry Composition (wt%) | Physical Properties | ||||||
|---|---|---|---|---|---|---|---|
| Hydrogel | G | PEG | HEC | Apparent Density (g/cc) | Porosity (%) | Gel Fraction (%) | Equilibrium Swelling Ratio (%) |
| G-PEG-HEC | 66 | 15 | 19 | 0.120 ± 0.01 | 83.09 ± 4.4 | 82.54 ± 1.9 | 720.00 ± 32.0 |
| Tensile Properties | Compressive Properties | ||
|---|---|---|---|
| Tensile elastic modulus (MPa) | 0.12 ± 0.001 | Compressive elastic modulus (MPa) | 0.06 ± 0.003 |
| Tensile strength (MPa) | 0.14 ± 0.03 | Compressive stress (MPa) at 50% strain | 0.09 ± 0.01 |
| Elongation at break (%) | 56.10 ± 8.61 | Compression energy (kJ/m3) | 8.96 ± 0.38 |
| Relaxation energy (kJ/m3) | 7.55 ± 0.38 | ||
| Dissipation energy (kJ/m3) | 1.40 ± 0.01 | ||
| Percentage dissipation energy (%) | 15.67 ± 0.78 | ||
| Time (Days) | Modulus (MPa) | Stress (MPa) at 50% Strain |
|---|---|---|
| 2 | 0.060 ± 0.01 | 0.140 ± 0.02 |
| 7 | 0.023 ± 0.005 | 0.055 ± 0.01 |
| 14 | 0.022 ± 0.002 | 0.047 ± 0.01 |
| 21 | 0.0162 ± 0.001 | 0.031 ± 0.001 |
| 28 | 0.010 ± 0.002 | 0.020 ± 0.004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, K.; Agnelli, S.; Borsani, E.; Sartore, L. Degradation-Dependent Stress Relaxing Semi-Interpenetrating Networks of Hydroxyethyl Cellulose in Gelatin-PEG Hydrogel with Good Mechanical Stability and Reversibility. Gels 2021, 7, 277. https://doi.org/10.3390/gels7040277
Dey K, Agnelli S, Borsani E, Sartore L. Degradation-Dependent Stress Relaxing Semi-Interpenetrating Networks of Hydroxyethyl Cellulose in Gelatin-PEG Hydrogel with Good Mechanical Stability and Reversibility. Gels. 2021; 7(4):277. https://doi.org/10.3390/gels7040277
Chicago/Turabian StyleDey, Kamol, Silvia Agnelli, Elisa Borsani, and Luciana Sartore. 2021. "Degradation-Dependent Stress Relaxing Semi-Interpenetrating Networks of Hydroxyethyl Cellulose in Gelatin-PEG Hydrogel with Good Mechanical Stability and Reversibility" Gels 7, no. 4: 277. https://doi.org/10.3390/gels7040277
APA StyleDey, K., Agnelli, S., Borsani, E., & Sartore, L. (2021). Degradation-Dependent Stress Relaxing Semi-Interpenetrating Networks of Hydroxyethyl Cellulose in Gelatin-PEG Hydrogel with Good Mechanical Stability and Reversibility. Gels, 7(4), 277. https://doi.org/10.3390/gels7040277









