Spatially-Resolved Network Dynamics of Poly(vinyl alcohol) Gels Measured with Dynamic Small Angle Light Scattering
Abstract
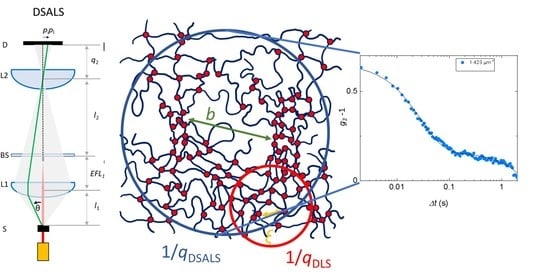
:1. Introduction
2. Results and Discussion
2.1. Unstretched Gels
2.2. Stretched Gels
3. Conclusions
4. Materials and Methods
4.1. Materials
4.2. Dynamic Light Scattering
4.3. Optical Design
4.4. DSALS Sample Preparation
4.5. Stretching Experiments
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morozova, S.; Hitimana, E.; Dhakal, S.; Wilcox, K.G.; Estrin, D. Scattering Methods for Determining Structure and Dynamics of Polymer Gels. J. Appl. Phys. 2021, 129, 071101. [Google Scholar] [CrossRef]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering; Dover Publications, Inc.: Mineola, NY, USA, 2000. [Google Scholar]
- Shibayama, M. Spatial Inhomogeneity and Dynamic Fluctuations of Polymer Gels. Macromol. Chem. Phys. 1998, 199, 1–30. [Google Scholar] [CrossRef]
- Narita, T.; Knaebel, A.; Munch, J.P.; Candau, S.J. Microrheology of Poly(vinyl alcohol) Aqueous Solutions and Chemically Cross-Linked Gels. Macromolecules 2001, 34, 8224–8231. [Google Scholar] [CrossRef]
- Narita, T.; Mayumi, K.; Ducouret, G.; Hébraud, P. Viscoelastic Properties of Poly(vinyl alcohol) Hydrogels Having Permanent and Transient Cross-Links Studied by Microrheology, Classical Rheometry, and Dynamic Light Scattering. Macromolecules 2013, 46, 4174–4183. [Google Scholar] [CrossRef]
- Horkay, F.; Basser, P.J. Composite Hydrogel Model of Cartilage Predicts Its Load-Bearing Ability. Sci. Rep. 2020, 10, 8103. [Google Scholar] [CrossRef]
- Horkay, F. Interactions of Cartilage Extracellular Matrix Macromolecules. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1699–1705. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Storr-Paulsen, T.; Wang, A.L.; Ghezzi, C.E.; Wang, S.; Fullana, M.; Karamichos, D.; Utheim, T.P.; Islam, R.; Griffith, M.; et al. Artificial Polymeric Scaffolds as Extracellular Matrix Substitutes for Autologous Conjunctival Goblet Cell Expansion. Investig. Ophthalmol. Vis. Sci. 2016, 57, 6134–6146. [Google Scholar] [CrossRef] [Green Version]
- Molyneaux, K.; Wnek, M.D.; Craig, S.E.L.; Vincent, J.; Rucker, I.; Wnek, G.E.; Brady-Kalnay, S.M. Physically-cross-linked Poly Vinyl Alcohol Cell Culture Plate Coatings Facilitate. J. Biomed. Mat. Res. 2020, 109, 1744–1753. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, S.; Feng, W. PVA Hydrogel Properties for Biomedical Application. J. Mech. Behav. Biomed. Mater. 2011, 4, 1228–1233. [Google Scholar] [CrossRef]
- Peppas, N.A.; Hilt, J.Z.; Khademhosseini, A.; Langer, R. Hydrogels in Biology and Medicine: From Molecular Principles to Bionanotechnology. Adv. Mater. 2006, 18, 1345–1360. [Google Scholar] [CrossRef]
- Fang, L.; Brown, W. Dynamic Light Scattering by Permanent Gels: Partial Heterodyne and Nonergodic Medium Methods for Data Evaluation. Macromolecules 1992, 25, 6897. [Google Scholar] [CrossRef]
- Horkay, F.; Burchard, J.W.; Geissler, E.; Hecht, A. Thermodynamic Properties of Poly(vinyl alcohol) and Poly(vinyl alcohol-vinyl acetate) Hydrogels. Macromolecules 1993, 26, 1296–1303. [Google Scholar] [CrossRef]
- Geissler, E.; Horkay, F.; Hecht, A.M. Osmotic and Scattering Properties of Chemically Cross-Linked Poly(vinyl alcohol) Hydrogels. Macromolecules 1991, 24, 6006–6011. [Google Scholar] [CrossRef]
- Ikkai, F.; Shibayama, M. Inhomogeneity Control in Polymer Gels. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 617–628. [Google Scholar] [CrossRef]
- Norisuye, T.; Tran-Cong-Miyata, Q.; Shibayama, M. Dynamic Inhomogeneities in Polymer Gels Investigated by Dynamic Light Scattering. Macromolecules 2004, 37, 2944–2953. [Google Scholar] [CrossRef]
- Xue, J.Z.X.; Pine, D.J.; Milner, S.T.; Wu, X.I.; Chaikin, P.M. Nonergodicity and Light Scattering from Polymer Gels. Phys. Rev. A 1992, 46, 6550–6563. [Google Scholar] [CrossRef]
- Dannhauser, D.; Romeo, G.; Causa, F.; Netti, P.A. Small Angle Light Scattering Characterization of Single Micrometric Particles in Microfluidic Flows. Opt. Methods Insp. Charact. Imaging Biomater. 2013, 8792, 879212. [Google Scholar] [CrossRef]
- Hashimoto, T.; Tomoaki, T.; Suehiro, S. Apparatus to Measure Small-Angle Light Scattering Profiles of Polymers under Shear Flow. Polym. J. 1986, 18, 123–130. [Google Scholar] [CrossRef] [Green Version]
- Cipelletti, L.; Weitz, D.A. Ultralow-Angle Dynamic Light Scattering with a Charge Coupled Device Camera Based Multispeckle, Multitau Correlator. Rev. Sci. Instrum. 1999, 70, 3214–3221. [Google Scholar] [CrossRef] [Green Version]
- Ferri, F. Use of a Charge Coupled Device Camera for Low-Angle Elastic Light Scattering. Rev. Sci. Instrum. 1997, 68, 2265–2274. [Google Scholar] [CrossRef] [Green Version]
- Block, I.D.; Scheffold, F. Modulated 3D Cross-Correlation Light Scattering: Improving Turbid Sample Characterization. Rev. Sci. Instrum. 2010, 81, 123107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sacks, M.S.; Smith, D.B.; Hiester, E.D. A Small Angle Light Scattering Device for Planar Connective Tissue Microstructural Analysis. Ann. Biomed. Eng. 1997, 25, 678–689. [Google Scholar] [CrossRef] [PubMed]
- Robitaille, M.C.; Zareian, R.; DiMarzio, C.A.; Wan, K.T.; Ruberti, J.W. Small-Angle Light Scattering to Detect Strain-Directed Collagen Degradation in Native Tissue. Interface Focus 2011, 1, 767–776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rhodes, M.B.; Stein, R.S. Light Scattering Study of the Annealing of Drawn Polyethylene. J. Appl. Phys. 1961, 32, 2344–2352. [Google Scholar] [CrossRef]
- Hindawi, I.A.; Higgins, J.S.; Weiss, R.A. Flow-Induced Mixing and Demixing in Polymer Blends. Polymer 1992, 33, 2522–2529. [Google Scholar] [CrossRef]
- Norman, A.I.; Zhang, W.; Beers, K.L.; Amis, E.J. Microfluidic Light Scattering as a Tool to Study the Structure of Aqueous Polymer Solutions. J. Colloid Interface Sci. 2006, 299, 580–588. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.; Mao, Y.; Prabhu, V.M. Pinhole Mirror-Based Ultra-Small Angle Light Scattering Setup for Simultaneous Measurement of Scattering and Transmission. Rev. Sci. Instrum. 2022, 93, 044104. [Google Scholar] [CrossRef]
- Kaplan, P.D.; Trappe, V.; Weitz, D.A. Light-Scattering Microscope. Appl. Opt. 1999, 38, 4151–4157. [Google Scholar] [CrossRef] [Green Version]
- Postnov, D.D.; Tang, J.; Erdener, S.E.; Kılıç, K.; Boas, D.A. Dynamic Light Scattering Imaging. Sci. Adv. 2020, 6, eabc4628. [Google Scholar] [CrossRef]
- Leheny, R.L. XPCS: Nanoscale Motion and Rheology. Curr. Opin. Colloid Interface Sci. 2012, 17, 3–12. [Google Scholar] [CrossRef]
- Quah, S.P.; Zhang, Y.; Fluerasu, A.; Yu, X.; Zheng, B.; Yin, X.; Liu, W.; Bhatia, S.R. Techniques to Characterize Dynamics in Biomaterials Microenvironments: XPCS and Microrheology of Alginate/PEO-PPO-PEO Hydrogels. Soft Matter 2021, 17, 1685–1691. [Google Scholar] [CrossRef] [PubMed]
- Ehrburger-Dolle, F.; Morfin, I.; Bley, F.; Livet, F.; Heinrich, G.; Chushkin, Y.; Sutton, M. Anisotropic and Heterogeneous Dynamics in Stretched Elastomer Nanocomposites. Soft Matter 2019, 15, 3796–3806. [Google Scholar] [CrossRef] [PubMed]
- Horkay, F.; Hecht, A.-M.M.; Geissler, E. Small Angle Neutron Scattering in Poly(vinyl alcohol) Hydrogels. Macromolecules 1994, 27, 1795–1798. [Google Scholar] [CrossRef]
- Shibayama, M. Small-Angle Neutron Scattering on Polymer Gels: Phase Behavior, Inhomogeneities and Deformation Mechanisms. Polym. J. 2011, 43, 18–34. [Google Scholar] [CrossRef] [Green Version]
- Hudson, S.D.; Hutter, J.L.; Nieh, M.P.; Pencer, J.; Millon, L.E.; Wan, W. Characterization of Anisotropic Poly(vinyl alcohol) Hydrogel by Small- and Ultra-Small-Angle Neutron Scattering. J. Chem. Phys. 2009, 130, 034903. [Google Scholar] [CrossRef] [Green Version]
- Matsunaga, T.; Sakai, T.; Akagi, Y.; Chung, U.I.; Shibayama, M. Structure Characterization of Tetra-PEG Gel by Small-Angle Neutron Scattering. Macromolecules 2009, 42, 1344–1351. [Google Scholar] [CrossRef]
- Shibayama, M.; Karino, T.; Miyazaki, S.; Okabe, S.; Takehisa, T.; Haraguchi, K. Small-Angle Neutron Scattering Study on Uniaxially Stretched Poly (n-isopropylacrylamide)-Clay Nanocomposite Gels. Macromolecules 2005, 38, 10772–10781. [Google Scholar] [CrossRef]
- Shibayama, M.; Kawakubo, K.; Ikkai, F.; Imai, M. Small-Angle Neutron Scattering Study on Charged Gels in Deformed State. Macromolecules 1998, 31, 2586–2592. [Google Scholar] [CrossRef]
- Takebe, T.; Nawa, K.; Suehiro, S.; Hashimoto, T. Quasielastic Light Scattering Studies of Swollen and Stretched Polymer Gels. J. Chem. Phys. 1989, 91, 4360–4368. [Google Scholar] [CrossRef]
- Matsunaga, T.; Asai, H.; Akagi, Y.; Sakai, T.; Chung, U., II; Shibayama, M. SANS Studies on Tetra-PEG Gel under Uniaxial Deformation. Macromolecules 2011, 44, 1203–1210. [Google Scholar] [CrossRef]
- Joosten, J.G.H.; McCarthy, J.L.; Pusey, P.N. Dynamic and Static Light Scattering by Aqueous Polyacrylamide Gels. Macromolecules 1991, 24, 6690–6699. [Google Scholar] [CrossRef]
- Brenner, S.L.; Gelman, R.A.; Nossal, R. Laser Light Scattering from Soft Gels. Macromolecules 1978, 11, 202–207. [Google Scholar] [CrossRef]
- Geissler, E.; Hecht, A. The Poisson Ratio in Polymer Gels. Macromolecules 1980, 13, 1276–1280. [Google Scholar] [CrossRef]
- Horkay, F.; Falus, P.; Hecht, A.-M.; Geissler, E. Length Scale Dependence of the Dynamic Properties of Hyaluronic Acid Solutions in the Presence of Salt. J. Phys. Chem. B 2010, 114, 15445–15450. [Google Scholar] [CrossRef] [Green Version]
- Fujii, K.; Ueki, T.; Niitsuma, K.; Matsunaga, T.; Watanabe, M.; Shibayama, M. Structural Aspects of the LCST Phase Behavior of Poly(benzyl methacrylate) in Room-Temperature Ionic Liquid. Polymer 2011, 52, 1589–1595. [Google Scholar] [CrossRef]
- Shibayama, M.; Okamoto, M. Dynamic Light Scattering Study on Gelatin Aqueous Solutions and Gels. J. Chem. Phys. 2001, 115, 4285–4291. [Google Scholar] [CrossRef]
- Burne, P.M.; Sellen, D.B. A Laser Light Scattering Study of Gellan Gels. Biopolymers 1994, 34, 371–382. [Google Scholar] [CrossRef]
- Shibayama, M.; Fujikawa, Y.; Nomura, S. Dynamic Light Scattering Study of Poly (n-isopropylacrylamide-co-acrylic acid) Gels. Macromolecules 1996, 29, 6535–6540. [Google Scholar] [CrossRef]
- Shibayama, M.; Takeuchi, T.; Nomura, S. Swelling/Shrinking and Dynamic Light Scattering Studies on Chemically Cross-Linked Poly(vinyl alcohol) Gels in the Presence of Borate Ions. Macromolecules 1994, 24, 5350–5358. [Google Scholar] [CrossRef]
- Toyoichi, T.; Hocker, L.O.; Benedek, G.B. Spectrum of Light Scattered From Viscoelastic Gels. J. Chem. Phys. 1973, 14, 5151–5159. [Google Scholar] [CrossRef]
- Tokita, M.; Tanaka, T. Friction Coefficient of Polymer Networks of Gels. J. Chem. Phys. 1991, 95, 4613–4619. [Google Scholar] [CrossRef]
- Rochas, C.; Geissler, E. Measurement of Dynamic Light Scattering Intensity in Gels. Macromolecules 2014, 47, 8012–8017. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.; Oppermann, W. Spatial Inhomogeneities of Polystrene Gels Prepared from Semidilute Solutions. Macromolecules 2006, 39, 4159–4167. [Google Scholar] [CrossRef]
- Wong, A.P.Y.; Wiltzius, P. Dynamic Light Scattering with a CCD Camera. Rev. Sci. Instrum. 1993, 64, 2547–2549. [Google Scholar] [CrossRef]






| Technique | Contrast | q-Range | Sample Volume | 1D or 2D |
|---|---|---|---|---|
| DSALS | Refractive index | 0.00035–0.035 nm−1 | ~10–500 µL | 1D |
| XPCS | Electron density | 0.05–10 nm−1 | ~10–500 µL | 2D |
| DLS | Refractive index | 0.00–0.025 nm−1 | ~1–10 µL | 2D |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhakal, S.; Chen, Z.; Estrin, D.; Morozova, S. Spatially-Resolved Network Dynamics of Poly(vinyl alcohol) Gels Measured with Dynamic Small Angle Light Scattering. Gels 2022, 8, 394. https://doi.org/10.3390/gels8070394
Dhakal S, Chen Z, Estrin D, Morozova S. Spatially-Resolved Network Dynamics of Poly(vinyl alcohol) Gels Measured with Dynamic Small Angle Light Scattering. Gels. 2022; 8(7):394. https://doi.org/10.3390/gels8070394
Chicago/Turabian StyleDhakal, Sujata, Zehao Chen, Daniel Estrin, and Svetlana Morozova. 2022. "Spatially-Resolved Network Dynamics of Poly(vinyl alcohol) Gels Measured with Dynamic Small Angle Light Scattering" Gels 8, no. 7: 394. https://doi.org/10.3390/gels8070394
APA StyleDhakal, S., Chen, Z., Estrin, D., & Morozova, S. (2022). Spatially-Resolved Network Dynamics of Poly(vinyl alcohol) Gels Measured with Dynamic Small Angle Light Scattering. Gels, 8(7), 394. https://doi.org/10.3390/gels8070394