Rheological Properties of Organic Kerosene Gel Fuel
Abstract
:1. Introduction
2. Results and Discussion
2.1. Shear-Thinning and Yield
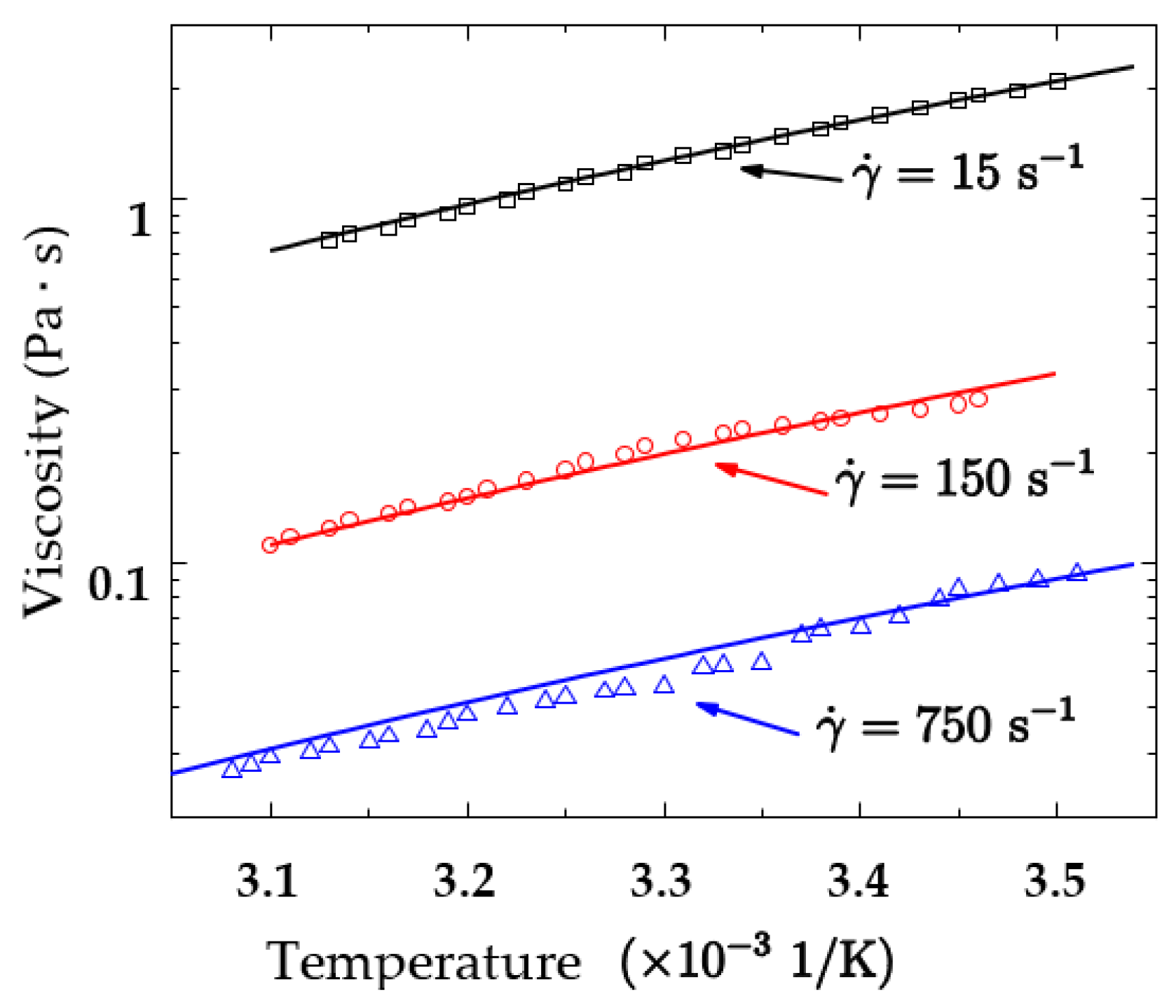
2.2. Shear-Thinning Coupled with Temperature
2.3. Thixotropic Loop Test
2.4. Second-Order Dynamic Thixotropic Model
3. Conclusions
- (1)
- The experimental measurements suggest that the thixotropic behavior of the kerosene gel would be exhausted by continuous shear effect, degenerating into a standard shear-thinning fluid with relatively simple mechanical behavior. This is beneficial to not only the study of its constitutive relationship, but also the engineering application where the friction of transportation is one of the major concerns.
- (2)
- After sufficient pre-shearing, the shear-thinning property could be approximated by a power law relationship between the equilibrium viscosity and the shear rate, where the consistency index increases with the gellant mass fraction, while the power law exponent remains almost constant.
- (3)
- A constitutive model of the viscosity affected by both temperature and shear rate is fitted. The fitted model can accurately predict the viscosity of kerosene gel affected at a variety of temperatures and shear rates. The difference in the fitted consistency indexes between this model and the previous shear-thinning model is less than 5%.
- (4)
- The time-dependent behavior of shear-thinning properties is investigated by thixotropic loops, based on which a second-order kinetic model is fitted. The expression of the model is consistent with the two power law relationships fitted previously, and the introduction of a structural parameter enables a reasonable prediction of the thixotropic characteristics of the kerosene gel.
4. Gel Preparation and Measurement Method
4.1. Materials and Instruments
4.2. Formulation of Constitutive Models
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Putz, A.; Frigaard, I.A.; Martinez, D.M. On the lubrication paradox and the use of regularisation methods for lubrication flows. J. Nonnewton. Fluid Mech. 2009, 163, 62–77. [Google Scholar] [CrossRef]
- Xue, K.; Cao, J.; Pan, L.; Zhang, X.; Zou, J.-J. Review on design, preparation and performance characterization of gelled fuels for advanced propulsion. Front. Chem. Sci. Eng. 2022, 16, 819–837. [Google Scholar] [CrossRef]
- Natan, B.; Hasan, D. ADVANCES IN GEL PROPULSION. Int. J. Energ. Mater. Chem. Propuls. 2019, 18, 303–323. [Google Scholar] [CrossRef]
- Ciezki, H.K.; Naumann, K.W.; Weiser, V. Status of Gel Propulsion in the Year 2010 with a Special View on the German Activities. In Proceedings of the Deutscher Luft- und Raumfahrtkongress 2010, Hamburg, Germany, 31 August–20 September 20210. [Google Scholar]
- Yang, D.; Xia, Z.; Huang, L.; Ma, L.; Chen, B.; Feng, Y. Synthesis of metallized kerosene gel and its characterization for propulsion applications. Fuel 2020, 262, 116684. [Google Scholar] [CrossRef]
- Song, W.; Hwang, J.; Koo, J. Atomization of gelled kerosene by multi-hole pintle injector for rocket engines. Fuel 2021, 285, 119212. [Google Scholar] [CrossRef]
- Padwal, M.B.; Natan, B.; Mishra, D.P. Gel propellants. Prog. Energy Combust. Sci. 2021, 83, 100885. [Google Scholar] [CrossRef]
- Mishra, D.P.; Patyal, A.; Padhwal, M. Effects of gellant concentration on the burning and flame structure of organic gel propellant droplets. Fuel 2011, 90, 1805–1810. [Google Scholar] [CrossRef]
- Glowinski, R.; Wachs, A. On the numerical simulation of viscoplastic fluid flow. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2011; Volume 6, pp. 483–717. ISBN 1570-8659. [Google Scholar]
- Solomon, Y.; Natan, B.; Cohen, Y. Combustion of gel fuels based on organic gellants. Combust. Flame 2009, 156, 261–268. [Google Scholar] [CrossRef]
- Saberi Moghaddam, A.; Manourizadeh, F.; Valizadeh, E. Investigation of Effect of Rheological Behavior of Gelled Propellant on Atomization Characteristics of Swirl Injector. J. Technol. Aerosp. Eng. 2021, 5, 43–56. [Google Scholar]
- Glushkov, D.O.; Pleshko, A.O.; Yashutina, O.S. Influence of heating intensity and size of gel fuel droplets on ignition characteristics. Int. J. Heat Mass Transf. 2020, 156, 119895. [Google Scholar] [CrossRef]
- Rahimi, S.; Natan, B. Flow of gel fuels in tapered injectors. J. Propuls. Power 2000, 16, 458–464. [Google Scholar] [CrossRef]
- Rahimi, S.; Natan, B. Atomization Characteristics of Gel Fuels. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Reston, VA, USA, 13–15 July 1998; p. 3830. [Google Scholar]
- Von Kampen, J.; Madlener, K.; Ciezki, H.K. Characteristic Flow and Spray Properties of Gelled Fuels with Regard to the Impinging Jet Injector Type. Collect. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006; Volume 4, pp. 2639–2650. [Google Scholar] [CrossRef]
- Madlener, K.; Ciezki, H. Theoretical Investigation of the Flow Behavior of Gelled Fuels of the Extended Herschel Bulkley Type. In Proceedings of the 1st European Conference for Aerospace Science (EUCASS), Moscow, Russia, 5–7 July 2005. [Google Scholar]
- Martinez-Pastor, J.; Franco, P.; Franco-Menchon, J.A. Optimization of extrusion process of double-base propellants from their rheological properties. Int. J. Mater. Form. 2019, 12, 307–320. [Google Scholar] [CrossRef]
- Cross, M.M. Relation between viscoelasticity and shear-thinning behaviour in liquids. Rheol. Acta 1979, 18, 609–614. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of polymeric liquids—Volume 1: Fluid Mechanics, 2. Ausgabe. 649 Seiten, Preis: £64.15. In Berichte der Bunsengesellschaft für Physikalische Chemie; Wiley: New York, NY, USA, 1987; Volume 91, p. 1397. [Google Scholar] [CrossRef]
- Yoon, C.; Heister, S.D.; Xia, G.; Merkle, C.L. Numerical modeling of injection of shear-thinning gel propellants through plain-orifice atomizer. J. Propuls. Power 2011, 27, 944–954. [Google Scholar] [CrossRef]
- Yoon, C.; Heister, S.; Sojka, P.; Watson, C.; Xia, G.; Merkle, C. Injector Flow Characteristics for Gel Propellants. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Yoon, C.; Heister, S.D.; Merkle, C.L.; Xia, G. Simulations of Plain-Orifice Injection of Gelled Propellants Under Manifold Crossflow Conditions. J. Propuls. Power 2012, 29, 136–146. [Google Scholar] [CrossRef]
- Andrade, E.N.d.C. The viscosity of liquids. Nature 1930, 125, 309–310. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, plasticity, and diffusion as examples of absolute reaction rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Rahimi, S.; Peretz, A.; Natan, B. On Shear Rheology of Gel Propellants. Propellants Explos. Pyrotech. 2007, 32, 165–174. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Thixotropy. Adv. Colloid Interface Sci. 2009, 147, 214–227. [Google Scholar] [CrossRef]
- Barnes, H.A. Thixotropy—A review. J. Nonnewton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- de Souza Mendes, P.R. Modeling the thixotropic behavior of structured fluids. J. Non-Newton. Fluid Mech. 2009, 164, 66–75. [Google Scholar] [CrossRef]
- Moore, F. The rheology of ceramic slip and bodies. Trans. Brit. Ceram. Soc. 1959, 58, 470–492. [Google Scholar]
- Hahn, S.J.; Ree, T.; Eyring, H. Flow mechanism of thixotropic substances. Ind. Eng. Chem. 1959, 51, 856–857. [Google Scholar] [CrossRef]
- Peter, S. Zur Theorie der Rheopexie. Rheol. Acta 1964, 3, 178–180. [Google Scholar] [CrossRef]
- Santos, P.H.S.; Carignano, M.A.; Campanella, O. Effect of shear history on rheology of time-dependent colloidal silica gels. Gels 2017, 3, 45. [Google Scholar] [CrossRef]
- Dullaert, K.; Mewis, J. A structural kinetics model for thixotropy. J. Non-Newton. Fluid Mech. 2006, 139, 21–30. [Google Scholar] [CrossRef]
- Barnes, H.A.; Nguyen, Q.D. Rotating vane rheometry—A review. J. Non-Newton. Fluid Mech. 2001, 98, 1–14. [Google Scholar] [CrossRef]
- Padwal, M.B.; Mishra, D.P. Synthesis of Jet A1 gel fuel and its characterization for propulsion applications. Fuel Process. Technol. 2013, 106, 359–365. [Google Scholar] [CrossRef]
- Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Massoudi, M. A Review of Rheological Modeling of Cement Slurry in Oil Well Applications. Energies 2020, 13, 570. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Tsamopoulos, J. Numerical simulations of complex yield-stress fluid flows. Rheol. Acta 2017, 56, 231–258. [Google Scholar] [CrossRef]
- Cao, Q.-L.; Wu, W.-T.; Liao, W.-H.; Feng, F.; Massoudi, M. Effects of temperature on the flow and heat transfer in gel fuels: A numerical study. Energies 2020, 13, 821. [Google Scholar] [CrossRef]
- Grillet, A.M.; Rao, R.R.; Adolf, D.B.; Kawaguchi, S.; Mondy, L.A. Practical application of thixotropic suspension models. J. Rheol. 2009, 53, 169–189. [Google Scholar] [CrossRef]
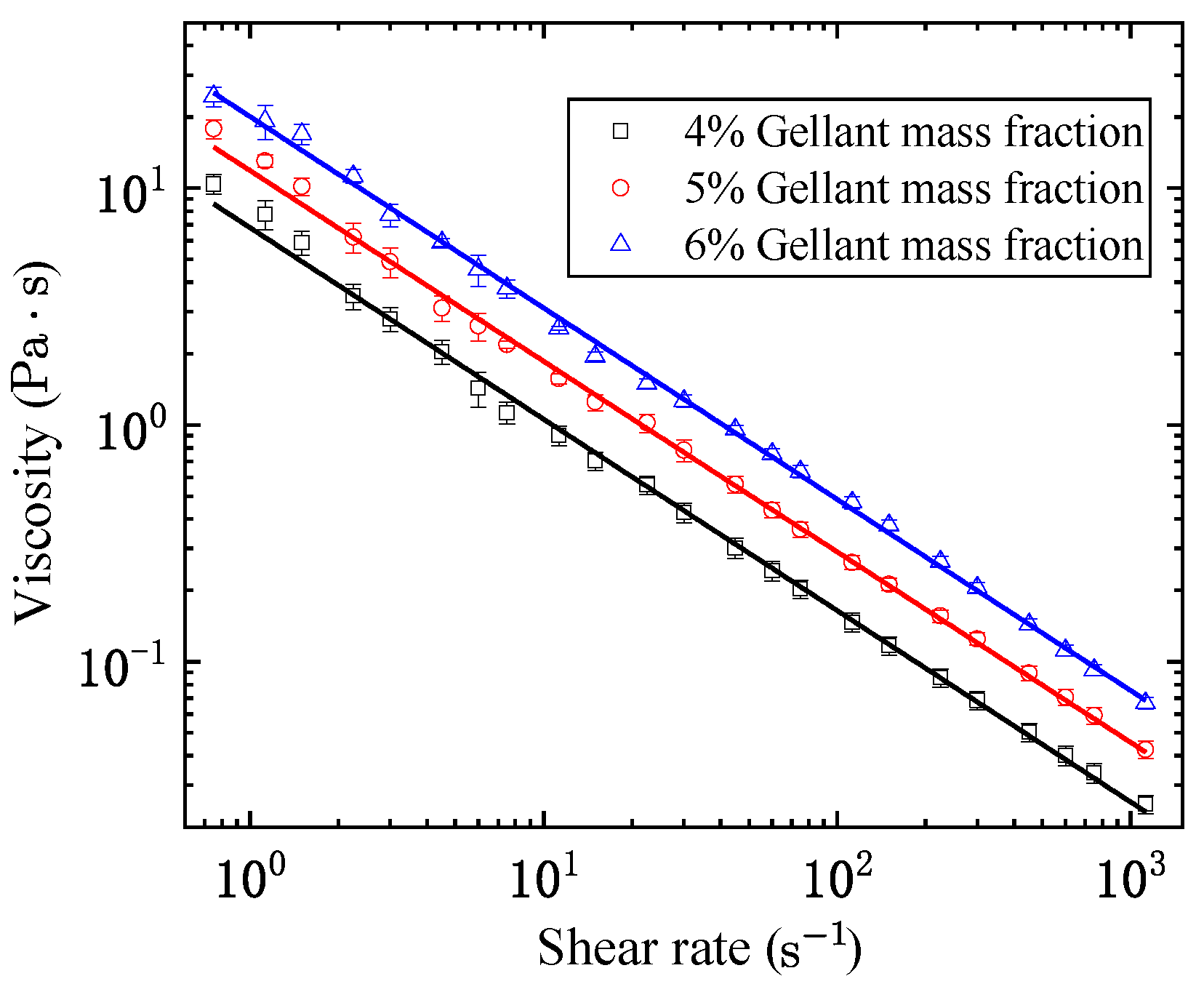






| Gellant Mass Fraction | R2 | ||
|---|---|---|---|
| 4% | 6.804 | 0.191 | 0.991 |
| 5% | 11.847 | 0.195 | 0.991 |
| 6% | 20.042 | 0.192 | 0.990 |
| 0.4725 | 0.1696 | 1.8957 | 25.073 | 0.195 |
| Kerosene (wt%) | THIXATROL ST (wt%) | Anhydrous Ethanol (wt%) |
|---|---|---|
| 92 | 4 | 4 |
| 90 | 5 | 5 |
| 88 | 6 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.-G.; Wu, Y.; Cao, Q.-L.; Yuan, X.-Y.; Chen, X.; Han, J.-L.; Wu, W.-T. Rheological Properties of Organic Kerosene Gel Fuel. Gels 2022, 8, 507. https://doi.org/10.3390/gels8080507
Li M-G, Wu Y, Cao Q-L, Yuan X-Y, Chen X, Han J-L, Wu W-T. Rheological Properties of Organic Kerosene Gel Fuel. Gels. 2022; 8(8):507. https://doi.org/10.3390/gels8080507
Chicago/Turabian StyleLi, Meng-Ge, Yan Wu, Qin-Liu Cao, Xin-Yi Yuan, Xiong Chen, Jun-Li Han, and Wei-Tao Wu. 2022. "Rheological Properties of Organic Kerosene Gel Fuel" Gels 8, no. 8: 507. https://doi.org/10.3390/gels8080507







