Exergy and Irreversibility Analysis in Non-Equilibrium Thermal Porous Rectangular Channel

Abstract

This paper deals with laminar forced convection in a rectangular channel through a non-equilibrium thermal gas saturated porous medium. The thermodynamic aspects of this flow, including the entropy generation rate, irreversibility, and exergy, are carefully investigated. The governing conservation equations of momentum, mass, and energy are solved numerically using the finite volume method. The effects of Reynolds number $Re$ (ranging from 100 to 2000), Darcy number $Da$ $\left(\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m} {10}^{-6} \mathrm{t}\mathrm{o} {10}^{-1}\right)$, and Biot number $Bi$ (from 10⁻³ to 10³) on the entropy generation, exergy, and irreversibility, for which the Gouy-Stodola relation is employed, are then presented. The results reveal that at low $Re$ and high $Bi$, thermal equilibrium between the two phases is achieved, leading to a reduction in entropy generation and, consequently, less exergy destruction. However, in the limit of high $Re$ and low $Da$, irreversibility is significant due to large velocity gradients, leading to greater exergy destruction. Furthermore, it was observed that the thermal non-equilibrium intensity (LNTE) significantly influences entropy generation, leading to critical exergy destruction.

1. Introduction

Accurately heat transfer is of primary interest in both academic and industrial points of view [1,2,3,4,5,6]. In these recent years, particular attention has been increasingly brought to conserving energy resources and their efficient and optimal use for several applications such as cryogenics, storage systems and power plants [7,8]. In this context, the entropy generation has attracted the attention of the scientific community because of its ability to describe irreversible dissipative phenomena [9]. In particular, the minimization of entropy generation (EGM theory) [8] has become the main method for thermodynamic optimization of energy systems, both theoretically and in engineering practice.

The works of Onsager [10], Keenan [11] and Glansdorff et al. [12] can be considered as the pioneering studies for developing the out-of-equilibrium thermodynamics that deals with irreversible dissipative processes, in which the classical thermodynamics fails to describe. The efforts have focused on determining entropy generation, irreversibility using Gouy-Stodola theorem, exergy, and available work to minimize energy losses [13,14].

On the other hand, the use of porous media in fluid flows has raised interest in various applications with the perspective of improving heat transfer processes [15,16,17,18,19]. Depending on how the thermal interaction between the fluid and the porous media through which it flows is modeled, two approaches are generally used. The first one adopts the assumption of local thermal equilibrium (LTE), in which the solid and fluid phases have the same temperature. The second approach disregards this assumption—valid only in specific cases—by considering the general situation where thermal equilibrium is no longer imposed, meaning the solid and fluid phases are in a state of thermal non-equilibrium (LTNE) [20].

Concerning the LTE approach, several formulations and researches on entropy generation in porous media have been subsequently performed [21,22,23,24,25,26]. These studies notably analyzed the entropy production in forced convection flows through rectangular horizontal porous channels with heated walls. The relative importance of viscous and thermal effects on entropy generation were shown. These numerical investigations allowed to report that the entropy generation occurs mainly in the region adjacent to the walls where strong velocity and temperature gradients exist. Note that similar findings were also obtained in circular pipes flows [27,28,29] and in curved rectangular channels [30,31,32]. In addition, the aspect ratio and turbulence effects on the entropy generation were also depicted by Ko and Yu [32]. Furthermore, Wu et al. [33,34], and Yessad and Souidi [35] performed an exergy analysis of the fully developed forced convection flow through a duct with heated horizontal walls. The main results obtained by the authors indicate that the Reynolds number increases entropy production, which leads to a rise in the system’s irreversibility, thereby reducing its available amount of work, i.e., its exergy.

Currently, the LTE approach is considered insufficient since it is only valid within a specific range of parameters where thermal equilibrium can be considered. Consequently, although more expensive in computational resources, the LTNE approach appears to be a better alternative to describe the complex flow phenomena in ducts containing porous media. For instance, Vafai and Sozen [36], who performed a comparative study of the results predicted by the LTE and LTNE models, highlighted that the LTE assumption is invalid in the range of high Reynolds and Darcy numbers values. Based on this statement, several works employed the LNTE approach to describe fluid flows through rectangular channels such as [27,28,29,30,31]. The entropy generation of forced convection in a rectangular channel filled with a porous medium using a non-equilibrium thermal assumption was also analyzed by [32,33] and in the case of partially filled channels by [34,35,37]. The cited studied showed that the thermal irreversibility decreases with the increase of the Biot number. Chee et al. [38] investigated entropy generation in a dissipative Darcy-Brinkman flow through a rectangular channel heated by an asymmetric heat flux using LTNE approach. Their study focused on the influence of the heat flux ratio, the effective thermal conductivity ratio $\kappa$, the Darcy number $Da$, the Biot number $Bi$, and the mean fluid velocity on the entropy generation rate. They concluded that thermal irreversibility, which dominates the dissipation mechanisms in the system, decreases for low thermal conductivity ratios $\kappa$ and low Brinkman numbers $Br$. In contrast, an increase in the Péclet number reduces the entropy generation rates.

Torabi et al. [39] conducted a bibliographic review concerning the second law of thermodynamics in forced convection flows in the presence of a porous medium, with particular attention to the LTE and LTNE approaches in the modeling and physical analysis of these flows. Torabi and his coworkers highlighted the rapid development and deployment of porous thermochemical system for several applications. This statement reinforces the importance to pursue efforts to perform exergetic analysis for better optimizing the efficiency of the systems.

To the best of the authors’ knowledge, exergy analysis has only been studied using the LTE approach in the literature. Based on this statement, the present study aims to investigate the effect of thermal non-equilibrium on the thermodynamic aspects of a system by employing the LTNE method. More specifically, we investigate the laminar forced convection flow through a rectangular channel. where the horizontal walls are maintained at a constant temperature. The influence of the Reynolds $Re$, Darcy $Da$, and Biot $Bi$ numbers on the behavior of LTNE intensity, irreversibility as well as exergy is thoroughly investigated. First, we present the mathematical model that describes this physical problem. Then, the thermal and dynamical behavior of the flow is examined as a function of the Reynolds, Darcy, and Biot numbers. Finally, a detailed thermodynamic analysis is conducted to evaluate the entropy generation within the studied configuration.

2. Formulation of the Problem

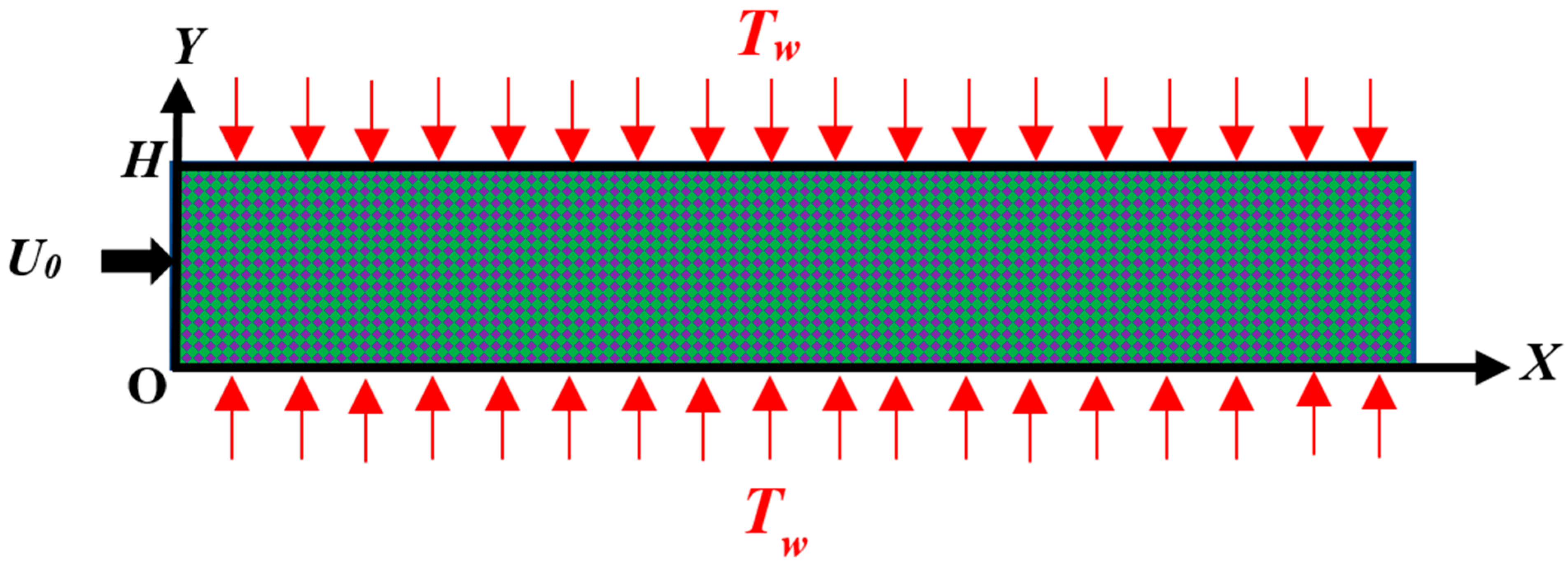
2.1. Description of the System

We consider the laminar and incompressible forced convection of a Newtonian fluid with constant thermophysical properties. The flow is considered to be steady and crosses a two-dimensional rectangular channel of height $H$ and length $L=9H$ with a purely longitudinal entering velocity $U_0$, filled with a saturated, homogeneous and isotropic porous medium of permeability $K$ and porosity $\epsilon$. The horizontal walls delimiting the channel are maintained at a uniform temperature $T_w$ (see Figure 1).

2.2. Mathematical Formulation and Governing Equations

The dimensionless governing equations are obtained using $H,U_0,T_w$, $\rho U_0^2$ as reference scales for lengths, velocities, temperatures, and pressure, respectively. Consequently, the fluid dynamics is monitored by the Reynolds $Re$, Darcy $Da$, Prandtl $Pr$, and Biot $Bi$ numbers, along with the thermal conductivities ratio of the fluid and the solid phases $\kappa$

$$Da={\displaystyle \frac{K}{H^2}},Bi={\displaystyle \frac{h_{sf}{a}_{sf}{H}^2}{k_s}},Re={\displaystyle \frac{{\rho }_f{U}_{0}H}{{\mu }_f}},Pr={\displaystyle \frac{{\mu }_f{C}_{pf}}{k_{f,eff}}},\kappa ={\displaystyle \frac{k_{f,eff}}{k_{s,eff}}}$$

where ${\rho }_f, {\mu }_f$, and $C_{pf}$ are the fluid’s density, viscosity, and heat capacity, respectively. In the present study, the porosity of the medium is fixed at $\epsilon =0.8$, the effective thermal conductivity ratio is set at $\kappa =0.2$, and the Prandtl number at $Pr=0.7$.

The fluid-solid interface is characterized by the ratio of the effective thermal conductivities of the solid $k_{s,eff}=(1-\epsilon )k_s$ and the fluid $k_{f,eff}=\epsilon k_f$ phases, the heat transfer coefficient $h_{sf}$ and the specific surface area $a_{sf}$ [40]. Furthermore, in the case of weak Forchheimer inertial effects, the following volume-related macroscopic equations then govern the steady two-dimensional laminar forced convection flow in a porous rectangular channel:

The mass conservation equation

$${\displaystyle \frac{\partial U}{\partial X}}+{\displaystyle \frac{\partial V}{\partial Y}}=0$$

(1)

The momentum conservation equation

$$\left\{\begin{array}{c}{\displaystyle \frac{1}{{\epsilon }^2}}\left(U{\displaystyle \frac{\partial U}{\partial X}}+V{\displaystyle \frac{\partial U}{\partial Y}}\right)=-{\displaystyle \frac{\partial P}{\partial X}}+{\displaystyle \frac{1}{Re}}\left[{\displaystyle \frac{{\partial }^{2}U}{\partial X^2}}+{\displaystyle \frac{{\partial }^{2}U}{\partial Y^2}}\right]-{\displaystyle \frac{1}{ReDa}}U\\ {\displaystyle \frac{1}{{\epsilon }^2}}\left(U{\displaystyle \frac{\partial V}{\partial X}}+V{\displaystyle \frac{\partial V}{\partial Y}}\right)=-{\displaystyle \frac{\partial P}{\partial Y}}+{\displaystyle \frac{1}{Re}}\left[{\displaystyle \frac{{\partial }^{2}V}{\partial X^2}}+{\displaystyle \frac{{\partial }^{2}V}{\partial Y^2}}\right]-{\displaystyle \frac{1}{ReDa}}V\end{array}\right.$$

(2)

The energy conservation equations for both the solid (with subscript ’s’) and the fluid (with subscript ’f’) phases:

$$\left\{\begin{array}{c}RePr\left(U{\displaystyle \frac{\partial {\theta }_f}{\partial X}}+V{\displaystyle \frac{\partial {\theta }_f}{\partial Y}}\right)={\displaystyle \frac{{\partial }^2{\theta }_f}{\partial X^2}}+{\displaystyle \frac{{\partial }^2{\theta }_f}{\partial Y^2}}+{\displaystyle \frac{Bi}{\kappa }}\left({\theta }_s-{\theta }_f\right)\\ 0={\displaystyle \frac{{\partial }^2{\theta }_s}{\partial X^2}}+{\displaystyle \frac{{\partial }^2{\theta }_s}{\partial Y^2}}-Bi\left({\theta }_s-{\theta }_f\right)\end{array}\right.$$

(3)

The boundary conditions for the velocity are $U\left(0,Y\right)=1$ at the channel entry and ${\left.\partial U/\partial X\right|}_{X=A}={\left.\partial V/\partial X\right|}_{X=A}=0$ at its exit traducing the flow establishment, whereas a homogeneous Dirichlet conditions are considered at all the other boundary locations, i.e., $U\left(X,0\right)=U\left(X,1\right)=V\left(0,Y\right)=V\left(X,0\right)=V\left(X,1\right)=0$. Note that $A=L/H$ is the aspect ratio of the channel.

The thermal boundary conditions are the same for both solid and fluid; that is $\theta \left(0,Y\right)={\theta }_e$ at the entry, $\theta (X,1)=\theta (X,0)=1$ at the horizontal isotherm walls, and ${\left.\partial \theta /\partial X\right|}_{X=A}=0$ at the exit of the channel.

A measure of the thermal non-equilibrium can be obtained from the local temperature difference between the fluid and the solid phases, defined as [41]:

$$\Delta NE=\left|{\theta }_s-{\theta }_f\right|$$

(4)

2.3. Thermodynamic Transport Properties

2.3.1. Entropy Generation

The volumetric entropy generation rate is connected to two physical phenomena: heat diffusion and viscous dissipation. In porous media, the entropy generation rate in the fluid phase under local thermal non-equilibrium (LTNE) is given, using dimensional quantities by [38]

$$\begin{array}{c}{s}_{f,gen}={\displaystyle \frac{k_{f,eff}}{{T_f}^2}}.{\left(𝛻T_f\right)}^2+{\displaystyle \frac{1}{T_f}}\left[a_{sf{h}_{sf}}\left(T_s-T_f\right)\right]+{\displaystyle \frac{\mu }{T}}\left[\left[{\left({\displaystyle \frac{\partial u}{\partial x}}\right)}^2+{\left({\displaystyle \frac{\partial v}{\partial y}}\right)}^2\right]+{\left({\displaystyle \frac{\partial u}{\partial y}}+{\displaystyle \frac{\partial v}{\partial x}}\right)}^2\right]\\ +{\displaystyle \frac{\mu }{KT}}{(u^2+v}^2)\end{array}$$

(5)

The first two terms are linked to the thermal energy degradation, whereas the remaining terms are related to mechanical energy transformation into heat by viscous dissipation.

The entropy generation of the porous medium solid phase can be expressed as:

$$s_{s,gen}={\displaystyle \frac{k_{s,eff}}{{T_s}^2}}.{\left(𝛻T_s\right)}^2-{\displaystyle \frac{1}{T_s}}\left[a_{sf}{h}_{sf}\left(T_s-T_f\right)\right]$$

(6)

Hence, the dimensionless forms of the local volumetric entropy generation, using $k_{f,eff}/H^2$ as a reference scale, may be expressed as the sum of all the above contributions:

$${S_{gen}=S}_{\theta }+S_{\psi }$$

where $S_{\theta }$ is the sum of the thermal entropy production rates in the fluid $S_{\theta ,f}$ and the solid $S_{\theta ,s}$ phases, such as:

$$S_{\theta ,f}={\displaystyle \frac{1}{{{\theta }_f}^2}}\left[{\left({\displaystyle \frac{\partial {\theta }_f}{\partial X}}\right)}^2+{\left({\displaystyle \frac{\partial {\theta }_f}{\partial Y}}\right)}^2\right]+{\displaystyle \frac{Bi}{{\kappa \theta }_f}}\left({\theta }_s-{\theta }_f\right)$$

(7)

and

$$S_{\theta ,s}={\displaystyle \frac{1}{{{\kappa \theta }_s}^2}}\left[{\left({\displaystyle \frac{\partial {\theta }_s}{\partial X}}\right)}^2+{\left({\displaystyle \frac{\partial {\theta }_s}{\partial Y}}\right)}^2\right]-{\displaystyle \frac{Bi}{{\kappa \theta }_s}}\left({\theta }_s-{\theta }_f\right),$$

(8)

$S_{\psi }$ represents the dynamical entropy generation rate, and it is given as:

$$S_{\psi }={\displaystyle \frac{E_{k}Pr}{{\theta }_f}}\left\{\left[\left({\left({\displaystyle \frac{\partial U}{\partial X}}\right)}^2+{\left({\displaystyle \frac{\partial V}{\partial Y}}\right)}^2\right)+{\left({\displaystyle \frac{\partial U}{\partial Y}}+{\displaystyle \frac{\partial V}{\partial X}}\right)}^2\right]+{\displaystyle \frac{1}{Da}}\left(U^2+V^2\right)\right\}$$

(9)

with $E_k$ is the Eckert number given by:

$$E_k={\displaystyle \frac{U_0^2}{C_{pf}{T}_W}}$$

2.3.2. Bejan Number

The ratio of the entropy generation of thermal origins to the total entropy generation is given by the Bejan number $Be$, defined as:

$$Be={\displaystyle \frac{S_{\theta }}{S_{\theta }+S_{\psi }}}$$

(10)

Hence, the Bejan number can be interpreted as follows: if $Be>1/2$, then the entropy generation is mostly of thermal origins. In contrast, if $Be<1/2,$ the entropy is mainly of dynamical [42].

2.3.3. Irreversibility

The irreversibility of the phenomenon can be evaluated using the Gouy-Stodola theorem, developed by Keenan [11], and given by the following expression:

$$I={\theta }_{\mathrm{\infty }}{S}_{gen}$$

(11)

where ${\theta }_{\mathrm{\infty }}$ is the temperature of the surrounding environment.

2.3.4. Exergy

It gives the maximum (minimum) valuable work that the system can produce (absorb) when the fluid flows from the inlet to the outlet of the channel. According to [18,34,35], the dimensionless exergy variation is then given by [11,35,43].

$$\lambda =\left(h_{out}-h_{in}\right)-{\theta }_{\mathrm{\infty }}\left(S_{out}-S_{in}\right)$$

(12)

where $h$ and $S$ denote the dimensionless enthalpy and entropy of the fluid, and $in/out$ subscripts refer to the inlet/outlet of the channel.

3. Validation

The governing conservation equations of momentum, mass, and energy (Equations (1)–(3)) with their boundary conditions are solved numerically using the finite volume method. For instance, a second-order upwind scheme is used for the momentum and energy variables discretization, along with a second-order interpolation scheme for the pressure. Finally, the pressure-velocity coupling is achieved using the SIMPLE segregated algorithm [44].

A grid dependency of the obtained solution is then performed for several cases with four different mesh resolutions noted M1, M2, M3 and M4. Considering that our study focuses on both hydrodynamic and heat transfer phenomena, we chose to use the two parameters center-line velocity and average Nusselt number obtained at the fully developed flow for the grid dependence analysis. A summary of the obtained values for the four meshes studied is given in

Table 1. Accuracy tests for the simulations. The Fully developed center-line velocity and Averege Nusselt number for Re = 2000, Pr = 0.7, and Da = 10⁻⁵ are given for different numbers of grid points in X and Y directions, respectively.

Mesh	Grid Points	Fully Developed Center-Line Velocity	Average Nusselt Number
M1	$720\times 320$	0.9999	89.1630
M2	$1200\times 320$	0.9999	93.5876
M3	$1440\times 320$	0.9999	95.7540
M4	$1440\times 640$	0.9999	95.7541

. From the values obtained, we selected the mesh M3 for this study.

In Figure 2a, we plot the evolution of the developed center-line velocity obtained numerically with the results of Hadim et al. [45] as function of Da. The numerical study by Hadim et al. [45] concerns forced convection flow in a channel that is either fully or partially filled with a porous medium, under different conditions and various physical parameters. As it appears clearly, the results are perfectly aligned. The comparison of the obtained average Nusselt number depicted in Figure 2b shows a fairly good agreement. Indeed, our numerical simulation can capture the decreasing trend occurring at Da = 0.001. From these two plots, one can confirm the validity of our simulations.

4. Results and Discussion

In this section, we examine the influence of the Reynolds number $\left(Re\right)$, Darcy number $\left(Da\right)$, and Biot number $\left(Bi\right)$ on the dynamical, thermal, and thermodynamic aspects of the flow.

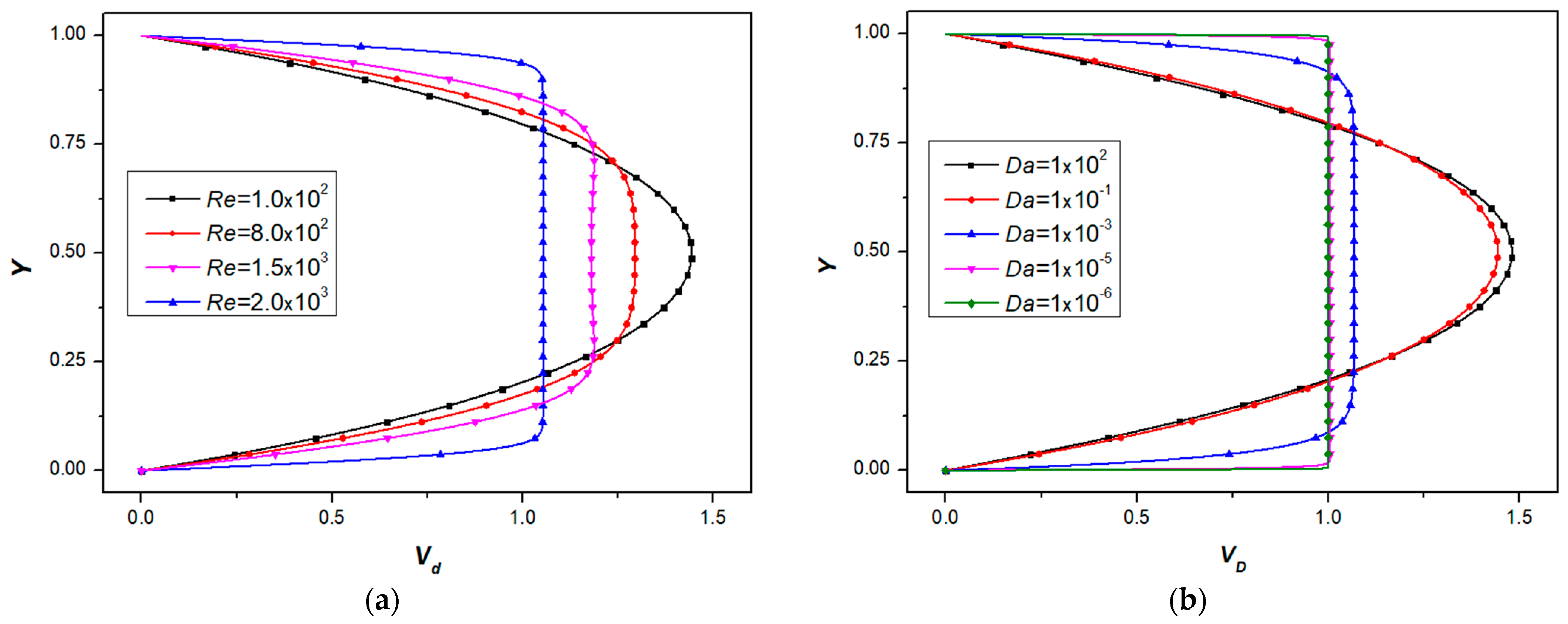
4.1. Flow Characteristics

Figure 3a presents the longitudinal component of the dimensionless velocity profile along the $Y$ direction at the channel outlet for different Reynolds numbers. The presence of the porous matrix regulates the flow within the channel cross-section. The obtained profiles indicate that an increase in the Reynolds number extends the flow establishment phase, with the establishment length being proportional to $Re(L\sim Re)$.

Figure 3b illustrates the influence of the Darcy number on the fully developed velocity profile. In the case of $Re=100$, the velocity profile exhibits a perfectly parabolic shape, characteristic of Poiseuille flow. As the permeability of the porous medium decreases, the velocity magnitude decreases, the profile flattens, and the boundary layer thickness reduces. This observation highlights the role of the porous medium in homogenizing the velocity distribution across the channel height. A lower permeability results in a thinner boundary layer. Similar trends have been previously reported in [7,13,38,39].

Figure 4 illustrates the evolution of the mean temperature difference, $\Delta NE$, between the solid and fluid phases, indicating thermal non-equilibrium, for different Biot, Reynolds, and Darcy numbers. Figure 4a shows the variation of $\Delta NE$ as a function of the Biot number ($Bi$) for $Da={10}^{-1}$ and $Da={10}^{-5}$ at $Re=100$. Two distinct regions are observed, where $\Delta NE$ varies slightly, separated by an abrupt transition around $Bi=1$. Overall, $\Delta NE$ decreases as the Biot number increases, indicating a tendency of the system toward thermal equilibrium. This behavior is explained by the fact that thermal equilibrium is primarily governed by the Biot number, defined here as the ratio of the solid’s internal conductive thermal resistance to the convective thermal resistance at the solid-fluid interface. Thus, for high Biot numbers, the interfacial convective thermal resistance becomes negligible compared to the conductive resistance within the solid, promoting thermal equilibrium. Conversely, for low $Bi$ values, the trend reverses, leading to thermal non-equilibrium.

The effect of the Reynolds number on $\Delta NE$ is illustrated in Figure 4b for two Biot values, $Bi=0.1$ and $Bi=100$, with $Da=1e-1$. For $Bi=0.1$, representing a thermal non-equilibrium situation, an increase in the Reynolds number further amplifies the thermal imbalance. A similar trend is observed for $Bi=100$, corresponding to a thermal equilibrium condition, but with a much weaker and therefore less noticeable effect.

Figure 4c depicts the influence of the Darcy number on $\Delta NE$ for $Re=100$ and $Re=2000$ at $Bi=0.1$. The results indicate that variations in the Darcy number have no significant impact on thermal non-equilibrium. From a physical perspective, the parameters $Re$ and $Da$ indirectly influence this equilibrium through the residence time of fluid particles at a given point, thus affecting heat exchange between the fluid and solid. For high $Re$ values, the residence time is short, minimizing heat exchange and leading to thermal non-equilibrium. Conversely, for low $Re$ values, the residence time increases, enhancing heat transfer and, consequently, promoting thermal equilibrium.

Finally, for fixed values of $Re$ and $Biot$, $Da$ mainly flattens the velocity profile while maintaining the mass flow rate and thus the residence time of fluid particles. This explains the negligible effect of $Da$ on thermal equilibrium/non-equilibrium between the solid and fluid phases.

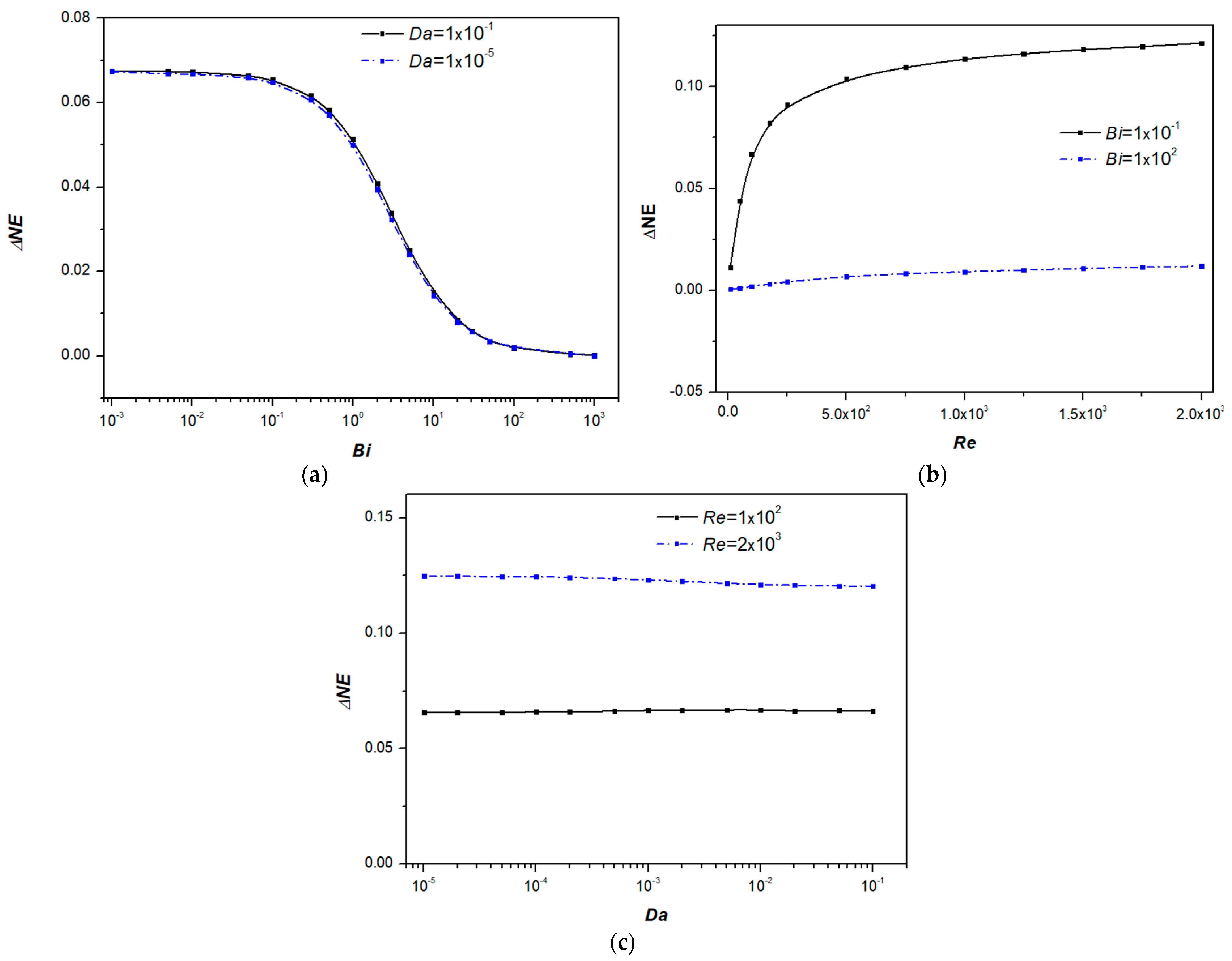
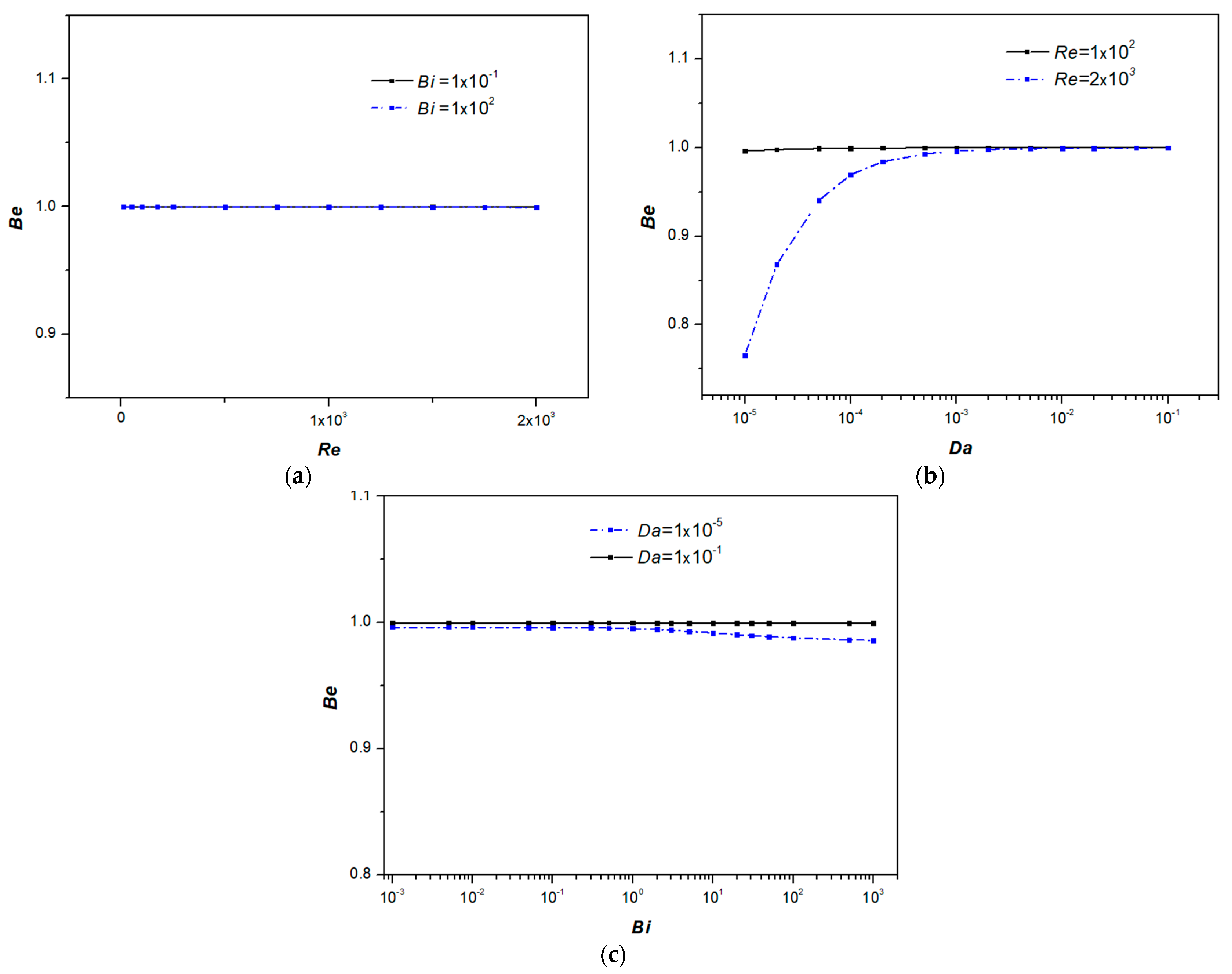
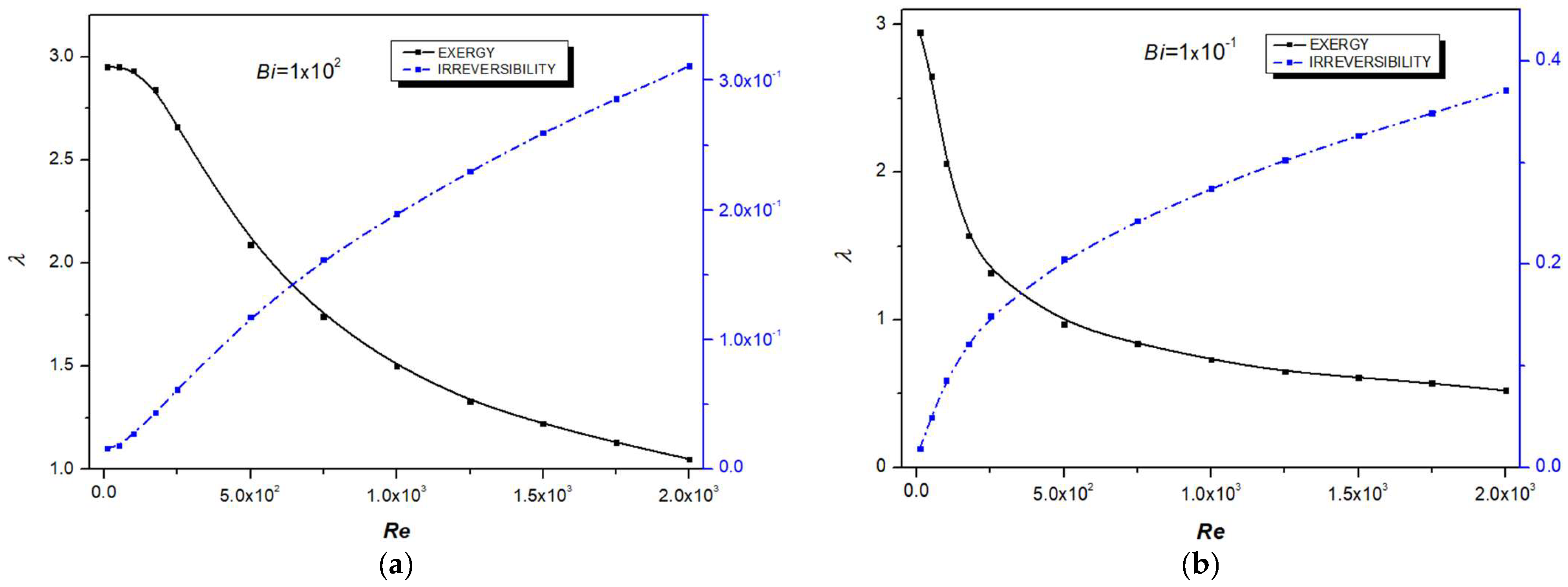
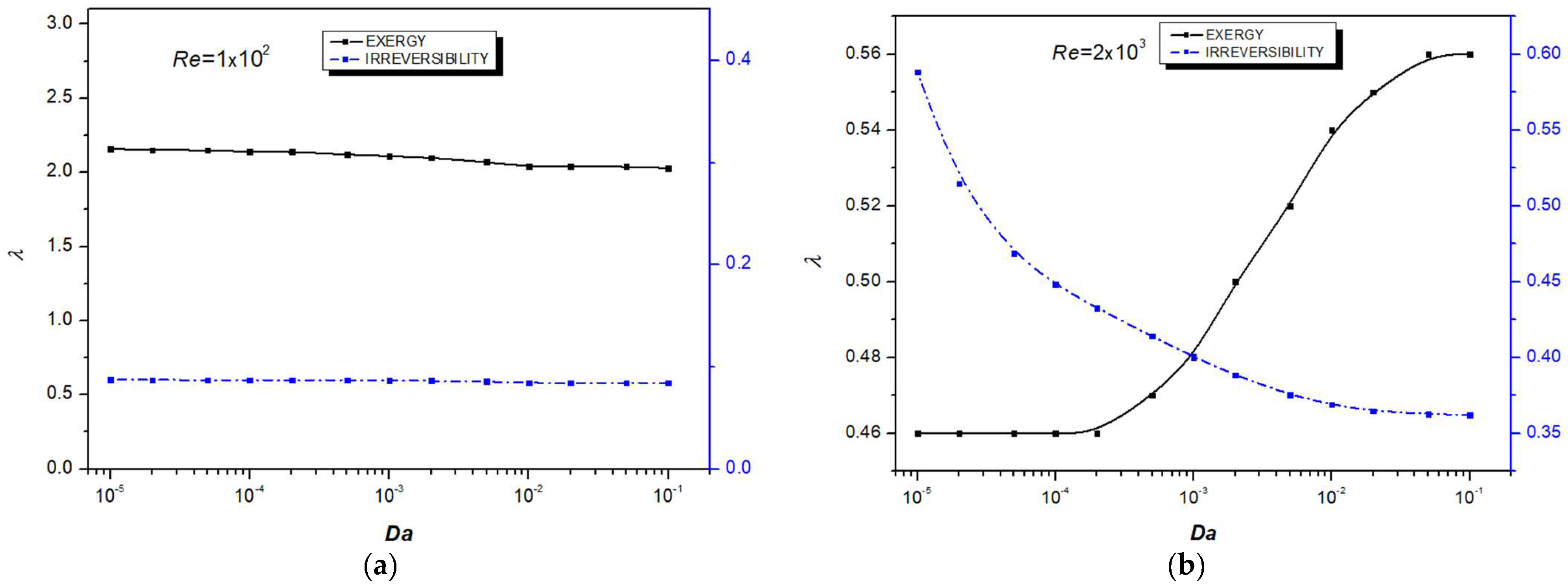
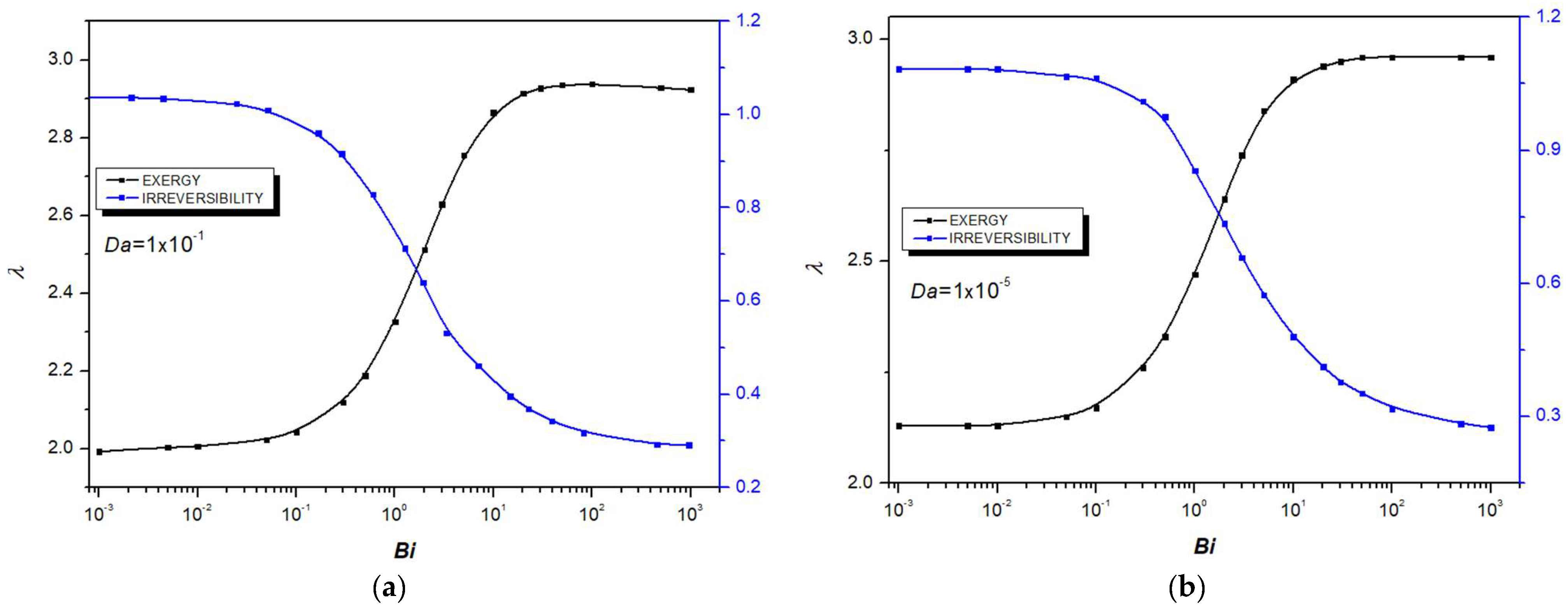
4.2. Thermodynamic Analysis

Figure 5a,c illustrate the variation of the Bejan number as a function of the Reynolds number and the Biot number, respectively. The analysis of these figures indicates that irreversibility is primarily dominated by thermal transport. Across the entire range of Reynolds and Biot numbers considered, the Bejan number approaches unity, which can be attributed to the very small Eckert number $(Ek\approx {10}^{-6})$ for air at moderate velocities.

Figure 5b presents the effect of the Darcy number on the Bejan number for two Reynolds numbers $Re=100$ and $Re=2000$. The previous observations remain valid for large Darcy numbers and low Reynolds numbers. However, for large Reynolds numbers and low Darcy numbers, a noticeable decrease in the Bejan number is observed. This indicates that, in this specific range of $Da$ and $Re$, entropy generation due to viscous dissipation becomes significantly more pronounced.

Figure 6 illustrates the variations of total exergy and irreversibility as a function of the Reynolds number $Re$ for two different Biot number $Bi$ values. As previously discussed in Figure 5a, thermal irreversibility remains dominant across the entire range of Reynolds numbers considered. Furthermore, an increase in $Re$ leads to a higher temperature gradient due to thermal non-equilibrium between the solid and fluid phases. This intensified thermal non-equilibrium results in significant irreversibility, ultimately contributing to the destruction of the system’s total exergy.

Figure 7a,b depict the variations of total exergy and irreversibility as a function of the Darcy number $Da$ for $Re=100$ and $Re=2000$, respectively.

Figure 7a shows that for $Re=100$, variations in Da have a negligible impact on irreversibility, indicating that the total exergy of the system remains nearly conserved. In contrast, Figure 7b demonstrates that for $Re=2000$, irreversibility increases as permeability decreases. This behavior is attributed to dynamic entropy generation, as previously observed in Figure 5b, leading to enhanced exergy degradation at lower $Da$ values.

Figure 8a,b illustrate the variations of irreversibility and total exergy $\lambda$ as a function of the Biot number $Bi$ for $Da={10}^{-1}$ and $Da={10}^{-5}$, respectively. As observed in Figure 5c, heat transfer irreversibility remains dominant across the entire range of $Bi$.

Figure 8a,b indicate that irreversibility decreases with increasing $Bi$. A higher Biot number enhances internal convective heat transfer, reducing the temperature difference between the solid and fluid phases (i.e., lowering LTNE intensity), which in turn results in a smaller temperature gradient.

Additionally, these figures illustrate the influence of $Bi$ on the total exergy $\lambda$ of the system. It is evident that $\lambda$ is significantly degraded at low $Bi$ due to high irreversibility. Beyond a certain threshold, the total exergy exhibits an approximately linear trend.

Finally, it is crucial to emphasize that thermal non-equilibrium has a significant impact on entropy generation, ultimately leading to substantial destruction of the system’s total exergy.

5. Conclusions

The primary objective of this study how to minimize total exergy destruction by reducing entropy generation through variations in key physical parameters, including the Reynolds number, Biot number, and Darcy number, in a porous medium using the thermal non-equilibrium LTNE model. The key findings can be summarized as follows:

• Thermal equilibrium between the fluid and solid phases is achieved at low Reynolds numbers and high Biot numbers, while the Darcy number has a negligible influence on thermal equilibrium.
• Irreversibilities are predominantly caused by heat transfer, except at low Darcy numbers and high Reynolds numbers, where entropy generation due to viscous dissipation becomes significant.
• For all investigated parameters, irreversibilities contribute to exergy destruction within the system.
• Finally, thermal non-equilibrium (LTNE intensity) plays a crucial role in entropy generation, leading to substantial exergy destruction.