Spectral Analysis of Confined Cylinder Wakes
Abstract
:1. Introduction
2. Methodology
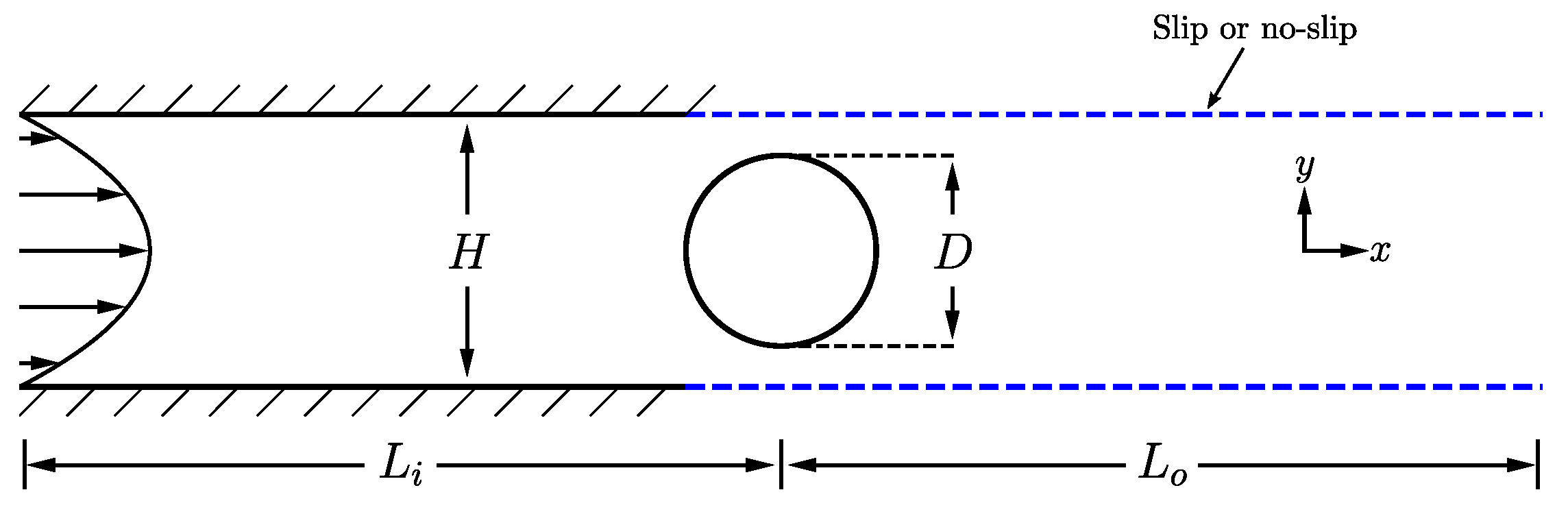
2.1. Numerical Dataset
2.2. Spectral Proper Orthogonal Decomposition
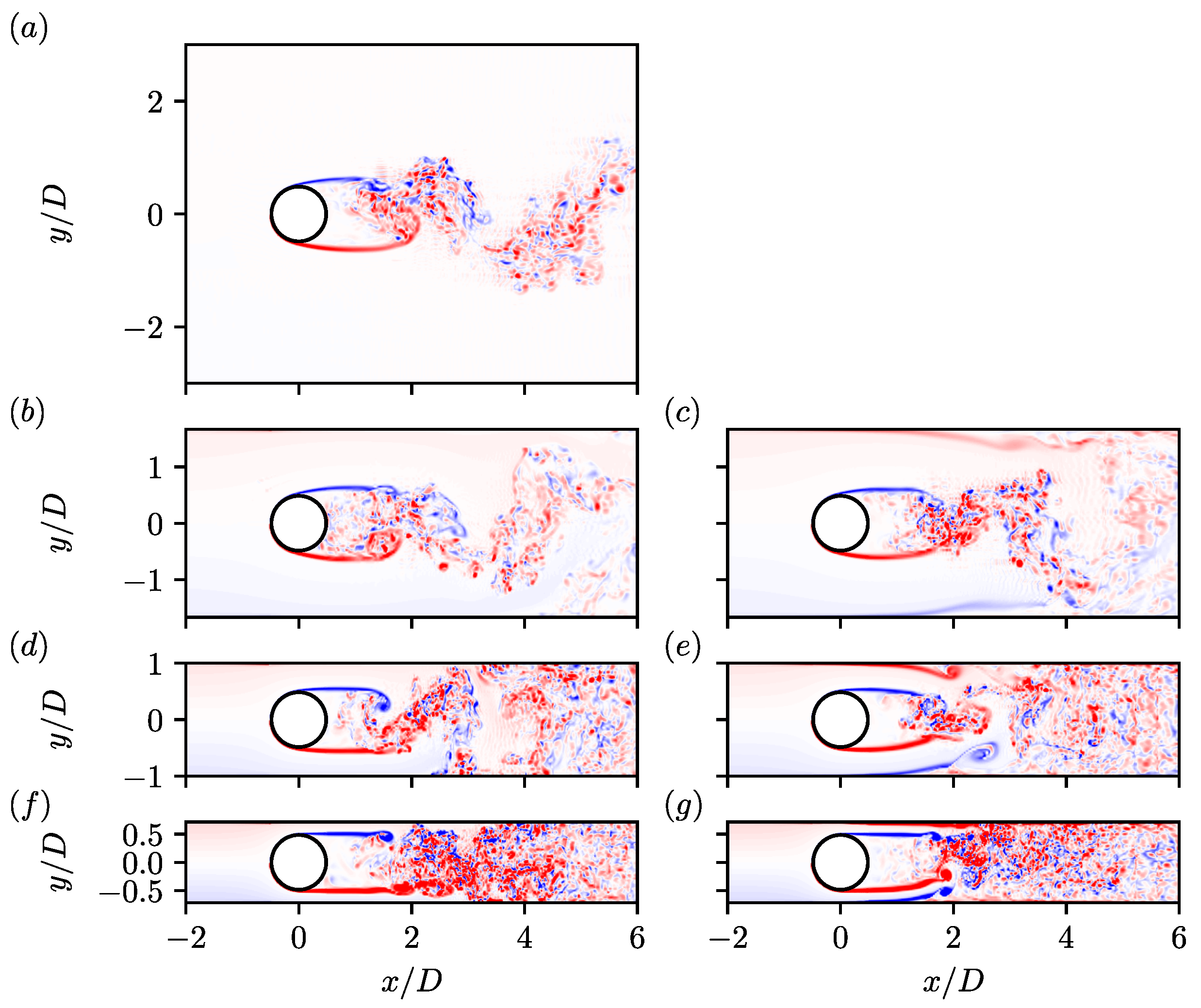
3. Flow Structures
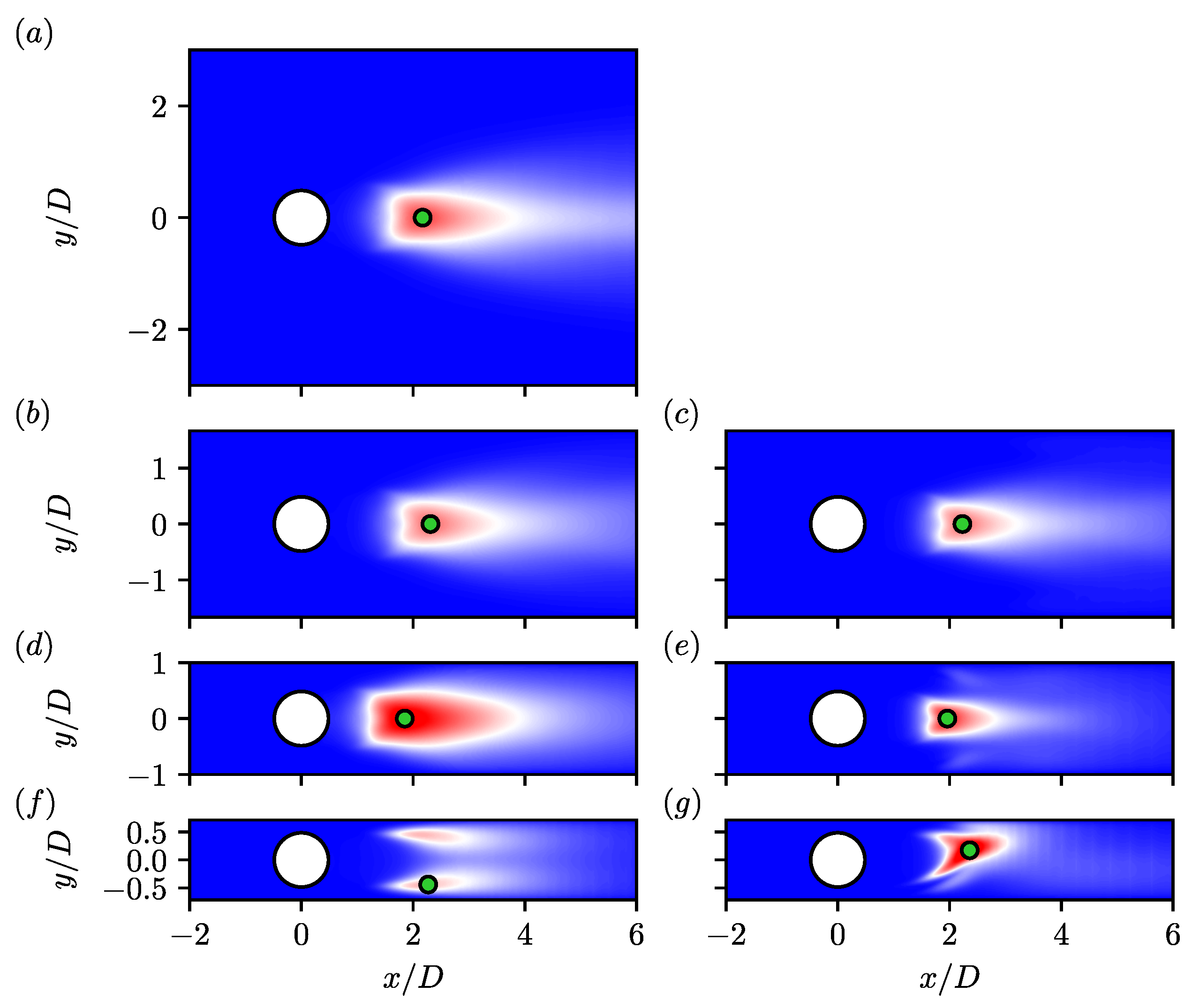
4. Flow Statistics
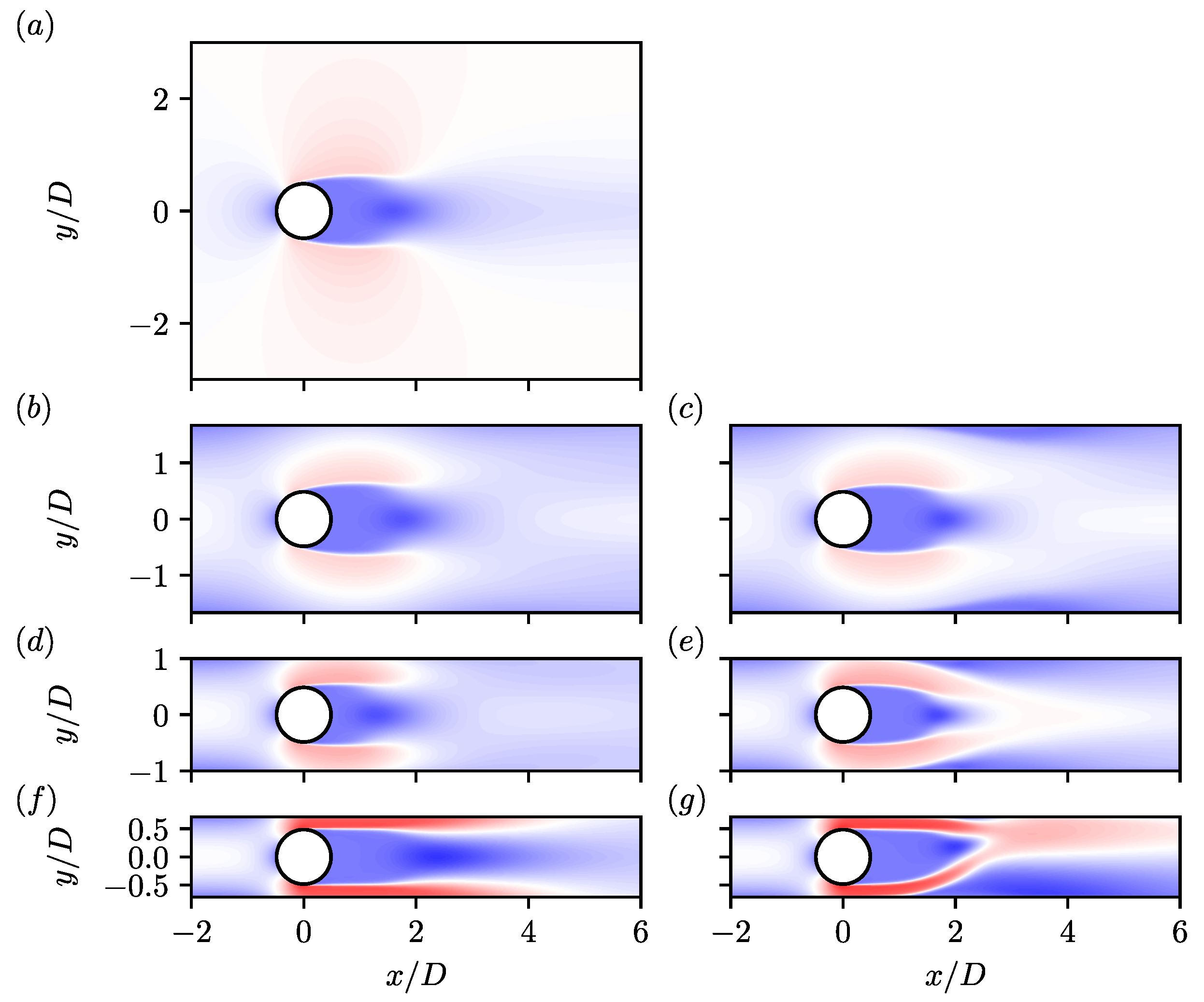
 ) and (
) and ( , along with at with slip (
, along with at with slip ( ) and no-slip (
) and no-slip ( ) boundary conditions. Profiles are taken along (a) the centreline along with (b) , (c) , (d) , and (e) .
) boundary conditions. Profiles are taken along (a) the centreline along with (b) , (c) , (d) , and (e) .
 ) and (
) and ( , along with at with slip (
, along with at with slip ( ) and no-slip (
) and no-slip ( ) boundary conditions. Profiles are taken along (a) the centreline along with (b) , (c) , (d) , and (e) .
) boundary conditions. Profiles are taken along (a) the centreline along with (b) , (c) , (d) , and (e) .
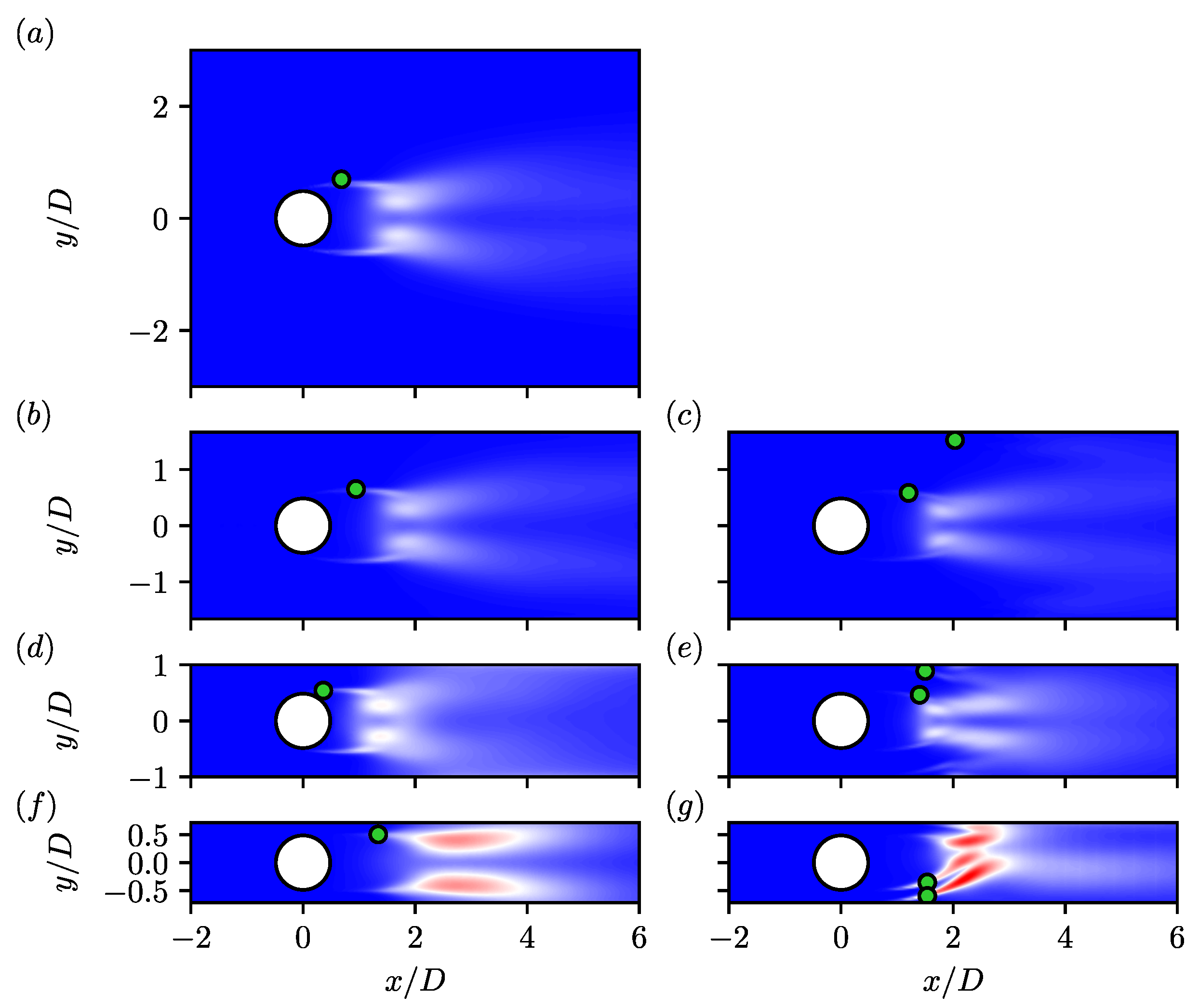
 ) and wall (
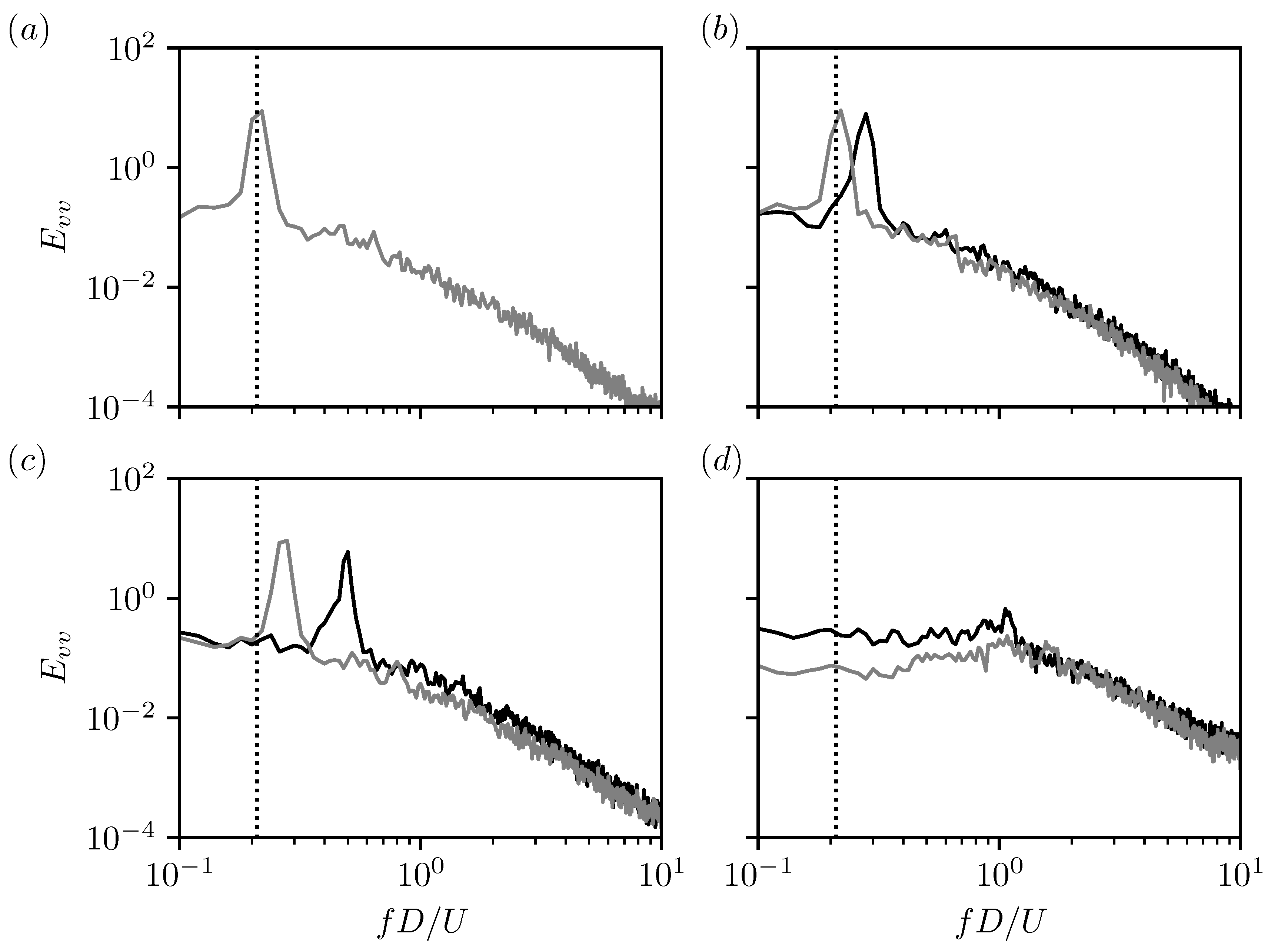
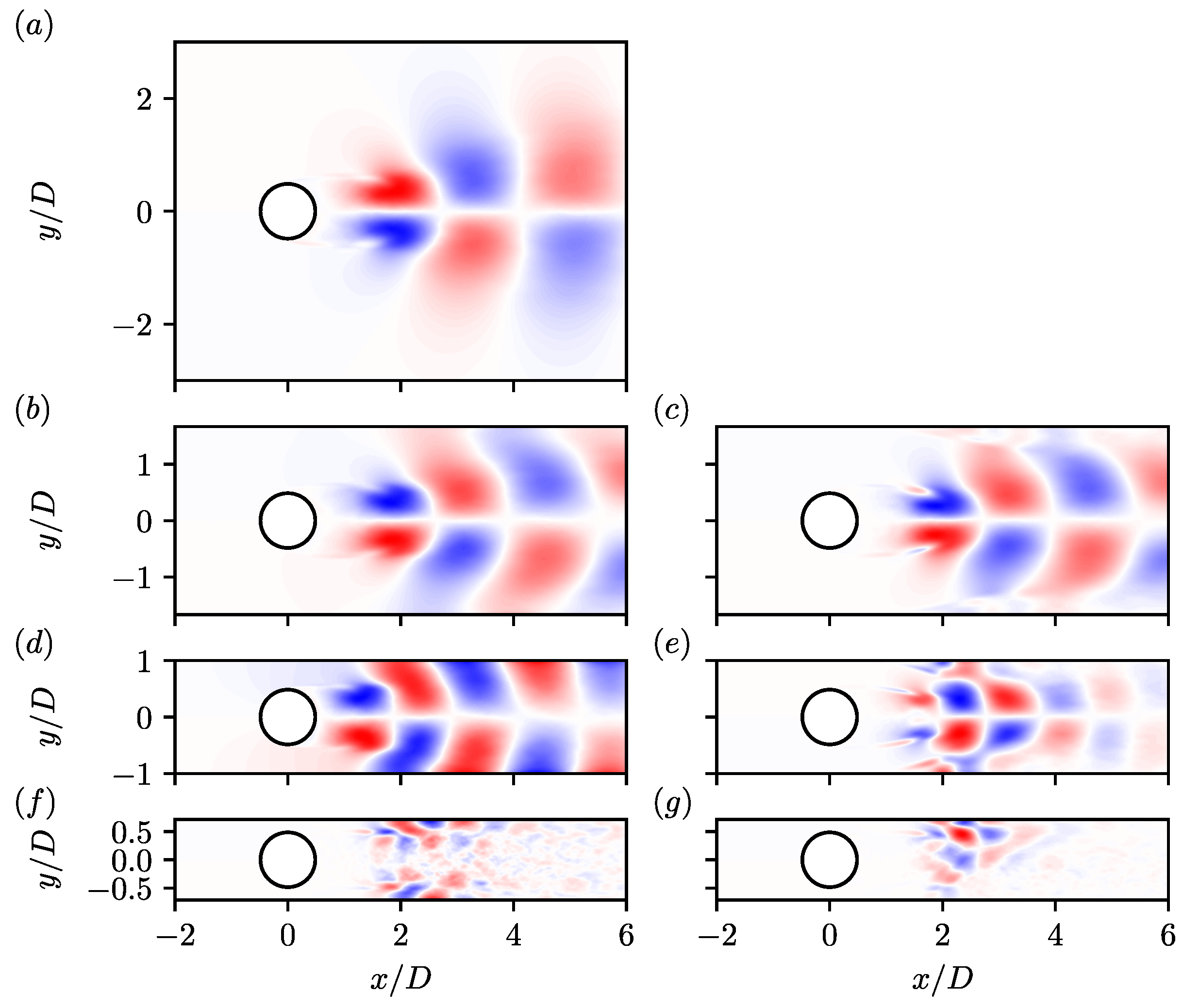
) and wall ( ) shear layers for slip (left column) and no-slip (right column) walls for (a) , (b,c) , (d,e) , and (f,g) . Locations where spectra are computed are denoted by the green dots in Figure 6. Vertical lines denote shedding frequency (
) shear layers for slip (left column) and no-slip (right column) walls for (a) , (b,c) , (d,e) , and (f,g) . Locations where spectra are computed are denoted by the green dots in Figure 6. Vertical lines denote shedding frequency ( ), second harmonic (
), second harmonic ( ), and shear layer frequency (
), and shear layer frequency ( ).
).
 ) and wall (
) and wall ( ) shear layers for slip (left column) and no-slip (right column) walls for (a) , (b,c) , (d,e) , and (f,g) . Locations where spectra are computed are denoted by the green dots in Figure 6. Vertical lines denote shedding frequency (
) shear layers for slip (left column) and no-slip (right column) walls for (a) , (b,c) , (d,e) , and (f,g) . Locations where spectra are computed are denoted by the green dots in Figure 6. Vertical lines denote shedding frequency ( ), second harmonic (
), second harmonic ( ), and shear layer frequency (
), and shear layer frequency ( ).
).
5. Spectral Analysis of the near Wake
5.1. Fourier Analysis
5.2. Spectral Proper Orthogonal Decomposition
6. Spectral Analysis of the Shear Layers
Fourier Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFL | Courant–Friedrichs–Lewy number |
| CSL | Cylinder shear layer |
| DNS | Direct numerical simulation |
| GLL | Gauss–Lobatto–Legendre |
| OIFS | Operator-integration-factor-splitting |
| SPOD | Spectral proper orthogonal decomposition |
| TKE | Turbulent kinetic energy |
| WSL | Wall shear layer |
References
- Williamson, C.H.K. Vortex Dynamics in the Cylinder Wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Derakhshandeh, J.; Alam, M.M. A review of bluff body wakes. Ocean. Eng. 2019, 182, 475–488. [Google Scholar] [CrossRef]
- Jackson, C. A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 1987, 182, 23–45. [Google Scholar] [CrossRef]
- Barkley, D.; Henderson, R.D. Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 1996, 322, 215–241. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at ReD = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox. Flow Turbul. Combust. 2012, 89, 491–518. [Google Scholar] [CrossRef]
- Pereira, F.; Vaz, G.; Eça, L.; Girimaji, S. Simulation of the flow around a circular cylinder at Re = 3900 with Partially-Averaged Navier-Stokes equations. Int. J. Heat Fluid Flow 2018, 69, 234–246. [Google Scholar]
- Molochnikov, V.; Mikheev, N.; Mikheev, A.; Paereliy, A.; Dushin, N.; Dushina, O. SIV measurements of flow structure in the near wake of a circular cylinder at Re = 3900. Fluid Dyn. Res. 2019, 51, 055505. [Google Scholar]
- Lehmkuhl, O.; Rodríguez, I.; Borrell, R.; Oliva, A. Low-frequency unsteadiness in the vortex formation region of a circular cylinder. Phys. Fluids 2013, 25, 085109. [Google Scholar] [CrossRef]
- Franke, J.; Frank, W. Large eddy simulation of the flow past a circular cylinder at ReD = 3900. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1191–1206. [Google Scholar]
- D’Alessandro, V.; Montelpare, S.; Ricci, R. Detached–eddy simulations of the flow over a cylinder at Re = 3900 using OpenFOAM. Comput. Fluids 2016, 136, 152–169. [Google Scholar]
- Lysenko, D.A. Free stream turbulence intensity effects on the flow over a circular cylinder at Re = 3900: Bifurcation, attractors and Lyapunov metric. Ocean. Eng. 2023, 287, 115787. [Google Scholar]
- Dong, S.; Karniadakis, G.E.; Ekmekci, A.; Rockwell, D. A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 2006, 569, 185–207. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, L. Large-eddy simulation of flow past a circular cylinder for Reynolds numbers 400 to 3900. Phys. Fluids 2021, 33, 034119. [Google Scholar] [CrossRef]
- Sahin, M.; Owens, R.G. A numerical investigation of wall effects up to high blockage ratios on two-dimensional flow past a confined circular cylinder. Phys. Fluids 2004, 16, 1305–1320. [Google Scholar] [CrossRef]
- Ooi, A.; Lu, W.; Chan, L.; Cao, Y.; Leontini, J.; Skvortsov, A. Turbulent flow over a cylinder confined in a channel at Re = 3900. Int. J. Heat Fluid Flow 2022, 96, 108982. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Lei, C. Hydrodynamic characteristics of a confined circular cylinder in cross-flows. Ocean. Eng. 2021, 221, 108567. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Lei, C. A particle image velocimetry measurement of flow over a highly confined circular cylinder at 60% blockage ratio. Phys. Fluids 2021, 33, 104111. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Lei, C. A PIV study of blockage ratio effects on flow over a confined circular cylinder at low Reynolds numbers. Exp. Fluids 2023, 64, 10. [Google Scholar]
- Lu, W.; Nguyen, Q.D.; Chan, L.; Lei, C.; Ooi, A. Flows past cylinders confined within ducts. Effects of the duct width. Int. J. Heat Fluid Flow 2023, 104, 109208. [Google Scholar]
- Lu, W.; Aljubaili, D.; Zahtila, T.; Chan, L.; Ooi, A. Asymmetric wakes in flows past circular cylinders confined in channels. J. Fluid Mech. 2023, 958, A8. [Google Scholar] [CrossRef]
- Lu, W.; Chan, L.; Ooi, A. Influence of upstream turbulence on flow past a confined circular cylinder. Submitted to Phys. Rev. Fluids, 2025; under review. [Google Scholar]
- Nguyen, Q.D.; Lu, W.; Chan, L.; Ooi, A.; Lei, C. A state-of-the-art review of flows past confined circular cylinders. Phys. Fluids 2023, 35, 071301. [Google Scholar]
- Ooi, A.; Chan, L.; Aljubaili, D.; Mamon, C.; Leontini, J.; Skvortsov, A.; Mathupriya, P.; Hasini, H. Some new characteristics of the confined flow over circular cylinders at low reynolds numbers. Int. J. Heat Fluid Flow 2020, 86, 108741. [Google Scholar] [CrossRef]
- Aljubaili, D.; Chan, L.; Lu, W.; Ooi, A. Numerical investigations of the wake behind a confined flat plate. Int. J. Heat Fluid Flow 2022, 94, 108924. [Google Scholar]
- Fischer, P.; Kerkemeier, S.; Min, M.; Lan, Y.H.; Phillips, M.; Rathnayake, T.; Merzari, E.; Tomboulides, A.; Karakus, A.; Chalmers, N.; et al. NekRS, a GPU-accelerated spectral element Navier–Stokes solver. Parallel Comput. 2022, 114, 102982. [Google Scholar] [CrossRef]
- Fischer, P.F.; Lottes, J.W.; Kerkemeier, S.G. nek5000 Web Page. 2008. Available online: https://nek5000.mcs.anl.gov/ (accessed on 12 April 2023).
- Zahtila, T.; Lu, W.; Chan, L.; Ooi, A. A systematic study of the grid requirements for a spectral element method solver. Comput. Fluids 2023, 251, 105745. [Google Scholar] [CrossRef]
- Zahtila, T.; Chan, L.; Ooi, A.; Philip, J. Particle transport in a turbulent pipe flow: Direct numerical simulations, phenomenological modelling and physical mechanisms. J. Fluid Mech. 2023, 957, A1. [Google Scholar] [CrossRef]
- Zahtila, T.; Chan, L.; Ooi, A.; Liu, K.; Benjamin, M.; Iaccarino, G. Influence of Miura-origami shapes on drag in turbulent flows. In Proceedings of the Summer Program 2022, Center for Turbulence Research, Bures-sur-Yvette, France, 11–29 July 2022. [Google Scholar]
- Chan, L.; Skvortsov, A.; Ooi, A. Effect of straight riblets of the underlying surface on wall bounded flow drag. Int. J. Heat Fluid Flow 2023, 102, 109160. [Google Scholar] [CrossRef]
- Chan, L.; Skvortsov, A.; Ooi, A. Flow over a confined mounted fence at low and moderate Reynolds number: A numerical study. Int. J. Heat Fluid Flow 2022, 96, 109001. [Google Scholar] [CrossRef]
- Lee, J.; Chan, L.; Zahtila, T.; Lu, W.; Iaccarino, G.; Ooi, A. Surrogate models for multiregime flow problems. Phys. Rev. Fluids 2025, 10, 024703. [Google Scholar] [CrossRef]
- Cui, G.; Cao, Y.; Yan, Y.; Wang, W. Hydrodynamic performance improvement on the hydrofoil using slotted configurations. Ocean. Eng. 2024, 299, 117350. [Google Scholar] [CrossRef]
- Cui, G.; Cao, Y.; Yan, Y.; Wang, W. Numerical study on high-fidelity flow field around vanes of a Francis turbine. Phys. Fluids 2024, 36, 045137. [Google Scholar] [CrossRef]
- Cao, Y.; Philip, J.; Ooi, A. Characteristics of a buoyant plume in a channel with cross-flow. Int. J. Heat Fluid Flow 2022, 93, 108899. [Google Scholar] [CrossRef]
- Zahtila, T.; Lam, W.K.; Chan, L.; Sutherland, D.; Moinuddin, K.; Dai, A.; Skvortsov, T.A.; Manasseh, R.; Ooi, A. On the propagation of planar gravity currents into a stratified ambient. Phys. Fluids 2024, 36, 036601. [Google Scholar] [CrossRef]
- Lam, W.K.; Chan, L.; Sutherland, D.; Manasseh, R.; Moinuddin, K.; Ooi, A. Effect of Stratification on the Propagation of a Cylindrical Gravity Current. J. Fluid Mech. 2024, 983, A43. [Google Scholar] [CrossRef]
- Lam, W.K.; Chan, L.; Cao, Y.; Sutherland, D.; Manasseh, R.; Moinuddin, K.; Ooi, A. Mixing of a Cylindrical Gravity Current in a Stratified Ambient. Int. J. Heat Fluid Flow 2024, 107, 109410. [Google Scholar] [CrossRef]
- Lu, W.; Ooi, A.; Thomas, L.; Zahtila, T.; Iaccarino, G. Application of multi-fidelity methods to prediction of gravity currents for uncertainty quantification. In Proceedings of the Summer Program, Center for Turbulence Research, Stanford University, Stanford, CA, USA, 19 June–23 July 2024. [Google Scholar]
- Cao, Y.; Ooi, A.; Philip, J. Characteristics of planar buoyant jets and plumes in a turbulent channel crossflow from direct numerical simulations. Environ. Fluid Mech. 2024, 24, 1047–1074. [Google Scholar] [CrossRef]
- Maday, Y.; Patera, A.T. Spectral element methods for the incompressible Navier-Stokes equations. In State-of-the-Art Surveys on Computational Mechanics (A90-47176 21–64); Amer Society of Mechanical: New York, NY, USA, 1989; pp. 71–143. [Google Scholar]
- Maday, Y.; Patera, A.T.; Rønquist, E.M. An operator-integration-factor splitting method for time-dependent problems: Application to incompressible fluid flow. J. Sci. Comput. 1990, 5, 263–292. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. Atmos. Turbul. Radio Wave Propag. 1967, 166–178. [Google Scholar]
- Lumley, J.L. Stochastic Tools in Turbulence; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef]
- Schmidt, O.T.; Colonius, T. Guide to Spectral Proper Orthogonal Decomposition. AIAA J. 2020, 58, 1023–1033. [Google Scholar] [CrossRef]
- Thompson, M.C.; Hourigan, K. The shear-layer instability of a circular cylinder wake. Phys. Fluids 2005, 17, 021702. [Google Scholar] [CrossRef]
- Unal, M.F.; Rockwell, D. On vortex formation from a cylinder. Part 1. The initial instability. J. Fluid Mech. 1988, 190, 491–512. [Google Scholar] [CrossRef]
- Aljure, D.; Lehmkhul, O.; Rodríguez, I.; Oliva, A. Three dimensionality in the wake of the flow around a circular cylinder at Reynolds number 5000. Comput. Fluids 2017, 147, 102–118. [Google Scholar]
- Moin, P.; Mahesh, K. DIRECT NUMERICAL SIMULATION: A Tool in Turbulence Research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Posdziech, O.; Grundmann, R. Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 2001, 15, 121–141. [Google Scholar]
- Posdziech, O.; Grundmann, R. A systematic approach to the numerical calculation of fundamental quantities of the two-dimensional flow over a circular cylinder. J. Fluids Struct. 2007, 23, 479–499. [Google Scholar] [CrossRef]
- Persillon, H.; Braza, M. Physical analysis of the transition to turbulence in the wake of a circular cylinder by three-dimensional Navier–Stokes simulation. J. Fluid Mech. 1998, 365, 23–88. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Triantafyllou, G.S. Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 1992, 238, 1–30. [Google Scholar] [CrossRef]
- Kumar, B.; Mittal, S. Effect of blockage on critical parameters for flow past a circular cylinder. Int. J. Numer. Methods Fluids 2006, 50, 987–1001. [Google Scholar]
- Behr, M.; Hastreiter, D.; Mittal, S.; Tezduyar, T. Incompressible flow past a circular cylinder: Dependence of the computed flow field on the location of the lateral boundaries. Comput. Methods Appl. Mech. Eng. 1995, 123, 309–316. [Google Scholar]
- Bloor, M.S. The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 1964, 19, 290–304. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Zhou, B.; Li, Y.; Xiang, Q. Experimental investigation of flow past a confined bluff body: Effects of body shape, blockage ratio and Reynolds number. Ocean. Eng. 2021, 220, 108412. [Google Scholar] [CrossRef]
- Schmidt, O.T.; Towne, A.; Rigas, G.; Colonius, T.; Brès, G.A. Spectral analysis of jet turbulence. J. Fluid Mech. 2018, 855, 953–982. [Google Scholar] [CrossRef]
- Siegel, S.G.; Seidel, J.; Fagley, C.; Luchtenburg, D.; Cohen, K.; McLaughlin, T. Low-dimensional modelling of a transient cylinder wake using double proper orthogonal decomposition. J. Fluid Mech. 2008, 610, 1–42. [Google Scholar]
- Thacher, E.; Van Ruymbeke, B.; Gabillet, C.; Jacques, N.; Mäkiharju, S.A. Flow topology changes with bubbly flow around a circular cylinder. Int. J. Multiph. Flow 2024, 179, 104917. [Google Scholar]
- Chu, S.; Xia, C.; Wang, H.; Fan, Y.; Yang, Z. Three-dimensional spectral proper orthogonal decomposition analyses of the turbulent flow around a seal-vibrissa-shaped cylinder. Phys. Fluids 2021, 33, 025106. [Google Scholar]
- Janocha, M.J.; Yin, G.; Ong, M.C. Modal analysis of wake behind stationary and vibrating cylinders. J. Offshore Mech. Arct. Eng. 2021, 143, 041902. [Google Scholar]
- Wu, J.; Xiao, D.; Luo, M. Deep-learning assisted reduced order model for high-dimensional flow prediction from sparse data. Phys. Fluids 2023, 35, 103115. [Google Scholar]
- Li, S.; Yang, J.; Teng, P. Data-driven prediction of cylinder-induced unsteady wake flow. Appl. Ocean. Res. 2024, 150, 104114. [Google Scholar]
- Provansal, M.; Mathis, C.; Boyer, L. Bénard-von Kármán instability: Transient and forced regimes. J. Fluid Mech. 1987, 182, 1–22. [Google Scholar]
- Henderson, R.D. Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 1997, 352, 65–112. [Google Scholar] [CrossRef]
- Brun, C.; Aubrun, S.; Goossens, T.; Ravier, P. Coherent structures and their frequency signature in the separated shear layer on the sides of a square cylinder. Flow Turbul. Combust. 2008, 81, 97–114. [Google Scholar]
- Prasad, A.; Williamson, C.H.K. The instability of the shear layer separating from a bluff body. J. Fluid Mech. 1997, 333, 375–402. [Google Scholar] [CrossRef]

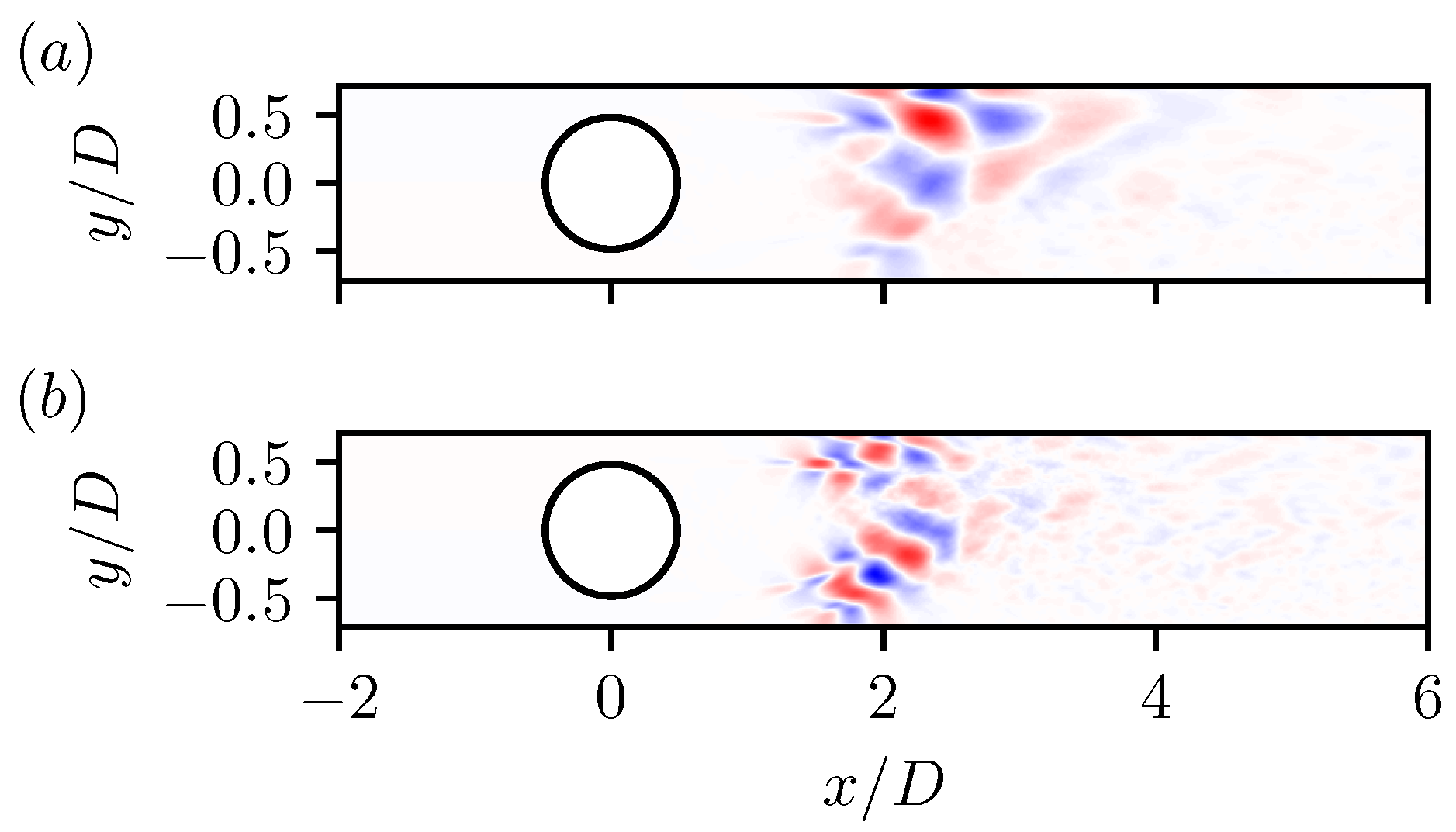
 ) (
) ( ), and (
), and ( ) with slip walls.
) with slip walls.
 ) (
) ( ), and (
), and ( ) with slip walls.
) with slip walls.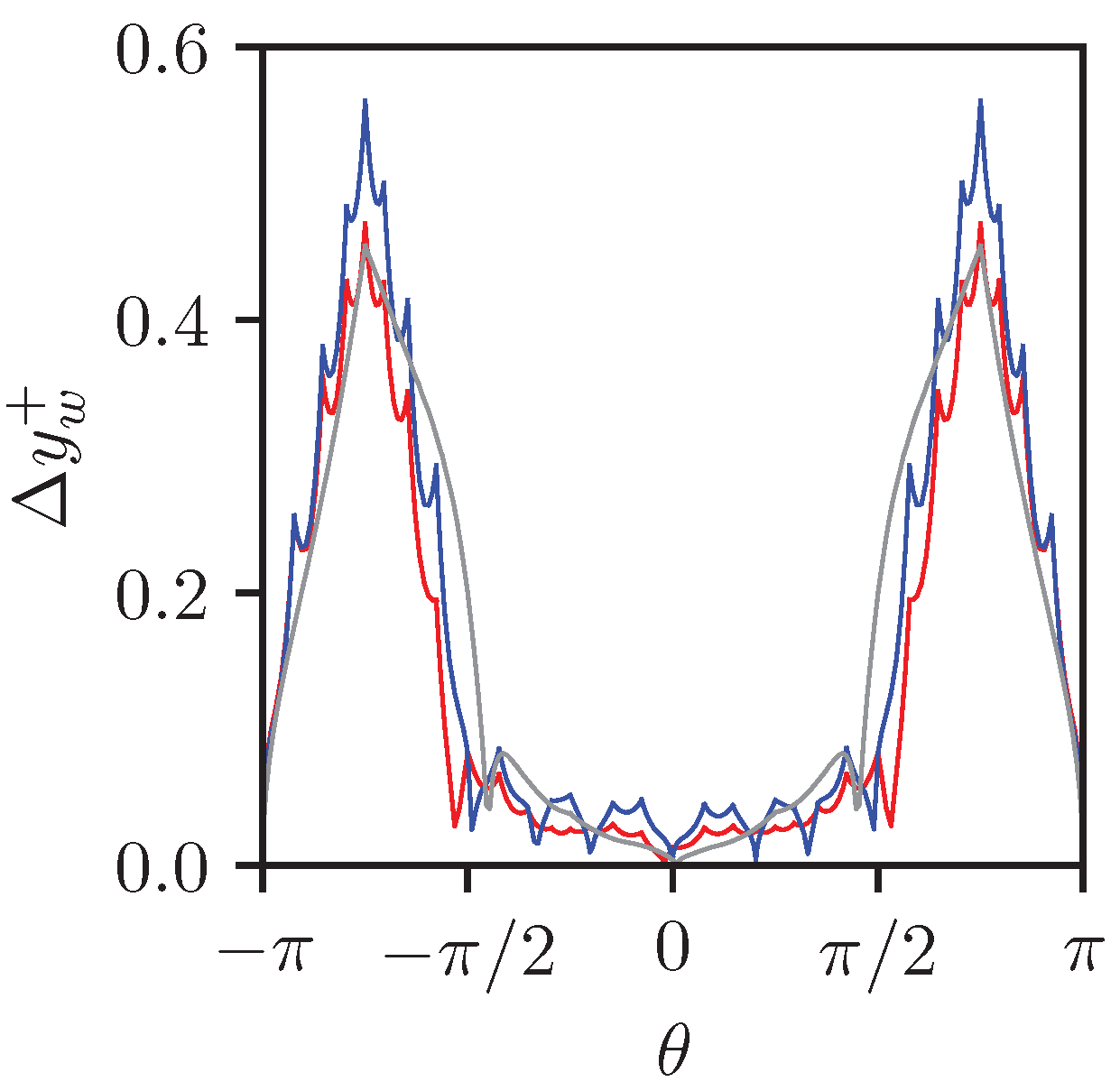

 ) and no-slip (
) and no-slip ( ) walls. Profiles are compared for blockages of (a) , (b) , and (c) . Dots denote the edge of the boundary layer, defined by the point of maximum velocity.
) walls. Profiles are compared for blockages of (a) , (b) , and (c) . Dots denote the edge of the boundary layer, defined by the point of maximum velocity.
 ) and no-slip (
) and no-slip ( ) walls. Profiles are compared for blockages of (a) , (b) , and (c) . Dots denote the edge of the boundary layer, defined by the point of maximum velocity.
) walls. Profiles are compared for blockages of (a) , (b) , and (c) . Dots denote the edge of the boundary layer, defined by the point of maximum velocity.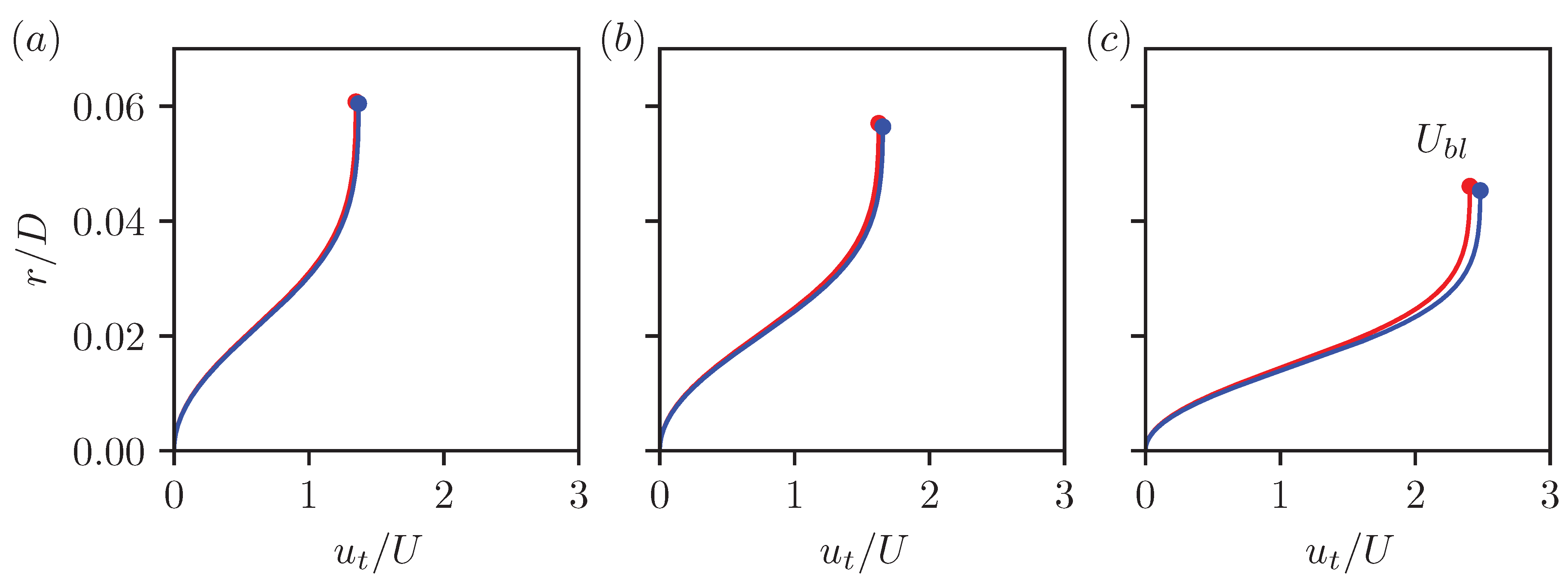
| Case | Wall BCs | E | Grid Points | |||
|---|---|---|---|---|---|---|
| SB0p0Re3900 | Slip | 3900 | 3900 | |||
| SB0p0Re2600 | Slip | 2600 | 2600 | 37,200 | ||
| NB0p3Re3900 | No-Slip | 2600 | 3900 | 42,600 | ||
| SB0p3Re3900 | Slip | 2600 | 3900 | 37,020 | ||
| NB0p5Re3900 | No-Slip | 2600 | 3900 | 39,780 | ||
| SB0p5Re3900 | Slip | 2600 | 3900 | 39,930 | ||
| NB0p7Re3900 | No-Slip | 2600 | 3900 | 85,120 | ||
| SB0p7Re3900 | Slip | 2600 | 3900 | 33,600 |
| No-Slip | Slip | No Shear | |
|---|---|---|---|
| − | |||
| − | |||
| − | |||
| − | − | − |
| Method | |||
|---|---|---|---|
| Present, Ooi et al. [17] | DNS | ||
| Dong et al. [14] | DNS | − | |
| Lysenko et al. [7] | LES | ||
| Lehmkuhl et al. [10] | DNS | ||
| Jiang and Cheng [15] | LES | ||
| Prasad and Williamson [71] | Empirical Fit | − |
| No-Slip | Slip | |
|---|---|---|
| − | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Chan, L.; Ooi, A. Spectral Analysis of Confined Cylinder Wakes. Fluids 2025, 10, 84. https://doi.org/10.3390/fluids10040084
Lu W, Chan L, Ooi A. Spectral Analysis of Confined Cylinder Wakes. Fluids. 2025; 10(4):84. https://doi.org/10.3390/fluids10040084
Chicago/Turabian StyleLu, Wilson, Leon Chan, and Andrew Ooi. 2025. "Spectral Analysis of Confined Cylinder Wakes" Fluids 10, no. 4: 84. https://doi.org/10.3390/fluids10040084
APA StyleLu, W., Chan, L., & Ooi, A. (2025). Spectral Analysis of Confined Cylinder Wakes. Fluids, 10(4), 84. https://doi.org/10.3390/fluids10040084






