Structural Optimization of the Venturi Fertilizer Applicator Using Head Loss Calculation Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Analysis on the Internal Flow of the Venturi Injector
2.2. Theoretical Analysis on Head Loss in the Venturi Tube
2.3. Numerical Simulation on the Interflow of the Venturi Tube
2.3.1. The Geometric Model
2.3.2. Governing Equation
2.3.3. Boundary Conditions
2.3.4. Grid Independence Verification
2.3.5. Comparison of Numerical and Experimental Results
3. Results
3.1. Internal Flow State of the Venturi Tube
3.2. Verification and Revision of the Loss Calculation Equation
3.3. Optimum Design Analysis of the Venturi Injector Based on the Head Loss Regression Formula
3.3.1. Optimal Throat Pipe Length
3.3.2. Optimal Reducing Angle and Expanding Angle
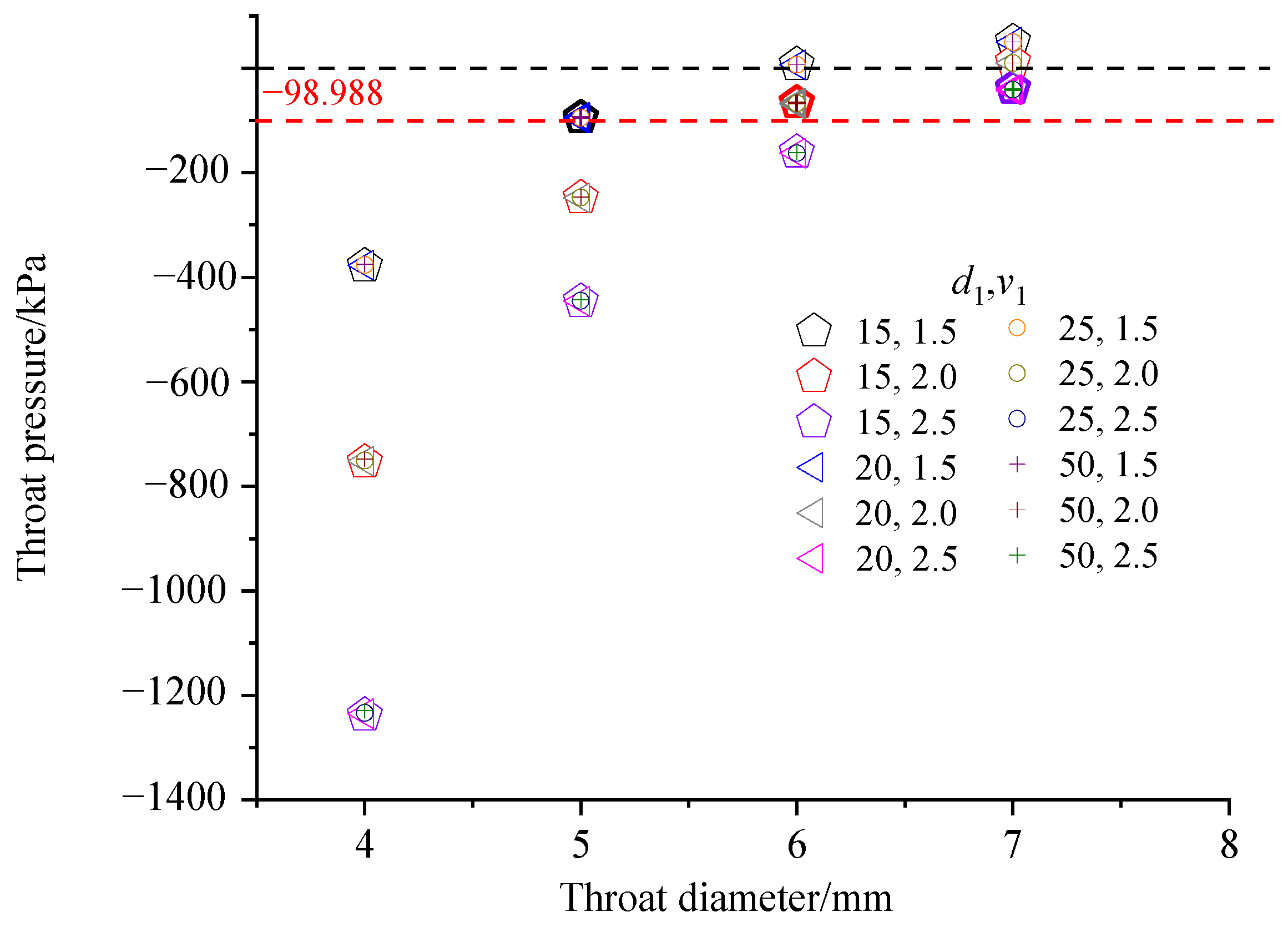
3.3.3. Optimal Throat Diameter
4. Discussion
5. Conclusions
- (1)
- Frictional losses and local head losses in the reducing, throat, and expanding sections of the Venturi injector were analyzed based on fluid mechanics. Subsequently, a theoretical equation for calculating the head loss between the inlet and outlet of the Venturi tube was proposed. To verify and refine the theoretical equation, simulations based on CFD methods were conducted. The coefficient of determination of the regression equation was 0.945. The average deviation between the simulated and calculated head loss was 4.43%. The regression equation can be reliably utilized for head loss calculations in the Venturi tube;
- (2)
- The equation for calculating the throat pressure of the Venturi injector was derived based on the regression equation for head loss. Subsequently, the optimal structure parameters of the Venturi injector were analyzed to maximize the suction flow rate of the Venturi injector under identical inlet and outlet pressures. The optimal throat length and suction pipe diameter were set equal to the throat diameter of the Venturi injector. The optimal range for the reducing angle and expanding angle of the Venturi injector were identified as 20–28° and 6–10°, respectively. Moreover, it was determined that the optimal throat diameter fell within the range of 5–7 mm when the inlet flow rate ranged from 1.5 to 2.5 m3/h. These results provide a theoretical framework for parameter optimization in diverse applications;
- (3)
- The throat pressure calculation model established in this study has significant engineering application value. When certain parameters (such as inlet flow rate and inlet diameter) have been determined in actual working conditions, the optimal structural parameters can be rapidly solved based on this model. For open systems with completely variable parameters, an optimization range is provided that includes the contraction angle, diffusion angle, and throat diameter. The model’s versatility extends to a range of applications, including agricultural irrigation and fertilization and industrial liquid mixing, among others.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| Ks | wall roughness constant |
| R2 | coefficient of determination |
| Re | Reynolds number |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| Y+ | wall-distance non-dimensional parameter |
References
- Li, P.; Li, H.; Li, J.; Huang, X.Q.; Liu, Y.; Jiang, Y. Effect of Aeration on Blockage Regularity and Microbial Diversity of Blockage Substance in Drip Irrigation Emitter. Agriculture 2022, 12, 1941. [Google Scholar] [CrossRef]
- Li, J.; Meng, Y.; Liu, Y. Hydraulic performance of differential pressure tanks for fertigation. Trans. ASAE 2006, 49, 1815–1822. [Google Scholar]
- Li, H.; Li, H.; Huang, X.; Han, Q.; Yuan, Y.; Qi, B. Numerical and Experimental Study on the Internal Flow of the Venturi Injector. Process 2020, 8, 64. [Google Scholar]
- Sobenko, L.R.; Frizzone, J.A.; Camargo, A.P.D.; Saretta, E.; Rocha, H.S.D. Characterization of venturi injector using dimensional analysis characterization of venturi injector using dimensional analysis. Rev. Bras. Eng. Agrícola Ambient. 2019, 23, 484–491. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Yan, S.; Xiang, Y. Evaluation of drip fertigation uniformity affected by injector type, pressure difference and lateral layout. Irrig. Drain. 2017, 66, 520–529. [Google Scholar]
- Li, J.; Meng, Y.; Li, B. Field evaluation of fertigation uniformity as affected by injector type and manufacturing variability of emitters. Irrig. Sci. 2007, 25, 117–125. [Google Scholar] [CrossRef]
- Yuan, Z.; Choi, C.Y.; Waller, P.M.; Colaizzi, P. Effects of liquid temperature and viscosity on venturi injectors. Trans. ASAE 2000, 43, 1441–1447. [Google Scholar]
- Neto, I.E.L.; Porto, R.D.M. Performance of low–cost ejectors. J. Irrig. Drain. Eng. 2004, 130, 122–128. [Google Scholar]
- Hu, G.; Guan, X.; Li, S.; Liu, N.; Zhang, J.; Zhang, J.; Wang, Z. Structure optimization and fertilizer injection performance analysis of a non–axisymmetric Venturi injector. Irrig. Drain. 2023, 73, 400–414. [Google Scholar] [CrossRef]
- Bartzanas, T.; Kacira, M.; Zhu, H.; Karmakar, S.; Tamimi, E.; Katsoulas, N.; Lee, I.B.; Kittas, C. Computational fluid dynamics applications to improve crop production systems. Comput. Electron. Agric. 2013, 93, 151–167. [Google Scholar]
- Dione, F.; Cong, T.; Jayeola, M. Open-FOAM CFD simulation of critical heat flux in vertical pipe under typically PWR conditions. Ann. Nucl. Energy 2022, 174, 109174. [Google Scholar] [CrossRef]
- Huang, X.; Li, G.; Wang, M. CFD simulation to the flow field of venturi injector. In Computer and Computing Technologies in Agriculture II, Volume 2: Proceedings of the Second IFIP International Conference on Computer and Computing Technologies in Agriculture (CCTA2008), 18–20 October 2008, Beijing, China; Li, D., Zhao, C., Eds.; Springer: New York, NY, USA, 2009; pp. 805–815. [Google Scholar]
- Wang, H.; Wang, J.; Yang, B.; Mo, Y.; Zhang, Y.; Ma, X. Simulation and optimization of venturi injector by machine learning algorithms. J. Irrig. Drain. Eng. 2020, 146, 04020021. [Google Scholar]
- Zhang, L.; Wei, Z.; Qian, Z. Structural optimization of the low-pressure venturi injector with double suction ports based on computational fluid dynamics and orthogonal test. Desalin. Water Treat. 2021, 214, 347–354. [Google Scholar]
- Liu, J.P.; Hussain, Z.; Wang, X.J.; Li, Y.F. Optimization and Numerical Simulation of the Internal Flow Field of Water–Pesticide Integrated Microsprinklers. Irrig. Drain. 2023, 72, 328–342. [Google Scholar]
- Chen, A.; Yu, Y. CFD-DEM simulation on the complex gas–solid flow in a closed chamber with particle groups. J. Mech. Sci. Technol. 2022, 36, 5523–5535. [Google Scholar]
- Im, K.; Kim, H.; Lai, M.; Tacina, R. Parametric study of the swirler/venturi spray injectors. J. Propuls. Power 2001, 17, 717–727. [Google Scholar]
- Manzano, J.; De Azevedo, B.M.; Do Bomfim, G.V.; Royuela, Á.; Palau, C.V.; De, A.; Viana, T.V. Design and prediction performance of Venturi injectors in drip irrigation. Rev. Bras. Eng. Agric. Ambient. 2014, 18, 1209–1217. [Google Scholar]
- Manzano, J.; Palau, C.; de Azevedo, B.; do Bomfim, G.; Vasconcelos, D. Characterization and selection method of Venturi injectors for pressurized irrigation. Rev. Cienc. Agron. 2018, 49, 201–210. [Google Scholar]
- Chen, L.; Sun, Z.; Ma, H.; Gao, K.; Ma, G.; Deng, Y. Structural parameters of venturi injector for periodic air recovery based on response surface methodology. Chem. Eng. Process. Intensif. 2023, 193, 109551. [Google Scholar]
- Valiantzas, J.D. Explicit power formula for the darcy–weisbach pipe flow Equation: Application in optimal pipeline design. J. Irrig. Drain. Eng. 2008, 134, 454–461. [Google Scholar] [CrossRef]
- Marui–Paloka, E.; Paanin, I. Effects of boundary roughness and inertia on the fluid flow through a corrugated pipe and the formula for the darcy–weisbach friction coefficient. Int. J. Eng. Sci. 2020, 152, 103293. [Google Scholar]
- Rettore Neto, O.; de Miranda, J.H.; Frizzone, J.A.; Workman, S.R. Local Head Loss of Non–Coaxial Emitters Inserted in Polyethylene Pipe. Trans. ASABE 2009, 52, 729–738. [Google Scholar]
- José, H.N.F.; Faria, L.C.; Neto, O.R.; Diotto, A.V.; Colombo, A. Methodology for determining the emitter local head loss in drip irrigation systems. J. Irrig. Drain. Eng. 2021, 147, 06020014. [Google Scholar]
- Xu, F. Influence of Valve on Flow Resistance of Piping System. China Nucl. Power 2017, 10, 64–68. [Google Scholar]
- Jiang, Y.; Li, H.; Xiang, Q.; Chen, C. Comparison of PIV Experiment and Numerical Simulation on the Velocity Distribution of Intermediate Pressure Jets with Different Nozzle Parameters. Irrig. Drain. 2017, 66, 510–519. [Google Scholar]
- Tang, P.; Juárez, J.M.; Li, H. Investigation on the effect of structural parameters on cavitation characteristics for the venturi tube using the CFD method. Water 2019, 11, 2194. [Google Scholar] [CrossRef]
- Hu, X.; Chen, X. Optimisation of fertiliser dissolution under differential pressure tank during fertigation. Biosyst. Eng. 2021, 206, 79–93. [Google Scholar]
- Dong, C.; Zhu, J.; Miller, C.F. Evaluation of six aerator modules built on venturi air injectors using clean water test. Water Sci. Technol. 2009, 60, 1353–1359. [Google Scholar]
- Mukesh, K.; Rajput, T.B.S.; Neelam, P. Effect of system pressure and solute concentration on fertilizer injection rate of a venturi for fertigation. J. Agric. Eng. 2012, 49, 9–13. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Y.; Wang, Z.; Zhou, L.; Yan, H. Investigation of the cavitation fluctuation characteristics in a Venturi injector. Fluid Dyn. Res. 2015, 47, 025506. [Google Scholar]
- Simpson, A.; Ranade, V.V. Modeling hydrodynamic cavitation in venturi: Influence of venturi configuration on inception and extent of cavitation. AIChE J. 2019, 65, 421–433. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, M.; Jiang, X.; Jiang, K.; Feng, Q. Structure Optimization of Suction Device and Performance Test of Integrated Water and Fertilizer Fertigation Machine. Trans. Chin. Soc. Agric. Mach. 2015, 11, 76–81+48. [Google Scholar]
- Qiu, Z.; Bao, A. Numerical Study on Concentration Affected by Structure Parameters—Based on Parallel Venturi Fertilizer Applicator. J. Agric. Mechan. Res. 2012, 4, 42–45. [Google Scholar]
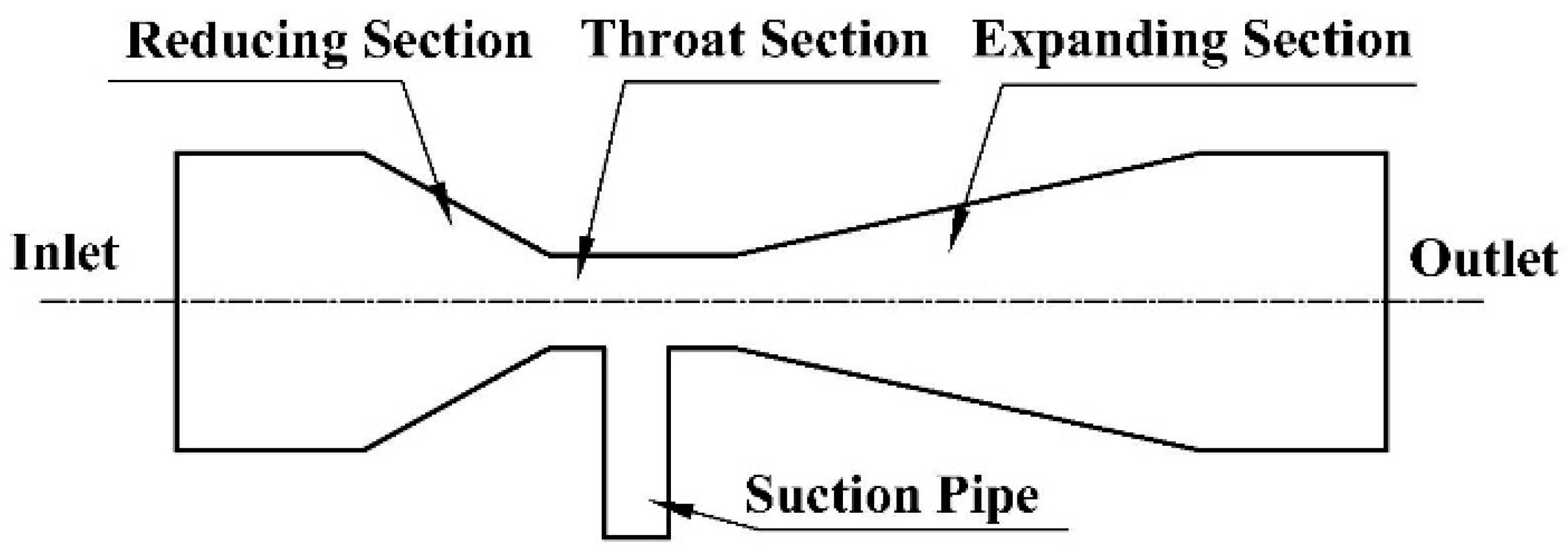
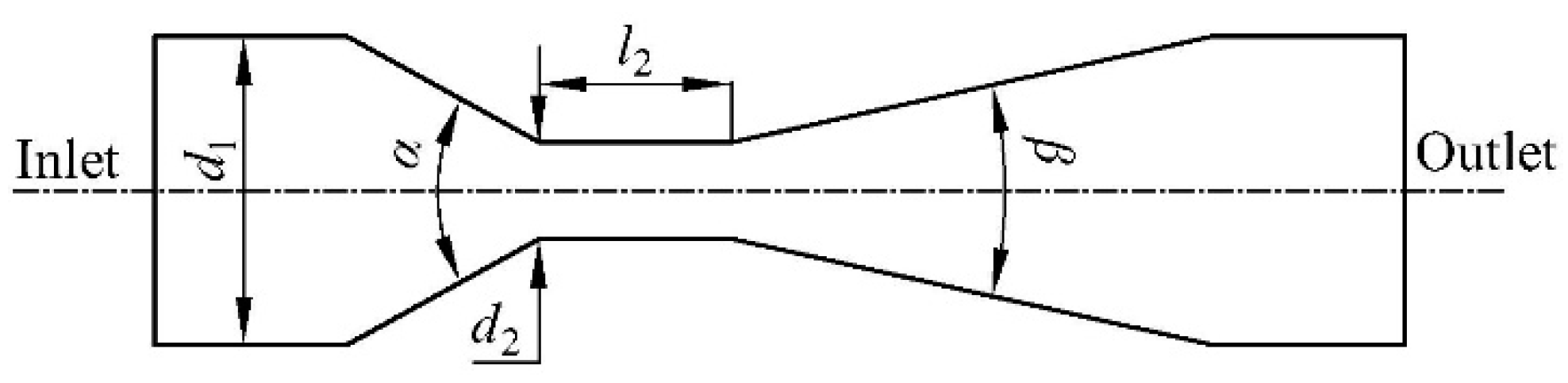

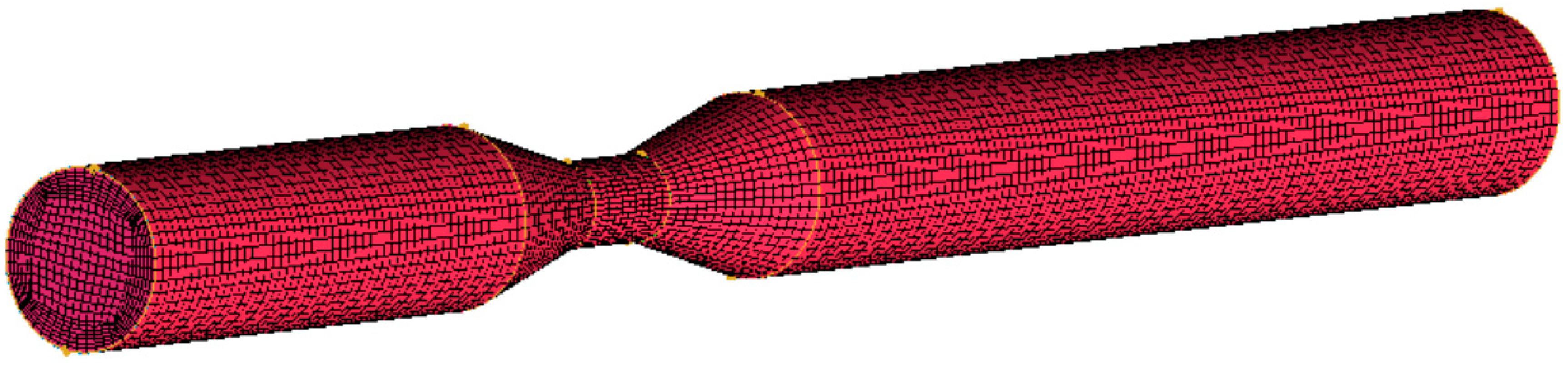
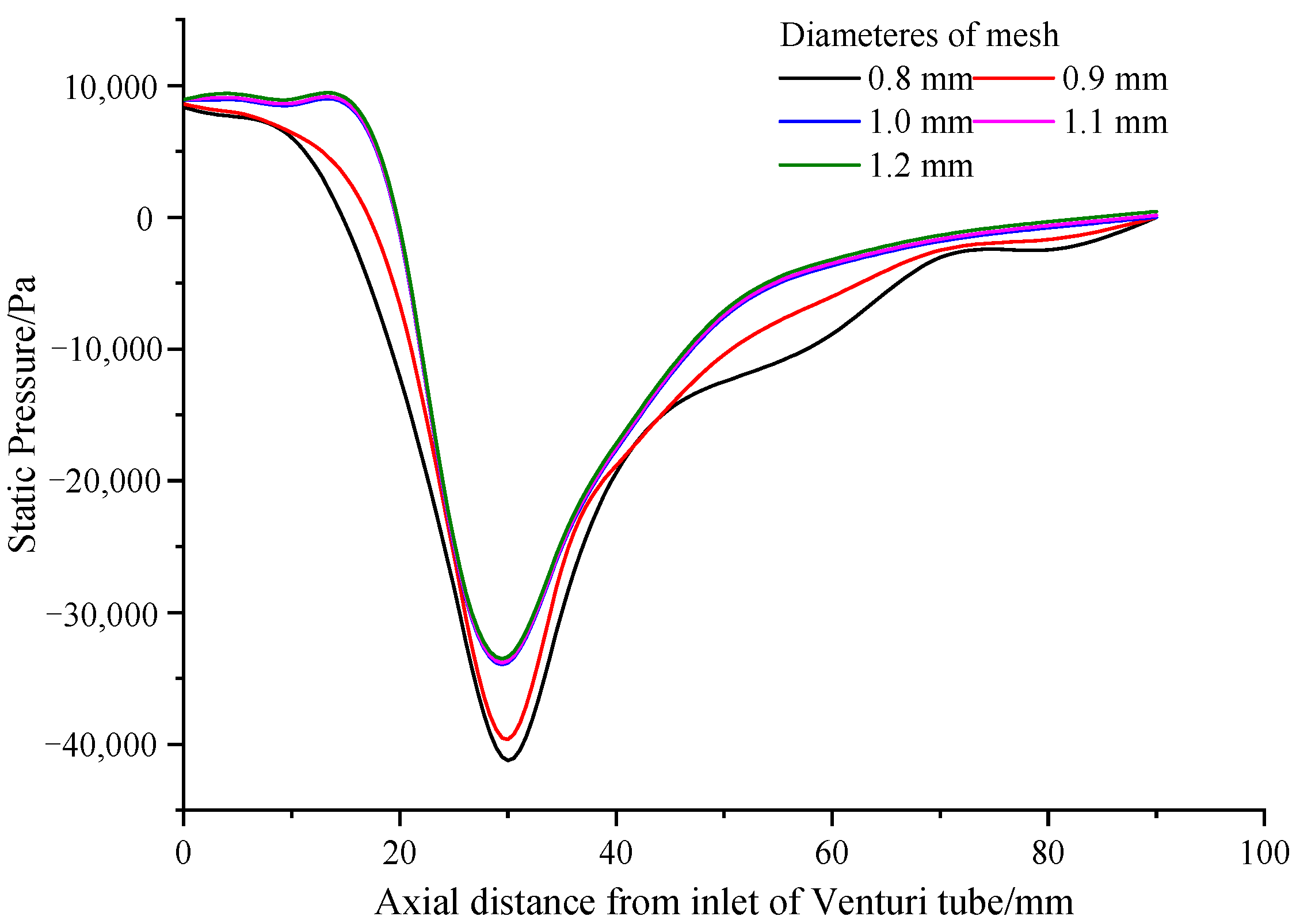

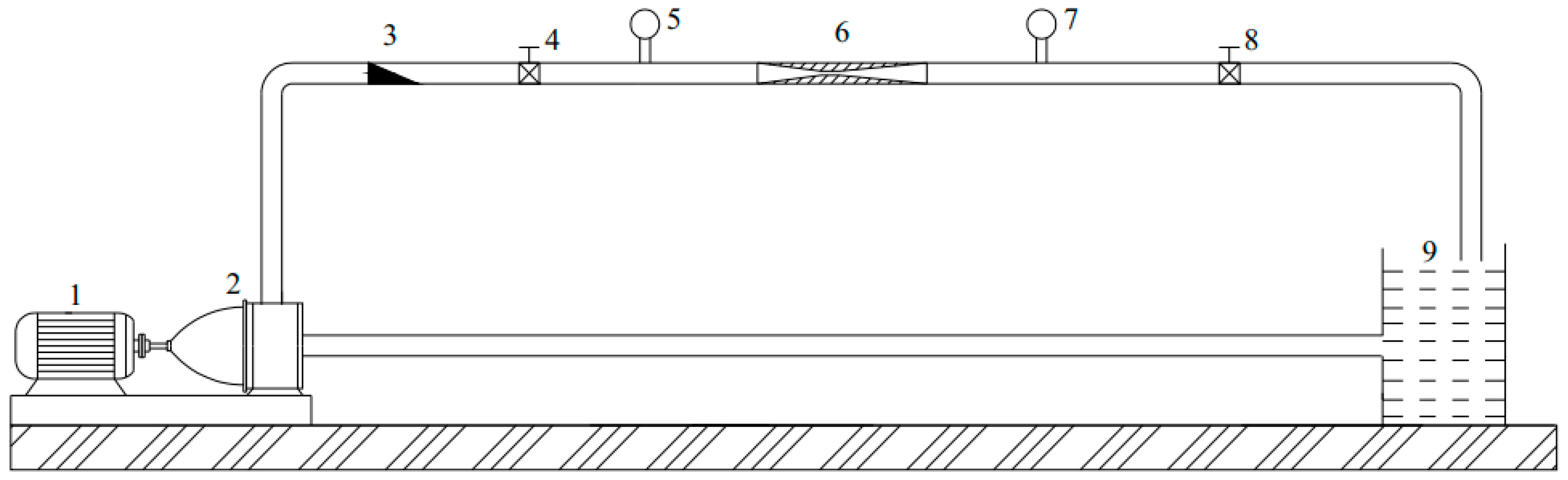
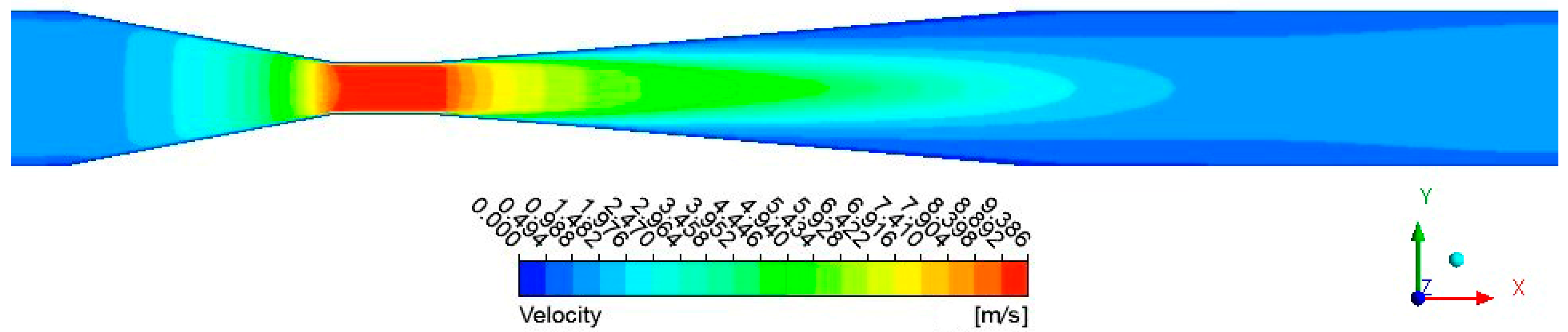
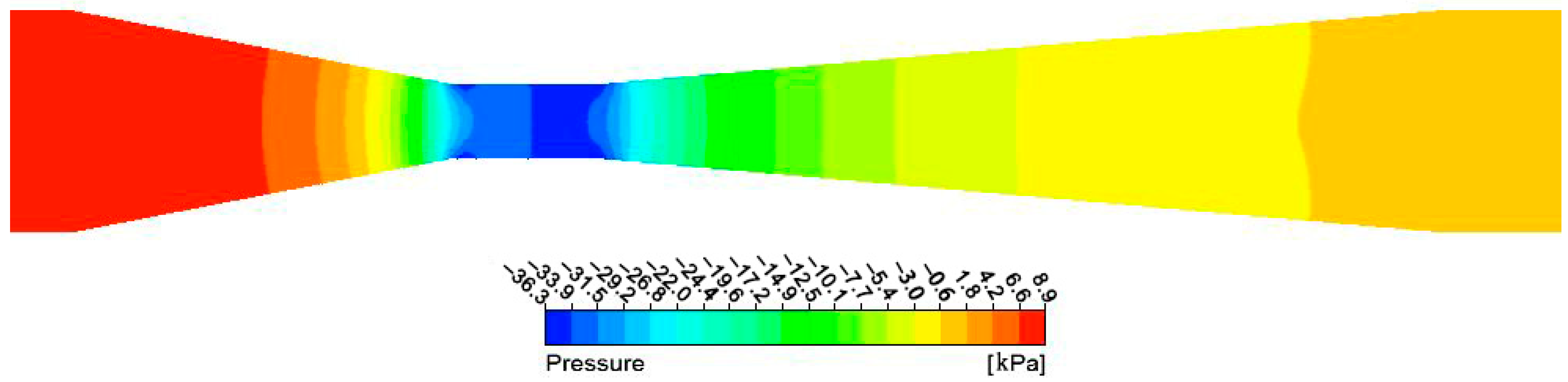
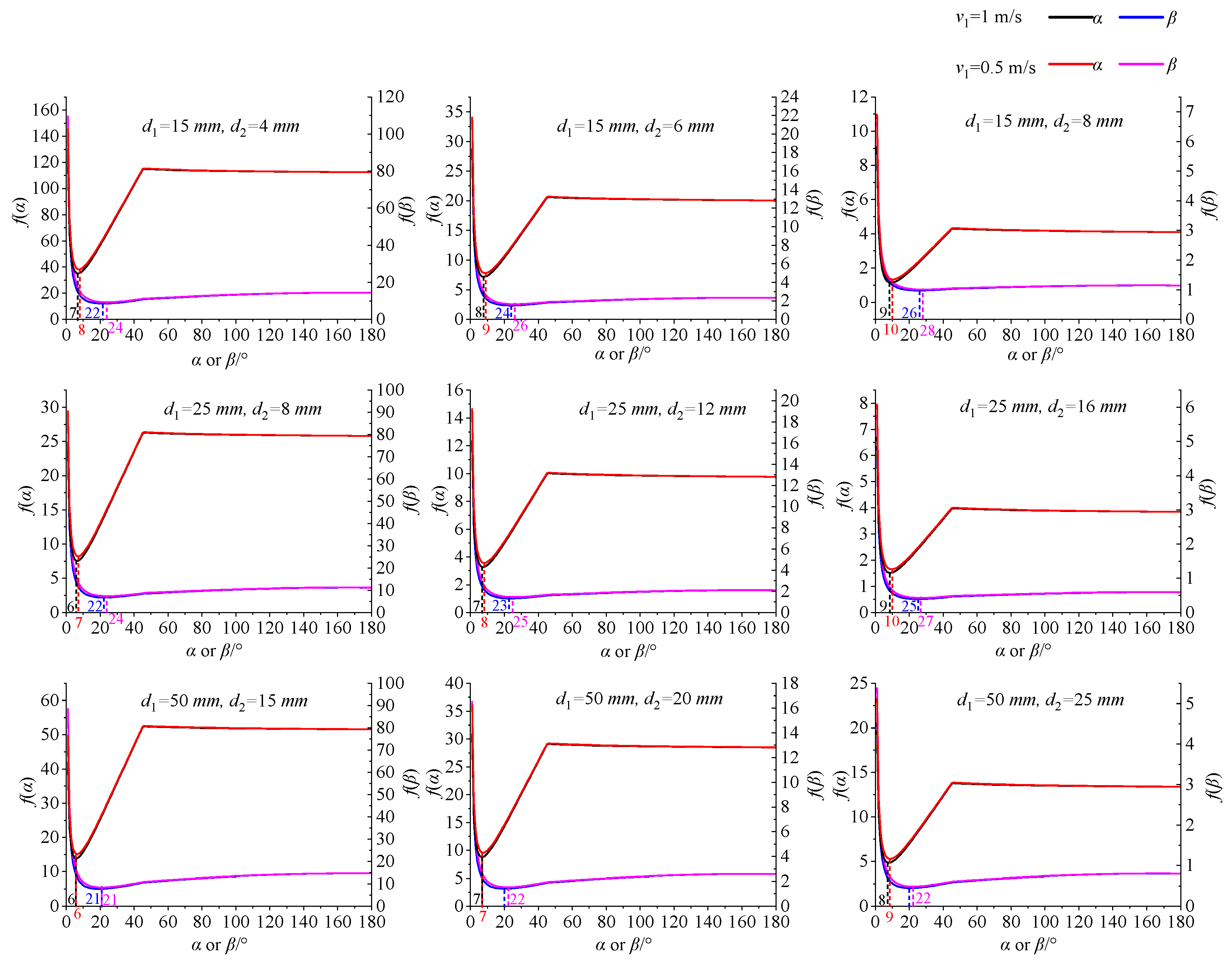
| Author | Specific Operating Conditions | Optimal Structural Parameters of the Venturi Fertilizer Applicator |
|---|---|---|
| Huang et al. [12] | A 3-factor 3-level full factor experiment | Throat diameter of 8 mm, Slot diameter of 18.5 mm, Throat length of 14 mm |
| Wang et al. [13] | Inlet diameter of 14 mm, Throat diameter of 15 mm, Inlet pressure of 0.3 MPa, Outlet pressure of 0.1 MPa | Contraction angle of 20–30°, Diffusion angle of 8–10°, Throat length of 40–50 mm, Ratio of throat diameter to nozzle diameter of 1.5–1.66 |
| Zhang et al. [14] | An orthogonal test of six factors and five levels | Convergence angle of 24°, Throat contraction ratio of 0.2, Throat length-diameter ratio of 2.0, Expanding angle of 6° |
| Factor | Level |
|---|---|
| Reducing angle (°) | 10, 20, 30, 40, 50 |
| Expanding angle (°) | 10, 20, 30, 40, 50 |
| Inlet diameter (mm) | 15, 20, 25, 30, 50 |
| Throat diameter (mm) | 5, 6, 7, 8, 9 |
| Inlet flow velocity (m/s) | 1, 1.2, 1.4, 1.6, 1.8 |
| Inlet Flow (m3/h) | Outlet Pressure (kPa) | Inlet Pressure | ||||
|---|---|---|---|---|---|---|
| Experiment (kPa) | Simulation (kPa) | Deviation | ||||
| Rs = 0.3 | Rs = 0.4 | Rs = 0.5 | ||||
| 1 | 0 | 19.8 ± 0.5 | 20.7 | 20.4 | 20.2 | 2.02%~4.55% |
| 1 | 50 | 67.2 ± 0.6 | 70.7 | 70.4 | 70.2 | 4.46%~5.21% |
| 1 | 100 | 115.5 ± 0.5 | 120.7 | 120.4 | 120.2 | 4.06%~4.50% |
| 1 | 150 | 162.4 ± 0.2 | 170.7 | 170.4 | 170.2 | 4.80%~5.11% |
| Velocity (m/s) | Simulation Loss (m) | Calculation Loss (m) | Deviation (%) |
|---|---|---|---|
| 1 | 0.912 | 1.602 | 43.07 |
| 1.2 | 1.282 | 2.287 | 62.73 |
| 1.4 | 1.707 | 3.092 | 86.45 |
| 1.6 | 2.188 | 4.015 | 114.04 |
| 1.8 | 2.724 | 5.056 | 145.57 |
| α (°) | β (°) | d1 (mm) | d2 (mm) | v1 (m/s) | hs1 (m) | h1 (m) | hs2 (m) | h2 (m) | hs3 (m) | h3 (m) | hs (m) | h1–3 (m) | δ (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 10 | 15 | 5 | 1 | 0.33 | 0.34 | 0.21 | 0.22 | 0.52 | 0.53 | 1.06 | 1.09 | 2.26 |
| 20 | 20 | 15 | 6 | 1.2 | 0.18 | 0.17 | 0.11 | 0.12 | 0.49 | 0.49 | 0.78 | 0.78 | 0.00 |
| 30 | 30 | 15 | 7 | 1.4 | 0.12 | 0.12 | 0.09 | 0.08 | 0.43 | 0.43 | 0.63 | 0.63 | 0.00 |
| 40 | 40 | 15 | 8 | 1.6 | 0.07 | 0.09 | 0.04 | 0.05 | 0.35 | 0.36 | 0.46 | 0.50 | 8.68 |
| 50 | 50 | 15 | 9 | 1.8 | 0.07 | 0.07 | 0.04 | 0.04 | 0.24 | 0.25 | 0.35 | 0.36 | 2.71 |
| 20 | 30 | 20 | 5 | 1.6 | 1.85 | 1.85 | 1.36 | 1.34 | 9.80 | 9.78 | 13.03 | 12.97 | 0.49 |
| 30 | 40 | 20 | 6 | 1.8 | 1.18 | 1.21 | 0.65 | 0.69 | 7.18 | 7.22 | 9.02 | 9.13 | 1.19 |
| 40 | 50 | 20 | 7 | 1 | 0.23 | 0.23 | 0.12 | 0.12 | 1.24 | 1.25 | 1.59 | 1.60 | 0.81 |
| 50 | 10 | 20 | 8 | 1.2 | 0.22 | 0.21 | 0.10 | 0.09 | 0.24 | 0.24 | 0.55 | 0.53 | 3.24 |
| 10 | 20 | 20 | 9 | 1.4 | 0.17 | 0.18 | 0.06 | 0.07 | 0.40 | 0.42 | 0.63 | 0.67 | 6.44 |
| 30 | 50 | 25 | 5 | 1.2 | 2.83 | 2.79 | 1.80 | 1.77 | 20.28 | 20.18 | 24.92 | 24.75 | 0.71 |
| 40 | 10 | 25 | 6 | 1.4 | 1.93 | 2.09 | 0.93 | 0.98 | 2.85 | 3.07 | 5.71 | 6.13 | 7.35 |
| 50 | 20 | 25 | 7 | 1.6 | 1.62 | 1.61 | 0.66 | 0.59 | 4.05 | 3.92 | 6.33 | 6.13 | 3.16 |
| 10 | 30 | 25 | 8 | 1.8 | 1.09 | 1.03 | 0.45 | 0.39 | 4.62 | 4.51 | 6.16 | 5.93 | 3.80 |
| 20 | 40 | 25 | 9 | 1 | 0.14 | 0.17 | 0.08 | 0.08 | 0.96 | 1.01 | 1.18 | 1.26 | 7.48 |
| 40 | 20 | 30 | 5 | 1.8 | 14.64 | 14.78 | 6.66 | 6.82 | 42.13 | 43.95 | 63.43 | 65.55 | 3.35 |
| 50 | 30 | 30 | 6 | 1 | 2.39 | 2.51 | 0.96 | 1.03 | 8.88 | 9.40 | 12.23 | 12.93 | 5.74 |
| 10 | 40 | 30 | 7 | 1.2 | 1.37 | 1.63 | 0.59 | 0.68 | 9.54 | 9.99 | 11.50 | 12.30 | 6.90 |
| 20 | 50 | 30 | 8 | 1.4 | 1.04 | 1.06 | 0.41 | 0.47 | 7.66 | 8.26 | 9.11 | 9.79 | 7.52 |
| 30 | 10 | 30 | 9 | 1.6 | 0.87 | 0.94 | 0.34 | 0.34 | 1.46 | 1.58 | 2.67 | 2.86 | 7.09 |
| 50 | 40 | 50 | 5 | 1.4 | 73.55 | 77.7 | 23.22 | 26.27 | 382.35 | 409.59 | 479.12 | 513.56 | 7.19 |
| 10 | 50 | 50 | 6 | 1.6 | 25.74 | 31.94 | 12.65 | 13.96 | 286.13 | 299.18 | 324.52 | 345.08 | 6.33 |
| 20 | 10 | 50 | 7 | 1.8 | 18.59 | 20.6 | 7.63 | 8.25 | 45.32 | 48.6 | 71.54 | 77.44 | 8.25 |
| 30 | 20 | 50 | 8 | 1 | 4.25 | 4.56 | 1.44 | 1.56 | 15.34 | 16.23 | 21.03 | 22.36 | 6.33 |
| 40 | 30 | 50 | 9 | 1.2 | 4.63 | 4.80 | 1.16 | 1.23 | 20.44 | 20.97 | 26.23 | 27.00 | 2.95 |
| α (°) | β (°) | d1 (mm) | d2 (mm) | v1 (m/s) | hs (m) | h1–3 (m) | Deviation (%) |
|---|---|---|---|---|---|---|---|
| 60 | 180 | 15 | 10 | 1 | 0.13 | 0.12 | 6.71 |
| 80 | 160 | 20 | 11 | 2 | 1.62 | 1.54 | 5.13 |
| 90 | 140 | 25 | 12 | 2.2 | 3.96 | 3.69 | 6.75 |
| 100 | 120 | 25 | 13 | 2.4 | 2.81 | 2.73 | 3.00 |
| 120 | 100 | 30 | 14 | 2.6 | 5.57 | 5.12 | 8.11 |
| 140 | 90 | 30 | 15 | 2.4 | 2.99 | 2.92 | 2.34 |
| 160 | 80 | 50 | 16 | 2 | 15.77 | 15.44 | 2.06 |
| 180 | 60 | 50 | 17 | 1.8 | 8.21 | 7.90 | 3.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, Y.; Gao, J.; Tang, P.; Huang, F. Structural Optimization of the Venturi Fertilizer Applicator Using Head Loss Calculation Methods. Fluids 2025, 10, 87. https://doi.org/10.3390/fluids10040087
Zhang Z, Li Y, Gao J, Tang P, Huang F. Structural Optimization of the Venturi Fertilizer Applicator Using Head Loss Calculation Methods. Fluids. 2025; 10(4):87. https://doi.org/10.3390/fluids10040087
Chicago/Turabian StyleZhang, Zhiyang, Yang Li, Juling Gao, Pan Tang, and Feng Huang. 2025. "Structural Optimization of the Venturi Fertilizer Applicator Using Head Loss Calculation Methods" Fluids 10, no. 4: 87. https://doi.org/10.3390/fluids10040087
APA StyleZhang, Z., Li, Y., Gao, J., Tang, P., & Huang, F. (2025). Structural Optimization of the Venturi Fertilizer Applicator Using Head Loss Calculation Methods. Fluids, 10(4), 87. https://doi.org/10.3390/fluids10040087





