Hydrodynamic Resistance Analysis of Large Biomimetic Yellow Croaker Model: Effects of Shape, Body Length, and Material Based on CFD
Abstract
1. Introduction
2. Materials and Methods
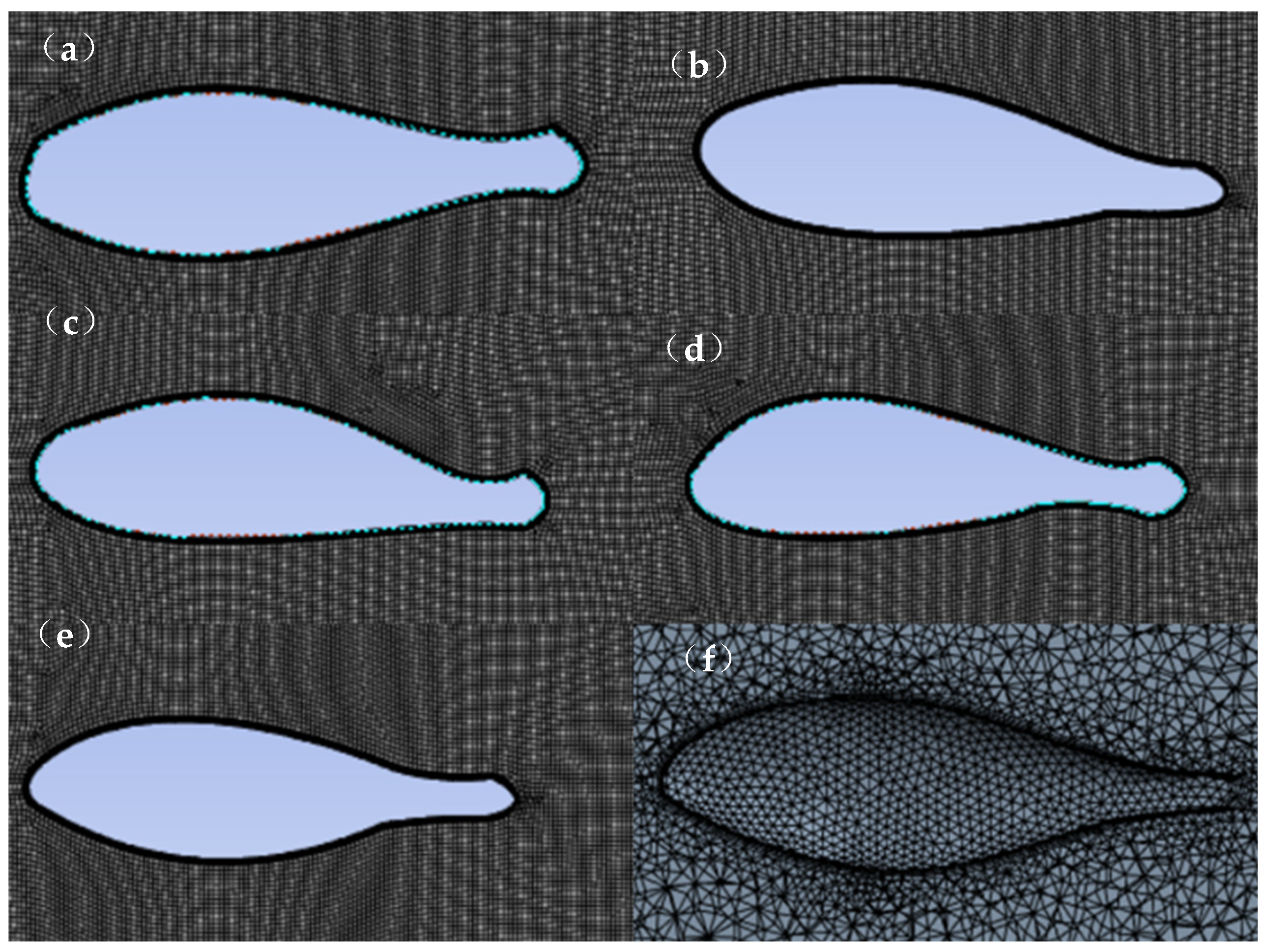
2.1. Establishment of the Large Yellow Croaker Model
2.1.1. Model Data Processing
2.1.2. Establishment of the Large Yellow Croaker Model
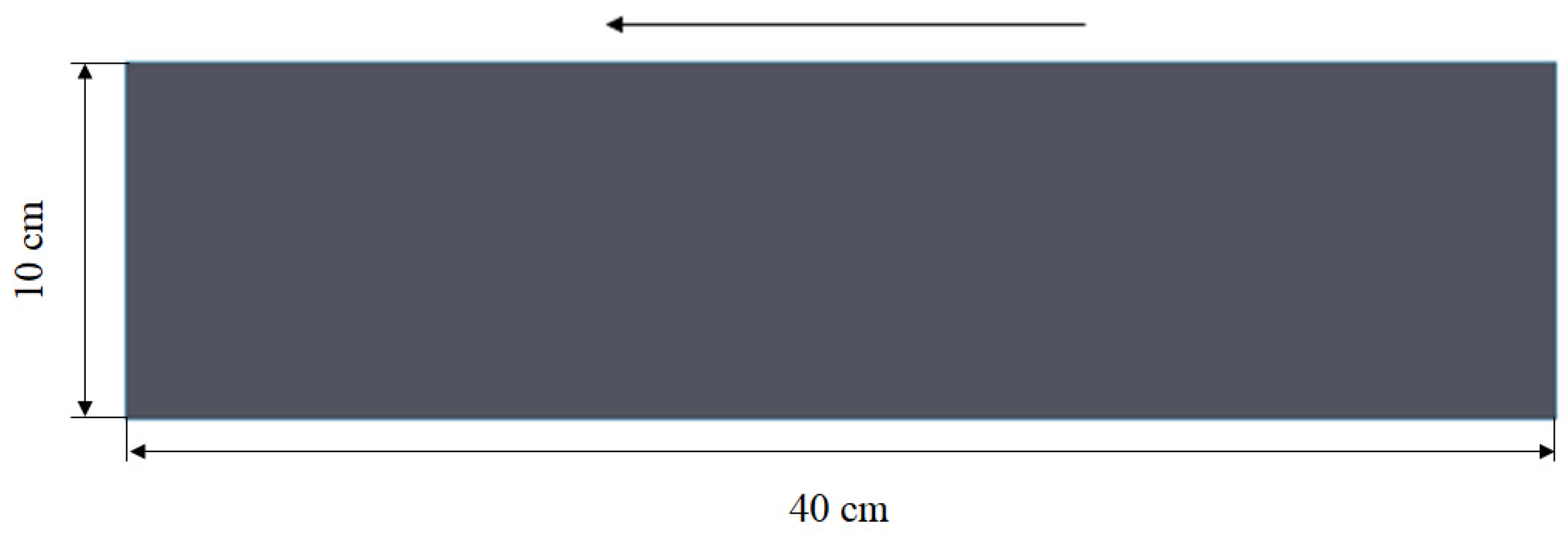
2.2. Creation of Fluid Domains and Meshes
2.2.1. Creation of Fluid Domains
2.2.2. Creation of Fluid Meshes
2.3. Test Methods
2.4. Test Procedure
2.5. Method Validation
3. Results
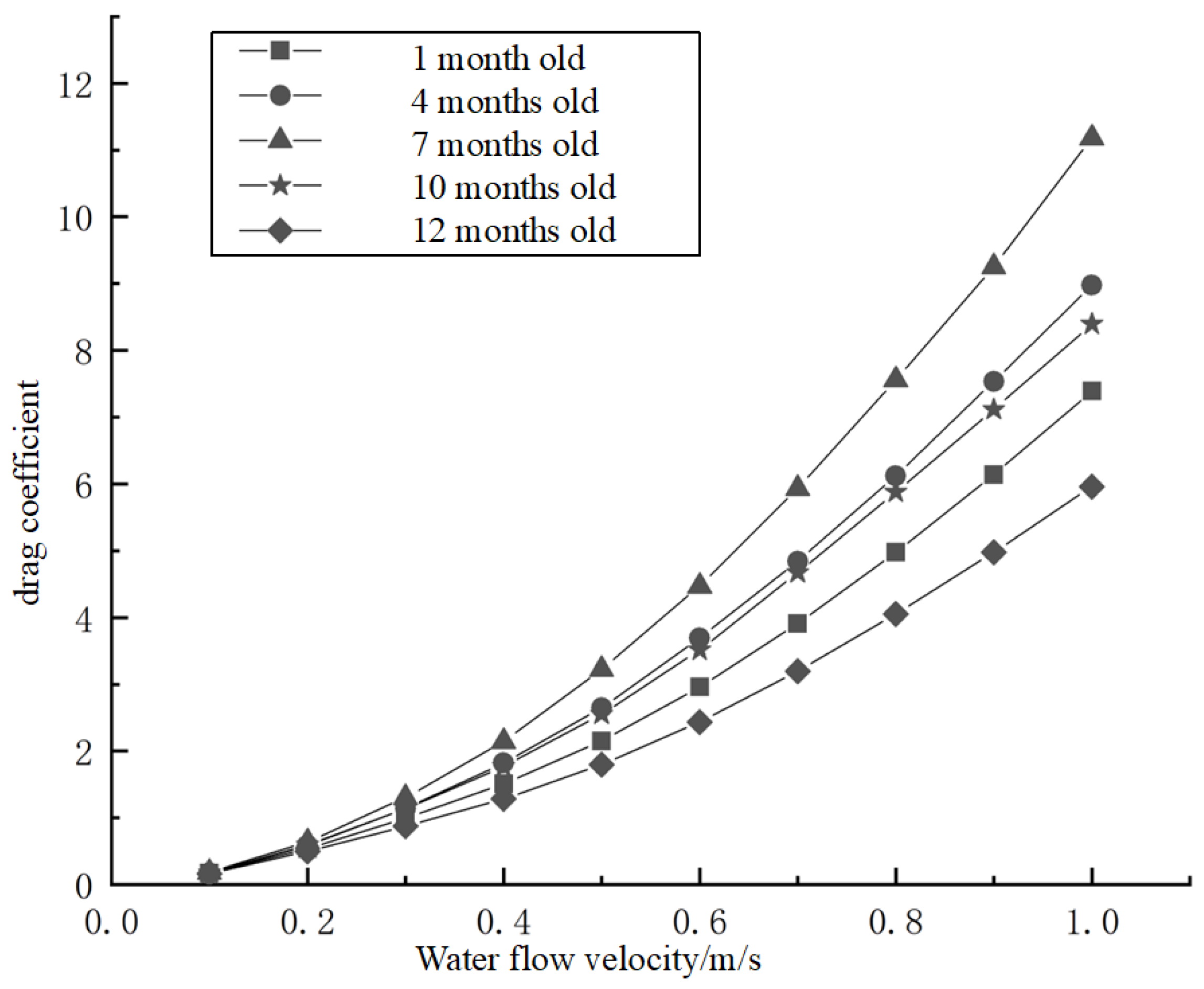
3.1. Differences in Water Resistance in Large Yellow Croaker Models at Different Ages
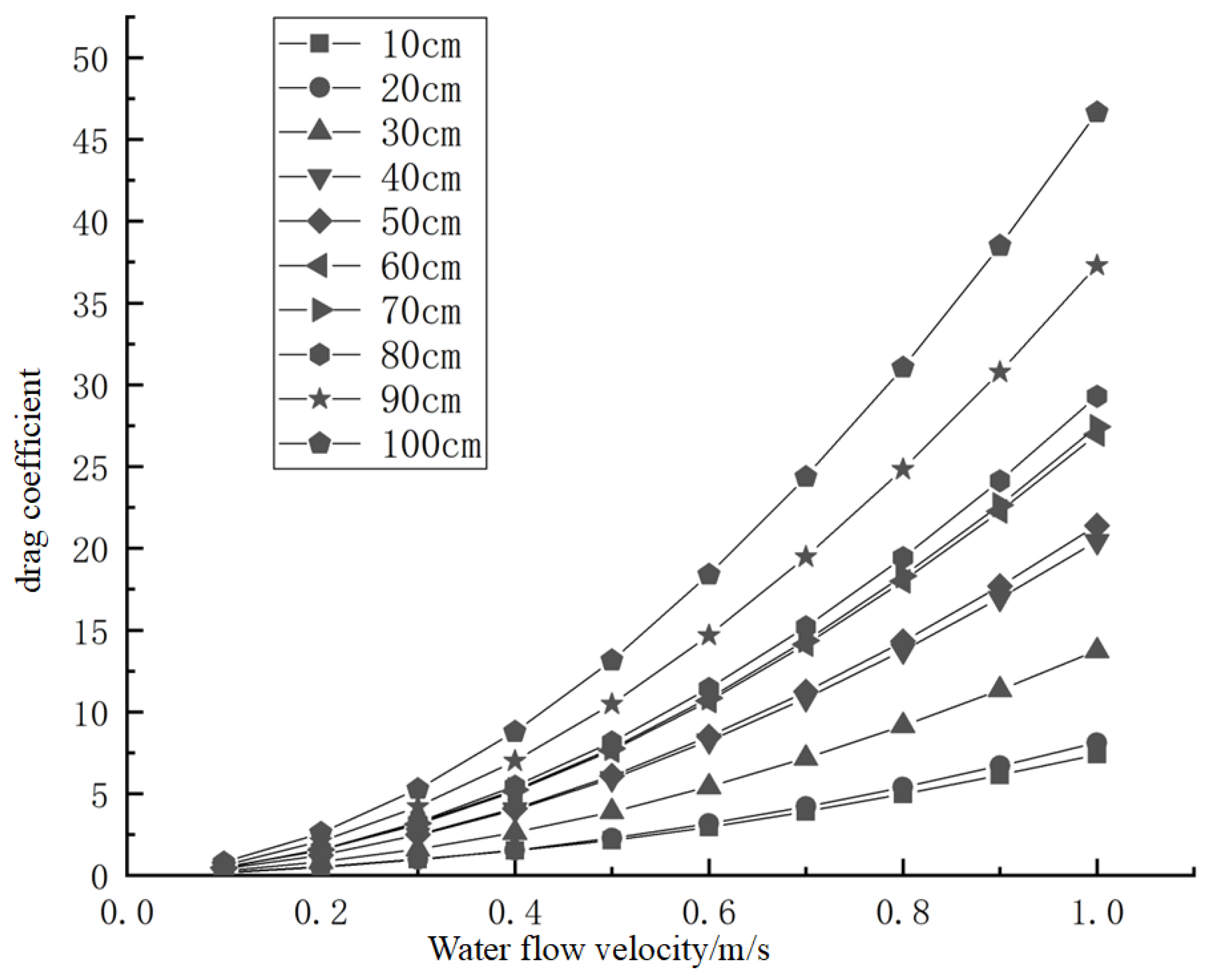
3.2. Differences in Water Resistance in Large Yellow Croaker Models at Different Body Lengths
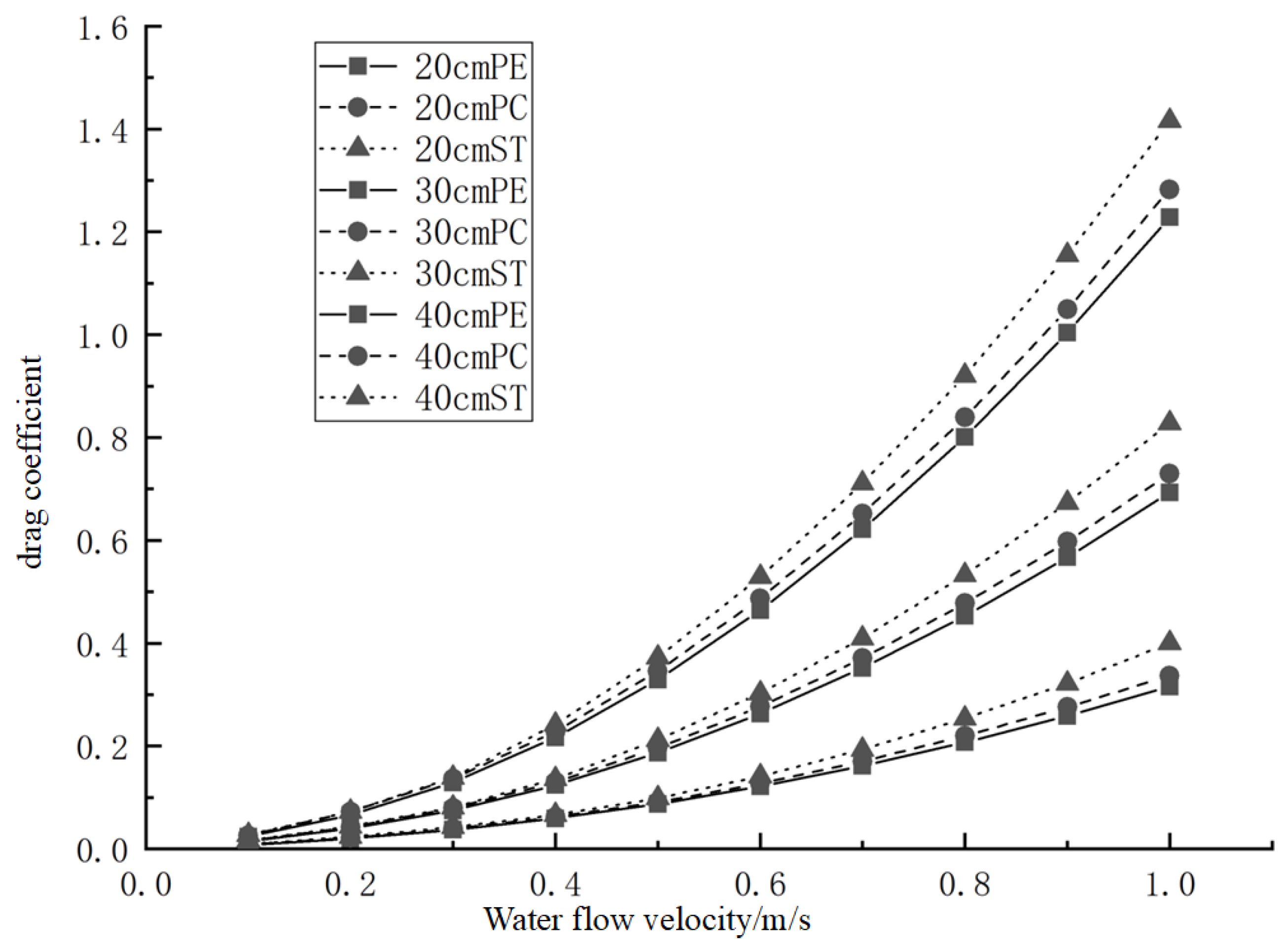
3.3. Differences in Water Resistance in Large Yellow Croaker Models of Different Materials
4. Discussion
4.1. Analysis of the Difference in Water Resistance Between Large Yellow Croaker Models of Different Ages
4.2. Analysis of the Difference in Water Resistance Between Large Yellow Croaker Models of Different Body Lengths
4.3. Analysis of the Difference in Water Resistance Between Large Yellow Croaker Models of Different Materials
5. Conclusions
- (1)
- Under the same size ratio, for each of the large yellow croaker models at different ages, as the water velocity increases, the total water resistance gradually increases and the rate of increase in water resistance gradually decreases.
- (2)
- Under different size ratios, the water resistance, rate of increase in water resistance, and drag coefficient increase as the body length ratio increases.
- (3)
- For the skin material of the large yellow croaker model, the water resistance of the PE material is better than those of the PC and ST materials. At low water velocities, the influence of the different skin materials on the water resistance, range of increase in the water resistance, and drag coefficient is significant; at high water velocities, this influence gradually decreases.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| PE | Polyethylene |
| PC | Polycarbonate |
| ST | Structural steel |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
References
- Lu, Q.; Fang, Z.; Chen, X.J. Evaluation of Sustainable Utilization of Fishery Resources in the Indian Ocean Based on Grey Relational Analysis. J. Guangdong Ocean Univ. 2021, 41, 61–66. [Google Scholar]
- Li, J.L.; Shen, M.H.; Ma, R.F.; Yang, H.S.; Chen, Y.N.; Sun, C.Z.; Liu, M.; Han, X.Q.; Hu, Z.D.; Ma, X.G. Marine resource economy and strategy under the background of marine ecological civilization construction. J. Nat. Resour. 2022, 37, 829–849. [Google Scholar] [CrossRef]
- Shi, K.W. The current situation and prospects of the development of ocean science popularization in China under the strategy of building a maritime power. Public Commun. Sci. Technol. 2024, 16, 35–37. [Google Scholar]
- Fang, N.; Huang, Z.; Zhao, T.Q.; Wang, S.H.; Chen, H.Q.; Han, G.D.; Sun, Y.Q. Dynamic Characteristic of Anti-swing Hook on Quad-rotor of Marine Crane. J. Guangdong Ocean Univ. 2024, 44, 129–138. [Google Scholar]
- Wang, Y.W.; Wang, Z.L.; Li, J. Research progress and development trend of biomimetic robotic fish. Mach. Des. Res. 2011, 27, 22–25. [Google Scholar]
- Sun, W.; Liu, S.P.; Wu, G.; Zhou, Y.X.; Ren, X.Z. Research progress and prospect of fish swimming mechanism: A review. J. Dalian Fish. Univ. 2024, 39, 698–707. [Google Scholar]
- Liu, J.K.; Chen, Z.L.; Chen, W.S.; Wang, L. A new type of underwater turbine imitating fish fin for underwater robot. Robot 2000, 22, 427–432. [Google Scholar]
- de Sousa, J.V.N.; De Macêdo, A.R.L.; de Amorim Junior, W.F.; De Lima, A.G.B. Numerical Analysis of Turbulent Fluid Flow and Drag Coefficient for Optimizing the AUV Hull Design. Open J. Fluid Dyn. 2014, 4, 263–277. [Google Scholar] [CrossRef]
- Kramer, M.O. Boundary Layer Stabilization by Distributed Damping. Nav. Eng. J. 2010, 72, 25–34. [Google Scholar]
- Divsalar, K. Improving the hydrodynamic performance of the SUBOFF bare hull model: A CFD approach. Acta Mech. Sin. 2019, 36, 44–56. [Google Scholar] [CrossRef]
- Yan, C. Computational Fluid Dynamics Methods and Applications; Beihang University Press: Beijing, China, 2006. [Google Scholar]
- Mao, H.F.; He, Y.L.; Yuan, J.P.; Pan, X.X.; Jia, B.Z. Hydrodynamic Coefficients of a Horizontal Circular Cylinder near Free Surface under Wave Action. J. Guangdong Ocean Univ. 2020, 40, 109–115. [Google Scholar]
- Huang, X.S.; Liu, F.; Sun, W.J.; Kong, X.H.; Liu, B.L.; Chen, X.J. Numerical simulation of hydrodynamics of bionic squid in pitching posture. J. Shanghai Ocean Univ. 2021, 30, 884–892. [Google Scholar]
- Yang, J.L.; Deng, Z.P.; Hou, L.; Shang, Y.L. Propulsive Performance of High Rotation Speed Paddlewheels with Different Numbers of Paddles. J. Guangdong Ocean Univ. 2024, 44, 136–142. [Google Scholar]
- Zhang, Z.; Wang, Q.; Zhang, S. Review of Computational Fluid Dynamics Analysis in Biomimetic Applications for Underwater Vehicles. Biomimetics 2024, 9, 79. [Google Scholar] [CrossRef]
- Rostamzadeh-Renani, M.; Rostamzadeh-Renani, R.; Baghoolizadeh, M.; Azarkhavarani, N.K. The effect of vortex generators on the hydrodynamic performance of a submarine at a high angle of attack using a multi-objective optimization and computational fluid dynamics. Ocean. Eng. 2023, 282, 114932. [Google Scholar] [CrossRef]
- Rostamzadeh-Renani, M.; Baghoolizadeh, M.; Sajadi, S.M.; Rostamzadeh-Renani, R.; Azarkhavarani, N.K.; Salahshour, S.; Toghraie, D. A multi-objective and CFD based optimization of roof-flap geometry and position for simultaneous drag and lift reduction. Propuls. Power Res. 2024, 13, 26–45. [Google Scholar] [CrossRef]
- Bahadir Olcay, A.; Tabatabaei Malazi, M.; Okbaz, A.; Heperkan, H.; Fırat, E.; Ozbolat, V.; Gokhan Gokcen, M.; Sahin, B. Experimental and numerical investigation of a longfin inshore squid’s flow characteristics. J. Appl. Fluid Mech. 2017, 10, 21–30. [Google Scholar]
- Barrett, D.S.; Triantafyllou, M.S.; Yue, D.K.P.; Grosenbaugh, M.A.; Wolfgang, M. Drag Reduction in Fish-Like Locomotion. J. Fluid Mech. 1999, 392, 183–212. [Google Scholar] [CrossRef]
- Xiao, H.P.; Fang, Z.F.; Zhu, C.; He, K.D.; Yang, W.H.; Ding, H.Z. Structural Drag Characteristic and Application Research of Underwater Streamlined Body. J. China Three Gorges Univ. (Nat. Sci.) 2013, 35, 92–96. [Google Scholar]
- Liu, J.X.; He, B.; Yan, T.H. Study on Hydrodynamic of Flounder Dual-Drive Bionic Robotic Fish. Ship Eng. 2023, 45, 84–90. [Google Scholar]
- Kaidong, M.; Ruirong, Z.; Xin, G.; Mingyang, X.; Yuxue, P. Shape design and flow field characteristics of a robotic fish imitating the head of a hammerhead. Chin. J. Theor. Appl. Mech. 2021, 53, 3389–3398. [Google Scholar]
- Tian, X.J.; Liu, Y.X.; Liu, G.J. Tuna 3D-Modeling and Stress Calculation in Flow Field. Period. Ocean Univ. China 2019, 49, 139–144. [Google Scholar]
- Zhou, P.X.; Hu, Q.S. Carp 3D-modeling and stress calculation in flow field. J. Shanghai Ocean Univ. 2013, 22, 855–861. [Google Scholar]
- Chen, H.K. Mechanism Research on the Swimming and Maneuvering of Robot Fish; University of Science and Technology of China: Hefei, China, 2006. [Google Scholar]
- Han, Z.Z.; Wang, J.; Lan, X.P. Fluent: Fluid Engineering Simulation Calculation Examples and Applications; Beijing Institute of Technology Press: Beijing, China, 2004. [Google Scholar]
- Wang, F.X. Computational Fluid Dynamics Analysis: Principles and Applications of CFD Software; Qinghua University Press: Beijing, China, 2004. [Google Scholar]
- Candelier, F.; Boyer, F.; Leroyer, A. Three-dimensional extension of Lighthill’s large-amplitude elongated-body theory of fish locomotion. J. Fluid Mech. 2011, 674, 196–226. [Google Scholar] [CrossRef]
- Liu, Q.Z. Research on Hydrodynamics of Tidal Turbine Bionic Blades; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Geng, W.B.; Wei, Y.K.; Hong, S.F.; Huang, J.J. Shape Design and Numerical Analysis of Flow Field Resistance of Bionic Robot Fish. Digit. Ocean Underw. Warf. 2024, 7, 318–325. [Google Scholar]
- Feng, Y.K.; Liu, H.X.; Su, Y.Y.; Su, Y.M. Numerical simulation on hydrodynamic preformance of fast-start for bionic robotic fish. J. Huazhong Univ. Sci. Technol. 2020, 48, 33–39. [Google Scholar]
- Li, G.H.; Feng, N.; Liu, G.J. Flat Drag Reduction Method Based on Biomimetic Fish-body Structure. J. Unmanned Undersea Syst. 2021, 029, 80–87. [Google Scholar]
- He, J.H.; Zhang, Y.H.; Dong, S.W. Design and Thrust Analysis of Bionic Caudal Fin with Variable Area. Light Ind. Mach. 2022, 40, 8–16. [Google Scholar]
- Ge, F.F.; Shen, C.; Xie, O. Research on hydrodynamic characteristics of crescent-shaped tail fins based on bidirectional fluid-structure coupling simulation. J. Suzhou Univ. Sci. Technol. Eng. Technol. Ed. 2023, 36, 74–80. [Google Scholar]
- Zhao, D.S. Design and Realization of Tuna-like Software Robot; Shenyang University of Technology: Shenyang, China, 2021. [Google Scholar]
- Xie, O.; Sun, Z.G.; Shen, C.; Ge, F.F. The Underwater Dynamic Targets Coupled Hydrodynamic Field Characteristics of Flexible Motion Lateral Line Sensing. J. Detect. Control 2024, 46, 131–137. [Google Scholar]

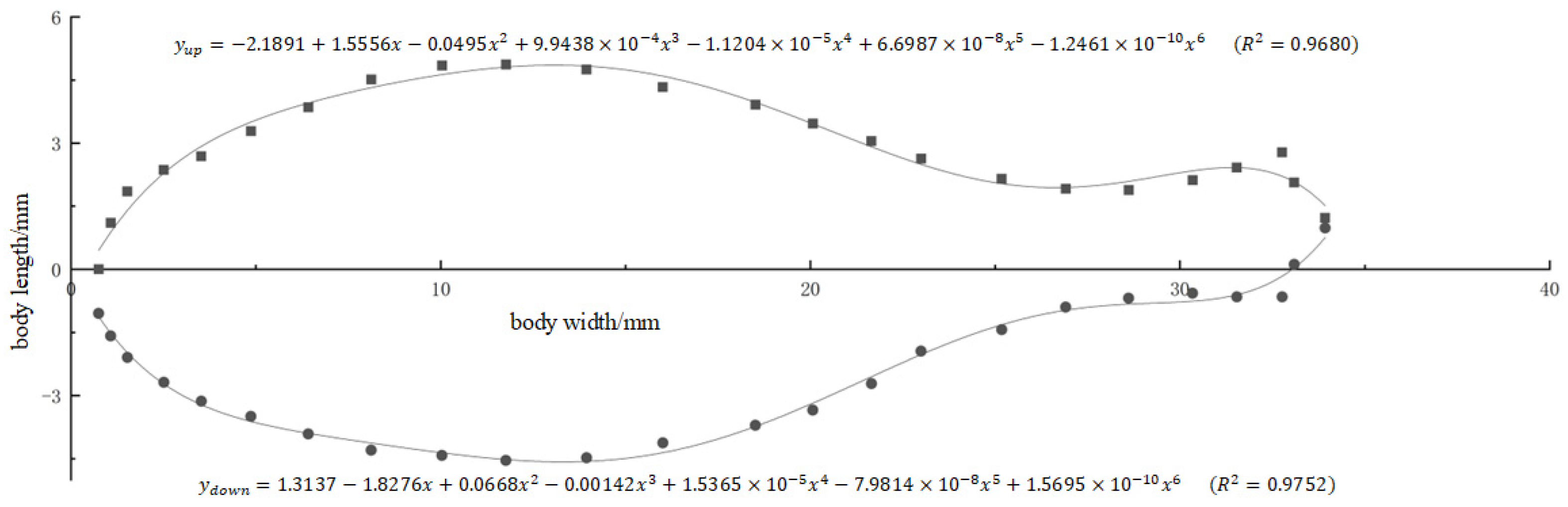
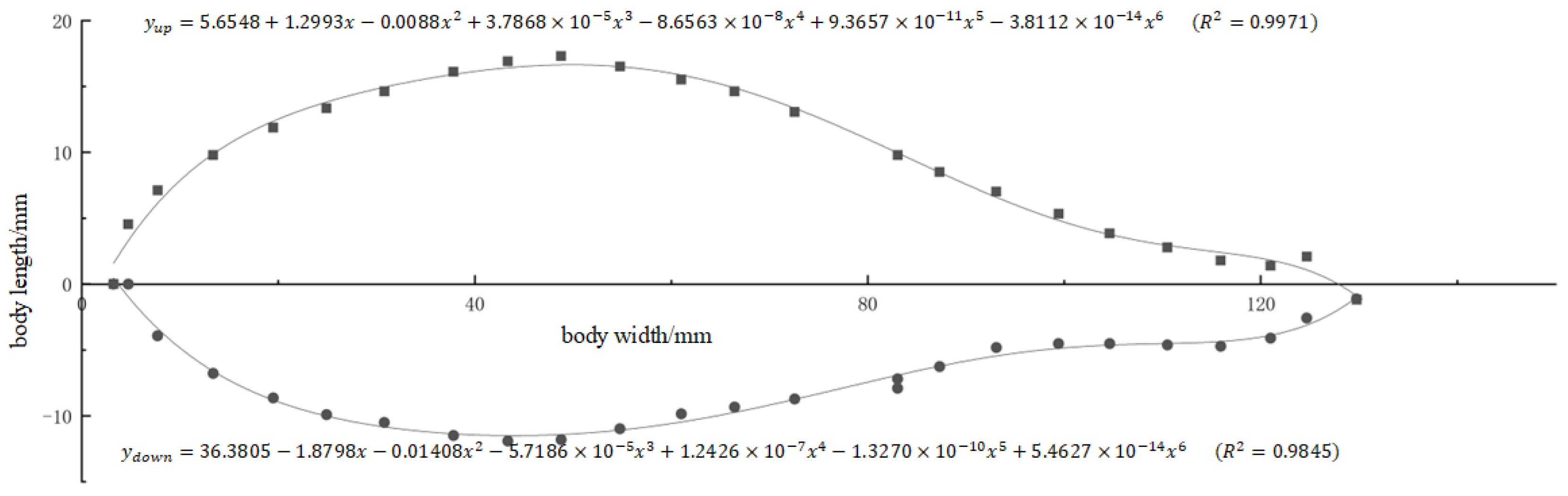
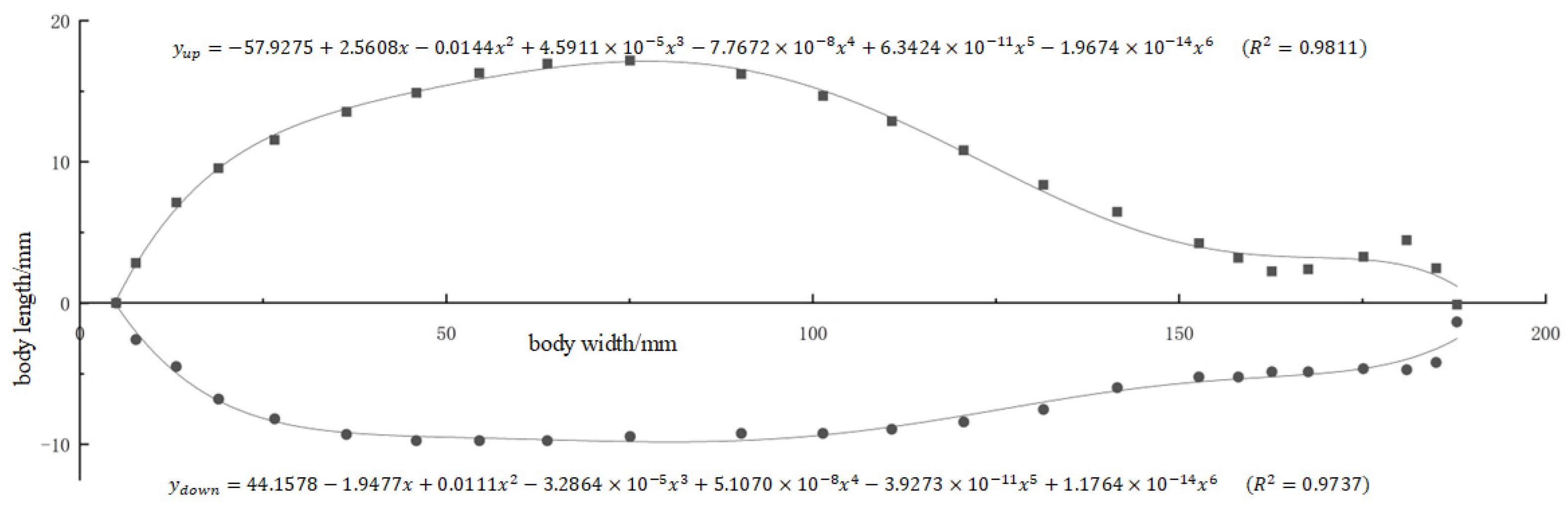
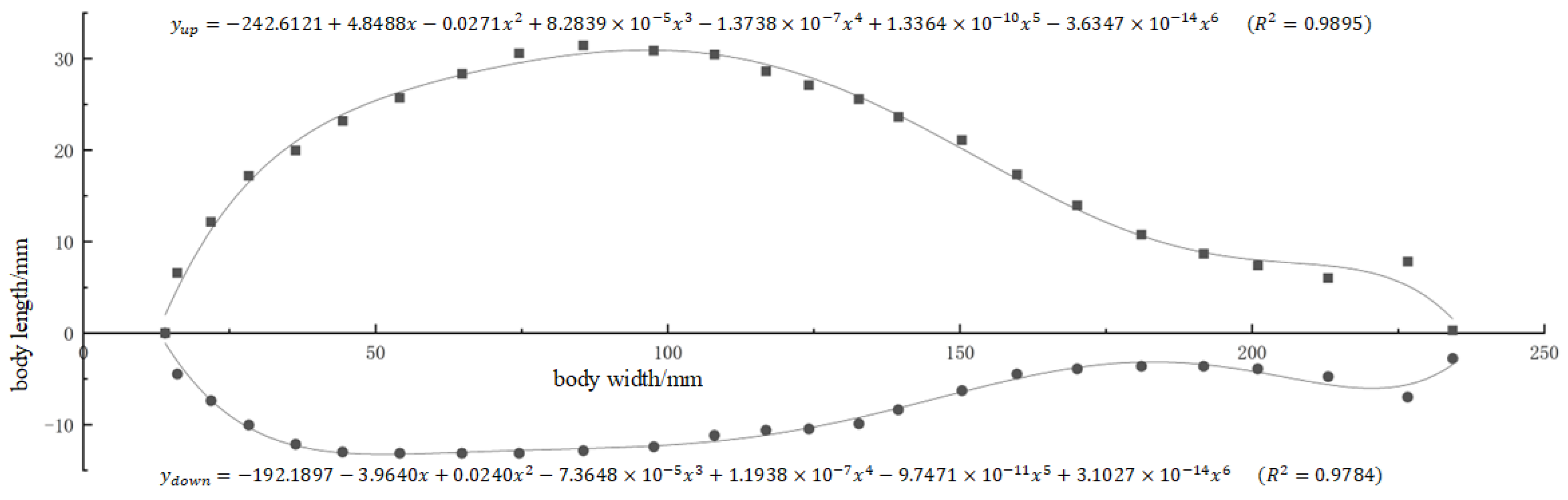







| Age of Large Yellow Croaker (Months) | Body Length (mm) | Body Width (mm) |
|---|---|---|
| 1 | 34.8 | 9 |
| 4 | 129.7 | 25.4 |
| 7 | 181.5 | 37 |
| 10 | 228.5 | 48.8 |
| 12 | 290 | 72.8 |
| Two-Dimensional | Three-Dimensional | ||
|---|---|---|---|
| Number of Grids | Relative Error/% | Number of Grids | Relative Error/% |
| 2,107,891 | 1.779 | 3,098,322 | 1.697 |
| 3,298,771 | 1.311 | 4,289,132 | 1.233 |
| 4,683,982 | 0.971 | 5,447,655 | 0.879 |
| Attack Angle/° | Drag Coefficient | |
|---|---|---|
| Sink Experiment | Simulation Test | |
| 0 | 0.0163 | 0.01467 |
| 3 | 0.0346 | 0.02975 |
| 6 | 0.0565 | 0.04955 |
| 9 | 0.0814 | 0.07505 |
| 12 | 0.0983 | 0.08818 |
| 15 | 0.2262 | 0.19880 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Lu, K.; Qian, W. Hydrodynamic Resistance Analysis of Large Biomimetic Yellow Croaker Model: Effects of Shape, Body Length, and Material Based on CFD. Fluids 2025, 10, 107. https://doi.org/10.3390/fluids10050107
Zhao D, Lu K, Qian W. Hydrodynamic Resistance Analysis of Large Biomimetic Yellow Croaker Model: Effects of Shape, Body Length, and Material Based on CFD. Fluids. 2025; 10(5):107. https://doi.org/10.3390/fluids10050107
Chicago/Turabian StyleZhao, Donglei, Kexiang Lu, and Weiguo Qian. 2025. "Hydrodynamic Resistance Analysis of Large Biomimetic Yellow Croaker Model: Effects of Shape, Body Length, and Material Based on CFD" Fluids 10, no. 5: 107. https://doi.org/10.3390/fluids10050107
APA StyleZhao, D., Lu, K., & Qian, W. (2025). Hydrodynamic Resistance Analysis of Large Biomimetic Yellow Croaker Model: Effects of Shape, Body Length, and Material Based on CFD. Fluids, 10(5), 107. https://doi.org/10.3390/fluids10050107





