Closure Relations for Fluxes of Flame Surface Density and Scalar Dissipation Rate in Turbulent Premixed Flames
Abstract
:1. Introduction
2. Method of Research
2.1. Model
= 〈u〉~ − 〈c〉~〈ρu″c〉″/[ρu(1 − 〈c〉~)] + 〈ρu″c″〉(1 − 〈c〉~)/[ρu〈c〉~]
= 〈u〉~ + (1 − 2〈c〉~)〈ρu″c″〉/[ρu〈c〉~(1 − 〈c〉~)].
2.2. Direct Numerical Simulations
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Candel, S.; Veynante, D.; Lacas, F.; Maistret, E.; Darabiha, N.; Poinsot, T. Coherent flame model: Applications and recent extensions. In Advances in Combustion Modeling; Larrouturou, B.E., Ed.; World Scientific: Singapore, 1990; pp. 19–64. [Google Scholar]
- Cant, S.R.; Pope, S.B.; Bray, K.N.C. Modelling of flamelet surface-to-volume ratio in turbulent premixed combustion. Proc. Combust. Inst. 1990, 23, 809–815. [Google Scholar] [CrossRef]
- Borghi, R. Turbulent premixed combustion: Further discussions of the scales of fluctuations. Combust. Flame 1990, 80, 304–312. [Google Scholar] [CrossRef]
- Veynante, D.; Vervisch, L. Turbulent combustion modeling. Prog. Energy Combust. Sci. 2002, 28, 193–266. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; Edwards: Philadelphia, PA, USA, 2005. [Google Scholar]
- Chakraborty, N.; Champion, M.; Mura, A.; Swaminathan, N. Scalar-dissipation-rate approach. In Turbulent Premixed Flames; Swaminathan, N., Bray, K.N.C., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 76–102. [Google Scholar]
- Moss, J.B. Simultaneous measurements of concentration and velocity in an open premixed turbulent flame. Combust. Sci. Technol. 1980, 22, 119–129. [Google Scholar] [CrossRef]
- Libby, P.A.; Bray, K.N.C. Countergradient diffusion in premixed turbulent flames. AIAA J. 1981, 19, 205–213. [Google Scholar] [CrossRef]
- Bray, K.N.C. Turbulent transport in flames. Proc. R. Soc. Lond. A 1995, 451, 231–256. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chomiak, J. Effects of premixed flames on turbulence and turbulent scalar transport. Prog. Energy Combust. Sci. 2010, 36, 1–102. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N. Recent advances in understanding of thermal expansion effects in premixed turbulent flames. Annu. Rev. Fluid Mech. 2017, 49, 91–117. [Google Scholar] [CrossRef]
- Bray, K.N.C. Turbulent flows with premixed reactants. In Turbulent Reacting Flows; Libby, P.A., Williams, F.A., Eds.; Springer-Verlag: Berlin, Germany, 1980; pp. 115–183. [Google Scholar]
- Lipatnikov, A.N. Conditionally averaged balance equations for modeling premixed turbulent combustion in flamelet regime. Combust. Flame 2008, 152, 529–547. [Google Scholar] [CrossRef]
- Yu, R.; Bai, X.-S.; Lipatnikov, A.N. A direct numerical simulation study of interface propagation in homogeneous turbulence. J. Fluid Mech. 2015, 772, 127–164. [Google Scholar] [CrossRef]
- Nishiki, S.; Hasegawa, T.; Borghi, R.; Himeno, R. Modeling of flame-generated turbulence based on direct numerical simulation databases. Proc. Combust. Inst. 2002, 29, 2017–2022. [Google Scholar] [CrossRef]
- Nishiki, S.; Hasegawa, T.; Borghi, R.; Himeno, R. Modelling of turbulent scalar flux in turbulent premixed flames based on DNS databases. Combust. Theory Model. 2006, 10, 39–55. [Google Scholar] [CrossRef]
- Im, Y.H.; Huh, K.Y.; Nishiki, S.; Hasegawa, T. Zone conditional assessment of flame-generated turbulence with DNS database of a turbulent premixed flame. Combust. Flame 2004, 137, 478–488. [Google Scholar] [CrossRef]
- Mura, A.; Tsuboi, K.; Hasegawa, T. Modelling of the correlation between velocity and reactive scalar gradients in turbulent premixed flames based on DNS data. Combust. Theory Model. 2008, 12, 671–698. [Google Scholar] [CrossRef]
- Mura, A.; Robin, V.; Champion, M.; Hasegawa, T. Small scale features of velocity and scalar fields in turbulent premixed flames. Flow Turbul. Combust. 2009, 82, 339–358. [Google Scholar] [CrossRef]
- Robin, V.; Mura, A.; Champion, M.; Hasegawa, T. Modeling of the effects of thermal expansion on scalar turbulent fluxes in turbulent premixed flames. Combust. Sci. Technol. 2010, 182, 449–464. [Google Scholar] [CrossRef]
- Robin, V.; Mura, A.; Champion, M. Direct and indirect thermal expansion effects in turbulent premixed flames. J. Fluid Mech. 2011, 689, 149–182. [Google Scholar] [CrossRef]
- Bray, K.N.C.; Champion, M.; Libby, P.A.; Swaminathan, N. Scalar dissipation and mean reaction rates in premixed turbulent combustion. Combust. Flame 2011, 158, 2017–2022. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. A direct numerical simulation study of vorticity transformation in weakly turbulent premixed flames. Phys. Fluids 2014, 26, 105104. [Google Scholar] [CrossRef] [Green Version]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T.; Chakraborty, N. DNS assessment of a simple model for evaluating velocity conditioned to unburned gas in premixed turbulent flames. Flow Turbul. Combust. 2015, 94, 513–526. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. DNS assessment of relation between mean reaction and scalar dissipation rates in the flamelet regime of premixed turbulent combustion. Combust. Theory Model. 2015, 19, 309–328. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chomiak, J.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T. Unburned mixture fingers in premixed turbulent flames. Proc. Combust. Inst. 2015, 35, 1401–1408. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N.; Chakraborty, N.; Nishiki, S.; Hasegawa, T. A transport equation for reaction rate in turbulent flows. Phys. Fluids 2016, 28, 081701. [Google Scholar] [CrossRef] [Green Version]
- Sabelnikov, V.A.; Lipatnikov, A.N.; Chakraborty, N.; Nishiki, S.; Hasegawa, T. A balance equation for the mean rate of product creation in premixed turbulent flames. Proc. Combust. Inst. 2017, 36, 1893–1901. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T. Flamelet perturbations and flame surface density transport in weakly turbulent premixed combustion. Combust. Theory Model. 2017, 21, 205–227. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Chakraborty, N.; Nishiki, S.; Hasegawa, T. A DNS study of closure relations for convection flux term in transport equation for mean reaction rate in turbulent flow. Flow Turbul. Combust. 2018, 100, 75–92. [Google Scholar] [CrossRef] [PubMed]
- Lipatnikov, A.N.; Chomiak, J.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T. A DNS study of the physical mechanisms associated with density ratio influence on turbulent burning velocity in premixed flames. Combust. Theory Model. 2018, 22, 131–155. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T. Combustion-induced local shear layers within premixed flamelets in weakly turbulent flows. Phys. Fluids 2018, 30, 085101. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T. Does flame-generated vorticity increase turbulent burning velocity? Phys. Fluids 2018, 30, 081702. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. Application of conditioned structure functions to exploring influence of premixed combustion on two-point turbulence statistics. Proc. Combust. Inst. 2019, 37, 2433–2441. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. A DNS assessment of linear relations between filtered reaction rate, flame surface density, and scalar dissipation rate in a weakly turbulent premixed flame. Combust. Theory Model. 2019, 23. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. Investigation of the influence of combustion-induced thermal expansion on two-point turbulence statistics using conditioned structure functions. J. Fluid Mech. 2019, in press. [Google Scholar]
- Veynante, D.; Trouvé, A.; Bray, K.N.C.; Mantel, T. Gradient and counter-gradient scalar transport in turbulent premixed flames. J. Fluid Mech. 1997, 332, 263–293. [Google Scholar] [CrossRef]
- Kuznetsov, V.R.; Sabelnikov, V.A. Turbulence and Combustion; Hemisphere Publishing Corporation: New York, NY, USA, 1990. [Google Scholar]
- Lipatnikov, A.N.; Chomiak, J. Molecular transport effects on turbulent flame propagation and structure. Prog. Energy Combust. Sci. 2005, 31, 1–73. [Google Scholar] [CrossRef]
- Lipatnikov, A.N. Fundamentals of Premixed Turbulent Combustion; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Venkateswaran, P.; Marshall, A.; Seitzman, J.; Lieuwen, T. Scaling turbulent flame speeds of negative Markstein length fuel blends using leading points concepts. Combust. Flame 2015, 162, 375–387. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N. Transition from pulled to pushed fronts in premixed turbulent combustion: Theoretical and numerical study. Combust. Flame 2015, 162, 2893–2903. [Google Scholar] [CrossRef]
- Kim, S.H. Leading points and heat release effects in turbulent premixed flames. Proc. Combust. Inst. 2017, 36, 2017–2024. [Google Scholar] [CrossRef]
- Dave, H.L.; Mohan, A.; Chaudhuri, S. Genesis and evolution of premixed flames in turbulence. Combust. Flame 2018, 196, 386–399. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chakraborty, N.; Sabelnikov, V.A. Transport equations for reaction rate in laminar and turbulent premixed flames characterized by non-unity Lewis number. Int. J. Hydrog. Energy 2018, 43, 21060–21069. [Google Scholar] [CrossRef]

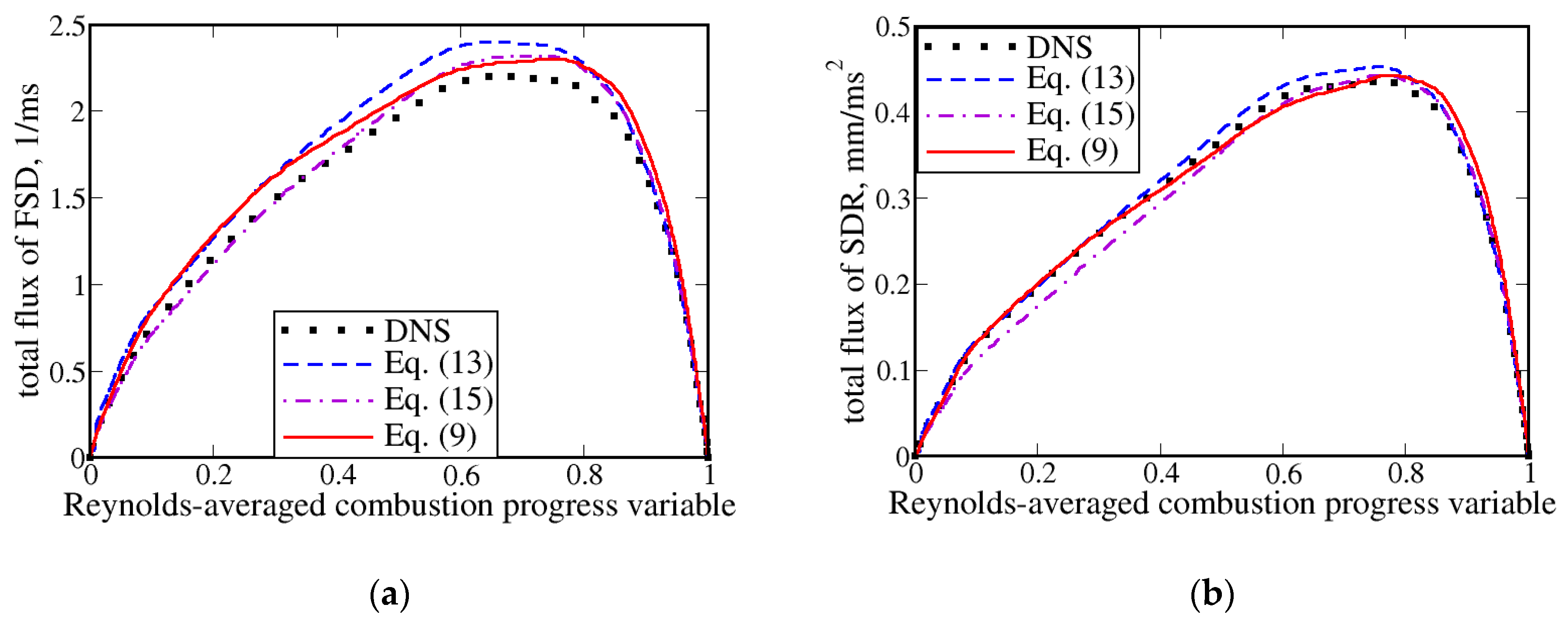
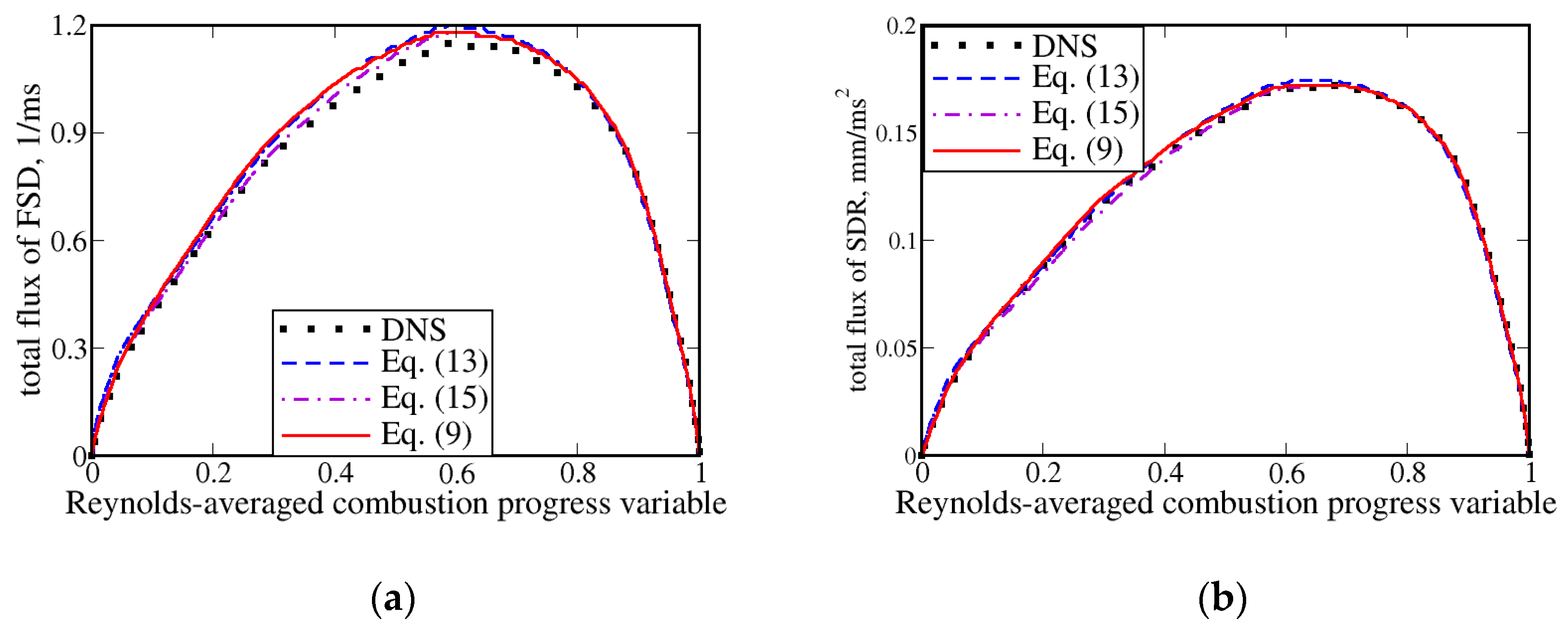

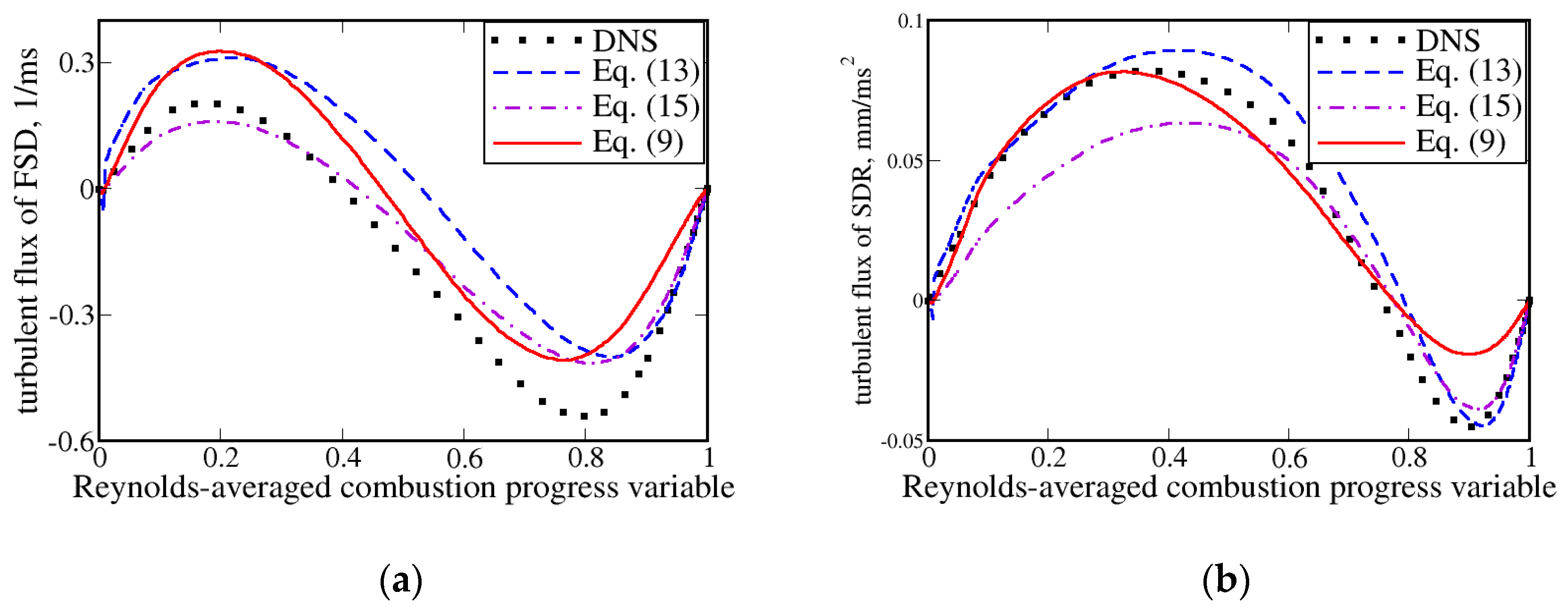

| Case | σ | Ret | u′/SL | L11/δF | Da | Ka | 〈UT〉/SL |
|---|---|---|---|---|---|---|---|
| H | 7.53 | 96 | 0.88 | 15.9 | 18.1 | 0.24 | 1.91 |
| M | 5.0 | 96 | 1.0 | 18.0 | 18.0 | 0.24 | 1.90 |
| L | 2.50 | 96 | 1.26 | 21.8 | 17.3 | 0.24 | 1.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. Closure Relations for Fluxes of Flame Surface Density and Scalar Dissipation Rate in Turbulent Premixed Flames. Fluids 2019, 4, 43. https://doi.org/10.3390/fluids4010043
Lipatnikov AN, Nishiki S, Hasegawa T. Closure Relations for Fluxes of Flame Surface Density and Scalar Dissipation Rate in Turbulent Premixed Flames. Fluids. 2019; 4(1):43. https://doi.org/10.3390/fluids4010043
Chicago/Turabian StyleLipatnikov, Andrei N., Shinnosuke Nishiki, and Tatsuya Hasegawa. 2019. "Closure Relations for Fluxes of Flame Surface Density and Scalar Dissipation Rate in Turbulent Premixed Flames" Fluids 4, no. 1: 43. https://doi.org/10.3390/fluids4010043
APA StyleLipatnikov, A. N., Nishiki, S., & Hasegawa, T. (2019). Closure Relations for Fluxes of Flame Surface Density and Scalar Dissipation Rate in Turbulent Premixed Flames. Fluids, 4(1), 43. https://doi.org/10.3390/fluids4010043






