Numerical Investigation of Pressure Influence on the Confined Turbulent Boundary Layer Flashback Process
Abstract
1. Introduction
2. Numerical Model
2.1. Inert Simulations
2.2. Reactive Simulations
2.3. Les Regimes for Hydrogen Combustion
3. Results
3.1. Pressure Influence on Confined Flashback Limits
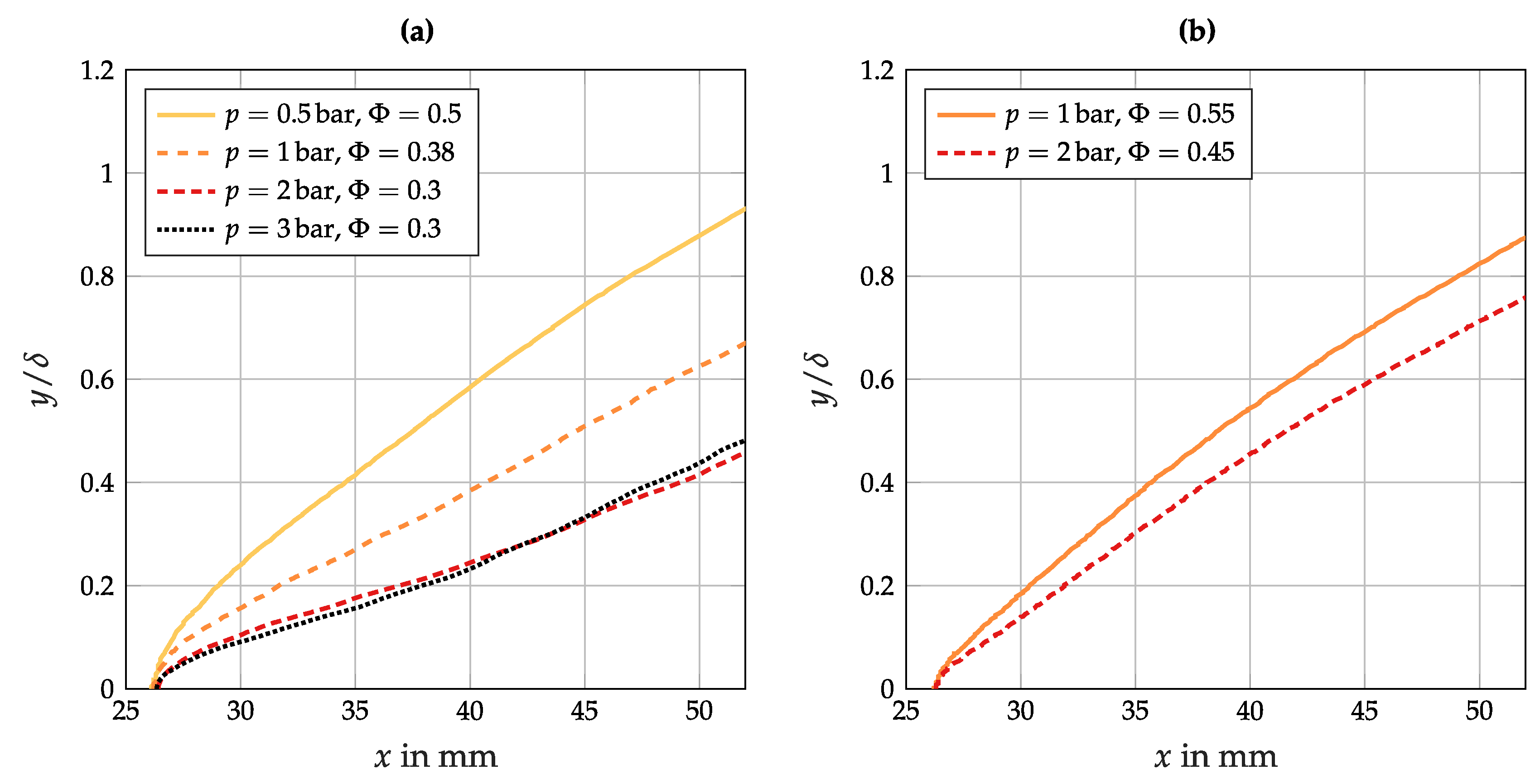
3.2. Macroscopic Flame Structure and Turbulent Flame Speed
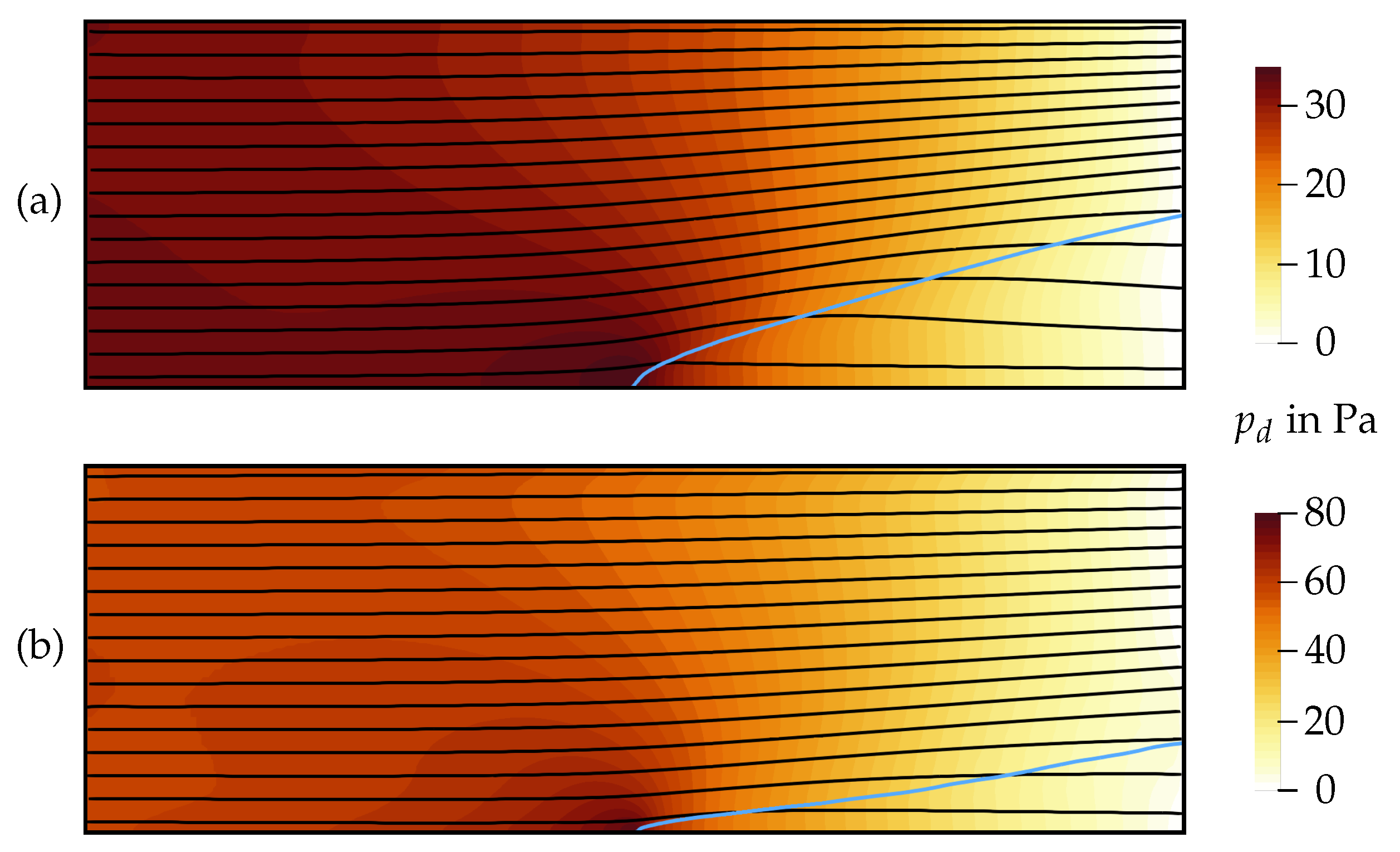
3.3. Average Pressure and Velocity Fields
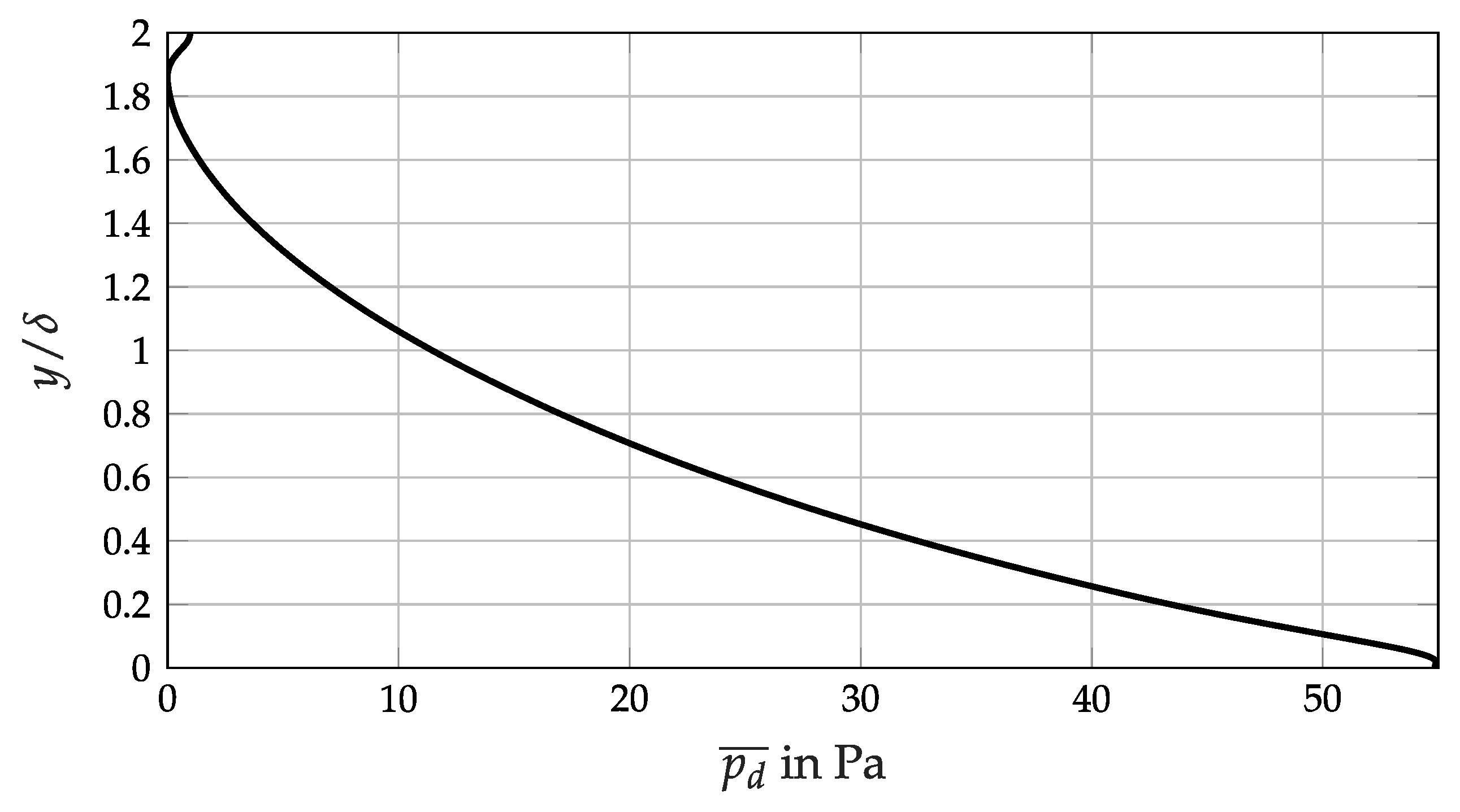
3.4. Quenching Distance and Local Flow Separation
3.5. Implications for Analytical Flashback Prediction
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BLF | Boundary Layer Flashback |
| LES | Large Eddy Simulation |
| ILES | Implicit LEL |
| ODE | Ordinary Differential Equations |
| SGS | Subgrid Scale |
Appendix A
| p | m | D | ||||||
|---|---|---|---|---|---|---|---|---|
| in bar | in K | in m s | in m s | in m s | in m s | |||
| 0.5 | 0.55 | 1741.4 | 0.76 | −0.26 | 7.275 | 3.722 | 0.458 | 1.587 |
| 1 | 0.4 | 1422.3 | 0.35 | −0.35 | 3.248 | 1.754 | 0.394 | 8.246 |
| 1 | 0.6 | 1838.6 | 0.92 | −0.24 | 3.698 | 1.864 | 0.484 | 7.640 |
| 1 | 0.75 | 2096.8 | 1.40 | −0.18 | 4.003 | 1.944 | 0.572 | 7.000 |
| 2 | 0.33 | 1257.2 | 0.20 | −0.40 | 1.559 | 8.689 | 0.370 | 4.212 |
| 2 | 0.5 | 1640.7 | 0.61 | −0.29 | 1.763 | 9.166 | 0.435 | 4.053 |
| 3 | 0.33 | 1257.2 | 0.20 | −0.40 | 1.039 | 5.793 | 0.370 | 2.808 |
References
- Bolland, O.; Undrum, H. A novel methodology for comparing CO2 capture options for natural gas-fired combined cycle plants. Adv. Environ. Res. 2003, 7, 901–911. [Google Scholar] [CrossRef]
- Voldsund, M.; Jordal, K.; Anantharaman, R. Hydrogen production with CO2 capture. Int. J. Hydrogen Energy 2016, 41, 4969–4992. [Google Scholar] [CrossRef]
- Schorr, M.M.; Chalfin, J. Gas Turbine NOx Emissions Approaching Zero — Is It Worth the Price? General Electric Power Generation, Report No. GER 4172; General Electric Power: Schenectady, NY, USA, 1999. [Google Scholar]
- Gruber, A.; Chen, J.H.; Valiev, D.; Law, C.K. Direct numerical simulation of premixed flame boundary layer flashback in turbulent channel flow. J. Fluid Mech. 2012, 709, 516–542. [Google Scholar] [CrossRef]
- Daniele, S.; Jansohn, P.; Boulouchos, K. Flashback Propensity of Syngas Flames at High Pressure: Diagnostic and Control. In Combustion, Fuels and Emissions, Parts A and B; ASME: Glasgow, UK, 2010; Volume 2, pp. 1169–1175. [Google Scholar] [CrossRef]
- Kalantari, A.; Sullivan-Lewis, E.; McDonell, V. Flashback Propensity of Turbulent Hydrogen–Air Jet Flames at Gas Turbine Premixer Conditions. J. Eng. Gas Turbines Power 2016, 138, 061506. [Google Scholar] [CrossRef]
- Eichler, C.; Sattelmayer, T. Experiments on flame flashback in a quasi-2D turbulent wall boundary layer for premixed methane-hydrogen-air mixtures. J. Eng. Gas Turbines Power 2011, 133, 011503. [Google Scholar] [CrossRef]
- Hoferichter, V.; Sattelmayer, T. Boundary Layer Flashback in Premixed Hydrogen–Air Flames with Acoustic Excitation. J. Eng. Gas Turbines Power 2018, 140, 051502. [Google Scholar] [CrossRef]
- Hoferichter, V.; Hirsch, C.; Sattelmayer, T. Prediction of Confined Flame Flashback Limits Using Boundary Layer Separation Theory. J. Eng. Gas Turbines Power 2017, 139, 021505. [Google Scholar] [CrossRef]
- Stratford, B.S. The prediction of separation of the turbulent boundary layer. J. Fluid Mech. 1959, 5, 1–16. [Google Scholar] [CrossRef]
- Eichler, C.T. Flame Flashback in Wall Boundary Layers of Premixed Combustion Systems; Verlag Dr. Hut: München, Germany, 2011. [Google Scholar]
- Gruber, A.; Richardson, E.S.; Aditya, K.; Chen, J.H. Direct numerical simulations of premixed and stratified flame propagation in turbulent channel flow. Phys. Rev. Fluids 2018, 3. [Google Scholar] [CrossRef]
- Clemens, N. Large Eddy Simulation Modeling of Flashback and Flame Stabilization in Hydrogen-Rich Gas Turbines Using a Hierarchical Validation Approach; University of Texas: Austin, TX, USA, 2015. [Google Scholar] [CrossRef]
- Lietz, C.; Hassanaly, M.; Raman, V.; Kolla, H.; Chen, J.; Gruber, A. LES of Premixed Flame Flashback in a Turbulent Channel. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Endres, A.; Sattelmayer, T. Large Eddy simulation of confined turbulent boundary layer flashback of premixed hydrogen-air flames. Int. J. Heat Fluid Flow 2018, 72, 151–160. [Google Scholar] [CrossRef]
- Eichler, C.; Baumgartner, G.; Sattelmayer, T. Experimental Investigation of Turbulent Boundary Layer Flashback Limits for Premixed Hydrogen-Air Flames Confined in Ducts. J. Eng. Gas Turb. Power 2012, 134, 011502. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for Finite Volume Method with Applications to Fluid Flow. Ph.D. Thesis, University of London, London, UK, June 1996. [Google Scholar]
- Nozaki, F. Smagorinsky SGS Model in OpenFOAM. Available online: https://caefn.com/openfoam/smagorinsky-sgs-model (accessed on 1 June 2019).
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Lilly, D.K. The representation of small scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences, Yorktown Heights, NY, USA, 14–16 November 1966; pp. 195–210. [Google Scholar]
- van Driest, E.R. On turbulent flow near a wall. J. Aerosp. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- Mukha, T.; Liefvendahl, M. Large-Eddy Simulation of Turbulent Channel Flow; Technical Report Number 2015-014; Uppsala University: Uppsala, Sweden, 2015. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Duwig, C.; Nogenmyr, K.J.; Chan, C.k.; Dunn, M.J. Large Eddy Simulations of a piloted lean premix jet flame using finite-rate chemistry. Combust. Theory Model. 2011, 15, 537–568. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 1996; Volume 14. [Google Scholar] [CrossRef]
- Burke, M.P.; Chaos, M.; Ju, Y.; Dryer, F.L.; Klippenstein, S.J. Comprehensive H2/O2 kinetic model for high-pressure combustion. Int. J. Chem. Kinet. 2012, 44, 444–474. [Google Scholar] [CrossRef]
- Contino, F.; Jeanmart, H.; Lucchini, T.; D’Errico, G. Coupling of in situ adaptive tabulation and dynamic adaptive chemistry: An effective method for solving combustion in engine simulations. Proc. Combust. Inst. 2011, 33, 3057–3064. [Google Scholar] [CrossRef]
- Pope, S. Computationally efficient implementation of combustion chemistry using in situ adaptive tabulation. Combust. Theory Model. 1997, 1, 41–63. [Google Scholar] [CrossRef]
- Krüger, O.; Duwig, C.; Terhaar, S.; Paschereit, C.O. Ultra-Wet Operation of a Hydrogen Fueled GT Combustor: Large Eddy Simulation Employing Detailed Chemistry. In Proceedings of the Seventh International Conference on Computational Fluid Dynamics (ICCFD7), ICCFD7-3403, Big Island, HI, USA, 9–13 July 2012. [Google Scholar]
- Fureby, C. Comparison of flamelet and finite rate chemistry LES for premixed turbulent combustion. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 8–11 January 2007; p. 1413. [Google Scholar]
- Pitsch, H.; Duchamp de Lageneste, L. Large-eddy simulation of premixed turbulent combustion using a level-set approach. Proc. Combust. Inst. 2002, 29, 2001–2008. [Google Scholar] [CrossRef]
- Heimerl, J.M.; Coffee, T.P. Transport Algorithms for Methane Flames. Combust. Sci. Technol. 1983, 34, 31–43. [Google Scholar] [CrossRef]
- Kee, R.J.; Rupley, F.M.; Meeks, E.; Miller, J.A. CHEMKIN-III: A FORTRAN Chemical Kinetics Package for the Analysis of Gas-Phase Chemical and Plasma Kinetics; Sandia National Laboratories Report SAND96-8216; Sandia National Laboratories: Albuquerque, NW, USA, 1996. [Google Scholar]
- Hirschfelder, J.O.; Bird, R.B.; Spotz, E.L. The Transport Properties of Gases and Gaseous Mixtures. II. Chem. Rev. 1949, 44, 205–231. [Google Scholar] [CrossRef] [PubMed]
- Welty, J.R. Fundamentals of Momentum, Heat, and Mass Transfer, 5th ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kuo, K.K.; Acharya, R. Applications of Turbulent and Multiphase Combustion; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Goodwin, D.G.; Moffat, H.K.; Speth, R.L. Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. 2017. Available online: http://www.cantera.org/ (accessed on 1 June 2019). [CrossRef]
- Sutherland, W. LII. The viscosity of gases and molecular force. Philos. Mag. Ser. 5 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge Monographs on Mechanics, Cambridge University Press: Cambridge, UK; New York, NY, USA, 2000. [Google Scholar]
- Böck, L.R. Deflagration-to-Detonation Transition and Detonation Propagation in H2-Air Mixtures with Transverse Concentration Gradients. Ph.D. Thesis, Technische Universität München, München, Germany, 2015. [Google Scholar]
- Bradley, D.; Lawes, M.; Liu, K.; Verhelst, S.; Woolley, R. Laminar burning velocities of lean hydrogen–air mixtures at pressures up to 1.0 MPa. Combust. Flame 2007, 149, 162–172. [Google Scholar] [CrossRef]
- Bechtold, J.K.; Matalon, M. The dependence of the Markstein length on stoichiometry. Combust. Flame 2001, 127, 1906–1913. [Google Scholar] [CrossRef]
- Dabireau, F.; Cuenot, B.; Vermorel, O.; Poinsot, T. Interaction of flames of H2 + O2 with inert walls. Combust. Flame 2003, 135, 123–133. [Google Scholar] [CrossRef]
- Gruber, A.; Sankaran, R.; Hawkes, E.R.; Chen, J.H. Turbulent flame–wall interaction: A direct numerical simulation study. J. Fluid Mech. 2010, 658, 5–32. [Google Scholar] [CrossRef]

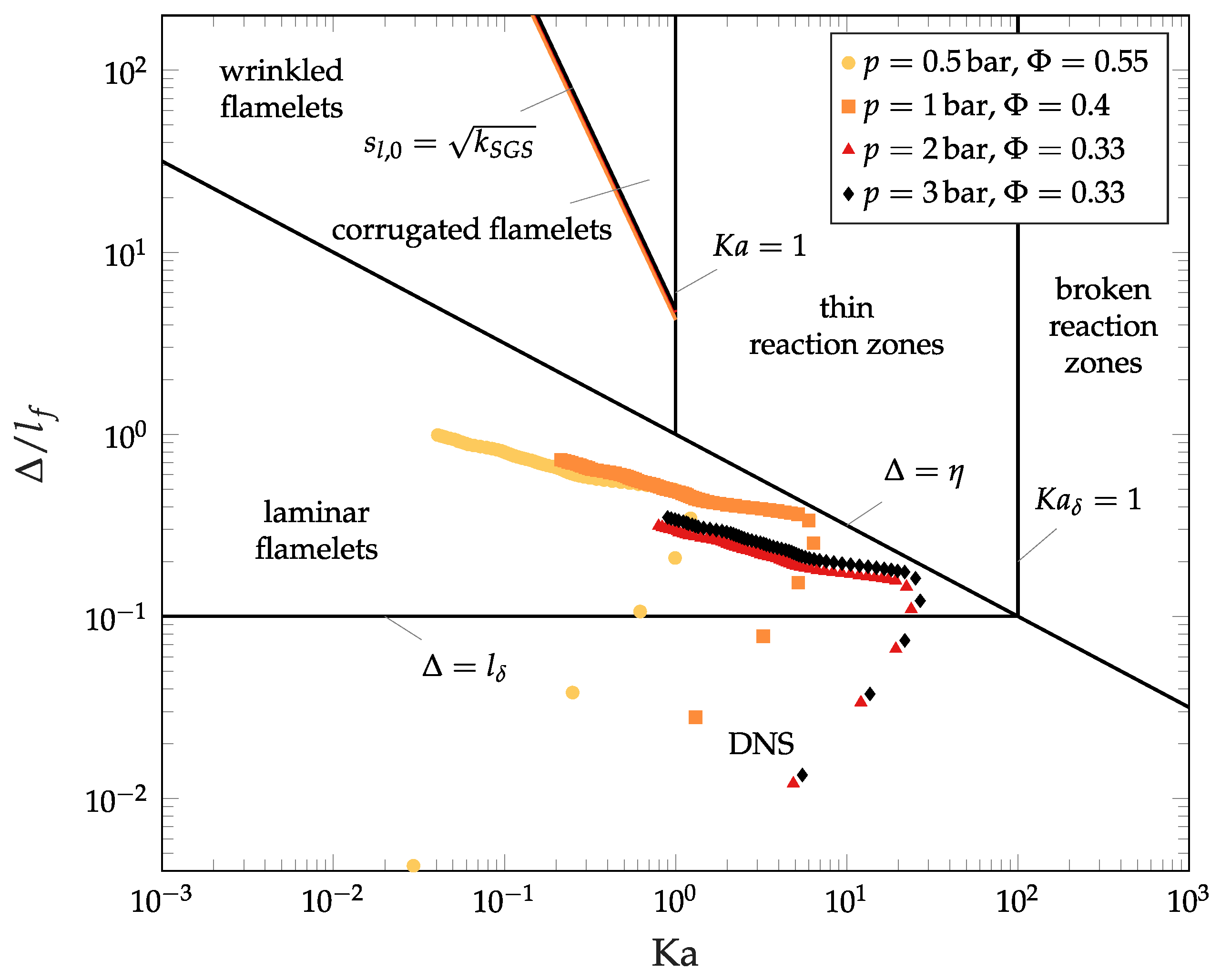
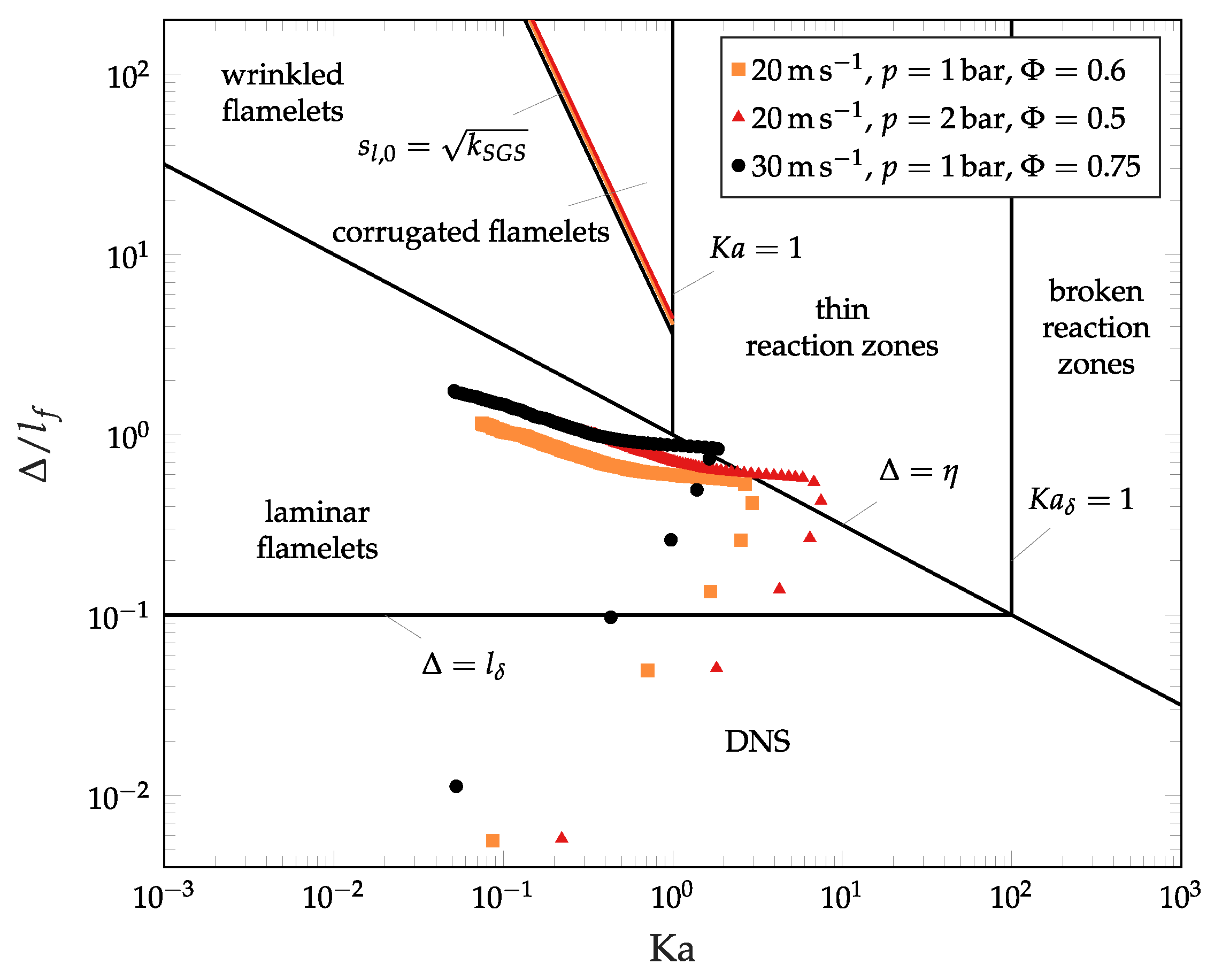
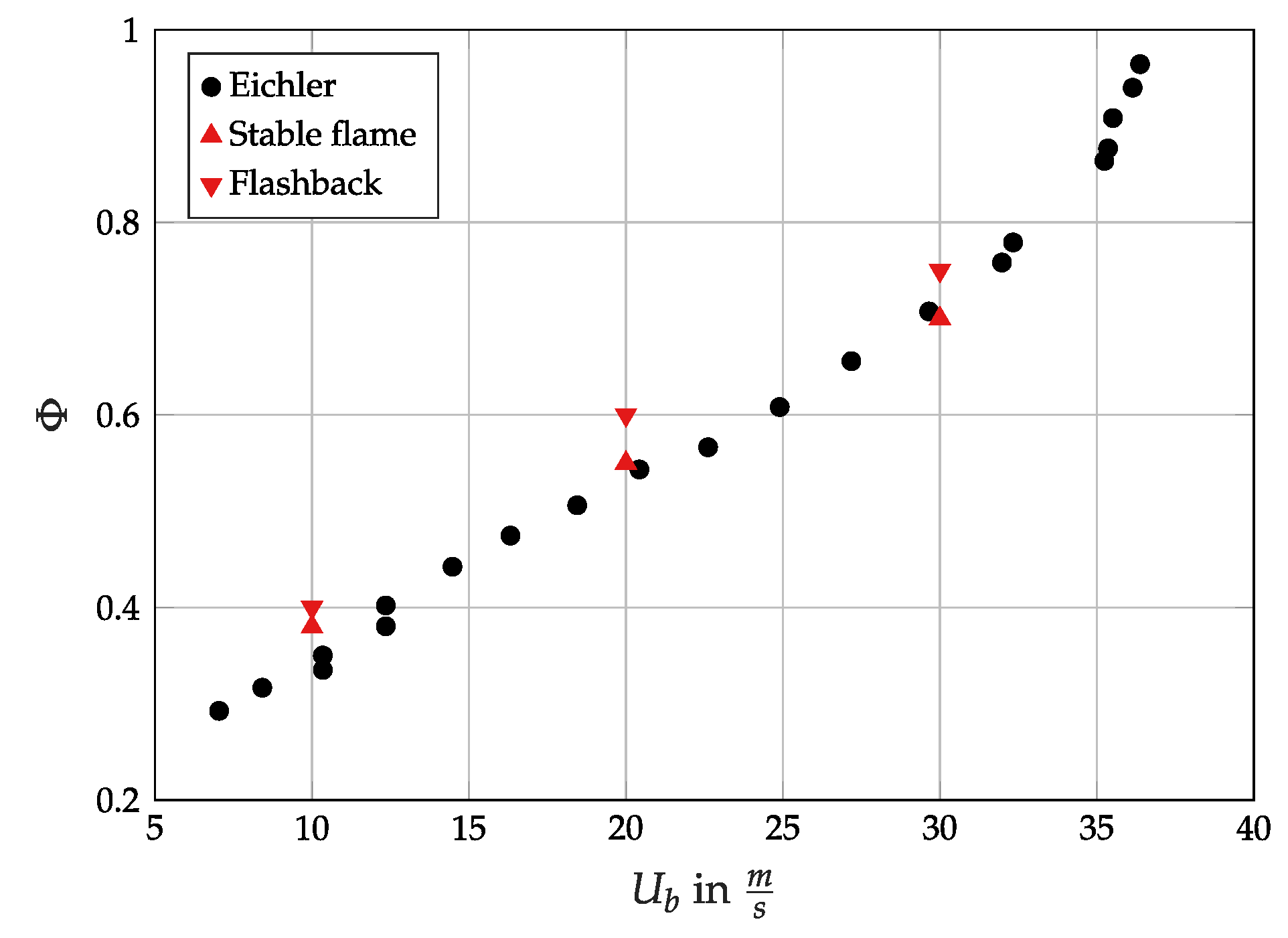


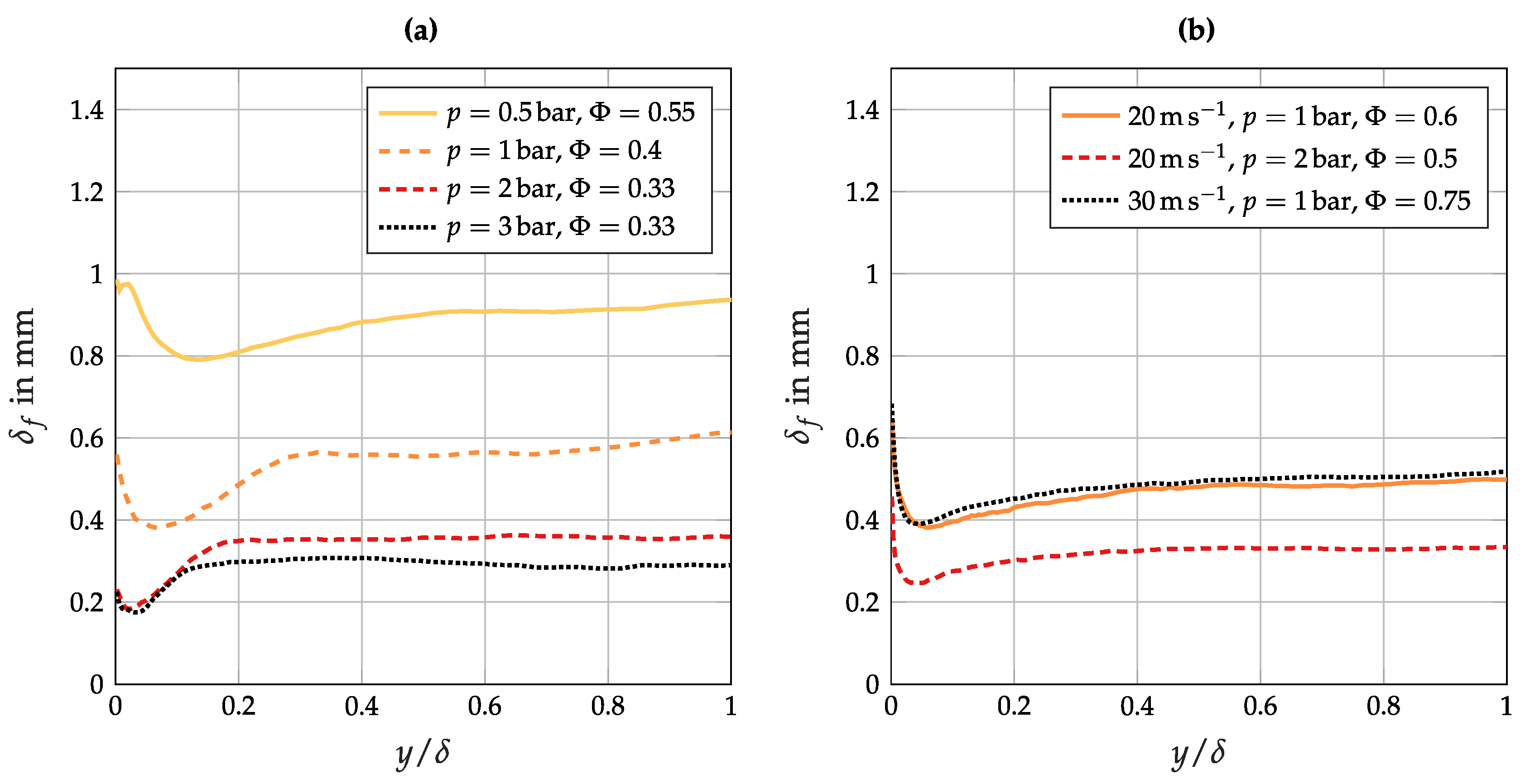




| Re | ||||||||
|---|---|---|---|---|---|---|---|---|
| 9722 | 0.598 | 290.7 | 0.63 | 13.42 | 12.52 | 8.90 | ||
| 19,444 | 1.101 | 535.2 | 0.66 | 13.72 | 13.11 | 9.02 | ||
| 29,167 | 1.573 | 764.4 | 0.79 | 18.35 | 16.24 | 12.07 |
| p | |||||||
|---|---|---|---|---|---|---|---|
| in bar | in m s | in mm | in mm | in mm | |||
| 0.5 | 10 | 0.55 | 0.78 | 0.81 | 0.96 | 0.66 | 0.84 |
| 1 | 10 | 0.4 | 0.42 | 0.39 | 1.06 | 0.65 | 1.56 |
| 1 | 20 | 0.6 | 0.36 | 0.39 | 0.92 | 0.55 | 1.53 |
| 1 | 30 | 0.75 | 0.37 | 0.39 | 0.94 | 0.53 | 1.45 |
| 2 | 10 | 0.33 | 0.24 | 0.18 | 1.31 | 0.54 | 2.23 |
| 2 | 20 | 0.5 | 0.18 | 0.26 | 0.68 | 0.28 | 1.58 |
| 3 | 10 | 0.33 | 0.18 | 0.18 | 1.00 | 0.39 | 2.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Endres, A.; Sattelmayer, T. Numerical Investigation of Pressure Influence on the Confined Turbulent Boundary Layer Flashback Process. Fluids 2019, 4, 146. https://doi.org/10.3390/fluids4030146
Endres A, Sattelmayer T. Numerical Investigation of Pressure Influence on the Confined Turbulent Boundary Layer Flashback Process. Fluids. 2019; 4(3):146. https://doi.org/10.3390/fluids4030146
Chicago/Turabian StyleEndres, Aaron, and Thomas Sattelmayer. 2019. "Numerical Investigation of Pressure Influence on the Confined Turbulent Boundary Layer Flashback Process" Fluids 4, no. 3: 146. https://doi.org/10.3390/fluids4030146
APA StyleEndres, A., & Sattelmayer, T. (2019). Numerical Investigation of Pressure Influence on the Confined Turbulent Boundary Layer Flashback Process. Fluids, 4(3), 146. https://doi.org/10.3390/fluids4030146





