1. Introduction
The knock phenomenon limits the compression ratio and the thermodynamic efficiency of a spark ignition (SI) engine. At some operating conditions, avoiding it will force the spark advance away from the maximum brake torque point further lowering engine performance. If knock occurs, it can be severely damaging to the engine components. Knock, i.e., onset of strong pressure oscillations, has been known to be caused by the autoignition of the end gas ahead of the propagating flame which is controlled by chemical kinetics. Therefore, numerical modelling of autoignition may be used to predict knock onset. This has been demonstrated in various studies by modelling the autoignition chemistry of a simpler gasoline surrogate such as primary reference fuels (PRFs), i.e., a mixture of iso-octane and n-heptane [
1,
2,
3].
Chemical kinetic mechanisms are routinely validated against shock tube and rapid compression machine measurements of the ignition delay times (
) of various gasoline surrogate fuels. The conditions for these laboratory measurements are similar to those which prevail before ignition in homogeneous charge compression ignition (HCCI) or controlled autoignition (CAI) engine, and the recent kinetic mechanisms, e.g., [
4,
5,
6], perform remarkably well in these regimes. Application of such gasoline surrogate mechanisms have been seen in various studies demonstrating autoignition predictions in HCCI and CAI engines, [
4,
7]. The question arises of whether the reduced chemical mechanisms will perform equally well in predicting autoignition in SI engines. This work attempts to address this subject.
2. Practical Gasoline Surrogates
The simplest surrogate, a primary reference fuel (PRF), i.e., mixture of iso-octane and n-heptane, is used in the well known Research and Motored Octane Number (RON and MON) tests to quantify the knock resistance of a gasoline by matching knock intensities in a standard engine. Compared to the RON test, in the MON test the end gas temperature is higher at the same pressures and therefore, unless gasoline exhibits a negative temperature coefficient (NTC) phase at those temperatures, the MON value tends to be lower than RON. The sensitivity
S, i.e., the difference of octane numbers (
) is a measure of fuel’s response to varying pressures and temperatures. PRF’s have zero sensitivity by definition. However, gasoline, owing to its complex composition, is likely to exhibit autoignition behaviour different from that of the PRF which matches its RON or the MON value, when the pressure and temperature history of the end gas does not match the standard RON and MON tests. Blends of iso-octane, n-heptane with toluene (Toluene Reference Fuels, TRFs) have an advantage of having non-zero sensitivity. Binary blends of toluene with iso-octane and n-heptane have also been studied in order to isolate their cross-oxidation chemistry [
8], however such blends have found little application as gasoline surrogates.
Use of iso-octane and n-heptane as components of a surrogate is hardly avoidable as they represent linear and branched alkanes, major gasoline components. Besides, the chemistry leading to their auto-ignition is relatively well understood. However, gasoline does not consists only of alkanes. Thus, EN228, the European standard for gasoline specifies aromatic content of up to 35% by volume, it also allows 5% oxygenates by volume. Therefore, it seems natural to seek surrogates going beyond PRF’s and TRF’s which contain compounds approximating various families of hydrocarbons present in the gasoline [
9].
Table 1 presents a list of such gasoline surrogates for which the auto-igntion delay times were experimentally determined using rapid compression machines (RCM), shock tubes (ST) and HCCI engines. The work of Gauthier et al. [
10] presents a fairly comprehensive shock tube study of two TRFs for
conditions of 12–25 and 45–60 atm at 850–1280 K. Two TRF’s were proposed to approximate a standard research gasoline, RD387, with an anti knock index (AKI) of 87. The measurements demonstrated a good similarity between the surrogates and the gasoline. However the RON and MON of these surrogates were later determined by Knop et al. [
11] and the AKI of the surrogates were found to be lower than 87, see
Table 1. But, even more importantly, the sensitivity
S of the two TRFs was found to be much lower than the usual gasoline range of
S of 8 to 12 points.
While shock tube measurements offer an important benchmark for validation of the chemical kinetic mechanisms, they are difficult to perform at temperatures below 850 K and this makes validation of chemical kinetic mechanisms at engine conditions difficult. At these temperatures, many individual components of gasolines have ignition delays decreasing with temperature, the phenomenon known as negative temperature coefficient (NTC) behaviour. Work of Mehl et al. [
12] demonstrated that the sensitivity of a surrogate can be correlated to the slope of the NTC region,
, while the values of the auto-ignition delay time
in the NTC region depend on the AKI of the surrogate. These two correlations and knowledge of the gasoline composition provides constraints for the aromatic and olefinic content of the surrogate which are key to achieving a realistic NTC behaviour and thus sensitivity. The PRF content was then varied to achieve the correct H/C ratio and the octane numbers. This approach was applied to another RD387 gasoline [
12], for which a 4-component surrogate (
Table 1, last entry) was proposed. Work of Kukkadapu et al. [
13] further investigated one of the TRF formulation proposed in [
10]; this surrogate is referred to as Gauthier TRF-A (iso-octane 63%, n-heptane 17%, toluene 20% by volume). Comparison of igntion delays for Gauthier TRF-A and the 4-component surrogate proposed by Mehl et al. [
12], measured in an RCM, Kukkadapu et al. [
13] revealed that the correlations of Mehl et al. [
12] overestimate the fuel sensitivity thereby indicating a weakness of an empirical prediction of octane numbers.
Ethanol addition to gasoline is now common mainly due to legislative impetus. Ethanol acts as an octane improver and is commonly blended in amounts of up to 10% by volume. Works of Fikri et al. [
14] and Cancino et al. [
15] performed shock tube measurements of four multicomponent gasoline surrogates including ethanol, see
Table 1.
The EN 228 gasoline standard specifies a maximum olefin content of 18% vol. Most European gasolines have olefin content between 5% and 9% vol, mostly branched rather than straight or cyclic compounds [
9]. Oxidation characteristics of some olefins, such as 1-hexene, cyclohexene and 1-pentene have been studied, however, other very common ones, e.g., 2-methyl-2-butene are little studied. It is because of this lack of understanding of common gasoline olefins that proposed chemical kinetic schemes differ significantly in olefine oxidation pathways. For autoignition simulations, the choice of olefin is crucial for producing correct ignition delays while also matching the H/C ratio. Surrogates tabulated in
Table 1 have therefore only limited capability to emulate gasoline in SI engine conditions.
3. Chemical Kinetics Schemes for Gasoline Surrogates
An earlier study [
16] compared autoignition predictions in an adiabatic homogeneous reactor and an HCCI engine using 8 chemical kinetics mechanisms of different sizes. However, these mechanisms can describe only a limited amount of gasoline compounds, this is why this work turns to more comprehensive, semi-detailed kinetic schemes referred to as Andrae’s [
4], Golovitchev’s [
5], and Reitz’ [
6], mechanisms. For individual substances, all these three mechanisms are capable of producing ignition delay times in fairly good agreement to experiments, see
Figure 1. It may be inferred from this Figure that biggest discrepancy between experiments and models arises at high pressures and low, 600–850 K, temperatures. The observed difference would amount to a substantial deviation in terms of crank angle timing, e.g., at 1500 rpm, 1 ms equals 9
of the crank rotation. The integrated error along the complete
history of the end gas may therefore result in a substantial difference between the predicted and observed autoignition onsets.
Performance of the three reduced mechanisms studied in this work for the ignition delay time predictions for the gasoline surrogates remains similar to the one for the individual icomponents. Ignition delay times for the stoichiometric mixtures of two surrogates at high pressures is presented in
Figure 2. The over-prediction of the NTC behaviour of iso-octane by Golovitchev model as seen in
Figure 1a is inheriteded in the surrogate simulations as well and, as a consequence, considerably lower ignition delay times are produced for both surrogates. It can be seen that Andrae’s mechanism outperforms the others at low, 600–850 K, temperatures crucial for the prediction of autoignition in SI engines.
The chemical kinetic calculations presented in this work have been done using a solver routine written in Fortran as part of the library of 1-D engine modelling code at Leeds University, refered to as LUSIE (Leeds University Spark Ignition Engine). For chemical kinetics, the solution of the stiff-type differential equations is carried out by using an implementation of the modified extended backward differentiation formulas developed by Cash [
20]. The chemistry solver has been coupled with the engine simulation package in which the main combustion event is modelled using a multi-zone thermodymanic approach to flame propagation [
21].
4. Gasoline Surrogate Formulation
Optimal surrogate formulation depends on its application. A large number of physical and chemical properties of the target fuel can be targeted in the surrogate, among those are the distillation curve, RON, MON, stoichiometric air-to-fuel ratio, molecular weight, thermal conductivity and laminar burning velocity. At the same time, the number of components in gasoline surrogate is limited by the availability of chemical kinetic data and complexity of blending rules. Since gasoline constituents belong to one of the five main classes it seems natural to seek surrogate with the same number of components. One mathematical constraint which must always be met while determining the composition of a surrogate is that the sum of the mole or volume fractions of its constituents must be one. This means that for a n component surrogate, properties can be used as constraints to optimise the surrogate composition. For a correct prediction of the cumulative heat release the stoichiometric air to fuel ratio () and the calorific value of the gasoline must also be matched. The correct H/C/O atomic proportions and the molar mass, M will automatically produce the desired .
For the quasi-dimensional combustion modelling in SI engine coupled with chemical kinetic modelling of surrogate autoignition in the end gas, the H/C and O/C ratios are crucial. Therefore, these constraints are used in the determination of the surrogate composition:
Reproducing the autoignition behaviour of the gasoline is the biggest challenge in surrogate formulation. The capablity of the surrogate to represent the anti-knock properties of the petrol is only partially dependent on the used model for octane number. A true surrogate for gasoline autoignition will match ignition delay of the gasoline at all conditions. It will show the emergence of similar ignition precursors at similar rates to that of the gasoline and therefore it will have, not only the same RON and MON as the gasoline, but similar octane index no matter which engine the two are compared in. Matching just the RON and MON of the surrogate with that of the gasoline does not guarantee that the surrogate will reproduce the autoignition behaviour of the gasoline universally in all engines. To make matters worse, the empirical/theoretical octane number models are far from perfect.
Detailed composition-based octane number models such as [
22] account for the non-linear blending interactions of surrogate constituents. The model developed in [
22] accounts for the paraffin-olefin and paraffin-naphthene interactions. The non-linear octane blending between ethanol and other gasoline constituents is a subject of on-going research [
23] but as yet no well tested octane number model has emerged. Pera and Knop [
9] advocated the use of a linear-by-moles additivity rule for the TRF blends shown to perform better than the non-linear model of Morgan et al. [
24] or the composition-based octane model of Ghosh et al. [
22]. Pera and Knop [
9] proposed an improvement to the linear-by-moles expression for TRFs by suggesting blend octane numbers for toluene (RON 116/MON 101.8) and demonstrated that their expression yielded the lowest absolute errors in comparison to 7 other octane number models [
11]. Their approach has been found to produce appreciable octane numbers in the present work and due to its accuracy and simplicity it has been adopted in this work for the calculation of TRF octane numbers as well as surrogates containing olefin:
Equations (
1) and (
2) and the unity sum of molar fractions provide 5 constraints for the determination of the so-called properties-based surrogate. Alternative to this would be a composition-based surrogate formulated by representing major constituents of gasoline by a surrogate of that particular family. The resulting surrogate will be expected to have different properties from that of the target gasoline as the surrogate components do not correctly represent all of the substances in that family. However, one of the findings of this work is that a composition-based surrogate whose composition represents accurately fractions of the actual gasoline may perform superior in replicating the autoignition behaviour as compared with a purely properties based surrogate which may contain unrealistic amounts of aromatics and oxygenates.
5. Supporting Experiments
Experiments were performed in a single cylinder optical engine (LUPOE2-D) at Leeds University with a disc shaped combustion chamber, the details of the engine and the experimental methods has been presented in [
25]. Iso-octane, as well as three fuels of very different compositions, commercial unleaded petrol ULG90, PRF and TRF, with the same RON of 90 were tested in the knocking regime to assess the differences in their auto-ignition behaviour. For all fuels stoichiometric mixtures were tested. TRF90 was blended with toluene and n-heptane only as most of the octane quality of ULG90 came from its branched paraffin content.
For autoignition modelling, cycles with similar pressure traces were chosen for the different fuels to allow a comparison of the knocking tendencies of different fuels at similar conditions,
Figure 3. The subject of autoignition modelling with predictive combustion for the full range of slow and fast burning cycles has been covered in [
1,
2,
3]. For this study, because fuel composition has only a small effect on the heat loss during compression phase, matching the cycle pressure effectively means very similar end-gas temperatures will result.
Difference in the reactivity of the two fuels was expected to manifest as different knock onsets regardless of the equivalent RON. However, TRF90 resulted in similar knock onset as ULG90 unlike PRF90 (
Figure 4). The effective octane rating of ULG90 and TRF90 appears to be superior than the corresponding PRF of ON 90.
6. Results and Discussion
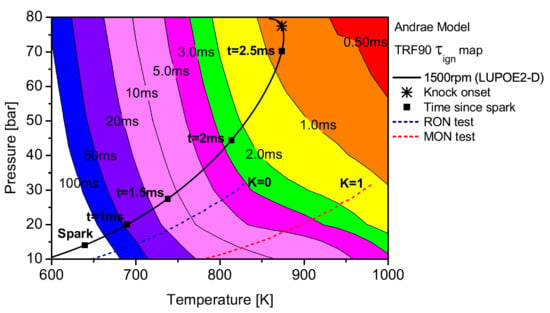
The relationship between the end gas thermodynamic state and the autoignitive tendency of a fuel can be depicted as ignition delay time (
) contours on a
carpet plot as shown in
Figure 5,
Figure 6 and
Figure 7.
The end gas thermodynamic path in LUPOE2-D as well as the RON and MON tests are superimposed on the
maps for PRF90 and TRF90; the latter calculated using Andrae’s model. The differences in fuel reactivity are shown by the shape of the contours and the extent to which the regions of different
span. In the case of PRF90, the LUPOE2-D
trajectory follows a path before the start of NTC phase where the regions of shorter
are met earlier. Combustion phasing with respect to the top dead centre (TDC) is such that the regions of longer
are passed relatively slowly as the pressure increase is initially slower. This phase of combustion corresponds to the period of the initial acceleration of the flame after spark until it reaches a steady turbulent burning velocity after which it starts to decelerate approaching the wall [
26].
The integration of the individual
along an engine’s
trajectory using the Livengood-Wu integral suggests that it is the short ignition delay region towards the later stages of combustion when the
are at their highest, which contribute the most in producing ignition. Comparison of the
contours for PRF90, TRF90 and iso-octane shows that the regions of short
are situated at lower
domain for PRF90 and a significant portion of the LUPOE2-D trajectory lies in these critical regions bringing the knock onset to an earliest value of 2.8
CA after TDC (aTDC) among the four fuels studied. Iso-octane shows the latest knock onset as the
trajectory stays within fairly long
regions,
Figure 7.
The end gas thermodynamic path in a RON test passes the same amount of time in regions of very similar for both PRF90 and TRF90, thus giving them the same RON values. This means that PRF90 can be regarded as a surrogate for TRF90 and ULG90 at only such the unburned zone conditions as encountered in the RON test. Similarly a PRF with octane number of 84.7 may be regarded as a surrogate for ULG90 at conditions of MON test. However, a single multi-component blend can be used to reproduce the autoignition behaviour of a gasoline at both RON and MON test conditions. Such a blend which has been matched to the RON/MON of a gasoline will have the same reactivity for only a narrow region of the landscape. It is therefore tempting to consider such a blend as a surrogate at all conditions. The fact that most modern SI engines operate with temperature and pressure history very similar to LUPOE2-D or at even higher pressures resulting from turbocharging, RON and MON are not sufficient to characterise auto-ignition of gasoline in such engines. Moreover, weaknesses in the empirical octane number models and the lack of ignition delay time data for gasolines reduces the surrogate formulation for SI engine autoignition to guess work.
Autoignition predictions of the three RON 90 fuels have been made for the LUPOE2-D conditions of
Figure 3 using the three reduced mechanisms and the comparison to the observed knock onsets is presented in
Figure 8. The three fuels are subject to that same end gas
and equivalence ratio history. Since LUPOE2-D was operated in skip firing mode, all trapped residual gases were expunged, hence an ideal scavenging was assumed in the modelling. Owing to this, the differences in the predicted autoignition times are caused solely by differences in the autoignition chemistry of the three fuels. Across the range of studied conditions, the Andrae’s model appears to perform consistently better than competitors, however more accurate PRF submodel in the Reitz model produces accurate autoignition prediction in the case of PRF90. Golovitchev’s model predicts shorter delays in contrast to what can be seen in the ignition delay time calculations at the constant pressure, see
Figure 1.
Table 2 lists the possible surrogates for ULG90. The constraints discussed in
Section 4 have been optimised for ULG90 to formulate a properties-based surrogate. Only the Reitz model has pathways for a naphthene, here cyclohexane, a suitable surrogate component. A composition-based surrogate is also studied whose composition is the same as that of the major gasoline constituent families. A tri-component TRF with the same RON and MON as ULG90 has also been studied. The autoignition onsets of the composition and properties based surrogates for the ULG90
history in LUPOE2-D have been simulated using the Reitz model. The autoignition onset of the TRF has been predicted by the three mechanisms. It is found that it is the TRF with Andrae model which predicts the closest autoignition to that of the ULG90. Among the two 4-component surrogates, it is the composition based surrogate which yields predictions closer to the observed knock onset.