An Introduction of Droplet Impact Dynamics to Engineering Students
Abstract
1. Introduction
Key Dimensionless Numbers in Droplet Impact Dynamics
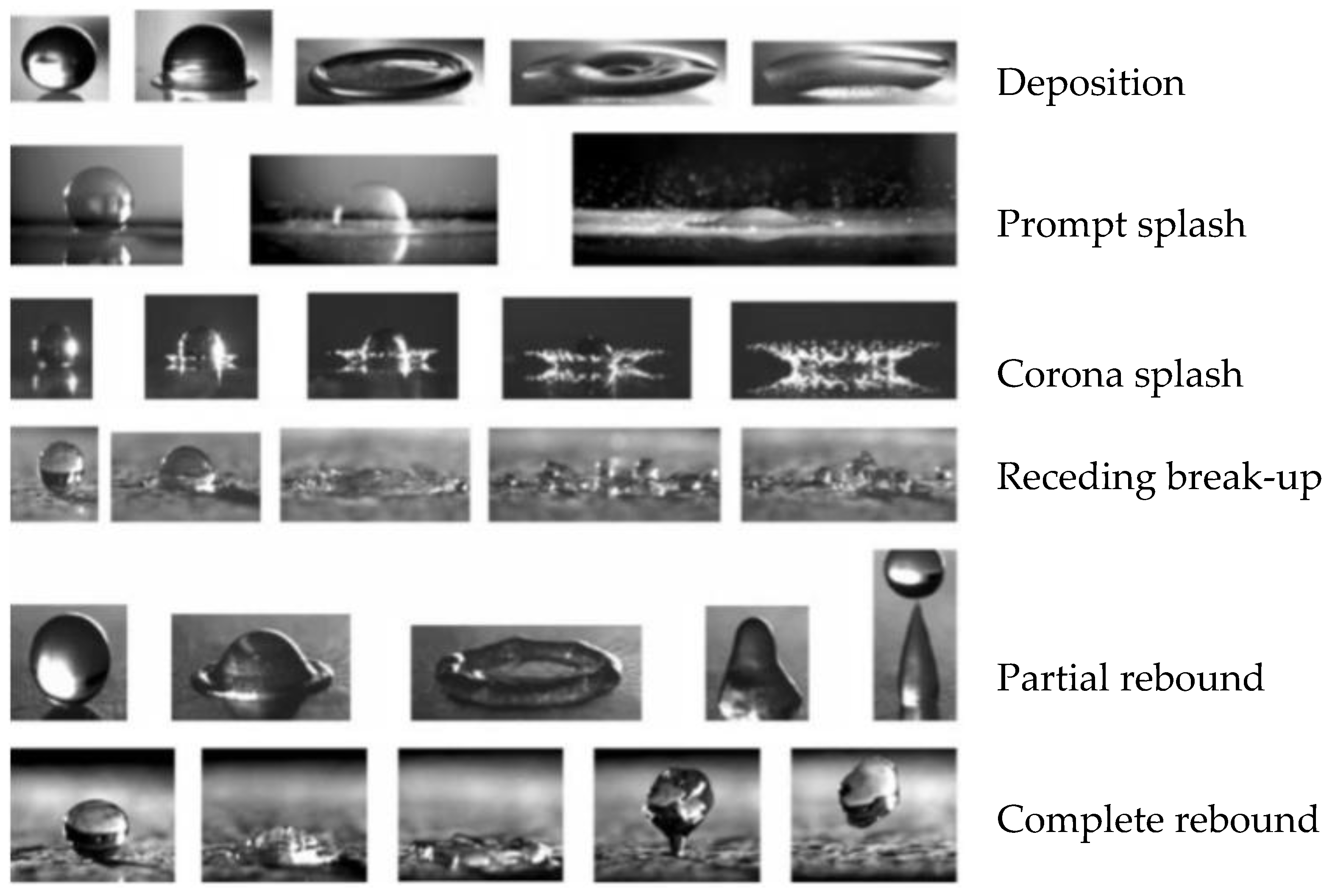
2. Droplet Impact on Static Solid Surfaces
2.1. Effect of Surface Temperature
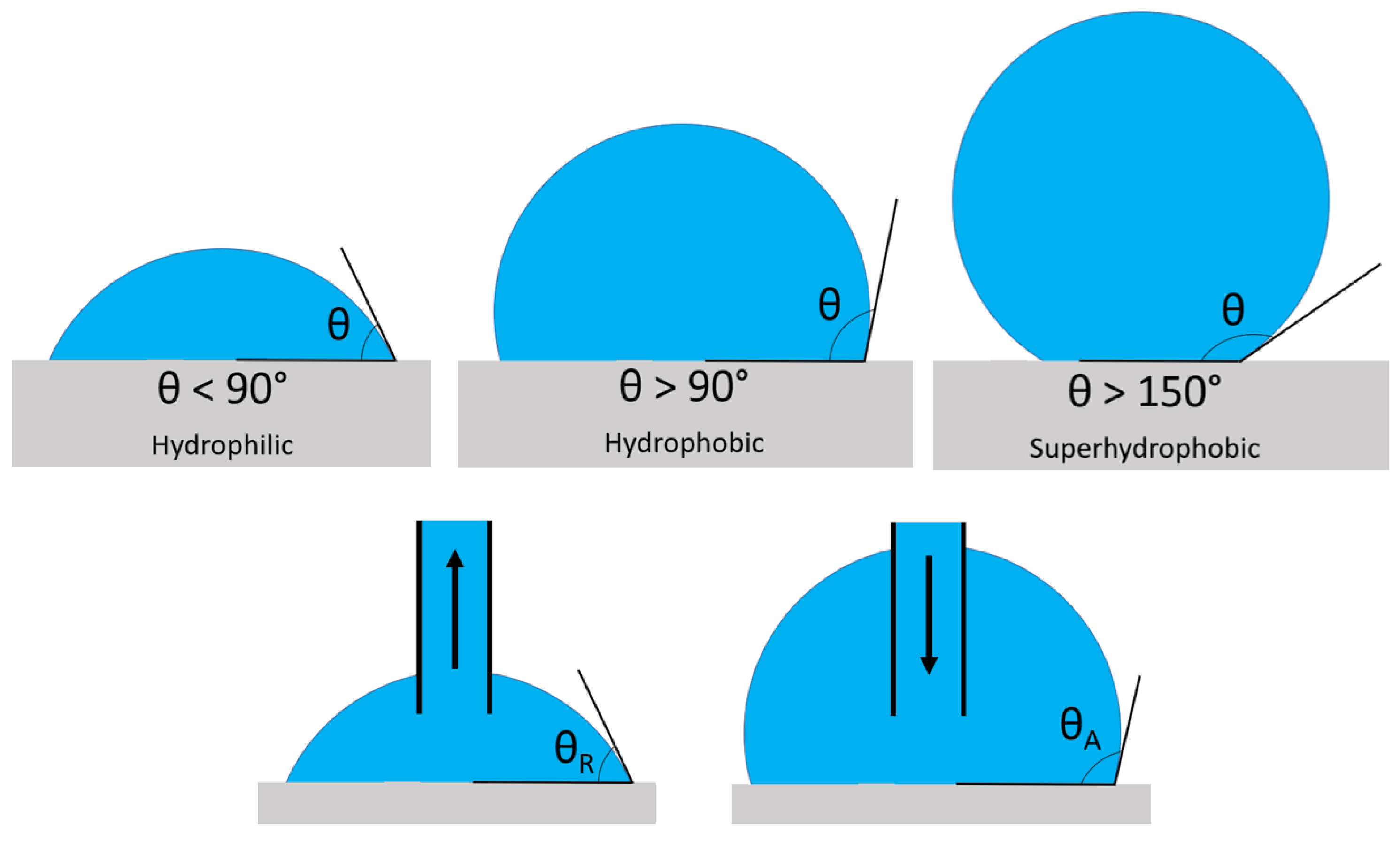
2.2. Effect of Surface Wettability
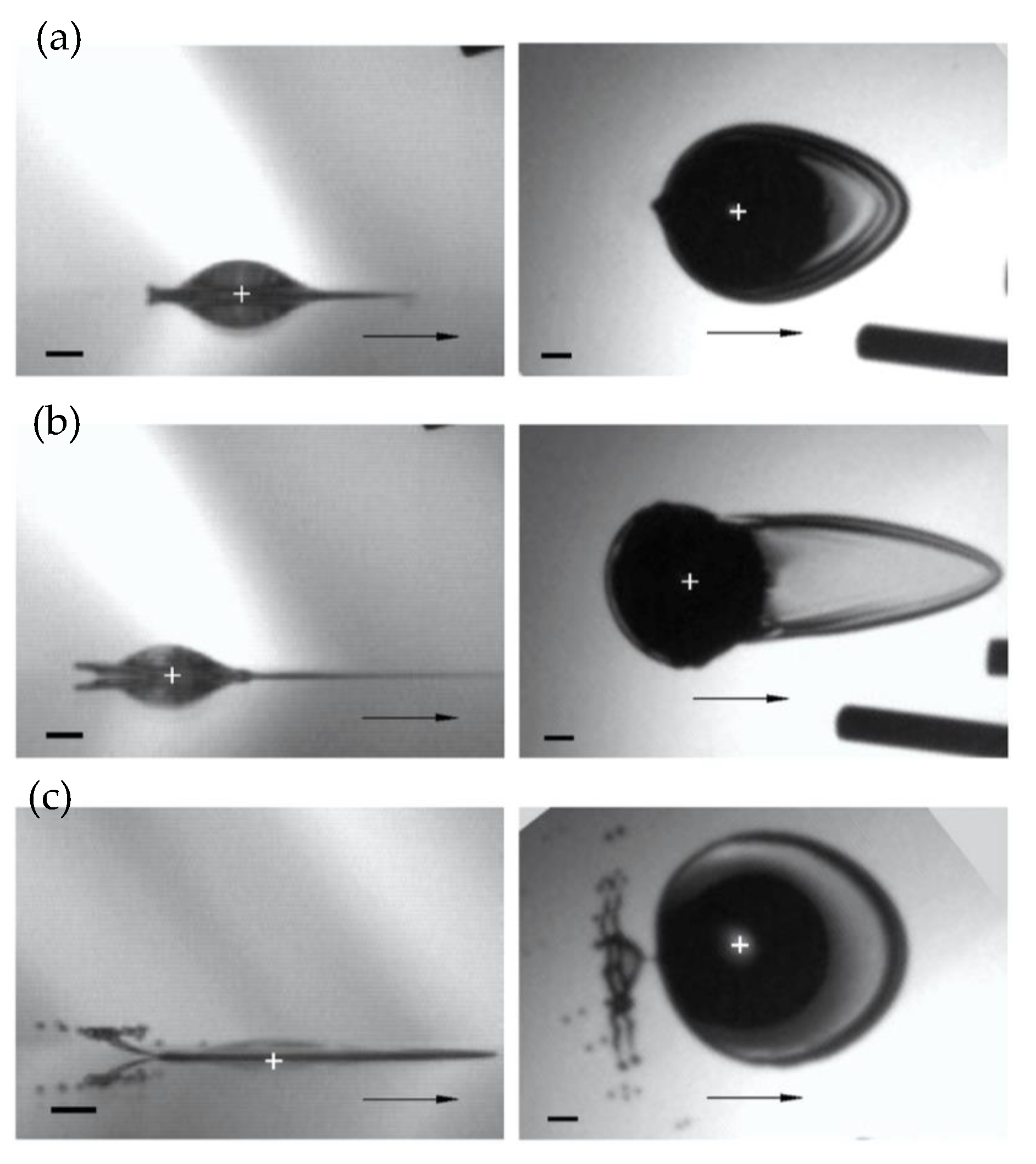
2.3. Effect of Impact Velocity
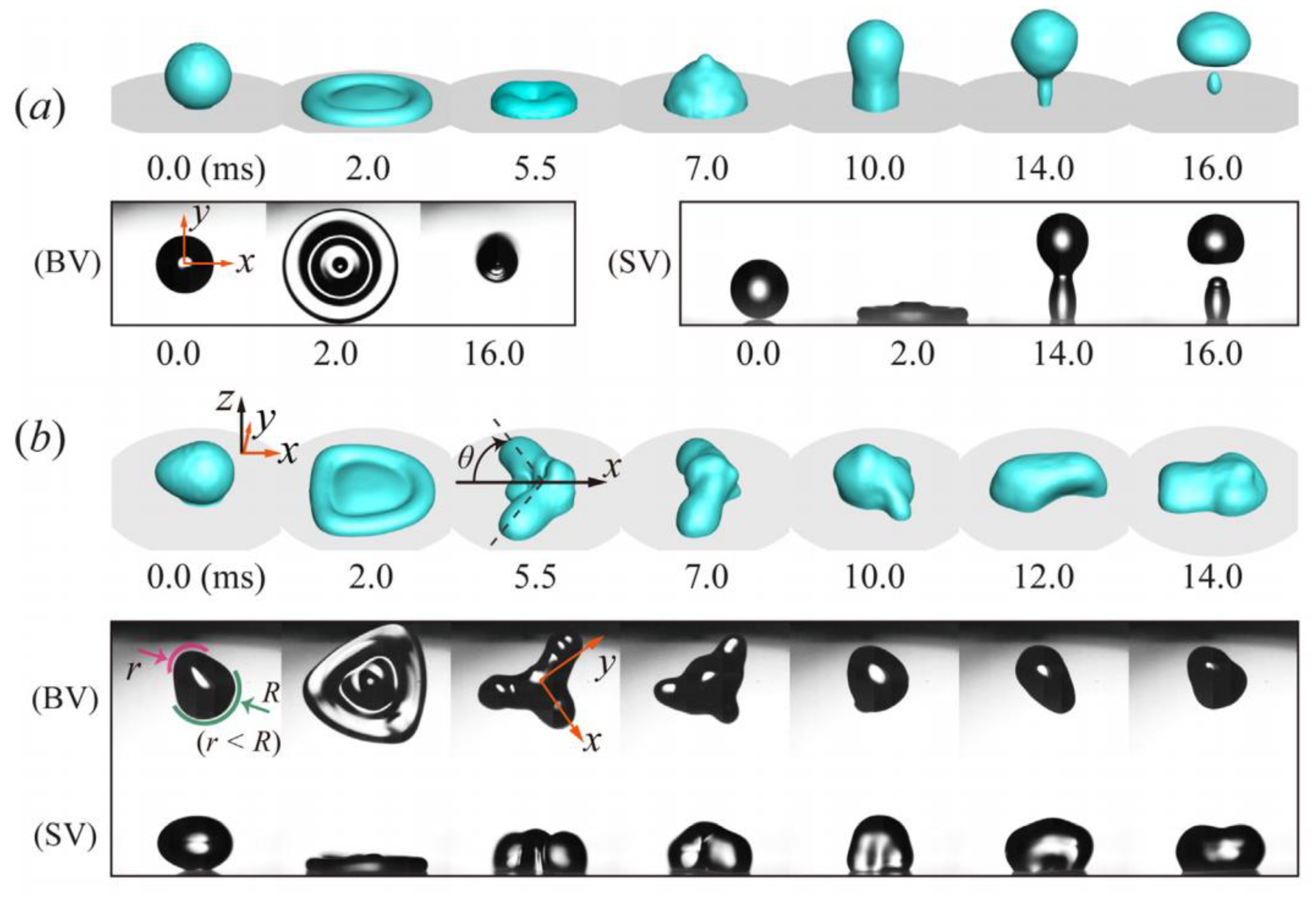
2.4. Effects of Droplet Shape and Volume
2.5. Effect of Relative Humidity
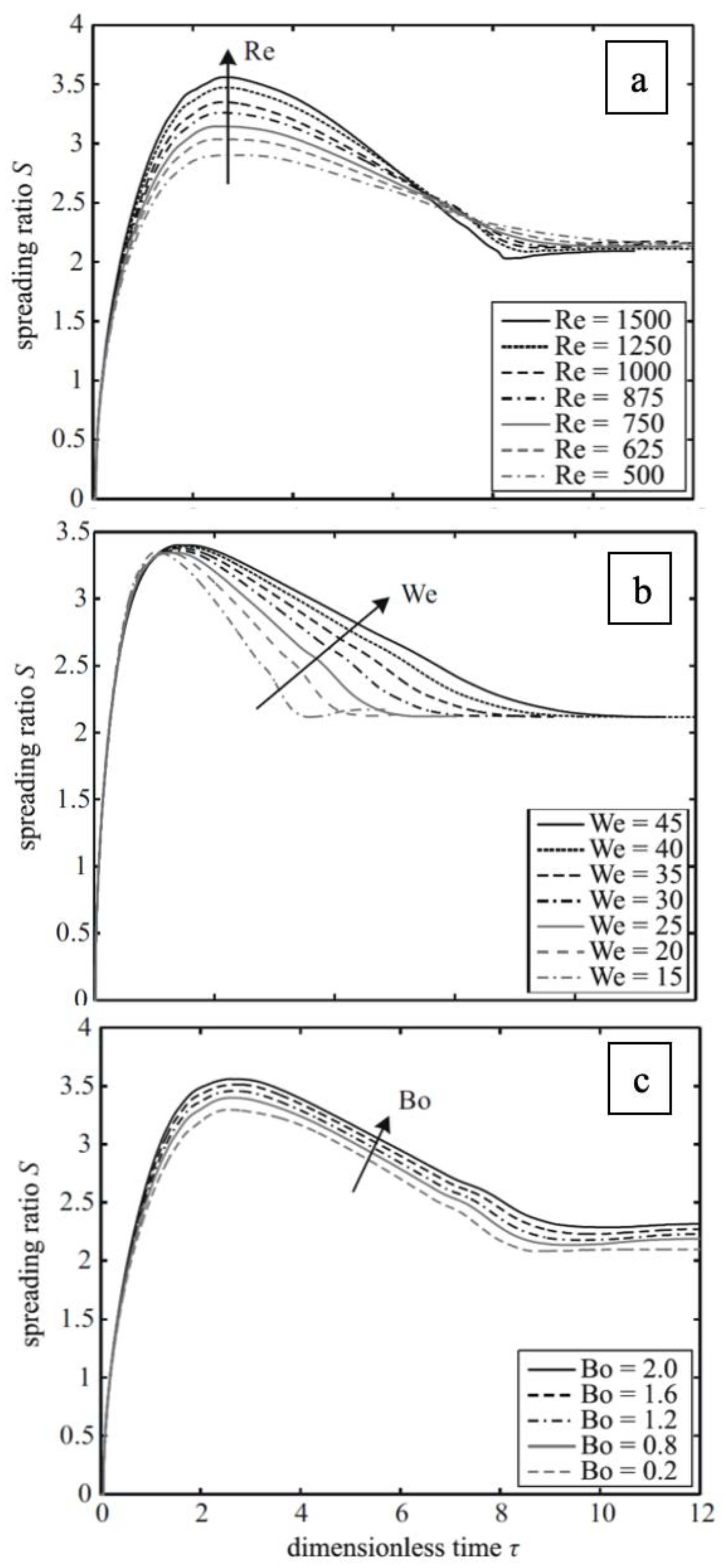
2.6. Effect of Dimensionless Numbers
3. Droplet Impact on Moving Surfaces
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Worthington, A.M. On the forms assumed by rops of liquids falling vertically on a horizontal plate. Proc. R. Soc. Lond. 1876, 25, 261–272. [Google Scholar]
- Worthington, A.M. A Study of Splashes; Longmans, Green, and Company: London, UK, 1908; Available online: https://archive.org/details/studyofsplashes00wortrich/mode/2up (accessed on 1 July 2020).
- Yarin, A.L. Drop Impact Dynamics: Splashing, Spreading, Receding, Bouncing…. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Khojasteh, D.; Kazerooni, M.; Salarian, S.; Kamali, R. Droplet impact on superhydrophobic surfaces: A review of recent developments. J. Ind. Eng. Chem. 2016, 42, 1–14. [Google Scholar] [CrossRef]
- Bolleddula, D.A.; Berchielli, A.; Aliseda, A. Impact of a heterogeneous liquid droplet on a dry surface: Application to the pharmaceutical industry. Adv. Colloid Interface Sci. 2010, 159, 144–159. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Esmail, N.; Dolatabadi, A. Shear-driven droplet coalescence and rivulet formation. Proc. Inst. Mech. Eng. Part. C J. Mech. Eng. Sci. 2016. [Google Scholar] [CrossRef]
- Moghtadernejad, S. Dynamics of Droplet Shedding and Coalescence under the Effect of Shear Flow; Concordia University: Montréal, QC, Canada, 2014. [Google Scholar]
- Bragg, M.B. Aicraft aerodynamic effects due to large droplet ice accretions. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996. [Google Scholar] [CrossRef][Green Version]
- Bragg, M.; Basar, T.; Perkins, W.; Selig, M.; Voulgaris, P.; Melody, J.; Sarter, N. Smart icing systems for aircraft icing safety. In Proceedings of the 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Tembely, M.; Esmail, N.; Dolatabadi, A. Concurrent droplet coalescence and solidification on surfaces with various wettabilities. J. Fluids Eng. Trans. ASME 2015. [Google Scholar] [CrossRef]
- Myong, R.S. Droplet impingement in aircraft icing. In Progress in Aircraft Icing and Aircraft Erosion Research; Springs of Dreams Corporation: Orange County, CA, USA, 2017. [Google Scholar]
- Potapczuk, M.G. Aircraft icing research at NASA Glenn research center. J. Aerosp. Eng. 2013. [Google Scholar] [CrossRef]
- Liu, Y.C.; Farouk, T.; Savas, A.J.; Dryer, F.L.; Avedisian, C.T. On the spherically symmetrical combustion of methyl decanoate droplets and comparisons with detailed numerical modeling. Combust. Flame 2013, 160, 641–655. [Google Scholar] [CrossRef]
- Cen, C.; Wu, H.; Lee, C.f.; Liu, F.; Li, Y. Experimental investigation on the characteristic of jet break-up for butanol droplet impacting onto a heated surface in the film boiling regime. Int. J. Heat Mass Transf. 2018, 123, 129–136. [Google Scholar] [CrossRef]
- Zama, Y.; Odawara, Y.; Furuhata, T. Experimental investigation on velocity inside a diesel spray after impingement on a wall. Fuel 2017, 203, 757–763. [Google Scholar] [CrossRef]
- Pei, Y.; Qin, J.; Li, X.; Zhang, D.; Wang, K.; Liu, Y. Experimental investigation on free and impingement spray fueled with methanol, ethanol, isooctane, TRF and gasoline. Fuel 2017, 208, 174–183. [Google Scholar] [CrossRef]
- Labergue, A.; Gradeck, M.; Lemoine, F. Experimental investigation of spray impingement hydrodynamic on a hot surface at high flow rates using phase Doppler analysis and infrared thermography. Int. J. Heat Mass Transf. 2016, 100, 65–78. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Tembely, M.; Jadidi, M.; Esmail, N.; Dolatabadi, A. Shear driven droplet shedding and coalescence on a superhydrophobic surface. Phys. Fluids 2015. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Mohammadi, M.; Jadidi, M.; Tembely, M.; Dolatabadi, A. Shear Driven Droplet Shedding on Surfaces with Various Wettabilities. SAE Int. J. Aerosp. 2013. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Ahmmed, K.M.T.; Lee, C.; Dolatabadi, A.; Kietzig, A.M. Experimental study of droplet shedding on laser-patterned substrates. Phys. Fluids 2019. [Google Scholar] [CrossRef]
- Knausgård, K. Superhydrophobic Anti-Ice Nanocoatings. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg. Sci. Technol. 2011. [Google Scholar] [CrossRef]
- Sarkar, D.K.; Farzaneh, M. Superhydrophobic coatings with reduced ice adhesion. J. Adhes. Sci. Technol. 2009. [Google Scholar] [CrossRef]
- Cao, L.; Jones, A.K.; Sikka, V.K.; Wu, J.; Gao, D. Anti-Icing superhydrophobic coatings. Langmuir 2009, 25, 12444–12448. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Jadidi, M.; Dolatabadi, A.; Esmail, N. SPH Simulation of Rivulet Dynamics on Surfaces with Various Wettabilities. SAE Int. J. Aerosp. 2015. [Google Scholar] [CrossRef]
- Chandra, S.; Fauchais, P. Formation of solid splats during thermal spray deposition. J. Therm. Spray Technol. 2009. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Pershin, V.; Chandra, S.; Mostaghimi, J. Splat shapes in a thermal spray coating process: Simulations and experiments. J. Therm. Spray Technol. 2002. [Google Scholar] [CrossRef]
- Jadidi, M.; Moghtadernejad, S.; Dolatabadi, A. A comprehensive review on fluid dynamics and transport of suspension/liquid droplets and particles in High-Velocity Oxygen-Fuel (HVOF) thermal spray. Coatings 2015, 5, 576–645. [Google Scholar] [CrossRef]
- Jadidi, M.; Vardelle, A.; Dolatabadi, A.; Moreau, C. Heat transfer in suspension plasma spraying. In Handbook of Thermal Science and Engineering; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Fauchais, P.L.; Heberlein, J.V.R.; Boulos, M.I. Thermal Spray Fundamentals: From Powder to Part; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Jadidi, M.; Moghtadernejad, S.; Dolatabadi, A. Penetration and breakup of liquid jet in transverse free air jet with application in suspension-solution thermal sprays. Mater. Des. 2016. [Google Scholar] [CrossRef]
- Jabbari, F.; Jadidi, M.; Wuthrich, R.; Dolatabadi, A. A numerical study of suspension injection in plasma-spraying process. J. Therm. Spray Technol. 2014. [Google Scholar] [CrossRef]
- Jadidi, M.; Yeganeh, A.Z.; Dolatabadi, A. Numerical Study of Suspension HVOF Spray and Particle Behavior Near Flat and Cylindrical Substrates. J. Therm. Spray Technol. 2018. [Google Scholar] [CrossRef]
- Parizi, H.B.; Rosenzweig, L.; Mostaghimi, J.; Chandra, S.; Coyle, T.; Salimi, H.; Pershin, L.; McDonald, A.; Moreau, C. Numerical simulation of droplet impact on patterned surfaces. J. Therm. Spray Technol. 2007. [Google Scholar] [CrossRef]
- Jadidi, M.; Moghtadernejad, S.; Dolatabadi, A. Numerical Modeling of Suspension HVOF Spray. J. Therm. Spray Technol. 2016. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Chandra, S.; Mostaghimi, J. A three-dimensional model of droplet impact and solidification. Int. J. Heat Mass Transf. 2002. [Google Scholar] [CrossRef]
- Jadidi, M.; Mousavi, M.; Moghtadernejad, S.; Dolatabadi, A. A Three-Dimensional Analysis of the Suspension Plasma Spray Impinging on a Flat Substrate. J. Therm. Spray Technol. 2014. [Google Scholar] [CrossRef]
- Yan, Z.; Zhao, R.; Duan, F.; Wong, T.N.; Toh, K.C.; Choo, K.F.; Chan, P.K.; Chua, Y.S. Spray Cooling. In Two Phase Flow, Phase Change and Numerical Modeling; Ahsan, A., Ed.; IntechOpen: London, UK, 2011; Available online: https://www.intechopen.com/books/two-phase-flow-phase-change-and-numerical-modeling/spray-cooling (accessed on 1 July 2020). [CrossRef]
- Horacek, B.; Kiger, K.T.; Kim, J. Single nozzle spray cooling heat transfer mechanisms. Int. J. Heat Mass Transf. 2005. [Google Scholar] [CrossRef]
- Jia, W.; Qiu, H.H. Experimental investigation of droplet dynamics and heat transfer in spray cooling. Exp. Therm. Fluid Sci. 2003. [Google Scholar] [CrossRef]
- Kim, J. Spray cooling heat transfer: The state of the art. Int. J. Heat Fluid Flow 2007. [Google Scholar] [CrossRef]
- Sodtke, C.; Stephan, P. Spray cooling on micro structured surfaces. Int. J. Heat Mass Transf. 2007. [Google Scholar] [CrossRef]
- Breitenbach, J.; Roisman, I.V.; Tropea, C. From drop impact physics to spray cooling models: A critical review. Exp. Fluids 2018. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wijshoff, H. Drop dynamics in the inkjet printing process. Curr. Opin. Colloid Interface Sci. 2018. [Google Scholar] [CrossRef]
- Gan, H.Y.; Shan, X.; Eriksson, T.; Lok, B.K.; Lam, Y.C. Reduction of droplet volume by controlling actuating waveforms in inkjet printing for micro-pattern formation. J. Micromech. Microeng. 2009. [Google Scholar] [CrossRef]
- Castrejón-Pita, J.R.; Martin, G.D.; Hoath, S.D.; Hutchings, I.M. A simple large-scale droplet generator for studies of inkjet printing. Rev. Sci. Instrum. 2008. [Google Scholar] [CrossRef]
- Daly, R.; Harrington, T.S.; Martin, G.D.; Hutchings, I.M. Inkjet printing for pharmaceutics—A review of research and manufacturing. Int. J. Pharm. 2015. [Google Scholar] [CrossRef]
- Yusof, A.; Keegan, H.; Spillane, C.D.; Sheils, O.M.; Martin, C.M.; O’Leary, J.J.; Zengerle, R.; Koltay, P. Inkjet-like printing of single-cells. Lab. Chip 2011. [Google Scholar] [CrossRef]
- Williams, C. Ink-jet printers go beyond paper. Phys. World 2006. [Google Scholar] [CrossRef]
- Fan, Y.Q.; Wang, H.L.; Gao, K.X.; Liu, J.J.; Chai, D.P.; Zhang, Y.J. Applications of Modular Microfluidics Technology. Chin. J. Anal. Chem. 2018, 46, 1863–1871. [Google Scholar] [CrossRef]
- Teh, S.Y.; Lin, R.; Hung, L.H.; Lee, A.P. Droplet microfluidics. Lab. Chip. 2008. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chang, C.L.; Wang, Y.N.; Fu, L.M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed]
- Grant, G.; Brenton, J.; Drysdale, D. Fire suppression by water sprays. Prog. Energy Combust. Sci. 2000. [Google Scholar] [CrossRef]
- Moon, J.H.; Kim, D.Y.; Lee, S.H. Spreading and receding characteristics of a non-Newtonian droplet impinging on a heated surface. Exp. Therm. Fluid Sci. 2014. [Google Scholar] [CrossRef]
- Rein, M. Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 1993. [Google Scholar] [CrossRef]
- Moon, J.H.; Lee, J.B.; Lee, S.H. Dynamic Behavior of Non-Newtonian Droplets Impinging on Solid Surfaces. Mater. Trans. 2013. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016. [Google Scholar] [CrossRef]
- Herbert, S.; Gambaryan-Roisman, T.; Stephan, P. Influence of the governing dimensionless parameters on heat transfer during single drop impingement onto a hot wall. Colloids Surf. A Physicochem. Eng. Asp. 2013. [Google Scholar] [CrossRef]
- Marengo, M.; Antonini, C.; Roisman, I.V.; Tropea, C. Drop collisions with simple and complex surfaces. Curr. Opin. Colloid Interface Sci. 2011. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, X.; Chen, R.; Liao, Q.; Ding, B. How supercooled superhydrophobic surfaces affect dynamic behaviors of impacting water droplets? Int. J. Heat Mass Transf. 2018, 124, 1025–1032. [Google Scholar]
- Bange, P.G.; Patil, N.D.; Bhardwaj, R. Impact Dynamics of a Droplet on a Heated Surface. In Proceedings of the 5th International Conference of Fluid Flow, Heat and Mass Transfer (FFHMT‘18), Niagara Falls, ON, Canada, 7–9 June 2018; Volume 190, pp. 232–247. [Google Scholar] [CrossRef]
- Guo, Y.; Shen, S.; Yang, Y.; Liang, G.; Zhen, N. Rebound and spreading during a drop impact on wetted cylinders. Exp. Therm. Fluid Sci. 2013, 52, 97–103. [Google Scholar] [CrossRef]
- Rioboo, R.; Tropea, C.; Marengo, M. Outcomes from a drop impact on solid surfaces. At. Sprays 2001. [Google Scholar] [CrossRef]
- Zhao, P.; Hargrave, G.K.; Versteeg, H.K.; Garner, C.P.; Reid, B.A.; Long, E.J.; Zhao, H. The dynamics of droplet impact on a heated porous surfac. Chem. Eng. Sci. 2018. [Google Scholar] [CrossRef]
- Rajesh, R.S.; Naveen, P.T.; Krishnakumar, K.; Ranjith, S.K. Dynamics of single droplet impact on cylindrically-curved superheated surfaces. Exp. Therm. Fluid Sci. 2019, 101, 251–262. [Google Scholar] [CrossRef]
- Pan, Y.; Shi, K.; Duan, X.; Naterer, G.F. Experimental investigation of water droplet impact and freezing on micropatterned stainless steel surfaces with varying wettabilities. Int. J. Heat Mass Transf. 2019, 129, 953–964. [Google Scholar] [CrossRef]
- Laan, N.; de Bruin, K.G.; Bartolo, D.; Josserand, C.; Bonn, D. Maximum diameter of impacting liquid droplets. Phys. Rev. Appl. 2014, 2, 044018. [Google Scholar] [CrossRef]
- Lee, J.B.; Laan, N.; de Bruin, K.G.; Skantzaris, G. Universal rescaling of drop impact on smooth and rough surfaces. J. Fluid Mech. 2016, 786, R4. [Google Scholar] [CrossRef]
- Jones, H. Cooling, freezing and substrate impact of droplets formed by rotary atomization. J. Phys. D Appl. Phys. 1971. [Google Scholar] [CrossRef]
- Chandra, S.; Avedisian, C.T. On the collision of a droplet with a solid surface. Proc. R. Soc. A Math. Phys. Eng. Sci. 1991. [Google Scholar] [CrossRef]
- Asai, A.; Shioya, M.; Hirasawa, S.; Okazaki, T. Impact of an ink drop on paper. J. Imaging Sci. Technol. 1993, 37, 205–207. [Google Scholar]
- Pasandideh-Fard, M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary effects during droplet impact on a solid surface. Phys. Fluids 1996. [Google Scholar] [CrossRef]
- Mao, T.; Kuhn, D.C.S.; Tran, H. Spread and Rebound of Liquid Droplets upon Impact on Flat Surfaces. AIChE J. 1997. [Google Scholar] [CrossRef]
- Ukiwe, C.; Kwok, D.Y. On the maximum spreading diameter of impacting droplets on well-prepared solid surfaces. Langmuir 2005. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Qin, M.; Weng, X.; Zhang, X.; Zhang, P.; Li, J.; Huang, Z.; Qin, M.; Weng, X.; Zhang, X.; et al. Dynamics of droplet impact on solid surface with different roughness. Int. J. Multiph. Flow 2017, 96, 56–69. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, H.; Yang, Z. International Journal of Heat and Mass Transfer The impact and freezing processes of a water droplet on different cold cylindrical surfaces. Int. J. Heat Mass Transf. 2017, 113, 318–323. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, Z.; Sui, D.; Yang, Z. The impact and freezing processes of a water droplet on different inclined cold surfaces. Int. J. Heat Mass Transf. 2016, 97, 211–223. [Google Scholar]
- Zhang, H.; Jin, Z.; Jiao, M.; Yang, Z. Experimental investigation of the impact and freezing processes of a water droplet on different cold concave surfaces. Int. J. Therm. Sci. 2018, 132, 498–508. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, H.; Yang, Z. Experimental investigation of the impact and freezing processes of a water droplet on an ice surface. Int. J. Heat Mass Transf. 2017. [Google Scholar] [CrossRef]
- Ju, J.; Jin, Z.; Zhang, H.; Yang, Z.; Zhang, J. The impact and freezing processes of a water droplet on different cold spherical surfaces. Exp. Therm. Fluid Sci. 2018. [Google Scholar] [CrossRef]
- Zhang, R.; Hao, P.; Zhang, X.; He, F. Supercooled water droplet impact on superhydrophobic surfaces with various roughness and temperature. Int. J. Heat Mass Transf. 2018, 122, 395–402. [Google Scholar] [CrossRef]
- Liang, G.; Guo, Y.; Mu, X.; Shen, S. Experimental investigation of a drop impacting on wetted spheres. Exp. Therm. Fluid Sci. 2014, 55, 150–157. [Google Scholar] [CrossRef]
- Burzynski, D.A.; Bansmer, S.E. Droplet splashing on thin moving films at high Weber numbers. Int. J. Multiph. Flow 2018, 101, 202–211. [Google Scholar] [CrossRef]
- Zen, T.S.; Chou, F.C.; Ma, J.L. Ethanol drop impact on an inclined moving surface. Int. Commun. Heat Mass Transf. 2010, 37, 1025–1030. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, W.W.; Nagel, S.R. Drop splashing on a dry smooth surface. Phys. Rev. Lett. 2005. [Google Scholar] [CrossRef]
- Allen, R.F. The role of surface tension in splashing. J. Colloid Interface Sci. 1975. [Google Scholar] [CrossRef]
- Thoroddsen, S.T.; Sakakibara, J. Evolution of the fingering pattern of an impacting drop. Phys. Fluids 1998. [Google Scholar] [CrossRef]
- Breitenbach, J.; Roisman, I.V.; Tropea, C. Drop collision with a hot, dry solid substrate: Heat transfer during nucleate boiling. Phys. Rev. Fluids 2017. [Google Scholar] [CrossRef]
- Leidenfrost, J.G. On the fixation of water in diverse fire. Int. J. Heat Mass Transf. 1966. [Google Scholar] [CrossRef]
- Kim, S.H.; Jiang, Y.; Kim, H. Droplet impact and LFP on wettability and nanostructured surface. Exp. Therm. Fluid Sci. 2018, 99, 85–93. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, W.l.; Peng, Y.h.; Jiang, L.j. Dynamic Leidenfrost temperature increase of impacting droplets containing high-alcohol surfactant. Int. J. Heat Mass Transf. 2018, 118, 1160–1168. [Google Scholar] [CrossRef]
- Chaudhary, G.; Li, R. Freezing of water droplets on solid surfaces: An experimental and numerical study. Exp. Therm. Fluid Sci. 2014. [Google Scholar] [CrossRef]
- Jung, S.; Tiwari, M.K.; Doan, N.V.; Poulikakos, D. Mechanism of supercooled droplet freezing on surfaces. Nat. Commun. 2012. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Roisman, I.V.; Tropea, C. Influence of solidification on the impact of supercooled water drops onto cold surfaces. Exp. Fluids 2015. [Google Scholar] [CrossRef]
- Mishchenko, L.; Hatton, B.; Bahadur, V.; Taylor, J.A.; Krupenkin, T.; Aizenberg, J. Design of ice-free nanostructured surfaces based on repulsion of impacting water droplets. ACS Nano 2010. [Google Scholar] [CrossRef] [PubMed]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944. [Google Scholar] [CrossRef]
- Gundersen, H.; Leinaas, H.P.; Thaulow, C. Surface structure and wetting characteristics of Collembola cuticles. PLoS ONE 2014, 9, e86783. [Google Scholar] [CrossRef]
- Vakarelski, I.U.; Patankar, N.A.; Marston, J.O.; Chan, D.Y.C.; Thoroddsen, S.T. Stabilization of Leidenfrost vapour layer by textured superhydrophobic surfaces. Nature 2012. [Google Scholar] [CrossRef]
- Phan, H.T.; Caney, N.; Marty, P.; Colasson, S.; Gavillet, J. Surface wettability control by nanocoating: The effects on pool boiling heat transfer and nucleation mechanism. Int. J. Heat Mass Transf. 2009. [Google Scholar] [CrossRef]
- Kandlikar, S.G. A Theoretical Model to Predict Pool Boiling CHF Incorporating Effects of Contact Angle and Orientation. J. Heat Transf. 2001. [Google Scholar] [CrossRef]
- Hamdan, K.S.; Kim, D.E.; Moon, S.K. Droplets behavior impacting on a hot surface above the Leidenfrost temperature. Ann. Nucl. Energy 2015, 80, 338–347. [Google Scholar] [CrossRef]
- Yun, S.; Hong, J.; Kang, K.H. Suppressing drop rebound by electrically driven shape distortion. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013. [Google Scholar] [CrossRef]
- Yun, S.; Lim, G. Ellipsoidal drop impact on a solid surface for rebound suppression. J. Fluid Mech. 2014. [Google Scholar] [CrossRef]
- Yun, S.; Lim, G. Control of a bouncing magnitude on a heated substrate via ellipsoidal drop shape. Appl. Phys. Lett. 2014. [Google Scholar] [CrossRef]
- Yun, S. Bouncing of an ellipsoidal drop on a superhydrophobic surface. Sci. Rep. 2017. [Google Scholar] [CrossRef]
- Yun, S. Impact dynamics of egg-shaped drops on a solid surface for suppression of the bounce magnitude. Int. J. Heat Mass Transf. 2018, 127, 172–178. [Google Scholar] [CrossRef]
- Bobinski, T.; Sobieraj, G.; Gumowski, K.; Rokicki, J.; Psarski, M.; Marczak, J.; Celichowski, G. Droplet impact in icing conditions—The influence of ambient air humidity. Arch. Mech. 2014. [Google Scholar] [CrossRef]
- Jadidi, M.; Trepanier, J.Y.; Farzad, M.A.; Dolatabadi, A. Effects of ambient air relative humidity and surface temperature on water droplet spreading dynamics. FEDSM 2018. [Google Scholar] [CrossRef]
- Povarov, O.A.; Nazarov, O.I.; Ignat’evskaya, L.A.; Nikol’skii, A.I. Interaction of drops with boundary layer on rotating surface. J. Eng. Phys. 1976. [Google Scholar] [CrossRef]
- Mundo, C.; Sommerfeld, M.; Tropea, C. Droplet-wall collisions: Experimental studies of the deformation and breakup process. Int. J. Multiph. Flow 1995. [Google Scholar] [CrossRef]
- Yao, S.C.; Cai, K.Y. The dynamics and leidenfrost temperature of drops impacting on a hot surface at small angles. Exp. Therm. Fluid Sci. 1988. [Google Scholar] [CrossRef]




| Dimensionless Number | Formulation |
|---|---|
| Weber number (ratio of inertial to surface tension forces) | |
| Reynolds number (ratio of inertial to viscous forces) | |
| Ohnesorge number | |
| Bond number (ratio of gravitational to surface tension forces) | |
| Dimensionless time | |
| Spreading ratio | |
| Prandtl number | |
| Stefan number | |
| Ratio of the thermal effusivity of the liquid and the solid | |
| Ratio of specific heat capacities | |
| Ratio of the total heat Q transferred to the droplet to the maximal possible heat transfer | |
| Evaporation efficiency |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghtadernejad, S.; Lee, C.; Jadidi, M. An Introduction of Droplet Impact Dynamics to Engineering Students. Fluids 2020, 5, 107. https://doi.org/10.3390/fluids5030107
Moghtadernejad S, Lee C, Jadidi M. An Introduction of Droplet Impact Dynamics to Engineering Students. Fluids. 2020; 5(3):107. https://doi.org/10.3390/fluids5030107
Chicago/Turabian StyleMoghtadernejad, Sara, Christian Lee, and Mehdi Jadidi. 2020. "An Introduction of Droplet Impact Dynamics to Engineering Students" Fluids 5, no. 3: 107. https://doi.org/10.3390/fluids5030107
APA StyleMoghtadernejad, S., Lee, C., & Jadidi, M. (2020). An Introduction of Droplet Impact Dynamics to Engineering Students. Fluids, 5(3), 107. https://doi.org/10.3390/fluids5030107







