The Effect of the Vadasz Number on the Onset of Thermal Convection in Rotating Bidispersive Porous Media

Abstract

The onset of thermal convection in uniformly rotating bidispersive horizontal porous layer, uniformly heated from below, is analyzed. A generalized Darcy equation for the macro-phase is considered to take the Vadasz number into account. It is proved that the presence of the Vadasz number can give rise to oscillatory motion at the loss of stability of thermal conduction solution.

1. Introduction

The onset of thermal convection is a very active research field due to the numerous applications in real world phenomena (see, for example, [1,2,3] and references therein). Recently, a great attention has been played to bidispersive porous media. A bidispersive porous medium is composed by clusters of large particles that are agglomerations of small particles that can be looked as a porous medium in which fractures or tunnels are introduced (see [4,5,6]). Denoting by $\mathsf{\Phi }$ and $\epsilon$ the porosity associated with the macro pores between the clusters and the porosity of the micro pores within the clusters, respectively, the fraction of volume occupied by the micro pores is $\epsilon (1-\mathsf{\Phi })$ while the solid skeleton occupies the fraction of volume $(1-\epsilon )(1-\mathsf{\Phi })$. Bidispersive porous media may be artificial [6] and they are involved in many real engineering processes and geophysical applications, such as, for example, in thermal convection in heat pipes [7], in the theory of landslides [8], as catalyst in the production of high octane petrol [9].

Recently, in [10], the effect of Vadasz number on thermohaline convection in a horizontal bidispersive layer, has been investigated. In particular, the destabilizing effect of heating from below opposite to the stabilizing effect of the layer salted from below is studied. The effect of Vadasz number has been widely studied for a single porosity medium [11,12,13,14,15,16,17,18,19], together with other effects, such as the influence of an external magnetic field acting on an electrically conducting fluid [15] and the presence of a chemical dissolved in the fluid [16]. In these models, a generalized Darcy equation is employed to include the time derivative term, multiplied by a positive constant, of the seepage velocity. In [18], Vadasz pointed out that the inertia term has a strong effect on the onset of convection in a rotating porous layer. The uniform rotation in porous media finds relevant applications in the food process industry, in geophysics, and in the chemical industry dealing with rotating machinery. For this reason, many papers are devoted to the onset of thermal convection in rotating porous media (see, for example, [20,21,22,23,24,25,26] and references therein). As it is well known, convection can be named steady or oscillatory according to the secondary motion, arising when the initial rest state loses its stability, is steady or oscillatory. The transition from the steady rest state to an oscillatory solution (i.e., the onset of oscillatory convection) captures the interest of many researchers, because it is “less continuous” with respect to the onset of steady convection and because the oscillatory convection is used in various fields that involve industrial and geophysical processes. Recently, in [27], the Coriolis effect has been analyzed in bidispersive porous layers showing that the thermal convection can only arise via a steady state (i.e., the principle of exchange of stability holds).

In this paper we reconsider the problem analyzed in [27], and investigate the effect of inertia in a rotating bidispersive porous medium. We consider the inertia term in the macro-phase only (since inertia effect can be neglected in the micro-phase) and show that inertia allows oscillatory convection at the instability threshold, as done in [10]. The plan of the paper is as follows. Section 2 is devoted to the introduction of mathematical model. To this aim, we consider the generalized Darcy equation for the macro-phase only [10] and assume the same temperature in the macro and micro pores [28]. The linear instability is performed in Section 3. In particular, Section 3.1 and Section 3.2 are respectively devoted to the determination of the critical Rayleigh number for the onset of steady and oscillatory convection, where the steady or oscillatory convection respectively means that—when the rest state loses its stability—the convection arises via a steady or via an oscillatory (in time) state. In Section 4 the behaviour of the Rayleigh number for the onset of oscillatory convection with respect to the Taylor number and the acceleration coefficients is numerically investigated. The paper ends with a conclusion section in which the obtained results are summarized.

2. Preliminaries

Let us consider a homogeneous incompressible fluid filling a horizontal bidisperse porous layer $\mathtt{L}$ of depth d, uniformly heated from below and rotating about a vertical axis. Let us introduce $Oxyz$, which is an orthogonal frame of reference with fundamental unit vectors $\mathbf{i},\mathbf{j},\mathbf{k}$ ($\mathbf{k}$ pointing vertically upwards) and denote by $\mathsf{\Omega }=\mathsf{\Omega }\mathbf{k}$ the constant angular velocity of $\mathtt{L}$. The aim of this paper is to investigate the influence of inertia effect on the onset of convection in bidispersive rotating porous medium, but considering the effect of a non-zero inertia term in the macro fluid velocity equation. In such a way, we restrict our attention to the more mathematically difficult, but contemporarily more physically interesting, case: in the analyzed situation, the heating wishes to destabilize the layer and initiate convective overturning, whereas the rotation of the layer acts in the opposite manner and it is stabilizing. The inertia term will be seen to have a very strong effect on the convection thresholds and we believe this is a justification for the analysis. When the inertial term is taken into account in the momentum equation of the macro-phase, the fluid motion is governed by the equations ([6,10,27])

$$\left\{\begin{array}{c}{\displaystyle {\rho }_0{c}_a{\mathbf{U}}_{,t}^f=-\frac{\mu }{k_f}{\mathbf{U}}^f-\delta ({\mathbf{U}}^f-{\mathbf{U}}^p)-\mathsf{\nabla }{p}^f+{\rho }_{0}g\alpha T\mathbf{k}-\frac{2{\rho }_0\mathsf{\Omega }}{\mathsf{\Phi }}\mathbf{k}\times {\mathbf{U}}^f,}\hfill \\ \\ {\displaystyle -\frac{\mu }{k_p}{\mathbf{U}}^p-\delta ({\mathbf{U}}^p-{\mathbf{U}}^f)-\mathsf{\nabla }{p}^p+{\rho }_{0}g\alpha T\mathbf{k}-\frac{2{\rho }_0\mathsf{\Omega }}{\epsilon }\mathbf{k}\times {\mathbf{U}}^p=\mathbf{0},}\hfill \\ \\ {\left(\rho c\right)}_m{T}_{,t}+{\left(\rho c\right)}_f({\mathbf{U}}^f+{\mathbf{U}}^p)·\mathsf{\nabla }T=k_m\mathsf{\Delta }T,\hfill \\ \\ \mathsf{\nabla }·{\mathbf{U}}^f=0,\mathsf{\nabla }·{\mathbf{U}}^p=0,\hfill \end{array}\right.$$

(1)

with

$${\displaystyle p^s=P^s-\frac{{\rho }_0}{2}{|\mathsf{\Omega }\mathbf{k}\times \mathbf{x}|}^2}$$

$${\left(\rho c\right)}_m=(1-\mathsf{\Phi })(1-\epsilon ){\left(\rho c\right)}_s+\mathsf{\Phi }{\left(\rho c\right)}_f+\epsilon (1-\mathsf{\Phi }){\left(\rho c\right)}_p$$

$$k_m=(1-\mathsf{\Phi })(1-\epsilon )k_s+\mathsf{\Phi }{k}_f+\epsilon (1-\mathsf{\Phi })k_p$$

and ${\mathbf{U}}^s$ is the seepage velocity, T is the temperature, $P^s$ is the pressure, $c_a$ is the acceleration coefficient, $\delta$ is the interaction coefficient, $\mathbf{g}=-g\mathbf{k}$ is the gravity, $\mathbf{x}=(x,y,z)$, $\mu$ is the fluid viscosity, ${\rho }_0$ is the reference (constant) density, $k_r$ is the permeability, $\alpha$ is the thermal expansion coefficient, c is the specific heat, $c_p$ is the specific heat at a constant pressure, and $k_m$ is the thermal conductivity. Moreover, ${(·)}_{,t}$ denotes the partial derivative with respect to t and $s=\{f,p\}$ being the subscript f and p referring to the macro and micro pore effects. To (1), we append the boundary conditions

$$\begin{array}{c}T(x,y,0,t)=T_L,T(x,y,d,t)=T_U,T_L>T_U,\hfill \\ \\ {\mathbf{U}}^s·\mathbf{n}=0,\mathrm{on}z=0,d,s=\{f,p\},\hfill \end{array}$$

(2)

being $\mathbf{n}$ the unit vector in the upward vertical direction. Model (1)–(2) admits the thermal conduction solution

$${\displaystyle {\mathbf{U}}_b^f=\mathbf{0},{\mathbf{U}}_b^p=\mathbf{0},T_b=-\beta z+T_L,\beta =\frac{T_L-T_U}{d}.}$$

(3)

Introducing the perturbation fields

$${\mathbf{u}}^s={\mathbf{U}}^s-{\mathbf{U}}_b^s,{\pi }^s=P^s-p_b,\theta =T-T_b,s=\{f,p\}$$

(4)

setting

$$\left\{\begin{array}{c}\mathbf{x}=d{\mathbf{x}}_{*},t=\mathcal{I}{t}_{*},\theta ={\theta }_{*}{T}^{♯},{\mathbf{u}}^s=U{\mathbf{u}}_{*}^s,{\pi }^s=P{\pi }_{*}^s,s=\{f,p\},\hfill \\ {\displaystyle \mathcal{I}=\frac{{\left(\rho c\right)}_m{d}^2}{k_m},U=\frac{k_m}{{\left(\rho c\right)}_{f}d},T^{♯}=\beta d,P=\frac{k_m\mu }{k_f{\left(\rho c\right)}_f}}\hfill \end{array}\right.$$

(5)

the non-dimensional system (omitting the asterisks) governing the evolution of perturbation fields is

$$\left\{\begin{array}{c}-J{\mathbf{u}}_{,t}^f-{\mathbf{u}}^f-\gamma ({\mathbf{u}}^f-{\mathbf{u}}^p)-\mathsf{\nabla }{\pi }^f+R\theta \mathbf{k}-\mathcal{T}\mathbf{k}\times {\mathbf{u}}^f=\mathbf{0},\hfill \\ \\ -k_r{\mathbf{u}}^p-\gamma ({\mathbf{u}}^p-{\mathbf{u}}^f)-\mathsf{\nabla }{\pi }^p+R\theta \mathbf{k}-\eta \mathcal{T}\mathbf{k}\times {\mathbf{u}}^p=\mathbf{0},\hfill \\ \\ {\theta }_{,t}+({\mathbf{u}}^f+{\mathbf{u}}^p)·\mathsf{\nabla }\theta =w^f+w^p+\mathsf{\Delta }\theta ,\hfill \\ \\ \mathsf{\nabla }·{\mathbf{u}}^f=0,\mathsf{\nabla }·{\mathbf{u}}^p=0,\hfill \end{array}\right.$$

(6)

with ${\mathbf{u}}^f=(u^f,v^f,w^f),{\mathbf{u}}^p=(u^p,v^p,w^p)$ and

$$\left\{\begin{array}{c}{\displaystyle J=\frac{{\rho }_0{c}_a{k}_f{k}_m}{{\left(\rho c\right)}_m\mu d^2}=\mathrm{Vadasz}\mathrm{number},}\hfill \\ {\displaystyle \gamma =\frac{\delta k_f}{\mu },\mathcal{T}=\frac{2{\rho }_0\mathsf{\Omega }{k}_f}{\mu \mathsf{\Phi }}=\mathrm{Taylor}\mathrm{number},k_r=\frac{k_f}{k_p},\eta =\frac{\mathsf{\Phi }}{\epsilon },}\hfill \\ {\displaystyle R=\frac{{\rho }_0\alpha g\beta d^2{k}_f{\left(\rho c\right)}_f}{\mu k_m}=\mathrm{Rayleigh}\mathrm{thermal}\mathrm{number}.}\hfill \end{array}\right.$$

(7)

To (6) we append smooth initial data

$${\mathbf{u}}^s(\mathbf{x},0)={\mathbf{u}}_0^s\left(\mathbf{x}\right);{\pi }^s(\mathbf{x},0)={\pi }_0^s\left(\mathbf{x}\right);\theta (\mathbf{x},0)={\theta }_0\left(\mathbf{x}\right)$$

(8)

with $\mathsf{\nabla }·{\mathbf{u}}_0^s=0,s=\{f,p\}$ and the boundary conditions

$$w^f=w^p=\theta =0,\mathrm{on}z=0,1.$$

(9)

In the sequel, we perform the linear stability analysis of the null solution of (6)–(9) under the assumption that the perturbations $\{u^s,v^s,w^s,{\pi }^s,\theta \}$ ($s=\{f,p\}$) are periodic in the horizontal directions x and y, respectively, of period $2\pi /a_x$, $2\pi /a_y$ and denote by

$$V=\left[{\displaystyle 0,\frac{2\pi }{a_x}}\right]\times \left[{\displaystyle 0,\frac{2\pi }{a_y}}\right]\times [0,1]$$

the periodicity cell.

3. Linear Instability

Neglecting the nonlinear terms, (6) reduces to

$$\left\{\begin{array}{c}-J{\mathbf{u}}_{,t}^f-{\mathbf{u}}^f-\gamma ({\mathbf{u}}^f-{\mathbf{u}}^p)-\mathsf{\nabla }{\pi }^f+R\theta \mathbf{k}-\mathcal{T}\mathbf{k}\times {\mathbf{u}}^f=\mathbf{0},\hfill \\ \\ -k_r{\mathbf{u}}^p-\gamma ({\mathbf{u}}^p-{\mathbf{u}}^f)-\mathsf{\nabla }{\pi }^p+R\theta \mathbf{k}-\eta \mathcal{T}\mathbf{k}\times {\mathbf{u}}^p=\mathbf{0},\hfill \\ \\ {\theta }_{,t}=w^f+w^p+\mathsf{\Delta }\theta ,\hfill \\ \\ \mathsf{\nabla }·{\mathbf{u}}^f=0,\mathsf{\nabla }·{\mathbf{u}}^p=0,\hfill \end{array}\right.$$

(10)

under the boundary conditions (9). Setting

$${\zeta }^s=(\mathsf{\nabla }\times {\mathbf{u}}^s)·\mathbf{k},s=\{f,p\},$$

(11)

the third components of the curl of (10)${}_1$ and (10)${}_2$, respectively, lead to the following equations:

$$\left\{\begin{array}{c}J{\zeta }_{,t}^f+{\zeta }^f+\gamma ({\zeta }^f-{\zeta }^p)-\mathcal{T}{w}_{,z}^f=0,\hfill \\ \\ k_r{\zeta }^p+\gamma ({\zeta }^p-{\zeta }^f)-\eta \mathcal{T}{w}_{,z}^p=0.\hfill \end{array}\right.$$

(12)

Since the system (10) is autonomous, setting $\forall \phi \in \{u^s,v^s,w^s,{\pi }^s,\theta \}$

$$\phi (x,y,z,t)=\tilde{\phi }(x,y,z)e^{\sigma t}$$

(13)

with $\sigma \in \mathbb{C}$ and substituting, respectively, in (12)${}_1$ and in (12)${}_2$, one has that:

$$\left\{\begin{array}{c}(J\sigma +1+\gamma ){\zeta }^f-\gamma {\zeta }^p-\mathcal{T}{w}_{,z}^f=0,\hfill \\ \\ (\gamma +k_r){\zeta }^p-\gamma {\zeta }^f-\eta \mathcal{T}{w}_{,z}^p=0,\hfill \end{array}\right.$$

(14)

i.e.,

$$\left\{\begin{array}{c}{\displaystyle {\zeta }^f=\frac{\mathcal{T}(\gamma +k_r)}{A}{w}_{,z}^f+\frac{\eta \gamma \mathcal{T}}{A}{w}_{,z}^p,}\hfill \\ \\ {\displaystyle {\zeta }^p=\frac{\eta \mathcal{T}(1+\sigma J+\gamma )}{A}{w}_{,z}^p+\frac{\gamma \mathcal{T}}{A}{w}_{,z}^f,}\hfill \end{array}\right.$$

(15)

being

$$A=(\gamma +k_r)(1+\sigma J)+\gamma k_r.$$

(16)

The third components of the double curl of (10)${}_1$–(12)${}_2$ are, respectively

$$\left\{\begin{array}{c}(1+\sigma J+\gamma )\mathsf{\Delta }{w}^f-\gamma \mathsf{\Delta }{w}^p-R{\mathsf{\Delta }}_1\theta +\mathcal{T}{\zeta }_{,z}^f=0,\hfill \\ \\ -\gamma \mathsf{\Delta }{w}^f+(\gamma +k_r)\mathsf{\Delta }{w}^p-R{\mathsf{\Delta }}_1\theta +\eta \mathcal{T}{\zeta }_{,z}^p=0,\hfill \end{array}\right.$$

(17)

with

$${\displaystyle {\mathsf{\Delta }}_1=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2},\mathsf{\Delta }={\mathsf{\Delta }}_1+\frac{{\partial }^2}{\partial z^2}.}$$

The derivative with respect to z of (15)${}_1$ and (15)${}_2$ leads to:

$$\left\{\begin{array}{c}{\displaystyle {\zeta }_{,z}^f=\frac{\mathcal{T}(\gamma +k_r)}{A}{w}_{,zz}^f+\frac{\eta \gamma \mathcal{T}}{A}{w}_{,zz}^p,}\hfill \\ \\ {\displaystyle {\zeta }_{,z}^p=\frac{\gamma \mathcal{T}}{A}{w}_{,zz}^f+\frac{\eta \mathcal{T}(1+\sigma J+\gamma )}{A}{w}_{,zz}^p}\hfill \end{array}\right.$$

(18)

and substituting (18) into (17), one has that

$$\left\{\begin{array}{c}(1+\sigma J+\gamma )\mathsf{\Delta }{w}^f-\gamma \mathsf{\Delta }{w}^p-R{\mathsf{\Delta }}_1\theta +{\mathcal{T}}^2\left[{\displaystyle \frac{\gamma +k_r}{A}{w}_{,zz}^f+\frac{\eta \gamma }{A}{w}_{,zz}^p}\right],\hfill \\ \\ -\gamma \mathsf{\Delta }{w}^f+(\gamma +k_r)\mathsf{\Delta }{w}^p-R{\mathsf{\Delta }}_1\theta +\eta {\mathcal{T}}^2\left[{\displaystyle \frac{\gamma }{A}{w}_{,zz}^f+\frac{\eta (1+\sigma J+\gamma )}{A}{w}_{,zz}^p}\right].\hfill \end{array}\right.$$

(19)

On taking into account (19) and (10)${}_3$–(10)${}_5$, let us consider the following initial-boundary value problem

$$\left\{\begin{array}{c}(1+\sigma J+\gamma )\mathsf{\Delta }{w}^f-\gamma \mathsf{\Delta }{w}^p-R{\mathsf{\Delta }}_1\theta +{\mathcal{T}}^2\left[{\displaystyle \frac{\gamma +k_r}{A}{w}_{,zz}^f+\frac{\eta \gamma }{A}{w}_{,zz}^p}\right],\hfill \\ \\ -\gamma \mathsf{\Delta }{w}^f+(\gamma +k_r)\mathsf{\Delta }{w}^p-R{\mathsf{\Delta }}_1\theta +\eta {\mathcal{T}}^2\left[{\displaystyle \frac{\gamma }{A}{w}_{,zz}^f+\frac{\eta (1+\sigma J+\gamma )}{A}{w}_{,zz}^p}\right],\hfill \\ \\ \sigma \theta =w^f+w^p+\mathsf{\Delta }\theta ,\hfill \\ \\ \mathsf{\nabla }·{\mathbf{u}}^f=0,\mathsf{\nabla }·{\mathbf{u}}^p=0,\hfill \end{array}\right.$$

(20)

$${\mathbf{u}}^s(\mathbf{x},0)={\mathbf{u}}_0^s\left(\mathbf{x}\right);{\pi }^s(\mathbf{x},0)={\pi }_0^s\left(\mathbf{x}\right);\theta (\mathbf{x},0)={\theta }_0\left(\mathbf{x}\right)$$

(21)

$$w^f=w^p=\theta =0,\mathrm{on}z=0,1$$

(22)

and let us look for normal modes solutions, i.e.,:

$$\phi (x,y,z,t)=\tilde{\phi }\left(z\right)e^{i(a_{x}x+a_{y}y)+\sigma t},\forall \phi \in \{w^f,w^p,\theta \}.$$

(23)

Setting ${\displaystyle D=\frac{d}{dz},a^2=a_x^2+a_x^2}$, it follows that

$${\mathsf{\Delta }}_1\phi =-a^2\phi ,\mathsf{\Delta }\phi =(D^2-a^2)\phi ,\forall \phi \in \{w^f,w^p,\theta \}.$$

(24)

Then, by virtue of (23) and (24), (20)${}_1$–(20)${}_3$ can be written as

$$\left\{\begin{array}{c}(1+\sigma J+\gamma )(D^2-a^2){\tilde{w}}^f-\gamma (D^2-a^2){\tilde{w}}^p+R{a}^2\tilde{\theta }+\frac{{\mathcal{T}}^2}{A}\left[(\gamma +k_r)D^2{\tilde{w}}^f+\eta \gamma D^2{\tilde{w}}^p\right]=0,\hfill \\ \\ {\displaystyle -\gamma (D^2-a^2){\tilde{w}}^f+(\gamma +k_r)(D^2-a^2){\tilde{w}}^p+R{a}^2\tilde{\theta }+\frac{\eta {\mathcal{T}}^2}{A}\left[\gamma D^2{\tilde{w}}^f+\eta (1+\sigma J+\gamma )D^2{\tilde{w}}^p\right]=0,}\hfill \\ \\ \sigma \tilde{\theta }={\tilde{w}}^f+{\tilde{w}}^p+(D^2-a^2)\tilde{\theta }.\hfill \end{array}\right.$$

(25)

In view of the boundary conditions, since the set ${\{sinn\pi z\}}_{n\in \mathbb{N}}$ is a complete orthogonal system for $L^2(0,1)$, $\forall \tilde{\phi }\left(z\right)\in \{{\tilde{w}}^f,{\tilde{w}}^p,\tilde{\theta }\}$ there exists a sequence ${\left\{{\tilde{\phi }}_n\left(z\right)\right\}}_{n\in \mathbb{N}}$ such that ${\displaystyle \tilde{\phi }\left(z\right)=\sum _{n=1}^{\infty }{\tilde{\phi }}_{0}sinn\pi z}$. Subsequently, setting ${\mathsf{\Lambda }}_n=a^2+n^2{\pi }^2$, (25) becomes

$$\left\{\begin{array}{c}-\left[{\displaystyle {\mathsf{\Lambda }}_n(1+\sigma J+\gamma )+\frac{n^2{\pi }^2{\mathcal{T}}^2(\gamma +k_r)}{A}}\right]w_0^f+\left({\displaystyle {\mathsf{\Lambda }}_n\gamma -\frac{n^2{\pi }^2{\mathcal{T}}^2\eta \gamma }{A}}\right)w_0^p+R{a}^2{\theta }_0=0,\hfill \\ \\ \left({\displaystyle \gamma {\mathsf{\Lambda }}_n-\frac{n^2{\pi }^2{\mathcal{T}}^2\eta \gamma }{A}}\right)w_0^f-\left[{\displaystyle \mathsf{\Lambda }(\gamma +k_r)+\frac{n^2{\pi }^2{\mathcal{T}}^2{\eta }^2(1+\sigma J+\gamma )}{A}}\right]w_0^p+R{a}^2{\theta }_0=0,\hfill \\ \\ w_0^f+w_0^p-({\mathsf{\Lambda }}_n+\sigma ){\theta }_0=0.\hfill \end{array}\right.$$

(26)

From (26), the condition guaranteeing the existence of a non null solution is the following

$${\displaystyle R=\frac{{\mathsf{\Lambda }}_n+\sigma }{a^2}\frac{{\mathsf{\Lambda }}_n^2{A}^2+n^2{\pi }^2{\mathcal{T}}^2{\mathsf{\Lambda }}_{n}B+n^4{\pi }^4{\mathcal{T}}^4{\eta }^2}{{\mathsf{\Lambda }}_{n}AC+n^2{\pi }^2{\mathcal{T}}^{2}E},}$$

(27)

being

$$\begin{array}{c}B={(1+\sigma J+\gamma )}^2{\eta }^2+{(\gamma +k_r)}^2+2\eta {\gamma }^2,\hfill \\ \\ C=4\gamma +k_r+1+\sigma J,E=\gamma {(\eta -1)}^2+{\eta }^2(1+\sigma J)+k_r.\hfill \end{array}$$

(28)

As it is well known, the onset of convection occurs or via a steady state –associated to $\sigma =0$—and named “steady convection”, or via an oscillatory state—associated to $\sigma =\pm i{\sigma }_1$ with ${\sigma }_1\in {\mathbb{R}}^{+}\backslash \left\{0\right\}$—and named “oscillatory convection”. In the sequel, we determine the critical Rayleigh thermal number for the onset of steady and oscillatory convection.

3.1. Steady Convection

In order to determine the critical Rayleigh thermal number for the onset of steady convection, say $R_S$, we substitute $\sigma =0$ in (27). Then

$${\displaystyle R_S=\underset{(n,a^2)\in \mathbb{N}\times {\mathbb{R}}^{+}}{min}\frac{{\mathsf{\Lambda }}_n}{a^2}\frac{{\mathsf{\Lambda }}_n^2{A}_1^2+{\pi }^2{\mathcal{T}}^2{\mathsf{\Lambda }}_n{B}_1+n^4{\eta }^2{\pi }^4{\mathcal{T}}^4}{{\mathsf{\Lambda }}_n{A}_1{C}_1+n^2{\pi }^2{\mathcal{T}}^2{E}_1},}$$

(29)

with $A_1,B_1,C_1,E_1$ given by (16), (28) when $\sigma =0$, i.e.,

$$A_1=\gamma +k_r+\gamma k_r,B_1={(1+\gamma )}^2{\eta }^2+{(k_r+\gamma )}^2+2\eta {\gamma }^2,C_1=4\gamma +k_r+1,E_1=\gamma {(\eta -1)}^2+{\eta }^2+k_r.$$

(30)

The minimum with respect to $n\in \mathbb{N}$ of the right-hand side of (29) is attained at $n=1$. Then, setting $\mathsf{\Lambda }={\mathsf{\Lambda }}_1=a^2+{\pi }^2$, one has that

$${\displaystyle R_S=\underset{a^2\in {\mathbb{R}}^{+}}{min}{f}_s\left(a^2\right):=\underset{a^2\in {\mathbb{R}}^{+}}{min}\frac{{\mathsf{\Lambda }}^2{A}_1^2+{\pi }^2{\mathcal{T}}^2\mathsf{\Lambda }{B}_1+{\eta }^2{\pi }^4{\mathcal{T}}^4}{\mathsf{\Lambda }{A}_1{C}_1+{\pi }^2{\mathcal{T}}^2{E}_1}.}$$

(31)

Let us remark that $R_S$ does not depend on J, i.e., $R_S$ does not depend on the inertial term. Hence, $R_S$ coincides with the critical Rayleigh thermal number for the onset of steady convection in the absence of inertia term found in [27]. Furthermore, ${\displaystyle \frac{\partial R_S}{\partial {\mathcal{T}}^2}>0}$, i.e., ${\mathcal{T}}^2$ has a stabilizing effect on the onset of steady convection, as one is expected. When ${\mathcal{T}}^2=0$, $R_S$ reduces to

$${\displaystyle {\left(R_S\right)}_{{\mathcal{T}}^2=0}=\underset{a^2\in {\mathbb{R}}^{+}}{min}\frac{{\mathsf{\Lambda }}^2{A}_1}{a^2{C}_1},}$$

(32)

that is the critical Rayleigh number for the onset of steady convection found in [10] in the absence of rotation. The minimum of R evaluated for $\sigma =0$ with respect to $a^2$ is attained at $a^2=a_s^2$, with $a_s^2$ being a positive root of a fourth-order degree polynomial:

$$f\left(x\right):=A_1{C}_1{x}^4+c_1{x}^3+c_2{x}^2+c_{3}x-{\pi }^6{c}_4,$$

(33)

with $c_i$ constants and

$$c_4=\left({\displaystyle {\pi }^2{C}_1+\frac{{\pi }^2{\mathcal{T}}^2{E}_1}{A_1}}\right)\left({\displaystyle A_1+\frac{{\mathcal{T}}^2{B}_1}{A_1}+{\mathcal{T}}^4{\eta }^2}\right).$$

Since ${\displaystyle \underset{x\to \infty }{lim}f\left(x\right)=\infty ,f\left(0\right)<0}$, $a_s^2$ exists.

3.2. Oscillatory Convection

In order to determine the critical Rayleigh thermal number for the onset of oscillatory convection, say $R_O$, then we substitute $\sigma =i{\sigma }_1$ in (27), with i being the imaginary unit and ${\sigma }_1\in {\mathbb{R}}^{+}\backslash \left\{0\right\}$. Subsequently, we take the real and imaginary parts of R, require the vanishing of the imaginary part of R, substitute ${\sigma }_1^2$ into the real part of R, and determine the minimum—with respect to $(n,a^2)\in \mathbb{N}\times {\mathbb{R}}^{+}$—of the obtained number. Setting

$$\begin{array}{c}{A}_2=\gamma +k_r,B_2=2(1+\gamma ){\eta }^2,\hfill \end{array}$$

(34)

and

$$\begin{array}{c}{k}_{1n}={\mathsf{\Lambda }}_n^2{A}_1^2+n^2{\pi }^2{\mathcal{T}}^2{\mathsf{\Lambda }}_n{B}_1+n^4{\pi }^4{\mathcal{T}}^4{\eta }^2,k_{2n}={\mathsf{\Lambda }}_n({\mathsf{\Lambda }}_n{A}_2^2+n^2{\pi }^2{\mathcal{T}}^2{\eta }^2),\hfill \\ \\ k_{3n}={\mathsf{\Lambda }}_n(2{\mathsf{\Lambda }}_n{A}_1{A}_2+n^2{\pi }^2{\mathcal{T}}^2{B}_2),k_{4n}={\mathsf{\Lambda }}_n{A}_1{C}_1+n^2{\pi }^2{\mathcal{T}}^2{E}_1,\hfill \\ \\ k_{5n}={\mathsf{\Lambda }}_n{A}_2,k_{6n}={\mathsf{\Lambda }}_n(A_2{C}_1+A_1)+n^2{\pi }^2{\mathcal{T}}^2{\eta }^2,\hfill \end{array}$$

(35)

one obtains

$${\displaystyle R=\frac{{\mathsf{\Lambda }}_n+i{\sigma }_1}{a^2}\frac{k_{1n}-{\sigma }_1^2{J}^2{k}_{2n}+i{\sigma }_{1}J{k}_{3n}}{k_{4n}-{\sigma }_1^2{J}^2{k}_{5n}+i{\sigma }_{1}J{k}_{6n}}.}$$

(36)

Subsequently, one has that $R=R_e\left(R\right)+i{\sigma }_{1}Im\left(R\right)$ with

$$\begin{array}{c}{\displaystyle R_e\left(R\right)=f_o\left(a^2\right):=\frac{1}{a^2[{(k_{4n}-{\sigma }_1^2{J}^2{k}_{5n})}^2+{\sigma }_1^2{J}^2{k}_{6n}^2]}\left\{{\mathsf{\Lambda }}_n\left[(k_{1n}-{\sigma }_1^2{J}^2{k}_{2n})(k_{4n}-{\sigma }_1^2{J}^2{k}_{5n})+{\sigma }_1^2{J}^2{k}_{3n}{k}_{6n}\right]\right.+}\hfill \\ \\ -\left.J{\sigma }_1^2\left[k_{3n}(k_{4n}-{\sigma }_1^2{J}^2{k}_{5n})-k_{6n}(k_{1n}-{\sigma }_1^2{J}^2{k}_{2n})\right]\right\}.\hfill \end{array}$$

$$\begin{array}{c}{\displaystyle Im\left(R\right)=\frac{\left\{(k_{1n}-{\sigma }_1^2{J}^2{k}_{2n})(k_{4n}-{\sigma }_1^2{J}^2{k}_{5n})+{\sigma }_1^2{J}^2{k}_{3n}{k}_{6n}+{\mathsf{\Lambda }}_{n}J\left[k_{3n}(k_{4n}-{\sigma }_1^2{J}^2{k}_{5n})-k_{6n}(k_{1n}-{\sigma }_1^2{J}^2{k}_{2n})\right]\right\}}{a^2\left[{(k_{4n}-{\sigma }_1^2{J}^2{k}_{5n})}^2+{\sigma }_1^2{J}^2{k}_{6n}^2\right]}.}\hfill \end{array}$$

The vanishing of the imaginary part of R implies that ${\sigma }_1^2$ has to satisfy

$$k_{2n}{k}_{5n}{J}^4{x}^2-J^2(k_{2n}{k}_{4n}+k_{1n}{k}_{5n}-k_{3n}{k}_{6n}+{\mathsf{\Lambda }}_{n}J{k}_{3n}{k}_{5n}-{\mathsf{\Lambda }}_{n}J{k}_{2n}{k}_{6n})x+k_{1n}{k}_{4n}+{\mathsf{\Lambda }}_{n}J(k_{3n}{k}_{4n}-k_{1n}{k}_{6n})=0.$$

(37)

Subsequently, if

$$k_{2n}{k}_{4n}+k_{1n}{k}_{5n}-k_{3n}{k}_{6n}+{\mathsf{\Lambda }}_{n}J{k}_{3n}{k}_{5n}-{\mathsf{\Lambda }}_{n}J{k}_{2n}{k}_{6n}<0,k_{1n}{k}_{4n}+{\mathsf{\Lambda }}_{n}J(k_{3n}{k}_{4n}-k_{1n}{k}_{6n})>0,$$

(38)

or if

$${(k_{2n}{k}_{4n}+k_{1n}{k}_{5n}-k_{3n}{k}_{6n}+{\mathsf{\Lambda }}_{n}J{k}_{3n}{k}_{5n}-{\mathsf{\Lambda }}_{n}J{k}_{2n}{k}_{6n})}^2-4k_{2n}{k}_{5n}\left[k_{1n}{k}_{4n}+{\mathsf{\Lambda }}_{n}J(k_{3n}{k}_{4n}-k_{1n}{k}_{6n})\right]<0,$$

(39)

oscillatory convection can not occur. When the complementary case to (38) and (39) holds, substituting the value of ${\sigma }_1^2$ (positive solution of (37)) in the real part of R and minimizing with respect to $(n,a^2)\in \mathbb{N}\times {\mathbb{R}}^{+}$, one obtains the critical Rayleigh thermal number for the onset of oscillatory convection. Numerical simulations show that the minimum—with respect to $n\in \mathbb{N}$—is attained at $n=1$ and, hence

$$\begin{array}{c}{\displaystyle R_O=\underset{a^2\in {\mathbb{R}}^{+}}{min}{f}_o\left(a^2\right):=\frac{1}{a^2[{(k_4-{\sigma }_1^2{J}^2{k}_5)}^2+{\sigma }_1^2{J}^2{k}_6^2]}\left\{\mathsf{\Lambda }\left[(k_1-{\sigma }_1^2{J}^2{k}_2)(k_4-{\sigma }_1^2{J}^2{k}_5)+{\sigma }_1^2{J}^2{k}_3{k}_6\right]\right.+}\hfill \\ \\ -\left.J{\sigma }_1^2\left[k_3(k_4-{\sigma }_1^2{J}^2{k}_5)-k_6(k_1-{\sigma }_1^2{J}^2{k}_2)\right]\right\}=f_o\left(a_o^2\right),\hfill \end{array}$$

(40)

with $k_j=k_{1j},j\in \{1,2,\cdots ,6\}$.

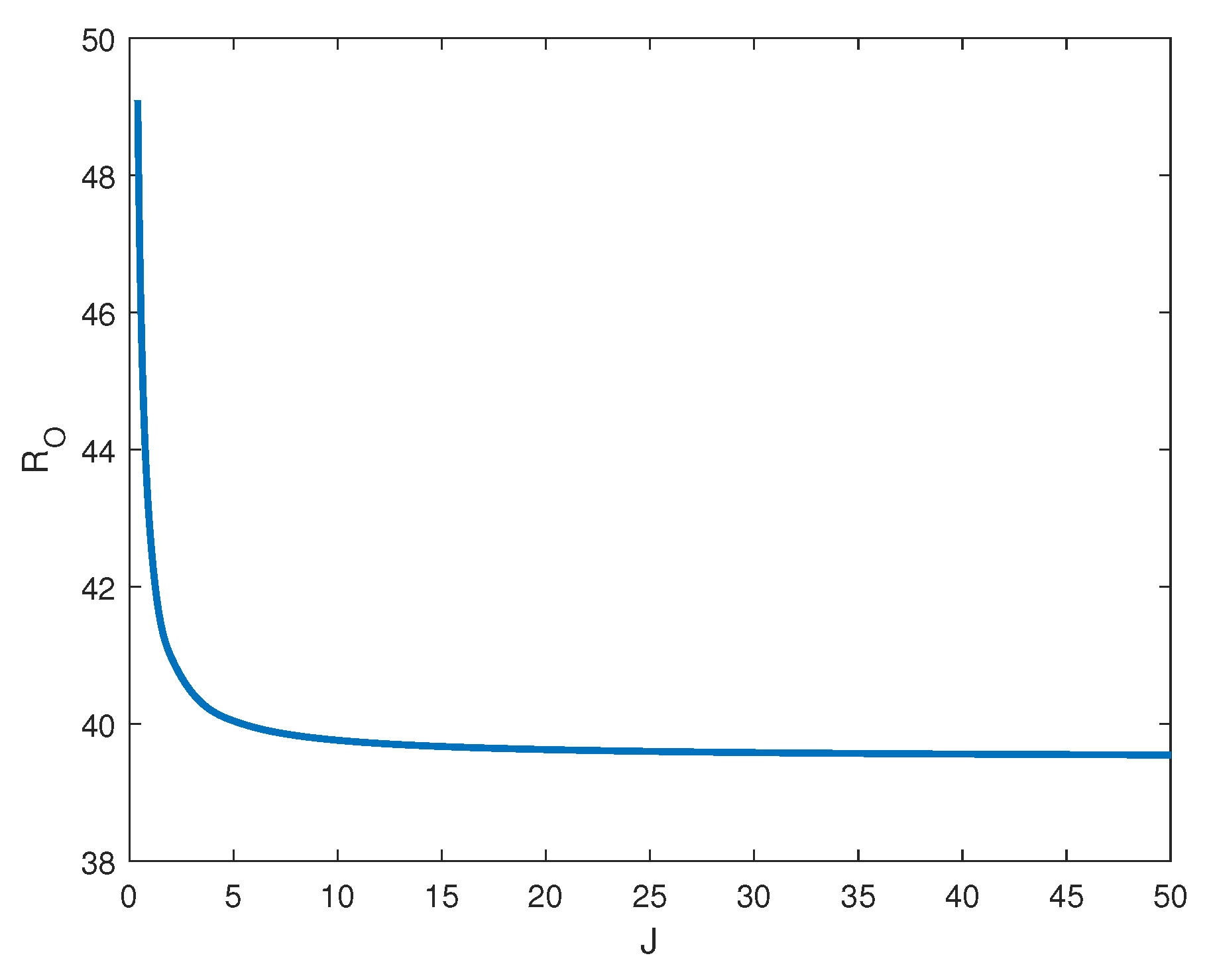
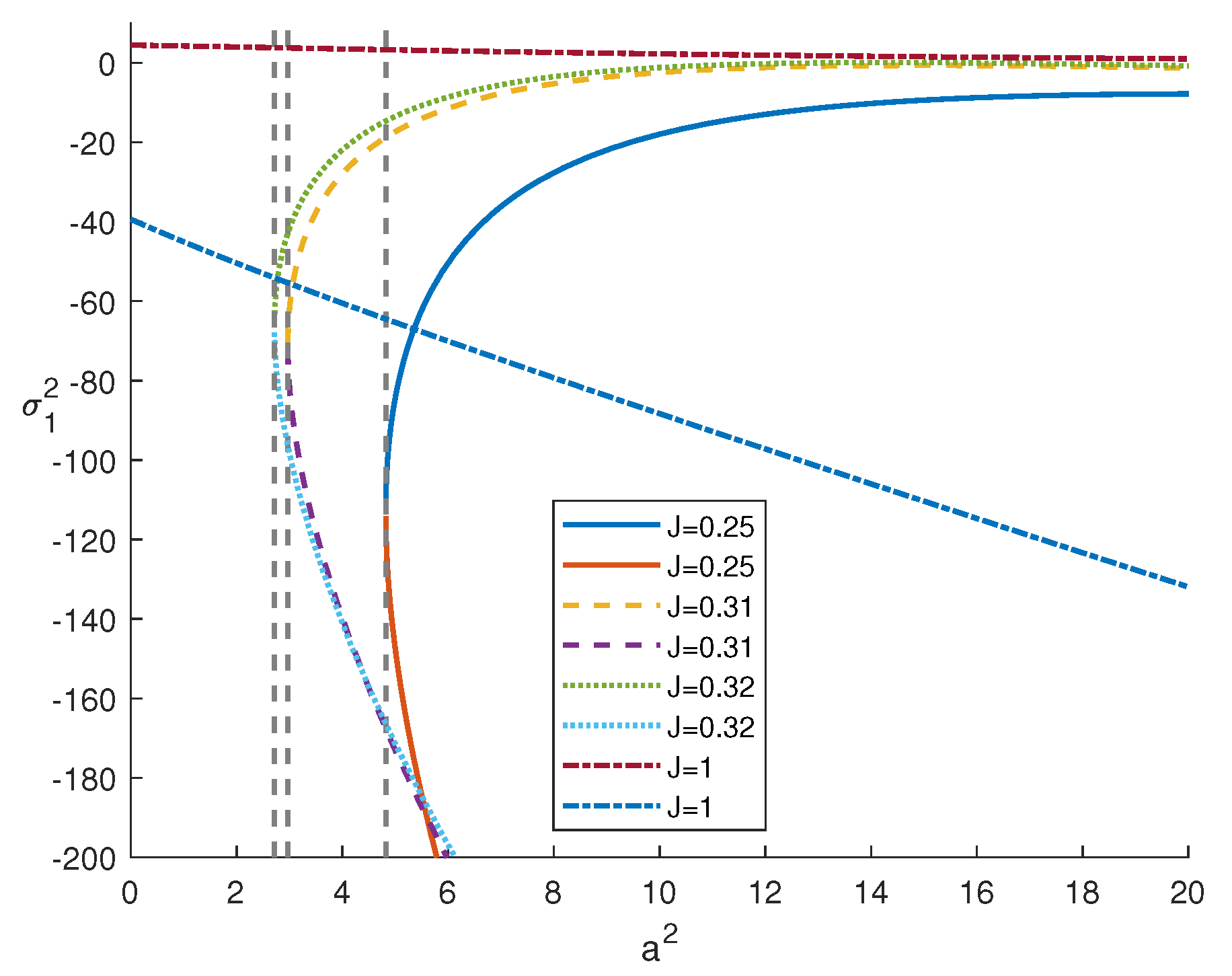
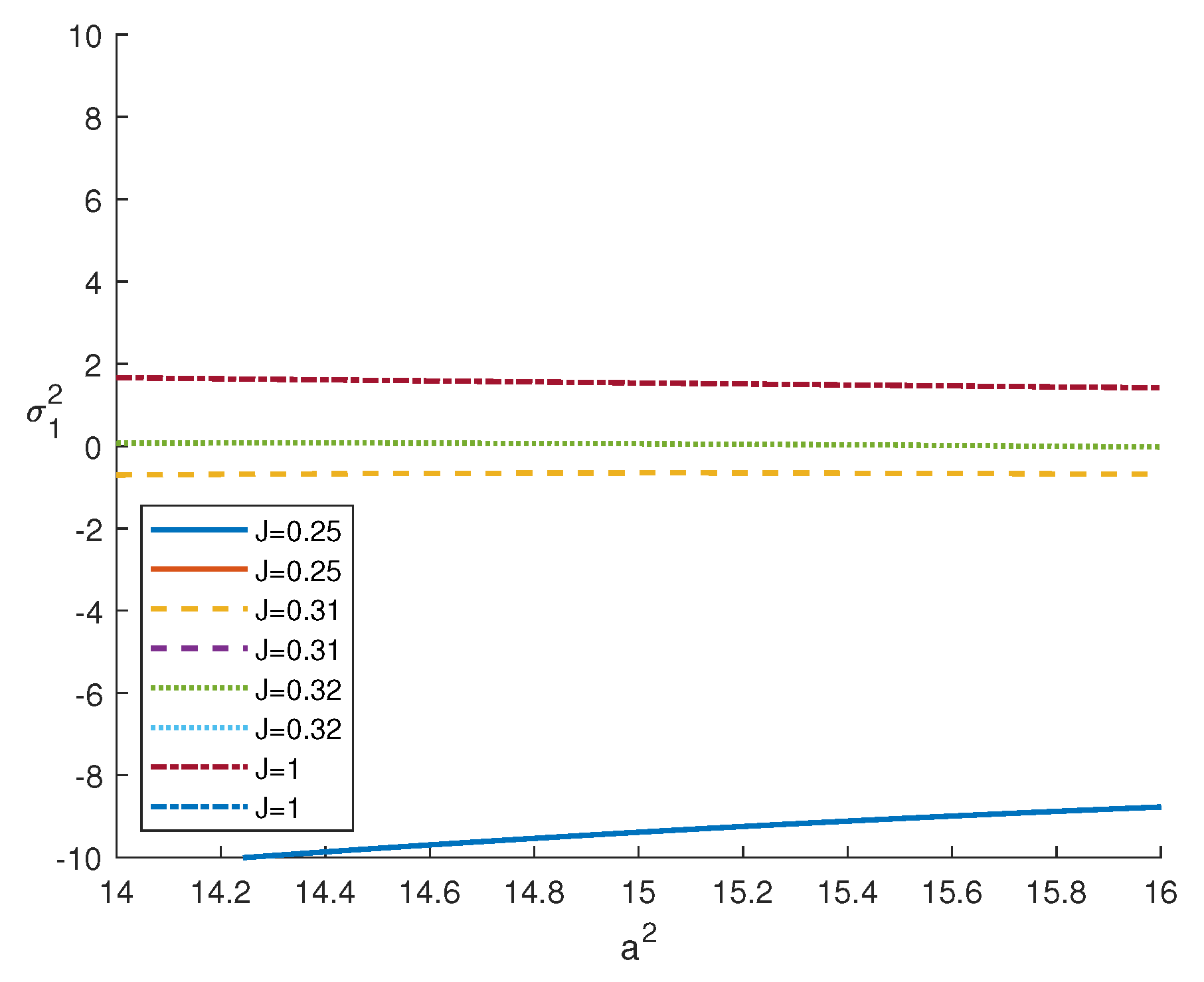
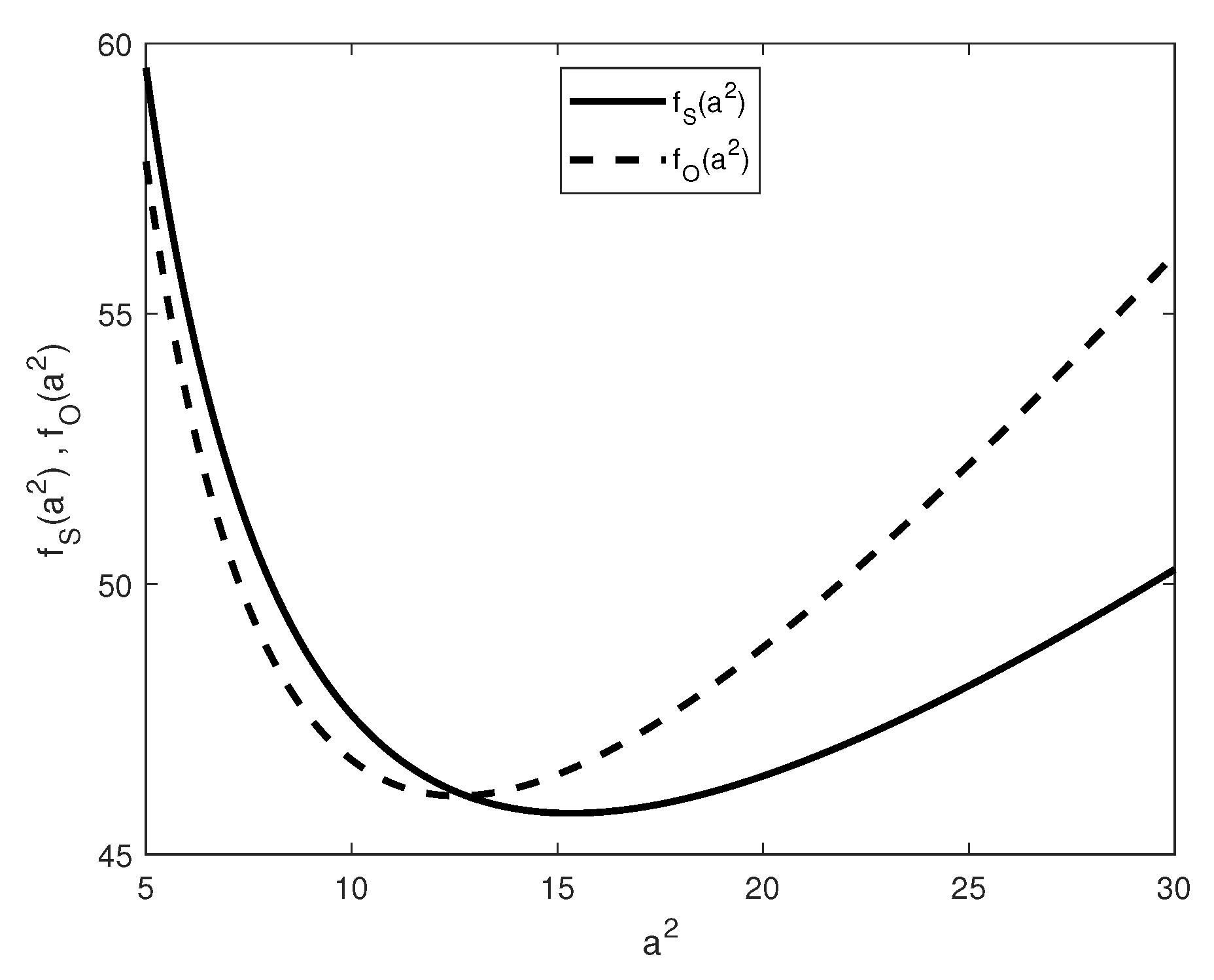
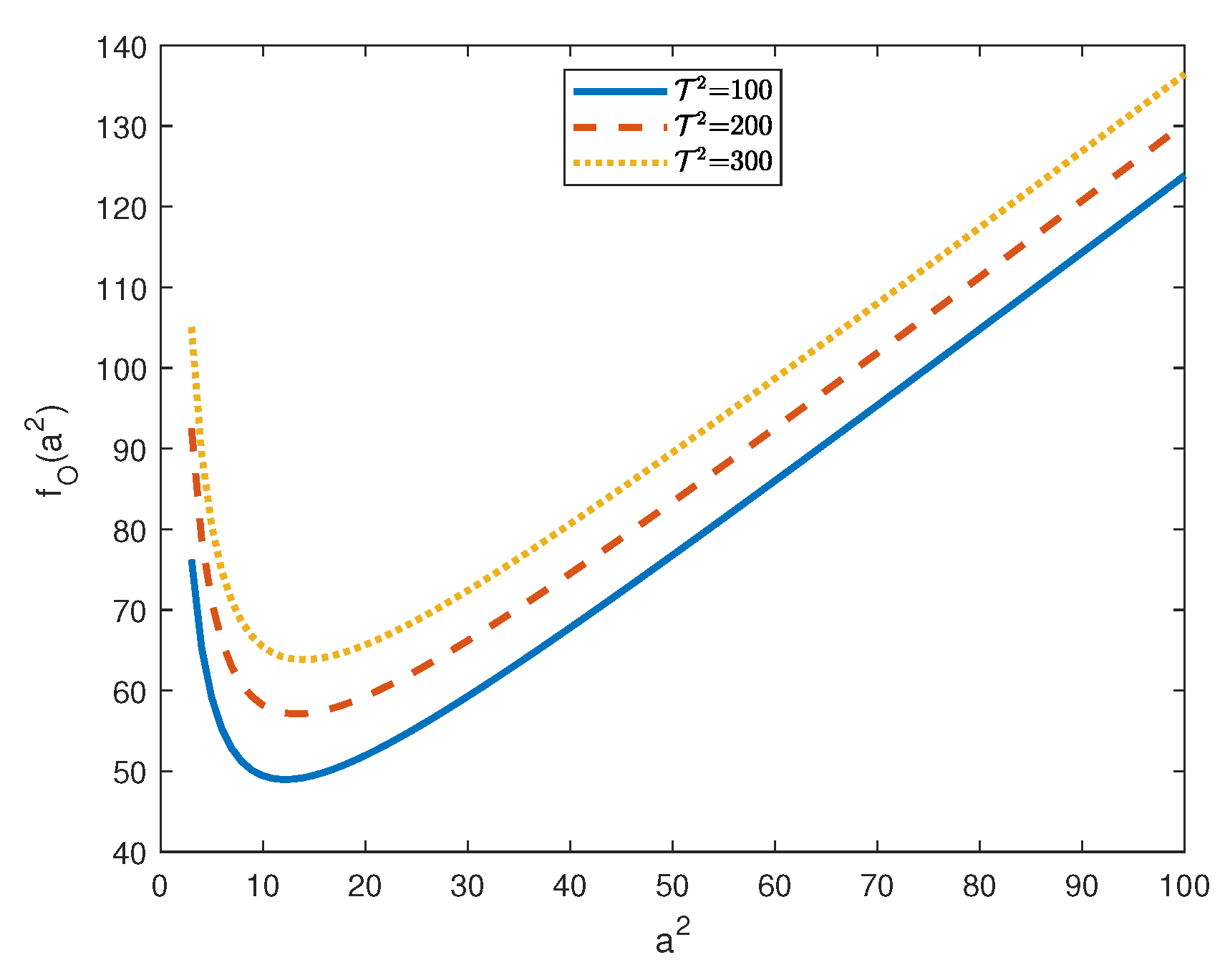
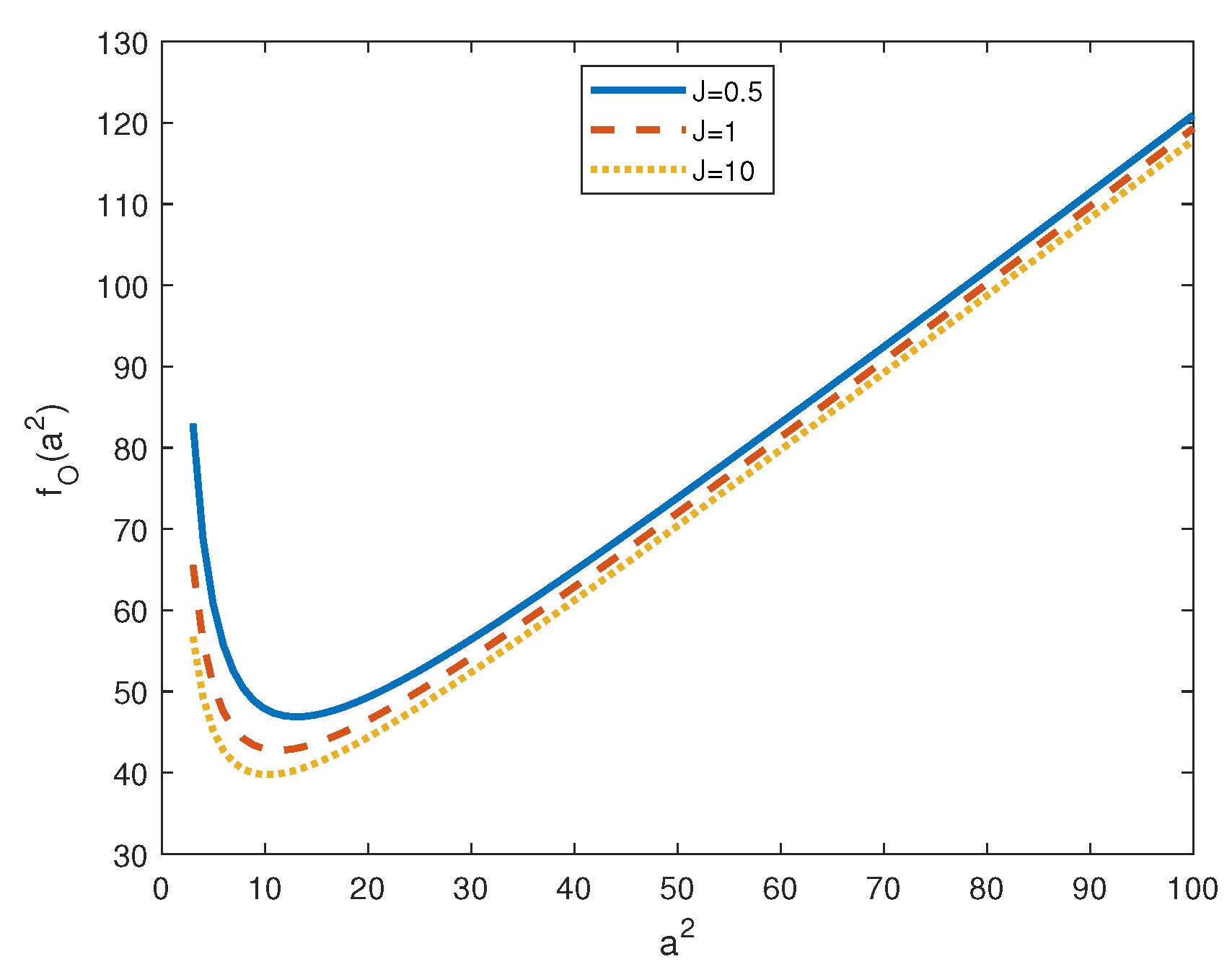
4. Numerical Results

Because of the complexity in writing $R_O$ in algebraic closed form, in this section—via Matlab software—we perform some numerical simulations in order to:

(1)

analyze the asymptotic behaviour of $R_O$ with respect to ${\mathcal{T}}^2$ and J; and,

(2)

compare $R_S$ and $R_O$ to establish whether the convection arises through a steady state (stationary convection) or via an oscillatory state (oscillatory convection).

Let us fix $\{\gamma =0.8,k_r=1.5,\eta =0.2\}$ (see [10]) and let ${\mathcal{T}}^2$ and J vary separately.

Let us fix ${\mathcal{T}}^2=10$ and let J vary in order to analyze the behaviour of $R_O$ with respect to J. In this case, one has that $a_s^2=15.919,R_S=51.9256$ and there exists a threshold $J^{*}\in (0.31,0.32)$ for the inertia coefficient, such that $R_O$ exists and convection arises via an oscillatory state (see

Table 1. Critical threshold of J, from which $R_O$ exists and convection occurs via an oscillatory state in the case $\{\gamma =0.8,k_r=1.5,\eta =0.2,{\mathcal{T}}^2=10$}.

J	${\mathit{a}}_{\mathit{o}}^2$	${\mathit{R}}_{\mathit{O}}$
0	∄	∄
0.25	∄	∄
0.31	∄	∄
0.32	15.3410	51.9150
0.35	14.7812	59.7010
0.4	14.0459	49.0951
0.7	11.9923	44.4657
1	11.2881	42.7649
5	10.3196	40.0417
10	10.2433	39.7591

). Furthermore, $R_O$ is a decreasing function of J (see Figure 1).

In Figure 2 and Figure 3, we plot the frequency ${\sigma }_1^2$ of oscillation motions (solution of (37)) with respect to $a^2$ for different values of J: the graphs show that the existence of ${\sigma }_1^2$(>0) and, hence, of $R_O$ is guaranteed for $J>0.31$.

Let us consider the following parameters set $\{\gamma =0.8,k_r=1.5,\eta =0.2,J=0.5\}$ and let ${\mathcal{T}}^2$ vary in order to analyze the behaviour of $R_O$ with respect to ${\mathcal{T}}^2$. In

Table 2. Critical threshold of ${\mathcal{T}}^2$ from which $R_O$ exists and convection occurs via an oscillatory state in the case $\{\gamma =0.8,k_r=1.5,\eta =0.2,J=0.5$}.

${\mathcal{T}}^2$	${\mathit{a}}_{\mathit{s}}^2$	${\mathit{a}}_{\mathit{o}}^2$	${\mathit{R}}_{\mathit{S}}$	${\mathit{R}}_{\mathit{O}}$
7	15.3031	∄	45.5293	∄
7.07	15.3234	12.5623	45.6906	46.0730
7.1	15.3320	12.5674	45.7596	46.0815
7.2	15.3603	12.5844	45.9885	46.1098
7.26	15.3769	12.5946	46.1253	46.1268
7.27	15.2796	12.5963	46.1480	46.1296
7.3	15.3878	12.6014	46.2162	46.1381
7.5	15.4410	12.6353	46.6677	46.1945
10	15.919	13.0503	51.9256	46.8876
20	16.1538	14.5717	67.9956	49.4695
50	15.2776	18.2109	95.5668	55.9909

the numerical values of $R_O$, computed through Matlab software are collected. In particular, we found that: (i) $R_O$ and $R_S$ are increasing functions of ${\mathcal{T}}^2$ (see Figure 4); (ii) there exists a threshold ${{\mathcal{T}}^{*}}^2\in (7.26,7.27)$ for the Taylor number, such that, if ${\mathcal{T}}^2>{{\mathcal{T}}^{*}}^2$, then the convection arises via an oscillatory state (see Figure 5).

To compare the asymptotic behaviour of $R_O$ versus $R_S$ to look for the occurrence of steady or oscillatory convection, we have numerically studied some specific cases. For example, on fixing the parameters $\{\gamma =0.8,k_r=1.5,\eta =0.2,J=1.5\}$ it arises that: for ${\mathcal{T}}^2=30$, convection sets in via an oscillatory state at $R=R_O=51.8111$ (Figure 5); while, for ${\mathcal{T}}^2=7.1$, there is a switch in the onset of convection that sets in through a steady state $R=R_S=45.7596$ (Figure 6).

The asymptotic behaviour of $f_o\left(a^2\right)$ with respect to ${\mathcal{T}}^2$ and J is shown in Figure 7 and Figure 8, respectively. In particular, Figure 7 shows that, for $\{\gamma =0.8,k_r=1.5,\eta =0.2,J=10\}$, $R_O$ increases with ${\mathcal{T}}^2$ and, hence, as one is expected, rotation has a stabilizing effect on the onset of convection. Figure 8 shows that, for $\{\gamma =0.8,k_r=1.5,\eta =0.2,{\mathcal{T}}^2=10\}$, $R_O$ decreases with J and, hence, J has a destabilizing effect on the onset of oscillatory convection.

Table 3. Onset of steady or oscillatory convection.

$\mathit{\gamma }$	${\mathit{k}}_{\mathit{r}}$	$\mathit{\eta }$	${\mathcal{T}}^2$	J	${\mathit{a}}_{\mathit{s}}^2$	${\mathit{a}}_{\mathit{o}}^2$	${\mathit{R}}_{\mathit{S}}$	${\mathit{R}}_{\mathit{O}}$	CONVECTION
10	7	2	30	1.3	22.74	15.78	198.64	202.89	STEADY
10	7	2	100	1.3	37.07	21.08	437.66	289.54	OSCILLATORY
0.8	1.5	0.2	300	10	19.25	13.92	193.25	63.84	OSCILLATORY
0.8	0.5	0.2	100	1	21.27	∄	120.07	∄	STEADY
0.8	0.5	0.2	100	1.5	21.27	17.10	120.07	44.72	OSCILLATORY

displays the numerical values of $a_s^2,a_o^2,R_S$ and $R_O$ of the previous examples.

On summarizing we have found numerically some thresholds ${\mathcal{T}}_c^2$ and $J_c$ such that:

(i)

if ${\mathcal{T}}^2<{\mathcal{T}}_c^2$ or if $\{{\mathcal{T}}^2>{\mathcal{T}}_c^2,J<J_c\}$, then convection can only arise via a steady state;

(ii)

if $\{{\mathcal{T}}^2>{\mathcal{T}}_c^2,J>J_c\}$, convection can only arise via an oscillatory state.

5. Conclusions

In this paper, the onset of thermal convection in a horizontal bidispersive porous layer, uniformly heated from below and rotating about a vertical axis, is analyzed in the presence of inertial effects.

The critical Rayleigh number for the onset of steady convection, $R_S$, has been found in algebraic closed form and it has been found that:

• $R_S$ does not depend on the acceleration coefficient, i.e., inertial effects do not affect $R_S$;
• $R_S$ increases with the Taylor number, i.e., ${\mathcal{T}}^2$ has—as one is expected—a stabilizing effect on the onset of steady convection; and,
• $R_S$ reduces to the critical Rayleigh number for the onset of steady convection found in [27] in the absence of inertia and to the critical Rayleigh number for the onset of steady convection found in [10] in the absence of rotation.

Moreover, due to the complexity in evaluating exactly the threshold for the onset of oscillatory convection $R_O$, we have performed some numerical simulations through Matlab software in order to analyze the influence of rotation and acceleration coefficient on $R_O$. In particular, we have found that:

• $R_O$ is a decreasing function of J and there exists a threshold $J^{*}\in (0.31,0.32)$ for the inertia coefficient, such that $R_O$ exists and convection arises via an oscillatory state; and,
• $R_O$ is an increasing functions of ${\mathcal{T}}^2$ and there exists a threshold ${{\mathcal{T}}^{*}}^2$ for the Taylor number, such that, for ${\mathcal{T}}^2>{{\mathcal{T}}^{*}}^2$, the convection arises via an oscillatory state.

Finally, we have compared $R_S$ and $R_O$ to establish whether the convection arises through a steady state (stationary convection) or via an oscillatory state (Hopf bifurcation).