Stability Analysis for an Interface with a Continuous Internal Structure
Abstract
1. Introduction
2. General Algorithm
- (a)
- Compute the steady-state solution and obtain the 1D profile;
- (b)
- Derive the linearized system of equations in 2D;
- (c)
- Fix k;
- (d)
- Fix ;
- (e)
- Compute the eigenvalues (modes ) with eigenvectors of the perturbed system;
- (f)
- For every mode, integrate the perturbed system and gather the perturbation amplitudes into a matrix;
- (g)
- Compute the determinant of this matrix;
- (h)
- Change and repeat steps (e–g), searching for the zero determinant;
- (i)
- Repeat steps (d–h) for different k to complete the dispersion relation.
- (a)
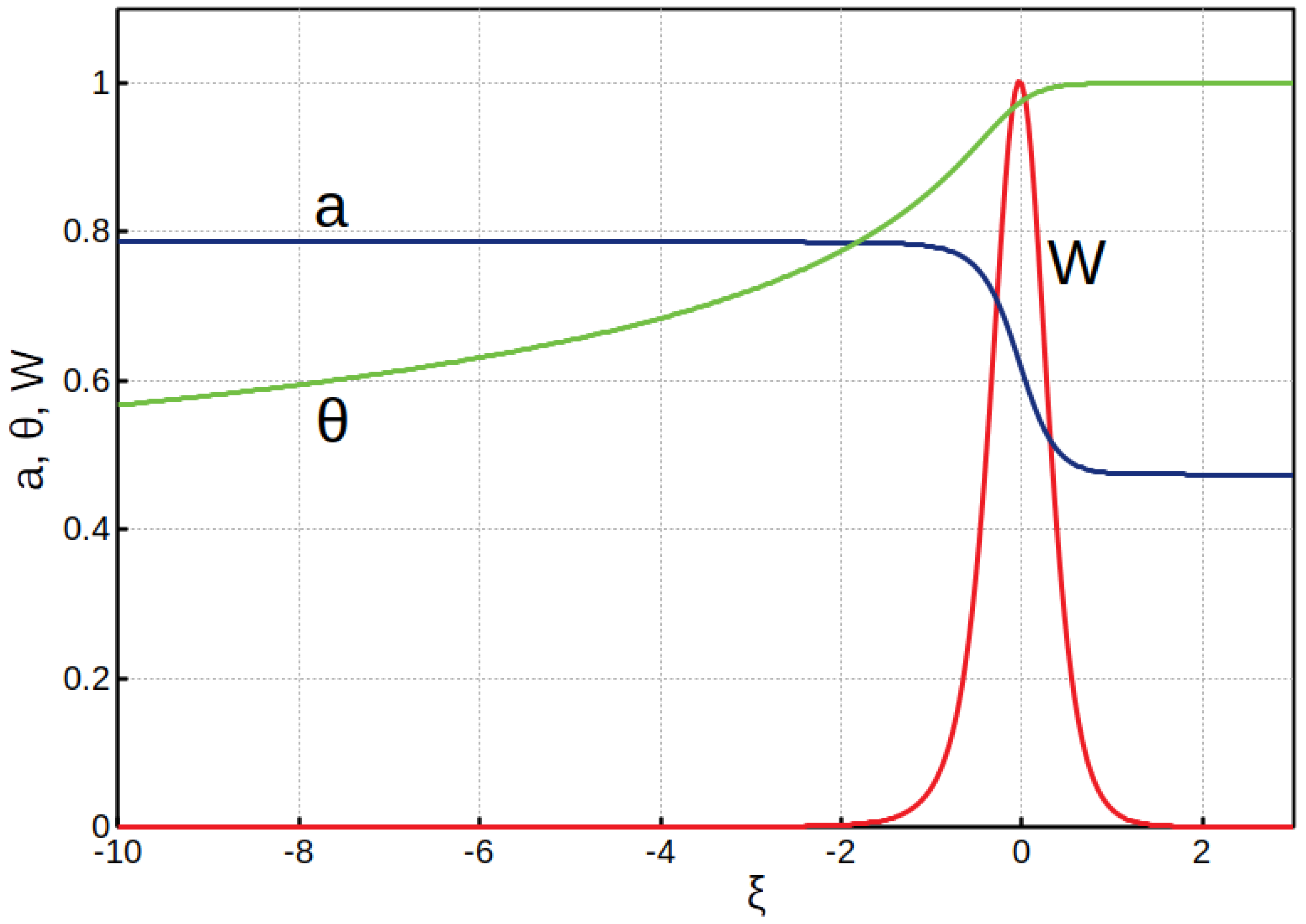
- The internal structure of the stationary front profile is defined by transport mechanisms and sources, if there are any; dissipative processes, like viscous dissipation, are omitted, as they do not allow a steady-state solution. Finding a steady state is a separate and standalone problem, which is not covered by this paper; typical profiles are shown in Figures 1 and 3.The profile can be virtually split into three parts: a central one—the actual front, where the media changes its phase—and the two uniform regions (tails) far from the central part.
- (b)
- Next, we apply small perturbations to the steady-state solution. In the 2D case, every system independent variable (such as density, temperature, and velocity) is written aswhere is a stead-state solution varying along the x coordinate, is the instability growth rate, k is the perturbation wave number, t stands for time, and y is a coordinate normal to the profile. It is important to notice that the perturbed part () varies along the profile, while in the perpendicular direction, it is determined by the wave number. In general, the instability growth rate is a complex number, with the real part standing for the growth or damping rate of the perturbations, and the imaginary part standing for the oscillation frequency. If the real part of is positive, the perturbations grow, leading to an unstable solution. Negative real implies damping of the perturbations and stable configuration of the front. Usually, the stability analysis resolves only either the pure real or pure imaginary part of the instability.A necessary condition for the applicability of the method is the possibility of writing down the linearized system in the following form:This system has N independent variables. It is important to notice that the matrix F depends on the steady-state variables and varies along the profile. It also depends on and k.
- (c,d)
- For the sake of clarity, it is convenient to postpone the explanation of the aim of steps (c,d) in the algorithm. The way to vary and k depends on the particular problem, its stability limits, the cutoff wave number, existence of multiple roots, etc.
- (e)
- The solution to the stability problem arises as an eigenvalue of system (2). Prior to the numerical integration, it is necessary to find proper boundary conditions for this system. The existence of the uniform tails with negligible gradients where all the variables remain nearly constant is an essential feature of this analysis. In these tails, the coefficients of matrix F from Equation (2) become constant in space, and with fixed and k, the above system has a trivial exponential solution:where is an eigenvalue (a “mode”) of matrix F and is a corresponding eigenvector. In order to find eigenvalues , we substitute expression (3) into the system (2) and equate the obtained determinant to zero:It is often possible to write down this equation as a polynomial with respect to and solve it analytically; in more realistic and complicated systems, the modes can only be calculated numerically. There are N different eigenvalues at each side of the front; however, not all of them are physical. The instability develops at the central part of the front, while in the uniform tails, all the perturbations must vanish. This determines the choice for proper mode selection by its sign. On the left side of the front in Figure 1, a mode with a positive sign grows towards the central part of the front and vanishes at . A negative mode has the opposite behavior, growing in the uniform tails, which is unphysical; therefore, it should be excluded. Hence, we obtain a set of positive modes for the left side of the front and a set of negative modes for the right side of the front,The number of suitable modes can be different at each side of the front, but their total number must be equal to the order of the system N. Every mode produces its eigenvector. This means that one perturbation amplitude is chosen arbitrary, while the others are derived from that amplitude. It is worth mentioning that if some modes are complex or purely imaginary, this method cannot be applied in its current form.
- (f)
- The above modes and eigenvectors constitute the boundary conditions for the numerical integration of the system (2) along the steady-state profile. Suppose that there are positive modes and negative modes. Next, we choose a “matching point” at the stationary profile, say ; from a numerical viewpoint, it is advisable to choose a point within a region of maximal gradients. Then, for each positive mode, the system (2) is integrated from the left side of the front until the point; in total, integrations are to be performed. Similarly, for every negative mode, the system is integrated backwards, from the right front side until the point; in total, integrations are to be performed. Integration can be done by any suitable computational method, like the explicit Runge–Kutta 4 or others.
- (g)
- Every integration produces a vector of perturbation amplitudes. At the matching point, we build an matrix from these amplitudes and compute its determinant; its value depends on k and .
- (h)
- (i)
- Finally, steps (d–h) are repeated for different k to compute the whole dispersion relation.
3. One-Dimensional Pulsating Instability in Molecular Magnets
- (a)
- There are several ways to find a steady-state solution to the system (7). We write those equations in the reference frame of the moving front, integrate them from both sides, and use the shooting method to find the front eigenvalue and compute the profiles. The profiles of concentration and temperature together with the energy release for the stationary magnetic deflagration front are shown in Figure 1.
- (b)
- Next, we apply small perturbations to this equilibrium state and derive a system of linearized equations. All the variables take the form , and the perturbed linearized system (7) iswhereis introduced for brevity.
- (c)
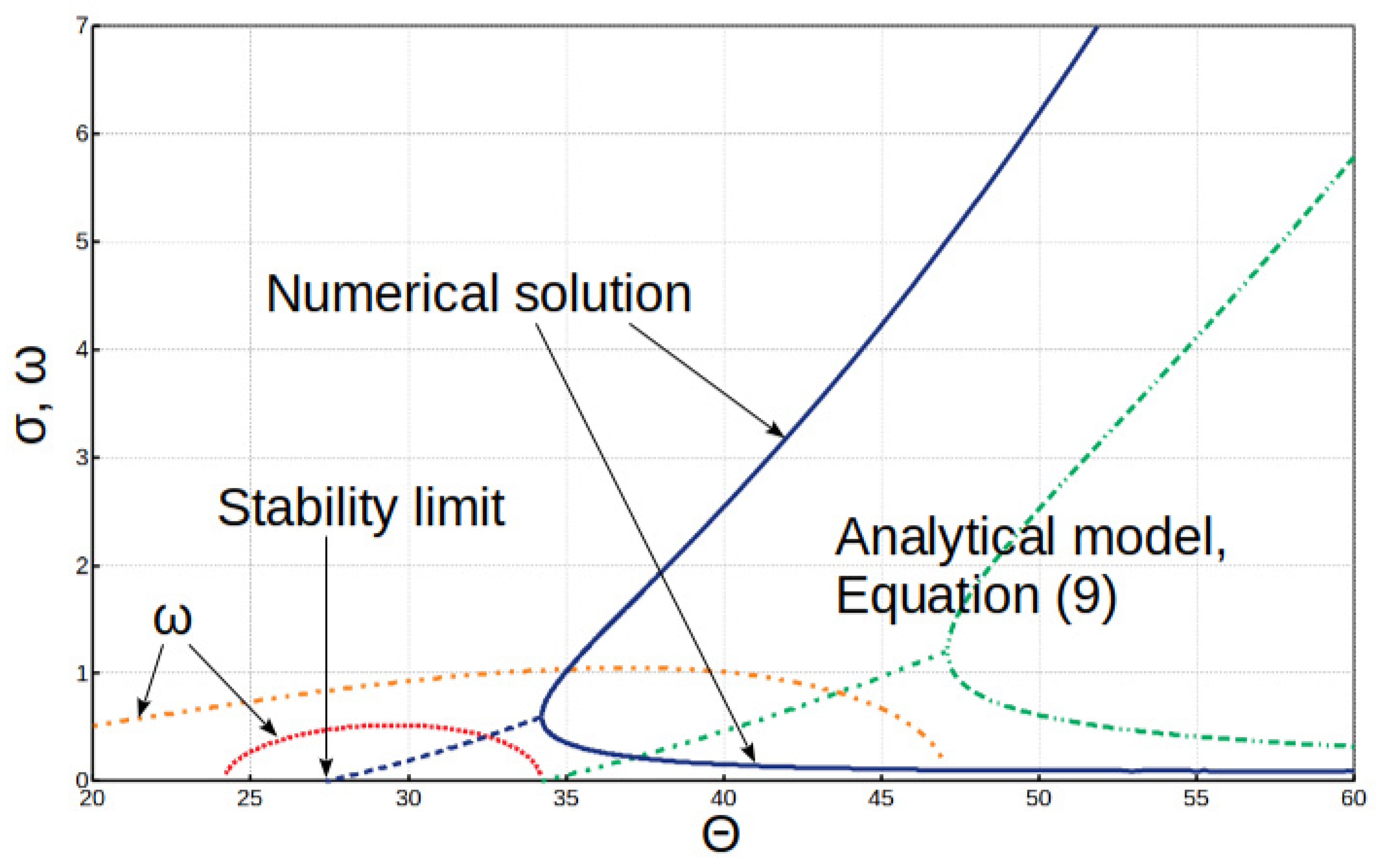
- In this problem, we investigate stability of the system with respect to the activation energy. Neglecting the width of the energy release zone, it is possible to solve the problem analytically. The corresponding analysis is performed in Section III of Ref. [11]; it results in a quadratic equation for ,where plays the role of the Zeldovich number [4], and is a constant parameter. From this equation, it is known that the system is stable () if the activation energy is below a certain critical value, and above this value, it becomes unstable () and demonstrates pulsating behavior (). In addition, at high values of the activation energy, there are two real solutions to Equation (9). We will use this fact and start searching for a numerical solution in the region of high activation energy (see Figure 2).Since this is a 1D problem and there is no k mentioned in the general algorithm, we fix the activation energy and search for the growth rate .
- (d)
- Fix and compute the system modes.
- (e)
- Substituting expression (3) into system (8), we obtain the following determinant:which is equivalent to Equation (4). This determinant of the third order can easily be expanded into a polynomial, and the modes can be found analytically. Each side of the front has three distinct roots, though only some of them stand for a physical solution. In particular, this system has two modes in the “hot” region (, ) and one mode in the “cold” region (, ). Looking at the stationary profiles in Figure 1, we choose limiting points for the profile. To be specific, we take as the left border and as the right border of the front.The computed modes are the eigenvalues of the system. Next, it is necessary to build corresponding eigenvectors. For that, the system (8) is rewritten asHaving fixed the amplitude of one particular perturbation, the others are derived in a straightforward way. For example, if one fixes , then is easily derived from the third equation of (11) asIn a similar way, is derived from the second equation. It is worth reminding the reader that these relations depend on the mode and on the particular location at the profile (equilibrium variables and ).
- (f)
- Hence, we obtain a vector of perturbation for each mode—three in total. They are the boundary conditions for the integration of the system (8) along the profile. As mentioned in the previous section, the integration can be done by any suitable numerical method. First, we are to define a matching point at the front. According to Figure 1, is a suitable choice; physical results do not depend on the choice of the matching point. There is one mode in the cold (left) region, so the system (8) is integrated once from until . The result of integration is a vector with three perturbation amplitudes, Then, we integrate the system (8) backwards twice from till for the two positive modes and collect the resulting vectors of perturbations.
- (g,h)
- At the matching point, we build a matrix from those vectors and compute its determinant:The value of this determinant depends on (the activation energy is kept fixed). The zero determinant (12) defines the solution for a specific activation energy value.
4. Two-Dimensional Darrieus–Landau Instability in Laser Ablation
- (a)
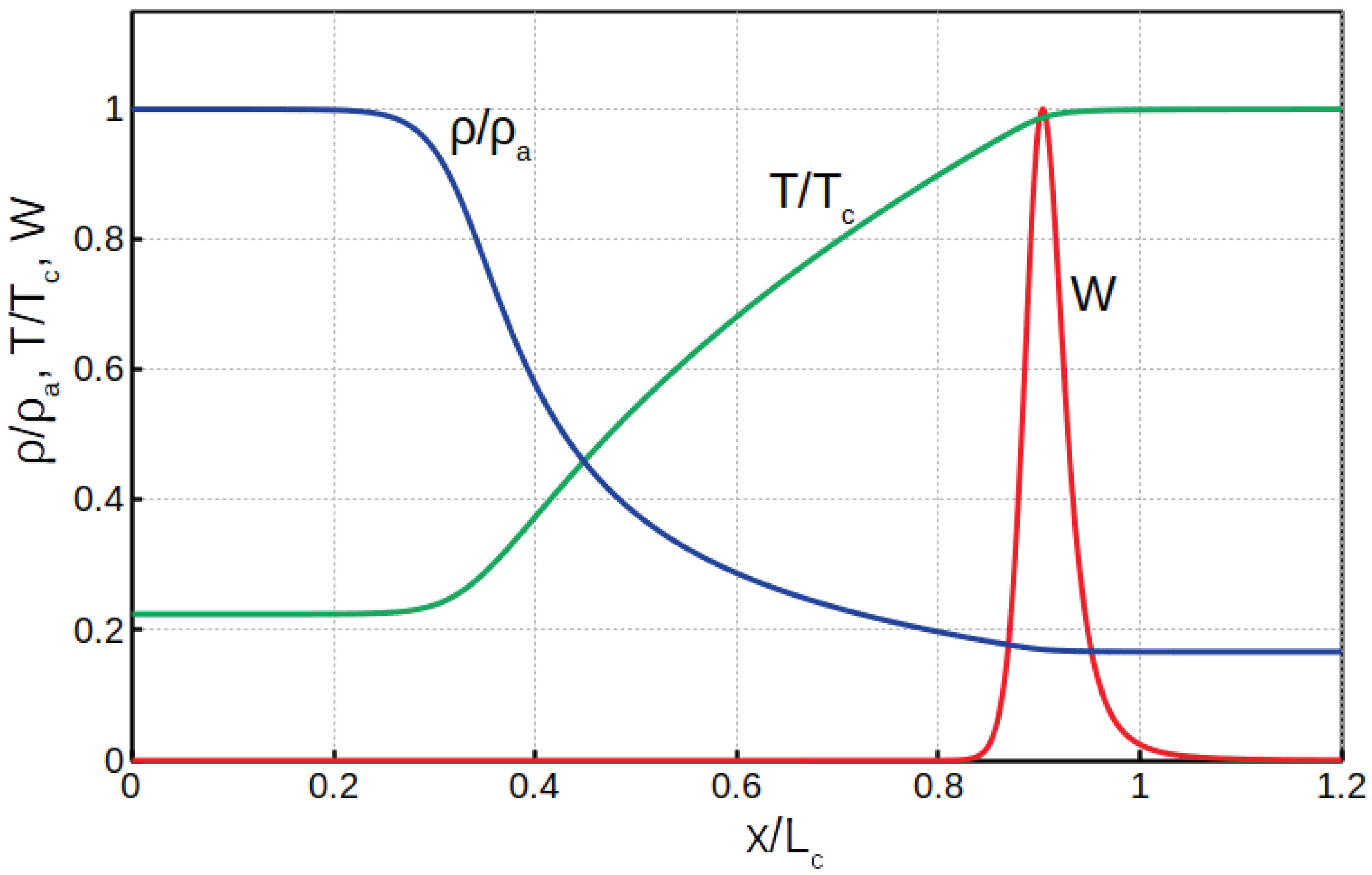
- We describe laser plasma within the one-fluid approximation using the ideal gas equation with a single temperature. This is a traditional approach for studying hydrodynamic instabilities in inertial fusion and is employed in the absolute majority of works on the subject [3]. We model an ablation wave with the Navier–Stokes equations for density, momentum, and energy:and the equation of state of ideal gas completes the system, . Electron thermal conduction depends on temperature as , the subscript “c” stands for the critical surface where the laser irradiance is absorbed. The energy release due to laser absorption is taken in a form similar to the Arrhenius law in combustion:where plays a role of the scaled activation energy. This particular form for is constructed to model very localized energy release, so the activation energy is set very high: in this sample.The typical internal structure of the stationary deflagration front is illustrated in Figure 3. It is mostly determined by the energy equation. Scale separation in the front structure is an important feature of laser ablation. One can identify a narrow region of the energy release and another region of the maximal density gradient. Both regions are separated from each other, and they are significantly smaller than the overall front width.
- (b)
- Such a complicated structure cannot be taken into account by usual analytical stability analysis. To be specific, we consider a wave of laser ablation propagating along the x direction, and the instability evolves along the y coordinate. Small perturbations are written as . Then, the linearized system (14) takes the following form:It is important to notice that the shape of the system differs from the necessary form (2) of the general algorithm (compare also with (8)). To overcome this limitation, we introduce new perturbation variables [9] and rewrite everything in dimensionless form:with the scaled wave number, , and the perturbation growth rate, ; is the characteristic width of the front determined by thermal conduction in the hot region. We also introduce an auxiliary variable ; this step is a common way to rewrite a second-order Equation () as two equations of the first order. Then, the linearized system (16)–() can be presented in a matrix form (2), withwhere dimensionless variables are , , , , and ; is the flow Mach number defined in the hot region, and coefficients depend on the steady-state solution and vary along the profile. For their exact expressions, see the Appendix in Ref. [8]. It is worth mentioning that for this problem, presenting the perturbed linearized equation in this proper form is the most tricky part.
- (c,d)
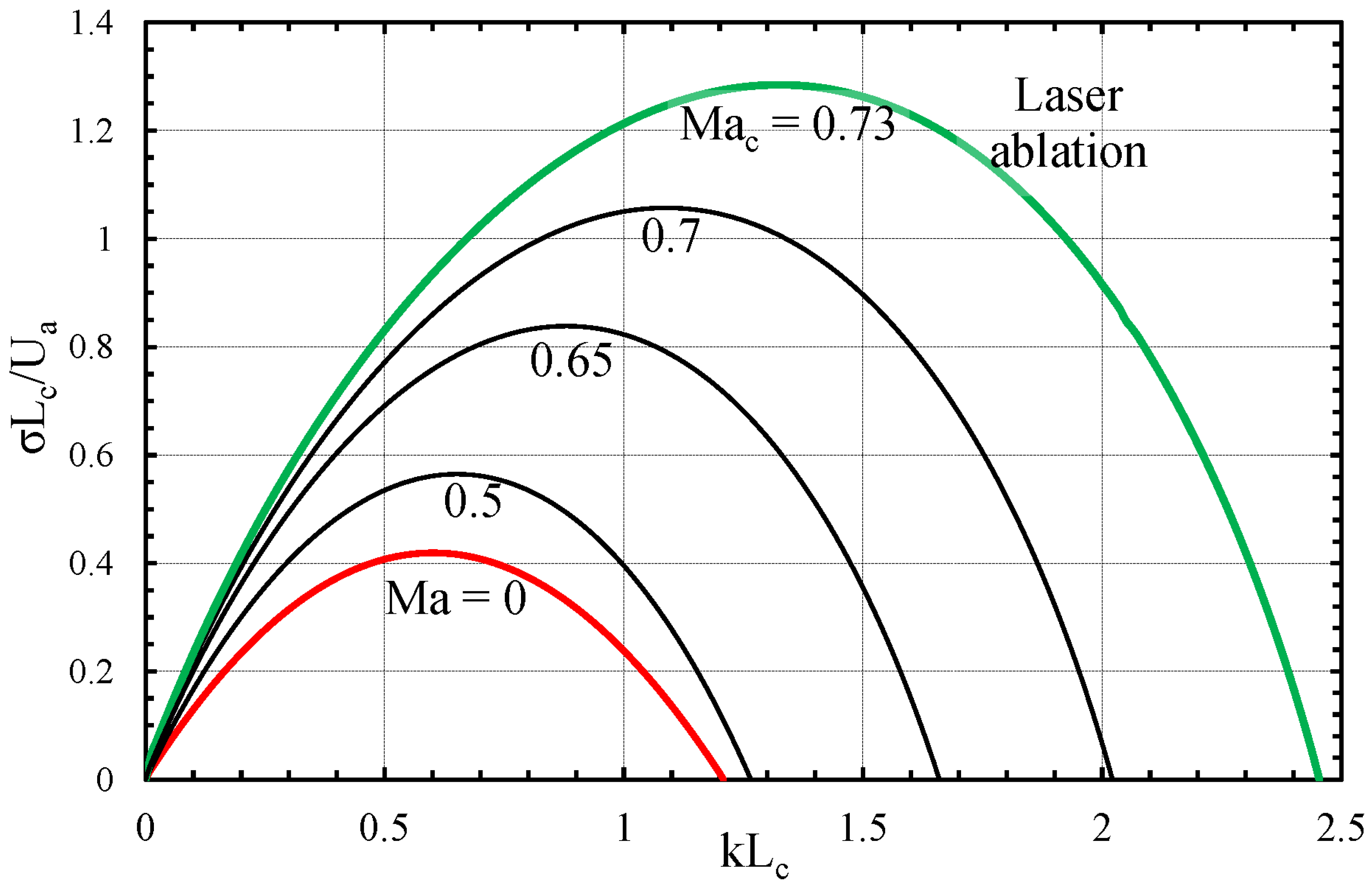
- For a chosen Mach number, we fix K and S and proceed according to the algorithm. In the incompressible case, the dispersion relation of the DL instability has a parabolic shape with a certain cutoff wavelength. Hence, it is advisable to start computing the dispersion relation from small values of the wavenumber K and increase it gradually until the cutoff (negative ) is found.
- (e)
- Next, we solve Equation (4) and compute five modes of the system. The equation for can be written as a fifth-order polynomial. In the incompressible case (), it simplifies a lot and can be solved analytically; in the general case, it is solved numerically. The system has two positive ( for ) and three negative modes ( for ). For each mode, we compute the corresponding eigenvector at its boundary. It is advisable to derive relationships between different perturbation amplitudes, as one mode may either nullify one perturbation amplitude or lead to division by zero error. The derived expressions help to identify which perturbation amplitude can be set to a small arbitrary value so that the others can be computed.
- (f)
- (g–i)
- At the matching point, we gather the results of the integrations into a matrix of perturbation amplitudes and compute its determinant. The zero determinant stands for the solution for the stability problem. Varying K and repeating steps (e,f), we compute the whole dispersion relation. In Figure 4, the resulting curves are illustrated for different Mach numbers. This clearly demonstrates that a compressible deflagration flow is more unstable. It has a higher maximal growth rate and a broader scale range where the front is unstable.
5. Discussions and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Landau, L.; Lifshitz, E. Fluid Mechanics; Pergamon: Oxford, UK, 1989. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover Publications: New York, NY, USA, 1981. [Google Scholar]
- Bychkov, V.; Modestov, M.; Law, C.K. Combustion phenomena in modern physics: I. Inertial confinement fusion. Prog. Energy Combust. Sci. 2015, 47, 32. [Google Scholar] [CrossRef]
- Zeldovich, Y.; Barenblatt, G.; Librovich, V.; Makhviladze, G. The Mathematical Theory of Combustion and Explosion; Consultants Bureau: New York, NY, USA, 1985. [Google Scholar]
- Bychkov, V.; Marklund, M.; Modestov, M. The Rayleigh-Taylor instability and internal waves in quantum plasmas. Phys. Lett. A 2008, 372, 3042. [Google Scholar] [CrossRef]
- Bodner, S. Rayleigh-Taylor Instability and Laser-Pellet Fusion. Phys. Ref. Lett. 1974, 33, 761. [Google Scholar] [CrossRef]
- Bychkov, V.; Modestov, M.; Marklund, M. The Darrieus-Landau instability in fast deflagration and laser ablation. Phys. Plasmas 2008, 15, 032702. [Google Scholar] [CrossRef]
- Modestov, M.; Bychkov, V.; Valiev, D.; Marklund, M. Growth rate and the cutoff wavelength of the Darrieus-Landau instability in laser ablation. Phys. Rev. E 2009, 80, 046403. [Google Scholar] [CrossRef] [PubMed]
- Liberman, M.A.; Bychkov, V.V.; Goldberg, S.M.; Book, D.L. Stability of a planar flame front in the slow combustion regime. Phys. Rev. E 1994, 49, 445. [Google Scholar] [CrossRef] [PubMed]
- Travnikov, O.Y.; Liberman, M.A.; Bychkov, V.V. Stability of a planar flame front in a compressible flow. Phys. Fluids 1997, 9, 12. [Google Scholar] [CrossRef]
- Modestov, M.; Bychkov, V.; Marklund, M. Pulsating regime of magnetic deflagration in crystals of molecular magnets. Phys. Rev. B 2011, 80, 214417. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chem. Int. Ed. 2003, 42, 268. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y.; Sarachik, M.P.; Chudnovsky, E.M.; McHugh, S.; Gonzalez-Rubio, R.; Avraham, N.; Myasoedov, Y.; Zeldov, E.; Shtrikman, H.; Chakov, N.E.; et al. Propagation of Avalanches in Mn12-Acetate: Magnetic Deflagration. Phys. Rev. Lett. 2005, 95, 147201. [Google Scholar] [CrossRef] [PubMed]
- Garanin, D.A.; Chudnovsky, E.M. Theory of magnetic deflagration in crystals of molecular magnets. Phys. Rev. B 2007, 76, 054410. [Google Scholar] [CrossRef]
- Kadowaki, S. Instability of a deflagration wave propagating with finite Mach number. Phys. Fluids 1995, 7, 220. [Google Scholar] [CrossRef]
- He, L. Analysis of compressibility effects on Darrieus-Landau instability of deflagration wave. Europhys. Lett. 2000, 49, 576. [Google Scholar] [CrossRef]
- Lesur, M.; Médina, J.; Sasaki, M.; Shimizu, A. Subcritical Instabilities in Neutral Fluids and Plasmas. Fluids 2018, 3, 89. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Modestov, M. Stability Analysis for an Interface with a Continuous Internal Structure. Fluids 2021, 6, 18. https://doi.org/10.3390/fluids6010018
Modestov M. Stability Analysis for an Interface with a Continuous Internal Structure. Fluids. 2021; 6(1):18. https://doi.org/10.3390/fluids6010018
Chicago/Turabian StyleModestov, Mikhail. 2021. "Stability Analysis for an Interface with a Continuous Internal Structure" Fluids 6, no. 1: 18. https://doi.org/10.3390/fluids6010018
APA StyleModestov, M. (2021). Stability Analysis for an Interface with a Continuous Internal Structure. Fluids, 6(1), 18. https://doi.org/10.3390/fluids6010018



