Improving the Performance of Surface Flow Generated by Bubble Plumes
Abstract
:1. Introduction
2. Experimental Apparatus, Method, and Conditions
3. Calculation of Bubble Parameters
3.1. The Mean Bubble Diameter
3.2. The Bubble Velocity
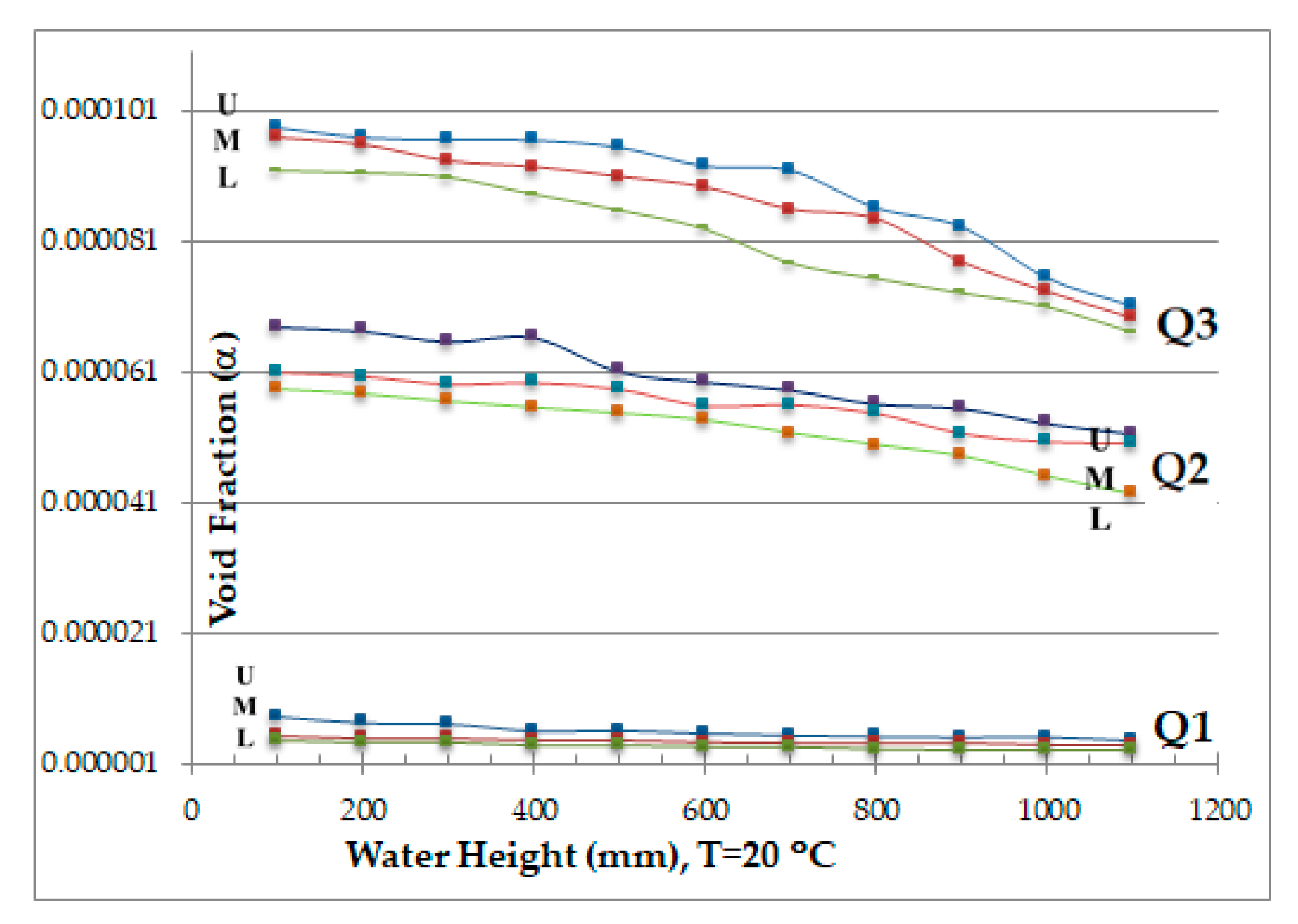
3.3. The Void Fraction
4. Results Interpretation and Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bankovic, A.; Currie, I.G.; Martin, W.W. Laser-doppler measurements of bubble plumes. Phys. Fluids 1984, 27, 348–355. [Google Scholar] [CrossRef]
- Hara, S.; Ikai, M.; Namie, S. Fundamental study on an air bubble type of oil boom. Trans. Ship Making Soc. Kansai Jpn. 1984, 194. [Google Scholar]
- Abdulmouti, H. Surface Flow Generation Mechanism Induced by Bubble Plume. Yanbu J. Eng. Sci. 2011, 2, 50–67. [Google Scholar]
- Bulson, P.S. The Theory and Design of Bubble Breakwaters. In Proceedings of the 11th International Conference on Coastal Engineering, London, UK, September 1968; pp. 995–1015. [Google Scholar]
- McDougall, T.J. Bubble Plumes in Stratified Environments. J. Fluid Mech. 1978, 85, 655–672. [Google Scholar] [CrossRef]
- Goosens, L.H.J.; Smith, J.M. The Hydrodynamics of Unconfined Bubble Columns for Mixing Lakes and Reservoirs. Chem. Eng. Tech. 1975, 47, 249. [Google Scholar]
- Abdulmouti, H.; Jassim, E. Visualization and Measurements of Bubbly Two-Phase Flow Structure Using Particle Imaging Velocimetry (PIV). Eur. Sci. J. 2013, 9. [Google Scholar]
- Abdulmouti, H.; Murai, Y.; Ohta, J.; Yamamoto, F. PIV Measurement of Bubbly Flow Interaction with Water Surface. J. Vis. Soc. Jpn. 1999, 19, 209–210. [Google Scholar]
- Yuichi, M.; Yasushi, O.; Hassan, A.; Junichi, O.; Fujio, Y. Numerical Prediction of a Horizontal Surface Flow Generated by Bubbles. In Proceedings of the Asian Symposium on Multiphase Flow (ASMF’99), Osaka, Japan, November 1999; pp. 45–50. [Google Scholar]
- Jones, W.T. Air Barriers as Oil-Spill Containment Devices. Soc. Pet. Eng. J. 1972, 126–142. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.-Y.; Yang, Y.-M.; Zhang, H.S. Surface tension effects on the behavior of a rising bubble driven by buoyancy force. Chin. Phys. B 2010, 19, 026801. [Google Scholar]
- Talaia, M.A.R. Terminal velocity of a bubble rise in a liquid column. World Acad. Sci. Eng. Technol. 2007, 28, 264–268. [Google Scholar]
- Haberman, G.P.; Cumo, M.; D’Annibale, F.; Tomiyama, A. Terminal Bubble Rising Velocity in One-Component Systems; Paper F-3. In Proceedings of the 39th European Two-Phase Flow Group Meeting, Aveiro, Portugal, 19–20 February 2001. [Google Scholar]
- Talaia, M.A.R. Uma análise dimensional: Ascensão de uma bolha num líquido parado. Gaz. Fís. 2000, 23, 9. [Google Scholar]
- Hussain, N.A.; Narang, B.S. Simplified Analysis of Air-Bubble Plumes in Moderately Stratified Environments. J. Heat Transfer. 1984, 106, 543–551. [Google Scholar] [CrossRef]
- Sheng, Y.Y.; Irons, G.A. Measurements of the Internal Structure of Gas-Liquid Plumes. Metall. Trans. B 1992, 23, 779–788. [Google Scholar] [CrossRef]
- Taylor, G. The action of a Surface Current Used as a Breakwater. Proc. R. Soc. Lond. A 1955, 231, 466–478. [Google Scholar]
- Peebles, F.; Garber, H. Studies on the motion of gas bubbles in liquid. Chem. Eng. Prog. 1953, 49, 88–97. [Google Scholar]
- Talaia, M.A.R. Predicting the Rise Velocity of Single Gas Slugs in Stagnant Liquid: Influence of Liquid Viscosity and Tube Diameter. In Proceedings of the 3rd International Symposium on Two-Phase Flow Modelling and Experimentation, Edizioni ETS. Pisa, Italy, 22–25 September 2004. [Google Scholar]
- Tomiyama, A. Drag, Lift and Virtual Mass Forces Acting on a Single Bubble. In Proceedings of the 3rd International Symposium on Two-Phase Flow Modelling and Experimentation, Edizioni ETS. Pisa, Italy, 22–25 September 2004. [Google Scholar]
- Tomiyama, A.; Celata, G.P.; Hosokawa, S.; Yoshida, S. Terminal Velocity of Single Bubbles in Surface Tension Force Dominant Regime. Paper F-2. In Proceedings of the 39th European Two-Phase Flow Group Meeting, Aveiro, Portugal, 19–20 February 2001. [Google Scholar]
- de Swart, J.W.A.; Krishna, R. Effect of particles concentration on the hydrodynamics of bubble column slurry reactors. Chem. Eng. Res. Design Trans. Ind. Chem. Eng. 1995, 73, 308–313. [Google Scholar]
- Shollenberger, K.A.; Torczynski, J.R.; Adkins, D.R.; O’Hem, T.J.; Jackson, N.B. Gamma-densitometry tomography of gas holdup spatial distribution in industrial scale bubble columns. Chem. Eng. Sci. 1997, 52, 2037–2048. [Google Scholar] [CrossRef] [Green Version]
- Eisenberg, B.; Ansel, L.L.; Fiato, R.A.; Bauman, R.F. Advanced gas conversion technology for remote natural gas utilization. In GPA Convention; GPA: New Orleans, LA, USA, 1994; p. 128. [Google Scholar]
- Grace, J.R.; Wairegi, T.; Nguyen, T.H. Shapes and velocities of single drops and bubbles moving freely Through Immiscible Liquids. Inst. Chem. Eng. 1976, 54, 167–173. [Google Scholar]
- Davis, B.H. Overview of reactors for liquid phase Fischer-Tropsch synthesis. Catal. Today 2002, 71, 249. [Google Scholar] [CrossRef]
- Magnaudet, J.J.M. The force acting on bubbles and rigid particles. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Vancouver, BC, Canada, 22–26 June 1997; Volume 97, pp. 22–26. [Google Scholar]
- Hussain, N.A.; Siegel, R. Liquid Jet Pumped by Rising Gas Bubbles. J. Fluids Eng. 1976, 98, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Murai, Y.; Ohno, Y.; Abdulmouti, H.; Yamamoto, F. Article of Fluid Dynamic Characteristics of Oil Fence Using Air Bubbles, “To Reduce the Damage of Heavy Oil Leakage at Sea” Nature and Environment of the Sea of Japan Districts; Fukui University: Fukui, Japan, 2000; Volume 7, pp. 63–68. [Google Scholar]
- Abdulmouti, H. Particle Imaging Velocimetry (PIV) Technique: Principles, the Typically Used Methods, Classification and Applications; Scholar’s Press: Atlanta, GA, USA, 2013. [Google Scholar]
- Jager, B.; Espinoza, R. Advances in low temperature Fisher-Tropsch synthesis. Catal. Today 1995, 23, 17. [Google Scholar] [CrossRef]
- White, S.J. Bubble Pump Design and Performance. Ph.D. Thesis, Georgia Institute of Technology, GA, USA, August 2001. [Google Scholar]
- Luewisutthichat, W.; Tsutsumi, A.; Yoshida, K. Chaotic hydrodynamics of continuous single-bubble flow systems. Chem. Eng. Sci. 1997, 52, 3685. [Google Scholar] [CrossRef]
- Bhaga, D.; Weber, M.E. Bubbles in viscous liquids: Shape, wakes and velocities. J. Fluid Mech. 1981, 105, 61–85. [Google Scholar] [CrossRef] [Green Version]
- Haberman, W.L.; Morton, R.K. An Experimental Study of Bubbles Moving in Liquids. Soc. Civ. Eng. 1956, 121, 227–250. [Google Scholar] [CrossRef]
- White, E.T.; Beardmore, R.H. The velocity of rise of single cylindrical air bubbles through liquids contained in vertical tubes. Chem. Eng. Sci. 1962, 17, 351–361. [Google Scholar] [CrossRef]
- Wallis, G.B. One-Dimensional Two-Phase Flow; Courier Dover Publications: New York, NY, USA, 1969; pp. 243–281. [Google Scholar]
- Krishna, R.; Wilkinson, P.M.; van Dierendonck, L.L. A model for gas holdup in bubble columns incorporating the influence of gas density on flow regime transitions. Chem. Eng. Sci. 1991, 46, 2491. [Google Scholar] [CrossRef]
- Sun, T.Y.; Faeth, G.M. Structure of Turbulent Bubbly Jets-I. Methods and Centerline properties. Int. J. Multiphase Flow 1989, 12, 99–114. [Google Scholar] [CrossRef]
- Al Tawell, A.M.; Landau, J. Turbulence Modulation in Two-Phase Jets. Int. J. Multiphase Flow 1977, 3, 341–351. [Google Scholar] [CrossRef]
- Junli, X. Bubble Velocity, Size and Interfacial Area Measurements in Bubble Columns; Washington University: Saint Louis, MI, USA, 2004. [Google Scholar]
- Gross, R.W.; Kuhlman, J.M. Three-Component Velocity Measurements in a Turbulent Recirculating Bubble-Driven Liquid Flow. Int. J. Multiphase Flow 1982, 18, 413–421. [Google Scholar] [CrossRef]
- Kataoka, I.; Serizawa, A.; Besnard, D.C. Prediction of Turbulence Suppression and Turbulence Modeling in Bubbly Two-Phase Flow. Nucl. Eng. Des. 1993, 141, 145–158. [Google Scholar] [CrossRef]
- Mao, Z.S.; Duckler, A. The motion of Taylor bubbles in vertical tubes: I. A numerical simulation for the shape and rise velocity of Taylor bubbles in stagnant and flowing liquid. J. Comp. Phys. 1990, 91, 132–160. [Google Scholar] [CrossRef]
- Chesters, A.K.; Van Doorn, M.; Goossens, L.H.J. A General Model of Unconfined Bubble Plumes from an Extended Source. Int. J. Multiphase Flow 1980, 6, 499–521. [Google Scholar] [CrossRef]
- Leitch, A.M.; Baines, W.D. Liquid Volume Flux in a Weak Bubble Plume. J. Fluid Mech. 1989, 205, 77–98. [Google Scholar] [CrossRef]
- Haberman, W.L.; Morton, R.K. An Experimental Investigation of the Drag and Shape of Air Bubbles Rising in Various Liquids; David, W., Ed.; Taylor Model Basin Report 802; Navy Dept.: Washington, DC, USA, 1953. [Google Scholar]
- Abdulmouti, H. Numerical simulation and fundamental characteristics of surface flow generated by bubbly flows. Int. J. Fluid Mech. Res. 2017, 44, 277. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Murai, Y. Numerical Simulation of Bubble Plume in a Tank with Free Surface. Trans. Jpn. Soc. Mech. Eng. 1995, 61, 2818–2825. [Google Scholar] [CrossRef]
- Abdel-Aal, H.K.; Stiles, G.B.; Holland, C.D. Formation of Interfacial Area at High Rates Gas Flow Through Submerged Orifices. ALCHE J. 1966, 12, 174–180. [Google Scholar] [CrossRef]
- Abdulmouti, H.; Murai, Y.; Ohno, Y.; Yamamoto, F. Measurement of bubble plume generated surface flow using PIV. J. Visual. Soc. Jpn. 2001, 21, 31. [Google Scholar]
- Abdulmouti, H. Bubbly two-phase flow: Part I-characteristics, structures, behaviors and flow patterns. Amer. J. Fluid Dyn. 2014, 4, 194. [Google Scholar]
- Garner, F.H.; Hammerton, D. Circulation inside gas bubbles. Chem. Eng. Sci. 1954, 3, 1–11. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Courier Dover Publications: New York, NY, USA, 2005. [Google Scholar]
- Magnaudet, J.; Eames, I. The motion of high-Reynolds-number bubbles in inhomogeneous flows. Ann. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Abdulmouti, H. Experimental measurements of bubble convection models in two-phase stratified liquids. Exp. Thermal Fluid Sci. 2017, 83C, 69. [Google Scholar] [CrossRef]
- Abdulmouti, H. The flow patterns in two immiscible stratified liquids induced by bubble plume. Int. J. Fluid Dyn. 2002, 6, 1. [Google Scholar]
- Murai, Y.; Ohno, Y.; Abdulmouti, H.; Yamamoto, F. Flow in the vicinity of free surface induced by a bubble plume. Jpn. Soc. Mech. Eng. 2001, 13, 1120–1127. [Google Scholar]
- Abdulmouti, H. Numerical simulation of bubble convection in two-phase stratified liquids multiphase science and technology by Begell House, Inc. USA. Home Sci. Eng. 2019, 31, 133–149. [Google Scholar] [CrossRef]
- Abdulmouti, H. Experimental measurement for surface flow characteristics generated by a bubble plume. J. Flow Visual. Image Proc. 2015, 22, 39. [Google Scholar] [CrossRef]
- Abdulmouti, H. 2D- numerical simulation of surface flow velocity and internal flow structure generated by bubbles. Multiph. Sci. Technol. 2016, 28, 153. [Google Scholar] [CrossRef]
- Abdulmout, H. Bubbly two-phase flow: Part II-characteristics and parameters. Am. J. Fluid Dyn. 2014, 4, 115–180. [Google Scholar] [CrossRef]
- Abdulmouti, H. Visualization and Image Measurement of Flow Structures Induced by a Bubbly Plume. Ph.D. Thesis, Fukui University, Fukui, Japan, 2003. [Google Scholar]
- Abdulmouti, H. Measurement of Flow Structures Induced by a Bubbly Plume Using Visualization, PIV, and Image Measurement; Scholar’s Press: Saarbrücken, Germany, 2013; ISBN-13: 978-3-639-51490-2. [Google Scholar]
- Abdulmouti, H.; Yamamoto, F.; Murai, Y.; Kobayashi, Y. Research and development for a new bubble curtain type of oil fence. J. Visual. Soc. Jpn. 1997, 17, 239. [Google Scholar]
- Abdulmouti, H. Measurements of Thermal Effect on Bubble Parameter. In Proceedings of the 3rd Thermal and Fluids Engineering Conference (TFEC), Fort Lauderdale, FL, USA, 4–7 March 2018. [Google Scholar]
- Abdulmouti, H. The measurements of bubble plume structure parameter. Int. J. Fluid Mech. Res. 2017, 44, 1. [Google Scholar] [CrossRef]
- Abdulmouti, H. Parameter Measurements of Bubble Plume Structure. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- Taylor, Y.; Matsumoto, Y. Eulerian analysis of bubbly two-phase flows using CIP scheme. Comput. Fluid Dyn. J. 1999, 8, 26–33. [Google Scholar]
- Murai, Y.; Ohno, Y.; Bae, D.S.; Abdulmouti, H.; Yamamoto, F. Bubble-Generated Convection in Immiscible Two-phase Stratified Liquids. In Proceeding of the ASME FEDSM-01, New Orleans, LA, USA, 29 May–1 June 2001. [Google Scholar]
- Abdulmouti, H.; Shinneeb, M. Investigation of Free-Surface Flow Induced by a Bubbly Plume Using PIV. In Proceeding of the Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4–6 February 2020; IEEE Xplore: Piscataway Township, NY, USA, 2020. [Google Scholar]
- Ohno, Y.; Murai, Y.; Abdulmouti, H.; Junichi, O.; Fujio, Y. Numerical analysis of the surface flow induced by a bubble curtain. In Proceedings of the CFD Symposium, Tokyo, Japan, 17–19 July 1998; pp. 235–236. [Google Scholar]
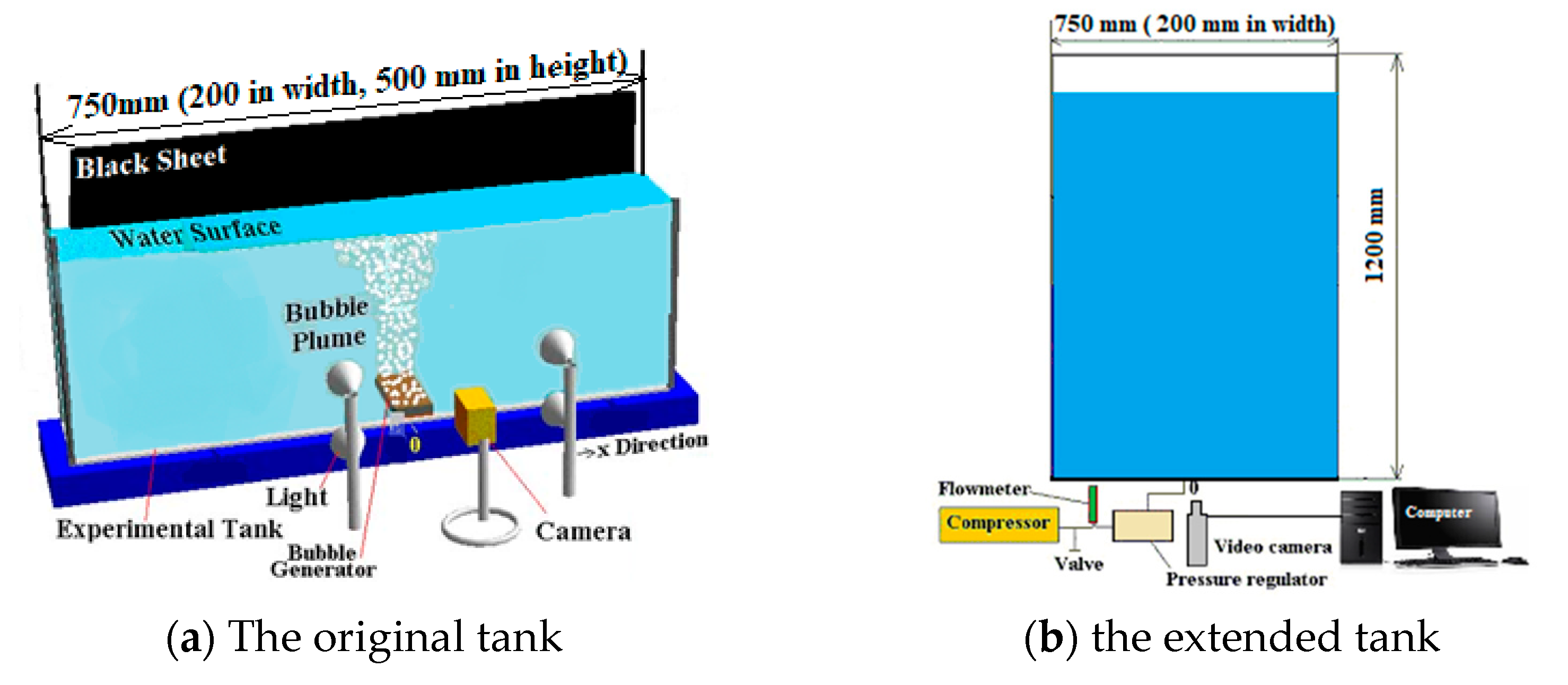



| Parameter | Value |
|---|---|
| Density of water | ρ = 1000 kg/m3 |
| Kinematic viscosity of water | υ = 0.547 × 10−6 to 1 × 10−6 m2/s |
| Initial water depth | H = 0.1 to 1.2 m |
| Atmospheric pressure | 101 kPa |
| Ambient temperature | 22–25 °C |
| Water temperature | 20–50 °C |
| The density of the gas (air) | 1.25 kg/m3 |
| Maximum gas flow rate | Q = 50 × 10−5 m3/s |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 20 | 3.600 | 3.700 | 3.800 | 0.01000–0.01010 | 3.920 | 4.100 | 4.230 | 0.01047–0.01051 | 4.400 | 4.580 | 4.720 | 0.01075–0.01079 |
| 200 | 3.690 | 3.750 | 3.820 | 0.01005–0.01011 | 3.990 | 4.150 | 4.250 | 0.01052–0.01053 | 4.440 | 4.600 | 4.760 | 0.01080–0.01083 | |
| 300 | 3.720 | 3.790 | 3.860 | 0.01014–0.01019 | 4.010 | 4.180 | 4.280 | 0.01055–0.01058 | 4.490 | 4.650 | 4.790 | 0.01084–0.01088 | |
| 400 | 3.750 | 3.810 | 3.890 | 0.01020–0.01023 | 4.100 | 4.210 | 4.310 | 0.01056–0.01058 | 4.510 | 4.690 | 4.830 | 0.01088–0.01093 | |
| 500 | 3.780 | 3.860 | 3.920 | 0.01024–0.01029 | 4.150 | 4.250 | 4.340 | 0.01057–0.01059 | 4.550 | 4.710 | 4.870 | 0.01094–0.01097 | |
| 600 | 3.801 | 3.890 | 3.950 | 0.01030–0.01032 | 4.180 | 4.280 | 4.360 | 0.01059–0.01061 | 4.590 | 4.750 | 4.901 | 0.01096–0.01098 | |
| 700 | 3.890 | 3.920 | 3.980 | 0.01033–0.01036 | 4.210 | 4.320 | 4.380 | 0.01062–0.01064 | 4.610 | 4.790 | 4.950 | 0.01097–0.01100 | |
| 800 | 3.920 | 3.990 | 4.080 | 0.01037–0.01039 | 4.250 | 4.360 | 4.420 | 0.01063–0.01065 | 4.660 | 4.820 | 5.020 | 0.01099–0.01105 | |
| 900 | 3.950 | 4.102 | 4.140 | 0.01039–0.01041 | 4.290 | 4.390 | 4.490 | 0.01065–0.01067 | 4.690 | 4.860 | 5.150 | 0.01107–0.01109 | |
| 1000 | 3.990 | 4.150 | 4.180 | 0.01042–0.01044 | 4.380 | 4.430 | 4.530 | 0.01066–0.01068 | 4.720 | 4.900 | 5.200 | 0.01115–0.01122 | |
| 1100 | 4.050 | 4.200 | 4.300 | 0.01045–0.01047 | 4.400 | 4.600 | 4.700 | 0.01069–0.01070 | 4.890 | 5.000 | 5.280 | 0.01128–0.01135 | |
| Water height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 30 | 4.445 | 4.531 | 4.577 | 0.01097–0.01099 | 4.609 | 4.683 | 4.888 | 0.01143–0.01147 | 4.994 | 5.030 | 5.100 | 0.01182–0.01188 |
| 200 | 4.453 | 4.534 | 4.583 | 0.01105–0.01109 | 4.609 | 4.729 | 4.894 | 0.01147–0.01151 | 5.048 | 5.050 | 5.200 | 0.01186–0.01191 | |
| 300 | 4.467 | 4.557 | 4.600 | 0.01114–0.01116 | 4.630 | 4.743 | 4.967 | 0.01152–0.01155 | 5.099 | 5.180 | 5.300 | 0.01190–0.01195 | |
| 400 | 4.470 | 4.564 | 4.600 | 0.01115–0.01117 | 4.638 | 4.867 | 4.980 | 0.01156–0.01159 | 5.159 | 5.250 | 5.400 | 0.01194–0.01198 | |
| 500 | 4.475 | 4.577 | 4.642 | 0.01116–0.01119 | 4.787 | 4.888 | 4.994 | 0.01160–0.01164 | 5.299 | 5.356 | 5.400 | 0.01197–0.01200 | |
| 600 | 4.479 | 4.583 | 4.653 | 0.01119–0.01123 | 4.809 | 4.894 | 5.048 | 0.01163–0.01167 | 5.299 | 5.410 | 5.500 | 0.01199–0.01205 | |
| 700 | 4.480 | 4.600 | 4.700 | 0.01124–0.01127 | 4.849 | 4.967 | 5.099 | 0.01169–0.01172 | 5.306 | 5.400 | 5.600 | 0.01209–0.01215 | |
| 800 | 4.485 | 4.609 | 4.720 | 0.01128–0.01131 | 4.897 | 4.980 | 5.159 | 0.01171–0.01175 | 5.432 | 5.600 | 5.600 | 0.01220–0.01228 | |
| 900 | 4.489 | 4.609 | 4.768 | 0.01133–0.01135 | 4.903 | 4.994 | 5.299 | 0.01173–0.01177 | 5.533 | 5.700 | 5.790 | 0.01225–0.01230 | |
| 1000 | 4.500 | 4.630 | 4.869 | 0.01135–0.01137 | 4.959 | 5.048 | 5.299 | 0.01175–0.01179 | 5.633 | 5.750 | 5.800 | 0.01228–0.01236 | |
| 1100 | 4.510 | 4.631 | 4.791 | 0.01139–0.01142 | 4.936 | 5.099 | 5.306 | 0.01178–0.01181 | 5.637 | 5.770 | 5.810 | 0.01231–0.01241 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 40 | 5.160 | 5.450 | 5.562 | 0.01204–0.01209 | 5.679 | 5.788 | 5.927 | 0.01239–0.01244 | 6.184 | 6.334 | 6.562 | 0.01279–0.01285 |
| 200 | 5.160 | 5.450 | 5.562 | 0.01206–0.01210 | 5.679 | 5.788 | 5.927 | 0.01245–0.01248 | 6.184 | 6.334 | 6.562 | 0.01282–0.01288 | |
| 300 | 5.377 | 5.476 | 5.582 | 0.01206–0.01210 | 5.695 | 5.810 | 5.970 | 0.01247–0.01251 | 6.232 | 6.461 | 6.599 | 0.01286–0.01290 | |
| 400 | 5.391 | 5.476 | 5.635 | 0.01212–0.01216 | 5.742 | 5.820 | 5.980 | 0.01250–0.01253 | 6.256 | 6.536 | 6.800 | 0.01289–0.01295 | |
| 500 | 5.437 | 5.536 | 5.676 | 0.01214–0.01219 | 5.754 | 5.927 | 6.044 | 0.01255–0.01259 | 6.321 | 6.557 | 6.790 | 0.01294–0.01299 | |
| 600 | 5.490 | 5.510 | 5.700 | 0.01218–0.01222 | 5.800 | 5.900 | 6.100 | 0.01258–0.01263 | 6.400 | 6.600 | 6.890 | 0.01298–0.01301 | |
| 700 | 5.510 | 5.540 | 5.670 | 0.01219–0.01225 | 5.900 | 5.990 | 6.090 | 0.01260–0.01266 | 6.380 | 6.800 | 6.950 | 0.01300–0.01309 | |
| 800 | 5.490 | 5.590 | 5.700 | 0.01221–0.01228 | 5.880 | 6.100 | 6.200 | 0.01266–0.01269 | 6.480 | 6.780 | 7.100 | 0.01308–0.01313 | |
| 900 | 5.560 | 5.650 | 5.800 | 0.01226–0.01232 | 5.990 | 6.200 | 6.400 | 0.01266–0.01270 | 6.500 | 6.850 | 7.170 | 0.01315–0.01320 | |
| 1000 | 5.550 | 5.723 | 5.900 | 0.01230–0.01235 | 6.002 | 6.400 | 6.600 | 0.01268–0.01274 | 6.700 | 6.900 | 7.250 | 0.01319–0.01325 | |
| 1100 | 5.590 | 5.690 | 5.990 | 0.01233–0.01238 | 6.200 | 6.450 | 6.700 | 0.01271–0.01276 | 6.900 | 7.050 | 7.340 | 0.01324–0.01335 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range Of uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 50 | 6.124 | 6.455 | 6.556 | 0.01310–0.01318 | 6.689 | 6.788 | 6.944 | 0.01350–0.01358 | 7.178 | 7.343 | 7.562 | 0.01401–0.01410 |
| 200 | 6.355 | 6.476 | 6.578 | 0.01315–0.01324 | 6.695 | 6.817 | 6.970 | 0.01354–0.01364 | 7.243 | 7.476 | 7.687 | 0.01410–0.01419 | |
| 300 | 6.389 | 6.490 | 6.646 | 0.01319–0.01328 | 6.762 | 6.832 | 6.978 | 0.01360–0.01366 | 7.256 | 7.576 | 7.709 | 0.01418–0.01428 | |
| 400 | 6.464 | 6.521 | 6.686 | 0.01324–0.01329 | 6.775 | 6.927 | 7.034 | 0.01365–0.01368 | 7.332 | 7.587 | 7.698 | 0.01427–0.01446 | |
| 500 | 6.400 | 6.600 | 6.700 | 0.01327–0.01332 | 6.800 | 7.010 | 7.100 | 0.01366–0.01370 | 7.400 | 7.600 | 7.892 | 0.01450–0.01466 | |
| 600 | 6.500 | 6.700 | 6.750 | 0.01330–0.01336 | 6.900 | 7.100 | 7.300 | 0.01370–0.01377 | 7.600 | 7.700 | 7.950 | 0.01466–0.01472 | |
| 700 | 6.550 | 6.650 | 6.800 | 0.01335–0.01339 | 6.850 | 7.050 | 7.350 | 0.01375–0.01380 | 7.550 | 7.900 | 8.019 | 0.01464–0.01471 | |
| 800 | 6.600 | 6.700 | 6.900 | 0.01336–0.01343 | 7.100 | 7.200 | 7.500 | 0.01379–0.01386 | 7.690 | 7.890 | 8.120 | 0.01475–0.01481 | |
| 900 | 6.700 | 6.800 | 7.020 | 0.01340–0.01347 | 7.200 | 7.400 | 7.700 | 0.01382–0.01389 | 7.800 | 8.010 | 8.130 | 0.01482–0.01487 | |
| 1000 | 6.800 | 6.900 | 7.100 | 0.01344–0.01349 | 7.290 | 7.500 | 7.800 | 0.01388–0.01395 | 7.900 | 8.200 | 8.340 | 0.01488–0.01490 | |
| 1100 | 6.750 | 6.890 | 7.090 | 0.01348–0.01354 | 7.250 | 7.480 | 7.780 | 0.01394–0.01400 | 7.910 | 8.150 | 8.314 | 0.01490–0.01500 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 20 | 0.090 | 0.138 | 0.170 | 0.00180–0.00340 | 0.205 | 0.229 | 0.239 | 0.00410–0.00478 | 0.253 | 0.257 | 0.271 | 0.00506–0.00542 |
| 200 | 0.102 | 0.149 | 0.180 | 0.00204–0.00360 | 0.207 | 0.231 | 0.242 | 0.00414–0.00484 | 0.257 | 0.260 | 0.272 | 0.00514–0.00544 | |
| 300 | 0.105 | 0.150 | 0.180 | 0.00209–0.00360 | 0.212 | 0.236 | 0.247 | 0.00424–0.00494 | 0.258 | 0.267 | 0.274 | 0.00516–0.00548 | |
| 400 | 0.124 | 0.160 | 0.199 | 0.00248–0.00398 | 0.210 | 0.235 | 0.251 | 0.00420–0.00502 | 0.258 | 0.270 | 0.282 | 0.00516–0.00564 | |
| 500 | 0.122 | 0.161 | 0.200 | 0.00244–0.00400 | 0.228 | 0.239 | 0.255 | 0.00456–0.00510 | 0.261 | 0.274 | 0.290 | 0.00522–0.00580 | |
| 600 | 0.132 | 0.174 | 0.210 | 0.00264–0.00420 | 0.234 | 0.250 | 0.260 | 0.00468–0.00520 | 0.269 | 0.279 | 0.300 | 0.00538–0.00600 | |
| 700 | 0.139 | 0.180 | 0.212 | 0.00278–0.00424 | 0.239 | 0.249 | 0.270 | 0.00478–0.00540 | 0.271 | 0.290 | 0.320 | 0.00542–0.00640 | |
| 800 | 0.145 | 0.182 | 0.230 | 0.00290–0.00460 | 0.248 | 0.255 | 0.280 | 0.00496–0.00560 | 0.289 | 0.295 | 0.330 | 0.00578–0.00660 | |
| 900 | 0.148 | 0.180 | 0.240 | 0.00296–0.00480 | 0.251 | 0.270 | 0.290 | 0.00502–0.00580 | 0.299 | 0.320 | 0.340 | 0.00598–0.00680 | |
| 1000 | 0.147 | 0.195 | 0.242 | 0.00294–0.00484 | 0.262 | 0.277 | 0.310 | 0.00524–0.00620 | 0.330 | 0.340 | 0.350 | 0.00660–0.00700 | |
| 1100 | 0.166 | 0.200 | 0.241 | 0.00332–0.00482 | 0.270 | 0.278 | 0.330 | 0.00540–0.00660 | 0.350 | 0.360 | 0.370 | 0.00700–0.00740 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 30 | 0.254 | 0.259 | 0.271 | 0.00508–0.00519 | 0.343 | 0.386 | 0.411 | 0.00686–0.00772 | 0.436 | 0.450 | 0.461 | 0.00871–0.00900 |
| 200 | 0.257 | 0.260 | 0.272 | 0.00514–0.00520 | 0.353 | 0.397 | 0.428 | 0.00706–0.00795 | 0.440 | 0.453 | 0.464 | 0.00880–0.00906 | |
| 300 | 0.258 | 0.267 | 0.274 | 0.00516–0.00534 | 0.376 | 0.399 | 0.430 | 0.00752–0.00798 | 0.443 | 0.454 | 0.467 | 0.00886–0.00908 | |
| 400 | 0.258 | 0.270 | 0.282 | 0.00516–0.00539 | 0.371 | 0.413 | 0.431 | 0.00742–0.00826 | 0.448 | 0.459 | 0.471 | 0.00895–0.00917 | |
| 500 | 0.260 | 0.270 | 0.289 | 0.00520–0.00540 | 0.388 | 0.412 | 0.439 | 0.00776–0.00824 | 0.460 | 0.460 | 0.490 | 0.00920–0.00920 | |
| 600 | 0.270 | 0.280 | 0.290 | 0.00540–0.00560 | 0.392 | 0.429 | 0.438 | 0.00784–0.00858 | 0.450 | 0.470 | 0.488 | 0.00900–0.00940 | |
| 700 | 0.280 | 0.290 | 0.310 | 0.00560–0.00580 | 0.403 | 0.422 | 0.440 | 0.00807–0.00844 | 0.465 | 0.490 | 0.500 | 0.00930–0.00980 | |
| 800 | 0.290 | 0.300 | 0.325 | 0.00580–0.00600 | 0.405 | 0.419 | 0.450 | 0.00810–0.00838 | 0.480 | 0.499 | 0.520 | 0.00960–0.00998 | |
| 900 | 0.300 | 0.301 | 0.330 | 0.00600–0.00602 | 0.409 | 0.430 | 0.451 | 0.00818–0.00860 | 0.470 | 0.500 | 0.540 | 0.00940–0.01000 | |
| 1000 | 0.310 | 0.320 | 0.340 | 0.00620–0.00600 | 0.414 | 0.435 | 0.460 | 0.00827–0.00870 | 0.490 | 0.530 | 0.550 | 0.00980–0.01060 | |
| 1100 | 0.320 | 0.330 | 0.350 | 0.00640–0.00660 | 0.411 | 0.434 | 0.459 | 0.00823–0.00868 | 0.480 | 0.499 | 0.549 | 0.00960–0.00998 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 40 | 0.416 | 0.473 | 0.488 | 0.00832–0.00947 | 0.498 | 0.518 | 0.555 | 0.00997–0.01037 | 0.597 | 0.650 | 0.737 | 0.01194–0.01299 |
| 200 | 0.436 | 0.479 | 0.491 | 0.00873–0.00957 | 0.500 | 0.528 | 0.562 | 0.00999–0.01056 | 0.603 | 0.660 | 0.758 | 0.01207–0.01321 | |
| 300 | 0.457 | 0.480 | 0.493 | 0.00913–0.00960 | 0.507 | 0.539 | 0.573 | 0.01014–0.01078 | 0.615 | 0.691 | 0.773 | 0.01230–0.01383 | |
| 400 | 0.467 | 0.485 | 0.494 | 0.00934–0.00971 | 0.511 | 0.549 | 0.582 | 0.01022–0.01099 | 0.625 | 0.716 | 0.793 | 0.01250–0.01433 | |
| 500 | 0.450 | 0.480 | 0.520 | 0.00900–0.00960 | 0.525 | 0.570 | 0.589 | 0.01050–0.01140 | 0.630 | 0.719 | 0.800 | 0.01260–0.01438 | |
| 600 | 0.459 | 0.488 | 0.515 | 0.00918–0.00976 | 0.550 | 0.574 | 0.590 | 0.01100–0.01148 | 0.660 | 0.720 | 0.835 | 0.01320–0.01440 | |
| 700 | 0.457 | 0.520 | 0.530 | 0.00914–0.01040 | 0.560 | 0.580 | 0.630 | 0.01120–0.01160 | 0.690 | 0.740 | 0.830 | 0.01380–0.01480 | |
| 800 | 0.468 | 0.510 | 0.540 | 0.00936–0.01020 | 0.590 | 0.596 | 0.660 | 0.01180–0.01192 | 0.700 | 0.760 | 0.890 | 0.01400–0.01520 | |
| 900 | 0.466 | 0.512 | 0.560 | 0.00932–0.01024 | 0.600 | 0.650 | 0.690 | 0.01200–0.01300 | 0.750 | 0.790 | 0.900 | 0.01500–0.01580 | |
| 1000 | 0.480 | 0.520 | 0.580 | 0.00960–0.01040 | 0.640 | 0.680 | 0.730 | 0.01280–0.01360 | 0.790 | 0.820 | 0.950 | 0.01580–0.01640 | |
| 1100 | 0.470 | 0.519 | 0.570 | 0.00940–0.01038 | 0.620 | 0.680 | 0.740 | 0.01240–0.01360 | 0.780 | 0.830 | 0.960 | 0.01560–0.01660 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 50 | 0.522 | 0.556 | 0.597 | 0.01044–0.01111 | 0.635 | 0.687 | 0.724 | 0.01270–0.01375 | 0.764 | 0.807 | 0.847 | 0.01527–0.01615 |
| 200 | 0.533 | 0.576 | 0.603 | 0.01066–0.01152 | 0.646 | 0.698 | 0.736 | 0.01292–0.01395 | 0.776 | 0.818 | 0.858 | 0.01552–0.01635 | |
| 300 | 0.544 | 0.587 | 0.615 | 0.01088–0.01175 | 0.659 | 0.707 | 0.747 | 0.01318–0.01415 | 0.787 | 0.828 | 0.877 | 0.01575–0.01655 | |
| 400 | 0.555 | 0.589 | 0.625 | 0.01110–0.01178 | 0.672 | 0.719 | 0.759 | 0.01343–0.01439 | 0.793 | 0.838 | 0.893 | 0.01586–0.01676 | |
| 500 | 0.560 | 0.590 | 0.630 | 0.01120–0.01180 | 0.670 | 0.720 | 0.760 | 0.01340–0.01440 | 0.780 | 0.820 | 0.880 | 0.01560–0.01640 | |
| 600 | 0.559 | 0.600 | 0.650 | 0.01118–0.01200 | 0.680 | 0.730 | 0.770 | 0.01360–0.01460 | 0.820 | 0.860 | 0.920 | 0.01640–0.01720 | |
| 700 | 0.580 | 0.590 | 0.660 | 0.01160–0.01180 | 0.700 | 0.770 | 0.780 | 0.01400–0.01540 | 0.830 | 0.890 | 0.950 | 0.01660–0.01780 | |
| 800 | 0.587 | 0.600 | 0.670 | 0.01174–0.01200 | 0.750 | 0.772 | 0.800 | 0.01500–0.01544 | 0.880 | 0.900 | 0.960 | 0.01760–0.01800 | |
| 900 | 0.600 | 0.650 | 0.700 | 0.01200–0.01300 | 0.790 | 0.820 | 0.880 | 0.01580–0.01640 | 0.900 | 0.950 | 0.990 | 0.01800–0.01900 | |
| 1000 | 0.650 | 0.700 | 0.750 | 0.01300–0.01400 | 0.820 | 0.850 | 0.890 | 0.01640–0.01700 | 0.950 | 0.980 | 1.000 | 0.01900–0.01960 | |
| 1100 | 0.660 | 0.710 | 0.760 | 0.01320–0.01420 | 0.830 | 0.860 | 0.900 | 0.01660–0.01720 | 0.960 | 0.978 | 1.010 | 0.01920–0.01956 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 20 | 0.0000083 | 0.0000054 | 0.0000044 | 0.000000166–0.000000162 | 0.0000679 | 0.0000608 | 0.0000583 | 0.000001358–0.000001824 | 0.0000982 | 0.0000967 | 0.0000917 | 0.000001965–0.000002901 |
| 200 | 0.0000073 | 0.0000050 | 0.0000041 | 0.000000146–0.000000150 | 0.0000673 | 0.0000602 | 0.0000575 | 0.000001345–0.000001806 | 0.0000967 | 0.0000956 | 0.0000914 | 0.000001935–0.000002869 | |
| 300 | 0.0000071 | 0.0000050 | 0.0000041 | 0.000000142–0.000000149 | 0.0000657 | 0.0000590 | 0.0000564 | 0.000001313–0.000001770 | 0.0000964 | 0.0000931 | 0.0000907 | 0.000001929–0.000002794 | |
| 400 | 0.0000060 | 0.0000047 | 0.0000037 | 0.000000120–0.000000140 | 0.0000663 | 0.0000592 | 0.0000555 | 0.000001326–0.000001777 | 0.0000964 | 0.0000922 | 0.0000882 | 0.000001927–0.000002767 | |
| 500 | 0.0000061 | 0.0000046 | 0.0000037 | 0.000000122–0.000000139 | 0.0000611 | 0.0000583 | 0.0000546 | 0.000001221–0.000001748 | 0.0000953 | 0.0000907 | 0.0000857 | 0.000001905–0.000002722 | |
| 600 | 0.0000056 | 0.0000043 | 0.0000035 | 0.000000113–0.000000128 | 0.0000595 | 0.0000557 | 0.0000536 | 0.000001190–0.000001671 | 0.0000924 | 0.0000891 | 0.0000829 | 0.000001849–0.000002673 | |
| 700 | 0.0000054 | 0.0000041 | 0.0000035 | 0.000000107–0.000000124 | 0.0000583 | 0.0000559 | 0.0000516 | 0.000001165–0.000001677 | 0.0000917 | 0.0000857 | 0.0000777 | 0.000001835–0.000002572 | |
| 800 | 0.0000051 | 0.0000041 | 0.0000032 | 0.000000103–0.000000123 | 0.0000561 | 0.0000546 | 0.0000497 | 0.000001123–0.000001638 | 0.0000860 | 0.0000843 | 0.0000753 | 0.000001721–0.000002528 | |
| 900 | 0.0000050 | 0.0000041 | 0.0000031 | 0.000000101–0.000000124 | 0.0000555 | 0.0000516 | 0.0000480 | 0.000001109–0.000001547 | 0.0000832 | 0.0000777 | 0.0000731 | 0.000001663–0.000002331 | |
| 1000 | 0.0000051 | 0.0000038 | 0.0000031 | 0.000000101–0.000000115 | 0.0000531 | 0.0000503 | 0.0000449 | 0.000001063–0.000001508 | 0.0000753 | 0.0000731 | 0.0000710 | 0.000001507–0.000002194 | |
| 1100 | 0.0000045 | 0.0000037 | 0.0000031 | 0.000000090–0.000000112 | 0.0000516 | 0.0000501 | 0.0000422 | 0.000001031–0.000001502 | 0.0000710 | 0.0000691 | 0.0000672 | 0.000001421–0.000002072 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 30 | 0.0000029 | 0.0000029 | 0.0000027 | 0.000000059–0.000000086 | 0.0000406 | 0.0000361 | 0.0000325 | 0.000000812–0.000001082 | 0.0000571 | 0.0000553 | 0.0000539 | 0.000001142–0.000001658 |
| 200 | 0.0000029 | 0.0000029 | 0.0000027 | 0.000000058–0.000000086 | 0.0000395 | 0.0000350 | 0.0000325 | 0.000000789–0.000001051 | 0.0000565 | 0.0000549 | 0.0000536 | 0.000001130–0.000001647 | |
| 300 | 0.0000029 | 0.0000028 | 0.0000027 | 0.000000058–0.000000084 | 0.0000370 | 0.0000349 | 0.0000324 | 0.000000741–0.000001047 | 0.0000561 | 0.0000547 | 0.0000533 | 0.000001123–0.000001642 | |
| 400 | 0.0000029 | 0.0000028 | 0.0000026 | 0.000000058–0.000000083 | 0.0000375 | 0.0000337 | 0.0000323 | 0.000000750–0.000001011 | 0.0000555 | 0.0000542 | 0.0000528 | 0.000001111–0.000001626 | |
| 500 | 0.0000029 | 0.0000028 | 0.0000026 | 0.000000057–0.000000083 | 0.0000359 | 0.0000338 | 0.0000317 | 0.000000717–0.000001014 | 0.0000541 | 0.0000541 | 0.0000507 | 0.000001081–0.000001622 | |
| 600 | 0.0000028 | 0.0000027 | 0.0000026 | 0.000000055–0.000000080 | 0.0000355 | 0.0000325 | 0.0000318 | 0.000000711–0.000000974 | 0.0000553 | 0.0000529 | 0.0000509 | 0.000001105–0.000001587 | |
| 700 | 0.0000027 | 0.0000026 | 0.0000024 | 0.000000053–0.000000077 | 0.0000345 | 0.0000330 | 0.0000316 | 0.000000690–0.000000990 | 0.0000535 | 0.0000507 | 0.0000497 | 0.000001069–0.000001522 | |
| 800 | 0.0000026 | 0.0000025 | 0.0000023 | 0.000000051–0.000000075 | 0.0000344 | 0.0000332 | 0.0000309 | 0.000000688–0.000000997 | 0.0000518 | 0.0000498 | 0.0000478 | 0.000001036–0.000001495 | |
| 900 | 0.0000025 | 0.0000025 | 0.0000023 | 0.000000050–0.000000074 | 0.0000340 | 0.0000324 | 0.0000309 | 0.000000681–0.000000971 | 0.0000529 | 0.0000497 | 0.0000460 | 0.000001058–0.000001492 | |
| 1000 | 0.0000024 | 0.0000023 | 0.0000022 | 0.000000048–0.000000070 | 0.0000337 | 0.0000320 | 0.0000303 | 0.000000673–0.000000960 | 0.0000507 | 0.0000469 | 0.0000452 | 0.000001015–0.000001407 | |
| 1100 | 0.0000023 | 0.0000023 | 0.0000021 | 0.000000047–0.000000068 | 0.0000338 | 0.0000321 | 0.0000303 | 0.000000677–0.000000962 | 0.0000518 | 0.0000498 | 0.0000453 | 0.000001036–0.000001495 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 40 | 0.0000018 | 0.0000016 | 0.0000015 | 0.0000000358–0.0000000472 | 0.0000279 | 0.0000269 | 0.0000251 | 0.0000005588–0.0000008059 | 0.0000416 | 0.0000383 | 0.0000337 | 0.0000008328–0.0000011480 |
| 200 | 0.0000017 | 0.0000016 | 0.0000015 | 0.0000000341–0.0000000467 | 0.0000279 | 0.0000264 | 0.0000248 | 0.0000005574–0.0000007910 | 0.0000412 | 0.0000377 | 0.0000328 | 0.0000008240–0.0000011295 | |
| 300 | 0.0000016 | 0.0000016 | 0.0000015 | 0.0000000326–0.0000000466 | 0.0000275 | 0.0000258 | 0.0000243 | 0.0000005491–0.0000007752 | 0.0000404 | 0.0000360 | 0.0000322 | 0.0000008086–0.0000010787 | |
| 400 | 0.0000016 | 0.0000015 | 0.0000015 | 0.0000000319–0.0000000461 | 0.0000273 | 0.0000253 | 0.0000239 | 0.0000005450–0.0000007604 | 0.0000398 | 0.0000347 | 0.0000314 | 0.0000007954–0.0000010414 | |
| 500 | 0.0000017 | 0.0000016 | 0.0000014 | 0.0000000331–0.0000000466 | 0.0000265 | 0.0000244 | 0.0000236 | 0.0000005304–0.0000007328 | 0.0000395 | 0.0000346 | 0.0000311 | 0.0000007893–0.0000010374 | |
| 600 | 0.0000016 | 0.0000015 | 0.0000014 | 0.0000000325–0.0000000458 | 0.0000253 | 0.0000243 | 0.0000236 | 0.0000005063–0.0000007277 | 0.0000377 | 0.0000345 | 0.0000298 | 0.0000007534–0.0000010360 | |
| 700 | 0.0000016 | 0.0000014 | 0.0000014 | 0.0000000326–0.0000000430 | 0.0000249 | 0.0000240 | 0.0000221 | 0.0000004973–0.0000007202 | 0.0000360 | 0.0000336 | 0.0000300 | 0.0000007207–0.0000010080 | |
| 800 | 0.0000016 | 0.0000015 | 0.0000014 | 0.0000000318–0.0000000438 | 0.0000236 | 0.0000234 | 0.0000211 | 0.0000004720–0.0000007008 | 0.0000355 | 0.0000327 | 0.0000279 | 0.0000007104–0.0000009814 | |
| 900 | 0.0000016 | 0.0000015 | 0.0000013 | 0.0000000320–0.0000000437 | 0.0000232 | 0.0000214 | 0.0000202 | 0.0000004641–0.0000006426 | 0.0000332 | 0.0000315 | 0.0000276 | 0.0000006630–0.0000009442 | |
| 1000 | 0.0000016 | 0.0000014 | 0.0000013 | 0.0000000310–0.0000000430 | 0.0000218 | 0.0000205 | 0.0000191 | 0.0000004351–0.0000006143 | 0.0000315 | 0.0000303 | 0.0000262 | 0.0000006294–0.0000009096 | |
| 1100 | 0.0000016 | 0.0000014 | 0.0000013 | 0.0000000317–0.0000000431 | 0.0000225 | 0.0000205 | 0.0000188 | 0.0000004491–0.0000006143 | 0.0000319 | 0.0000300 | 0.0000259 | 0.0000006375–0.0000008987 | |
| Water Height (mm) | Water Temperature (°C) | Gas Volume Flow Rate Q1 = 1.5 × 10−5 (m3/s) | Gas Volume Flow Rate Q2 = 28 × 10−5 (m3/s) | Gas Volume Flow Rate Q3 = 50 × 10−5 (m3/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | Lower | Middle | Upper | Range of Uncertainties | ||
| 100 | T = 50 | 0.0000014 | 0.0000013 | 0.0000012 | 0.0000000358–0.0000000472 | 0.0000219 | 0.0000203 | 0.0000192 | 0.0000005588–0.0000008059 | 0.0000326 | 0.0000308 | 0.0000293 | 0.0000008328–0.0000011480 |
| 200 | 0.0000014 | 0.0000013 | 0.0000012 | 0.0000000341–0.0000000467 | 0.0000216 | 0.0000200 | 0.0000189 | 0.0000005574–0.0000007910 | 0.0000320 | 0.0000304 | 0.0000290 | 0.0000008240–0.0000011296 | |
| 300 | 0.0000014 | 0.0000013 | 0.0000012 | 0.0000000326–0.0000000466 | 0.0000211 | 0.0000197 | 0.0000186 | 0.0000005491–0.0000007752 | 0.0000316 | 0.0000300 | 0.0000283 | 0.0000008086–0.0000010787 | |
| 400 | 0.0000013 | 0.0000013 | 0.0000012 | 0.0000000319–0.0000000461 | 0.0000207 | 0.0000194 | 0.0000183 | 0.0000005451–0.0000007604 | 0.0000314 | 0.0000297 | 0.0000278 | 0.0000007954–0.0000010414 | |
| 500 | 0.0000013 | 0.0000013 | 0.0000012 | 0.0000000331–0.0000000466 | 0.0000208 | 0.0000193 | 0.0000183 | 0.0000005304–0.0000007328 | 0.0000319 | 0.0000303 | 0.0000283 | 0.0000007893–0.0000010374 | |
| 600 | 0.0000013 | 0.0000012 | 0.0000011 | 0.0000000325–0.000000045 | 0.0000205 | 0.0000191 | 0.0000181 | 0.000000506–0.0000007277 | 0.0000303 | 0.0000289 | 0.0000270 | 0.0000007534–0.0000010360 | |
| 700 | 0.0000013 | 0.0000013 | 0.0000011 | 0.0000000326–0.0000000430 | 0.0000199 | 0.0000181 | 0.0000179 | 0.0000004973–0.0000007202 | 0.0000300 | 0.0000279 | 0.0000262 | 0.0000007207–0.0000010080 | |
| 800 | 0.0000013 | 0.0000012 | 0.0000011 | 0.0000000318–0.0000000438 | 0.0000186 | 0.0000180 | 0.0000174 | 0.0000004720–0.0000007008 | 0.0000283 | 0.0000276 | 0.0000259 | 0.0000007104–0.0000009814 | |
| 900 | 0.0000012 | 0.0000011 | 0.0000011 | 0.0000000320–0.0000000437 | 0.0000176 | 0.0000170 | 0.0000158 | 0.0000004641–0.0000006426 | 0.0000276 | 0.0000262 | 0.0000251 | 0.0000006630–0.0000009442 | |
| 1000 | 0.0000011 | 0.0000011 | 0.0000010 | 0.0000000310–0.0000000430 | 0.0000170 | 0.0000164 | 0.0000156 | 0.0000004351–0.0000006143 | 0.0000262 | 0.0000254 | 0.0000249 | 0.0000006294–0.0000009096 | |
| 1100 | 0.0000011 | 0.0000010 | 0.0000010 | 0.0000000317–0.0000000431 | 0.0000168 | 0.0000162 | 0.0000155 | 0.0000004491–0.0000006143 | 0.0000259 | 0.0000254 | 0.0000246 | 0.0000006375–0.0000008987 | |
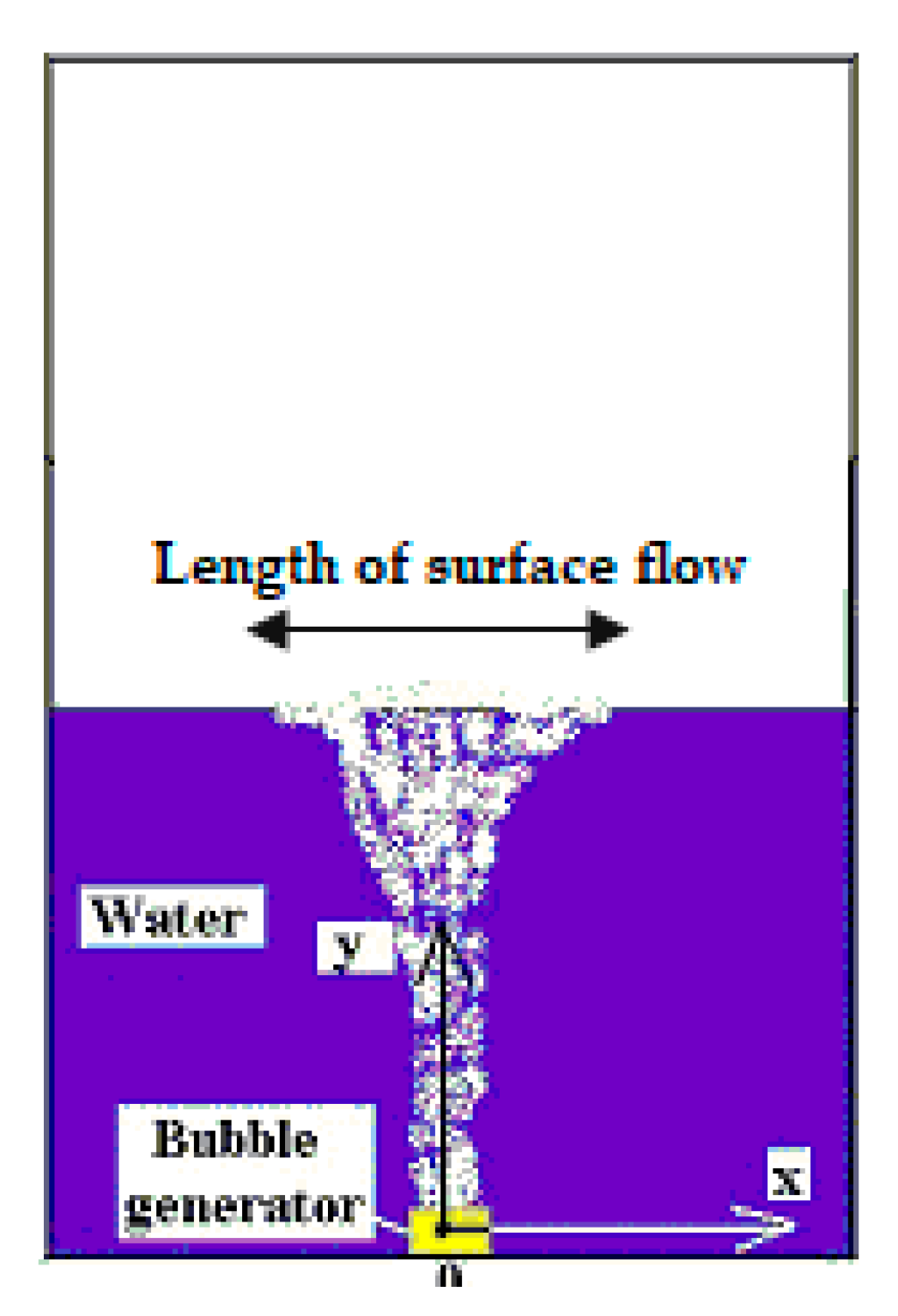
| Gas Volume Flow Rate Q (m3/s) | Water Temperature (°C) | Length of Surface Flow (mm) | Range of Uncertainties (mm) |
|---|---|---|---|
| Q1 = 1.5 × 10−5 | 20 | 320 | 0.4960 |
| 30 | 322 | 0.5120 | |
| 40 | 325 | 0.5265 | |
| 50 | 329 | 0.5593 | |
| Q2 = 28 × 10−5 | 20 | 345 | 0.6210 |
| 30 | 348 | 0.6612 | |
| 40 | 350 | 0.7000 | |
| 50 | 353 | 0.7766 | |
| Q3 = 50 × 10−5 | 20 | 369 | 0.0849 |
| 30 | 372 | 0.8928 | |
| 40 | 374 | 0.9350 | |
| 50 | 376 | 0.9776 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulmouti, H. Improving the Performance of Surface Flow Generated by Bubble Plumes. Fluids 2021, 6, 262. https://doi.org/10.3390/fluids6080262
Abdulmouti H. Improving the Performance of Surface Flow Generated by Bubble Plumes. Fluids. 2021; 6(8):262. https://doi.org/10.3390/fluids6080262
Chicago/Turabian StyleAbdulmouti, Hassan. 2021. "Improving the Performance of Surface Flow Generated by Bubble Plumes" Fluids 6, no. 8: 262. https://doi.org/10.3390/fluids6080262
APA StyleAbdulmouti, H. (2021). Improving the Performance of Surface Flow Generated by Bubble Plumes. Fluids, 6(8), 262. https://doi.org/10.3390/fluids6080262






