Microfluidics for Multiphase Mixing and Liposomal Encapsulation of Nanobioconjugates: Passive vs. Acoustic Systems

Abstract

One of the main routes to ensure that biomolecules or bioactive agents remain active as they are incorporated into products with applications in different industries is by their encapsulation. Liposomes are attractive platforms for encapsulation due to their ease of synthesis and manipulation and the potential to fuse with cell membranes when they are intended for drug delivery applications. We propose encapsulating our recently developed cell-penetrating nanobioconjugates based on magnetite interfaced with translocating proteins and peptides with the purpose of potentiating their cell internalization capabilities even further. To prepare the encapsulates (also known as magnetoliposomes (MLPs)), we introduced a low-cost microfluidic device equipped with a serpentine microchannel to favor the interaction between the liposomes and the nanobioconjugates. The encapsulation performance of the device, operated either passively or in the presence of ultrasound, was evaluated both in silico and experimentally. The in silico analysis was implemented through multiphysics simulations with the software COMSOL Multiphysics 5.5^® (COMSOL Inc., Stockholm, Sweden) via both a Eulerian model and a transport of diluted species model. The encapsulation efficiency was determined experimentally, aided by spectrofluorimetry. Encapsulation efficiencies obtained experimentally and in silico approached 80% for the highest flow rate ratios (FRRs). Compared with the passive mixer, the in silico results of the device under acoustic waves led to higher discrepancies with respect to those obtained experimentally. This was attributed to the complexity of the process in such a situation. The obtained MLPs demonstrated successful encapsulation of the nanobioconjugates by both methods with a 36% reduction in size for the ones obtained in the presence of ultrasound. These findings suggest that the proposed serpentine micromixers are well suited to produce MLPs very efficiently and with homogeneous key physichochemical properties.

1. Introduction

Over the past two decades, microfluidics has gained considerable attention owing to major technological breakthroughs allowing fluid manipulation at sub-millimeter scales for many applications in rapidly developing fields such as biotechnology and biomedical engineering [1]. In this context, microfluidic systems have permitted the high reproducibility of different processes involving the precise encapsulation of bioactive compounds with unique properties for the potential treatment of several conditions ranging from cancer to neurodegeneration. Some include mixing and interaction of liquid phases, sorting of particles, high-throughput screening, and novel drug delivery systems [2,3,4]. The growing interest in microfluidic systems can be attributed to the low volume samples, the size of the devices, and the ease of use, allowing a reduction in costs and fast prototyping and testing [5,6]. Using microfluidic platforms for drug delivery systems represents an opportunity for increasing the bioavailability of therapeutic agents to treat current health issues of growing concern, including immune disorders and the control of antibiotic-resistant bacteria [7,8]. Due to the ability to manipulate fluid interactions very precisely, microfluidic systems allow the development of droplet-based drug carriers as a result of the interaction between continuous and dispersed phases within highly controlled laminar flows in microchannels. Some of the most studied carriers prepared with this approach include emulsions and liposomes [9,10,11].

Liposomes have been of great interest due to their similarity to cells’ membranes and naturally occurring vesicles, having low cytotoxicity and high delivery rates [10,12,13,14]. Besides, their phospholipid bilayers allow the immobilization of both hydrophilic and hydrophobic molecules, providing an excellent resource for drug delivery systems. Liposomes can be easily synthesized with microfluidic devices by passive mixing methods such as microfluidic hydrodynamic focusing (MHF). This method relies on transport phenomena principles within microchannels by controlling flow ratios between an aqueous-based continuous phase and a dispersed phase with diluted lipids. Consequently, monodispersed liposomes can typically be obtained between 50–500 nm (diameter) [3,15]. The size and stability of liposomes depend upon experimental conditions related to flow parameters and the microfluidic device features (i.e., channel geometry and materials) [16]. Liposomes have been successfully employed to deliver biologically active compounds such as proteins, enzymes, nucleic acids, and small pharmacological molecules [9,17].

Furthermore, liposomes have been explored to prepare hybrid delivery encapsulates such as magnetoliposomes (MLPs), which combine the advantages of liposomes and nanostructured magnetic materials (e.g., magnetite). MLPs have found several biomedical and industrial applications, including molecule separation and targeted drug delivery [18,19]. We are particularly interested in preparing MLPs for drug delivery to potentiate even further a number of highly biocompatible cell-penetrating nanobioconjugates that we have synthesized by interfacing membrane active agents with the nanostructured material magnetite (e.g., the Outer Membrane Protein A (OmpA) of Escherichia coli and the translocating peptide Buforin II (BUF-II) [20,21,22]). Besides their ability to penetrate cell membranes very effectively, they exhibit high stability and biocompatibility, reducing the risk of undesired biological responses [23,24]. However, a more potent fusion with cell membranes might be advantageous to reduce the require dosage to achieve the same level of nanobioconjugates reaching the intracellular space.

For liposome encapsulation, conventional methods (e.g., rehydration of phospholipids in the presence of an aqueous suspension of the nanostructured material) lead to low encapsulation efficiencies and high polydispersity indexes as the process proceeds in an uncontrolled manner [3]. However, acoustofluidics has shown to be an efficient avenue for increasing mixing and enhancing the manipulation of particles suspended in fluids within microfluidic devices, by using integrated transducers and piezoelectric components aided by frequencies of up to 2 MHz [25,26,27,28,29]. For instance, with the aid of acoustic streaming and radiation forces in a cell–nanoparticle mixture, fluid–particle interactions are favored for reaching high cell uptakes [30,31]. Acoustic streaming refers to a steady flow caused by the absorption of non-linear acoustic waves with finite amplitude, forcing the fluid molecules within a microchannel to oscillate with the same frequency of the incident wave. When this happens, a time-independent flow velocity (DC flow) is produced by the wave propagation, leading particles to follow a specific movement direction, which depends on the microchannels’ geometry, boundary conditions, and the incident acoustic wave [32]. Considering this, we hypothesize that active mixing techniques based on acoustofluidics can enhance the interaction between liposomes and nanobioconjugates, consequently, leading to high encapsulation efficiencies without significantly altering the morphology of the obtained MLPs.

This contribution is therefore dedicated to study the potential of a simple and affordable acoustic mixing method for producing MLPs. Our approach takes advantage of general acoustic fields produced by ultrasonic baths and a low-cost manufacturing technique of microfluidic devices already mastered by our research groups that is based on laser-cutting techniques and poly (methyl methacrylate) (PMMA) as base material to engrave the micromixing channels of the device [33]. Prior to manufacturing, we studied the potential of acoustic energy for improving mixing and interaction between continuous and dispersed phases in silico aided by an approach implemented in the software COMSOL Multiphysics^®. This allowed us to have a better insight into the encapsulation efficiencies of magnetite nanoparticles (MNPs) into liposomes that are attainable with our device. The devices were then manufactured and tested at different operating regimes to experimentally validate the multiphysics simulations. Finally, the obtained MLPs were characterized via DLS and TEM.

2. Materials and Methods

The mechanistic details of the encapsulation process for producing MLPs via microfluidics was initially studied with a Eulerian approach, aided by the multiphysics simulation software COMSOL Multiphysics 5.5^® (COMSOL Inc., Stockholm, Sweden). This study considered the mixing phenomenon a multiphase problem where a continuous and a dispersed phase interacted according to the Navier–Stokes equations [34]. A ferrofluid containing cell-penetrating magnetite nanoparticles (MNPs) (1 mg/mL) was considered the dispersed phase. In contrast, an aqueous solution with liposomes was regarded as the continuous phase, having similar properties to water. The average particle size for MNPs was set at 10 nm.

An acoustic mixing method was also studied via multiphysics simulations in COMSOL by establishing a 2D geometry of the proposed experimental setup, including computational domains for the geometry of a serpentine micromixer and an ultrasonic bath, used as the source of the acoustic field. To evaluate the effect of acoustic streaming in micromixing, a multiphase flow model was implemented for both the acoustic mixing method and a passive mixing system in the absence of acoustic fields.

Furthermore, to predict the liposomal encapsulation of MNPs, a diluted species model with chemical reaction was considered, integrating a Michaelis–Menten-like equation for modeling the enzyme–substrate complex and the interaction between liposomes and MNPs. The properties of MNPs and forces within the ferrofluid were included as additional parameters for the dispersed phase within the physics settings in COMSOL Multiphysics. This mathematical model was then validated experimentally via fluorescence quenching analyses in a spectrofluorometer to quantify the encapsulation efficiency, and by estimating the mixing quality based on the standard deviation of the pixel intensity upon imaging the mixing process after injection of dye tracers into the device as proposed by Huanming et al. [35].

2.1. Mathematical Models

2.1.1. Macroscopic Flow of the Ferrofluid

A two-phase Eulerian laminar mixture model was implemented to simulate the macroscopic movement of MNPs (by considered them a ferrofluid) from the dispersed to the continuous phase, related to the translocation of particles through the liposomes’ lipid bilayer. In this model, it was assumed that both fluid phases’ densities are approximately constant. Moreover, it was assumed that both phases share the same pressure field and that the particle’s relaxation time is short compared to the timescales of the macroscopic flow [36].

First, the governing equation of the mixture model establishes the mixture density as a weighted average of both phases’ densities, as shown in Equation (1).

$$\rho ={\varphi }_c{\rho }_c+{\varphi }_d{\rho }_d$$

(1)

where ϕ_c, ϕ_d, and ρ_c, ρ_d represent the volume fraction and density of the continuous and dispersed phase, respectively. This leads to the volume flux equation for each phase given by Equations (2) and (3), respectively.

$$j_d={\varphi }_d{u}_d$$

(2)

$$j_c={\varphi }_c{u}_c$$

(3)

where u_c and u_d are the continuous and dispersed phase velocity vectors. Thus, the mixture velocity is given by the volume-averaged flux density or the volume-average mixture velocity j in Equation (4).

$$j=j_d+j_c$$

(4)

Considering the continuity equation for the mixture as

$$\nabla j=0$$

(5)

The Navier–Stokes equation for the momentum of the mixture is then rewritten as (Equation (6)).

$$\rho j_t+\rho \left(j\nabla \right)j+{\rho }_c\epsilon \left(j_{slip}\nabla \right)j=-\nabla P-\nabla {\tau }_{Gm}+\rho g+F-\nabla \left[{\rho }_c\left(1-{\varphi }_c\epsilon \right)u_{slip}{j}_{slip}^T\right]-{\rho }_c\epsilon \left[\left(j\nabla \right)j_{slip}-\frac{m_{dc}}{{\rho }_d}\right]$$

(6)

where ρ is the mixture density, P is the pressure, ε is the reduced density difference, u_slip is the slip velocity vector between the two phases, j_slip is the slip flux, τ_Gm is the sum of the viscous and turbulent stress, g is the gravity vector, m_dc is the mass transfer rate from dispersed to continuous phase, and F is the volume force due to the acoustic field (this is zero when the field is OFF). The slip flux is defined as shown in Equation (7).

$$j_{slip}={\varphi }_d{\varphi }_c{u}_{slip}$$

(7)

The reduced density difference is given by Equation (8).

$$\epsilon =\frac{{\rho }_d-{\rho }_c}{{\rho }_c}$$

(8)

The sum of the viscous and turbulent stress is given by Equation (9).

$${\tau }_{Gm}=\left(\mu \right)\left[\nabla j+\nabla j^T\right]$$

(9)

where μ is the mixture viscosity. Then, for the dispersed volume fraction, the following transport equation is valid (Equation (10)):

$$\frac{\partial }{\partial t}\left({\varphi }_d\right)+j\nabla {\varphi }_d+\nabla \left(j_{slip}\right)=0$$

(10)

The continuous phase volume fraction is given by Equation (11).

$${\varphi }_c=1-{\varphi }_d$$

(11)

Finally, the mixture viscosity Krieger model is solved with Equation (12).

$$\mu ={\mu }_c{(1-\frac{{\varphi }_d}{{\varphi }_{\max }})}^{-2.5{\varphi }_{\max }}$$

(12)

where ${\varphi }_{\max }$ is the maximum packing concentration.

2.1.2. Diluted Species

We approached the encapsulation process by considering the interaction and subsequent encapsulation as the reaction between two different chemical species present in the mixture. Thus, this model also accommodates all types of material transport through diffusion (modeled by Fick’s law) and convection, given the laminar flow described by Navier–Stokes equations. For this model, we assumed that all present species are fully dissolved in the solvent (i.e., the solvent’s concentration is more than 90% mol) [36]. The model solves the conservation of chemical species, which is described by Equation (13).

$$\frac{\partial C_i}{\partial t}+\nabla J_i+V\nabla C_i=R_i$$

(13)

This equation considers both transport mechanisms (diffusion and convection). C_i, V, and R_i represent the concentration of species i, the mass-average velocity vector, and the reaction rate expression for species i. Lastly, J_i is the diffusive flux vector given by Equation (14).

$$J_i=-D\nabla C$$

(14)

where D denotes the diffusion coefficient and C the concentration of the species i. Here, we considered that the R_i term models the liposome–ferrofluid interaction through the Michaelis–Menten-like reaction rate expression. Thus, Equation (15) describes the reaction rate of each species present in the mixture.

$$R_i=\frac{V_{max}\left[MNPs\right]}{K_m+\left[MNPs\right]}$$

(15)

where $K_m$ is the Michaelis constant and is given by Equation (16).

$$K_m=\frac{\left[Liposomes\right]\left[MNPs\right]}{\left[Complex\right]}=\frac{k_r+k_{cat}}{k_f}$$

(16)

where $k_f$ is the forward rate constant, $k_r$ is the reverse rate constant and $k_{cat}$ is the catalytic rate constant. For an initial concentration of liposomes, $V_{max}$ is given by Equation (17).

$$V_{max}=k_{cat}\left[Liposome{s}_o\right]$$

(17)

Considering this, R_i reflects the liposome–nanoparticle complex production following an irreversible reaction, resembling the translocation of the nanoparticles through the liposome lipid bilayer.

2.1.3. Acoustic Field Implementation

A thermoviscous acoustics model was implemented to understand and impose an acoustic field to alter the nanoparticles’ macroscopic movement. This approach was used to compute the acoustic variation pressure, velocity, and temperature within a microfluidic device’s microchannels. Furthermore, this model’s selection was based on its precision when modeling acoustic fields at small scales [37,38]. Two types of ultrasonic baths with different operating frequencies (i.e., 37 kHz and 45 kHz) were considered for the multiphysics model. The piezoelectric effect from the solid mechanics module was coupled with thermoviscous acoustics and electrostatics modules to introduce both sources.

The model solves the thickness of the viscous boundary layer and the thermal boundary layer given by Equations (18) and (19).

$${\delta }_v=\sqrt{\frac{\mu }{\pi f{\rho }_0}}:Viscous$$

(18)

$${\delta }_t=\sqrt{\frac{k}{\pi {\rho }_0{c}_p}}:Thermal$$

(19)

where f is the frequency, μ is the dynamic viscosity, ρ₀ is the equilibrium density, k is the thermal conductivity, and c_p is the heat capacity at constant pressure. The model solves the tangential harmonic oscillation of viscous waveform in terms of u₀ and frequency f by Equation (20).

$$u\left(z\right)=u_0\exp -\sqrt{\frac{Hf{\rho }_0}{\mu }}\left(i+1\right)z$$

(20)

where u₀ is given by the interaction of an ultrasonic transducer generated by the piezoelectric effect described by Equation (21).

$$u_0=i\omega u_{solid}$$

(21)

Once the previous equations are solved, the continuity, momentum, and energy equations in the frequency domain (Equations (22)–(24), respectively) are solved

$$i\omega \rho +\nabla \left({\rho }_{0}u\right)=0\hspace{1em}:\mathrm{Continuity}$$

(22)

$$i{\rho }_0\omega u=\nabla [-PI+\mu (\nabla u+(\nabla u{)}^T)-(\frac{2\mu }{3}-{\mu }_B)(\nabla u)I]\hspace{1em}:\mathrm{Momentum}$$

(23)

$$i\omega (\frac{1}{{\rho }_0})P+\nabla u=0\hspace{1em}:\mathrm{Energy}$$

(24)

Simultaneously, the constitutive Equations (25)–(27) are solved.

$$\sigma =-PI+\mu (\nabla u+(\nabla u{)}^T)-(\frac{2\mu }{3}-{\mu }_B)(\nabla u)I$$

(25)

$$q=-k\nabla T$$

(26)

$$\rho =\rho (P,T)\hspace{1em}:\mathrm{Constant}$$

(27)

where $\sigma$ is the stress tensor, P is the pressure, u is the velocity, q is the heat from the thermoviscous effect, T is the temperature, μ_B is the bulk viscosity, μ is the dynamic viscosity, and I is the intensity vector, which is defined as the time average of the instantaneous rate of energy per unit area by Equation (28).

$$I=\frac{1}{4}\left(P{u}^{*}+P^{*}u\right)$$

(28)

where * denotes complex conjugation, and u is the acoustic velocity that can be expressed as shown in Equation (29).

$$u=\frac{1}{i\omega P}\nabla P$$

(29)

Once the acoustic field was set, Newton’s second law was implemented. The mechanical force exerted to promote the particles’ macroscopic movement (F) can be estimated by following Equations (30) and (31).

$$m_{v}a=F+v_0\left({\rho }_p-{\rho }_f\right)g+F_d\hspace{1em}:\mathrm{Newton}’\mathrm{s} \mathrm{Sec}\mathrm{ond} \mathrm{Law}$$

(30)

where v₀ is the particle’s volume, ρ_p is the particle’s density, ρ_f is the fluid density, m_v is the particle’s virtual mass, and F_d is the virtual drag force. The force vector F is then calculated from Equation (31)

$$\overrightarrow{F}=-\langle \nabla \rangle E=-\nabla \langle E\rangle \hspace{1em}:\mathrm{Mechanical} \mathrm{force}$$

(31)

where E is the acoustic energy density as described by Equation (32).

$$E=\frac{1}{2}\frac{P_1^2}{{\rho }_0{C}_0^2}+\frac{1}{2}{\rho }_0\overrightarrow{u_1}\overrightarrow{v_1}$$

(32)

where P₁ is the first-order acoustic pressure, C₀ is the sound velocity in water, and u₁ and v₁ are the first-order acoustic velocity vectors in directions x and y, respectively [39,40].

2.2. Computational Implementation (In Silico Study)

A multiphysics model was implemented in COMSOL to simultaneously evaluate the momentum, mass, and energy transfer phenomena involved in our study. With this goal in mind, a geometry, boundary conditions, and mesh convergence were defined for our model. The simulations were computed for both passive (acoustic field OFF) and active mixing (acoustic field ON).

2.2.1. Geometry

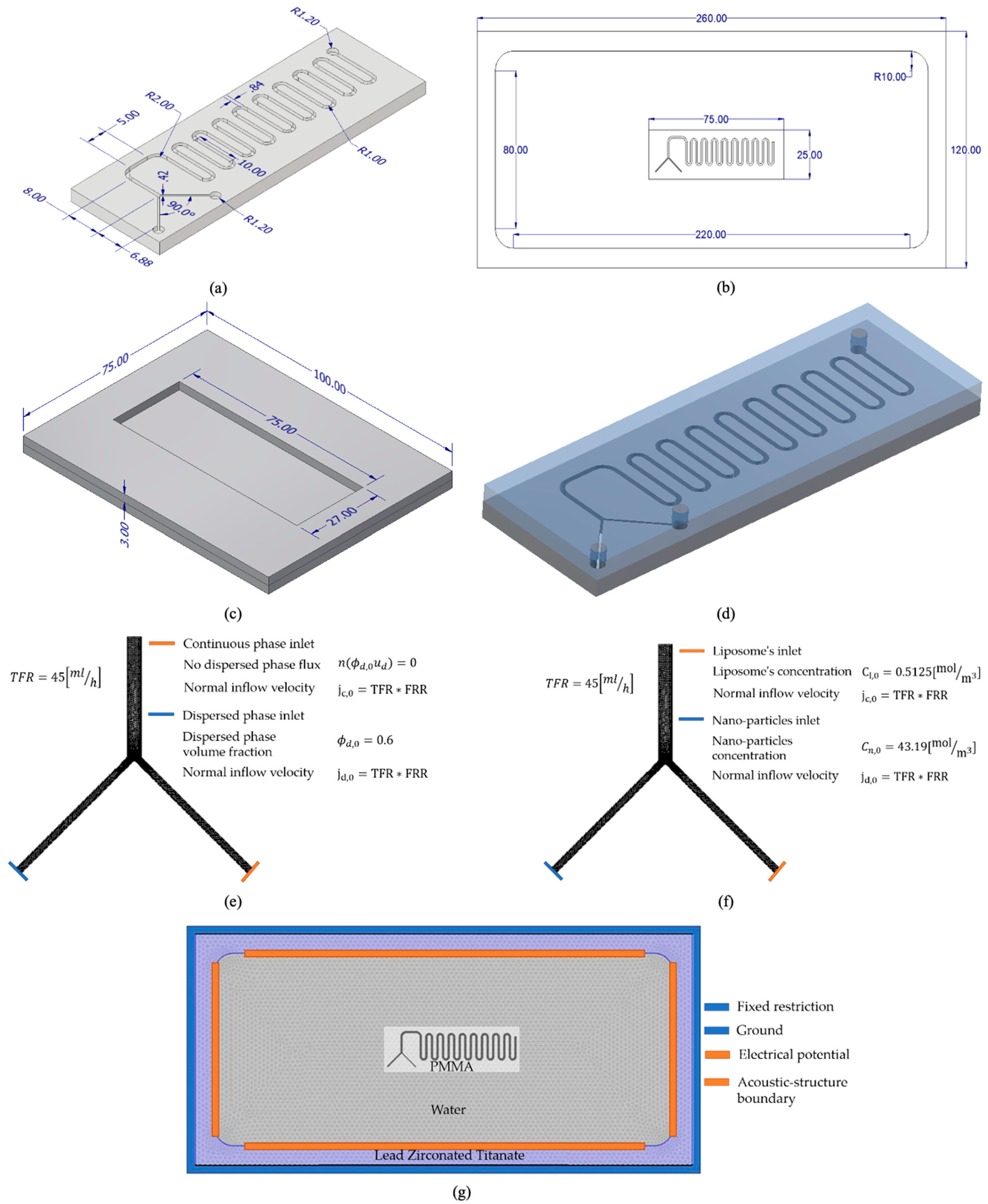
The microfluidic device’s geometry consists of a serpentine micromixer (SM) with two inlets and a single outlet, as shown in Figure 1a. This geometry was designed with the computer-aided design software Autodesk Inventor 2019 (Autodesk, San Rafael, CA, USA). The mixing serpentine channel diameter was 0.84 mm, while the inlets’ diameter was 0.42 mm. The angle between both inlets was 90°. Given the geometry features, the continuous and uniform mixing channel allows predominant laminar flow. At the same time, serpentine arcs contribute to the interaction of both fluid phases (continuous and dispersed) enhanced by the chaotic advection generated by Dean vortices [41]. Microchannels and device dimensions were defined based on the low-cost PMMA manufacturing technique with laser cutting considered for experimental validation. This technique allows a reduction in costs and time by avoiding complex cleanroom manufacturing methods such as soft lithography, injection molding, and spin-coating [42,43]. For the simulations, a 2D geometry of the SM (ignoring the depth of microchannels) was exported to COMSOL Multiphysics. For evaluating the acoustic mixing method, a top-view geometry of the proposed experimental setup of the microfluidic device within an ultrasonic bath was defined, as shown in Figure 1b.

2.2.2. Computational Domains, Materials and Boundary Conditions

For the mixture model, a single domain for the SM geometry was considered. In this case, multiphase flow and the interaction between the dispersed phase (MNPs) and the continuous phase (liposomes) were studied. The macroscopic properties of the continuous phase were assumed to be those of water as liposomes have been reported to have the same density [44]. As for the dispersed phase, magnetite properties (Fe₃O₄) were considered for modeling MNPs in the ferrofluid. Relevant material properties for the models are given in

Table 1. Material properties included in the multiphysics model ¹.

Material	Property	Value
PMMA	Density	1190 [kg/m3]
	Speed of Sound	2750 [m/s]
	Attenuation	0.0164 [dB/m]
Water	Density	997 [kg/m3]
	Speed of Sound	1483 [m/s]
	Dynamic Viscosity	8.9 × 10−4 [Pa*s]
	Attenuation	0.0025 [dB/m]
PZT-5H	Density	75,000 [kg/m3]
Liposomes	Density	1000 [kg/m3]
	Diffusivity	1.51 × 10−5 [m2/s]
Nanoparticles (Ferrofluid)	Density	1100 [kg/m3]
	Diffusivity	1.0 × 10−9 [m2/s]

¹ Materials properties taken from [45,46,47,48,49,50].

.

The initial pressure, dispersed phase volume fraction, and velocity field of the SM domain were set to zero. Boundary conditions were set according to Figure 1e. As shown, inlet flow velocities and inlet volume fractions were established. A total flow rate (TFR) of 45 mL/h was considered for assigning values to both inlets’ inflow velocities. A parametric sweep of the velocities was evaluated for different flow rate ratios (FRRs) of 1:3, 1:2, 1:1, 2:1, and 3:1 (MNPs: liposomes). Non-slip wall and non-dispersed phase flux boundary conditions were also included. For the outlet, a zero-pressure boundary condition was imposed.

Three chemical species were considered for the diluted species model: liposomes, MNPs, and the liposome–MNP complex (resembling MLPs formation). Boundary conditions introduced in the model are shown in Figure 1f. The liposome inlet concentration was regarded as a soy lecithin solution with a concentration of 0.78 mg/mL and a molecular weight of 643.9 g/mol [51]. The nanoparticle inlet concentration was considered as a Fe₃O₄ ferrofluid (1 mg/mL) with a molecular weight of 231.53 g/mol, given that, according to Martinez et al., cell-penetrating proteins such as OmpA have a negligible weight of 31 kDa [52]. Convective conditions were given by the computed laminar velocity field from the mixture model, based on the parametric sweep of inflow velocities for different FRRs. Reaction constants K_m and k_cat were assigned to 3 mM and 1.245 s⁻¹, respectively [53].

For the acoustic model implementation, four domains were considered. In addition to the SM channels geometry, the following domains were included: the ultrasonic bath basket made of lead zirconate titanate (PZT-5H), a water domain also inside the bath, and the microfluidic device made of PMMA. Material properties are shown in Table 1. Initial values for sound pressure, velocity field, and temperature variation were set to zero. Boundary conditions were established as shown in Figure 1g, including conditions for the piezoelectric effect (given by ultrasonic transducers found in ultrasonic baths) and the thermoviscous acoustic-structure boundary, between the piezoelectric transducers and the ultrasonic bath basket. The electric potential was set to 120 V.

2.2.3. Mesh and Convergence

A user-defined mesh was created for the mixture model within the microchannels domain and subsequently evaluated for convergence. Mesh elements were free triangular, and convergence was assessed for different default sizes calibrated for the CFD module, ranging from coarse to extremely fine. As shown in Figure S1a, the model converges at around 40,000 mesh elements, corresponding to the ultrafine element size. Boundary layers with a stretching factor of 0.7 and thickness adjustment factor of 3.0 were also defined for the geometry. Moreover, a corner refinement operation at both inlets and the outlet of the microfluidic device was applied with a number of elements distribution of 25. Regarding the ultrasonic bath’s external domains, a free triangular mesh calibrated for general physics with extremely fine size was selected (Figure S1b). Lastly, an adaptive meshing for local solution improvement was introduced, reducing the error by refining the mesh in three iterations and evaluating the solution, considering 40,000 mesh elements as the minimum number of mesh elements and 100,000 as the maximum.

2.3. Experimental Procedure

2.3.1. Design of the Microfluidic Device and Base Plate

Following the 3D geometry shown in Figure 1, the microfluidic device components for manufacturing and assembly were designed for a two-layer microfluidic device with 3-mm-thick PMMA sheets, as shown in Figure 1d. Both layers and the corresponding assembly were developed with Autodesk Inventor 2019 (Autodesk, San Rafael, CA, USA). As shown, the upper layer is attached to the lower one with the micromixer geometry (dimensions given in Figure 1), allowing inflow and outflow of fluids through connectors in both inlets and the outlet of the microfluidic device, respectively. For conducting the acoustic mixing experimental validation, a base plate for the microfluidic device was designed in Inventor. As shown in Figure 1c, the baseplate comprises two 3-mm-thick layers with a space in the middle for fixing the microdevice and to prevent unexpected displacements within the ultrasonic bath.

2.3.2. Manufacturing of Microfluidic Device and Baseplate

The microfluidic device and baseplate were manufactured with a low-cost PMMA laser cutting technique, previously reported by Aranguren et al. [32] as schematically shown in Figure 2. With this aim, 2D designs of each layer included in the microfluidic device and baseplate were prepared and exported to the computer-aided design software AutoCAD 2019 (Autodesk, San Rafael, CA, USA). Each 2D layer was adjusted to the following color convention: red lines for laser cutting and black lines for laser engraving (1 mm deep). This step was followed by exporting the 2D layers as PDF files and using them to obtain the microfluidic device and baseplate parts with a Trotec Speedy 100 (Marchtrenk, Austria) laser cutting machine engraving and cutting through 3-mm-thick PMMA sheets.

PMMA sheets were immersed in ethanol (96% v/v) for 3 min and sonicated for 10 min with the Gemoro Sparkle Spa (Dallas, TX, USA) stencil cleaning system to eliminate debris. Thereupon, sheets were immersed again in ethanol (96% v/v) for 3 min to conclude the debris removal process.

Layers were assembled according to computational designs. Ethanol (96% v/v) was then applied evenly onto the sheets, gluing them together with a handmade compression press at 110 °C for 15 min. Following assembly, hollow connectors were attached to the microdevice inlets and outlets with epoxy adhesive to allow fluid flow with probes.

2.3.3. Liposome and Nanoconjugate Synthesis

Liposomes were initially produced with the aid of the microfluidic device described by Aranguren et al. [33]. A lipid solution was prepared evaporating 100 mg of soybean lecithin (1-α-lecithin, soybean-cas 8002-43-5-calbiochem) (Merck, Kenilworth, NJ, USA) dissolved in 10 mL of chloroform c2432 > 99.5% (Merck, Kenilworth, NJ, USA) in a rotary evaporator Hei-VAP Value Digital Vertical (Heidolph, Schwabach, Germany), at 45 °C for 45 min at a vacuum environment. Then, the solution was resuspended in 15 mL of ethanol 96% (v/v). Simultaneously, an aqueous solution with NaCl (anhydrous, Redi-Dri™, free-flowing, ACS reagent, >99%) (0.05 M) (Merck, Kenilworth, NJ, USA) was prepared. Both solutions were mixed within the microsystem at a laminar flow regime using a total flow rate (TFR) of 300 mL/h and setting the flow rate ratio (FRR) at 3:1 between the aqueous phase and the dispersed phase (lipid). The solutions were pumped into the device with a syringe pump (Medcaptain MP-30, Shenzhen, China); 1 mL of the lipid solution was injected first into the microsystem to purge it and reach a stable fluid flow regime. This was followed by the injection of the aqueous solution to allow liposome formation by mixing bulk phases. The synthesized liposomes were finally collected at the output channel and characterized via DLS in a Malvern’s Zetasizer Nano Range (Malvern, UK) to determine particle size distribution and polydispersity index (PDI).

Magnetite nanoparticles (MNPs) were synthetized by the chemical coprecipitation method as reported by Lopez-Barbosa et al. [20]. For this, FeCl₂ (0.34 g) (J. T. Baker, Phillipsburg, NJ, USA) and FeCl₃ (0.93 g) (Merck, Kenilworth, NJ, USA) were solubilized in 60 mL of type I water. In addition, 0.69 g of NaOH (PanReac AppliChem, Darmstadt, Germany) was added to 17 mL of type I water and then both solutions were heated at 80 °C. Next, a NaOH solution was added dropwise to the iron chlorides solution at a rate of 5 mL/min under constant stirring. A black precipitate was observed corresponding to the formation of MNPs. The obtained MNPs were then washed four times with NaCl solution (1.5% (w/v)) and twice with type I water aided with a neodymium magnet; 100 mg of MNPs was silanized by adding 50 uL of glacial acetic acid followed by 400 uL of (3-aminopropyl) triethoxysilane (APTES, 98%, Sigma–Aldrich, St. Louis, MO, USA). The MNP solution was left to react under constant stirring (250 rpm) at 60 °C for 1 h and then washed as mentioned previously. Later, 100 mg of the silanized MNPs (MNP-APTES) was mixed with 2 mL of glutaraldehyde solution (2% (v/v)) (25% (v/v), Sigma–Aldrich, St. Louis, MO, USA) that was stirred (220 RPM) at room temperature for 1 h to allow glutaraldehyde activation (MNP-APTES-GA). Then, 5 mL of a NH2-PEG-Propionic acid (Merck, Darmstadt, Germany, 99%) solution (2 mg/mL) was added dropwise to the MNP-APTES-GA conjugates under constant stirring to obtain MNP-APTES-PEG conjugates. The solution was left to react at 220 rpm and room temperature for 24 h and washed four times with NaCl solution (1.5% (w/v)) and twice with type I water.

The resulting MNP-APTES-PEG conjugates were labeled with rhodamine B for the fluorescent-based assays. For this, 14 mg of N-[3-dimethylammino)-propyl]-N′-ethyl carbodiimide hydrochloride (EDC, 98%, Sigma–Aldrich, St. Louis, MO, USA), 7 mg of NHS, and 5 mg of Rhodamine B (RdB, 95%, Sigma–Aldrich, St. Louis, MO, USA) were dissolved in 5 mL of type I water containing 2 mL of DMF. The RdB solution was left under constant stirring for 15 min. Next, the previously activated rhodamine B solution was added to 50 mL of MNP-APTES-PEG conjugates aqueous solution (2 mg/mL) and left to react at 220 rpm, room temperature, and complete darkness for 24 h. The resulting MNP-APTES-PEG-RdB was washed several times with NaCl (1.5% (w/v)) and type I water to remove the excess of reagents. The nanoconjugates were then resuspended in type I water and stored in complete darkness at 4 °C until further use.

2.3.4. Encapsulation Test

Liposomal encapsulation of MNP-APTES-PEG-RdB nanoconjugates was evaluated with both passive and active mixing approaches based on Y-junction microfluidic devices with a serpentine or spiral-shaped geometry by controlling the FRRs between a sample of liposomes and the ferrofluid with the suspended nanoconjugates (1 mg/mL). Flow conditions were assigned according to finite element simulation parameters, considering a TFR of 45 mL/h and FRRs of 1:1, 1:2 and 1:3 (nanoconjugates: liposomes).

The nanoconjugate labeling with the fluorescent dye Rhodamine B was conducted to evaluate encapsulation efficiency by spectrofluorimetry (details below in Section 2.3.5.). The experimental setup was assembled according to Aranguren et al. [32]. Accordingly, both fluid phases were pumped into the microfluidic device with a Medcaptain MP-30 infusion pump (Shenzhen, China) connected to Nelaton probes of about 20 cm length (Medex, Smiths Medical Inc., Minneapolis, MN, USA) attached to the inlets. MLP samples were collected at the outlet of the device with a Nelaton probe falling into a container. This procedure was followed for the passive encapsulation test, which relied only on flow focusing and the membrane penetrating abilities of the nanoconjugates to achieve loading into liposomes.

As shown in Figure 3, the active encapsulation test with acoustics started by adjusting the microfluidic device to the baseplate. Subsequently, an ultrasonic bath (Elmasonic Easy 30 H, Elma Schmidbauer GmbH, Singen, Germany) was filled with water followed by the device arrangement immersion. The bath was then turned on, activating an ultrasonic field operating at 37 kHz and 80 W. With the ultrasonic field activated, the active test proceeded and the MLP samples were collected at the device outlet for FRRs of 1:1, 1:2, and 1:3.

2.3.5. Encapsulation Efficiency

The encapsulation efficiency percentage (EE%) was determined according to the experimental work by Simoes et al. [54]. In their approach, the fluorescence changes between nanoparticles’ concentration inside and outside the liposomes were the basis to quantify the percentage of non-encapsulated MNPs into the liposomes. Fluorescence emission tests were conducted with a Horiba FluoroMax Spectrofluorometer (Kyoto, Japan), using 546 nm for excitation and 568 nm for emission.

To evaluate encapsulation efficiency, Triton X-100 was added to the samples to induce liposome membrane rupture, which induces the exit of the MLPs contents. Then, a comparative fluorescence test was run where fluorescence emission of encapsulated samples was compared with that of the disrupted ones. With these results, the difference between fluorescence emission measurements was calculated to obtain the encapsulation efficiency as described by Equation (33).

$$\mathrm{EE}\%=\frac{\left(\left(E_F-E_T\right)-E_I\right)}{E_F}\times 100\hspace{0.25em}$$

(33)

where $E_I$ is the emission pre–Triton X-100 treatment and $E_F$ is the emission post-Triton X-100 treatment. $E_T$ is the blank emission of Triton X-100.

2.3.6. Mixing Evaluation

While operating the microfluidic system, a methylene blue solution was pumped into the channels to photographically track the mixing patterns as the fluid travels along the serpentine. A set of pictures was collected in seven regions along the mixing channel aided by a 1000× Digital USB Microscope (TM-DM4, TOMLOV, Wuhan, Hubei, China). Then, a Python code was implemented (Supplementary Script S1) to measure each pixel intensity within an evaluation window of 30 × 30 pixels, using all color channels to finally apply Equation (34) to calculate the pixel intensity’s standard deviation. According to Lopez R. et al., this approach is well suited to quantify the mixture quality [33].

$$\sigma =1-\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=0}^N{\left(\frac{I_i-I_{mix}}{I_{umix}-I_{mix}}\right)}^2}$$

(34)

where I_i is the pixel intensity within the evaluation window, I_mix is the intensity when a complete mix is achieved, I_umix is the intensity of a pixel in the basal state, and N is the total number of pixels within the window; pixel intensity is given by Equation (S1), while the color composition of mixed fluid and unmixed fluid is presented in Supplementary Figure S3. To set I_mix and I_umix values, a color histogram for the positive and negative controls was calculated.

2.3.7. Magnetoliposome (MLP) Characterization

Similar to liposomes, the particle size and polydispersity index (PDI) of MLPs were determined by dynamic light scattering (DLS), using a Malvern’s Zetasizer Nano Range (Malvern, UK). Transmission electron microscope (TEM) images of the MLPs were also collected in a Tecnai F20 Super Twin TMP instrument (FEI, Hillsboro, OR, USA) to analyze their morphology and size, aided by ImageJ software. The samples for TEM analysis were prepared by depositing a drop of the MLPs samples on a copper grid with carbon coating and drying for 1 h, followed by staining with 2% uranyl acetate. Finally, the grid was washed using deionized water and dried for later imaging at a total magnification of 145,000×.

3. Results

Figure 4 shows the acoustic pressure fields for both configurations of ultrasonic baths, in the presence and absence of the microfluidic system. Figure 4a,b relate to a 37-kHz operating frequency, while Figure 4c,d correspond to a 45-kHz operating frequency. As can be seen, although the acoustic field pattern is disrupted by introducing the microfluidic device, the acoustic pressure range values seem unaffected. This disruption is due to PMMA’s sound absorption properties as discussed by Seddeq et al. and Notario et al. [55,56], who reported a sound attenuation value of 0.0164 [dB/m].

Furthermore, as expected and reported by Tangsopha et al. [57], it can be seen that the number of nodes with maximum acoustic pressure increases in the operating frequency. Besides, the acoustic pressure pattern results are similar to those reported by Zhang et al. [58], and the wall’s pattern concurs with that described by Tudela et al. [59]. As shown in Figure 4c,d, the maximum acoustic pressure is 6E4 Pa, comparable to the acoustic pressure value reported by Tangsopha et al. at 48 kHz of 1E5 Pa.

3.1. Mixing Evaluation

Figure 5 shows the mixture model results for passive and active mixing under different operating FRRs. At the same time, Figure 6 illustrates the mixture quality achieved for different FRRs, at different microchannel lengths within the microfluidic system. As shown in Figure 5, the results suggest that a complete mixture is achieved earlier on the microchannel with the acoustic mixing (second loop) than with the passive mixing (third loop). This can be attributed to the energy introduced into the system and has been previously discussed and explained as the consequence of cavitation and microturbulence processes [60,61].

The obtained mixing pattern is similar to the one presented by Chen et al. and Clark et al. for a serpentine micromixer [62,63]. This was achieved with 1 as the maximum volume concentration of the dispersed phase; however, in our case this parameter approached to 0.6. As shown in Figure 6, our mixing quality appears superior most likely due to the Y- junction present in our system as has been discussed previously by Hessel et al. and Zhang et al. [60,64]. Chen et al. predicted a mixture performance for a serpentine micromixer of approximately 60% at a Reynolds number of 6 [62]. A close mixture quality of 0.5 was achieved by Clark et al. for a micromixer equipped with a T junction [63]. In our study, the Reynolds number was 5.97 for an FRR of 1:1, which allowed us to obtain a sigma value (indicative of the mixing performance) of 0.6. This mixing level is similar to the one obtained by Huanming et al. at a Reynolds number of 10. Besides, as has been reported previously, the mixture quality increased with distance traveled within the device [35]. Finally, as shown in Figure 6 by increasing the FRR, the quality of mixing increases. This has also been reported by Viktorov et al. for a similar Reynolds number [65].

3.2. Encapsulation Evaluation

Figure 7 illustrates liposomes and MNP concentration profiles for the first section of the microfluidic system when operating at different FRRs for a passive mixing configuration. Both species’ concentration decreased across the device until the liposome concentration reached 0 [mol/m³], and MNP concentration approached 0.5–1 [mol/m³]. Moreover, the concentration profiles indicate that higher FRRs led to a faster consumption of both species in close proximity to the first main loop of the serpentine.

Figure 8 shows the formation of the complex liposome–MNPs while operating at different FRRs in a passive and active in-silico configuration. The main difference between the two modes of encapsulation is that the active one occurs closer to the first main loop of the device for all FRRs, while the passive takes longer (Figure 8a–d). Nevertheless, both operation modes lead to the same maximum liposome–MNP complex concentration, which increased as a function of the FRR from 0.7 to 0.9 [mol/m³].

Similar reactive flows have been studied in detail both in silico and experimentally by several authors [66,67,68,69,70,71,72,73]. For instance, Brivio et al. discussed the underlying phenomena behind several reactive flows and discussed the significant effect of controlling the mass transfer processes for the involved reactants (via mixing) on the extent of a chemical reaction [66]. Figure 7 and Figure 8 show that by increasing the FRR and introducing energy to the system, mixing improves. This in turn leads to a concentration gradient that promotes the interaction between the involved chemical species and consequently, the rapid formation of the liposome–MNP complexes. Our reactive flow profiles agree well with experimental results obtained by Chan et al. and Zaher et al., who demonstrated that within the initial section of a serpentine micromixer, the reactants decrease in concentration and are confined to a narrow portion in close proximity to the microchannel wall. As the reaction mixture flows along the microchannel, its concentration increases substantially [67,70].

Figure 9a shows the in silico encapsulation efficiencies for different FRRs. The results show that while encapsulation efficiency increases at higher liposome to MNP ratios, the trend is reversed when the MNP to liposome ratio increases. A maximum encapsulation efficiency of about 95% was achieved for a device operating passively at a FRR = 1:3 but it was only 35% at a FRR = 3:1 in the same device. Differences with respect to the acoustic operation were not significant considering that the absolute errors approached 4.6 ± 1.70% and 8.3 ± 1.43% for the passive and acoustic devices, respectively (Figure 9b). Figure 9c compares the in silico and the experimental encapsulation efficiencies while operating at different FRRs. In the case of acoustic encapsulation, the most significant difference was found at a FRR = 1:1 at the highest agreement at FRR = 1:2. In contrast, for passive encapsulation, the agreement between the two approaches was higher, especially while operating at FRR = 1:1 and FRR = 1:2. Importantly, for most FRRs evaluated, the in silico approach overestimated the efficiencies obtained experimentally.

Several authors have studied efficiencies of liposome encapsulation thoroughly and reported efficiency values range from 10% to 90%, which agree well with our results [11,74,75,76,77]. Moreover, according to Aghaei et al., Delama et al., and Berger et al., the most relevant variables defining encapsulation efficiencies are liposomes size, polydispersity, and FRR [11,76,77]. In line with these works, our results indicate a marked influence of FRR on encapsulation efficiency.

3.3. Magnetoliposome Characterization

Figure 10a shows a TEM micrograph of a representative MLP obtained by passive encapsulation while an MLP obtained by the acoustic method is shown in Figure 10b. The selected MLPs exhibited diameters of 95.1 nm and 62.7 nm for the passive and acoustic method, respectively. In both cases, the MLPs show clustered nanoconjugates internalized and a few individual nanoconjugates (of about 3.5 nm and 2 nm for the passive and acoustic methods, respectively) intercalated within the outermost leaflet of the lipid bilayer. Importantly, the selected images are for the smallest MLPs obtained by each method, i.e., at the lower end of the particle size distributions.

The average particle hydrodynamic diameter for MLPs obtained by the passive device (while operating at FRR = 3:1) was 344 ± 40 nm with a PDI of 0.33 ± 0.07 nm. In the case of acoustic mixing (while operating at FRR = 1:3), the diameter was 219 ± 1.8 nm with a PDI of 0.31 ± 0.03. The complete particle size distribution for liposomes and MLPs obtained by both methods is shown in Supplementary Figure S4. The results indicate that upon application of ultrasound, the generated acoustic cavitation led to an MLP size reduction of about 36.3% compared with the passive method. These values agree with experiments reported by several authors, which describe a size reduction by ultrasonic field interaction [78,79,80].

It is important to point out that the DLS and TEM results differ from each other. This is because TEM is conducted on dry samples while DLS is used for samples suspended in a liquid medium. For this reason, DLS results generally report larger particles as they can interact with each other dynamically [81].

4. Discussion

The mixing process within a serpentine microfluidic device was modeled by two models implemented in COMSOL Multiphysics^®, which allowed us to estimate mixing profiles and consequently, the performance of nanobioconjugates encapsulated into liposomes. The profiles were successfully validated experimentally with a high degree of accuracy aided by tracer dyes. The models provided insights into the notion that encapsulation can be enhanced by adding external energy in the form of ultrasound waves. The findings are in line with previous results of similar systems and helped us to calculate the encapsulation efficiencies.

Considering the obtained encapsulation efficiency results from in silico experiments, we found that both the passive and active mixing methods had a similar performance. In this regard, efficiency results were about 2% higher at most FRRs for the passive mixing regarding acoustic mixing (Figure 9a). However, as shown in Figure 9c, passive mixing showed a better agreement with the encapsulation efficiencies obtained experimentally. These results can be attributed to the complexity of the encapsulation process and indicate that there is still room for further model refinement. With respect to the passive method, the absolute error of the acoustic simulations almost doubled, which was attributed to the complexity of the process where continuous cavitation caused by the impact of ultrasonic waves leads to certain randomness in MLP dynamic breakage and assembly [79,80,82,83]. This cavitation process represents a significant modeling challenge for accurately predicting experimental results that go beyond the scope of the present contribution. Despite this, the absolute error is still acceptable for the general purposes of the present proof-of-concept contribution.

A major finding is that the hydrodynamic diameter of MLPs obtained in the presence of ultrasound decreased by about 36% with respect to the passive method. To a large extent, this result can be attributed to the effect of the acoustic energy imparted to the synthesis device by the ultrasonic bath. In this regard, several studies have previously reported the effect of low ultrasonic frequencies on reducing liposomes size [79,80,82,83]. As described by Yamaguchi et al., after sonicating liposome samples with ultrasonic cleaners at 43 kHz, liposomes underwent a mean diameter reduction from about 300 nm to 150 nm after roughly 6 min of ultrasound exposure [80]. We established similar experimental conditions in our acoustic mixing setup (37 kHz, 5 min) where liposomes with a mean diameter of 344 nm were employed to produce MLPs with magnetite-based nanobioconjugates encapsulated.

Even though size reduction might lead to impeded encapsulation due to limited space availability, ultrasound positively enhances MNPs translocation most likely due to acoustic streaming. This was initially validated in silico as evidenced by the rapid formation of the nanobioconjugate-liposome complexes (as a result of homogeneous mixing) and the stable mixing quality parameters (e.g., sigma and dispersed phase volume fraction) obtained as the mixture flows through the microchannels. Other evidence has been reported previously according to which acoustic fields produce interfacial waves that result in enhanced mixing and superior dispersion of interacting phases [84]. This phenomenon can be explained by acoustic-streaming flows inducing micromixing by a steady fluid motion, which improves the diffusion process between two streams of laminar flows within a micromixer [84,85,86]. This indicates that in our case, the chances of superior interaction between the phases might be increased via acoustic streaming.

The obtained MLPs confirmed the success of the encapsulation process and hold much promise regarding the use of low-cost micromixers along with acoustically addressable systems to prepare high-quality MLPs, which are in high demand for the preparation of more effective drug delivery vehicles with superior pharmacological performance. Certainly, our MLP synthesis is superior in comparison with bulk methods such as reverse-phase evaporation and extrusion, which have failed to achieve optimal liposome encapsulation of MNPs for pharmacological purposes as evidenced by encapsulation efficiencies of only 10% [87]. Consequently, reflecting on the drawbacks of the classical methods for MNP liposome encapsulation, microfluidics achieve high encapsulation efficiencies.

5. Conclusions

Encapsulation of different materials, biomolecules, and bioactive compounds has become a common practice in various industries including food, cosmetics, and pharma. This is mainly due to the possibility of protecting these valuable components from harsh environments and therefore to assure their functionality in the final products. In this work, we were interested in developing an encapsulation strategy for our recently introduced cell-penetrating agents based on magnetite nanoparticles interfaced with translocating peptides and proteins. The selected encapsulating system was liposomes due to their ability to fuse with cell membranes to release cargoes and their ease of synthesis and manipulation. The produced encapsulates are known as magnetoliposomes (MLPs), and one of the main challenges is to ensure homogeneous morphologies and particle size distributions. To address this issue, we introduced microfluidic devices equipped with serpentine microchannels to promote the interactions between the nanostructured vehicles and the liposomes. Additionally, we explored both a passive approach and an active one based on applying ultrasound externally. Initially, we investigated the performance of the devices via multiphysics simulations implemented in COMSOL. We employed two modeling approaches, the first one based on a Eulerian approach and the second one on the transport of diluted species. The results allowed us to gain insights into the encapsulation performance as a function of one of the most significant operation parameters, the flow rate ratio (FRR). Our simulations indicated that for both the passive and active operation modes, it is possible to achieve about an 80% encapsulation efficiency for the highest FRRs.

This was corroborated experimentally where no significant differences in encapsulation efficiency were found between the two approaches. However, higher discrepancies were observed for the acoustic method between the in silico and the experimental results, which was attributed to the limited ability of the implemented models to capture the complete interplay of involved phenomena. The obtained MLPs were examined via TEM imaging and demonstrated successful encapsulation and entrapment of the nanobioconjugates within the outermost leaflet of the lipid bilayer. Despite the similar performance, the acoustic method led to MLPs with smaller hydrodynamic diameters most likely due to the acoustic streaming processes capable of altering the MLP assembly.

Even though recent research and this work have shown that acoustic fields enhance the mixing of fluid phases, some applications in liposomal encapsulation for drug delivery systems might not be an appropriate choice to achieve this goal. This is related to the detrimental impact of acoustic cavitation (even after shot exposure to ultrasound) on reducing liposome size and consequently their loading capacity. However, mixing improvement given by ultrasonic fields might be of interest for other applications such as sonoporation, where an enhanced cell membrane permeability is useful to facilitate the internalization of therapeutic molecules.

In future work, the multiphysics model for accurately predicting encapsulation can be increased by establishing a more reliable interaction description between liposomes and nanobioconjugates. In this context, a mathematical model based on real-time interaction needs to be developed, including stochastic behavior involved in the translocation of molecules through lipid bilayers.