1. Introduction
The desire to understand fluid motion in the Earth’s outer core, and ultimately the geodynamo, provides the physical motivation for our study. The magnetofluid in the outer core is primarily liquid iron and although its electrical conductivity and convective turbulence give rise to magnetic fields, we will ignore these here, but will include dissipation. Furthermore, the fluid will be treated as incompressible, as is usually done in geodynamo modeling (e.g., [
1,
2]). Velocity and vorticity will be expanded in terms of ‘toroidal’ and ‘poloidal’ functions, as they were first called and defined by [
3]; these will be detailed presently. Here, we use Galerkin toroidal–poloidal (T–P) expansions to focus on velocity and vorticity, where ‘Galerkin’ means each term satisfies designated boundary conditions (e.g., see [
4]). (We leave magnetic fields for future study. Understanding magnetohydrodynamic inertial modes through Galerkin T–P expansions is a further goal and the present work is viewed as a necessary step in that direction).
Our T–P model is based on that of [
5] and is similar to that used by [
6,
7], although these authors work with positive and negative helicity Chandrasekhar–Kendall (C–K) functions [
8], which are linear combinations of T–P functions, as will be seen explicitly in Equation (
10) below; also, our model system has an inner boundary, while theirs did not. When T–P functions are put into C–K form, again as seen in Equation (
10), we have ‘eigenfunctions of the curl’ [
9,
10] that also satisfy the Helmholtz equation and are Galerkin. The focus of either the T–P or C–K approach is on internal, free-stream turbulence and neither pretends to accurately address boundary layer motion. However, the work of [
11] indicates that interior solutions for spherical shell flows are independent of b.c.s in the limit of vanishing Ekman number. In addition, little is known about the nature of the core–mantle boundary or the inner core boundary, so it is uncertain as to what kind of boundary conditions actually apply. Thus, we have the latitude to choose b.c.s that are appropriate for a T–P expansion of an incompressible fluid confined within a spherical shell.
A critical feature of the velocity and vorticity expansions is that each term will be required to individually satisfy the Helmholtz equation as well as the b.c.s. Mathematically, this means that our T–P basis functions are a product of spherical Bessel functions and spherical harmonics. The benefit of this is that each term in the expansions has a unique wavenumber associated with it. However, this affects the nature of the boundary conditions that can be imposed. The first boundary condition will be, of course, that the normal component of velocity vanishes at the boundaries. Next, the choice of T–P basis functions that satisfy the Helmholtz equation in a spherical shell leads to the second boundary condition: the normal component of vorticity also vanishes at the boundaries. What is left on the bounding surfaces is a two-dimensional potential flow, as will be seen presently in (
29). If the fluid in the spherical shell was compressible, then velocity on the boundaries could be completely zeroed out by adding another term (related to compressibility) to the T–P expansion and the flow could be made to obey a no-slip condition (more details will appear in
Section 4) However, we wish to treat the flow as incompressible here, to make our work commensurate with previous work on the geodynamo.
Thus, we do not use the no-slip or stress-free or inviscid boundary conditions that were compared by [
11], but something else, which we will call
homogeneous boundary conditions, i.e., the normal components of velocity and vorticity vanish at the boundaries. In the case of no-slip or stress-free, there are conditions on all three velocity components, while for the inviscid case, there is only one condition, that on the normal component of velocity. Here, we have the two boundary conditions stated above plus a third boundary condition intrinsically linked to the condition of incompressibility, i.e., that there is a 2-D potential flow on the boundaries. (Again, more details are given in
Section 4).
At this point, let us set the context for our mathematical model and T–P vector basis functions (or equivalent C–K functions) that we use, followed by our results.
2. Historical Overview
Historically, it has long been recognized that stars and planets contain turbulent fluids. Turbulence theory and simulation began by using Fourier transformations by which the velocity and magnetic fields are represented by their Fourier coefficients. Fourier analysis, in using expansions in terms of sines and cosines, implies that physical motion is taking place in periodic box, i.e., a 3-torus which has no boundaries and hence no need for boundary conditions. Although usually called ‘periodic boundary conditions,’ this is a misnomer because, again, a 3-torus has no boundaries. The motivation for using Fourier analysis is well-described by [
12], though the topological ramifications are not. A 3-torus is a self-contained compact, closed space without boundary and there is no ‘outside’ to it, topologically speaking [
13]. A 3-torus is a mathematically useful space for studying fluid motion, though unphysical (except perhaps for our universe as a whole, which some conjecture may, in fact, be a 3-torus [
14]). However, a 3-torus is problematic when a magnetofluid is the object of study, as there is no outside into which the model magnetic field can emerge to be compared with geophysical or astrophysical observations. Nevertheless, the majority of research on fluid and magnetofluid turbulence has relied on ‘periodic boundary conditions.’ Although inertial waves in a periodic box have been examined using Fourier methods [
15], the vector basis functions are all uncoupled in the Fourier case, but, as we will see, in the rotating spherical shell, T–P functions are strongly coupled.
In regard to Galerkin methods, an important move away from Fourier analysis had been taken by [
6,
7], who numerically examined incompressible MHD inside a sphere (no inner boundary) using expansions in terms of positive and negative helicity C–K functions [
8]. (However, [
1,
2] and others had used non-Galerkin T–P methods previously, using Chebyshev polynomials instead of Bessel functions for radial dependence). C–K functions have also been used to treat astrophysical problems in a spherical geometry, rather a periodic box [
16]. Again, C–K and T–P functions satisfy ‘homogeneous’ boundary conditions (b.c.s): the velocity and magnetic field, as well as their curls (and the curls of those, and of those, ad infinitum) all have zero normal components on the boundary. This is analogous to Fourier analysis, where the velocity and all of its derivatives of every order are still periodic. A further analogy is that both the Fourier and C–K or T–P basis functions satisfy the Helmholtz equation, which is essential as it allows a specific wavenumber to be associated with each basis function. This, in turn, allows us to define precisely what is meant by the energy or power spectrum in fluid mechanics.
Extending the Galerkin approach of [
6,
7] was done in [
5] by providing the sphere with an inner boundary upon which homogeneous b.c.s are also applied, but using a T–P form rather than a C–K form. This system can be set rotating mathematically, giving us opportunity here to study waves within a spherical shell with homogeneous b.c.s. Using Galerkin T–P expansions to analyze the linearized Navier–Stokes equation for flows within a spherical shell with homogeneous b.c.s, leads us to explicit formulas for inertial waves, which are the new results that we present.
Rotation enters the Navier–Stokes equation through the Coriolis term and linearization gives the basic equation for inertial waves. Traditionally, for the case of a sphere with no-slip conditions, these waves have been studied and solutions provided by [
17,
18], building on the work of [
19], while [
20] have used a perturbation expansion to examine pressure oscillations, finding solutions that are ‘pathological.’ Moreover, in the case of flow in a rotating spherical shell, Ref. [
17] has stated that, “Explicit formulas for all the eigenmodes in the spherical annulus do not exist. Bryan’s transformation [p. 64], the essential step in the solution procedure for the spherical container, does not apply and for this reason very little is known about the inertial waves.” This sentiment concerning analytical solutions is echoed by [
21,
22], as well as by [
23], who, in their examination of inertial waves in a rotating spherical shell, used non-Galerkin T–P methods, as radial cofactors have primarily been Chebyshev polynomials, rather than Bessel functions. This may have its benefits numerically, but such basis functions do not satisfy the Helmholtz equation and wavenumbers cannot be precisely associated with them.
Our approach here varies in obvious and significant details from the traditional approaches that use, for example, no-slip [
17] or stress-free conditions [
24]. First, we use ‘homogeneous b.c.s’ and choose to avoid conjecturing about the nature of the boundary between, say, the Earth’s outer core and mantle or between the outer core and inner core, boundaries which are presently unknown, and possibly unknowable. Second, velocity and vorticity are represented by Galerkin T–P functions (or the equivalent C–K form), i.e., vector basis functions that have as radial cofactors a linear combination of spherical Bessel functions and vector spherical harmonics.
The results presented here are extensions of our previous work [
5,
25] in which T–P expansions using a Galerkin basis as defined by [
3] were used, while others may also have used a general T–P formulation, these were designed for computational efficacy and to satisfy no-slip b.c.s. For example, radial functions can be Chebyshev polynomials [
1,
2,
23] or be represented numerically by finite differences [
26], but again, these are not Galerkin methods. Here, we use a Galerkin expansion with spherical Bessel of the first and second kind (the second kind are also called Neumann functions) that describe radial variation.
Using our model, with velocity and vorticity expanded in terms of Galerkin T–P vector functions, we are able to find explicit formulas for all the eigenmodes of inertial waves in an incompressible, rotating fluid contained between concentric spherical surfaces with homogeneous b.c.s, rather than traditional no-slip or stress-free boundary conditions. Our method of solution appears robust as we find no pathologies. We determine eigenfrequencies which we compute using Earth-like parameters. We present these results following a brief discussion of the basic equations and the Galerkin method of solution. As an example, we consider a dissipative 25 eigenmode system in detail; the method can, of course, be expanded to any desired number of eigenmodes given sufficient computational resources.
3. Basic Equations
In non-dimensional form, the linearized incompressible Navier–Stokes equation in a rotating frame of reference with constant angular velocity
is
For the Earth,
rad/s and
is the Ekman number for the outer core [
27]. Although
E is very small, the dissipation term
will get large at a small enough length-scale, i.e., large enough wavenumber, which needs to be estimated.
We approximate the outer core to be a spherical shell with inner radius
m and outer radius
m [
27];
is the characteristic distance and the ratio
. The non-dimensional Equation (
1) will be examined in a spherical polar coordinate system
, with
,
and
. The boundary conditions at
and
are that the normal components of
and
are zero:
Thus, we appear to have two conditions: (a) a Dirichlet condition on
and (b) a Neumann condition linking angular derivatives of
and
on the model boundaries (we use the appellations ‘Dirichlet condition’ and ‘Neumann condition’ in a general sense); conditions (a) and (b) are implicit in the ‘homogeneous b.c.s’ given by (
2). It should be remembered, though, that the curl of the vorticity, the curl of that, etc., also satisfy homogeneous b.c.s; this is simply a property of T–P (or C–K) expansions. As stated earlier, a third condition could be imposed if the flow was not considered incompressible.
Again, many different boundary conditions have been employed for geodynamo studies, although the particular set used often does not appear to have significant effects on final results, as discussed by [
11,
28]. Mathematically, the choice (
2) allows us to employ the Galerkin expansion functions that are used for determining the structure of inertial waves in a rotating spherical shell. As mentioned before, the individual basis functions of T–P (or C–K) expansions each satisfy a different Helmholtz equation, allowing each to have a well-defined wavenumber.
4. Galerkin Expansion
It is well-known (e.g., see [
29]) that a divergence-less vector field in a spherical geometry can be represented as a ‘toroidal–poloidal decomposition’:
In order to satisfy the Helmholtz equation in a spherical shell, the functions
U and
W in (
3) must take the form
Here,
are spherical harmonics and the
are linear combinations of the spherical Bessel functions of the first kind,
, and of the second kind,
(also called spherical Neumann functions). The exact form of the
will be given below, while the wavenumbers
will be determined by the b.c.s. Note that if the flow were compressible, we would need to add a term
to (
3), where
would have an expansion similar to those in (
4), with radial derivative zero on the boundaries. Here, we only wish to outline a novel approach to studying compressible flow, while our main aim is to focus on incompressible flow.
Now, putting (
4) into (
3), we can write the toroidal–poloidal decomposition in the form:
Here,
is a normalizing constant, to be defined presently; also,
denotes complex conjugation. Furthermore, in (
5), the overall minus sign that occurred because
has been dropped. Furthermore, if one wanted to approach the problem with no-slip b.c.s. and compressibility, then one would still use the vector expansion functions
and
in addition to introducing a new set of expansion functions for the compressible term
.
Obviously,
, while (
8) is required by the realness of
and the definition of the toroidal and poloidal vector functions,
and
given below, where it will be seen that the
and
form an orthogonal set for
, each member of which will be seen to satisfy the boundary conditions (so that we have a Galerkin expansion), while the
are numerical constants and the summation indices
range over prescribed, finite range of integer values. It is evident that we have two sets of essential, generally complex, coefficients (
and
) to represent the velocity. The flow we are studying has vorticity
and using the relations given above, this is
We mention the vorticity because it is used to define the kinetic helicity which, along with energy, is an ideal invariant for (
1) with homogeneous boundary conditions [
30]. In what follows, we will use
to represent angular frequency, but there should be no confusion as the magnitude of
will not appear here, although its component
will.
Note that we could have written (
5) and (
9) in terms of an explicitly helical set of vector basis functions:
The
are Chandrasekhar-Kendall functions [
8], and are eigenfunctions of the curl operator [
9,
10]. Although we choose to use
and
instead, our toroidal-poloidal vector basis functions are essentially the same as those in (
10), differing only by a linear transformation.
In general, the various quantities used above can be defined as follows. First,
The orthonormal vector functions
,
and
are the (normalized) vector spherical harmonics of [
31] and are based on the spherical harmonics
described in [
32]:
The radial functions
in (
11) and (12) form an orthonormal set for
at each value of
l over the range
, and are linear combinations of the spherical Bessel and Neumann functions,
and
(see, e.g., [
33]):
Therefore,
and the zeroes
of
satisfy
(An equivalent form of this equation has been studied earlier by [
34]). Using the results above, along with (15) and (16), the normalizing constant in (
6) is seen to be
. The
in (
21) clearly depend on the ratio
; again, we use
, which is appropriate for the Earth’s outer core. The
are easily found numerically, and for
, they appear in
Table 1.
Let us define integrals over radius
r as
and over solid angle
as
, where
Thus, the integral over the volume of the spherical shell interior is
The orthonormality properties of the Galerkin basis functions are
Using these and the properties given in (
11) and (12), we see that the integrals of the inner products of
and
over the volume enclosed by the homogeneous boundaries are
These will be useful in determining the linear inertial waves of the system.
While we use a model with an inner core, refs. [
6,
7] perform numerical simulations on a model with no inner core. The results we present do not depend on whether there is an inner core or not. The only adjustment necessary is that the radial expansion functions (18) become
when there is no inner core. In this case, the numerical values of the
in
Table 1 change slightly, but this does not affect our analysis, which is independent of the exact values of the
, as these are always distinct and well-ordered solutions of
, as discussed by [
35].
As to the flow on the boundary, consider (
11) and (12) at
:
This indicates a 2-D potential flow on the bounding surfaces that could be negated if compressibility was assumed for the fluid, as mentioned earlier in the discussion following (
3) and (
4). The development of this possibility is beyond the scope of the present work and will be deferred.
5. Inertial Waves in a Spherical Shell
If we place Equation (
5) into the Navier–Stokes Equation (
1), take the inner product of both sides with
and
, then integrate over the spherical shell volume, using the orthogonality relations (
24) and (
25), we get
Note that pressure
p does not appear above because
, where
is either
or
. Here, we see that the dissipative term may be neglected in a model system with given
L and
N if
for
and
. For Earth-like parameters, the dissipative term is extremely small and dissipation wavenumber
. If the system of Equations (
30) and (31) is truncated at moderate sizes of
N and
L, where
the dissipative term may be ignored for earth-like
E, though we will study model systems here by making
E large enough to have significant effect.
Now, consider the integral
. We can use (
11) and (12), as well as standard vector identities, along with Gauss’s divergence theorem and the boundary conditions to determine that
These equations lead immediately to
Since the wavenumbers
are all distinct, and using the fact that
only has
-dependence through a factor
, where
, we arrive at
Next, we must determine and then .
The quantum mechanical angular momentum operator
, whose properties are well known, is (with
)
Using this, along with (
11) and (15), allows
to be expressed as
The differential operator
has the properties
The first term in (40) vanishes because of the identity .
Now, to determine the cross terms
. Using (
11), (12), (15) and (16), along with the recurrence relations of the spherical Bessel, Neumann and associated Legendre functions [
33], and after much algebra, we find
Note that the vector product is antisymmetric when
and
are interchanged, as it must be, and that
for
and
; for
,
. Furthermore, note that these cross terms do not vanish when
. Furthermore,
When needed, this will be of use in computing (44).
The cross terms in (
30) and (31), which have just been evaluated, pertain to a rotating spherical shell. Ref. [
7] consider a rotating sphere and in that case called these cross terms ‘coupling coefficients’ and although they stated that these were computed numerically, no analytical determination similar to ours was presented. In our previous work [
5], we did not consider these cross terms at all and in the work presented here, we make up for this deficiency.
Now, if we put all of these results into the set of ordinary differential Equations (
30) and (31), we correct and expand the Coriolis terms given in [
5]:
Here, we have set
to eliminate the dissipative term, which can be placed back later, if desired. The equations above are qualitatively different from the inertial wave equations that are obtained by Fourier analysis [
17,
24]. In particular, we see that moving from a periodic box to a more realistic spherical shell model reveals the intrinsic coupling amongst the toroidal and poloidal linear modes. For each
m, there are two separate, disjoint sets. In one set, toroidal
with
even couple to poloidal
with
odd; in the other set, toroidal
couple to poloidal
. This result is fundamentally different to the one derived from Fourier analysis where there is no coupling.
Again, in (
48) and (49), modes
and
are only coupled to modes with the same
m and opposite parity for
l and
. Toroidal modes
are coupled to poloidal modes
, and all modes with same
m are coupled to one another in their respective set; for a given
N and
L, each set will have
eigenmodes. We can examine these coupled systems by restricting (
48) and (49) to
and
. For
, we have, using the notation
,
For the wave numbers given in
Table 1,
. Using this, the set of coupled Equations (
50) and (51) gives the variables
and
a dimensional oscillation frequency of
and the set (
50) and (51) gives
and
an dimensional oscillation frequency of
. (Again,
rad/s). Note that
and
are not coupled and that
and
are not coupled either. Instead, the Coriolis force links dipole and quadrupole components here.
Now, let us consider the variables with
in the reduced system. Their equations are
Compared to (
50) and (51), these equations have an extra term on the right; without the coupling terms, the 111 coefficients would have a dimensional angular frequency of
and the 211 coefficients have a frequency of
. However, they are coupled and the eigenvalues of the coupling matrices provide the actual frequencies. Again using
, the set of coupled Equation (
52) gives the variables
and
frequencies of
and
, while the set (
50) and (51) gives
and
the frequencies are
and
. (For
, these eigenfrequencies have their signs reversed). Again, the Coriolis force links dipole and quadrupole components and allows them to oscillate at frequencies determined by the set of linked multipole equations.
The
Equations (
50) and (51) and
Equations (
52) and (53) define four independent coupled linear systems of two variables each. However, these systems were created by ignoring all variables with
. For example, the full equation for
, rather than (51), couples it to
, so that we have
Thus, even though we can create a closed system for and with all variables set to zero, a system can be set up with larger L and N, where and . The values of L and N, which set the spatial resolution, can be made as large as computationally practicable, while the closure problem for an ideal system can be addressed by using a suitable to determine the dissipation wave number , which (as in fluid turbulence) should be commensurate with the largest wavenumber of the system, . We now consider these two topics: resolution and dissipation.
6. General Solution
A uniform approximation of fluid velocity in a spherical shell would ostensibly require
; However, it may be beneficial to produce formulas that allow
L and
N to be independent. In this regard, let us define the following matrix elements (reintroducing dissipation):
Using these, (
48) and (49) can be written as
(Remember that
). Let us further define the
vectors (‘
’ is transpose),
and
matrices,
Note that and for .
At this point, we can write (
57) and (58) as
Continuing along this line, we construct the following ‘super vectors’:
We also define the following ‘super matrices’, which are Hermitian if
:
Finally, we get to the canonical forms:
In the ideal case
, the matrices
and
are Hermitian and thus have real eigenvalues. Furthermore, for each
m there are three ideal invariants, the energies
and
, as well as the kinetic helicity
because of (
56):
Here,
is ‘kinetic helicity’ and
is the diagonal matrix
Each inertial wave vector
or
as a whole conserves energy when
, but their individual modes do not. In the theory of ideal fluid turbulence [
36], the ideal invariance of total energy and kinetic helicity allow for a statistical description of a model system; here, the lack of an inertial term
in (
1) precludes turbulence. However, it turns out that there are
ideal invariants for each
m, rather than the three in (
68) and (
69).
Let
and
be the unitary matrices that diagonalize
and
:
The superscript ‘’ denotes, as usual, a Hermitian adjoint. The diagonal matrices and contain the eigenvalues, which are complex when . Multiplying these eigenvalues by 2 yields the non-dimensional eigenfrequencies; when these, in turn are multiplied by , they are the dimensional eigenfrequencies of the eigenmodes of the system.
The unitary matrices
and
in (
70) also produce the eigenmodes of the system by transforming the vectors
and
defined in (
63) and (64):
The eigenmodes are the components of and and they are linear combinations of the components of and , respectively. Thus, the eigenmodes are combinations of the various multipoles (dipole, quadrupole, etc.) which comprise the inertial waves of the system. The extent of this mixing will be considered in the next section for the case .
In terms of
and
, Equation (
67) become
These have immediate solution:
The eigenvectors
and
have components (eigenmodes) with constant magnitude and periodically varying phase, whereas including an inertial term in (
1) would connect them and subject both to statistical fluctuations. These
magnitudes plus the kinetic helicity (
69) are the ideal invariants of the model system, i.e., when
.
The case where
and
have been expressed in (
50)–(53), where it was seen that the eigenfrequencies for the former are different from those for the latter. In general. For large
L and
N, the matrices (
65) and (66) present a formidable eigenvalue problem, particularly with respect to accuracy. However, for small
L and
N, the eigenvalues are easily found numerically and we now turn to a discussion of these.
7. Eigenfrequencies and Eigenmodes
We have seen some examples already, in 2-dimensional systems (
50) and (
52) for modes
with
and
. Again, a more uniform approximation of fluid velocity in a spherical shell would ostensibly require
. So, let us first truncate (
63)–(66) to
and look at the systems
Let us set
and
. Using the matrix elements defined in (
56), along with
Table 1 and formulas (44)–(47), we compute (using MatLab) the following, where
is the zero
matrix,
Now, let us keep
but set
. Using the matrix elements defined in (
56), along with
Table 1 and Equations (44)–(47), we compute (using MatLab) the following, where
is the unit
matrix,
The numerical matrix elements given above are, of course, approximate values and presented for purposes of illustration and an example for verification. One feature to notice in the matrices (
78), (
79), (
81) and (
82) is that the first element
in each has the largest magnitude. This property appears to hold for all
and
, with
.
From the above results, we can form the matrices given in (75) and (
76), i.e.,
,
,
and
. (Again,
here). The eigenvalues of these, multiplied by 2, are the eigenfrequencies of associated truncated systems; these eigenfrequencies, written as vectors, are
Above, are the eigenfrequencies associated with and are the eigenfrequencies associated with for and 1; those associated with are the negative of those in (86). Here, these are all real because ; they become complex, with positive imaginary parts when . (The ordering of the eigenfrequencies and their corresponding eigenvectors is arbitrary; above, the choice is most positive to most negative eigenfrequency, but this is not essential).
The eigenmodes can be found using (
71), but this will not be done here; however, the case
will be considered presently and the structure of the eigenmodes will be examined graphically. Note the appearance of zero eigenfrequencies in (
83) and (84);
N zero values occur when
L is odd, but none when
L is even or when
(or when
, though the real part will be zero for any odd
L and become zero if
E is large enough, as will be seen presently).
Earlier, in the discussion following (
50) and (51), the eigenfrequencies associated with
,
were given, and similarly, following (
52) and (53), the eigenfrequencies associated with
,
were given, while above
was considered. Of course, we can find the eigenvalues of
and
for any values of
L and
N. As
L and
N increase, the number of eigenfrequencies (and eigenmodes) is
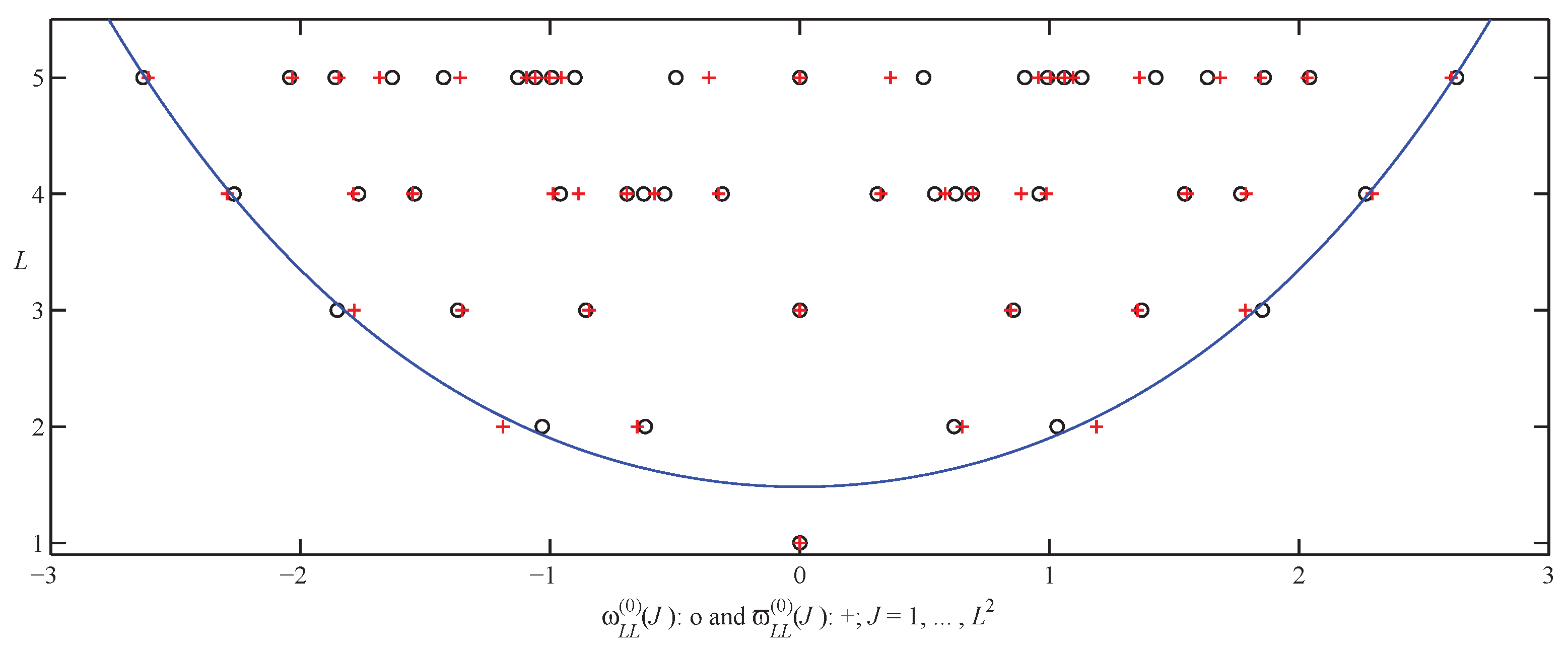
, and the presentation of either as an array of numbers would perhaps be overwhelming. Instead, results will be presented graphically (
Figure 1, 5 and 6) in what follows and will be limited to
for
and
.
8. Undamped and Damped Inertial Waves
Consider the cases with
and
. The case
is simple: for
, the eigenfrequencies are zero and for
, they are
(in units of
). For
, we use MatLab to find the eigenfrequencies from
and
. In the case where
, the eigenfrequencies are presented in
Figure 2. There it can be seen that the undamped eigenfrequencies appear to increase without bound for
. For
= 1, 3, 5 there are 1, 3 and 5 zero eigenfrequencies, respectively, although they are on top of each other for
.
However, in physical body such as the Earth,
E, though small, is not zero, but using
would require
, which from a standpoint of accuracy and computation time is not very feasible. So, for example, we look at the cases where
and
; the results of doing so gives us the sequence of plots shown in
Figure 3. There, each of the eigenfrequencies has gained a positive imaginary part, leading to damping of the eigenmode. As
E increases, more and more eigenfrequencies get a real part of zero, indicating overdamping. Thus, as
L increases beyond what is shown in
Figure 2, the bounding curve will reach a limit and eventually return to
.
In
Figure 4, the damped eigenfrequencies for
and the cases
are presented. Notice that in both
Figure 3 and
Figure 4, the five zeroes that were superimposed for the
case in
Figure 2 have now separated due to each gaining a different damping factor
. The same will occur for the multiple zeros of any odd
L when damping is introduced.
In (
71), the matrices
and
used to transform the primary vectors
and
in eigenvectors
and
, each of the components of which is an eigenmode. These eigenmodes are combinations of the components (modes) of
and
, as defined by (
59), (
60), (
63) and (64); the specific manner in which each mode goes in each eigenmode is determined by the
rows (
)
of
and
of
. The
elements (
)
of
and
of
are generally complex and for
would give an array of 25 complex numbers, too many perhaps to be very illuminating.
Instead, for
and
, we give the eigenfrequencies in
Figure 1 and
Table 2, and plot the magnitudes
and
for the
case in
Figure 5, which contains the 25 magnitudes for each
; the corresponding eigenfrequencies are given in
Table 2. In the
case, there is no need to give the magnitudes and eigenfrequencies for
because these are the same as those found in the range
(although the complex values for these
and
are different). Similar figures can be made for the
eigenmodes, but this will not be done here, where the
case is chosen as an example.
One interesting feature seen in plots
, of
Figure 5 is that the
and
have only three significant magnitudes, while the plots,
, have many.
Table 3 explores this feature in more detail by showing the actual values, rather than just the magnitudes, of these large magnitude
and
. In
Table 3, we see that actual values are all real and positive. Remember that for
,
and
; thus, these are non-oscillatory eigenmodes.
If we consider the structure of
and
given in (
63) and (64), we see that the three significant magnitudes for the eigenmodes
, in
Figure 5 which have
, are the toroidal parts of
and those which have
are the poloidal parts of
, while the eigenmodes whose frequencies have zero real part are almost purely either toroidal or poloidal, the eigenmodes
, have a mixture of toroidal and poloidal components; according to
Table 2, these also have
and
, and are thus time-dependent eigenmodes.
9. Physical Space Eigenfunctions
In order to visualize the non-oscillatory eigenmodes, we find their functional form in physical space. First, we define arrays containing the expansion functions
and
:
We use these to define larger arrays analogous to
and
:
Now, Equations (
1) and (
9) for
and
can be written, using (
69), as
Here, the factor of
appears because of (
8) and (
13).
The arrays
and
transform differently from the rule (
71) that applies to
and
:
In the case
, the elements of
and
are real, while those of
and
are generally complex. Under these transformations, (
91) and (92) become
However, in this example with
and
, the important elements of
and
associated with
and
are real (and positive) as
Table 3 shows. We can use these values and (
93) to find the approximate form of the physical space eigenfunctions
and
associated with each
, and
and
associated with each
,
. Since
, these have no
-dependence, plotting their shape on any
= constant slice of the spherical shell will reveal their structure. For this case, we make use of (
11)–(15) to see that
; thus, only the toroidal
in (
95) and (96) will contribute as
and
. Let us define
Here, is, of course, a Legendre polynomial.
Now, we can examine the physical space eigenfunctions associated with the
and
eigenmodes contained in the expansions for velocity (
91) and vorticity (92) using the data in
Table 3. In any
slice, the velocity eigenfunctions will be denoted
,
, where
The vorticity eigenfunctions associated with these are
,
,
Again, the numerical values of the
and
used above can be found in
Table 3.
The eigenfunctions
in (
99)–(
103) and
in (
104)–(108) that represent the
physical space eigenmodes of velocity and vorticity are pictured in
Figure 6. These are non-oscillatory flow patterns specific to the
system that was used as an example; they are ordered by the smallest (
) to the largest (
) dissipation factors of the non-oscillatory eigenmodes, which are also the five smallest dissipation factors of the 25 eigenmodes of the whole system. What they indicate is that the non-oscillatory inertial wave eigenmodes take the form of circular vortex structures that surround the rotation axis of the spherical shell. This is in contrast to the columnar, axially aligned vortices that numerical geodynamo simulations of a turbulent magnetofluid show occurring outside the so-called tangent cylinder of the rotating shell [
27,
28,
37]. However, it must be remembered that here we are dealing with linear inertial hydrodynamic waves, while the turbulent geodynamo simulations study a fully nonlinear magnetohydrodynamic (MHD) system. A connection to nonlinear MHD systems must await an analysis of the MHD analog of the hydrodynamic inertial wave Equation (
1).
10. Conclusions
In this paper, we determined the inertial waves found in an incompressible fluid in a rotating spherical shell with ‘homogeneous’ boundary conditions (b.c.s). A dynamical system has been defined and it has been shown that this system, with definite values of
L and
N, has exact solutions, e.g., definite eigenfrequencies and eigenmodes. If
L and
N are changed, then we have a new system which may have different values for the eigenfrequencies and shapes of eigenmodes. In this context, the question can be asked as to whether eigenfrequencies converge, at least for the largest scales, to definite values for a given
E, as
L and
N get larger and larger. The two largest-scale modes for
L =
N = 5 are identified by
as seen in
Figure 5; the eigenfrequencies of these two modes are
and
as given in
Table 2; these have the smallest magnitude of all eigenfrequencies in the case
L =
N = 5. Furthermore, in
Figure 2, it is evident that the smallest magnitude
have Re
= 0 for all odd
L, while for increasing even values of
L,
Figure 2 suggests that smallest magnitude
also have Re
. This indicates the convergence of the eigenfrequencies of the largest scale modes:
. This is interesting, as it appears that the largest-scale inertial waves are or become stationary as
L and
N increase. A fuller examination of this topic is beyond the scope of the present work and must be deferred.
In summary, we have found the analytical form of inertial waves in an incompressible, rotating fluid constrained by concentric inner and outer spherical surfaces with homogeneous boundary conditions by using a toroidal-poloidal basis equivalent to Chandrasekhar-Kendall functions. We have discovered formulas and procedures for determining eigenmodes and associated eigenfrequencies for both the ideal and dissipative cases. These eigenmodes are formed from linear combinations of the multipole components of the Bessel function-spherical harmonic series that represents the fluid velocity. We illustrated the use of our results with specific low-dimensional examples and discussed what may occur as one moves to larger systems. In particular, we have found in a specific example that the lowest dissipation eigenmodes, all of which are non-oscillatory, are vortex ring structures that encircle the rotation axis. Application of the approach presented here to the problem of determining magnetohydrodynamic inertial wave structure in a spherical shell with homogeneous b.c.s is expected to further increase our understanding of the geodynamo.
Finally, let us mention a few other points. First, we have outlined an approach to the case with no-slip b.c.s. and compressibility, where one would still use the vector expansion functions
and
in addition to introducing a new set of expansion functions suitable for including compressibility effects and enforcing the no-slip boundary condition. Second, the Galerkin basis used here is unique in that each term satisfies a Helmholtz equation, for the given b.c.s and incompressibility. One could use Chebyshev polynomials as is done by [
1,
2], or perhaps Legendre polynomials, but the individual terms no longer satisfy the Helmholtz equation, i.e., there are no longer unique wavenumbers for the modes. (Please see [
38] for formulas related to Chebyshev and Legendre methods). Third, the results developed here could be used to analyze data from numerical simulations, most directly from simulations based on the Galerkin vector basis functions defined in the paper, but also, data from finite-difference or finite-volume methods could also examined, particularly, but not necessarily, if these other methods employ the same b.c.s.