Impact of Respiratory Fluctuation on Hemodynamics in Human Cardiovascular System: A 0-1D Multiscale Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. 0-1D Modeling of Hemodynamics in Human CVS
2.2. Clinical Data Collection and Processing
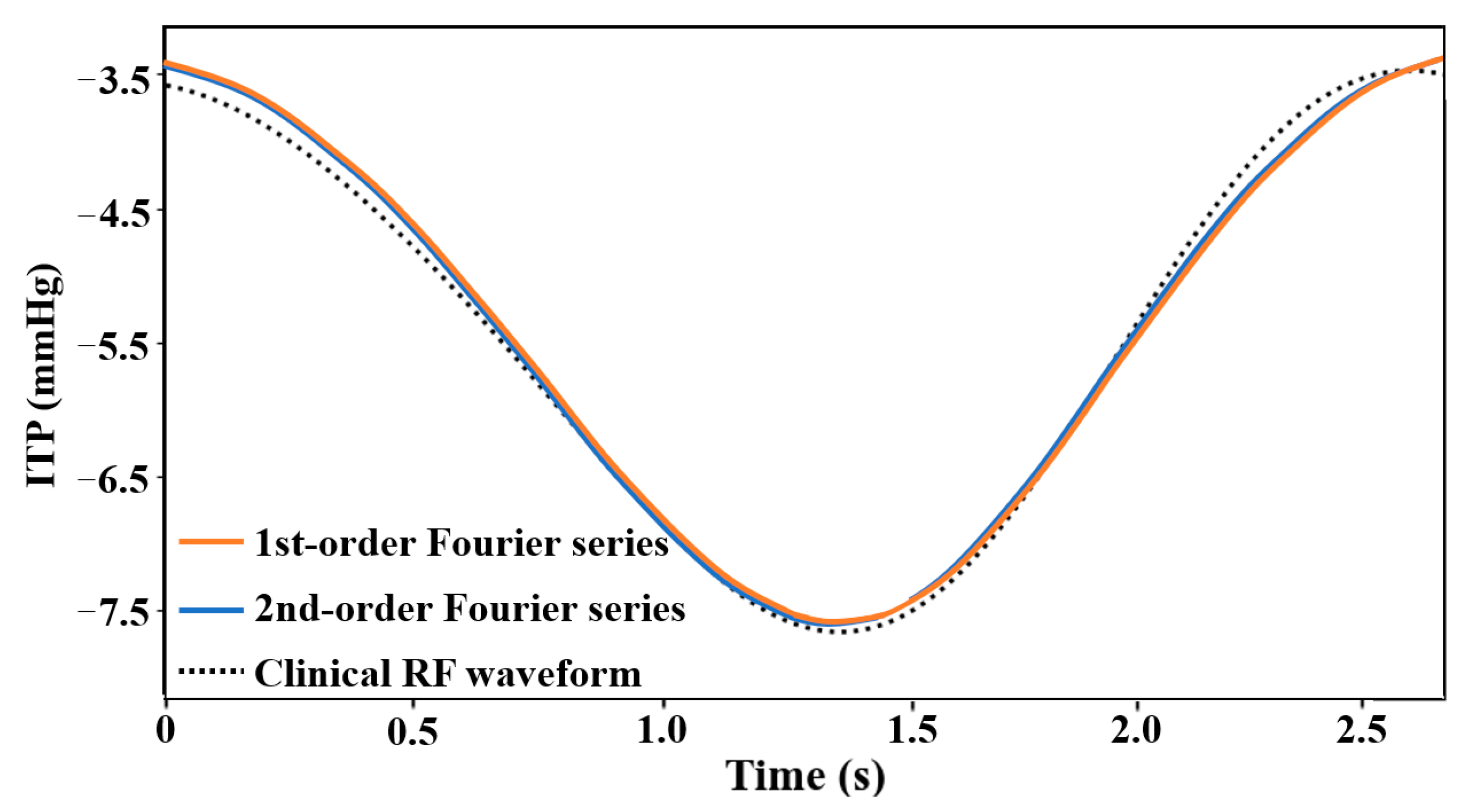
2.3. Submodule of Respiratory Fluctuations (RF)
2.4. Age Regulation
3. Results and Discussion
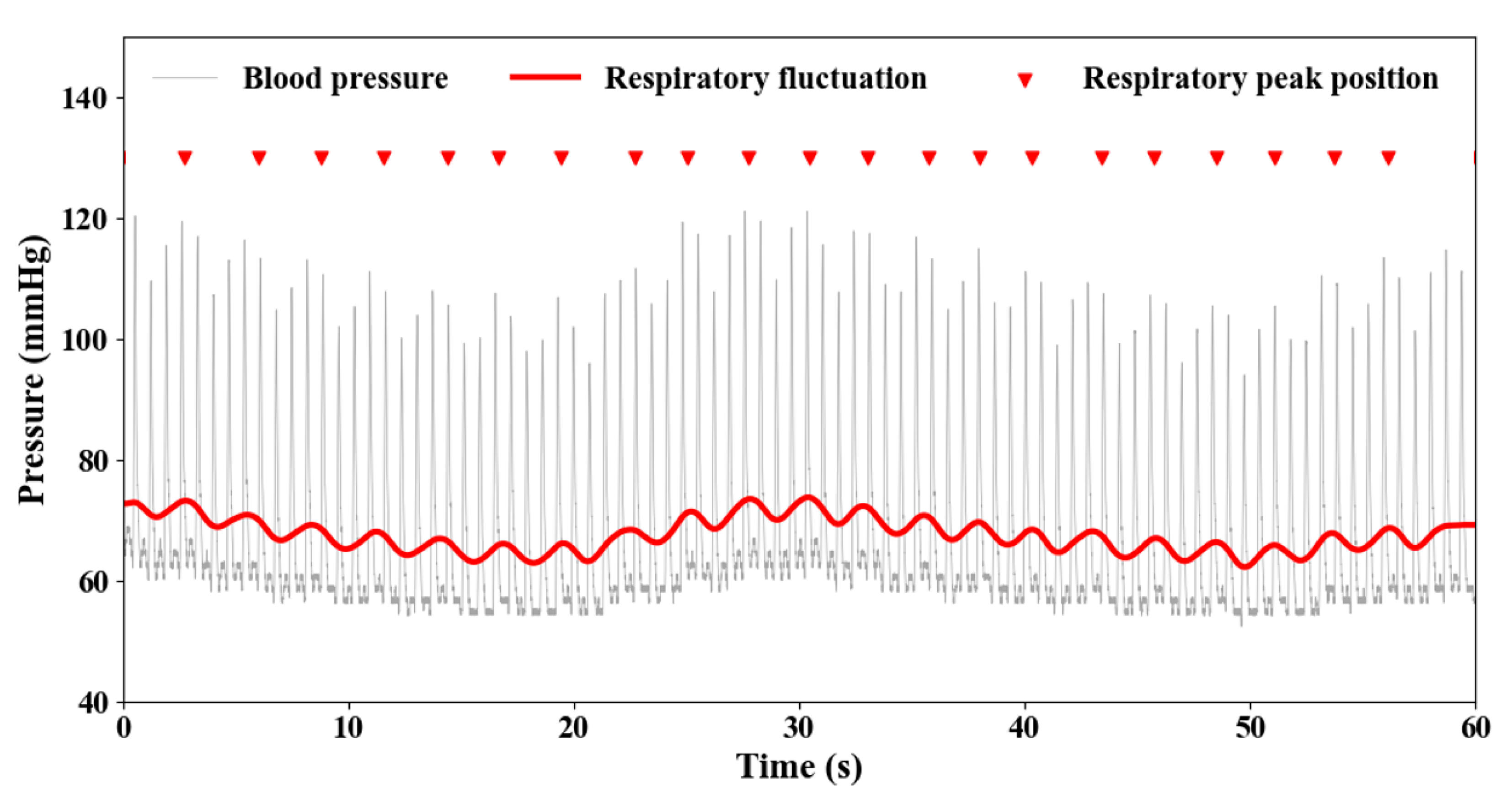
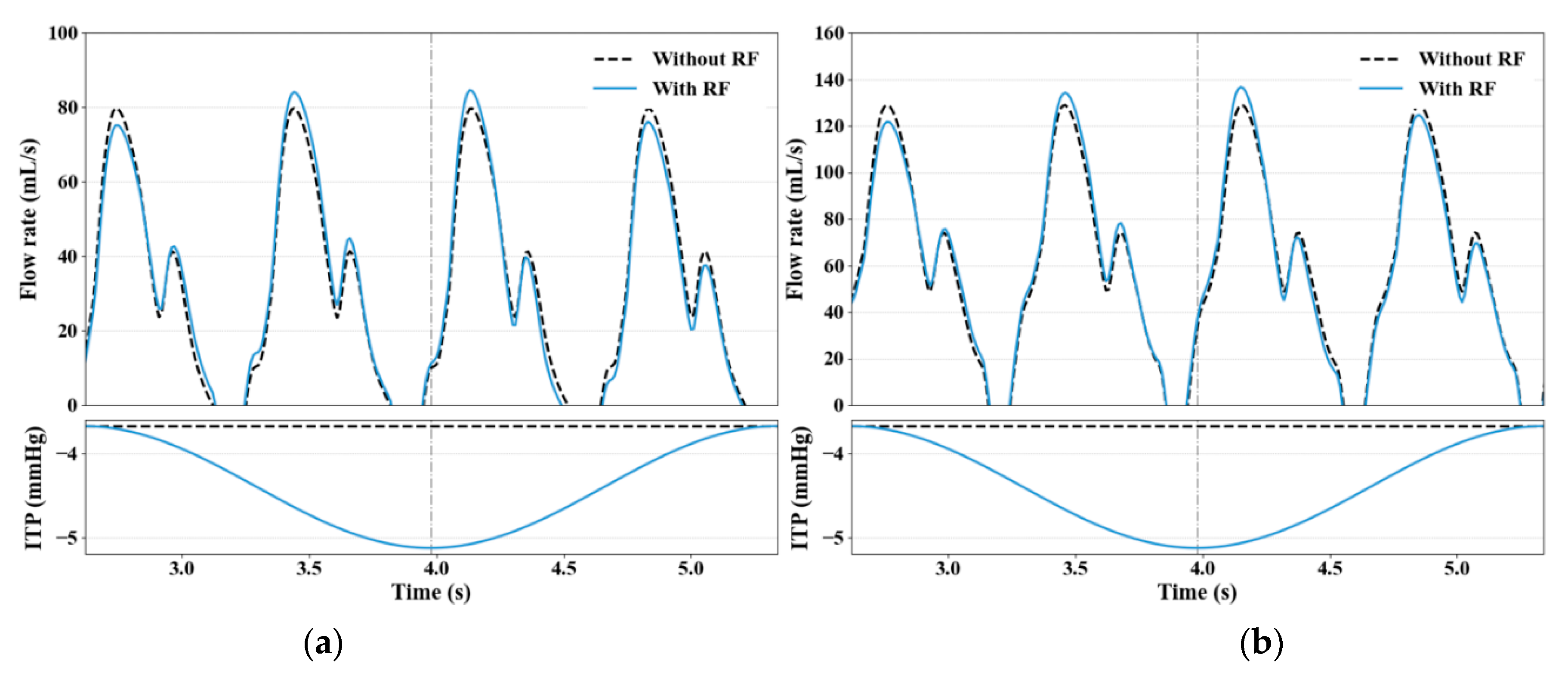
3.1. RF Modeling Validation
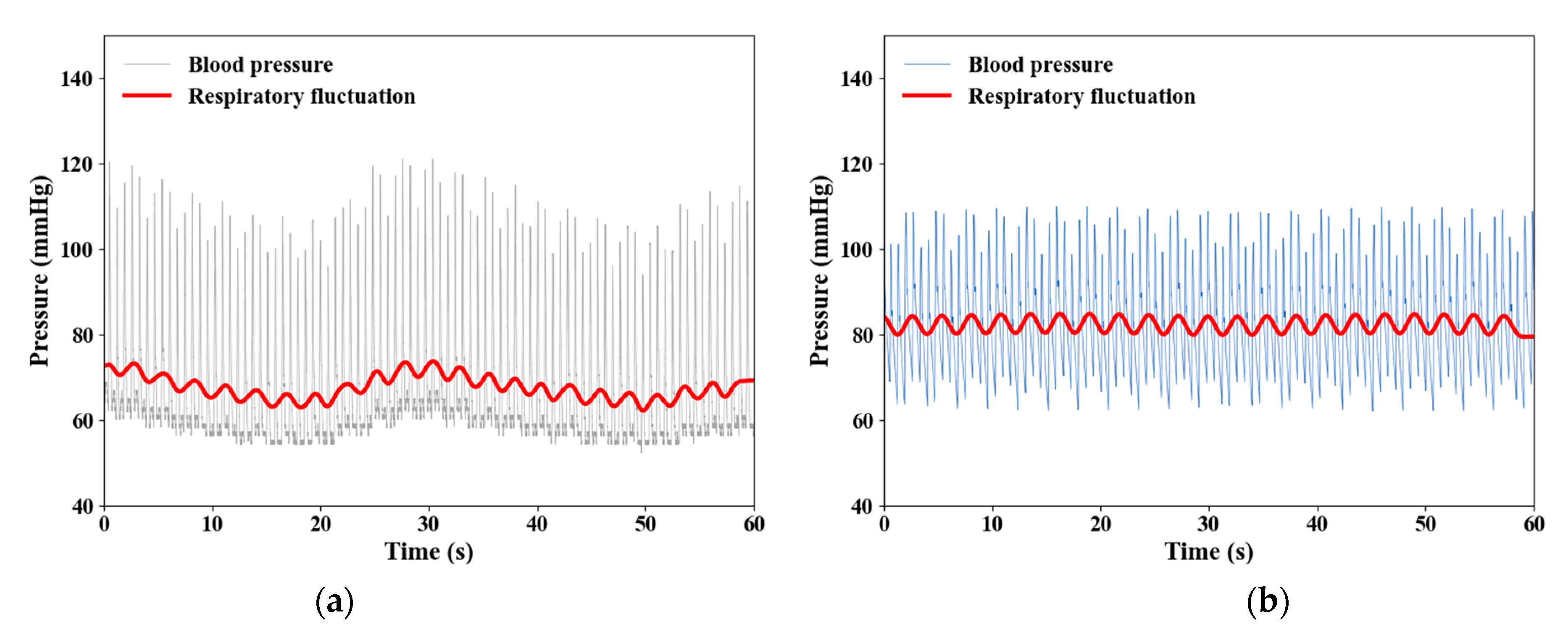
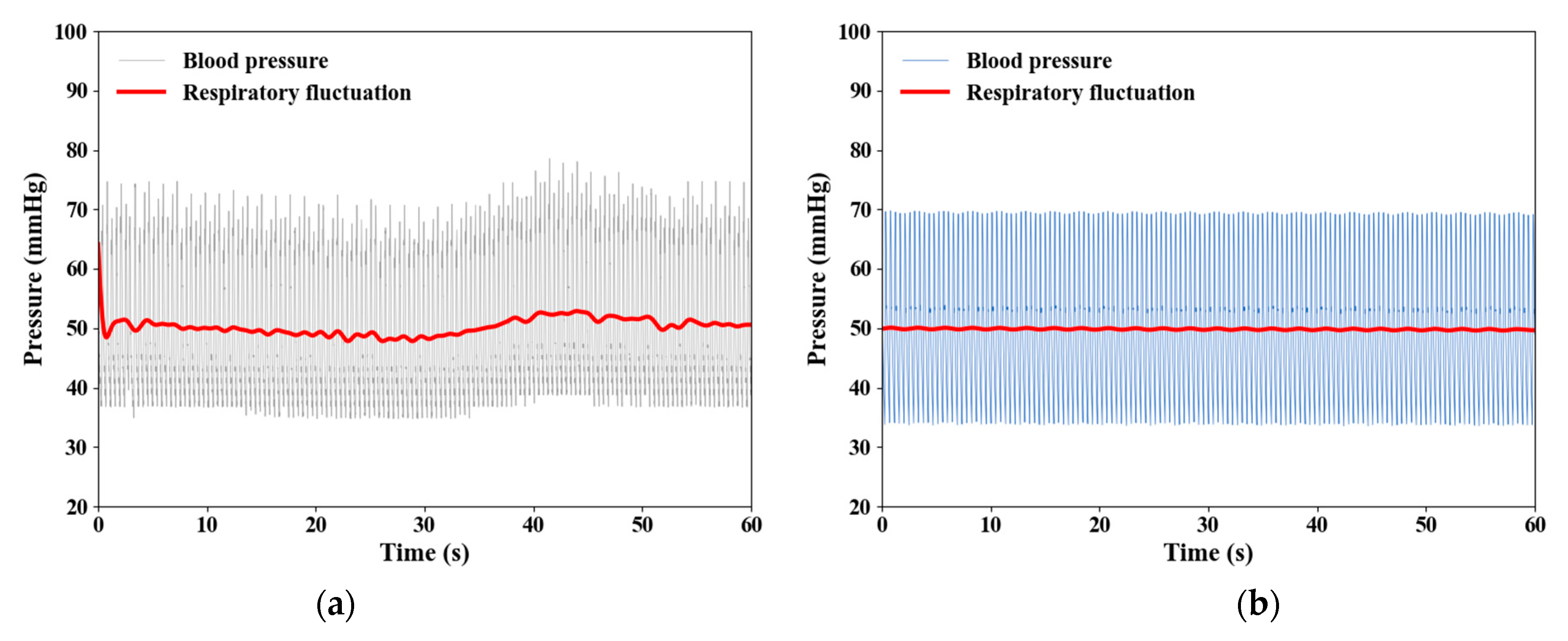
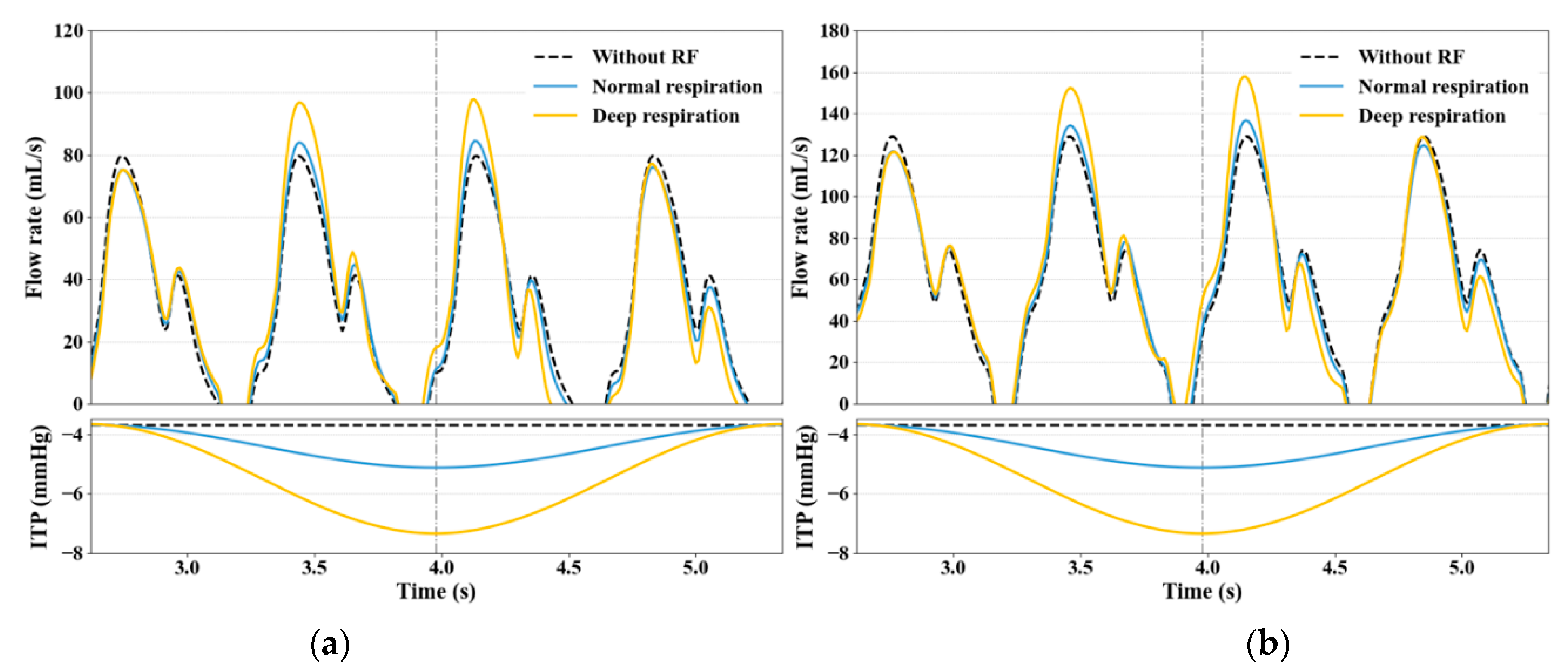
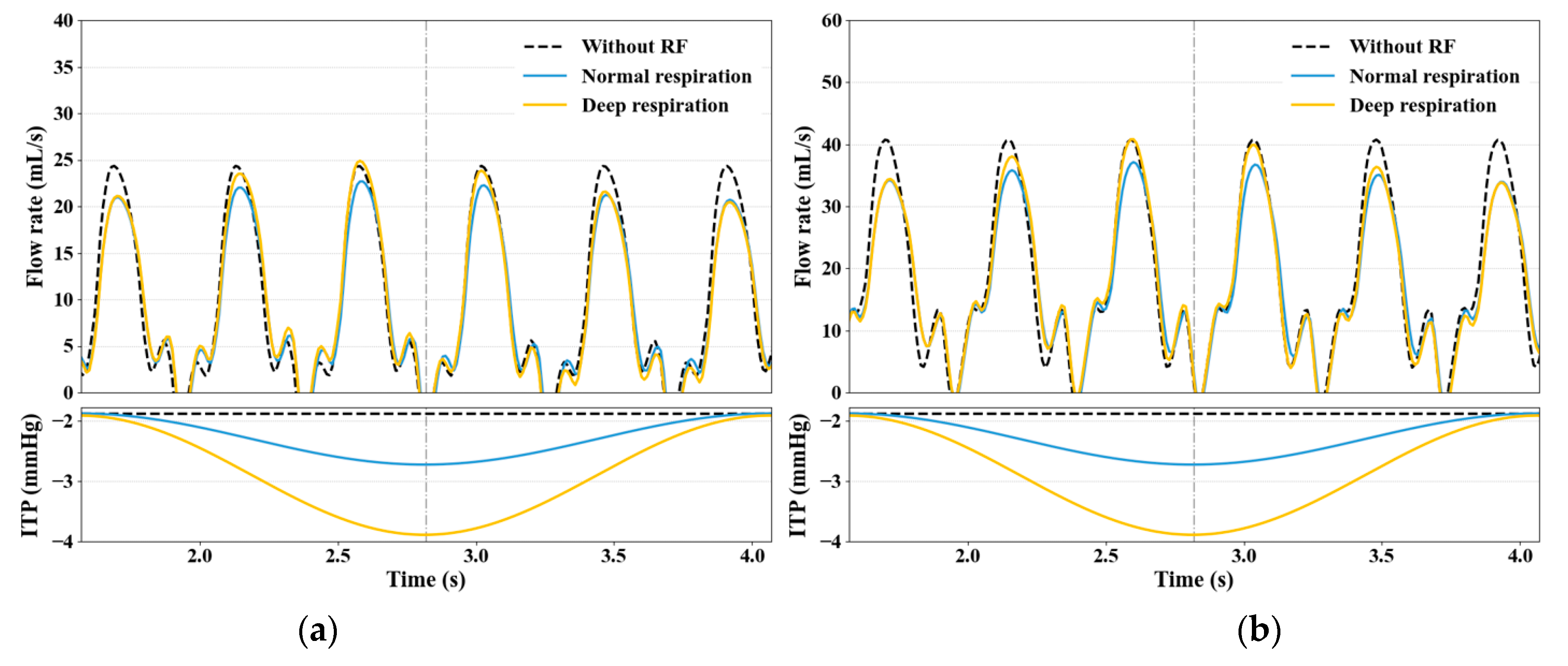
3.2. Impact of RF on Venous Return
3.3. Effect of Large ITP Reduction
3.4. Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dornhorst, A.C.; Howard, P.; Leathart, G.L. Respiratory variations in blood pressure. Circulation 1952, 6, 553–558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brecher, G.A.; Hubay, C.A. Pulmonary blood flow and venous return during spontaneous respiration. Circ. Res. 1955, 3, 210–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno, A.H.; Burchell, A.R.; Van der Woude, R.; Burke, J.H. Respiratory regulation of splanchnic and systemic venous return. Am. J. Physiol.-Leg. Content 1967, 213, 455–465. [Google Scholar] [CrossRef] [Green Version]
- Robotham, J.L.; Lixfeld, W.; Holland, L.; MacGregor, D.; Bryan, A.C.; Rabson, J. Effects of respiration on cardiac performance. J. Appl. Physiol. 1978, 44, 703–709. [Google Scholar] [CrossRef]
- Kim, B.H.; Ishida, Y.; Tsuneoka, Y.; Matsubara, N.; Hiraoka, T.; Takeda, H.; Inoue, M.; Kamada, T.; Kimura, K.; Kozuka, T. Effects of spontaneous respiration on right and left ventricular function: Evaluation by respiratory and ECG gated radionuclide ventriculography. J. Nucl. Med. 1987, 28, 173–177. [Google Scholar]
- Peters, J.; Fraser, C.; Stuart, R.S.; Baumgartner, W.; Robotham, J.L. Negative intrathoracic pressure decreases independently left ventricular filling and emptying. Am. J. Physiol.-Heart Circ. Physiol. 1989, 257, H120. [Google Scholar]
- Innes, J.A.; De Cort, S.C.; Kox, W.; Guz, A. Within-breath modulation of left ventricular function during normal breathing and positive-pressure ventilation in man. J. Physiol. 1993, 460, 487–502. [Google Scholar] [CrossRef]
- Convertino, V.A. Mechanisms of inspiration that modulate cardiovascular control: The other side of breathing. J. Appl. Physiol. 2019, 127, 1187–1196. [Google Scholar] [CrossRef]
- Liu, H.; Liang, F.; Wong, J.; Fujiwara, T.; Ye, W.; Tsubota, K.I.; Sugawara, M. Multi-scale modeling of hemodynamics in the cardiovascular system. Acta Mech. Sin. 2015, 31, 446–464. [Google Scholar] [CrossRef]
- Avolio, A.P. Multi-branched model of the human arterial system. Med. Biol. Eng. Comput. 1980, 18, 709–718. [Google Scholar] [CrossRef]
- Taylor, C.A.; Figueroa, C.A. Patient-specific modeling of cardiovascular mechanics. Annu. Rev. Biomed. Eng. 2009, 11, 109–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mynard, J.P.; Smolich, J.J. One-dimensional haemodynamic modeling and wave dynamics in the entire adult circulation. Ann. Biomed. Eng. 2015, 43, 1443–1460. [Google Scholar] [CrossRef] [PubMed]
- Sherwin, S.J.; Formaggia, L.; Peiro, J.; Franke, V. Computational modelling of 1D blood flow with variable mechanical properties and its application to the simulation of wave propagation in the human arterial system. Int. J. Numer. Methods Fluids 2003, 43, 673–700. [Google Scholar] [CrossRef]
- Sherwin, S.J.; Franke, V.; Peiró, J.; Parker, K. One-dimensional modelling of a vascular network in space-time variables. J. Eng. Math. 2003, 47, 217–250. [Google Scholar] [CrossRef]
- Van de Vosse, F.N.; Stergiopulos, N. Pulse wave propagation in the arterial tree. Annu. Rev. Fluid Mech. 2011, 43, 467–499. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Lawford, P.; Hose, R. Review of zero-D and 1-D models of blood flow in the cardiovascular system. Biomed. Eng. Online 2011, 10, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Westerhof, N.; Lankhaar, J.W.; Westerhof, B.E. The arterial windkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef] [Green Version]
- Formaggia, L.; Lamponi, D.; Tuveri, M.; Veneziani, A. Numerical modeling of 1D arterial networks coupled with a lumped parameters description of the heart. Comput. Methods Biomech. Biomed. Eng. 2006, 9, 273–288. [Google Scholar] [CrossRef]
- Liang, F.Y.; Takagi, S.; Himeno, R.; Liu, H. Biomechanical characterization of ventricular–arterial coupling during aging: A multi-scale model study. J. Biomech. 2009, 42, 692–704. [Google Scholar] [CrossRef]
- Liang, F.Y.; Takagi, S.; Himeno, R.; Liu, H. Multi-scale modeling of the human cardiovascular system with applications to aortic valvular and arterial stenoses. Med. Biol. Eng. Comput. 2009, 47, 743–755. [Google Scholar] [CrossRef]
- Liang, F.Y.; Liu, H.; Takagi, S. The effects of brachial arterial stiffening on the accuracy of oscillometric blood pressure measurement: A computational model study. J. Biomech. Sci. Eng. 2012, 7, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Liang, F.Y.; Takagi, S.; Liu, H. The influences of cardiovascular properties on suprasystolic brachial cuff wave studied by a simple arterial-tree model. J. Mech. Med. Biol. 2012, 12, 1250040. [Google Scholar] [CrossRef]
- Liang, F.Y.; Takagi, S.; Himeno, R.; Liu, H. A computational model of the cardiovascular system coupled with an upper-arm oscillometric cuff and its application to studying the suprasystolic cuff oscillation wave, concerning its value in assessing arterial stiffness. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 141–157. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.Y.; Fukasaku, K.; Liu, H.; Takagi, S. A computational model study of the influence of the anatomy of the circle of Willis on cerebral hyperperfusion following carotid artery surgery. Biomed. Eng. Online 2011, 10, 1–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, F.Y.; Oshima, M.; Huang, H.X.; Liu, H.; Takagi, S. Numerical study of cerebroarterial hemodynamic changes following carotid artery operation: A comparison between multiscale modeling and stand-alone three-dimensional modeling. J. Biomech. Eng. 2015, 137, 101011. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.Y.; Senzaki, H.; Yin, Z.F.; Fan, Y.Q.; Sughimoto, K.; Liu, H. Transient hemodynamic changes upon changing a BCPA into a TCPC in staged Fontan operation: A computational model study. Sci. World J. 2013, 2013, 486815. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.Y.; Senzaki, H.; Kurishima, C.; Sughimoto, K.; Inuzuka, R.; Liu, H. Hemodynamic performance of the Fontan circulation compared with a normal biventricular circulation: A computational model study. Am. J. Physiol.-Heart Circ. Physiol. 2014, 307, H1056–H1072. [Google Scholar] [CrossRef]
- Müller, L.O.; Toro, E.F. A global multiscale mathematical model for the human circulation with emphasis on the venous system. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 681–725. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.C.; Noda, S.; Himeno, R.; Liu, H. Gravitational effects on global hemodynamics in different postures: A closed-loop multiscale mathematical analysis. Acta Mech. Sin. 2017, 33, 595–618. [Google Scholar] [CrossRef]
- Zhang, X.C.; Haneishi, H.; Liu, H. Multiscale modeling of the cardiovascular system for infants, children, and adolescents: Age-related alterations in cardiovascular parameters and hemodynamics. Comput. Biol. Med. 2019, 108, 200–212. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Pennati, G.; Fumero, R. Scaling approach to study the changes through the gestation of human fetal cardiac and circulatory behaviors. Ann. Biomed. Eng. 2000, 28, 442–452. [Google Scholar] [CrossRef] [PubMed]
- Alastruey Arimon, J. Numerical Modelling of Pulse Wave Propagation in the Cardiovascular System: Development, Validation and Clinical Applications. Ph.D. Thesis, Imperial College London, London, UK, 2006. [Google Scholar]
- Armstrong, M.K.; Schultz, M.G.; Picone, D.S.; Black, J.A.; Dwyer, N.; Roberts-Thomson, P.; Sharman, J.E. Brachial and radial systolic blood pressure are not the same: Evidence to support the popeye phenomenon. Hypertension 2019, 73, 1036–1041. [Google Scholar] [CrossRef]
- Salim, M.A.; DiSessa, T.G.; Arheart, K.L.; Alpert, B.S. Contribution of superior vena caval flow to total cardiac output in children: A Doppler echocardiographic study. Circulation 1995, 92, 1860–1865. [Google Scholar] [CrossRef] [PubMed]
- Kimura, B.J.; Dalugdugan, R.; Gilcrease III, G.W.; Phan, J.N.; Showalter, B.K.; Wolfson, T. The effect of breathing manner on inferior vena caval diameter. Eur. J. Echocardiogr. 2011, 12, 120–123. [Google Scholar] [CrossRef] [PubMed]
- Natori, H.; Tamaki, S.; Kira, S. Ultrasonographic evaluation of ventilatory effect on inferior vena caval configuration. Am. Rev. Respir. Dis. 1979, 120, 421–427. [Google Scholar]
- Cheyne, W.S.; Gelinas, J.C.; Eves, N.D. The haemodynamic response to incremental increases in negative intrathoracic pressure in healthy humans. Exp. Physiol. 2018, 103, 581–589. [Google Scholar] [CrossRef]
- Singh, I.; Pinsky, M.R. Heart-lung interactions. In Mechanical Ventilation, 1st ed.; Papadakos, P.J., Lachmann, B., Visser-Isles, L., Eds.; W.B. Saunders: Philadelphia, PA, USA, 2007; pp. 173–184. [Google Scholar]
- Ryan, K.L.; Cooke, W.H.; Rickards, C.A.; Lurie, K.G.; Convertino, V.A. Breathing through an inspiratory threshold device improves stroke volume during central hypovolemia in humans. J. Appl. Physiol. 2008, 104, 1402–1409. [Google Scholar] [CrossRef]



| Types | Parameters | |
|---|---|---|
| Subject 1 | Subject 2 | |
| Age | 12-year-old | 1-year-old |
| Disease | Ventricular septal defect (VSD) | Atrial septal defect (VSD) |
| Weight | 40.8 kg | 9.3 kg |
| Heart rate | 86 beats/min | 135 beats/min |
| Cardiac cycle | 0.697 s | 0.444 s |
| Respiration | 22 beats/min | 24 beats/min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Sughimoto, K.; Zhang, X.; Wang, S.; Hiraki, Y.; Liu, H. Impact of Respiratory Fluctuation on Hemodynamics in Human Cardiovascular System: A 0-1D Multiscale Model. Fluids 2022, 7, 28. https://doi.org/10.3390/fluids7010028
Li R, Sughimoto K, Zhang X, Wang S, Hiraki Y, Liu H. Impact of Respiratory Fluctuation on Hemodynamics in Human Cardiovascular System: A 0-1D Multiscale Model. Fluids. 2022; 7(1):28. https://doi.org/10.3390/fluids7010028
Chicago/Turabian StyleLi, Ruichen, Koichi Sughimoto, Xiancheng Zhang, Sirui Wang, Yuto Hiraki, and Hao Liu. 2022. "Impact of Respiratory Fluctuation on Hemodynamics in Human Cardiovascular System: A 0-1D Multiscale Model" Fluids 7, no. 1: 28. https://doi.org/10.3390/fluids7010028
APA StyleLi, R., Sughimoto, K., Zhang, X., Wang, S., Hiraki, Y., & Liu, H. (2022). Impact of Respiratory Fluctuation on Hemodynamics in Human Cardiovascular System: A 0-1D Multiscale Model. Fluids, 7(1), 28. https://doi.org/10.3390/fluids7010028







