Evaluation of RANS-DEM and LES-DEM Methods in OpenFOAM for Simulation of Particle-Laden Turbulent Flows
Abstract
:1. Introduction
2. CFD-DEM Approach and the Governing Equations
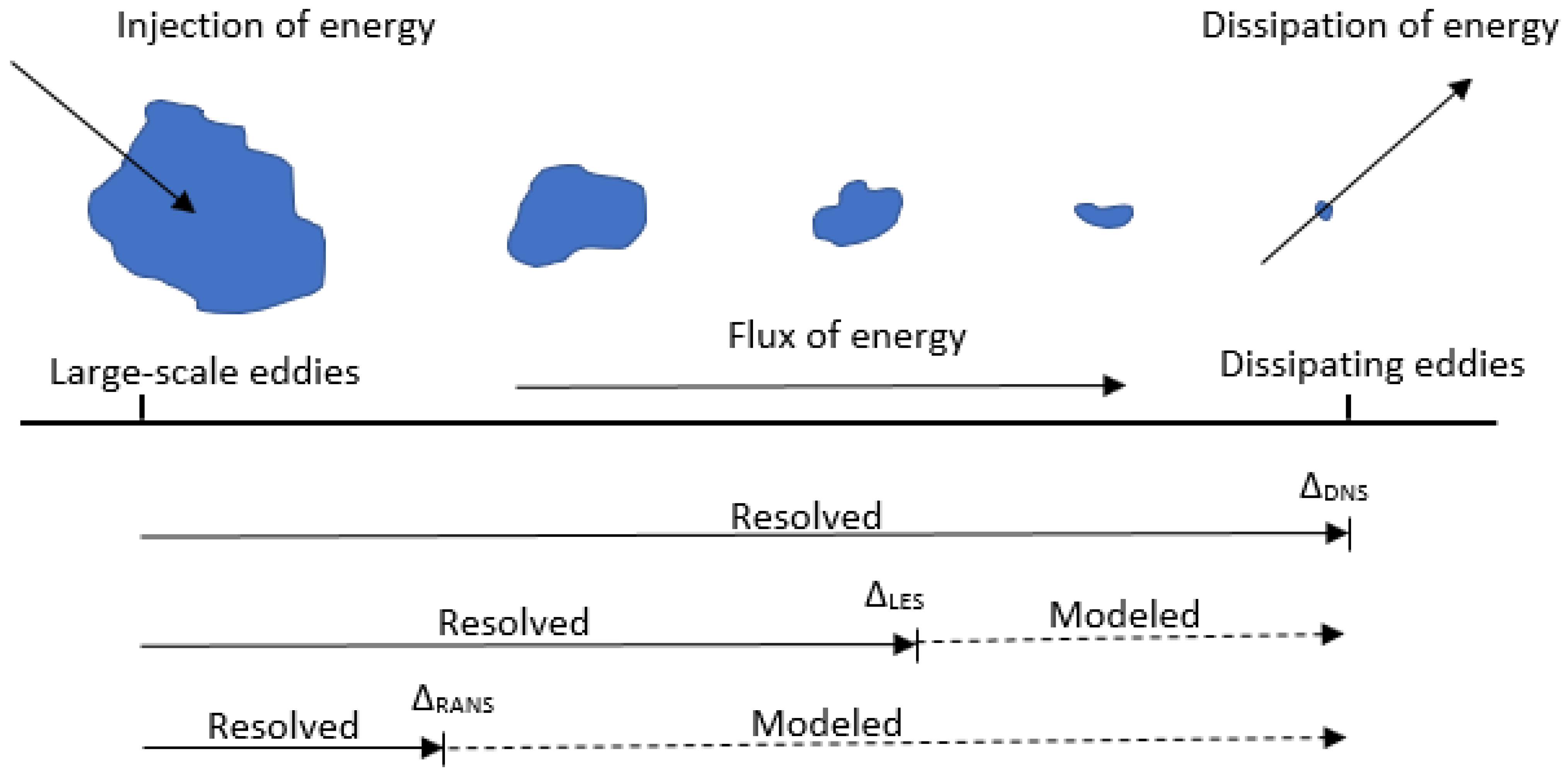
2.1. Direct Numerical Simulation (DNS)
2.2. Large-Eddy Simulation (LES)
2.3. Reynolds-Averaged Navier–Stokes Equations (RANS)
2.4. Particle Dispersion Modelling
2.5. Coupling between Continuum and Discrete Phases
- One-way coupling (fluid → particle): when the volumetric concentration of particles is small (αp < 0.0001%), the fluid flow fields affect the particle motion, but particles have a negligible effect on fluid flow fields. This results in only specific terms being considered in the governing CFD-DEM equations as follows:
- Two-way coupling (fluid ←→ particle): when the volumetric concentration of particles increases (0.1% < αp < 0.0001%), both fluid and particles affect each other’s motion. Two-way coupling can be further categorized into two categories, one in which particles enhance the turbulence dissipation and a second in which particles enhance turbulence production, which depends on the ratio of particle reaction time () to the Kolmogorov time scale () and to the turnover time of large eddies (), respectively, where is the density of particle, is the diameter of particle, is the density of fluid, υ is the kinematic viscosity of fluid, is turbulence dissipation rate, is turbulence length scale, and u is the fluid velocity. Two-way coupling results in the following CFD-DEM equations:
- Four-way coupling (fluid ←→ particle, particle ←→ particle): When the volumetric concentration of the particles further increases (αp > 0.1%), the interaction among particles becomes significant. In this regime, fluid and particle affect each other’s motion; additionally, the particle collision term needs to be included in the governing equations:
3. Method and Numerical Setup
4. Results and Discussion
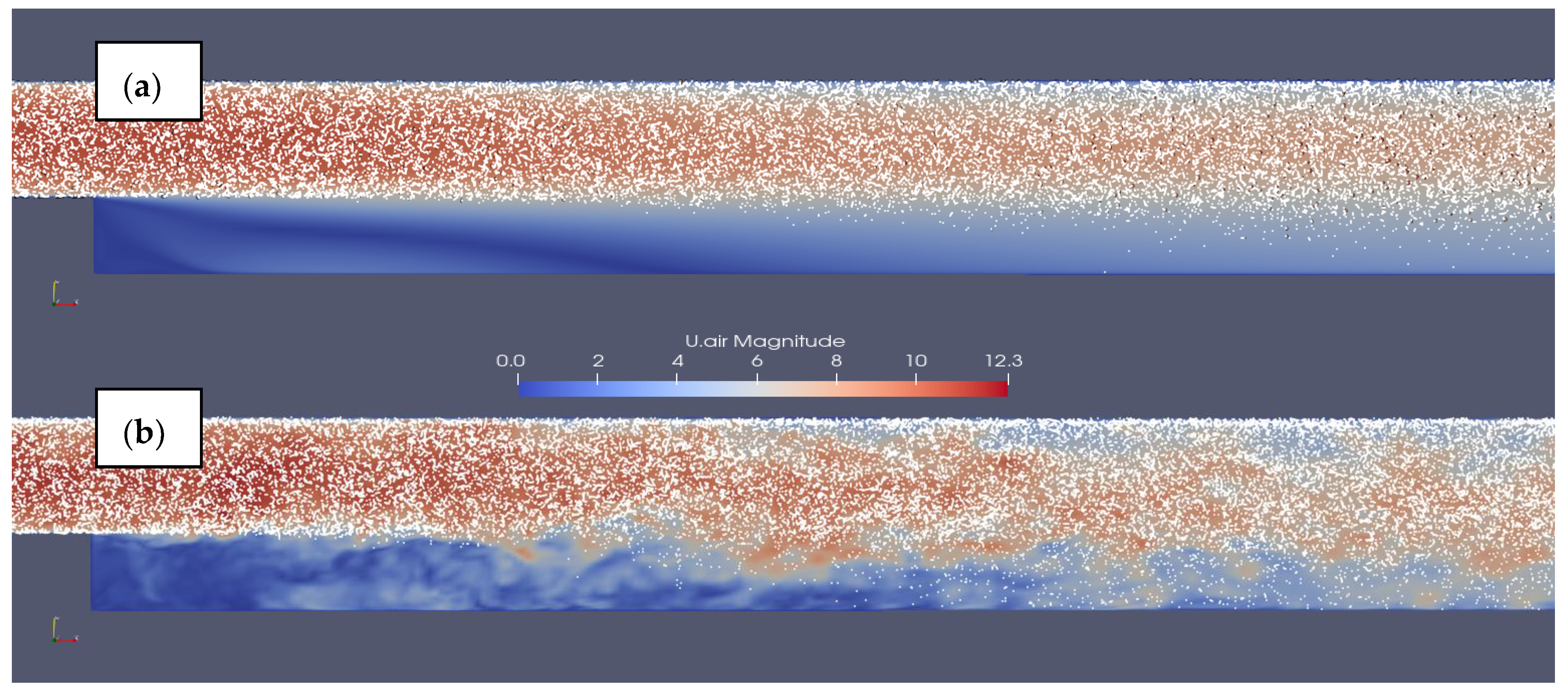
4.1. Single-Phase RANS and LES
4.2. RANS-DEM
4.3. LES-DEM
5. Summary and Conclusions
- We found that the threshold of coupling regime suggested by Elghobashi [4] is rigidly formulated and it might be sufficient to include one-way coupling even when the particle concentration is in O ~ , since we found almost no difference between the fluid and particle phase results for one-way and two-way coupling;
- Under the RANS-DEM framework, simple dispersion models based on DRW significantly underpredicted the particle dispersion. Consequently, more sophisticated dispersion models such as CRW must be used in conjunction with RANS-DEM. Previously claimed results about the ability of the simple dispersion models in accurately incorporating turbulence effects on particles were due to error in the numerical setup;
- When using relatively coarse mesh resolution (y+ > 1), Dynamic LES turbulence models seem to overcome the poor performance of static LES turbulence models in predicting the mean and fluctuating components of turbulent flow. We recommend using dynamic LES models when extreme mesh refinement is not possible due to the limitation of particles being smaller than CFD cell size in unresolved CFD-DEM;
- Resolved CFD-DEM (particle resolved DNS) requires huge computational resources and is restricted to a small number of particles. Point particle DNS-DEM is also computationally expensive and should not be applied for larger particles than Kolmogorov length scale. The LES-DEM seems to be a good compromise between accuracy and computational feasibility. However, its application is mostly restricted to simple cases (point-particles or small particles) due to the constraint of the particles being smaller than the CFD cells in unresolved CFD-DEM. In addition, the unresolved component of the turbulent velocity (SGS) seems to have a significant effect on particle dispersion and cannot be neglected, especially when using larger y+ in LES-DEM;
- Our analysis of different options for approximating the initial particle velocity (particle injection velocity) indicates that a suitable numerical approach might be to inject particles with (0, 0, 0) m/s of particle injection velocity. The difference between the results is small, but still might be appropriate so as to let the particles attain the real physical velocity according to physics, for the cases where the initial particle velocity is unavailable. However, this approach is case-dependent and software-specific. The best practice guidelines for CFD should still be the extension of the inlet channel length and allowing particles to develop real physical velocity, but this might be an extra computational overhead for CFD-DEM simulations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2011. [Google Scholar]
- Brennen, C.E. Fundamentals of Multiphase Flows; Cambridge University Press: Pasadena, CA, USA, 2005. [Google Scholar]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete Particle Simulation of Particulate Systems: Theoretical Developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Salih, S.Q.; Aldlemy, M.S.; Rasani, M.R.; Ariffin, A.K.; Ya, T.M.Y.S.T.; Al-Ansari, N.; Yaseen, Z.M.; Chau, K.W. Thin and sharp edges bodies-fluid interaction simulation using cut-cell immersed boundary method. Eng. Appl. Comput. Fluid Mech. 2019, 13, 860–877. [Google Scholar] [CrossRef] [Green Version]
- Squires, K.D.; Eaton, J.K. Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A Fluid Dyn. 1990, 2, 1191–1203. [Google Scholar] [CrossRef]
- Elghobashi, S.; Truesdell, G.C. On the two-way interaction between homogeneous turbulence and dispersed solid particles. I: Turbulence modification. Phys. Fluids A Fluid Dyn. 1993, 5, 1790–1801. [Google Scholar] [CrossRef]
- Chan, L.; Zahtila, T.; Ooi, A.; Philip, J. Turbulence Modification Due to Inertial Particles in a Rough-Wall Pipe. In Proceedings of the 22nd Australasian Fluid Mechanics Conference AFMC2020, Brisbane, Australia, 7–10 December 2020; The University of Queensland: Brisbane, Australia, 2020. [Google Scholar]
- Lee, J.; Lee, C. The Effect of Wall-Normal Gravity on Particle-Laden Near-Wall Turbulence. J. Fluid Mech. 2019, 873, 475–507. [Google Scholar] [CrossRef]
- Kuerten, J.G.M. Point-Particle DNS and LES of Particle-Laden Turbulent flow—A state-of-the-art review. Flow Turbul. Combust. 2016, 97, 689–713. [Google Scholar] [CrossRef] [Green Version]
- Bocksell, T.L.; Loth, E. Stochastic modeling of particle diffusion in a turbulent boundary layer. Int. J. Multiph. Flow 2006, 32, 1234–1253. [Google Scholar] [CrossRef]
- Loth, E. Numerical approaches for motion of dispersed particles, droplets and bubbles. Prog. Energy Combust. Sci. 2000, 26, 161–223. [Google Scholar] [CrossRef]
- Mofakham, A.A.; Ahmadi, G. On random walk models for simulation of particle-laden turbulent flows. Int. J. Multiph. Flow 2020, 122, 103157. [Google Scholar] [CrossRef]
- Xiang, L. RANS Simulations and Dispersion Models for Particles in Turbulent Flows. Master’s Thesis, KTH, School of Engineering Sciences (SCI), Mechanics, Stockholm, Sweden, 2019. [Google Scholar]
- Greifzu, F.; Kratzsch, C.; Forgber, T.; Lindner, F.; Schwarze, R. Assessment of particle-tracking models for dispersed particle-laden flows implemented in OpenFOAM and ANSYS FLUENT. Eng. Appl. Comput. Fluid Mech. 2016, 10, 30–43. [Google Scholar] [CrossRef] [Green Version]
- Innocenti, A.; Marchioli, C.; Chibbaro, S. Lagrangian filtered density function for LES-based stochastic modelling of turbulent particle-laden flows. Phys. Fluids 2016, 28, 115106. [Google Scholar] [CrossRef] [Green Version]
- Kuerten, J.G.M.; Vreman, A.W. Can turbophoresis be predicted by large-eddy simulation? Phys. Fluids 2005, 17, 011701. [Google Scholar] [CrossRef] [Green Version]
- Marchioli, C.; Salvetti, M.V.; Soldati, A. Some issues concerning large-eddy simulation of inertial particle dispersion in turbulent bounded flows. Phys. Fluids 2008, 20, 40603. [Google Scholar] [CrossRef] [Green Version]
- Salmanzadeh, M.; Rahnama, M.; Ahmadi, G. Effect of Sub-Grid Scales on Large Eddy Simulation of Particle Deposition in a Turbulent Channel Flow. Aerosol Sci. Technol. 2010, 44, 796–806. [Google Scholar] [CrossRef]
- Bianco, F.; Chibbaro, S.; Marchioli, C.; Salvetti, M.V.; Soldati, A. Intrinsic filtering errors of Lagrangian particle tracking in LES flow fields. Phys. Fluids 2012, 24, 45103. [Google Scholar] [CrossRef] [Green Version]
- Geurts, B.J.; Kuerten, J.G.M. Ideal stochastic forcing for the motion of particles in large-eddy simulation extracted from direct numerical simulation of turbulent channel flow. Phys. Fluids 2012, 24, 81702. [Google Scholar] [CrossRef] [Green Version]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD Simulations of Fixed Bed Reactors with Small Tube to Particle Diameter Ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Palzer, S. DEM–CFD modeling of a fluidized bed spray granulator. Chem. Eng. Sci. 2011, 66, 2340–2355. [Google Scholar] [CrossRef]
- Jajcevic, D.; Siegmann, E.; Radeke, C.; Khinast, J.G. Large-Scale CFD–DEM Simulations of Fluidized Granular Systems. Chem. Eng. Sci. 2013, 98, 298–310. [Google Scholar] [CrossRef]
- Mohammadreza, E. Experimental and Numerical Investigations of Horizontal Pneumatic Conveying. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2014. [Google Scholar]
- Spogis, N. Multiphase Modeling Using EDEM-CFD Coupling for FLUENT. In Proceedings of the 3rd Latin Americal CFD Workshop Applied to the Oil Industry, Rio de Janeiro, Brazil, 18–19 August 2008. [Google Scholar]
- Breuer, M.; Alletto, M. Efficient simulation of particle-laden turbulent flows with high mass loadings using LES. Int. J. Heat Fluid Flow 2012, 35, 2–12. [Google Scholar] [CrossRef]
- Capecelatro, J.; Desjardins, O. An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys. 2013, 238, 1–31. [Google Scholar] [CrossRef]
- Deb, S.; Tafti, D.K. A Novel Two-Grid Formulation for Fluid–Particle Systems Using the Discrete Element Method. Powder Technol. 2013, 246, 601–616. [Google Scholar] [CrossRef]
- Drake, T.G.; Calantoni, J. Discrete particle model for sheet flow sediment transport in the nearshore. J. Geophys. Res. 2001, 106, 19859–19868. [Google Scholar] [CrossRef]
- Wu, C.L.; Ayeni, O.; Berrouk, A.S.; Nandakumar, K. Parallel Algorithms for CFD-DEM Modeling of Dense Particulate Flows. Chem. Eng. Sci. 2014, 118, 221–244. [Google Scholar] [CrossRef]
- OpenCFD Limited. OpenFOAM, v1912; OpenCFD Limited: Bracknell, UK, 2019; Available online: https://www.openfoam.com/news/main-news/openfoam-v1906 (accessed on 4 September 2022).
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. 2012, 12, 140. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. SediFoam: A General-Purpose, Open-Source CFD-DEM Solver for Particle-Laden Flow with Emphasis on Sediment Transport. Comput. Geosci. 2016, 89, 207–219. [Google Scholar] [CrossRef] [Green Version]
- Bing, W.; Hui Qiang, Z.; Xi Lin, W. Large-Eddy Simulation of Particle-Laden Turbulent Flows over a Backward-Facing Step Considering Two-Phase Two-Way Coupling. Adv. Mech. Eng. 2013, 5, 325101. [Google Scholar] [CrossRef] [Green Version]
- Kasper, R.; Turnow, J.; Kornev, N. Numerical modeling and simulation of particulate fouling of structured heat transfer surfaces using a multiphase Euler-Lagrange approach. Int. J. Heat Mass Transf. 2017, 115, 932–945. [Google Scholar] [CrossRef]
- Wang, B.; Wei, W.E.; Zhang, H. A study on correlation moments of two-phase fluctuating velocity using direct numerical simulation. Int. J. Mod. Phys. C 2013, 24, 1350068. [Google Scholar] [CrossRef]
- Yu, K.F.; Lau, K.S.; Chan, C.K. Large eddy simulation of particle-laden turbulent flow over a backward-facing step. Commun. Nonlinear Sci. Numer. Simul. 2004, 9, 251–262. [Google Scholar] [CrossRef]
- Yu, K.F.; Lau, K.S.; Chan, C.K. Numerical simulation of gas-particle flow in a single-side backward-facing step flow. J. Comput. Appl. Math. 2004, 163, 319–331. [Google Scholar] [CrossRef] [Green Version]
- Yu, K.F.; Lee, E.W. Evaluation and modification of gas-particle covariance models by Large Eddy Simulation of a particle-laden turbulent flows over a backward-facing step. Int. J. Heat Mass Transf. 2009, 52, 5652–5656. [Google Scholar] [CrossRef]
- Armenio, V.; Fiorotto, V. The importance of the forces acting on particles in turbulent flows. Phys. Fluids 2001, 13, 2437–2440. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; Printing (with Corrections); DCW Industries: La Cãnada, CA, USA, 1998. [Google Scholar]
- Uijttewaal, W.S.J.; Oliemans, R.V.A. Particle dispersion and deposition in direct numerical and large eddy simulations of vertical pipe flows. Phys. Fluids 1996, 8, 2590–2604. [Google Scholar] [CrossRef]
- Yeh, F.; Lei, U. On the motion of small particles in a homogeneous isotropic turbulent flow. Phys. Fluids A Fluid Dyn. 1991, 3, 2571–2586. [Google Scholar] [CrossRef]
- Minier, J.P.; Chibbaro, S.; Pope, S.B. Guidelines for the Formulation of Lagrangian Stochastic Models for Particle Simulations of Single-Phase and Dispersed Two-Phase Turbulent Flows. Phys. Fluids 2014, 26, 113303. [Google Scholar] [CrossRef] [Green Version]
- Sodja, J. Turbulence models in CFD. Master’s Thesis, University of Ljubljana, Ljubljana, Slovenia, 2007. [Google Scholar]
- Kuczaj, A.K.; Geurts, B.J. Mixing in manipulated turbulence. J. Turbul. 2006, 7, N67. [Google Scholar] [CrossRef] [Green Version]
- Simonin, O.; Deutsch, E.; Minier, J.P. Eulerian prediction of the fluid/particle correlated motion in turbulent two-phase flows. Appl. Sci. Res. 1993, 51, 275–283. [Google Scholar] [CrossRef]
- Benra, F.K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A Comparison of One-Way and Two-Way Coupling Methods for Numerical Analysis of Fluid-Structure Interactions. J. Appl. Math. 2011, 2011, 853560. [Google Scholar] [CrossRef]
- Chen, S.F.; Lei, H.; Wang, M.; Yang, B.; Dai, L.J.; Zhao, Y. Two-way coupling calculation for multiphase flow and decarburization during RH refining. Vacuum 2019, 167, 255–262. [Google Scholar] [CrossRef]
- Kitagawa, A.; Murai, Y.; Yamamoto, F. Two-way coupling of Eulerian–Lagrangian model for dispersed multiphase flows using filtering functions. Int. J. Multiph. Flow 2001, 27, 2129–2153. [Google Scholar] [CrossRef]
- Ruetsch, G.R.; Meiburg, E. Two-way coupling in shear layers with dilute bubble concentrations. Phys. Fluids 1994, 6, 2656–2670. [Google Scholar] [CrossRef] [Green Version]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 394, 97–117. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef] [Green Version]
- Gimenez, J.M.; Idelsohn, S.R.; Oñate, E.; Löhner, R. A Multiscale Approach for the Numerical Simulation of Turbulent Flows with Droplets. Arch. Comput. Methods Eng. State Art Rev. 2021, 28, 4185–4204. [Google Scholar] [CrossRef]
- Hardalupas, Y.; Taylor, A.M.K.P.; Whitelaw, J.H. Particle Dispersion in a Vertical Round Sudden-Expansion Flow. Philos. Trans. Phys. Sci. Eng. 1992, 341, 411–442. [Google Scholar]
- Dehbi, A. Stochastic Models for Turbulent Particle Dispersion in General Inhomogeneous Flows; Paul Scherrer Institut: Villigen PSI, Switzerland, 2008. [Google Scholar]
- Pope, S.B. Turbulent Flows. Meas. Sci. Technol. 2001, 12, 2020–2021. [Google Scholar] [CrossRef]
- Peirano, E.; Chibbaro, S.; Pozorski, J.; Minier, J.P. Mean-field/PDF numerical approach for polydispersed turbulent two-phase flows. Prog. Energy Combust. Sci. 2006, 32, 315–371. [Google Scholar] [CrossRef] [Green Version]
- Durbin, P.A. A Reynolds stress model for near-wall turbulence. J. Fluid Mech. 1993, 249, 465. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B.E. A Reynolds stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 1972, 52, 609–638. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Kasper, R.; Turnow, J.; Kornev, N. Multiphase Eulerian–Lagrangian LES of particulate fouling on structured heat transfer surfaces. Int. J. Heat Fluid Flow 2019, 79, 108462. [Google Scholar] [CrossRef]








| Experimental Setup | Our Numerical Setup | |
|---|---|---|
| Geometry | Channel half-height, h = 20 mm | Channel half-height, h = 20 mm |
| Channel span, Lu = 457 mm | Channel span, Lu = 457 mm | |
| Step height, H = 26.7 mm | Expansion channel length, Ld = 935 mm | |
| Expansion ratio (H + 2h/2h) = 5:3 | Step height, H = 26.7 mm | |
| Aspect ratio (B/H) = 17:1 | Width (B) = 114.25 mm | |
| Continuum phase (air) | Centerline velocity, U0 = 10.5 m/s Friction velocity, uτ = 0.5 m/s Viscous length scale = 31 µm Dissipation, ϵ (centerline estimated) = 4.3 m2/s3 Kolmogorov length scale, η (Centerline estimated) = 170 µm Large eddy time scale, τf = 5H/U0 = 12.7 ms | Density () = 1.225 kg/m3 Kinematic viscosity (υ) = 1.5 × 10−5 m2/s Centerline velocity (U0) at Inlet = (10.5 0 0) m/s Average velocity (Uavg) at inlet = (9.39 0 0) m/s |
| Discrete phase (copper particle) | Nominal diameter, = 70 µm Material = copper Number mean diameter = 68.2 µm Standard deviation of diameter = 10.9 µm Density, = 8800 kg/m3 Mass flow rate of particle (Mass loading), = 10% Stokes mean particle time constant,= 130 ms Modified mean particle time constant,= 88 ms Particle Reynolds number, = 5.5 | Particle size distribution (PSD): Normal distribution with expected value of 68.2 µm and standard deviation of 10.9 µm Density, = 8800 kg/m3 Mass flow rate of particle (mass loading), = 10% |
| Description | RANS-DEM | LES-DEM |
|---|---|---|
| Solution domain | 3-Dimension | 3-Dimension |
| Turbulence model | kOmegaSST | dynamicKEqn with cubeRootVolume delta function |
| Dispersion model | StochasticDispersionRAS | - |
| Mesh resolution | 1,105,280 hexahedra cells | 3,533,376 hexahedra cells |
| y+ | - | ~3 |
| Resolved TKE | - | 80–90% |
| boundary condition at inlet (air) | mappedPatch (Mapped from 400 mm downstream of inlet) | mappedPatch (Mapped from 400 mm downstream of inlet) |
| Front and back boundary treatment | Cyclic | Cyclic |
| Wall treatment | Wallfunctions | Resolved |
| Particle injection velocity at inlet (particle boundary condition) | (10.5, 0, 0) m/s (0, 0, 0) m/s Varying as per fluid velocity distribution | (10.5, 0, 0) m/s (0, 0, 0) m/s Varying as per fluid velocity distribution |
| Mass loading of particles | 10% | 10% |
| Coupling regime | One-way and two-way | Two-way |
| Simulation duration | 1 s | 3 s |
| Simulation | Total CPU Computational Time (in Seconds) | |
|---|---|---|
| RANS-DEM (Run Time = 1 s) | LES-DEM (Run Time = 3 s) | |
| Single-phase | 3925 | 29,682 |
| Two-phase (one-way coupled) | 12,693 | - |
| Two-phase (two-way coupled) | 13,385 | 109,921 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaiswal, A.; Bui, M.D.; Rutschmann, P. Evaluation of RANS-DEM and LES-DEM Methods in OpenFOAM for Simulation of Particle-Laden Turbulent Flows. Fluids 2022, 7, 337. https://doi.org/10.3390/fluids7100337
Jaiswal A, Bui MD, Rutschmann P. Evaluation of RANS-DEM and LES-DEM Methods in OpenFOAM for Simulation of Particle-Laden Turbulent Flows. Fluids. 2022; 7(10):337. https://doi.org/10.3390/fluids7100337
Chicago/Turabian StyleJaiswal, Atul, Minh Duc Bui, and Peter Rutschmann. 2022. "Evaluation of RANS-DEM and LES-DEM Methods in OpenFOAM for Simulation of Particle-Laden Turbulent Flows" Fluids 7, no. 10: 337. https://doi.org/10.3390/fluids7100337
APA StyleJaiswal, A., Bui, M. D., & Rutschmann, P. (2022). Evaluation of RANS-DEM and LES-DEM Methods in OpenFOAM for Simulation of Particle-Laden Turbulent Flows. Fluids, 7(10), 337. https://doi.org/10.3390/fluids7100337








