Experimental Solid–Liquid Mass Transfer around Free-Moving Particles in an Air-Lift Membrane Bioreactor with Optical Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Properties of QQ Media
2.2. Mass Transfer Experiments
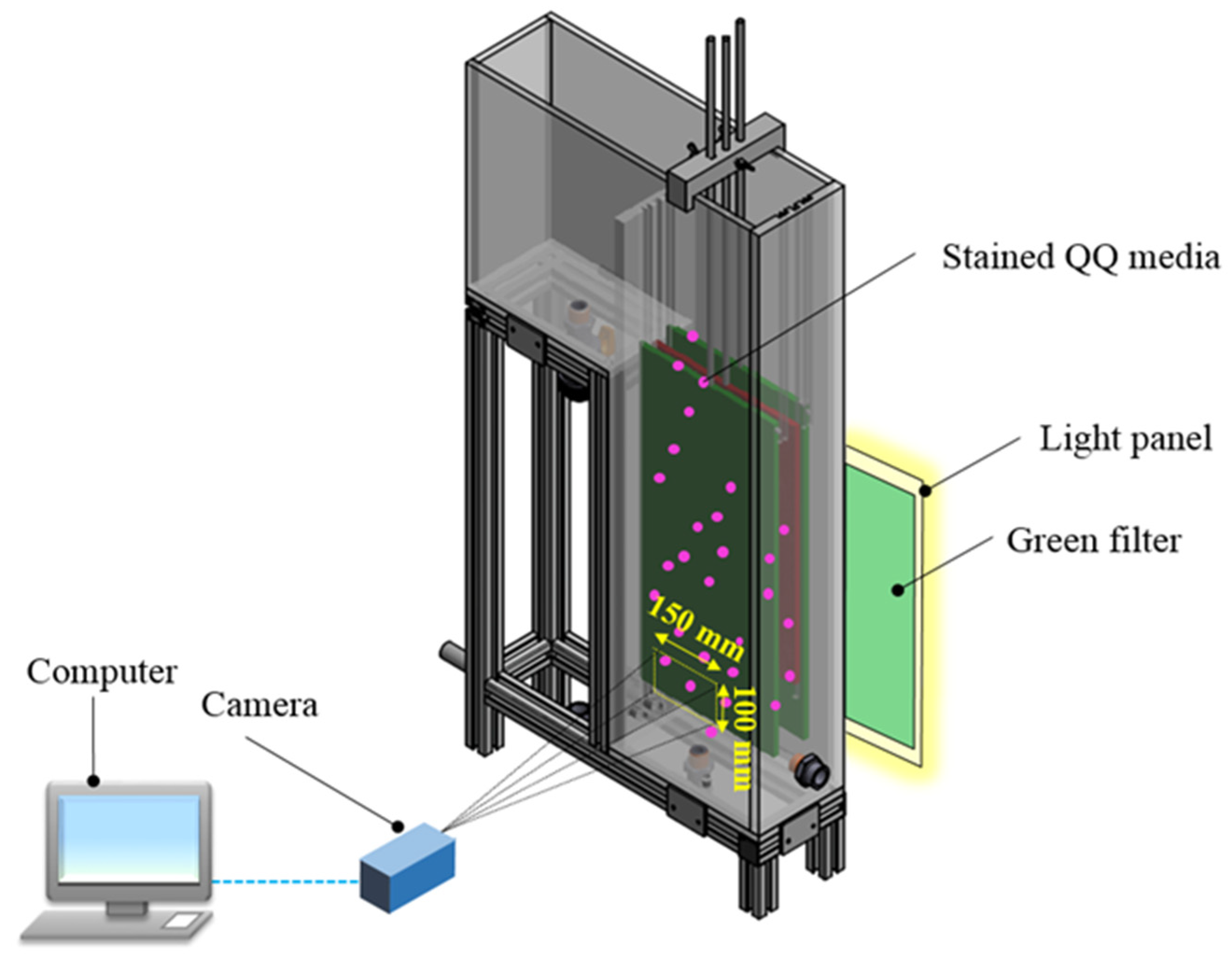
2.2.1. Mass Transfer from the Liquid to the Media
2.2.2. Mass Transfer from the Media to the Liquid
3. Liquid–Solid Mass Transfer from the Liquid to the Solid Medium
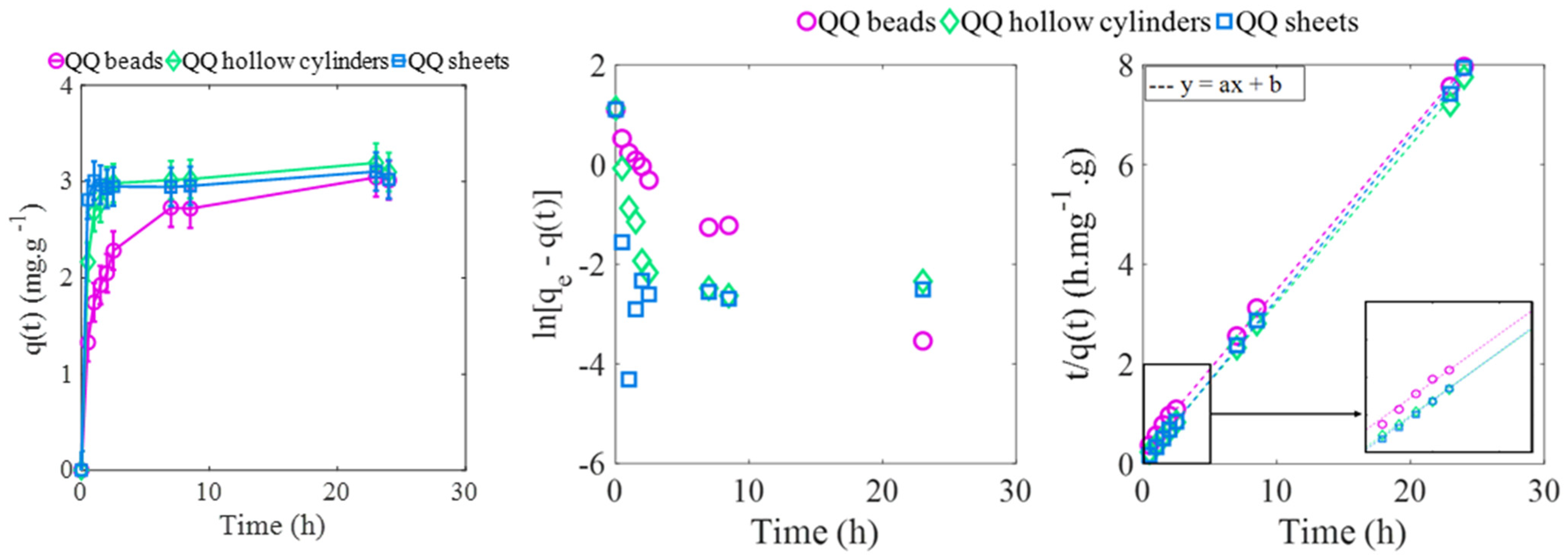
3.1. Analysis of the Adsorption Kinetics
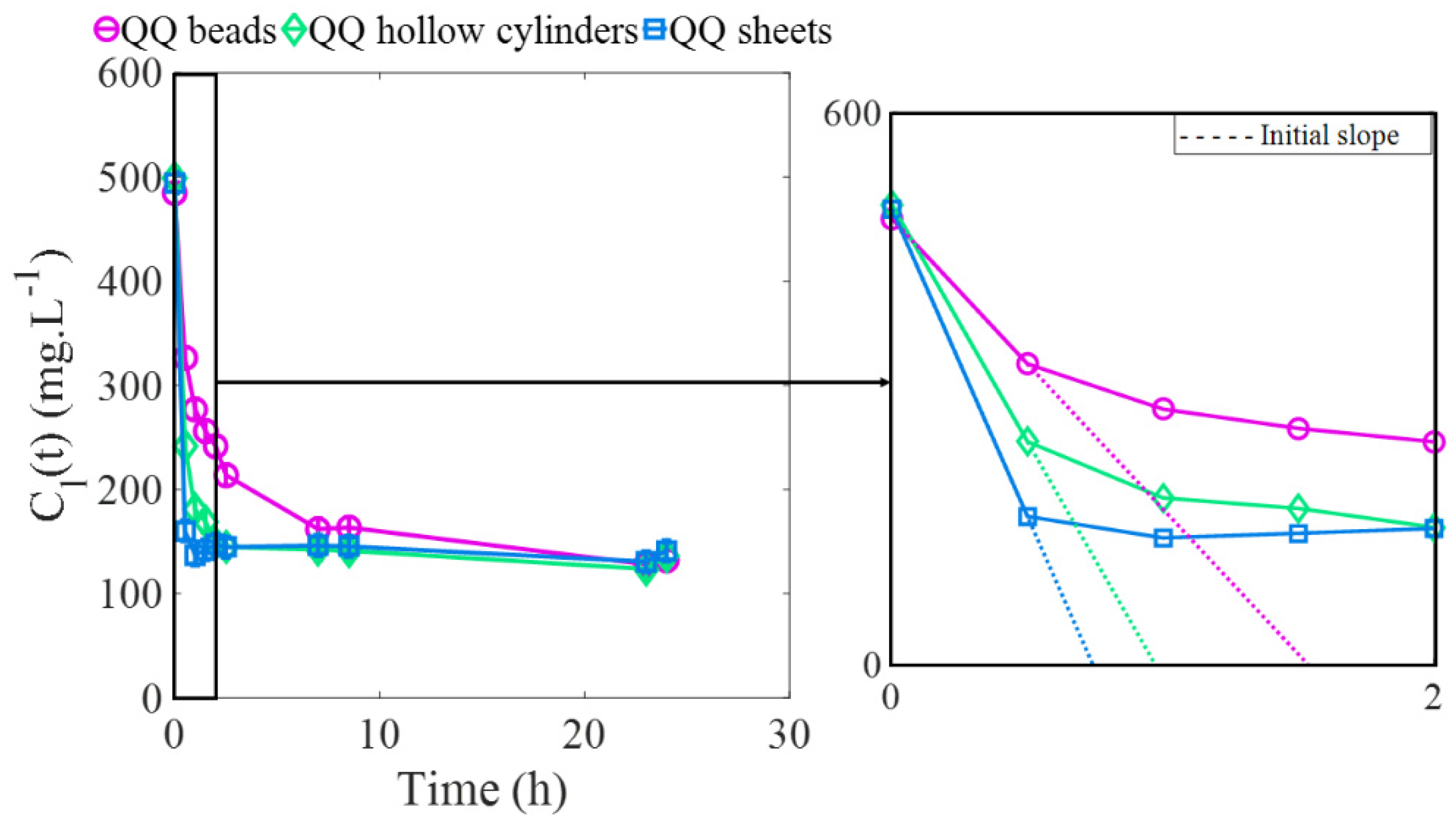
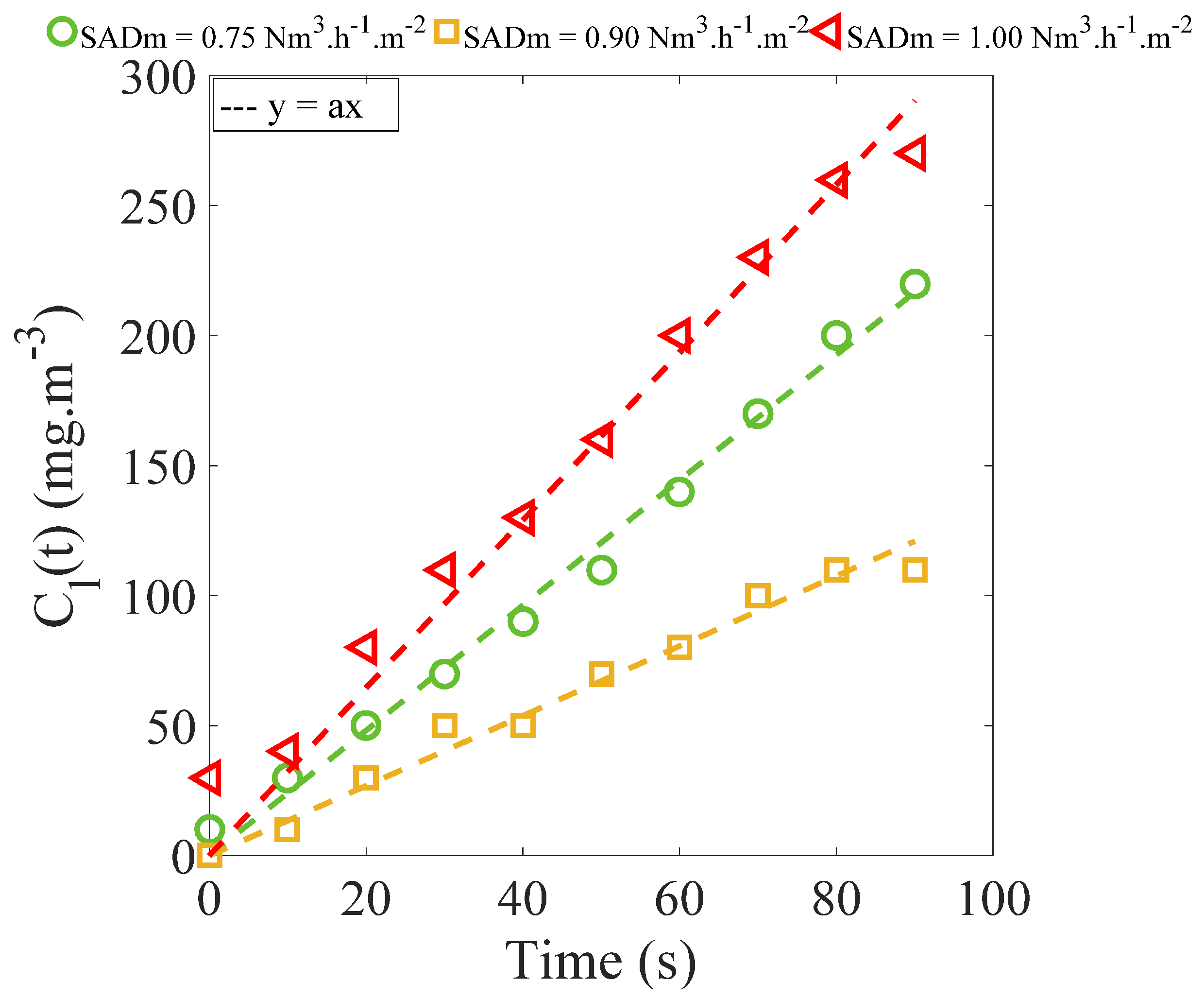
3.2. Analysis of the External Liquid–Solid Mass Transfer Mechanism
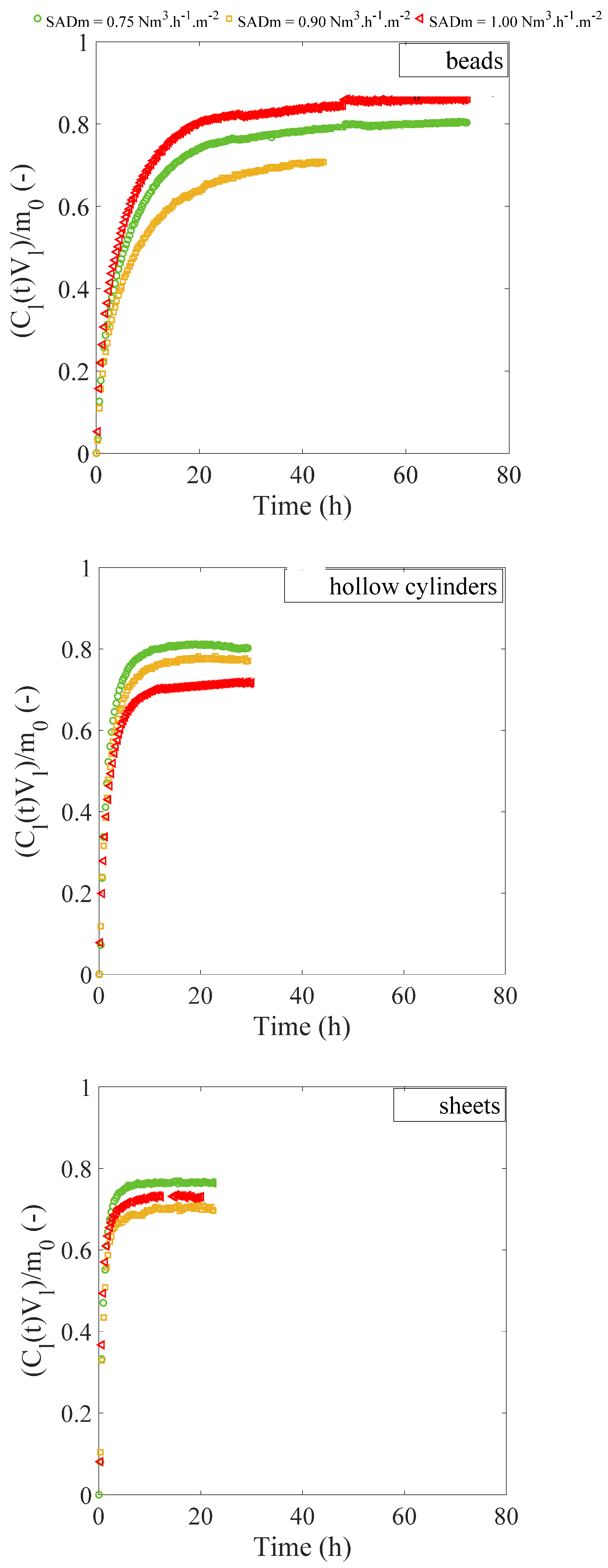
4. Solid–Liquid Mass Transfer from the Solid Media to the Liquid
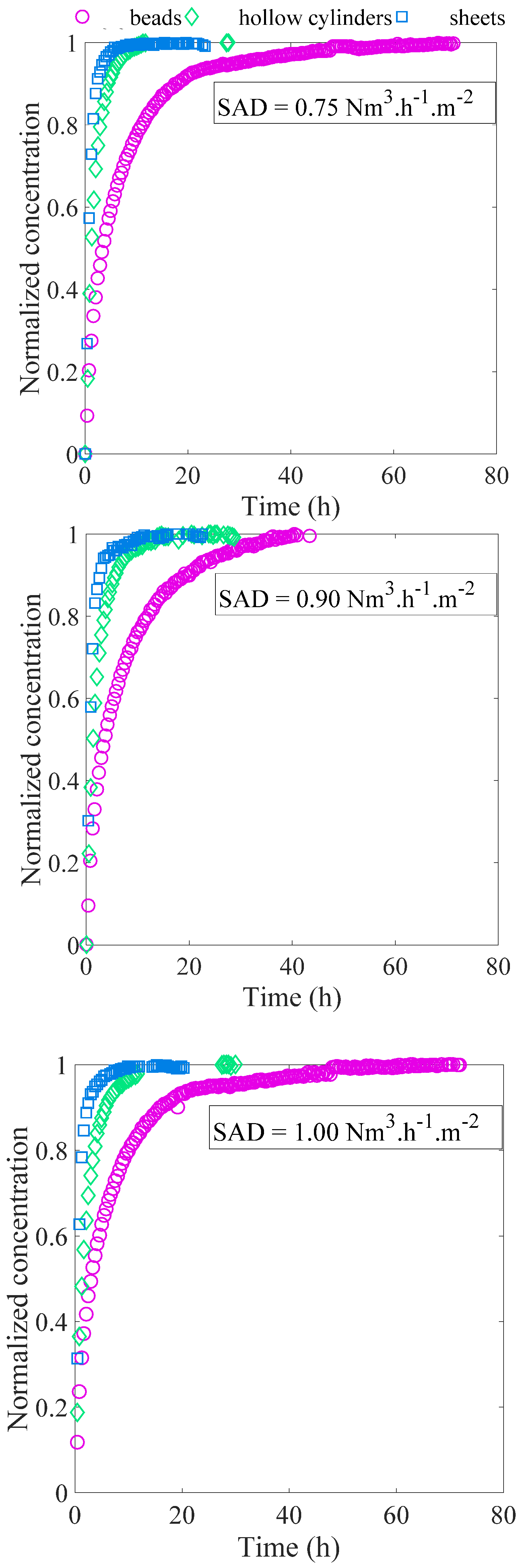
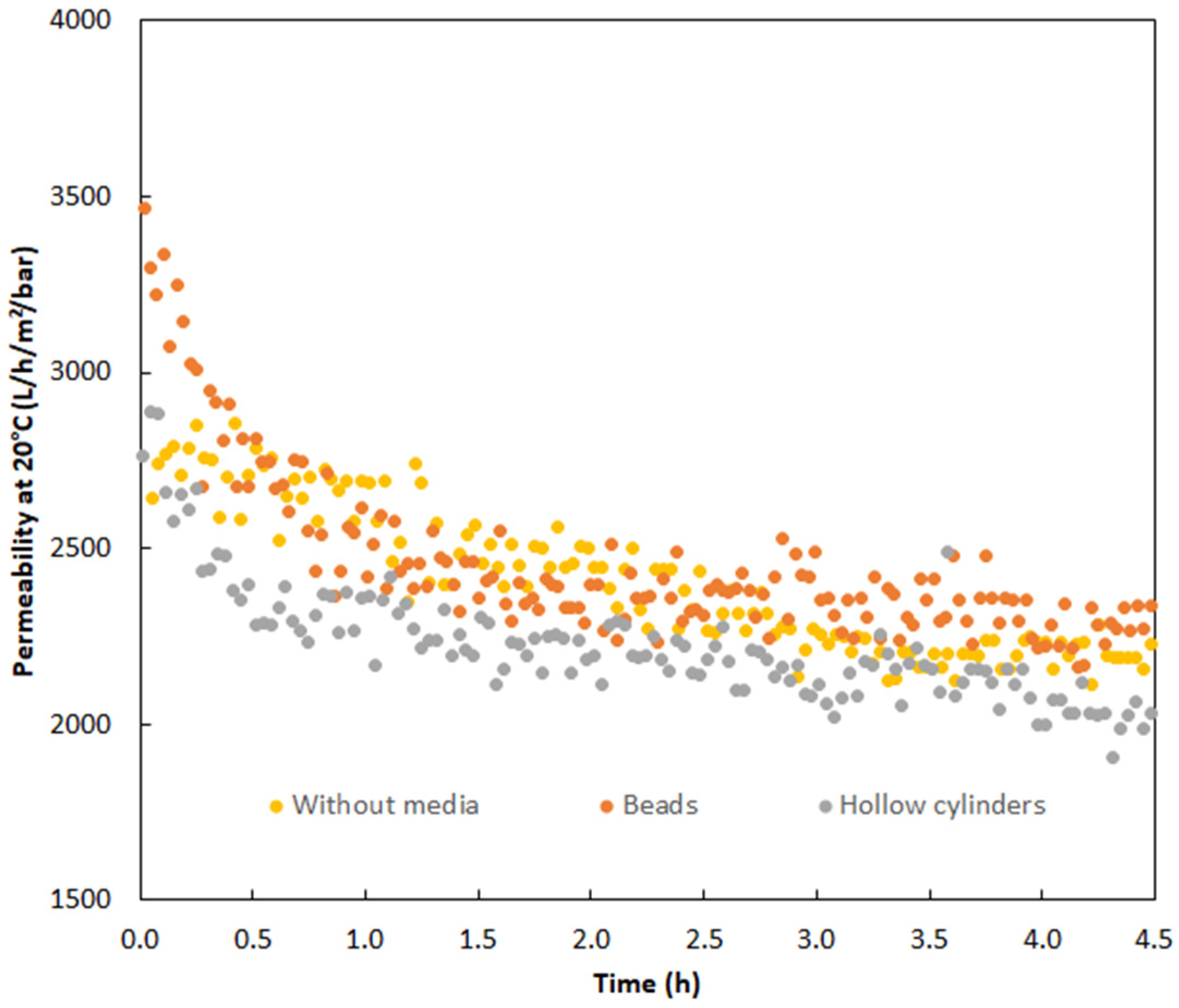
4.1. Effect of Hydrodynamics on Solid–Liquid Mass Transfer
4.2. Effect of Solid Particle Shapes on the Mass Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gander, M.; Jefferson, B.; Judd, S. Aerobic MBRs for Domestic Wastewater Treatment: A Review with Cost Considerations. Sep. Purif. Technol. 2000, 18, 119–130. [Google Scholar] [CrossRef]
- Melin, T.; Jefferson, B.; Bixio, D.; Thoeye, C.; Wilde, W.D.; Koning, J.D.; van der Graaf, J.; Wintgens, T. Membrane Bioreactor Technology for Wastewater Treatment and Reuse. Desalination 2006, 187, 271–282. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, S.; Shen, Y. Particle-Scale Modelling of Rapid Granular Filtration in a Dual-Media Filter. Sep. Purif. Technol. 2022, 302, 122076. [Google Scholar] [CrossRef]
- Liu, R.; Huang, X.; Wang, C.; Chen, L.; Qian, Y. Study on Hydraulic Characteristics in a Submerged Membrane Bioreactor Process. Process Biochem. 2000, 36, 249–254. [Google Scholar] [CrossRef]
- Liu, R.; Huang, X.; Sun, Y.F.; Qian, Y. Hydrodynamic Effect on Sludge Accumulation over Membrane Surfaces in a Submerged Membrane Bioreactor. Process Biochem. 2003, 39, 157–163. [Google Scholar] [CrossRef]
- Prieske, H.; Drews, A.; Kraume, M. Prediction of the Circulation Velocity in a Membrane Bioreactor. Desalination 2008, 231, 219–226. [Google Scholar] [CrossRef]
- Yan, X.; Wu, Q.; Sun, J.; Liang, P.; Zhang, X.; Xiao, K.; Huang, X. Hydrodynamic Optimization of Membrane Bioreactor by Horizontal Geometry Modification Using Computational Fluid Dynamics. Bioresour. Technol. 2016, 200, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Xiao, K.; Liang, S.; Lei, T.; Liang, P.; Xue, T.; Yu, K.; Guan, J.; Huang, X. Hydraulic Optimization of Membrane Bioreactor via Baffle Modification Using Computational Fluid Dynamics. Bioresour. Technol. 2015, 175, 633–637. [Google Scholar] [CrossRef]
- Wu, B.; Zamani, F.; Lim, W.; Liao, D.; Wang, Y.; Liu, Y.; Chew, J.W.; Fane, A.G. Effect of Mechanical Scouring by Granular Activated Carbon (GAC) on Membrane Fouling Mitigation. Desalination 2017, 403, 80–87. [Google Scholar] [CrossRef]
- Aslam, M.; Charfi, A.; Lesage, G.; Heran, M.; Kim, J. Membrane Bioreactors for Wastewater Treatment: A Review of Mechanical Cleaning by Scouring Agents to Control Membrane Fouling. Chem. Eng. J. 2017, 307, 897–913. [Google Scholar] [CrossRef]
- Kim, S.-R.; Lee, K.-B.; Kim, J.-E.; Won, Y.-J.; Yeon, K.-M.; Lee, C.-H.; Lim, D.-J. Macroencapsulation of Quorum Quenching Bacteria by Polymeric Membrane Layer and Its Application to MBR for Biofouling Control. J. Membr. Sci. 2015, 473, 109–117. [Google Scholar] [CrossRef]
- Kim, S.-R.; Oh, H.-S.; Jo, S.-J.; Yeon, K.-M.; Lee, C.-H.; Lim, D.-J.; Lee, C.-H.; Lee, J.-K. Biofouling Control with Bead-Entrapped Quorum Quenching Bacteria in Membrane Bioreactors: Physical and Biological Effects. Environ. Sci. Technol. 2013, 47, 836–842. [Google Scholar] [CrossRef] [PubMed]
- Köse-Mutlu, B.; Ergön-Can, T.; Koyuncu, İ.; Lee, C.-H. Quorum Quenching MBR Operations for Biofouling Control under Different Operation Conditions and Using Different Immobilization Media. Desalination Water Treat. 2016, 57, 17696–17706. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.-K.; Kwon, H.; Lee, S.H.; Lee, K.; Nahm, C.H.; Jo, S.J.; Oh, H.-S.; Park, P.-K.; Choo, K.-H.; et al. Crossing the Border between Laboratory and Field: Bacterial Quorum Quenching for Anti-Biofouling Strategy in an MBR. Environ. Sci. Technol. 2016, 50, 1788–1795. [Google Scholar] [CrossRef]
- Maqbool, T.; Khan, S.J.; Waheed, H.; Lee, C.-H.; Hashmi, I.; Iqbal, H. Membrane Biofouling Retardation and Improved Sludge Characteristics Using Quorum Quenching Bacteria in Submerged Membrane Bioreactor. J. Membr. Sci. 2015, 483, 75–83. [Google Scholar] [CrossRef]
- Yu, H.; Lee, K.; Zhang, X.; Choo, K.-H. In Situ versus Pre-Quorum Quenching of Microbial Signaling for Enhanced Biofouling Control in Membrane Bioreactors. J. Membr. Sci. 2019, 592, 117387. [Google Scholar] [CrossRef]
- Li, Y.-S.; Tian, T.; Li, B.-B.; Yu, H.-Q. Longer Persistence of Quorum Quenching Bacteria over Quorum Sensing Bacteria in Aerobic Granules. Water Res. 2020, 179, 115904. [Google Scholar] [CrossRef]
- Oh, H.-S.; Yeon, K.-M.; Yang, C.-S.; Kim, S.-R.; Lee, C.-H.; Park, S.Y.; Han, J.Y.; Lee, J.-K. Control of Membrane Biofouling in MBR for Wastewater Treatment by Quorum Quenching Bacteria Encapsulated in Microporous Membrane. Environ. Sci. Technol. 2012, 46, 4877–4884. [Google Scholar] [CrossRef]
- Siddiqui, M.F.; Rzechowicz, M.; Harvey, W.; Zularisam, A.W.; Anthony, G.F. Quorum Sensing Based Membrane Biofouling Control for Water Treatment: A Review. J. Water Process Eng. 2015, 7, 112–122. [Google Scholar] [CrossRef]
- Siddiqui, M.F.; Sakinah, M.; Singh, L.; Zularisam, A.W. Targeting N-Acyl-Homoserine-Lactones to Mitigate Membrane Biofouling Based on Quorum Sensing Using a Biofouling Reducer. J. Biotechnol. 2012, 161, 190–197. [Google Scholar] [CrossRef]
- Bouayed, N.; Dietrich, N.; Lafforgue, C.; Lee, C.-H.; Guigui, C. Process-Oriented Review of Bacterial Quorum Quenching for Membrane Biofouling Mitigation in Membrane Bioreactors (MBRs). Membranes 2016, 6, 52. [Google Scholar] [CrossRef] [PubMed]
- Kose-Mutlu, B.; Ergon-Can, T.; Koyuncu, I.; Lee, C.H. Quorum Quenching for Effective Control of Biofouling in Membrane Bioreactor: A Comprehensive Review of Approaches, Applications, and Challenges. Environ. Eng. Res. 2019, 24, 543–558. [Google Scholar] [CrossRef]
- Yu, H.; Lee, K.; Zhang, X.; Choo, K.-H. Core-Shell Structured Quorum Quenching Beads for More Sustainable Anti-Biofouling in Membrane Bioreactors. Water Res. 2019, 150, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, T.; Weerasekara, N.A.; Lee, K.; Choo, K.-H. Impact of Encapsulated Quorum-Quenching Bacterial Dose and Feed Type on Biofouling Control in Membrane Bioreactors. J. Environ. Eng. 2020, 146, 04019109. [Google Scholar] [CrossRef]
- Bouayed, N.; Cavalier, A.; Lafforgue, C.; Dietrich, N.; Lee, C.-H.; Guigui, C. Hydrodynamics Characterization of the Impact of Free-Moving Particles in an Air-Lift Membrane Bioreactor. Ind. Eng. Chem. Res. 2020, 59, 7943–7954. [Google Scholar] [CrossRef]
- Choo, K.-H.; Park, P.-K.; Oh, H.-S. 12—Quorum Sensing and Quorum Quenching in Membrane Bioreactors. In Current Developments in Biotechnology and Bioengineering; Ng, H.Y., Ng, T.C.A., Ngo, H.H., Mannina, G., Pandey, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 245–274. ISBN 978-0-12-819809-4. [Google Scholar]
- Liu, J.; Eng, C.Y.; Ho, J.S.; Chong, T.H.; Wang, L.; Zhang, P.; Zhou, Y. Quorum Quenching in Anaerobic Membrane Bioreactor for Fouling Control. Water Res. 2019, 156, 159–167. [Google Scholar] [CrossRef]
- Jiang, B.; Zeng, Q.; Hou, Y.; Liu, J.; Xu, J.; Li, H.; Du, C.; Shi, S.; Ma, F. Quorum Quenching Bacteria Bioaugmented GO/PPy Modified Membrane in EMBR for Membrane Antifouling. Sci. Total Environ. 2020, 718, 137412. [Google Scholar] [CrossRef]
- Dietrich, N.; Jimenez, M.; Xie, X.; Hébrard, G. Optical Techniques to Evaluate Hydrodynamics and Mass Transfer in Biorectors. 2015. Available online: https://www.sciencedirect.com/science/article/pii/S0017931019332399 (accessed on 18 October 2022).
- Dietrich, N.; Loubière, K.; Jimenez, M.; Hébrard, G.; Gourdon, C. A New Direct Technique for Visualizing and Measuring Gas–Liquid Mass Transfer around Bubbles Moving in a Straight Millimetric Square Channel. Chem. Eng. Sci. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Xu, F.; Hébrard, G.; Dietrich, N. Comparison of Three Different Techniques for Gas-Liquid Mass Transfer Visualization. Int. J. Heat Mass Transf. 2020, 150, 119261. [Google Scholar] [CrossRef]
- Oh, H.-S.; Kim, S.-R.; Cheong, W.-S.; Lee, C.-H.; Lee, J.-K. Biofouling Inhibition in MBR by Rhodococcus Sp. BH4 Isolated from Real MBR Plant. Appl. Microbiol. Biotechnol. 2013, 97, 10223–10231. [Google Scholar] [CrossRef]
- Wang, J.; Quan, C.; Wang, X.; Zhao, P.; Fan, S. Extraction, Purification and Identification of Bacterial Signal Molecules Based on N-Acyl Homoserine Lactones. Microb. Biotechnol. 2011, 4, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Yuh-Shan, H. Citation Review of Lagergren Kinetic Rate Equation on Adsorption Reactions. Scientometrics 2004, 59, 171–177. [Google Scholar] [CrossRef]
- Wu, F.-C.; Tseng, R.-L.; Huang, S.-C.; Juang, R.-S. Characteristics of Pseudo-Second-Order Kinetic Model for Liquid-Phase Adsorption: A Mini-Review. Chem. Eng. J. 2009, 151, 1–9. [Google Scholar] [CrossRef]
- Furusawa, T.; Smith, J.M. Fluid-Particle and Intraparticle Mass Transport Rates in Slurries. Ind. Eng. Chem. Fundam. 1973, 12, 197–203. [Google Scholar] [CrossRef]
- Dotto, G.L.; Moura, J.M.; Cadaval, T.R.S.; Pinto, L.A.A. Application of Chitosan Films for the Removal of Food Dyes from Aqueous Solutions by Adsorption. Chem. Eng. J. 2013, 214, 8–16. [Google Scholar] [CrossRef]
- Dotto, G.L.; Buriol, C.; Pinto, L.A.A. Diffusional Mass Transfer Model for the Adsorption of Food Dyes on Chitosan Films. Chem. Eng. Res. Des. 2014, 92, 2324–2332. [Google Scholar] [CrossRef]
- Sänger, P.; Deckwer, W.-D. Liquid—Solid Mass Transfer in Aerated Suspensions. Chem. Eng. J. 1981, 22, 179–186. [Google Scholar] [CrossRef]
- Noyes, A.A.; Whitney, W.R. The rate of solution of solid substances in their own solutions. J. Am. Chem. Soc. 1897, 19, 930–934. [Google Scholar] [CrossRef]

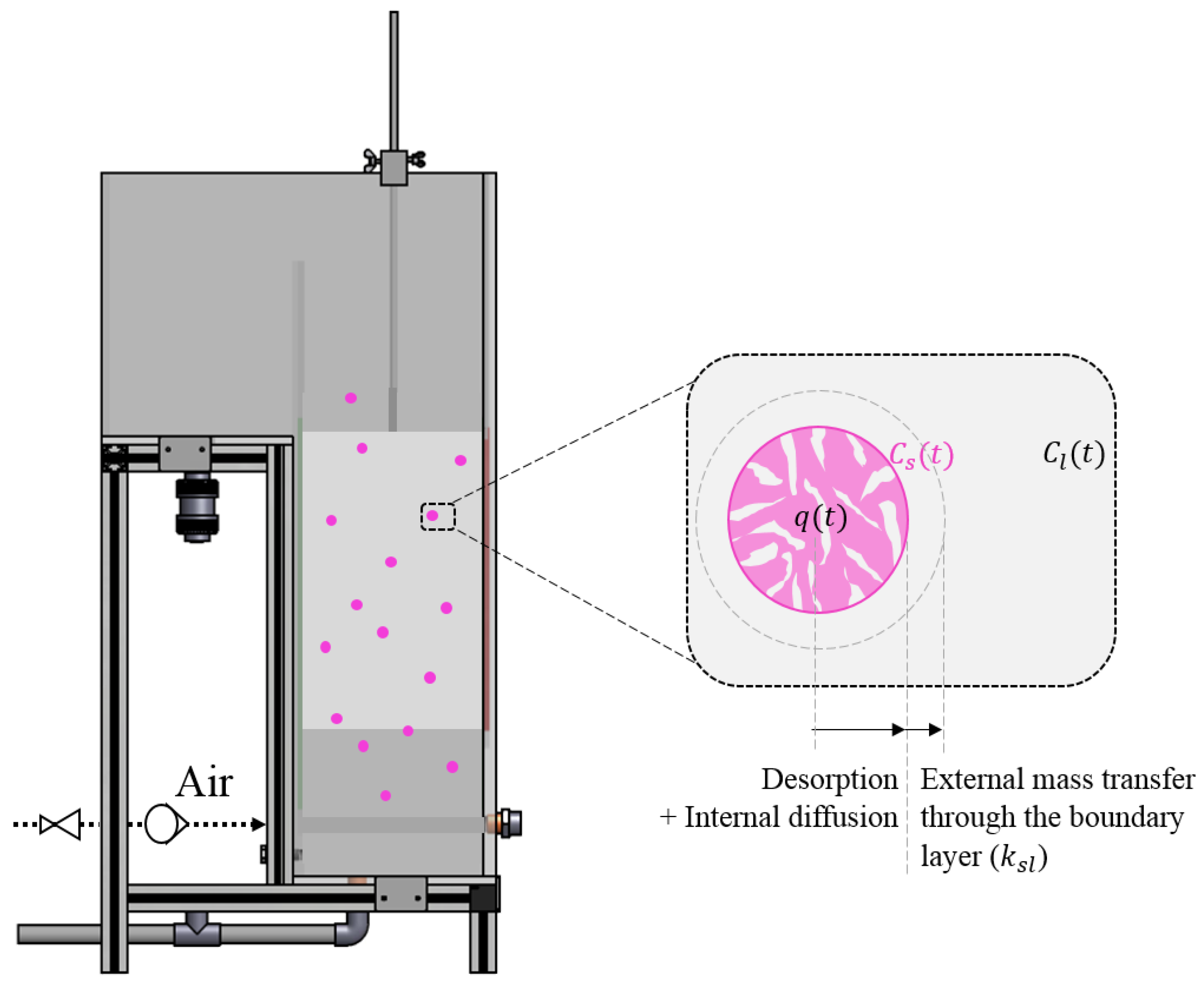

| Solid Medium | Beads | Hollow Cylinders | Sheets |
|---|---|---|---|
| Dimensions (mm) | Diameter: 3.5 | Inner diameter: 1.7 Outer diameter: 3.5 Length: 27 | Length: 20 Width: 10 Thickness: 0.5 |
| Volume of a particle (mm3) | 22.5 | 198.5 | 100 |
| Surface area of a particle (mm2) | 8.5 | 455.8 | 400 |
| Chemical formula/Molecular structure | C20H4Cl4I4O5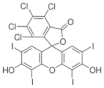 |
| Molecular weight (g.mol−1) | 973.67 |
| Appearance | Pink powder |
| Purity | ≥95% |
| Concentration of Dye Lactone Solution (g·L−1) | 0.0002 | 0.0006 | 0.0012 | 0.0023 | 0.0044 |
|---|---|---|---|---|---|
| Spectrophotometer | |||||
| Absorbance at 500 nm (-) | 0.0037 | 0.0088 | 0.0188 | 0.0346 | 0.0673 |
| Optical path length (cm) | 1.0 | ||||
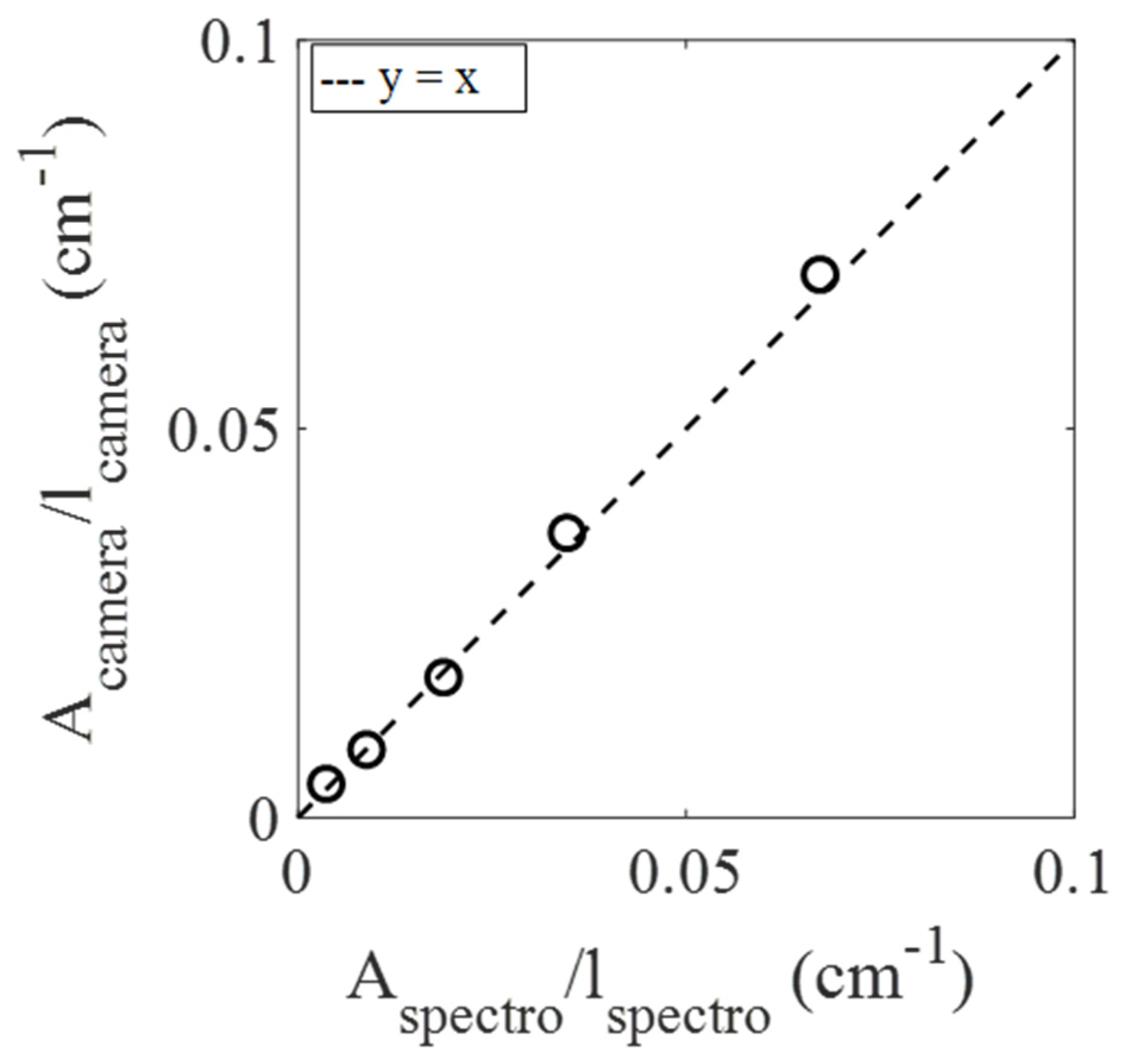
| (cm−1) | 0.0037 | 0.0088 | 0.0188 | 0.0346 | 0.0673 |
| (L·g−1·cm−1) | 15.136 | ||||
| Camera | |||||
| Absorbance at 500 nm (-) | 0.0490 | 0.1000 | 0.2050 | 0.4180 | 0.7960 |
| Optical path length (cm) | 11.6 | ||||
| (cm−1) | 0.0042 | 0.0086 | 0.0177 | 0.0360 | 0.0686 |
| (L·g−1·cm−1) | 15.425 | ||||
| Beads | Hollow Cylinders | Sheets | |
|---|---|---|---|
| Linear correlation parameters () | |||
| (g·mg−1) | 0.3187 | 0.3157 | 0.3260 |
| (h·mg−1·g) | 0.3015 | 0.0712 | 0.0376 |
| 0.9996 | 0.9995 | 0.9996 | |
| Model parameters | |||
| (calculated) (mg·g−1) | 3.14 | 3.17 | 3.07 |
| (experimental) (mg·g−1) | 3.0 ± 0.2 | 3.1 ± 0.2 | 3.0 ± 0.2 |
| (g·mg−1·h−1) | 0.34 | 1.40 | 2.83 |
| (10−5 g·mg−1·s−1) | 9.36 | 38.89 | 78.51 |
| (10−4 s−1) | 2.94 | 12.33 | 24.10 |
| Beads | Hollow Cylinders | Sheets | |
|---|---|---|---|
| Experiment 1 | |||
| (m2) | 0.100 | 0.135 | 0.234 |
| Cl(t = 0) (mg·L−1) | 484 | 499 | 495 |
| (dCl(t)dt)t = 0 (mg·L−1·h−1) | −316 | −514 | −668 |
| klsSs (10−7 m3·s-−1) | 0.95 | 1.51 | 1.98 |
| kls (10−6 m·s−1) | 0.95 | 1.12 | 0.85 |
| Experiment 2 | |||
| (m2) | 0.086 | 0.115 | 0.200 |
| Cl(t = 0) (mg·L−1) | 424 | 409 | 436 |
| (dCl(t)dt)t = 0 (mg·L−1·h−1) | −320 | −455 | −612 |
| klsSs (10−7 m3·s−1) | 0.94 | 1.39 | 1.75 |
| kls (10−6 m·s−1) | 1.12 | 1.21 | 0.88 |
| Experiment 3 | |||
| Ss (m2) | 0.086 | 0.115 | 0.200 |
| Cl(t = 0) (mg·L−1) | 506 | 492 | 503 |
| (dCl(t)dt)t = 0 (mg·L−1·h−1) | −300 | −456 | −639 |
| klsSs (10−7 m3·s−1) | 1.14 | 1.74 | 2.38 |
| kls (10−6 m·s−1) | 1.30 ± 0.1 | 1.51 ± 0.2 | 1.19 ± 0.1 |
| Average values over the three experiments ± standard deviation | |||
| (10−7 m3·s−1) | 1.0 ± 0.1 | 1.5 ± 0.2 | 2.0 ± 0.2 |
| (10−6 m·s−1) | 1.1 ± 0.2 | 1.3 ± 0.2 | 1.0 ± 0.2 |
| (10−3 m) | 1.75 | 0.45 | 0.25 |
| (10−10 m2·s−1) | 3.92 | ||
| 4.9 ± 0.4 | 1.5 ± 0.1 | 0.6 ± 0.08 | |
| SADm (Nm3·h−1·m−2) | 0.75 | 0.90 | 1.00 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Solid medium | Beads | Hollow cylinders | Sheets | Beads | Hollow cylinders | Sheets | Beads | Hollow cylinders | Sheets |
| Total exchange surface area, (m2) | 0.086 | 0.115 | 0.200 | 0.086 | 0.115 | 0.200 | 0.086 | 0.135 | 0.234 |
| Fluidization rate (%) | 6.2 | 26.2 | 30.1 | 10.9 | 53.2 | 47.8 | 16.1 | 63.3 | 55.9 |
| Fluidized surface area, (m2) | 0.0062 | 0.0354 | 0.0704 | 0.0109 | 0.0718 | 0.1118 | 0.0161 | 0.0845 | 0.1308 |
| Fluidized volume, (10−5 m3) | 0.31 | 1.53 | 1.76 | 0.64 | 3.11 | 2.79 | 0.94 | 3.70 | 3.27 |
| SADm (Nm3·h−1·m−2) | 0.75 | 0.90 | 1.00 |
| Solid–liquid mass transfer parameters for beads | |||
| Total exchange surface area, (m2) | 0.086 | 0.086 | 0.086 |
| Fluidization rate (%) | 6.2 | 10.9 | 16.1 |
| Fluidized surface area, (m2) | 0.062 | 0.0109 | 0.01611 |
| Fluidized volume, (10−5 m3) | 0.31 | 0.64 | 0.94 |
| (10−8 m3·s−1) | 1.00 | 0.62 | 1.52 |
| (considering ) (10−7 m·s−1) | 1.17 ± 0.1 | 0.72 ± 0.06 | 1.78 ± 0.15 |
| (considering ) (10−7 m·s−1) | 18.8 ± 1 | 6.8 ± 0.5 | 11 ± 1 |
| (10−3 m) | 3.50 | ||
| (considering ) (-) | 1.04 | 0.66 | 1.59 |
| (considering ) (-) | 16.80 | 6.08 | 9.86 |
| Solid–liquid mass transfer parameters for hollow cylinders | |||
| Total exchange surface area, (m2) | 0.115 | 0.115 | 0.135 |
| Fluidization rate (%) | 26.2 | 53.2 | 63.3 |
| Fluidized surface area, (m2) | 0.0354 | 0.0718 | 0.0845 |
| Fluidized volume, (10−5 m3) | 1.53 | 3.11 | 3.70 |
| (10−8 m3·s−1) | 2.16 | 1.70 | 1.87 |
| (considering ) (10−7 m·s−1) | 1.88 ± 0.1 | 1.48 ± 0.1 | 1.39 ± 0.1 |
| (considering ) (10−7 m·s−1) | 7.16 ± 0.6 | 2.86 ± 0.3 | 2.20 ± 0.2 |
| (10−3 m) | 0.90 | ||
| (considering ) (-) | 0.43 | 0.35 | 0.32 |
| (considering ) (-) | 1.65 | 0.66 | 0.50 |
| Solid-liquid mass transfer parameters for sheets | |||
| Total exchange surface area, (m2) | 0.200 | 0.200 | 0.234 |
| Fluidization rate (%) | 30.1 | 47.8 | 55.9 |
| Fluidized surface area, (m2) | 0.0704 | 0.01118 | 0.1308 |
| Fluidized volume, (10−5 m3) | 1.76 | 2.79 | 3.27 |
| (10−8 m3·s−1) | 4.03 | 3.23 | 4.58 |
| (considering ) (10−7 m·s−1) | 2.02 ± 0.2 | 1.62 ± 0.1 | 1.95 ± 0.2 |
| (considering ) (10−7 m·s−1) | 6.63 ± 0.5 | 3.37 ± 0.3 | 3.50 ± 0.3 |
| (10−3 m) | 0.50 | ||
| (considering ) (-) | 0.26 | 0.21 | 0.25 |
| (considering ) (-) | 0.85 | 0.43 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouayed, N.; Montaner, M.; Le Men, C.; Teychené, J.; Lafforgue, C.; Dietrich, N.; Lee, C.-H.; Guigui, C. Experimental Solid–Liquid Mass Transfer around Free-Moving Particles in an Air-Lift Membrane Bioreactor with Optical Techniques. Fluids 2022, 7, 338. https://doi.org/10.3390/fluids7100338
Bouayed N, Montaner M, Le Men C, Teychené J, Lafforgue C, Dietrich N, Lee C-H, Guigui C. Experimental Solid–Liquid Mass Transfer around Free-Moving Particles in an Air-Lift Membrane Bioreactor with Optical Techniques. Fluids. 2022; 7(10):338. https://doi.org/10.3390/fluids7100338
Chicago/Turabian StyleBouayed, Naila, Manon Montaner, Claude Le Men, Johanne Teychené, Christine Lafforgue, Nicolas Dietrich, Chung-Hak Lee, and Christelle Guigui. 2022. "Experimental Solid–Liquid Mass Transfer around Free-Moving Particles in an Air-Lift Membrane Bioreactor with Optical Techniques" Fluids 7, no. 10: 338. https://doi.org/10.3390/fluids7100338
APA StyleBouayed, N., Montaner, M., Le Men, C., Teychené, J., Lafforgue, C., Dietrich, N., Lee, C.-H., & Guigui, C. (2022). Experimental Solid–Liquid Mass Transfer around Free-Moving Particles in an Air-Lift Membrane Bioreactor with Optical Techniques. Fluids, 7(10), 338. https://doi.org/10.3390/fluids7100338






