Crater Depth after the Impact of Multiple Drops into Deep Pools
Abstract
:1. Introduction
- A single fluid (water) at a fixed temperature was selected.
- Repeated simulations about the impact of four to 30 drops were performed, with the drops having the same diameter and impact velocity, but random positions in the domain, including the vertical distance from the pool, so that they hit the liquid–gas interface at slightly different time instants.
2. Materials and Methods
2.1. Experimental Setup
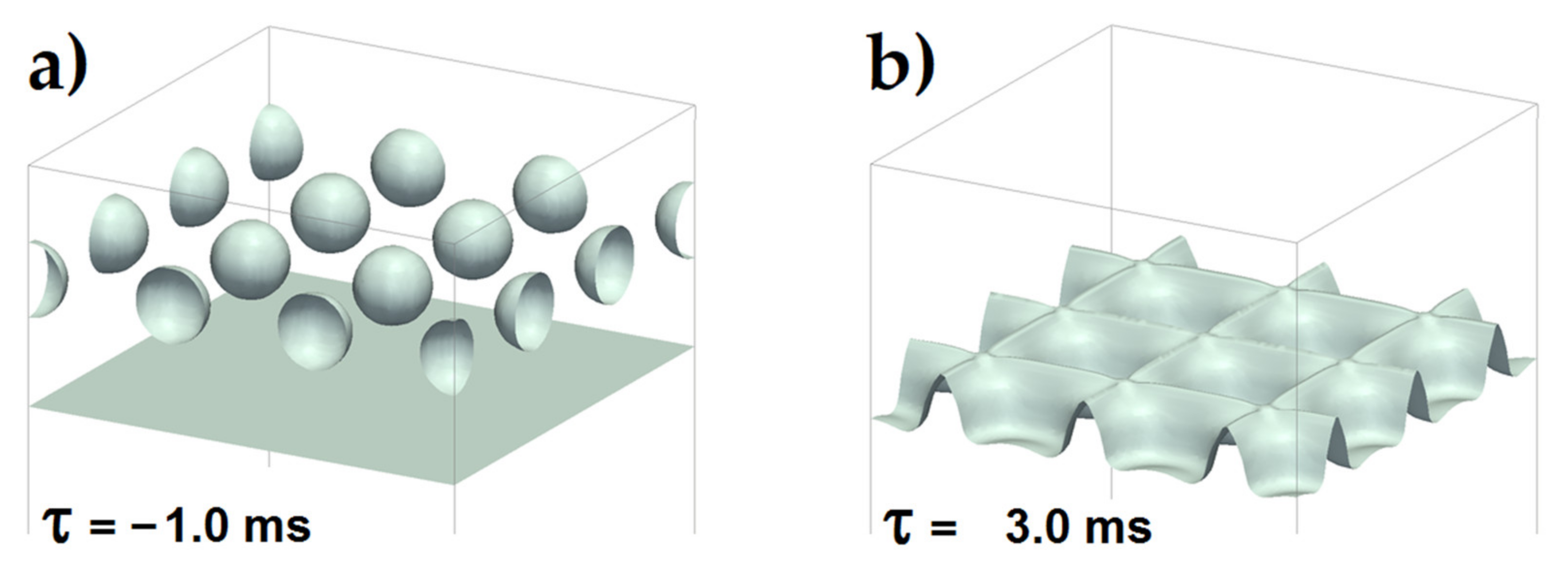
2.2. Numerical Simulations
- The bottom boundary was set as a wall, i.e., fixed value equal to 0 for the velocity, zero gradient for the pressure, volume fraction equal to 1 (water always present).
- The top boundary was set as an open boundary, i.e., zero gradient for the velocity, fixed value equal to 0 for the pressure, volume fraction equal to 0 (air always present).
- The side boundaries were set as symmetry boundaries for all the variables, to reduce the computational effort for single and double drop impacts, and to model the control volume as a “tile” of a larger physical domain for multiple drop impacts.
3. Results and Discussion
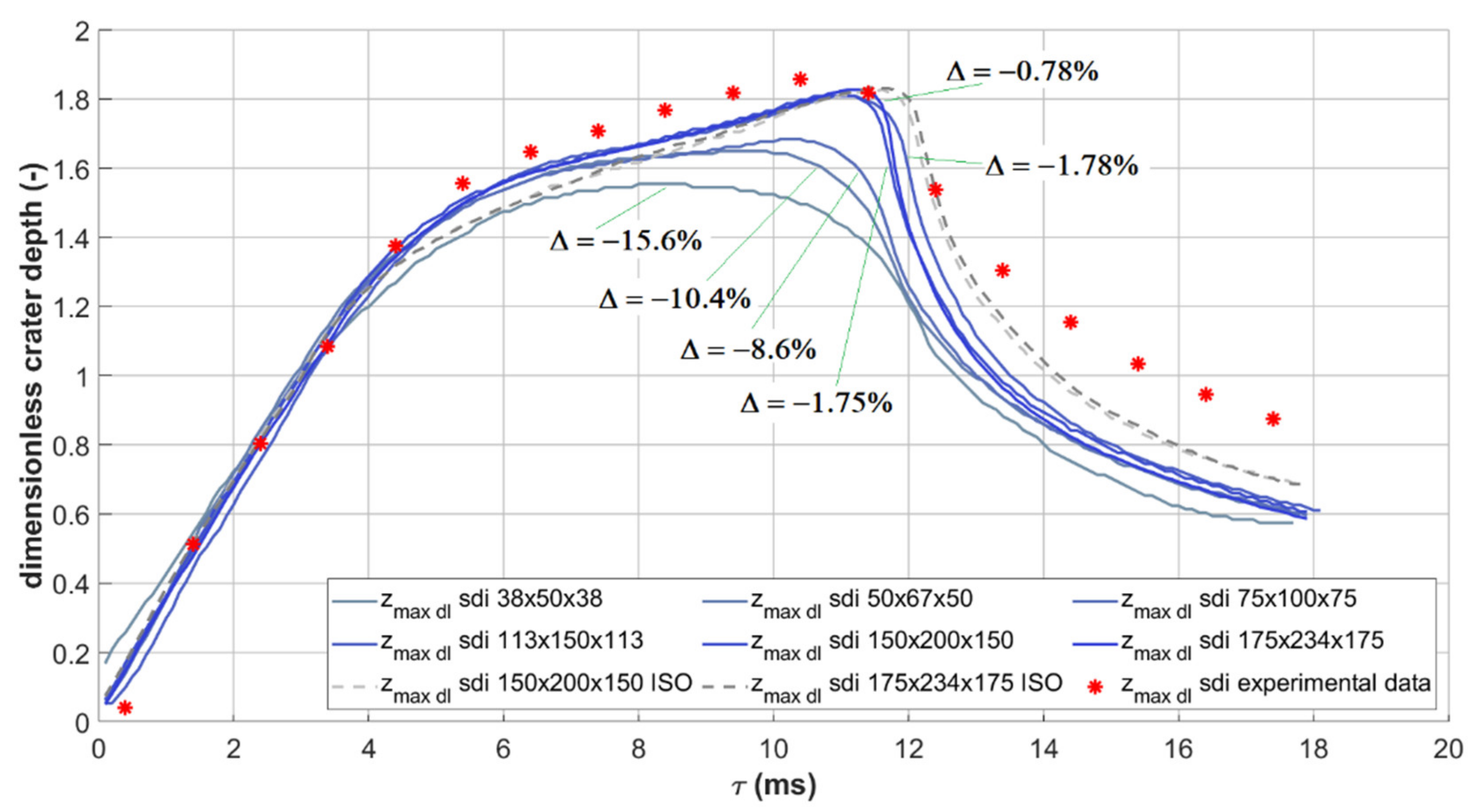
3.1. Mesh Independence and Validation against Experimental Data
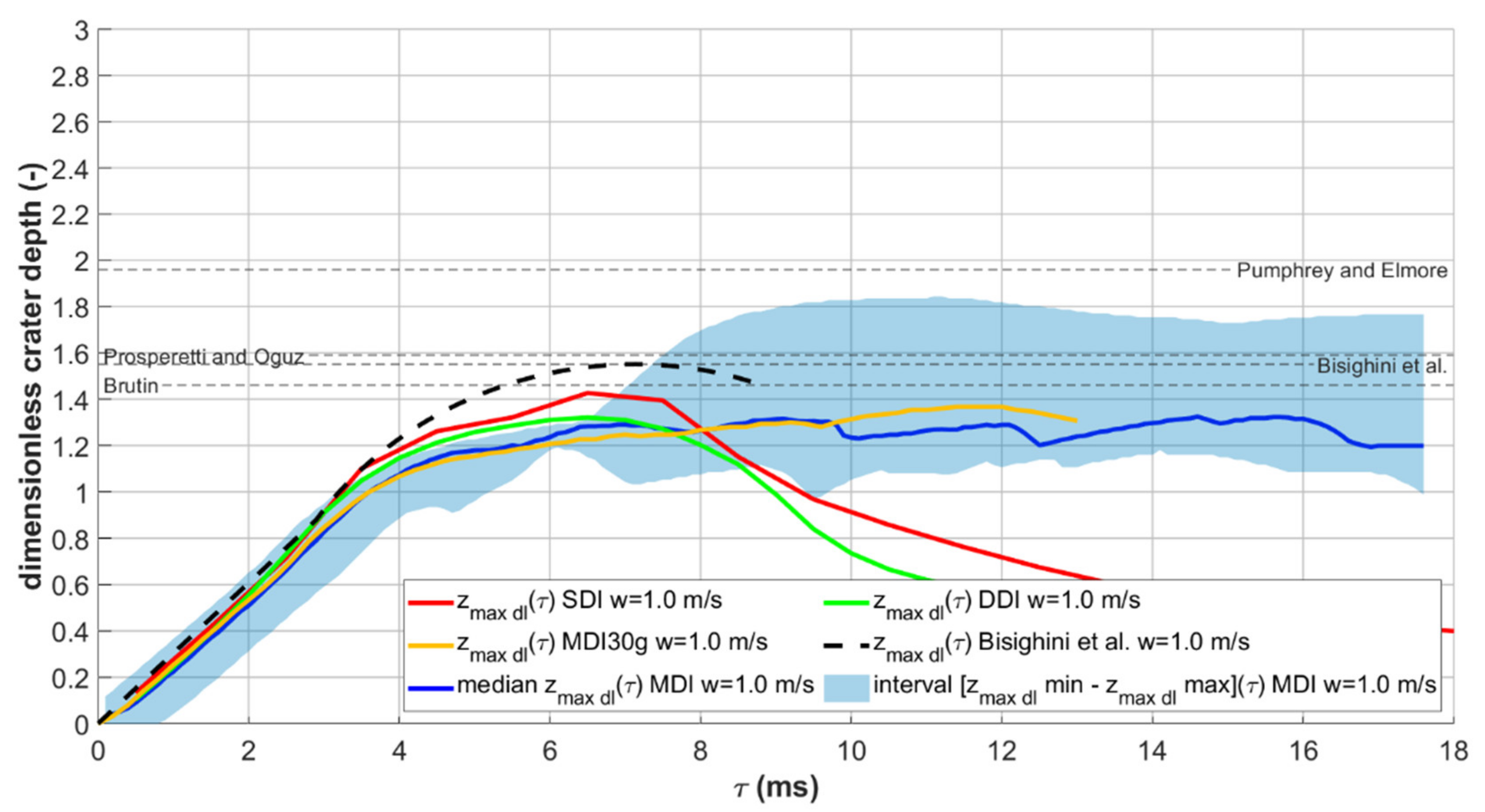
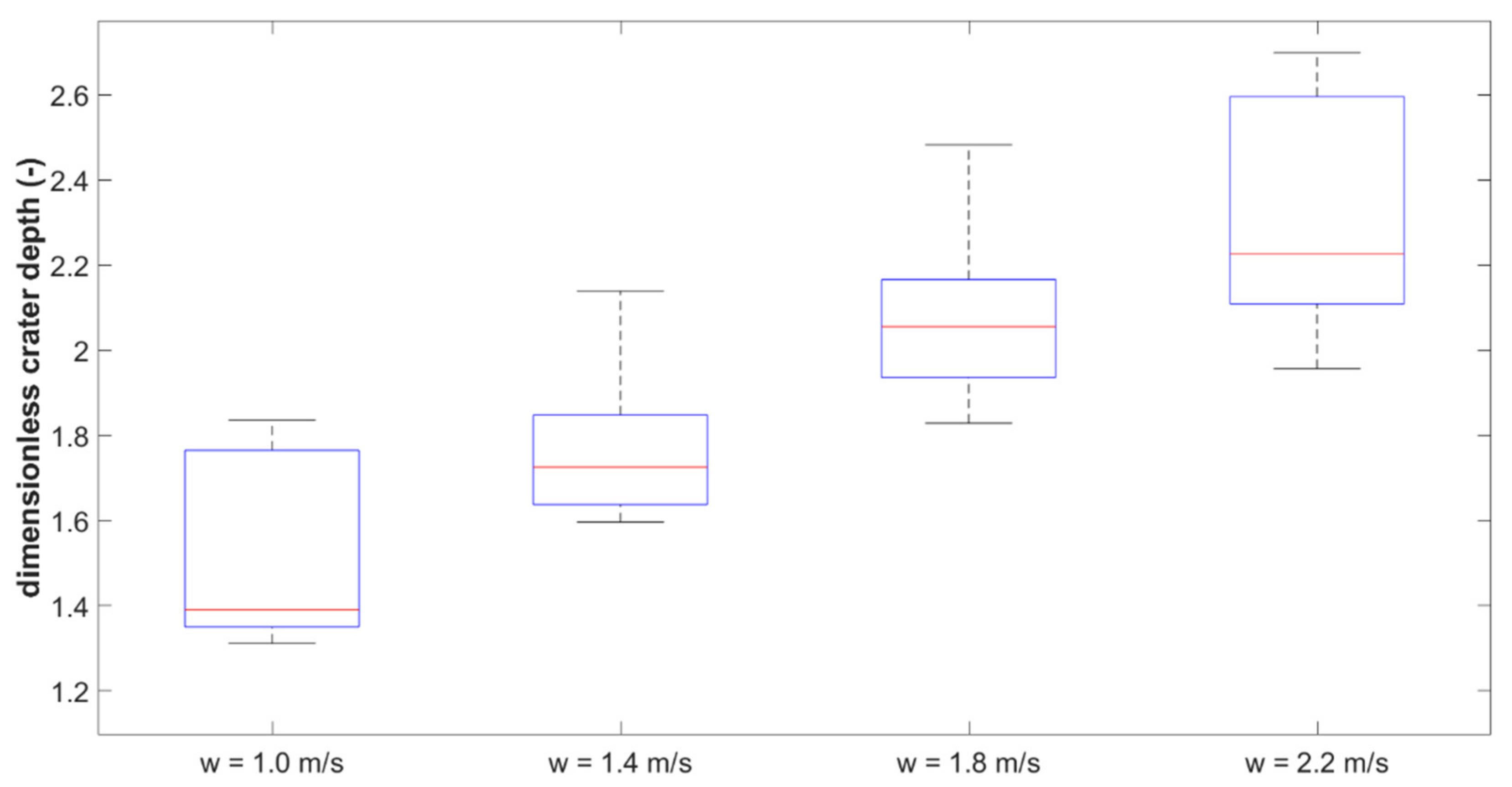
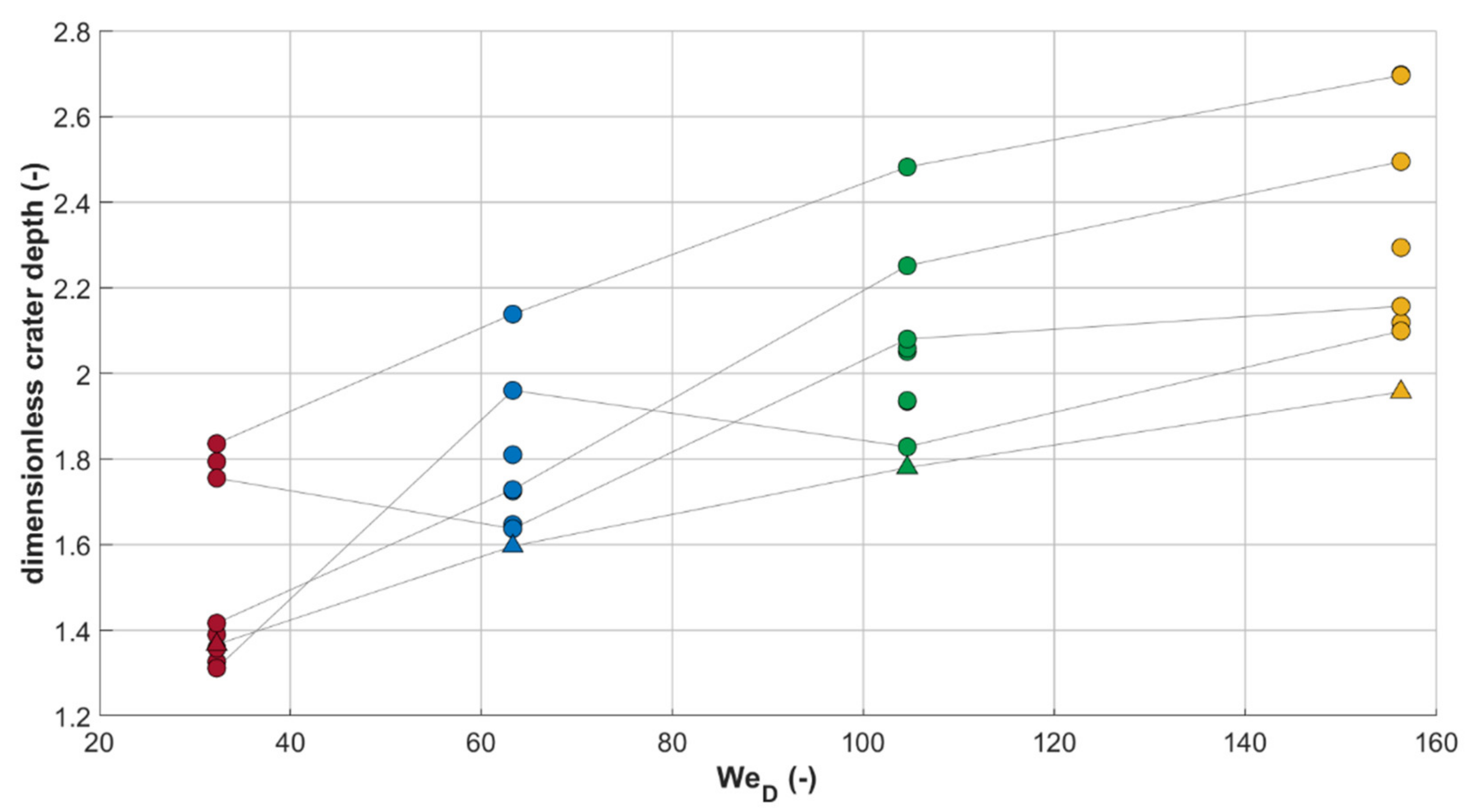
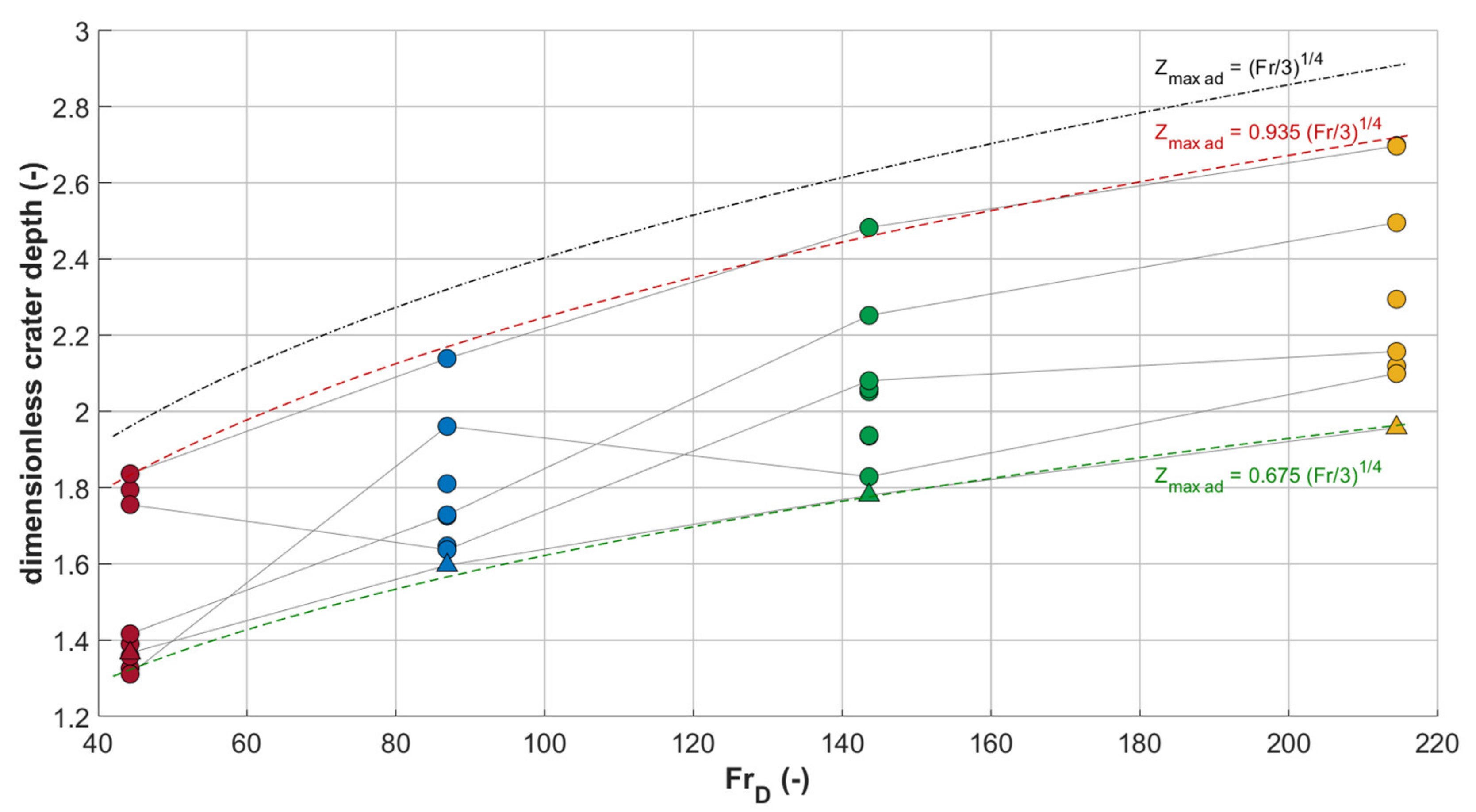
3.2. Results for Multiple Drop Impacts
- the line corresponding to Zmax ad = (FrD/3)1/4—that, as already said, is the “basis” of many of the literature models—is also shown as a dash-dot line.
- the two lines corresponding to Zmax ad = 0.675 (FrD/3)1/4 and Zmax ad = 0.935 (FrD/3)1/4, that can be used as “rounded” boundaries of the simulation results. A larger number of simulations would be needed to perform a significant fitting of the minimum, maximum, and median values of the maximum crater depths in order to propose a new model with reliable coefficients.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Worthington, A.M. On impact with a liquid surface. Proc. R. Soc. Lond. 1882, 34, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Worthington, A.M. A Study of Splashes; Longmans Green and Co.: London, UK, 1908. [Google Scholar]
- Rein, M. Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 1993, 12, 61–93. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Ashgriz, N. (Ed.) Handbook of Atomization and Sprays: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 2011; ISBN 9781441972644. [Google Scholar] [CrossRef]
- Cole, D. The Splashing Morphology of Liquid-Liquid Impacts. Ph.D. Thesis, James Cook University, Townsville, Australia, 2007. [Google Scholar]
- Bisighini, A.; Cossali, G.E. High-speed visualization of interface phenomena: Single and double drop impacts onto a deep liquid. J. Vis. 2011, 14, 103–110. [Google Scholar] [CrossRef]
- Santini, M.; Fest-Santini, S.; Cossali, G.E. Experimental study of vortices and cavities from single and double drop impacts onto deep pools. Eur. J. Mech. B Fluids 2017, 62, 21–31. [Google Scholar] [CrossRef]
- Guilizzoni, M.; Santini, M.; Fest-Santini, S. Synchronized Multiple Drop Impacts into a Deep Pool. Fluids 2019, 4, 141. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Chen, G.; Shen, S.; Zhang, J. Double Droplets Simultaneous Impact on Liquid Film. IOP Conf. Ser. Mater. Sci. Eng. 2015, 88, 012016. [Google Scholar] [CrossRef]
- Santini, M.; Cossali, G.E.; Marengo, M. Splashing characteristics of multiple and single drop impacts onto a thin liquid film. In Proceedings of the International Conference on Multiphase Flows, Leipzig, Germany, 9–13 July 2007. [Google Scholar]
- Fest-Santini, S.; Steigerwald, J.; Santini, M.; Cossali, G.E.; Weigand, B. Multiple drops impact onto a liquid film: Direct numerical simulation and experimental validation. Comput. Fluids 2021, 214, 104761. [Google Scholar] [CrossRef]
- Roisman, I.V.; Prunet-Foch, B.; Tropea, C.; Vignes-Adler, M. Multiple Drop Impact onto a Dry Solid Substrate. J. Colloid Interface Sci. 2002, 256, 396–410. [Google Scholar] [CrossRef]
- Trujillo, M.F.; Lewis, S.R. Thermal boundary layer analysis corresponding to droplet train impingement. Phys. Fluids 2012, 24, 112102. [Google Scholar] [CrossRef]
- Ray, B.; Biswas, G.; Sharma, A.; Welch, S.W.J. CLSVOF method to study consecutive drop impact on liquid pool. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 143–158. [Google Scholar] [CrossRef]
- Bouwhuis, W.; Huang, X.; Chan, C.U.; Frommhold, P.E.; Ohl, C.-D.; Lohse, D.; Snoeijer, J.H.; van der Meer, D. Impact of a high-speed train of microdrops on a liquid pool. J. Fluid Mech. 2016, 792, 850–868. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Kim, S.; Kim, J.; Kim, H.; Kim, H.-Y. From an elongated cavity to funnel by the impact of a drop train. J. Fluid Mech. 2021, 921, A8. [Google Scholar] [CrossRef]
- Oguz, H.N.; Prosperetti, A. Bubble entrainment by impact of a liquid drop on liquid surfaces. J. Fluid Mech. 1990, 219, 143–179. [Google Scholar] [CrossRef] [Green Version]
- Rieber, M.; Frohn, A. A numerical study on the mechanism of splashing. Int. J. Heat Fluid Flow 1999, 20, 455–461. [Google Scholar] [CrossRef]
- Bussmann, M.; Mostaghimi, J.; Chandra, S. On a three-dimensional volume tracking model of droplet impact. Phys. Fluids 1999, 11, 1406. [Google Scholar] [CrossRef]
- Morton, D.; Rudman, M.; Liow, J.M. An investigation of the flow regimes resulting from splashing drops. Phys. Fluids 2000, 12, 747. [Google Scholar] [CrossRef]
- Thoraval, M.-J.; Takehara, K.; Etoh, T.G.; Popinet, S.; Ray, P.; Josserand, C.; Zaleski, S.; Thoroddsen, S.T. von Karman Vortex Street within an Impacting Drop. Phys. Rev. Lett. 2012, 108, 264506. [Google Scholar] [CrossRef] [Green Version]
- Thoraval, M.-J.; Li, Y.; Thoroddsen, S. Vortex-ring induced large bubble entrainment during drop impact. Phys. Rev. E 2016, 93, 033128. [Google Scholar] [CrossRef] [Green Version]
- Reijers, S.A.; Liu, B.; Lohse, D.; Gelderblom, H. Oblique droplet impact onto a deep liquid pool. arXiv 2019, arXiv:1903.08978. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S.J. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. A front tracking algorithm for accurate representation of surface tension. Int. J. Numer. Methods Fluid 1999, 30, 775–793. [Google Scholar] [CrossRef]
- Bonometti, T.; Magnaudet, J. An interface-capturing method for incompressible two-phase flows. Validation and application to bubble dynamics. Int. J. Multiph. Flow 2007, 33, 109–133. [Google Scholar] [CrossRef] [Green Version]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.-J. A Front-Tracking Method for the Computations of Multiphase Flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef] [Green Version]
- Albadawi, A.; Donoghue, D.B.; Robinson, A.J.; Murray, D.B.; Delauré, Y.M.C. Influence of surface tension implementation in Volume of Fluid and coupled Volume of Fluid with Level Set methods for bubble growth and detachment. Int. J. Multiph. Flow 2013, 53, 11–28. [Google Scholar] [CrossRef]
- Taqieddin, A.; Liu, Y.; Alshawabkeh, A.N.; Allshouse, M.R. Computational modeling of bubbles growth using the coupled Level Set—Volume of Fluid method. Fluids 2020, 5, 120. [Google Scholar] [CrossRef] [PubMed]
- Menard, T.; Tanguy, S.; Berlemont, A. Coupling level set/VOF/ghost fluid methods: Validation and application to 3D simulation of the primary break-up of a liquid jet. Int. J. Multiph. Flow 2007, 33, 510–524. [Google Scholar] [CrossRef]
- Fuster, D.; Agbaglah, G.; Josserand, C.; Popinet, S.; Zaleski, S. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dyn. Res. 2009, 41, 065001. [Google Scholar] [CrossRef]
- Zheng, H.W.; Shu, C.; Chew, Y.T.; Sun, J.H. Three-dimensional lattice Boltzmann interface capturing method for incompressible flows. Int. J. Numer. Methods Fluids 2008, 56, 1653–1671. [Google Scholar] [CrossRef]
- Huang, J.J.; Shu, C.; Chew, Y.T. Lattice Boltzmann study of bubble entrapment during droplet impact. Int. J. Numer. Methods Fluids 2011, 65, 655–682. [Google Scholar] [CrossRef]
- Gentner, F.; Rioboo, R.; Baland, J.P.; De Coninck, J. Low Inertia Impact Dynamics for Nanodrops. Langmuir 2004, 20, 4748–4755. [Google Scholar] [CrossRef] [PubMed]
- OpenFOAM®. Available online: https://openfoam.org (accessed on 5 December 2021).
- Brackbill, J.U.; Khote, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Gopala, V.R.; van Wachem, B.G.M. Volume of fluid methods for immiscible-fluid and free-surface flows. Chem. Eng. J. 1998, 141, 204–211. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Trujillo, M.F. Distinguishing features of shallow angle plunging jets. Phys. Fluids 2013, 25, 082103. [Google Scholar] [CrossRef]
- Costa, A.B.; Graham Cooks, R. Simulated splashes: Elucidating the mechanism of desorption electrospray ionization mass spectrometry. Chem. Phys. Lett. 2008, 464, 1–8. [Google Scholar] [CrossRef]
- Roisman, I.V.; Weickgenannt, C.M.; Lembach, A.N.; Tropea, C. Drop impact close to a pore: Experimental and numerical investigations. In Proceedings of the ILASS—Europe 2010, 23rd Annual Conference on Liquid Atomization and Spray Systems, Brno, Czech Republic, 6–9 September 2010. [Google Scholar]
- Berberovic, E.; van Hinsberg, N.P.; Jakirlic, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79, 036306. [Google Scholar] [CrossRef]
- Castillo-Orozco, E.; Davanlou, A.; Choudhury, P.K.; Kumar, R. Droplet impact on deep liquid pools: Rayleigh jet to formation of secondary droplets. Phys. Rev. E 2015, 92, 053022. [Google Scholar] [CrossRef]
- Brambilla, P.; Guardone, A. Automatic tracking of corona propagation in three-dimensional simulations of non-normal drop impact on a liquid film. Computing 2013, 95, 415–424. [Google Scholar] [CrossRef]
- Trujillo, M.F.; Alvarado, J.; Gehring, E.; Soriano, G.S. Numerical simulations and experimental characterization of heat transfer from a periodic impingement of droplets. J. Heat Transf. 2011, 133, 122201. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Trujillo, M.F.; Wu, X.; Chahine, G. Computational and experimental characterization of a liquid jet plunging into a quiescent pool at shallow inclination. Int. J. Heat Fluid Flow 2012, 34, 1–14. [Google Scholar] [CrossRef]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R.; Tryggvason, G. Fluid Mechanics, 6th ed.; Academic Press: New York, NY, USA, 2015; ISBN 9780124059351. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 9783540420743. [Google Scholar] [CrossRef]
- Márquez Damián, S. Description and Utilization of InterFoam Multiphase Solver. Universidad Nacional del Litoral, Argentina. Available online: http://infofich.unl.edu.ar/upload/5e6dfd7ff282e2deabe7447979a16d49b0b1b675.pdf (accessed on 5 December 2021).
- InterFoam. in the Unofficial OpenFOAM Wiki. Available online: https://openfoamwiki.net/index.php/InterFoam (accessed on 5 December 2021).
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Jasak, H.; Weller, H.G. Interface-Tracking Capabilities of the InterGamma Differencing Scheme; Technical Report; Imperial College of Science, Technology and Medicine, University of London: London, UK, 1995. [Google Scholar]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gamet, L.; Scala, M.; Roenby, J.; Scheufler, H.; Pierson, J.-L. Validation of volume-of-fluid OpenFOAM® isoAdvector solvers using single bubble benchmarks. Comput. Fluids 2020, 213, 104722. [Google Scholar] [CrossRef]
- Krause, F.; Li, X.; Fritsching, U. Simulation of droplet-formation and -interaction in emulsification processes. Eng. Appl. Comput. Fluid Mech. 2011, 5, 406–415. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Hao, J.; Lu, J.; Xu, L.; Hu, G.; Floryan, J.M. Small droplet bouncing on a deep pool. Phys. Fluids 2020, 32, 012107. [Google Scholar] [CrossRef]
- Rodriguez, F.; Mesler, R. The penetration of drop-formed vortex rings into pools of liquid. J. Colloid Interface Sci. 1988, 121, 121–129. [Google Scholar] [CrossRef]
- Pumphrey, H.C.; Elmore, P.A. The entrainment of bubbles by drop impacts. J. Fluid Mech. 1990, 220, 539–567. [Google Scholar] [CrossRef]
- Prosperetti, A.; Oguz, H.N. The impact of drops on liquid surfaces and the underwater noise of rain. Annu. Rev. Fluid Mech. 1993, 25, 577–602. [Google Scholar] [CrossRef]
- Leng, J.L. Splash formation by spherical drops. J. Fluid Mech. 2001, 427, 73–105. [Google Scholar] [CrossRef]
- Brutin, D. Drop impingement on a deep liquid surface: Study of a crater’s sinking dynamics. C. R. Mec. 2003, 331, 61–67. [Google Scholar] [CrossRef]
- Bisighini, A.; Cossali, G.E.; Tropea, C.; Roisman, I.V. Crater evolution after the impact of a drop onto a semi-infinite liquid target. Phys. Rev. E 2010, 82, 036319. [Google Scholar] [CrossRef] [PubMed]
- Fedorchenko, A.I.; Wang, A.-B. On some common features of drop impact on liquid surfaces. Phys. Fluids 2004, 16, 1349–1365. [Google Scholar] [CrossRef]
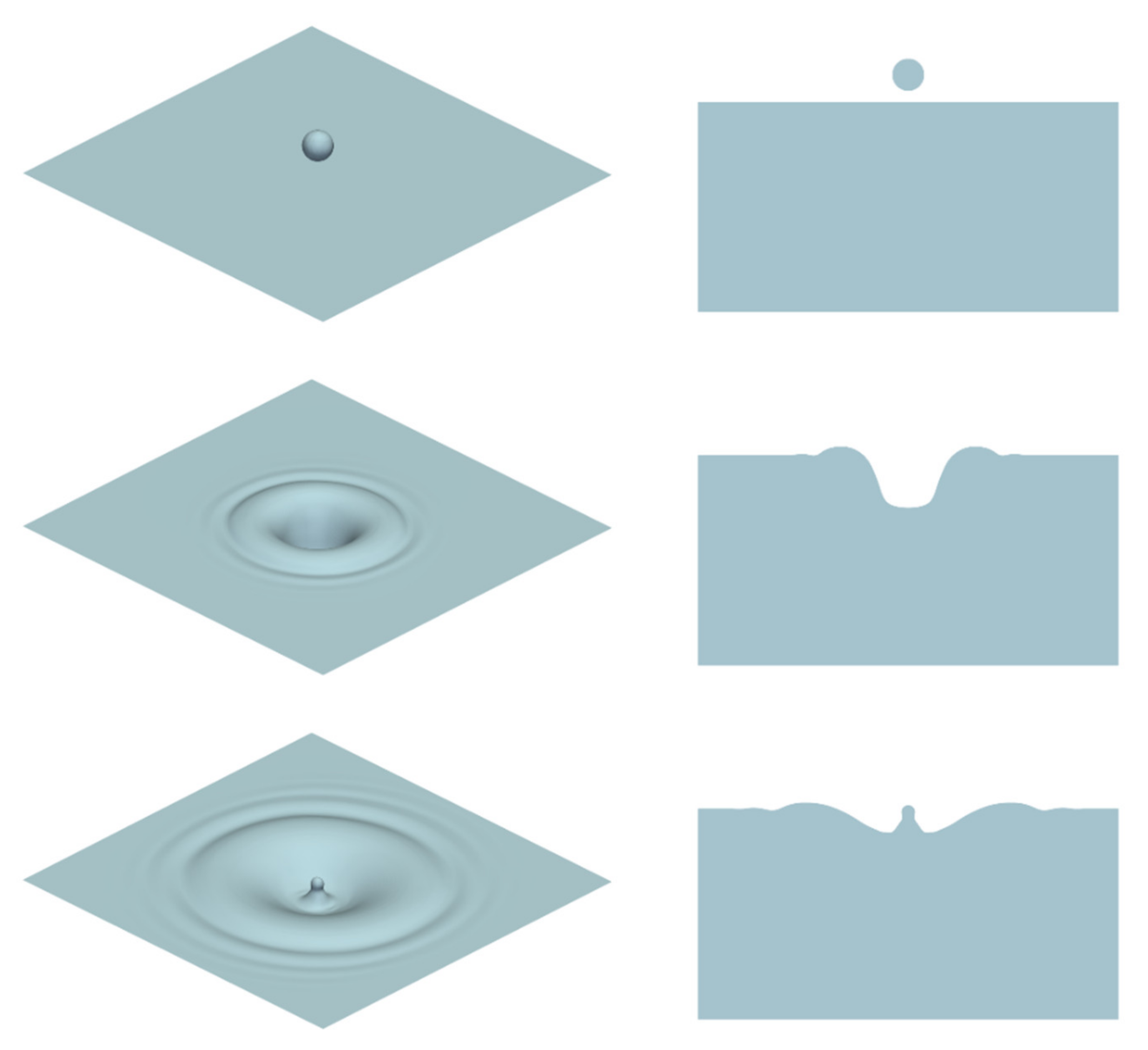






| Test | w = 1.0 m/s | w = 1.4 m/s | w = 1.8 m/s | w = 2.2 m/s |
|---|---|---|---|---|
| 1 |  |  |  |  |
| 2 |  |  |  |  |
| 3 |  |  |  |  |
| 4 |  |  |  |  |
| 5 |  |  |  |  |
| 6 |  |  |  |  |
| 7 |  |  |  |  |
| 8 |  |  |  |  |
| 9 |  |  |  |  |
| Model | Equation[s] |
|---|---|
| Pumphrey and Elmore (1990) [60] | |
| Prosperetti and Oguz (1993) [61] | |
| Leng (2001) [62] | |
| Brutin (2003) [63] | |
| Bisighini et al. (2010) [64] | with initial conditions: |
| Model | 1.0 m/s | 1.4 m/s | 1.8 m/s | 2.2 m/s |
|---|---|---|---|---|
| Pumphrey | 49.49 | 41.68 | 43.84 | 38.54 |
| Prosperetti and Oguz | 22.22 | 18.03 | 23.00 | 20.99 |
| Leng | 8.68 | 3.00 | 4.57 | 0.72 |
| Brutin | 11.41 | 0.55 | −1.10 | −6.97 |
| Bisighini | 18.26 | 8.41 | 10.86 | 7.54 |
| Model | 1.0 m/s | 1.4 m/s | 1.8 m/s | 2.2 m/s |
|---|---|---|---|---|
| Pumphrey | 39.71 | 34.31 | 27.99 | 21.44 |
| Prosperetti and Oguz | 13.29 | 11.89 | 9.44 | 6.05 |
| Leng | 1.57 | −2.35 | −6.95 | −11.72 |
| Brutin | 4.21 | −4.67 | −12.00 | −18.45 |
| Bisighini | 10.52 | 2.78 | −1.36 | −5.74 |
| Model | 1.0 m/s | 1.4 m/s | 1.8 m/s | 2.2 m/s |
|---|---|---|---|---|
| Pumphrey | 6.78 | 8.47 | 5.96 | 7.78 |
| Prosperetti and Oguz | −13.41 | −9.64 | −9.39 | −5.87 |
| Leng | −22.37 | −21.14 | −22.96 | −21.64 |
| Brutin | −20.42 | −23.02 | −27.14 | −27.62 |
| Bisighini | −15.53 | −17.00 | −18.33 | −16.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guilizzoni, M.; Frontera, G. Crater Depth after the Impact of Multiple Drops into Deep Pools. Fluids 2022, 7, 50. https://doi.org/10.3390/fluids7020050
Guilizzoni M, Frontera G. Crater Depth after the Impact of Multiple Drops into Deep Pools. Fluids. 2022; 7(2):50. https://doi.org/10.3390/fluids7020050
Chicago/Turabian StyleGuilizzoni, Manfredo, and Giuseppe Frontera. 2022. "Crater Depth after the Impact of Multiple Drops into Deep Pools" Fluids 7, no. 2: 50. https://doi.org/10.3390/fluids7020050
APA StyleGuilizzoni, M., & Frontera, G. (2022). Crater Depth after the Impact of Multiple Drops into Deep Pools. Fluids, 7(2), 50. https://doi.org/10.3390/fluids7020050








