Rim Breakups of Impacting Drops on a Superhydrophobic Surface and a Superheated Surface
Abstract
:1. Introduction
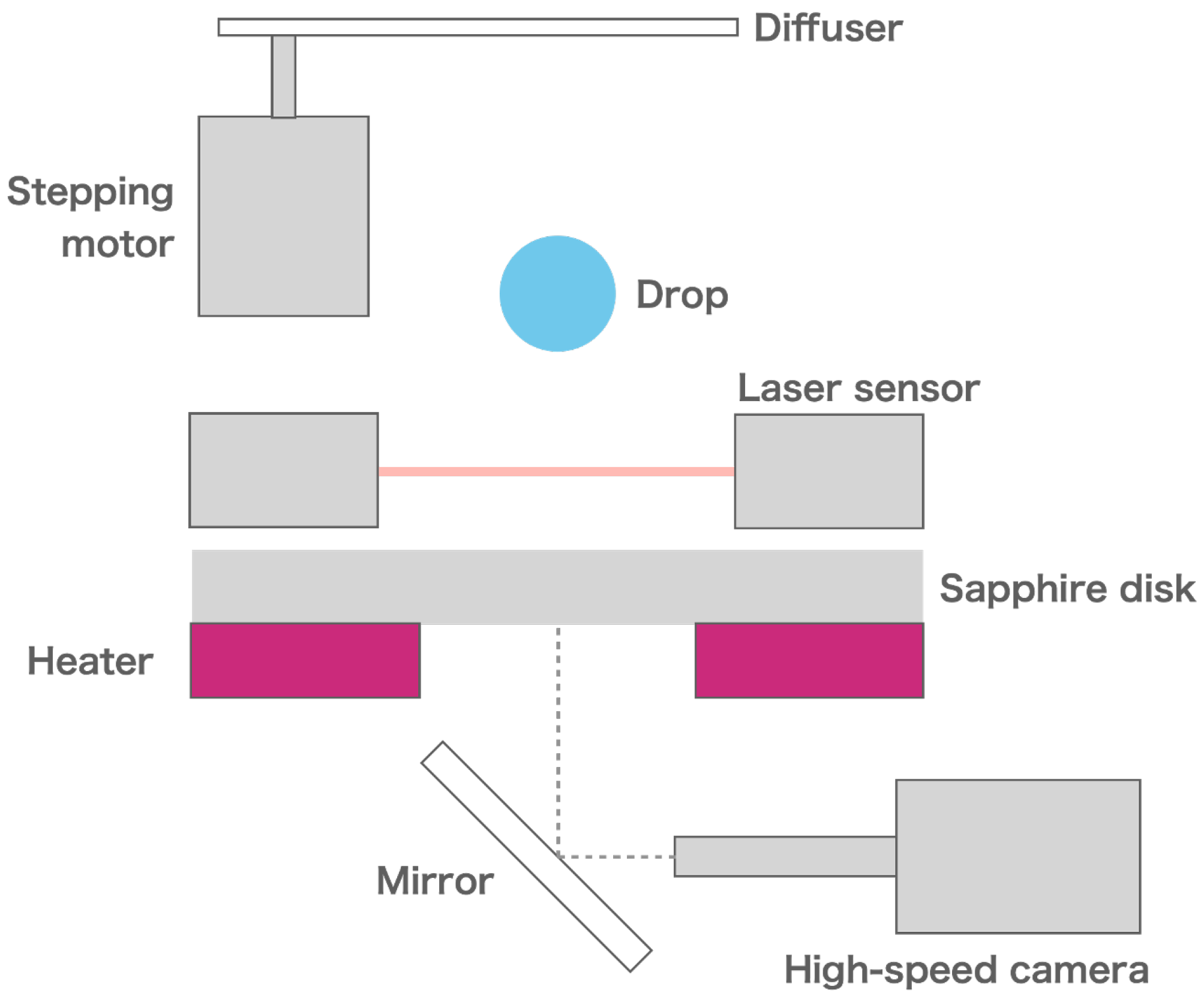
2. Materials and Methods
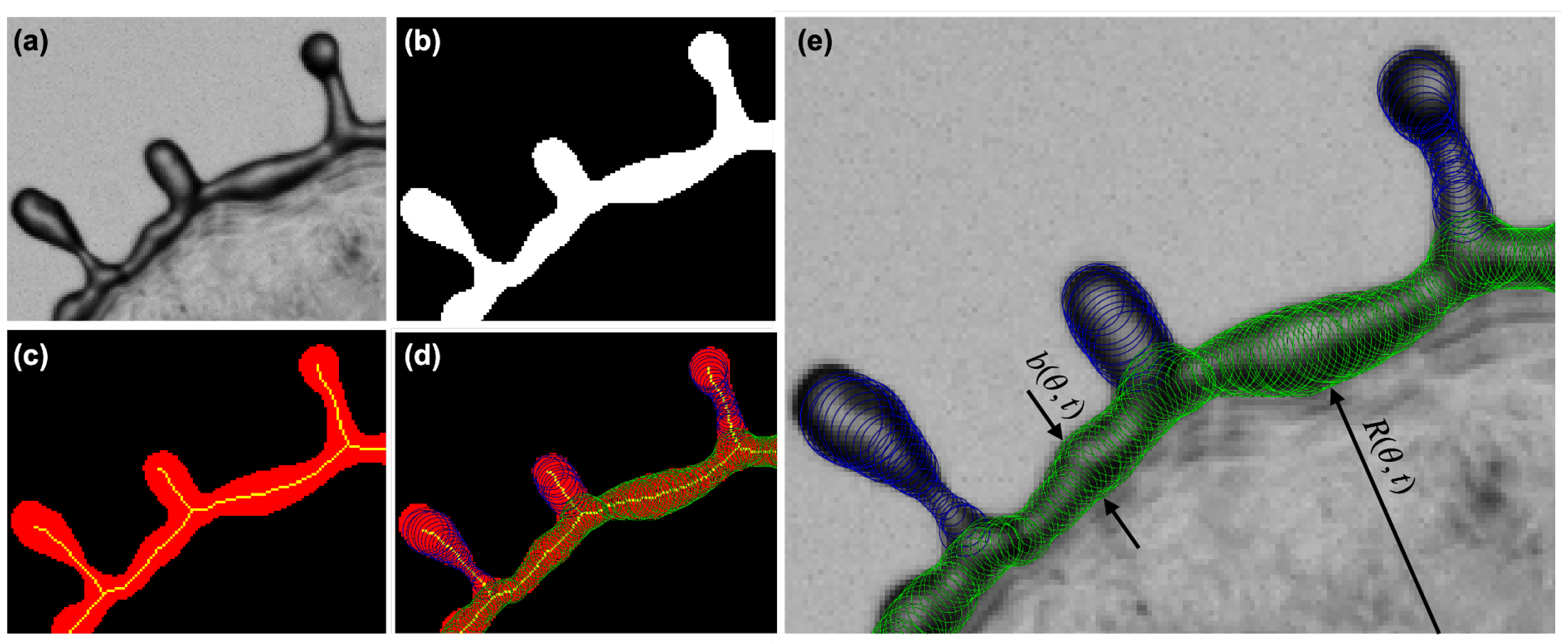
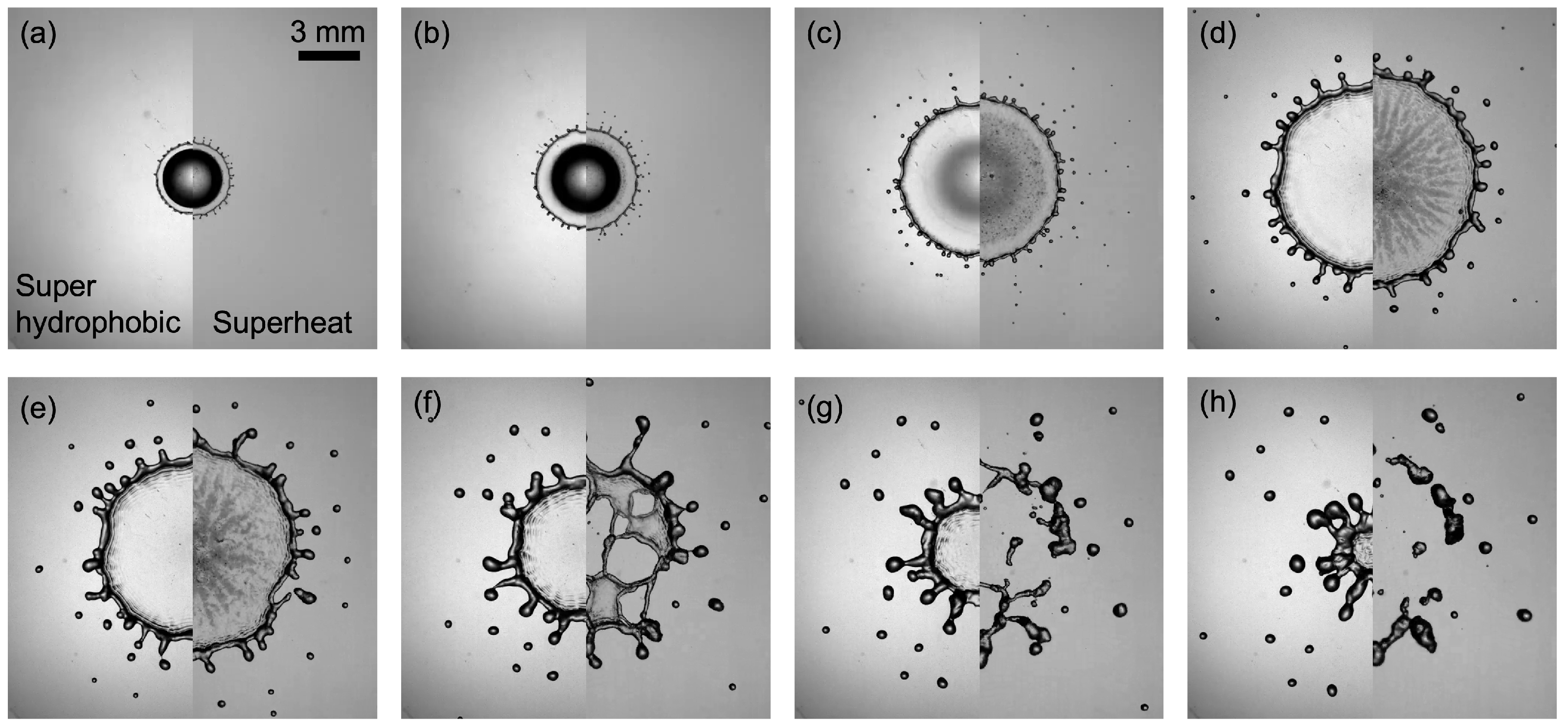
3. Results
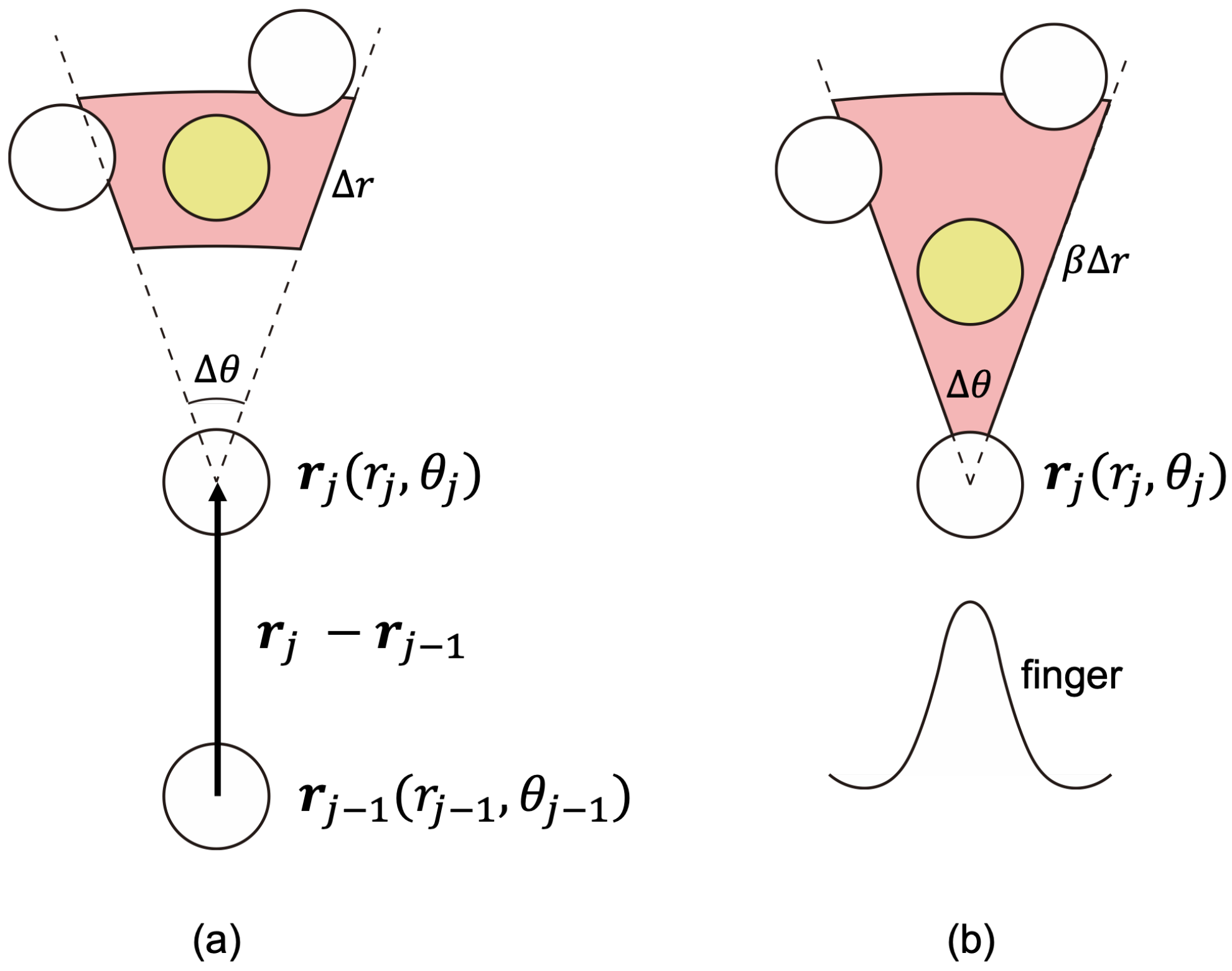
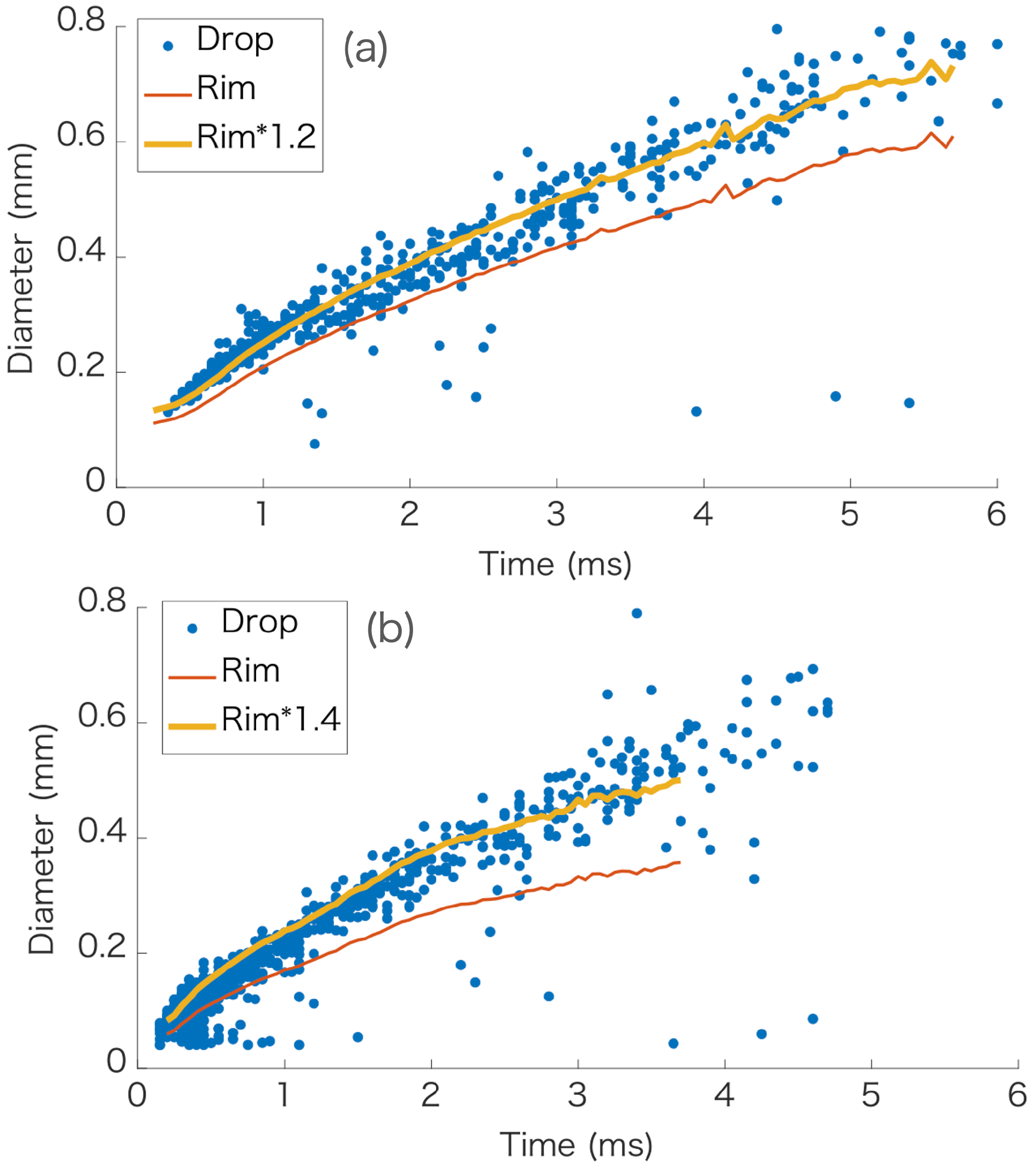
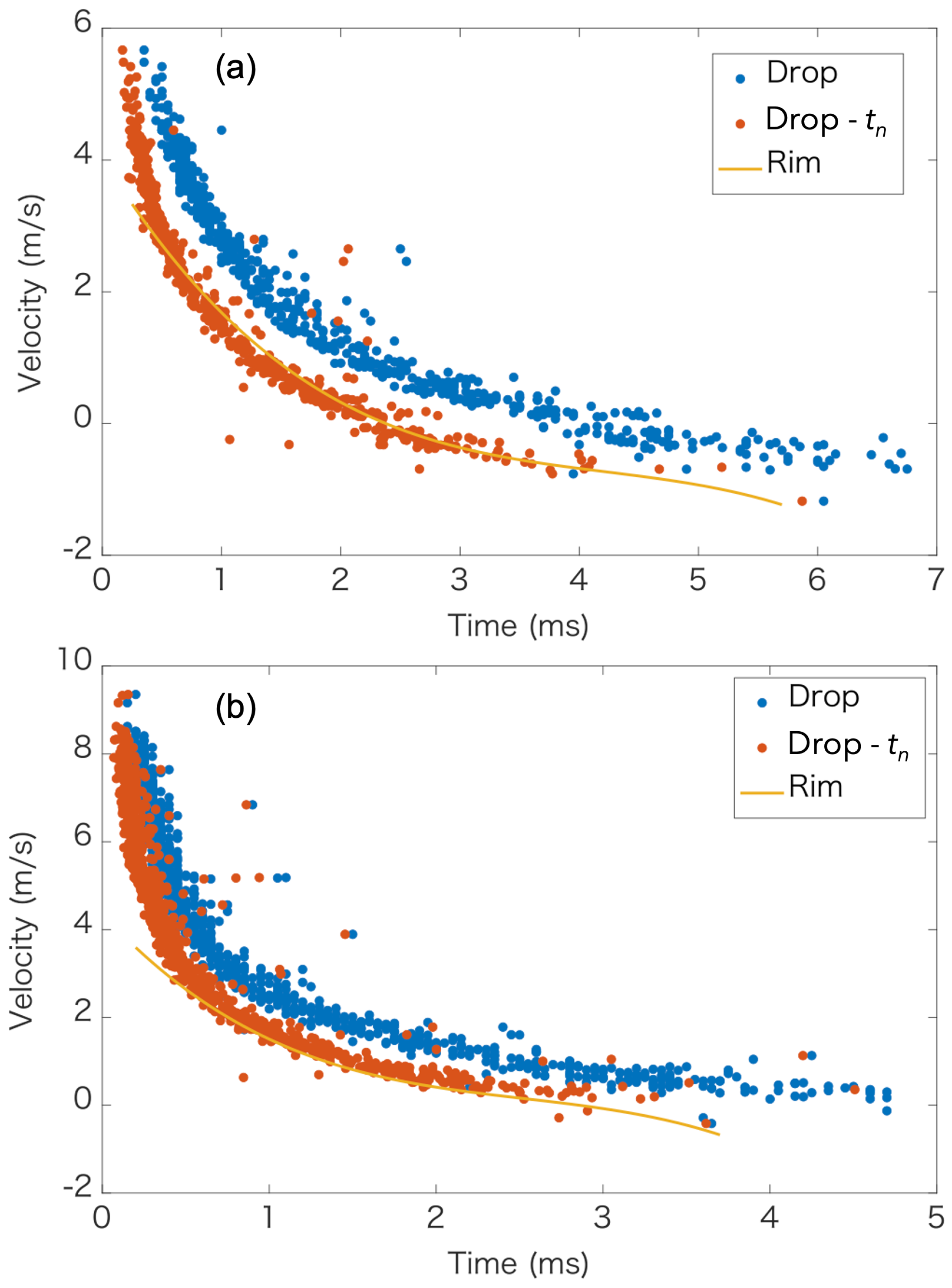
3.1. Local Bo of the Rim
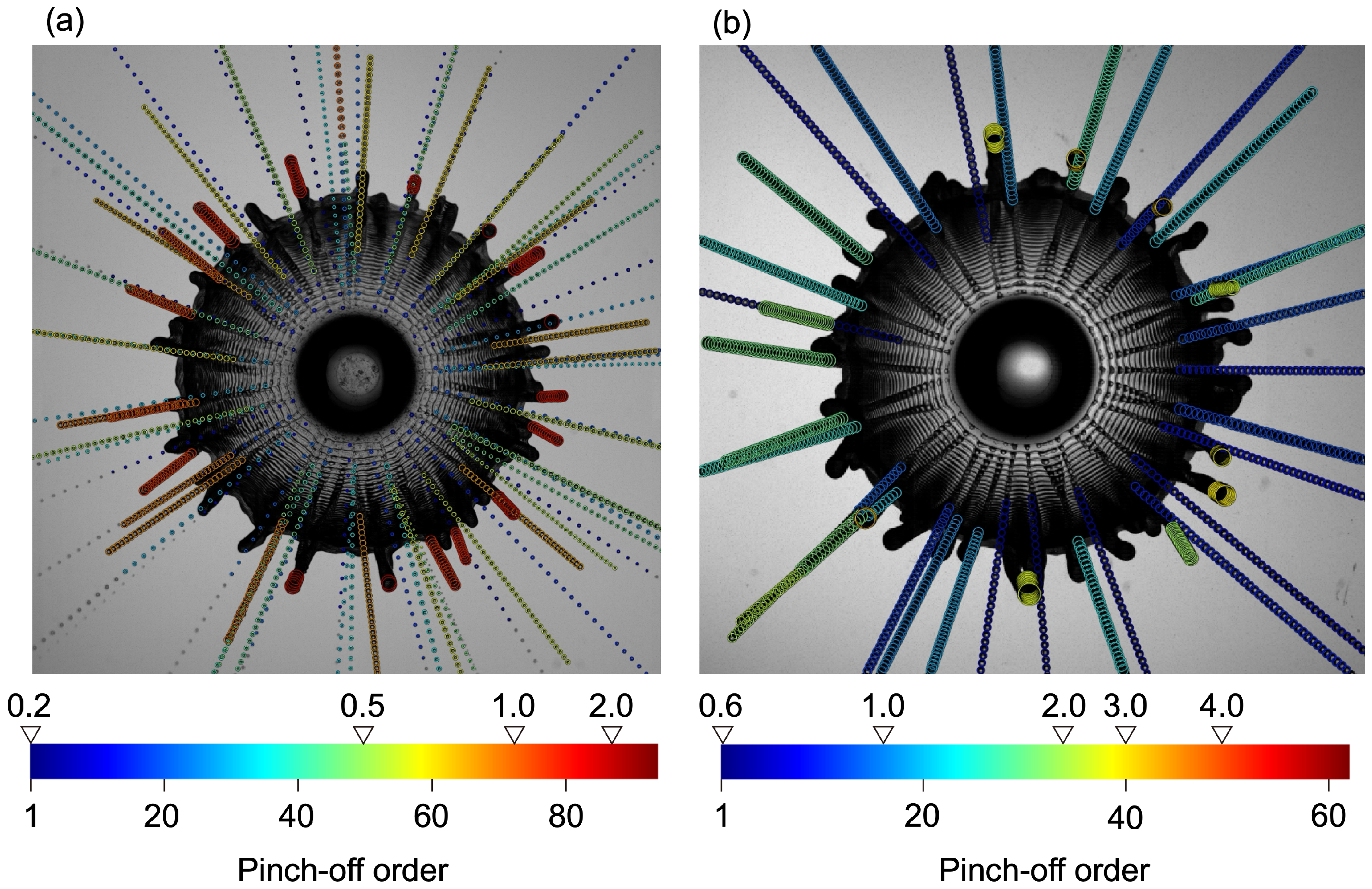
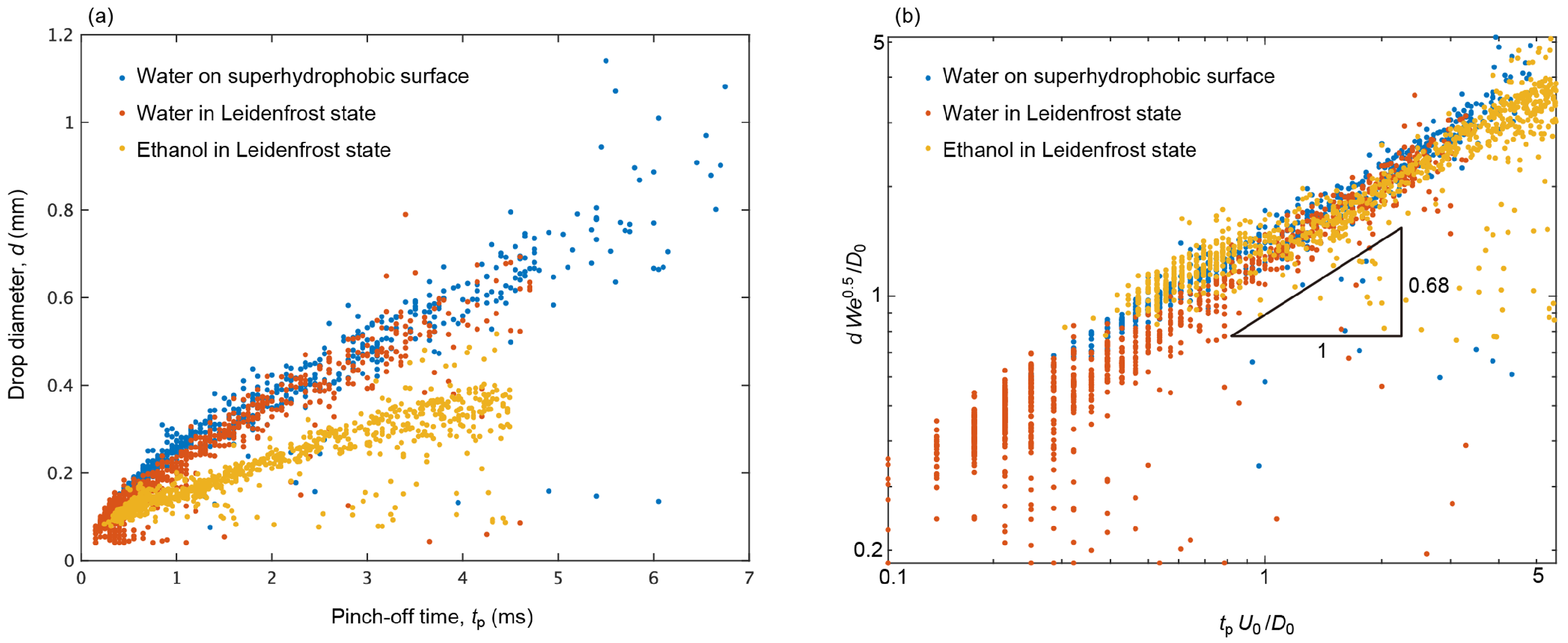
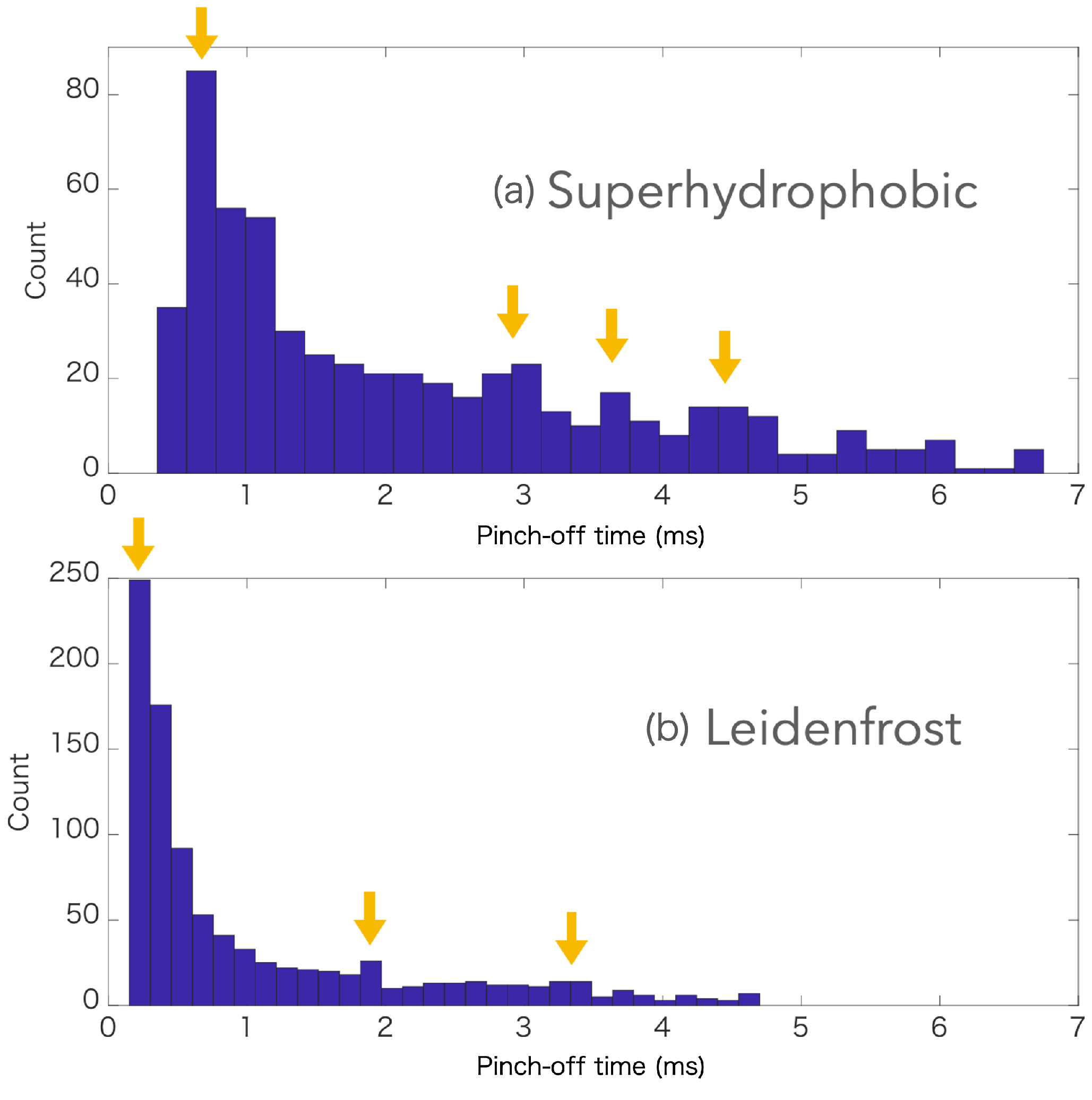
3.2. Pinch-Off of the Daughter Drops from the Rim
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SH | Superheated |
| SHPB | Superhydrophobic |
References
- Chandra, S.; Avedisian, C. On the collision of a droplet with a solid surface. Proc. R. Soc. Lond. A 1991, 432, 13–41. [Google Scholar] [CrossRef]
- Aziz, S.D.; Chandra, S. Impact, recoil and splashing of molten metal droplets. Int. J. Heat Mass Transf. 2000, 43, 2841–2857. [Google Scholar] [CrossRef]
- Roisman, I.V.; Berberović, E.; Tropea, C. Inertia dominated drop collisions. I. On the universal flow in the lamella. Phys. Fluids 2009, 21, 052103. [Google Scholar] [CrossRef]
- Roisman, I.V. Inertia dominated drop collisions. II. An analytical solution of the Navier-Stokes equations for a spreading viscous film. Phys. Fluids 2009, 21, 052104. [Google Scholar] [CrossRef]
- Eggers, J.; Fontelos, M.a.; Josserand, C.; Zaleski, S. Drop dynamics after impact on a solid wall: Theory and simulations. Phys. Fluids 2010, 22, 062101. [Google Scholar] [CrossRef] [Green Version]
- Laan, N.; De Bruin, K.G.; Bartolo, D.; Josserand, C.; Bonn, D. Maximum diameter of impacting liquid droplets. Phys. Rev. Appl. 2014, 2. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.B.; Derome, D.; Guyer, R.; Carmeliet, J. Modeling the Maximum Spreading of Liquid Droplets Impacting Wetting and Nonwetting Surfaces. Langmuir 2016, 32, 1299–1308. [Google Scholar] [CrossRef]
- Yonemoto, Y.; Kunugi, T. Analytical consideration of liquid droplet impingement on solid surfaces. Sci. Rep. 2017, 7, 2362. [Google Scholar] [CrossRef] [Green Version]
- Wildeman, S.; Visser, C.W.; Sun, C.; Lohse, D. On the Spreading of Impacting Drops. J. Fluid Mech. 2016, 805, 636–655. [Google Scholar] [CrossRef] [Green Version]
- Gordillo, J.M.; Riboux, G.; Quintero, E.S. A theory on the spreading of impacting droplets. J. Fluid Mech. 2019, 866, 298–315. [Google Scholar] [CrossRef]
- Villermaux, E.; Bossa, B. Drop fragmentation on impact. J. Fluid Mech. 2011, 668, 412–435. [Google Scholar] [CrossRef]
- Lastakowski, H.; Boyer, F.; Biance, A.L.; Pirat, C.; Ybert, C. Bridging local to global dynamics of drop impact onto solid substrates. J. Fluid Mech. 2014, 747, 103–118. [Google Scholar] [CrossRef]
- Tran, T.; Staat, H.J.J.; Prosperetti, A.; Sun, C.; Lohse, D. Drop Impact on Superheated Surfaces. Phys. Rev. Lett. 2012, 108, 036101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, T.; Staat, H.J.J.; Susarrey-Arce, A.; Foertsch, T.C.; van Houselt, A.; Gardeniers, H.J.G.E.; Prosperetti, A.; Lohse, D.; Sun, C. Droplet impact on superheated micro-structured surfaces. Soft Matter 2013, 9, 3272–3282. [Google Scholar] [CrossRef]
- Shirota, M.; van Limbeek, M.A.J.; Sun, C.; Prosperetti, A.; Lohse, D. Dynamic Leidenfrost Effect: Relevant Time and Length Scales. Phys. Rev. Lett. 2016, 116, 1–5. [Google Scholar] [CrossRef] [Green Version]
- van Limbeek, M.A.J.; Shirota, M.; Sleutel, C.P.; Sun, C.; Prosperetti, A. Vapour cooling of poor conducting hot substrates increases the dynamic Leidenfrost temperature. Int. J. Heat Mass Transf. 2016, 97, 101–109. [Google Scholar] [CrossRef] [Green Version]
- van Limbeek, M.A.J.; Hoefnagels, P.B.; Shirota, M.; Sun, C.; Lohse, D. Boiling regimes of impacting drops on a heated substrate under reduced pressure. Phys. Rev. Fluids 2018, 3, 053601. [Google Scholar] [CrossRef] [Green Version]
- van Limbeek, M.A.J.; Nes, T.H.; Vanapalli, S. Impact dynamics and heat transfer characteristics of liquid nitrogen drops on a sapphire prism. Int. J. Heat Mass Transf. 2020, 148, 118999. [Google Scholar] [CrossRef]
- Visser, C.W.; Pohl, R.; Sun, C.; Römer, G.W.; Huis In ’T Veld, B.; Lohse, D. Toward 3D Printing of Pure Metals by Laser-Induced Forward Transfer. Adv. Mater. 2015, 27, 4087–4092. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.H.; Tsai, H.L.; Wu, Y.C.; Hwang, W.S. Investigation of molten metal droplet deposition and solidification for 3D printing techniques. J. Micromech. Microeng. 2016, 26, 95012. [Google Scholar] [CrossRef]
- Gielen, M.V.; de Ruiter, R.; Koldeweij, R.B.J.; Lohse, D.; Snoeijer, J.H.; Gelderblom, H. Solidification of liquid metal drops during impact. J. Fluid Mech. 2020, 883, A32. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Bourouiba, L. Unsteady Sheet Fragmentation: Droplet Sizes and Speeds. J. Fluid Mech. 2018, 848, 946–967. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Dandekar, R.; Bustos, N.; Poulain, S.; Bourouiba, L. Universal Rim Thickness in Unsteady Sheet Fragmentation. Phys. Rev. Lett. 2018, 120, 204503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Bourouiba, L. Drop impact on small surfaces: Thickness and velocity profiles of the expanding sheet in the air. J. Fluid Mech. 2017, 814, 510–534. [Google Scholar] [CrossRef] [Green Version]
- Villermaux, E.; Marmottant, P.; Duplat, J. Ligament-Mediated Spray Formation. Phys. Rev. Lett. 2004, 92, 074501. [Google Scholar] [CrossRef] [Green Version]
- Marmottant, P.; Villermaux, E. Fragmentation of stretched liquid ligaments. Phys. Fluids 2004, 16, 2732–2742. [Google Scholar] [CrossRef]
- Visser, C.W.; Frommhold, P.E.; Wildeman, S.; Mettin, R.; Lohse, D.; Sun, C. Dynamics of high-speed micro-drop impact: Numerical simulations and experiments at frame-to-frame times below 100 ns. Soft Matter 2015, 11, 1708–1722. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shirota, M.; Kato, M.; Ishio, A. Rim Breakups of Impacting Drops on a Superhydrophobic Surface and a Superheated Surface. Fluids 2022, 7, 79. https://doi.org/10.3390/fluids7020079
Shirota M, Kato M, Ishio A. Rim Breakups of Impacting Drops on a Superhydrophobic Surface and a Superheated Surface. Fluids. 2022; 7(2):79. https://doi.org/10.3390/fluids7020079
Chicago/Turabian StyleShirota, Minori, Masaki Kato, and Ai Ishio. 2022. "Rim Breakups of Impacting Drops on a Superhydrophobic Surface and a Superheated Surface" Fluids 7, no. 2: 79. https://doi.org/10.3390/fluids7020079
APA StyleShirota, M., Kato, M., & Ishio, A. (2022). Rim Breakups of Impacting Drops on a Superhydrophobic Surface and a Superheated Surface. Fluids, 7(2), 79. https://doi.org/10.3390/fluids7020079




