A Numerical Study on Distant Tsunami Propagation Considering the Strong Nonlinearity and Strong Dispersion of Waves, or the Plate Elasticity and Mantle Fluidity of Earth

Abstract

Numerical simulations were generated to investigate the propagation processes of distant tsunamis, using a set of wave equations based on the variational principle considering both the strong nonlinearity and strong dispersion of waves. First, we proposed estimate formulae for the time variations of the tsunami height and wavelength of the first distant tsunami, by assuming that the initial tsunami profile was a long crest in a uniform bathymetry. Second, we considered the plate elasticity and upper-mantle fluidity of Earth, to examine their effects on the distant tsunami propagation. When the plate and upper mantle meet certain conditions with both a large depth and moderately large density of the upper mantle, the internal-mode tsunamis with a significant tsunami height propagated slower than the tsunamis in the corresponding one-layer problems, leading to the delay of the arrival time observed in distant tsunamis from that evaluated by the one-layer calculation.

1. Introduction

The 2011 mega East Japan earthquake triggered huge tsunamis that caused enormous damage mainly to the eastern coasts of Japan, as reported by the field surveys (e.g., [1]). The tsunamis generated by the seabed rise or subsidence due to the submarine earthquakes had wavelengths as long as the fault widths, to the extent that they also arrived all the way to the north coasts of Australia and the west coasts of North America. Such large distant tsunamis can be affected by not only wave nonlinearity but also wave dispersion during their propagation. Therefore, when applying wave equations to reproduce distant tsunamis, appropriate dispersion terms should be considered [2,3,4,5,6,7].

Moreover, when the tsunamis due to the 1960 Chile earthquake and 2010 Chile Maule earthquake spread widely to the Pacific Rim regions, the arrival time of the distant tsunamis on Japanese coasts was later than the estimated arrival time through the numerical calculations with the shallow water equations [8]; there were several beaches on which the arrival-time difference was more than an hour. Although the effect of density stratification in the ocean on the propagation of long tsunamis was not as large as expected [9], it was revealed that considering both the seawater compressibility and Earth elasticity improves the estimated arrival time of distant tsunamis [10,11,12,13,14,15]. In the 2011 Tohoku tsunami case, the effects of weak dispersion, seawater density stratification, elastic loading, and gravitational potential change were considered in the numerical calculation for the tsunami propagation [16]. However, these factors alone cannot explain the arrival-time difference of around one hour in transoceanic propagation of tsunamis in other several cases.

In the present study, we first numerically simulated distant tsunamis using a set of wave equations based on a variational principle considering both the strong nonlinearity and strong dispersion of waves, and proposed formulae for estimating the time variations of the tsunami height and wavelength of the first wave. In the computation, we assumed that the initial tsunami profile was a sinusoidal crest with a relatively long wavelength, and the still seawater depth was uniform, for simplicity.

Second, we investigated the effects of the plate and upper mantle of Earth on the phase velocity of distant tsunamis, by assuming that the plate under the sea was an elastic body, and the upper layer of the mantle under the plate behaved like a fluid, to consider the motion of the plate and upper mantle. Although a tsunami generated as the first wave may be delayed or extinguished based on the effects of refraction, reflection, dispersion, etc. during transoceanic travel, the cause of the travel-time delay of the first tsunami without these effects was assumed to be the mantle motion. The state of mantle has not been elucidated, so it is undeniable that the hot mantle, which behaves like a fluid even in a limited area, affects tsunami propagation. We tried several thought experiments in which the mantle behavior was considered throughout the tsunami propagation process.

2. Numerical Calculation Method

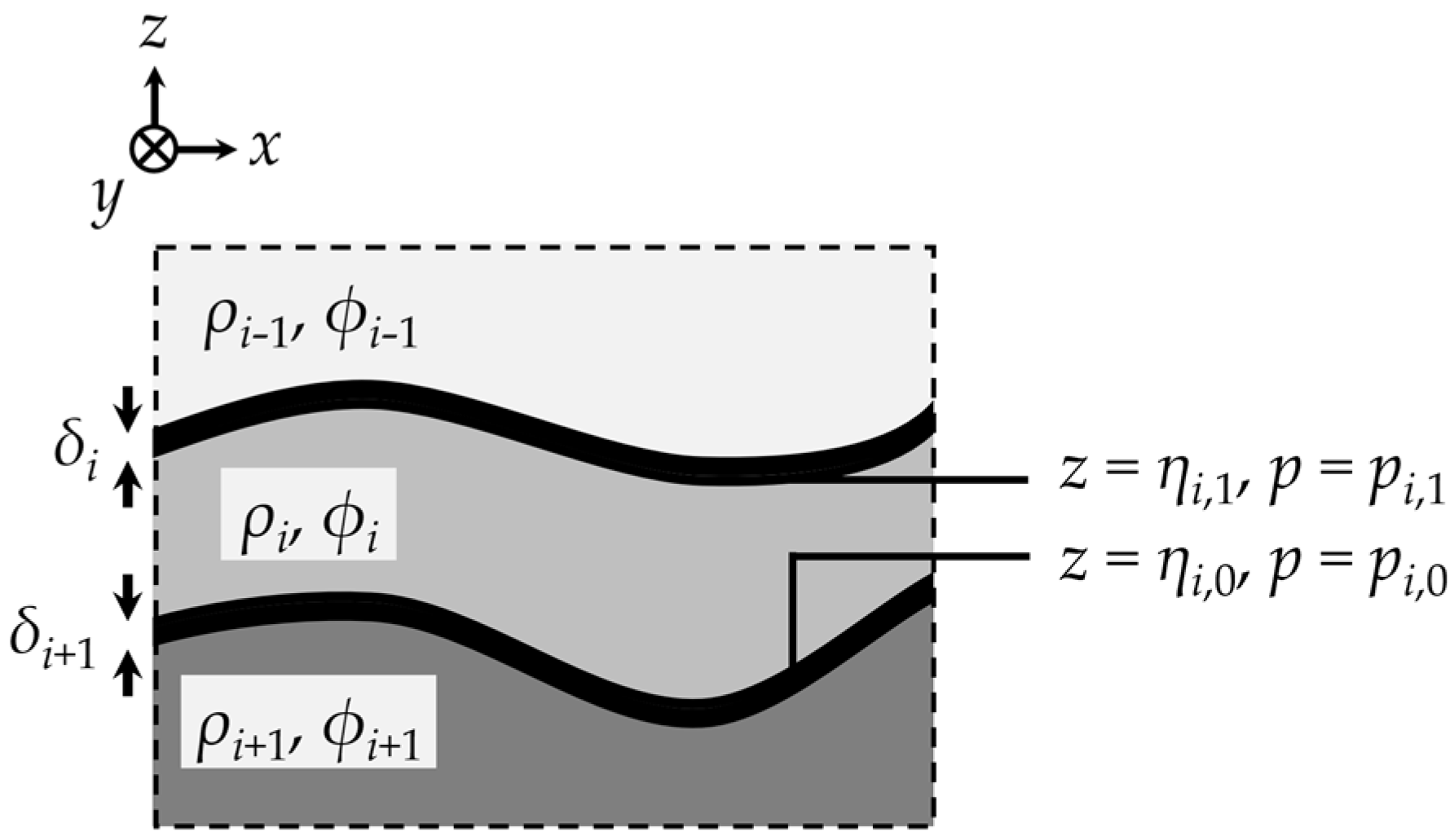
2.1. Governing Equations

Figure 1 depicts our schematic for a system consisting of multilayer fluids and thin plates, where the fluid layers and thin plates are represented as the i-layers and i-plates (i = 1, 2, …, I) from top to bottom, respectively. The method of deriving the present governing equations is described below. It was assumed that none of the fluids mixed even in motion without plates, and the density ρ_i (ρ₁ < ρ₂ < … < ρ_I) of the i-layer was spatially uniform and temporally constant. The thickness of the i-layer was h_i(x) in the stationary state, where x was the coordinate in the horizontal plane, i.e., (x, y). The origin of the vertical axis z was located at the top surface of the system in the stationary state, and the positive direction of z was vertically upward. The elevations of the lower and upper interfaces of the i-layer were expressed by z = η_i,0 (x, t) and z = η_i,1 (x, t), respectively, and the pressures at the lower and upper interfaces of the i-layer were denoted by p_i,0 (x, t) and p_i,1 (x, t), respectively.

The thin plate touching the upper interface of the i-layer is called the i-plate. The density and vertical width of the i-plate were m_i and δ_i, respectively. When m_i, δ_i, and the flexural rigidity of the i-plate are zero, the plate yielded no resistance to fluid motion, where two immiscible fluids touched each other directly without any plate. Both surface tension and capillary action were ignored. Although the friction was also ignored for simplicity in the present study, the seabed friction affected tsunami propagation in various stages, including propagation and run-up, e.g., [17,18,19], so the terms regarding bottom friction should be introduced in the governing equations in future.

Fluid motion was assumed to be inviscid, incompressible, and irrotational, resulting in the existence of velocity potential ϕ_i, which was expanded into a power series of z with weightings f_i,α as

$${\varphi }_i\left(x, z, t\right)={\displaystyle \sum }_{\alpha =0}^{N-1}[f_{i,\alpha }\left(x, t\right)·z^{\alpha }].$$

(1)

In the i-layer, when both the displacement of one interface, z = η_i,1−j(x, t) (j = 0 or 1), and the pressure on the other interface, p_i,j(x, t), are known, the unknown variables were the velocity potential ϕ_i(x, z, t) and interface displacement η_i,j(x, t). Then, the definition of the functional for the variational problem in the i-layer, F_i, was as follows [20]:

$$F_i\left[{\varphi }_i,{\eta }_{i,j}\right]={{\displaystyle \int }}_{t_0}^{t_1}{{\displaystyle \iint }}_A{{\displaystyle \int }}_{{\eta }_{i,0}}^{{\eta }_{i,1}}\left[\frac{\partial {\varphi }_i}{\partial t}+\frac{1}{2}{\left(\nabla {\varphi }_i\right)}^2+\frac{1}{2}{\left(\frac{\partial {\varphi }_i}{\partial z}\right)}^2+gz+\frac{p_{i,j}+P_i+W_i}{{\rho }_i}\right]\hspace{0.17em}dz\hspace{0.17em}dA\hspace{0.17em}dt,$$

(2)

where the gravitational acceleration g was assumed to be constant at 9.8 m/s² regardless of latitude in this study, and ∇ = (∂/∂x, ∂/∂y) was a horizontal partial differential operator. The plane A which was the orthogonal projection of the object domain on to the x-y plane was assumed to be independent of time. The Coriolis force is ignored for simplicity along the paths of one-dimensional tsunami propagation in this paper, although it is an important factor for transoceanic tsunamis [6].

In comparison with the functional referred to in [21] for the rotational motion of a fluid, Equation (2) introduced an additional term of the integral of (p_i,j + P_i + W_i)/ρ_i as an interfacial-pressure term, without the terms related to vorticity. Using the functional of [21], after omitting the vorticity terms, the set of nonlinear equations for one-layer problems without thin plates was derived by [22].

P_i and W_i in Equation (2) were expressed by

$$P_i={{\displaystyle \sum }}_{k=1}^{i-1}\left[\left({\rho }_i-{\rho }_k\right)g{h}_k\right],$$

(3)

$$W_i={{\displaystyle \sum }}_{k=1}^i\left(-m_{k}g{\delta }_k\right),$$

(4)

respectively.

After substituting the velocity potential ϕ_i expanded in Equation (1) into Equation (2), the Euler-Lagrange equations on f_i,α and η_i,α were derived as

$${\eta }_{i,1}^{\alpha }\frac{\partial {\eta }_{i,1}}{\partial t}-{\eta }_{i,0}^{\alpha }\frac{\partial {\eta }_{i,0}}{\partial t}+\nabla \left[\left({\eta }_{i,1}^{\alpha +\beta +1}-{\eta }_{i,0}^{\alpha +\beta +1}\right)\nabla f_{i,\beta }\right]-\frac{\alpha \beta }{\alpha +\beta -1}\left({\eta }_{i,1}^{\alpha +\beta -1}-{\eta }_{i,0}^{\alpha +\beta -1}\right)f_{i,\beta }=0,$$

(5)

$${\eta }_{i,j}^{\beta }\frac{\partial f_{i,\beta }}{\partial t}+\frac{1}{2}{\eta }_{i,j}^{\beta +\gamma }\nabla f_{i,\beta }\nabla f_{i,\gamma }+\frac{1}{2}\beta \gamma {\eta }_{i,j}^{\beta +\gamma -2}{f}_{i,\beta }{f}_{i,\gamma }+g{\eta }_{i,j}+\frac{p_{i,j}+P_i+W_i}{{\rho }_i}=0 \left(j=0 \mathrm{or} 1\right),$$

(6)

where the sum rule of product was adopted for subscripts β and γ. For example, f_2,3 was the weighting of z³ in the 2nd layer.

In the derivation process of the equations, no assumption was used for the wave nonlinearity and dispersion of fluids without viscosity and compressibility, so the application of this model is expected to be theoretically free from limitations concerning the relative thickness of fluid layers or the frequency band of surface/internal waves. For long surface waves in one-layer problems without thin plates, the accuracy of the above equations was investigated by [23]: when the maximum order of equations is 2n, the order of error in the set of Equations (5) and (6) was σ^{4n + 2}, where σ was the representative ratio of water depth to wavelength. Conversely, the order of error in the extended Green-Naghdi equation [24] was σ^{2n + 2}. Therefore, especially when O(σ) ≪ 1, the accuracy of the former is significantly higher than that of the latter for n ≥ 1.

Regarding the i-plate, the horizontal length scale was assumed to be much larger than the thickness of the thin plate, so the differences in curvature between the upper surface, neutral plane, and lower surface of the thin plate were ignored. Therefore, the governing equation of motion for the i-plate was the following classical equation to describe the oscillation of an elastic thin plate:

$$m_i{\delta }_i\frac{{\partial }^2{\eta }_{i,1}}{\partial t^2}+B_i{\nabla }^2{\nabla }^2{\eta }_{i,1}+m_{i}g{\delta }_i+p_{i-1,0}-p_{i,1}=0,$$

(7)

where B_i was the flexural rigidity of the i-plate. Both the plate density m_i and vertical width δ_i were assumed to be constant throughout the i-plate, for simplicity.

When the representative values of wave height, wavelength, fluid depth, and density are H, l, d, and ρ, respectively, the dimensionless quantities were

$$\begin{array}{c}{x}^{*}=\frac{x}{l}, t^{*}=\frac{\sqrt{gd}}{l}t, {\nabla }^{*}=l\nabla , \frac{\partial }{\partial t^{*}}={\left(\frac{\partial }{\partial t}\right)}^{*}=\frac{l}{\sqrt{gd}}\frac{\partial }{\partial t},\\ {\eta }_{i,e}^{*}=\frac{{\eta }_{i,e}}{H}, {\delta }_i^{*}=\frac{{\delta }_i}{H}, m_i^{*}=\frac{m_i}{\rho }, B_i^{*}=\frac{B_i}{\rho g{l}^4}, p_{i,e}^{*}=\frac{p_{i,e}}{\rho gd}\end{array} \},$$

(8)

where e = 0 and 1.

We substituted Equation (8) into Equation (7), and obtained

$${\epsilon }^2{\sigma }^2{m}_i^{*}{\delta }_i^{*}\frac{{\partial }^2{\eta }_{i,1}^{*}}{\partial t^{*2}}+\epsilon B_i^{*}{\nabla }^{*2}{\nabla }^{*2}{\eta }_{i,1}^{*}+\epsilon m_i^{*}{\delta }_i^{*}+p_{i-1,0}^{*}-p_{i,1}^{*}=0,$$

(9)

where ε = H/d and σ = d/l were the representative ratio of wave height to water depth, and that of water depth to wavelength, respectively. In the manner similar to that of [25], each layer was assumed to be relatively shallow, such that O(ε) = O(σ²) ≪ 1. Thus, the first term on the left-hand side of Equation (9) could be ignored. Without this term, we obtained the i-plate equation for the dimensional quantities as

$$B_i{\nabla }^2{\nabla }^2{\eta }_{i,1}+m_{i}g{\delta }_i+p_{i-1,0}-p_{i,1}=0.$$

(10)

In this study, we consider the one-dimensional propagation problems of waves in the x-axis direction.

2.2. Numerical Method

The governing equations, namely Equations (5), (6) and (10), were transformed to finite-difference equations, and solved to study the interaction of fluid layers with thin plates in the vertical two dimensions, by applying the implicit scheme, which was developed by [26] for internal waves, to the present equations including the terms regarding surface and interface displacements. In the initial state at t = 0 s, the weighting coefficients f_i,α(x, 0 s) of the expanded velocity potential in Equation (1) were all zero, so the initial velocity was zero everywhere. In this paper, the values are written without considering significant digits, although the calculation was conducted using 64-bit floating-point numbers.

The numerical model was verified by [27], in which the numerical results of the surface displacements were in good agreement with the existing experimental data obtained by [28] for the disintegration of the incident solitary wave due to a floating thin plate. Based on the results, the generation of the preceding short waves were simulated successfully when the number of terms for the velocity potential expanded as in Equation (1), N, is two, where both the linear vertical distribution of horizontal velocity u_i and the uniform vertical distribution of vertical velocity w_i were considered, with the balance between the nonlinearity and dispersion of the waves.

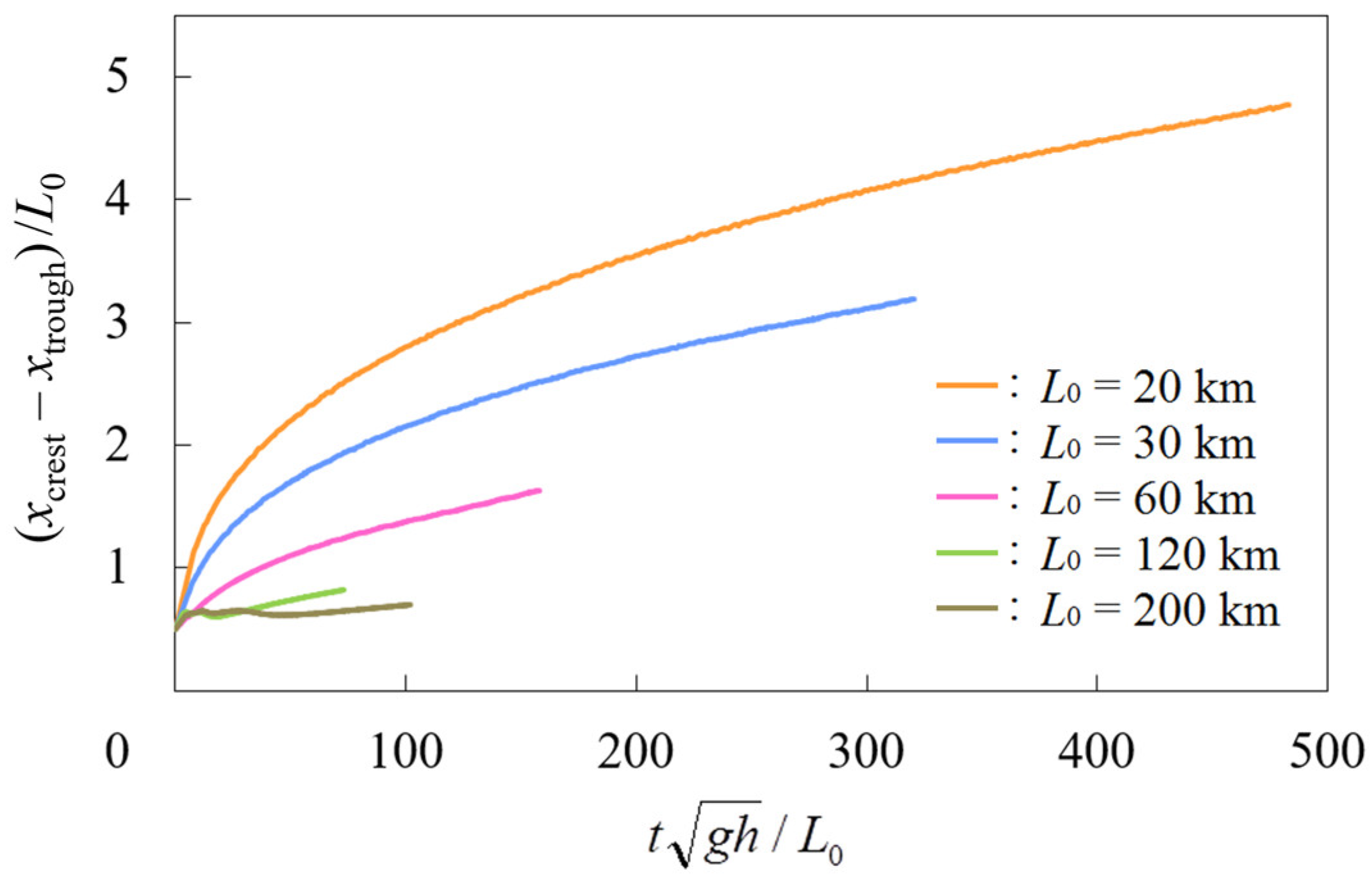
3. Estimate Formulae for the Time Variations of Tsunami Height and Wavelength in Distant Tsunami Propagation

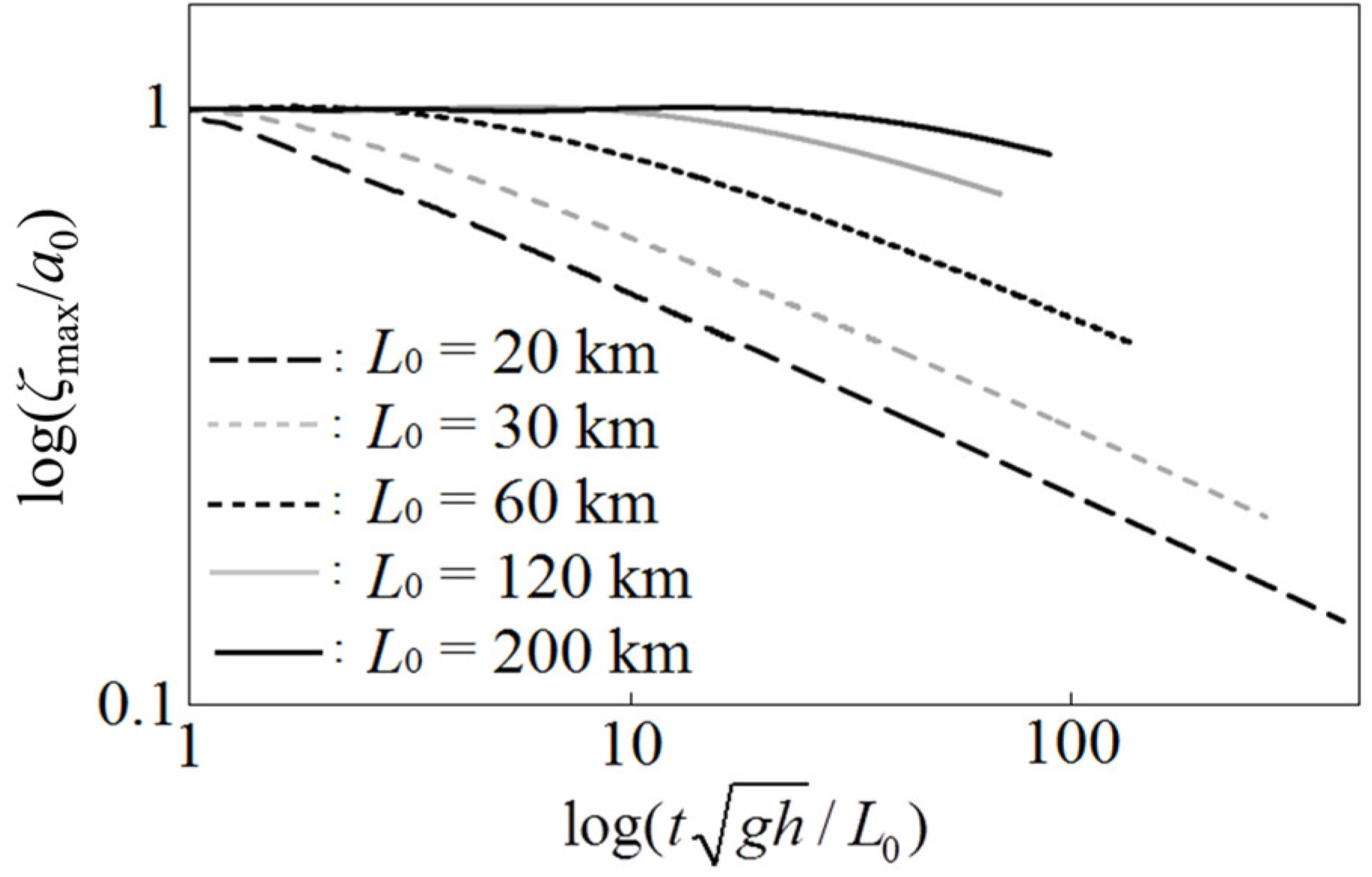
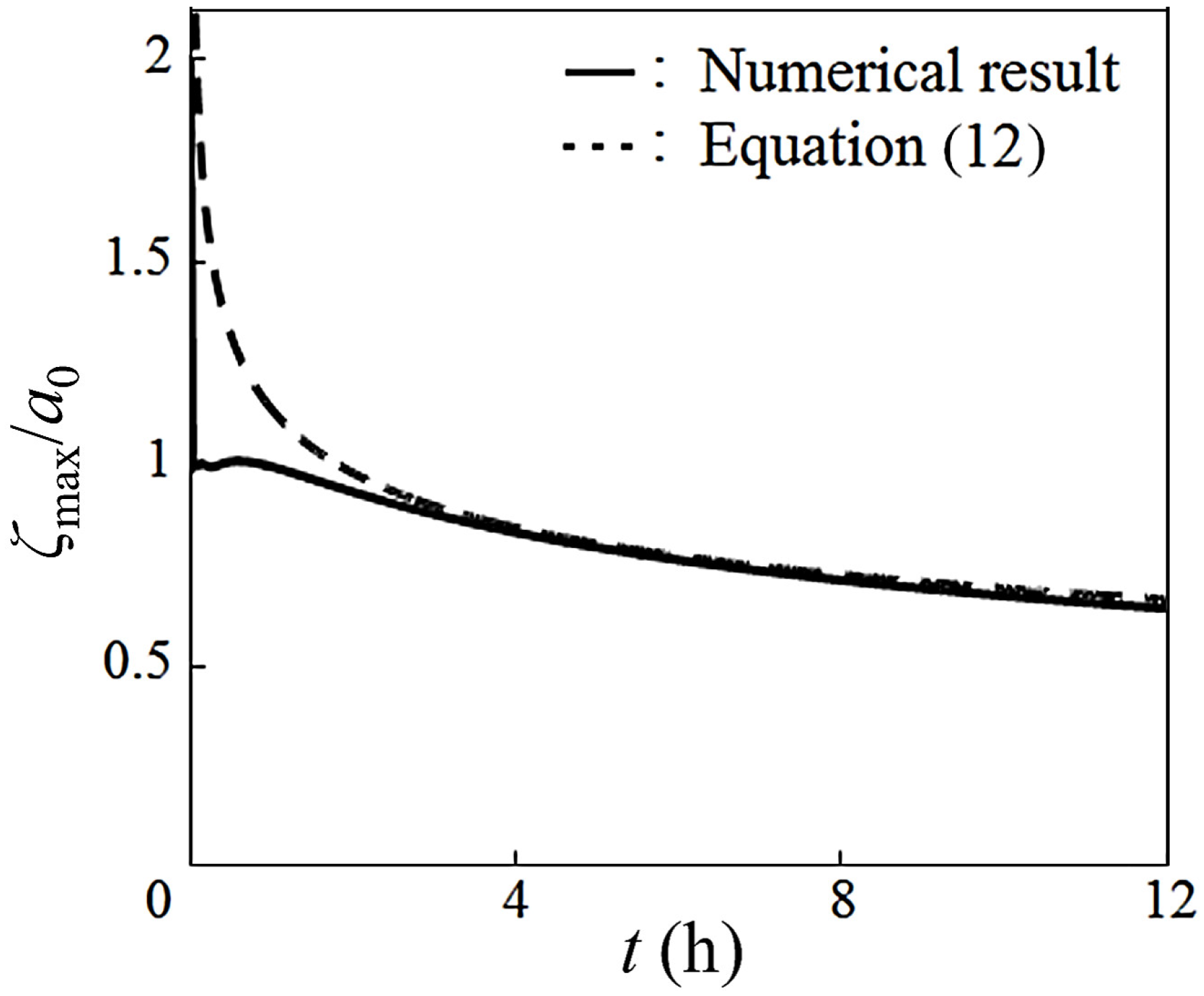
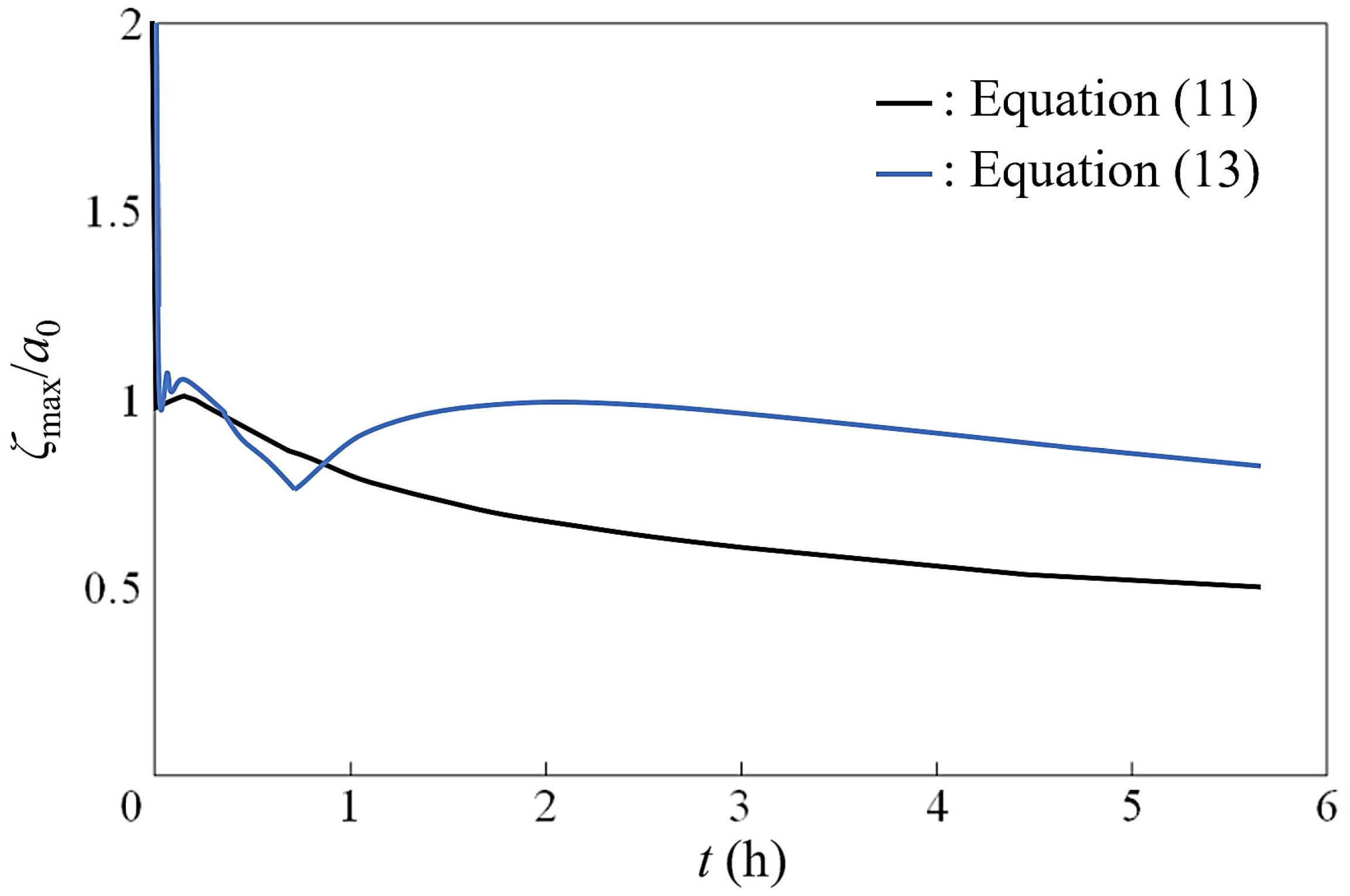
3.1. Estimate Formula for the Time Variation of Tsunami Height in Distant Tsunami Propagation

We focused on one-layer fluid problems without thin plates, to obtain a formula for estimating the tsunami height of distant tsunamis, based on the information on the initial water surface profile in a tsunami source area, namely the initial tsunami profile. In order to consider the dispersion of distant tsunamis, the number of terms for the velocity potential expanded as in Equation (1), N, was two, so the velocity potential ϕ(x, z, t) was represented by f₀(x, t) + z·f₁(x, t). We assumed that the initial tsunami profile was a relatively long crest caused by an uplift of the seabed. The perfect reflection was assumed as the boundary condition at x = 0 km, and the initial tsunami profile, namely z = η_1,1(x, t) = ζ(x, t) at t = 0 s, was given by

$$\zeta \left(x, 0 \mathrm{s}\right)/a_0=\{\begin{array}{c} 1+\cos \left[2\pi \left(x/L_0\right)\right] \mathrm{when} 0 \mathrm{km}\le x<L_0/2\\ 0 \mathrm{when} x\ge L_0/2\end{array},$$

(11)

where the initial tsunami height a₀ was 1 m, and L₀ was the initial tsunami wavelength. The initial water surface profile of a submarine-earthquake tsunami is determined by seabed uplift and subsidence, so a sinusoidal curve as described in Equation (11) was assumed regardless of the nonlinearity of the computational framework.

It should be noted that even if a crest is generated in the tsunami source area, when the wavelength is not sufficiently long, the crest will disappear based on the wave dispersion, creating a trough behind it, as described by [4]. Thus, in the present computation, L₀ was on the order of tens to hundreds of kilometers. The grid size Δx was 1.0 km and the time interval Δt was 0.05 s.

For simplicity, the bathymetry was uniform, where the still seawater depth h was uniformly 4000 m, similar to the average depth of the Pacific Ocean. Figure 2 depicts the numerical calculation results for the relative tsunami height of the leading wave, namely the first wave, where the tsunami height is defined by the maximum water surface displacement ζ_max at each location x. In the calculations, the initial tsunami wavelength L₀ was of 20 km, 30 km, 60 km, 120 km, and 200 km, although earthquakes may excite wavelengths longer than 200 km. Figure 2 indicates that the reduction rate of the tsunami height ζ_max of the first wave increased, as the initial tsunami wavelength L₀ was decreased.

Based on the calculation results, we created an estimate formula for the time variation of tsunami height. In any curve of the log-log graph depicted in Figure 2, the reduction rate was almost constant after a certain propagation time of the tsunamis, so we determined both the intercept k₁ on the vertical axis and the slope k₂ of the almost straight line. Then, we evaluated the general forms of k₁ and k₂ with respect to the ratio of still seawater depth to initial tsunami wavelength, h/L₀, and obtained the estimate formula for the time variation of the relative tsunami height of the first wave as

$$\begin{array}{c}{\zeta }_{\max }/a_0={10}^{k_1}{\left(t\sqrt{gh}/L_0\right)}^{k_2},\\ k_1=101.24{\left(h/L_0\right)}^3-35.77{\left(h/L_0\right)}^2+2.10\left(h/L_0\right)+0.22,\\ k_2=-97.56{\left(h/L_0\right)}^3+41.13{\left(h/L_0\right)}^2-5.67\left(h/L_0\right)-0.07\end{array}\}.$$

(12)

In Figure 3, we compare the relative tsunami height ζ_max/a₀ estimated by Equation (12) with that obtained using the numerical model, to verify the accuracy of Equation (12), for each value of L₀. When L₀ is 120 km and 200 km, the accuracy of the estimated values was good for t > 4 h and 12 h, respectively, where the tsunamis were generated at t = 0 h, although the accuracy was reduced near the tsunami source.

Equation (12) is an estimate formula obtained using the values of k₁ and k₂ when the initial tsunami wavelengths L₀ are 20 km, 30 km, 60 km, 120 km, and 200 km. When L₀ is 80 km, which is different from these values, we compare the estimated value and the corresponding numerical result in Figure 4. This figure indicates that when L₀ is 80 km, the accuracy of the estimated tsunami height was good for t > 2.5 h.

Furthermore, although Equation (12) was obtained when the still seawater depth h is 4000 m, the formula is described for the nondimensional values. In Figure 5, we compare the time variation of the relative tsunami height ζ_max/a₀ estimated by Equation (12) and the corresponding numerical result when h is 2000 m and L₀ is 60 km. Based on this figure, the formula was applicable for t > 3 h. When applying the estimate formula in the ocean with a distribution of still seawater depth h, it is recommended to use the most accurate mean of h possible, along tsunami propagation.

In the above discussion, the initial tsunami profile consisted of only one crest. If the initial tsunami profile includes both a long crest and a trough, several crests and troughs can be generated in the wave-transformation process with wave disintegration, so the crest generated from the initial long crest may overlap the crests generated from the initial trough, resulting in an increase in tsunami height. When the perfect reflection is assumed as the boundary condition at x = 0 km, and the initial tsunami profile z = ζ(x, 0 s) is given by

$$\zeta \left(x, 0 \mathrm{s}\right)/a_0=\{\begin{array}{c} 1+\cos \left[2\pi \left(x/L_0\right)\right] \mathrm{when} 0 \mathrm{km}\le x<L_0/2\\ -1+\cos \left[2\pi \left(x/L_0\right)-\pi \right] \mathrm{when} L_0/2\le x<3L_0/2\\ 0 \mathrm{when} 3L_0/2\le x\end{array},$$

(13)

the time variation of the relative tsunami height ζ_max/a₀ is presented in Figure 6, with the corresponding result using Equation (11), where a₀ was 1 m, the initial tsunami wavelength L₀ was 60 km, and the still seawater depth h was 4000 m. In this case, the long crest generated from the initial crest overlapped the preceding long crest generated from the initial trough, and the tsunami height increased when 0.7 h < t < 2.1 h. Therefore, it should be noted that the tsunami height estimated using Equation (12) is valid when the long crest generated from the initial crest continues to precede other waves, or after it overtakes all the other waves that were ahead of it.

3.2. Estimate Formula for the Time Variation of Wavelength in Distant Tsunami Propagation

We considered one-layer fluid problems without thin plates in order to obtain a formula for estimating the wavelength of distant tsunamis, using the information on the initial tsunami profile consisting only of a relatively long crest. The perfect reflection was assumed as the boundary condition at x = 0 km, and the initial tsunami profile was given by Equation (11), in which a₀ was 1 m.

Figure 7 depicts the numerical calculation results for the relative half wavelength (x_crest − x_trough)/L₀ of the first wave, for various values of the initial tsunami wavelength L₀, when the still seawater depth h is 4000 m. The half wavelength is defined by the horizontal interval between the locations of the highest and lowest water levels at each time, namely x_crest and x_trough, respectively, of the first wave.

Based on Figure 7, the estimate formula expressing the time variation of the relative half wavelength of the first wave was obtained as

$$\begin{array}{c}\left(x_{\mathrm{crest}}-x_{\mathrm{trough}}\right)/L_0=k_3\hspace{0.17em}{\left(t\sqrt{gh}/L_0\right)}^{k_4},\\ k_3=-191.77{\left(h/L_0\right)}^3+78.43{\left(h/L_0\right)}^2-8.33\left(h/L_0\right)+0.71,\\ k_4=133.28{\left(h/L_0\right)}^3-59.68{\left(h/L_0\right)}^2+8.87\left(h/L_0\right)-0.13\end{array}\}.$$

(14)

In Figure 8, we compare the time variation of the relative half wavelength (x_crest − x_trough)/L₀ of the first wave estimated by Equation (14) with the corresponding numerical result depicted in Figure 7, for each value of the initial tsunami wavelength L₀. This figure indicates that when t > 4.5 h, the relative half wavelength increased, as h/L₀ was increased, because of the stronger dispersion of waves. In particular, when L₀ is 200 km, the formula is applicable for a longer propagation distance of tsunamis.

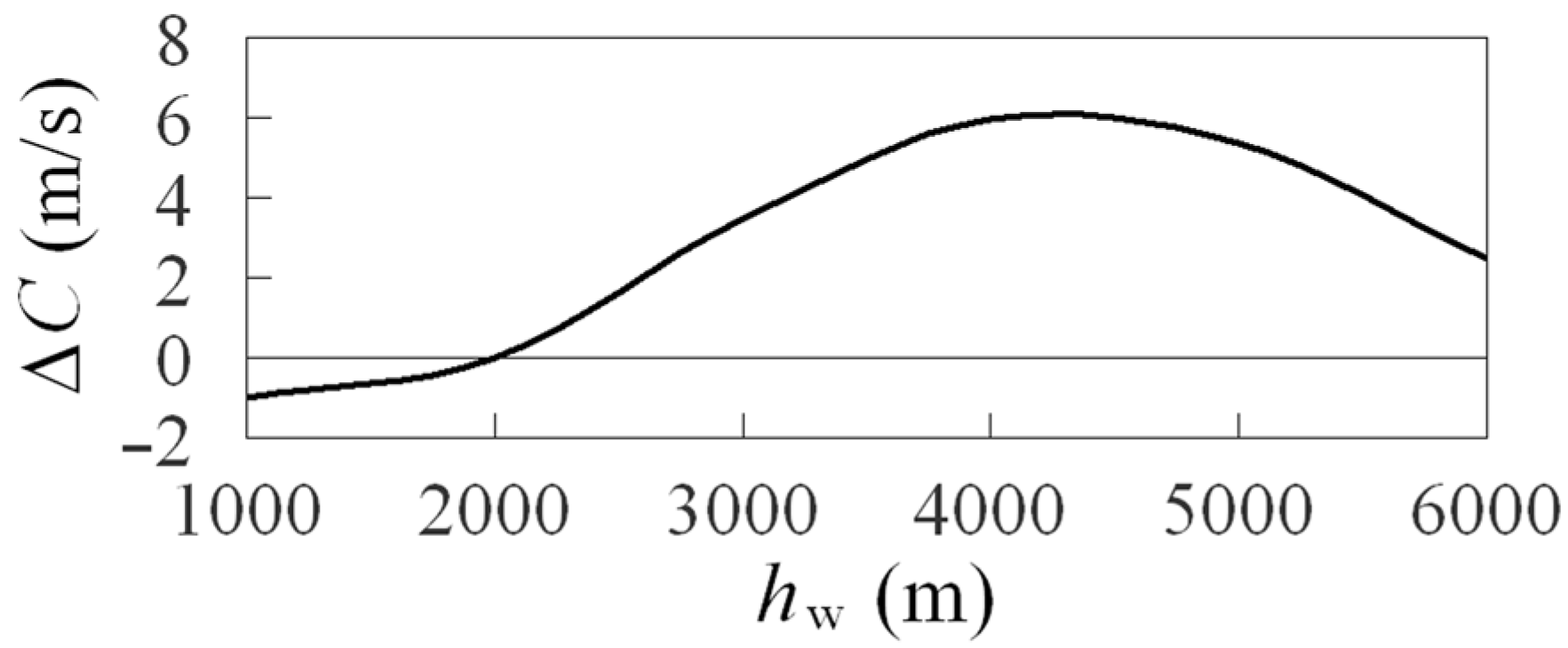
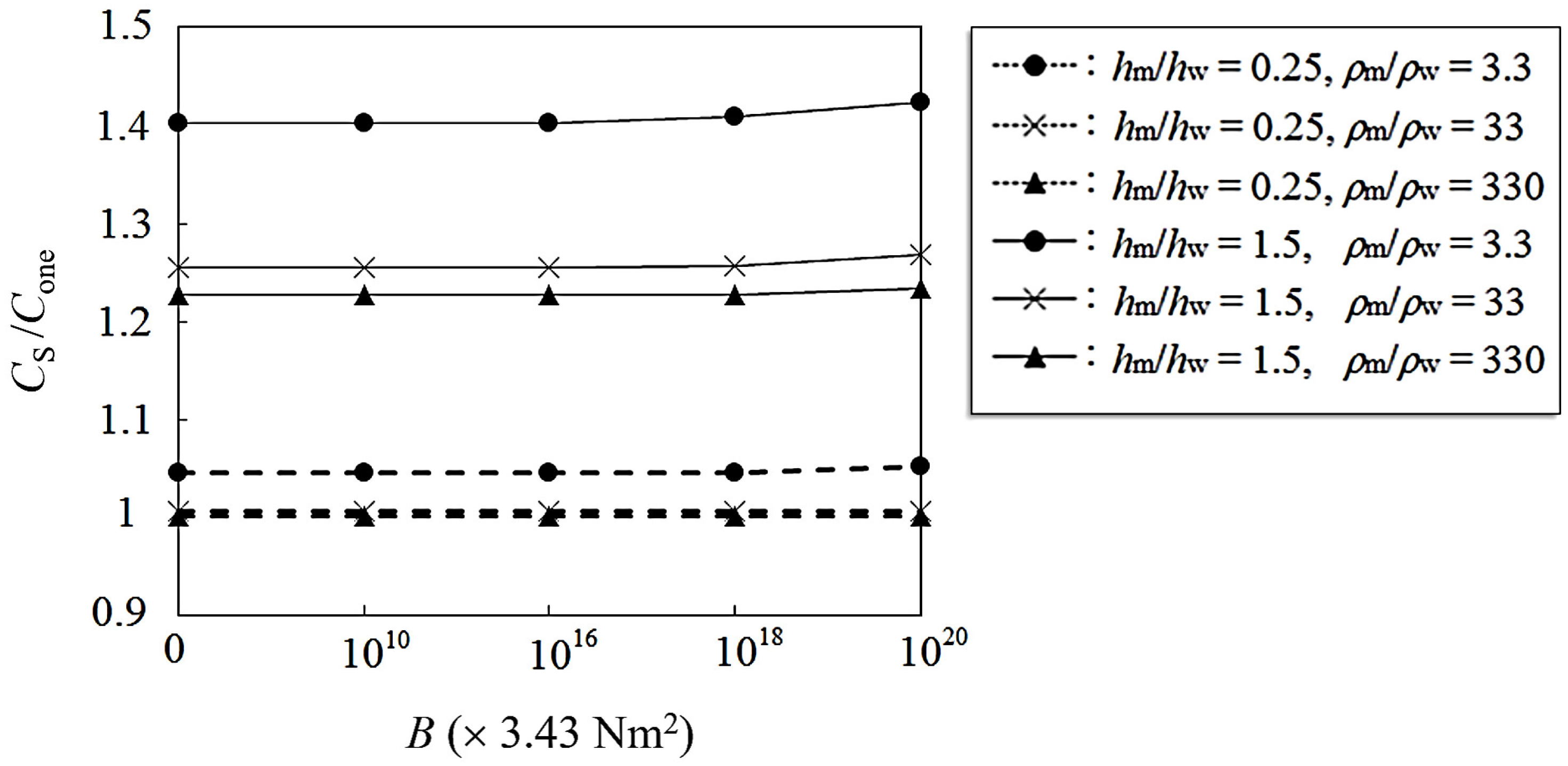
4. Effects of the Upper-Mantle and Plate Motion on Distant Tsunami Propagation

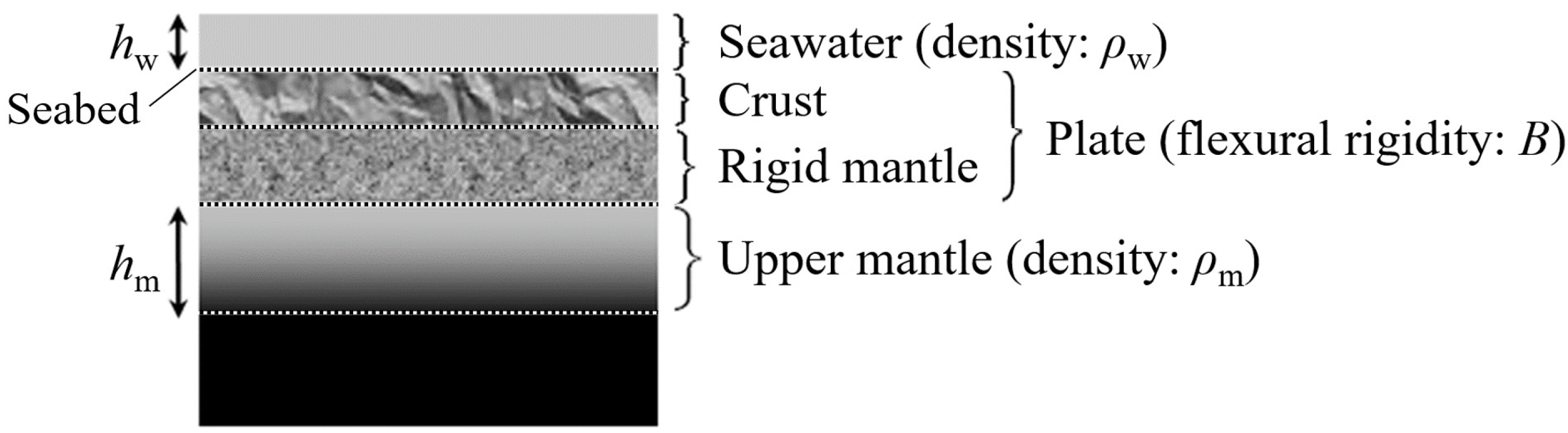
4.1. Structural Model of Earth

When the propagation distance of tsunamis is very large, the difference in propagation distance due to the difference in phase velocity appears greatly between calculated and measured values, even if both the nonlinearity and dispersion of tsunamis are considered as in Section 3. To consider the cause, the effects of the seawater compressibility and Earth elasticity on tsunami propagation have been examined in the numerical calculations, as mentioned in Section 1, with reference to the theoretical studies including [29,30,31]. However, there are still unknowns about the internal structure of Earth, and there is room for investigation to clarify the cause. In this study, we analyzed the effects of the upper-mantle and plate motion on the propagation processes of distant tsunamis. The present model of the internal structure near Earth surface is illustrated in Figure 9, in which under the bottom of seawater, namely the seabed, there is a plate consisting of a crust and a rigid surface layer of mantle, under which the upper mantle exists.

In the model, the assumptions are as follows:

(1)

The plate is an elastic body with a large horizontal scale, so the plate movement is considered at the neutral plane, regardless of the plate thickness. In the present computation, the discontinuity between multiple plates was ignored, and the flexural rigidity of the plate, B, was uniform.

(2)

The upper mantle under the plate behaves like a fluid, although it is a substantial idealization in the modeling. We have not proved that the upper mantle has fluid properties on the tsunami time scale, but there is no proof that it does not, because seismic-wave data on the surface of Earth alone do not clarify both the mechanism and accurate paths of seismic-wave propagation in the deeper part of Earth, and the internal structure of Earth has not been revealed. Although it is unclear whether molten mantle is under the entire plate, we consider that the areas of fluid mantle are connected under the paths of tsunamis in the present study.

(3)

The part below the upper mantle is less likely to affect tsunami propagation, and the upper-mantle bottom in a very deep position is a fixed horizontal plane.

Therefore, from bottom to top in the initial state of computation, on a fixed horizontal plane, there was a fluid corresponding to the upper mantle with a uniform depth of h_m; on this fluid, a thin plate representing a plate was lying; on this thin plate, the seawater with a uniform depth of h_w existed. The upper surface of the seawater was a free water surface, and the densities of the seawater and upper mantle, ρ_w and ρ_m, respectively, were assumed to be constant.

In the numerical model, the multilayer fluids were not viscous, so the viscosity of the upper mantle could not be considered. Therefore, instead of the unclear liquidity and movement range of the upper mantle, various values were used for both its density ρ_m and initial depth h_m. For example, when the upper mantle is difficult to move, the value of ρ_m was set to be large.

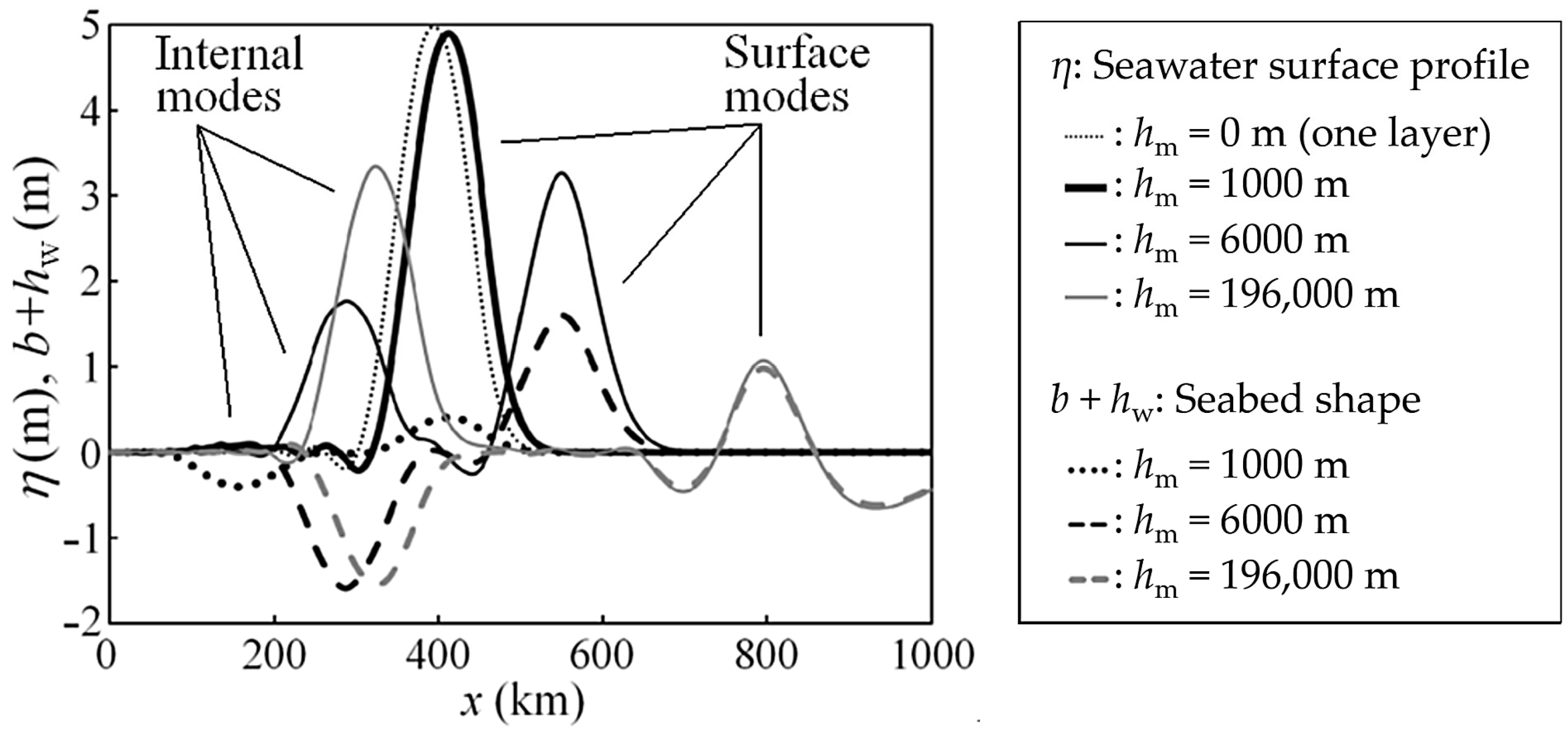
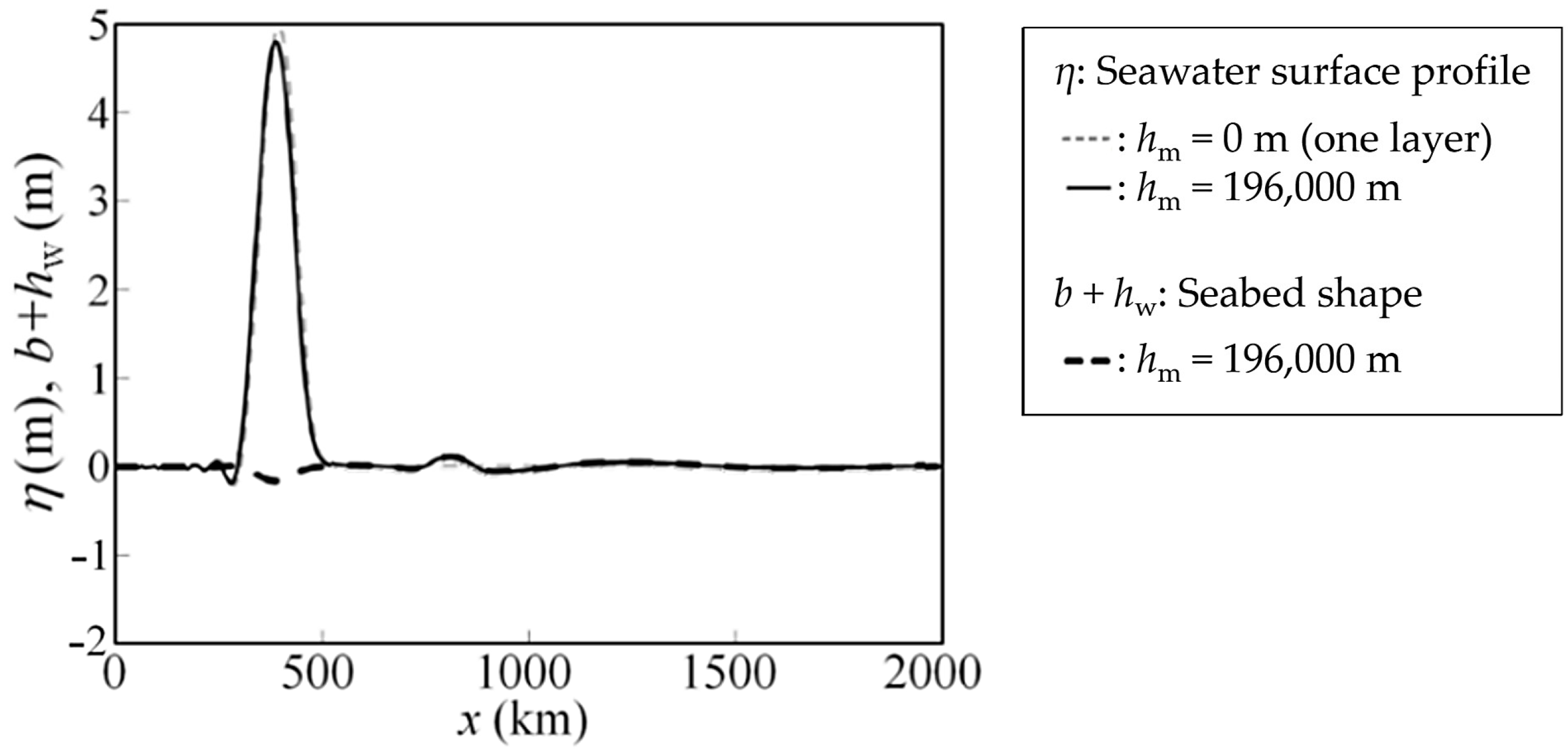
4.2. Effects of the Upper-Mantle and Plate Motion on Distant Tsunami Propagation

The seawater surface profile and seabed shape were expressed as z = η_1,1 = η and z = η_1,0 + h_w = b + h_w, respectively, using the displacements η and b from z = 0 m, respectively. The perfect reflection was assumed as the boundary condition at x = 0 km, and the initial water surface profile at t = 0 s was given by

$$\eta \left(x, 0 \mathrm{s}\right)/a_0=\{\begin{array}{c} 1+\cos \left[2\pi \left(x/L_0\right)\right] \mathrm{when} 0 \mathrm{km}\le x<L_0/2\\ 0 \mathrm{when} x\ge L_0/2\end{array},$$

(15)

where a₀ was 5 m, and the initial tsunami wavelength L₀ was 200 km.

In fluid motion, to consider both the nonlinearity and dispersion of waves, the number of terms for the velocity potential expanded as in Equation (1), N, was three, so ϕ_i(x, z, t) = f_i,0(x, t) + z·f_i,1(x, t) + z²·f_i,2(x, t) (i = 1 and 2).

We assumed that the seawater density ρ_w was 1000 kg/m³ and the still seawater depth h_w was uniformly 4000 m. Then, the remaining parameters were the upper-mantle density ρ_m, upper-mantle initial depth h_m, and plate flexural rigidity B. Assuming the values of these unclear parameters ρ_m, h_m, and B, several examples of the numerical calculation results for the water surface profile z = η and seabed shape z = b + h_w at t = 2000 s are presented in Figure 10, Figure 11, Figure 12 and Figure 13. In the figures, the water surface profiles of the corresponding tsunamis traveling in a one-layer problem without the motion of the upper mantle and plate are also depicted for comparison, where the one layer was the seawater layer with a density of ρ_w and an initial depth of h_w.

Depicted in Figure 10 are the numerical results at t = 2000 s, where the initial depth of the upper mantle, h_m, was of 1000 m, 6000 m, and 196,000 m, and the flexural rigidity of the plate, B, was 0 Nm². The density of the upper mantle, ρ_m, was 3300 kg/m³, which was determined with reference to [32]. Figure 10 indicates the propagation of both the surface-mode and internal-mode tsunamis in the two layers, in which the upper and lower layers consisted of the seawater and upper mantle, respectively. In the surface mode, the water surface profile and seabed shape were in phase, whereas in the internal mode, they were in opposite phase.

When the initial depth of the upper mantle, h_m, is 1000 m, the leading crest was the first crest in a surface mode, and appeared around x = 800 km at t = 2000 s. The phase velocities of the crests in surface modes were larger than that of the corresponding tsunami in the one-layer problem, because the total depth in the surface modes included the depths of both the seawater and upper mantle, and was larger than the total depth, which was the seawater depth, in the one-layer problem. At t = 2000 s, the location of the first crest peak in the surface mode, x_peak, was 550 km when h_m is 6000 m, and x_peak was 412 km when h_m is 1000 m, the latter of which was close to the location of the first peak in the corresponding one-layer problem because the upper mantle with a shallow depth was not effective.

Conversely, the phase velocities in the internal modes were slower than that in the corresponding one-layer problem, regardless of the values of the upper-mantle depth h_m, as indicated in Figure 10. As h_m was increased, both the phase velocity and tsunami height in the internal modes increased, where the tsunami height is defined by the maximum value of water surface displacement η in each mode at each location. When h_m is 196,000 m, the tsunami height in the internal mode was larger than that in the surface mode, whereas when h_m is 6000 m, the reverse was true.

Figure 11 depicts the numerical results at t = 2000 s, where h_m = 196,000 m, ρ_m = 3300 kg/m³, and B = 3.43 × 10¹⁰ Nm². Comparing the results in Figure 11 with the results for the case in which h_m = 196,000 m, ρ_m = 3300 kg/m³, and B = 0 Nm² in Figure 10, there was almost no difference, so the plate flexural rigidity B with an order of 10¹⁰ Nm² hardly affected the tsunami height and phase velocity in both the surface and internal modes.

Figure 12 presents the numerical results at t = 2000 s, where h_m = 196,000 m, ρ_m = 3300 kg/m³, and B = 3.43 × 10²⁰ Nm². The phase velocity of the second peak in the surface mode was approximately 407 m/s in Figure 12, whereas 397 m/s in Figure 11, in which h_m = 196,000 m, ρ_m = 3300 kg/m³, and B = 3.43 × 10¹⁰ Nm², so the phase velocity in the surface mode was affected by the plate flexural rigidity with an order of 10²⁰ Nm². However, the effect of the difference in the plate flexural rigidity was hardly observed in the internal modes depicted in Figure 11 and Figure 12.

Figure 13 depicts the numerical results at t = 2000 s, where h_m = 196,000 m, ρ_m = 33,000 kg/m³, and B = 3.43 × 10¹⁰ Nm². Based on the figure, the tsunami height in the surface mode was remarkably reduced owing to the large upper-mantle density ρ_m. Conversely, both the tsunami height and phase velocity in the internal mode were increased and closer to those in the corresponding one-layer problem.

We specifically consider the cases in which tsunamis generated near a Chilean coast reach a Japanese coast, assuming that the distance between the two coasts is 17,000 km, and the still seawater depth h_w is uniformly 4000 m.

Table 1. Tsunami height ratio (η_I)_max/(η_S)_max and arrival-time delay Δt_Chile, where (η_I)_max and (η_S)_max are the tsunami heights in the internal and surface modes, respectively, near a Japanese coast, and Δt_Chile represents the difference between the arrival time on the Japanese coast of the first crest with a significant tsunami height in the internal mode and that of the tsunami with a phase velocity of $\sqrt{{gh}_w}$. It was assumed that the distance from the tsunami source near a Chilean coast to the Japanese coast was 17,000 km, and the initial depth h_w and density ρ_w of seawater were uniformly 4000 m and 1000 kg/m³, respectively. The initial depth and density of the upper mantle are represented by h_m and ρ_m, respectively, and B is the flexural rigidity of the plate. The initial water surface profile was given by Equation (15), in which a₀ was 5 m and L₀ was 200 km.

Upper-Mantle Initial Depth hm (m)	Upper-Mantle Density ρm (kg/m3)	Plate Flexural Rigidity B (Nm2)	Tsunami Height Ratio (ηI)max/(ηS)max	Arrival-Time Delay ΔtChile	Figure	Category *
1000	3300	0	-	-	Figure 10	xx
		3.43 × 1018	-	-	-	xx
6000	3300	0	0.54	8 h 57 min	Figure 10	x
		3.43 × 1020	0.58	8 h 57 min	-	x
	33,000	0	4.9	1 h 16 min	-	S
		3.43 × 1016	3.9	45 min	-	S
		3.43 × 1020	4.0	45 min	-	S
	330,000	0	-	15 min	-	x
		3.43 × 1010	-	15 min	-	x
196,000	3300	0	3.2	4 h 57 min	Figure 10	x
		3.43 × 1010	3.2	4 h 57 min	Figure 11	x
		3.43 × 1020	3.2	4 h 57 min	Figure 12	x
	9900	0	12.3	1 h 49 min	-	x
		3.43 × 1010	12.3	1 h 49 min	-	x
	13,200	0	16.9	1 h 16 min	-	SI
		3.43 × 1010	18.2	1 h 16 min	-	SI
	33,000	0	43.5	45 min	-	I
		3.43 × 1010	48.0	45 min	Figure 13	I
		3.43 × 1020	48.0	45 min	-	I
	330,000	0	450	15 min	-	x
		3.43 × 1020	450	15 min	-	x

* The categories are as follows: xx: The internal-mode tsunami height is not significant. x: The internal-mode tsunami height is significant, but the arrival-time delay in the internal mode is not within the range of 30 min to 1 h 30 min. S: The arrival-time delay in the internal mode is within the range of 30 min to 1 h 30 min, but the surface-mode tsunami height is significantly large. SI: The arrival-time delay in the internal mode is within the range of 30 min to 1 h 30 min, but the surface-mode tsunami may be observed, although its tsunami height is not as large as in category S. I: The arrival-time delay in the internal mode is within the range of 30 min to 1 h 30 min, and the tsunami height is significant only in the internal mode.

describes the numerical results of the tsunami height ratio near the Japanese coast, (η_I)_max/(η_S)_max, where (η_I)_max and (η_S)_max are the tsunami heights in the internal and surface modes, respectively, near the Japanese coast. Table 1 also describes Δt_Chile, which represents the difference between the arrival time on the Japanese coast of the first crest with a significant tsunami height in the internal mode and that of the tsunami with a phase velocity of $\sqrt{{gh}_{\mathrm{w}}}$.

In Table 1, the velocity $\sqrt{{gh}_{\mathrm{w}}}$, which is the phase velocity of linear waves in shallow water, is used as a traveling speed to be compared, because the arrival time of tsunamis is often evaluated using a map created with $\sqrt{{gh}_{\mathrm{w}}}$ based on the bathymetry of the ocean.

For example, the internal-mode tsunami depicted in Figure 13 propagated at a phase velocity of approximately 192 m/s, slower than the one-layer tsunami with a phase velocity of $\sqrt{{gh}_{\mathrm{w}}}$ ≃ 198 m/s. Thus, in this case, a tsunami generated near the Chilean coast will reach the Japanese coast approximately 45 min later than the tsunami with a phase velocity of $\sqrt{{gh}_{\mathrm{w}}}$. However, when the upper-mantle density ρ_m is 330,000 kg/m³, the effect of the mantle fluidity is reduced, so the arrival-time delay Δt_Chile will not be so large, namely approximately 15 min, as indicated in Table 1.

Therefore, under certain conditions of the upper mantle and plate, internal-mode tsunamis with a significant wave height can propagate slower than the corresponding one-layer tsunamis. As reported in [8], at several Japanese coasts, the arrival time of the first wave due to 2010 Chile Maule earthquake was 30 min to 1 h 30 min later than that evaluated using the linear shallow water model. Based on the obtained arrival-time delay Δt_Chile, the cases in Table 1 are divided into five categories, including categories “S,” “SI,” and “I,” in which Δt_Chile of the first internal-mode tsunami with a significant tsunami height is 30 min to 1 h 30 min.

In category S, the tsunami height in the surface mode is significantly large, so the surface-mode tsunami with a phase velocity larger than that of the corresponding one-layer tsunami will be observed as the first tsunami at the Japanese coast.

In category SI, although the tsunami height in the surface mode is not as large as that in category S, the surface-mode tsunami may be first observed at the Japanese coast.

Conversely, in category I, when the upper-mantle initial depth h_m is large, namely 196,000 m, and the upper-mantle density ρ_m is moderately large, namely 33,000 kg/m³, the tsunami height ratio (η_I)_max/(η_S)_max is 43.5 or 48.0, which means that the internal-mode tsunami height is remarkably larger than the surface-mode tsunami height, so the internal-mode surface wave with a phase velocity slower than $\sqrt{{gh}_{\mathrm{w}}}$ will be recognized as the first tsunami at the Japanese coast. In this case, the arrival-time delay Δt_Chile of the internal-mode surface wave from the arrival time of the tsunami with a phase velocity of $\sqrt{{gh}_{\mathrm{w}}}$ is approximately 45 min.

When the initial total depth h_w + h_m, upper-mantle density ρ_m, and plate flexural rigidity B are 200,000 m, 33,000 kg/m³, and 0 Nm², respectively, Figure 14 depicts the traveling-velocity difference ΔC = $\sqrt{{gh}_{\mathrm{w}}}$ − C_I for different still seawater depth h_w, where C_I is the average value of the phase velocity in the internal mode for 0 s ≤ t ≤ 2000 s. In this case, ΔC becomes maximal when h_w is 4250 m, as indicated in Figure 14.

Furthermore, the initial water surface profile at t = 0 s was given by Equation (15), in which the perfect reflection was assumed as the boundary condition at x = 0 km, a₀ was 5 m, and the initial tsunami wavelength L₀ was 60 km. When the still seawater depth h_w is 4000 m and the seawater density ρ_w is 1000 kg/m³, Figure 15 presents the velocity ratios C_S/C_one for various values of the parameters h_m, ρ_m, and B, where C_S is the phase velocity in the surface mode, and C_one is that obtained using the present numerical model in the corresponding one-layer problem. It should be noted that C_one may not be $\sqrt{{gh}_{\mathrm{w}}}$. Figure 15 indicates that the phase velocity C_S was larger than C_one, and the velocity ratio C_S/C_one increased, as the upper-mantle initial depth h_m increased and the upper-mantle density ρ_m decreased. The velocity ratio C_S/C_one was almost unaffected by the plate flexural rigidity B when B ≤ 3.43 × 10¹⁶ Nm².

Conversely, Figure 16 depicts the velocity ratios C_I/C_one, where C_I was the phase velocity in the internal mode. Based on the figure, C_I was slower than C_one, and C_I/C_one increased as h_m and ρ_m increased. The velocity ratio C_I/C_one was almost independent of B when ρ_m/ρ_w = 330 and when ρ_m/ρ_w = 33 and h_m/h_w = 0.25, because the upper mantle was relatively difficult to move.

5. Conclusions

The numerical simulations were generated to investigate the propagation processes of distant tsunamis, using the set of wave equations based on the variational principle considering both the strong nonlinearity and strong dispersion of waves.

First, we proposed the estimate formulae for the time variations of the tsunami height and wavelength of the first distant tsunami with a uniform initial seawater depth, assuming the initial tsunami profile as a relatively long crest. The accuracy of the estimated tsunami height was good except near the tsunami source. The proposed estimate formulae were obtained on the assumption that the still seawater depth was constant, so the average water depth along the tsunami propagation path will be used in application. Furthermore, it should be noted that the effects of reflection and refraction caused by the spatial change of topography were not considered. Moreover, wave deformation due to shallowing on continental slopes and shelves was not considered, so the application range of the estimate formulae is limited to before tsunamis reach a continental slope.

Second, we considered the plate elasticity and upper-mantle fluidity of Earth, to examine their effects on distant tsunami propagation. When the plate and upper mantle meet certain conditions, in which the upper-mantle depth is large and the upper-mantle density is moderately large, internal-mode tsunamis with a significant tsunami height will propagate slower than the tsunamis in the corresponding one-layer problems.

Future work is required to improve the present model, based on information updated by the observations of distant tsunami propagation and investigations of Earth’s internal structure. Especially regarding the assumption of Earth’s internal structure, it is necessary to compare the results obtained through this model with those of other studies from various perspectives to deepen the discussion.