Next Article in Journal
Experimental and Numerical Study of Cavitation Number Limitations for Hydrodynamic Cavitation Inception Prediction
Previous Article in Journal
Thermohydraulic Performance of Chevron Pin-Fins
Previous Article in Special Issue
Efficiency and Aerodynamic Performance of Bristled Insect Wings Depending on Reynolds Number in Flapping Flight
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fluids
Volume 7
Issue 6
10.3390/fluids7060197
fluids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances

by
Amirtahà Taebi
Department of Agricultural and Biological Engineering, Mississippi State University, 130 Creelman Street, Starkville, MS 39762, USA
Fluids 2022, 7(6), 197; https://doi.org/10.3390/fluids7060197
Submission received: 20 April 2022 / Revised: 31 May 2022 / Accepted: 5 June 2022 / Published: 9 June 2022
(This article belongs to the Special Issue Advances in Biological Flows and Biomimetics, Volume II)
Browse Figures
Versions Notes

Abstract

:
Computational fluid dynamics (CFD) modeling of blood flow plays an important role in better understanding various medical conditions, designing more effective drug delivery systems, and developing novel diagnostic methods and treatments. However, despite significant advances in computational technology and resources, the expensive computational cost of these simulations still hinders their transformation from a research interest to a clinical tool. This bottleneck is even more severe for image-based, patient-specific CFD simulations with realistic boundary conditions and complex computational domains, which make such simulations excessively expensive. To address this issue, deep learning approaches have been recently explored to accelerate computational hemodynamics simulations. In this study, we review recent efforts to integrate deep learning with CFD and discuss the applications of this approach in solving hemodynamics problems, such as blood flow behavior in aorta and cerebral arteries. We also discuss potential future directions in the field. In this review, we suggest that incorporating physiologic understandings and underlying fluid mechanics laws in deep learning models will soon lead to a paradigm shift in the development novel non-invasive computational medical decisions.

1. Introduction

A fluid dynamics problem can be solved mathematically through governing equations, such as the Navier–Stokes equations of conservation of mass and conservation of momentum. For problems associated with a higher degree of complexity, it becomes challenging to solve the governing equations theoretically. This is usually the case in biomedical applications with the aim of investigating physiological flows where patient-specific geometries and conditions should be considered in order to achieve a personalized solution. In such cases, computational fluid dynamics (CFD) provides a powerful alternative based on numerical methods that can be applied to a large array of fluid dynamics equations and solve these complex problems either directly or iteratively [1].
CFD simulations have been increasingly used to analyze biomedical flows both in health and disease. Physiological flows, such as cardiovascular flow [2,3,4,5,6], respiratory flow [7,8,9], cerebrospinal flow [10,11], and intracellular flow [12,13], have been investigated through CFD simulations. In addition, CFD has been used to analyze and develop medical diagnostic methods [14,15,16,17], drug delivery systems [18,19], personalized treatments and treatment planning [20,21,22,23], and medical devices [24,25,26,27].
In the last decade, there was a resurgence in image-based CFD modeling [28], which brought the idea of patient-specific simulations closer to reality. The development of open-source software, such as SimVascular [29], made this transition faster. Such packages integrate the components of a patient-specific modeling pipeline from image segmentation and 3D modeling to mesh generation and simulation. In addition to personalized diagnostic and treatment solutions, patient-specific simulations could facilitate sensitivity studies to investigate the effect of a wide range of factor parameter spaces on hemodynamics [30].
Despite many research efforts and the predictive power of CFD-based solutions, they still suffer from important limitations that hinder their application in clinical settings. First, the more complex the problem and the computational domain are, the more computationally expensive the numerical simulation becomes, e.g., due to iterative optimization, complex geometries, patient-specific boundary conditions, and unsteady flow. Furthermore, the preprocessing, mesh generation, and postprocessing steps require more computational time and power. This computational cost hampers the utility of numerical simulations for a large cohort of patients or analyzing different risk factors in a single patient (e.g., different degrees of stenosis), especially when a time-sensitive clinical recommendation is required. One way to address this issue is to use 0D and 1D models, such as lumped-parameter networks [31,32]. Such abstractions of a 3D model could significantly decrease the computational cost at the expense of local flow field detail. For instance, whereas a 0D model can estimate blood flow rate and pressure at each cross section of the computational domain, it cannot provide information about the complex local hemodynamics in those cross sections. Therefore, when such details are required, the more costly 3D models should be still employed.
Another limitation of conventional CFD simulations is the complexity of the steps that are required to develop a numerical model. To carry out a patient-specific simulation, the computational domain should be segmented from medical images, such as computed tomography scans of the patient. In addition, realistic boundary conditions, initial conditions, and material properties are required. However, determining these conditions is usually challenging and sometimes becomes impossible if the measurement methods are invasive [33]. For example, the boundary conditions that are prescribed at the outlets of the computational domain should precisely model the downstream flow dynamics. However, measurement of these outlet conditions is prohibitively difficult in smaller vessels. Considering the significant effect of these conditions on the final CFD solution, their deviation from real conditions may drastically alter the personalized solutions suggested by the simulation, thus limiting the utility of numerical models to satisfy clinical needs [34]. Moreover, when boundary conditions are unknown, solving inverse problems is significantly more expensive.
Finally, recent advances in computational technologies and resources coupled with the reduced costs of computation and data storage have increased the use of CFD for biomedical applications. As a result, the volume of available data from clinical measurements, numerical simulations, and benchtop validations is rapidly growing. The analysis of such big data requires new strategies for translation into clinically relevant information. Deep learning (DL), as a subset of machine learning, offers a wide range of capabilities that can address these issues (Figure 1). DL techniques can reduce the expensive computational time required for complex biomedical CFD simulations. They can also assist in solving inverse problems where the boundary conditions are either unavailable or require invasive measurements. In addition, DL can be used for reduced-order modeling, dimensionality reduction, convergence time reduction, and shape optimization [35]. In this paper, a qualitative overview of the history and current advances of DL for biomedical fluid mechanics is presented. First, DL approaches for general fluid mechanics problems are briefly reviewed. Then, some of the current applications of DL approaches for hemodynamics simulations are discussed. The paper is concluded with suggestions for future research directions.

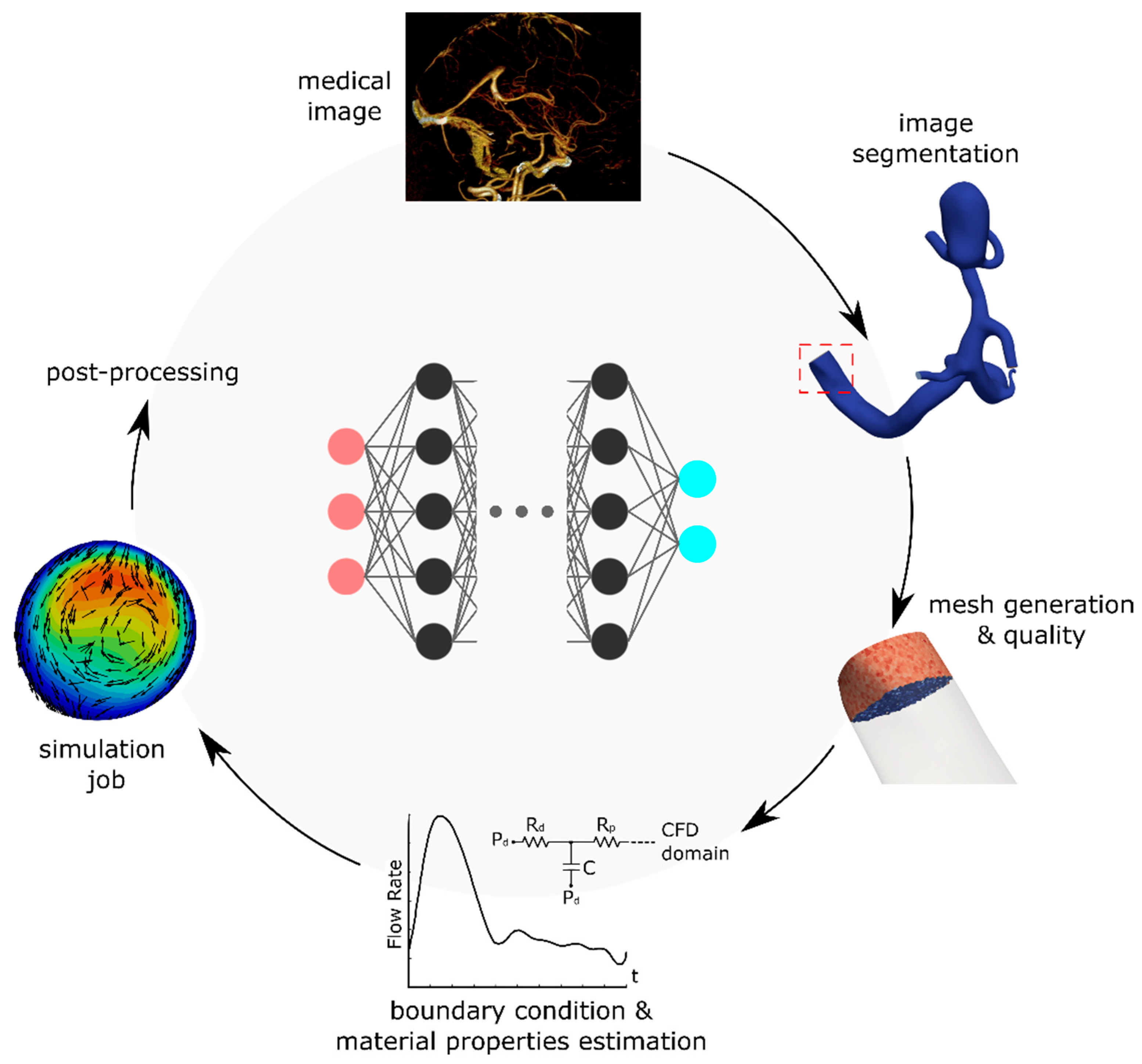
2. Methods

An electronic search (until February 2022) of the PubMed and Google Scholar databases was performed. The Boolean combination (i.e., AND and OR) of the following terms was used in the search: “computational fluid dynamics”, “numerical models”, “hemodynamics”, “blood flow”, “arteries”, “vessels”, “machine learning”, “deep learning”, and “neural networks”. Synonyms, alternate terms, different spellings (e.g., hemodynamics and haemodynamics), and medical subject headings (MeSH) were also considered to obtain more information. Search results were limited to English-language papers with no limitations for the publication year. Papers, including preprints, were screened for relevance using the title and abstract. Reference lists of included publications were examined for relevant citations. Search results were imported into Mendeley (version 1.19.8, Elsevier, London, UK). Based on the reviewed papers, the following applications of DL for computational hemodynamics were selected to be discussed in more detail in this review: hemodynamics of aorta, cerebral hemodynamics, and enhancement of 4D flow magnetic resonance imaging using CFD. Our bibliometric analysis indicates that ~87% of the papers that discuss the application of deep learning for hemodynamics problems were published after 2020, which indicates an increasing interest in this field.

3. Deep Learning for Fluid Mechanics

In this section, we provide a short review of DL-based approaches for the prediction of the solution of fluid mechanics problems. In general, DL models offer new solutions to reduce the computational time needed for expensive fluid mechanics problems, such as turbulent flows [36]. This can be achieved through modeling flow kinematics by extracting flow features or solving flow dynamics using learning architectures. DL models can describe the spatiotemporal evolution of the flow using reduced-order modeling. Furthermore, dominant flow features can be extracted through dimensionality reduction [37]. Model reduction methods, such as proper orthogonal decomposition and dynamic mode decomposition, can simplify the flow dynamics and capture its key patterns at a lower computational cost [38]. For example, proper orthogonal decomposition, which can be expressed as a two-layer neural network (i.e., autoencoder) [35], provides an orthogonal linear transformation from physical coordinates into a modal basis.
Turbulent flow modeling (when Reynolds number (Re) >> 1) is common in biomedical applications, e.g., due to the pulsatile nature of blood flow or the presence of stenosis in a vessel [39]. Neural networks have been developed to model features of turbulent flow, including the rotational and translational structures [40], as well as to reconstruct the near-wall flow fields [41]. DL is also used to enhance resolution and remove noise in the simulation of biomedical turbulent flows. In other words, high-resolution details within a low-resolution cell can be inferred in Reynolds-averaged Navier–Stokes and large-eddy simulations. To this end, various models, such as convolutional neural networks (CNNs) and generative adversarial networks (GANs), have been studied to reconstruct turbulent flow and estimate the flow field parameters [42,43,44].
Physics-informed neural network (PINN) models are also widely used in biomedical applications. In general, PINNs have been developed for both incompressible [45,46,47] and compressible flows [48]. They predict the underlying flow physics by integrating the concentration field of a passive scalar with fluid mechanics laws (e.g., Navier–Stokes equations), using them as constraints in the loss function of the neural network [49]. For example, any deviation from zero for the conservation of mass would be penalized by the model. These models are based on the notion of data assimilation. In fluid dynamics experiments, flow patterns can be qualitatively assessed by techniques such as dye or smoke visualizations. Here, dye or smoke behaves as a passive scalar, i.e., it is advected by the flow without affecting the flow dynamics. Sparse measurements of these passive scalars do not provide detailed information compared to high-resolution CFD simulation results. However, their combination with fluid mechanics laws and deep learning can form PINNs and lead to quantitative estimation of local and complex flow patterns. A PINN model can be trained using the flow data in an arbitrary training domain within the computational domain. This training domain should meet the following conditions [46]. First, the concentration field of the passive scalar should be available within the boundaries of the training domain. Second, the gradients of the concentration normal to the boundaries should be nonzero. The latter condition is specifically crucial in obtaining a single solution for the velocity field. Another characteristic of the PINN models that makes them suitable for biomedical applications is that they are agnostic to geometry, initial conditions, and boundary conditions. In other words, the selection of the computational and training domains is flexible, with their boundaries anywhere within the physical boundaries. PINNs eliminate the need for meshing, which is usually another time-consuming and challenging task in carrying out CFD simulations [34]. Altogether, the requirement of minimal training data is one of the major advantages of PINNs relative to other DL models, which typically require large training datasets.

4. Hemodynamics Applications

For hemodynamics simulations, machine learning techniques can be used for different steps of numerical modeling, including (1) automatic segmentation of the computational domain from medical images [50,51,52,53,54,55], (2) automatic mesh generation and mesh quality assessment [56,57,58,59,60], and (3) prediction of the numerical simulation results [46,61]. Machine learning has also assisted in estimating material properties and boundary conditions [62,63,64]. In addition, machine learning models have been developed for the postprocessing of the simulation results [65]. Table 1 lists DL studies in which the hemodynamics in human blood vessels were predicted. In these studies, DL models were proposed as an alternative to CFD for steady-state and unsteady blood flow analysis. Some studies used DL models to predict the results of reduced-order simulations, such as 1D CFD models [66,67,68]. These models are specifically helpful when only general information about the blood flow is required, such as flow rate or pressure at a cross section. Reduced models are significantly less computationally costly than 3D models. Therefore, they are convenient for generating large datasets for the training of DL models. However, such models cannot provide information about complex and local flow patterns. Thus, when such details are required, 3D models should be employed, although they are associated with more costly computational demand, which makes it more difficult to create adequately large training datasets. Some studies reported 3D CFD simulations in simplified geometries [33,69,70]. Although geometric simplification can reduce computational cost, simplified simulations may not provide a patient-specific clinical recommendation. In the remainder of this section, the application of deep learning in estimating aortic hemodynamics, cerebral hemodynamics, and enhancement of 4D flow magnetic resonance imaging (MRI) is discussed.

4.1. Hemodynamics of Aorta

DL models were developed to predict the hemodynamics in 3D patient-specific models of the aorta under different conditions. Liang et al. investigated the feasibility of using deep neural networks (DNNs) for hemodynamics modeling of the human thoracic aorta [61]. The steady-state distributions of velocity, velocity magnitude, and pressure were predicted using separate DNN models that were trained by hemodynamics data obtained from CFD simulations of 729 thoracic aorta models (built based on the real geometry of 25 patients) [81]. Each CFD simulation took about 15 min on an 8-core computer, which was significantly longer than the time needed to run a DL model to predict the same results. The DL models consisted of three steps of shape encoding using an autoencoder, nonlinear mapping of shape code to field code, and field decoding to predict the scalar values of velocity and pressure. In this study, the meshes had correspondence among different geometric models such that the surface mesh of all aorta models had the same number of mesh nodes. Some studies suggested that this method enhances the DL performance in large sample sizes compared to methods based on an image–pixel representation for interpolation [65,81,82]. On the other hand, some studies suggest this method may not be suitable for complex geometries consisting of both small and large vessels [73].
Li et al. developed a DL model to predict coronary hemodynamics before and after coronary artery bypass surgery with a high resolution [73]. The proposed model was a dual sampling channel network based on PointNet where the CFD mesh nodes defined the input point cloud [72]. The DL model was trained by the CFD results that were carried out for 110 patients with coronary heart disease. The trained model was then used to predict the velocity and pressure distributions for a given 3D geometry. The DL model performance was evaluated using normalized mean absolute error and mean relative error. Figure 2 is a comparison of the streamlines and velocity distributions estimated by CFD (i.e., the reference) with those predicted by the DL model for a patient with a stenosis rate of 85%. For example, Figure 2a–d shows the flow streamlines before and after bypass surgery. The study suggested that there was a good agreement between CFD and DL results. The DL model was able to predict complex structures, such as vortices (black arrows in Figure 2). However, it achieved lower accuracy in the regions with vortices and flow separations.
Aortic coarctation is a congenital heart defect characterized by the narrowing of the aorta. This condition causes a pressure gradient across the stenosed location (Figure 3), which can lead to further cardiovascular complications, such as heart failure and cerebral aneurysm [83]. Different risk factors have been suggested as indicators of aortic coarctation severity, such as pressure gradient, time-averaged wall shear stress, and flow rate [84,85,86]. However, CFD investigation of the combination of these risk factors would be time-consuming. Feiger et al. [30] developed a machine learning framework to study the effect of these factors in a 3D aorta geometry of an eight-year-old female patient. A second geometry was also created synthetically by increasing the degree of stenosis. For each geometry, a total of 50 CFD simulations were carried out for the combination of 10 blood viscosity and 5 flow-rate values. Machine learning models, including fully connected neural networks with a single hidden layer, support vector machines, and regression trees, were trained and tested by the results of 40 and 10 simulations, respectively. The performance of the predictive model was assessed by computing the correlation coefficient between the machine learning model predictions and the CFD results. The study reported a high accuracy for the pressure gradient and wall shear stress values predicted by the neural network model. However, despite the high computational cost of the numerical simulations that were used to train the neural networks (more than 70 million computation hours), general conclusions cannot be made about the model performance, given the limited number and variety of geometries. Another study investigated the aortic hemodynamics in a database of 228 images of the aorta consisting of healthy individuals and patients with aortic coarctation [75]. Additional geometries were also generated synthetically to improve the performance of the DL model. Unlike most of the current DL-based CFD studies that use general simplified boundary conditions, patient-specific boundary conditions were obtained from a 4D phase–contrast MRI in this study. Static pressure, wall shear stress, secondary flow degree, and specific kinetic energy were estimated using CFD and then averaged at the corresponding centerline point of the vessel. The DL model was trained using the vessel centerline geometry and CFD boundary conditions to predict the averaged hemodynamics parameters. The DL model consisted of a long–short-term memory architecture that is usually well-suited for the processing of time series. This architecture was used to predict the hemodynamics parameters of a centerline node based on the values of the adjacent nodes. It should be noted that although the DL model was able to estimate the hemodynamics parameters faster than a CFD simulation, long–short-term memory models usually require a long computational time and considerable resources for training. Thus, a lengthy training may contradict the primary goal of using DL for CFD estimation.

4.2. Cerebral Hemodynamics

The investigation of cerebral hemodynamics is essential for developing new diagnostic and treatment methods for cerebrovascular diseases. Clinical techniques for cerebral hemodynamics measurement include transcranial Doppler ultrasound, which is usually limited to measurements in a few cross sections of the cerebrovascular system. CFD simulations, on the other hand, can estimate the hemodynamics in the entire cerebrovascular system. However, such simulations are associated with expensive computational cost.
PINNs predict flow patterns quantitively based on the variation of a passive scalar over time that is usually acquired through measurements or experiments. In the medical setting, this information can become available from the propagation of contrast material (e.g., Iohexol, Omnipaque 300, GE Healthcare, Chicago, IL) that is routinely administered during diagnostic tests, such as angiography or contrast-enhanced computed tomography [87]. Raissi et al. [46] developed a PINN model to predict the 3D hemodynamics in a patient-specific intracranial aneurysm (Figure 4a). For model training, a uniform concentration for the passive scalar was only used in an arbitrary training domain (Figure 4b), and no additional boundary condition information was required. Figure 4c shows the architecture of the PINN model, which consisted of a densely connected physics-uninformed neural network, automatic differentiation operators, and a Navier–Stokes-informed neural network. The study suggested that the velocity and pressure predictions were in agreements with the reference solution, which was obtained from a CFD simulation with patient-specific boundary conditions (Figure 4d,e).
Sarabian et al. [68] developed a PINN model to estimate the flow rate and pressure distributions in the cerebrovascular system. To predict these parameters, the DL model used a 1D fluid dynamics model and limited measurements of transcranial Doppler ultrasound, which were acquired at several locations in the cerebral vasculature, as well as the baseline vessel cross-sectional areas. The DL results were compared and validated with the flow measurements obtained from a gold-standard 4D flow MRI. This study suggested that the 1D CFD results achieved less agreement with the clinical measurements than the PINN predictions, which could be due to the lack of patient-specific boundary conditions in the CFD simulations or the presence of noise in the 4D flow MRI data.

4.3. 4D Flow Magnetic Resonance Imaging

4D flow MRI can visualize and quantify the time variation of the 3D velocity field in the vessels [88]. Other parameters and geometric features, such as vessel tortuosity and cross-sectional area, can be calculated either directly or indirectly from these images [89]. However, 4D flow MRI is unable to provide information about some of the critical hemodynamics parameters, such as pressure, on its own merits. Furthermore, limitations such as patient scan time restrictions, intravoxel dephasing, and image noise can result in poor flow estimations from 4D flow MRI scans [80]. On the other hand, CFD simulations, as an alternative to 4D flow MRI, usually suffer from a lack of patient-specific boundary conditions. PINNs can combine the strengths of CFD and 4D flow MRI, boosting them further with the power of DL. For example, PINNs were used to estimate pressure wave propagation from 4D flow MRI using a reduced-order model of pulsatile flow [34]. Other DL models, such as CNNs, can be used to enhance the quality of 4D flow MRI data by CFD estimations [80]. Figure 5 compares DL-enhanced velocity fields with the original MRI estimations. In this example, the DL model was able to improve the near-wall velocity estimation, smooth the velocity gradient transitions in abnormalities such as cerebral aneurysms, and remove unrealistic velocity fluctuations. In another study, CFD simulations were used to generate synthetic 4D flow MRI data, which were subsequently used to train a deep super-resolution residual network designed to enhance the quality of real 4D flow MRI data [90].

5. Discussion and Future Directions

Recent advances in the field of DL for hemodynamics simulations indicate the strong potential of this computational method to address a wide variety of clinical needs. DL models do not replace conventional computational simulations but could assist them in mitigating some of their common bottlenecks, such as high computational costs. The best-case scenario for a DL model that is trained by the data obtained from CFD simulations is to achieve an accuracy as good as the CFD results (i.e., the training dataset). Considering the potential loss in accuracy, DL solutions are recommended, especially when either a quick medical decision is needed, or it is difficult or impossible to develop conventional computational models for a specific biomechanics problem.
DL usually requires large volumes of training data. When the training dataset is small, the trained model may be suitable for interpolation but may not perform well for new input data that represent different features than the training dataset (i.e., extrapolation). Many DL datasets in other applications have a large sample size. However, such a large database is not still available for fluid mechanics applications, specifically for biomedical CFD. Thus, the current DL models suffer from insufficient training data [73,75]. Estimating an appropriate size of training data for a specific application is usually difficult. Based on available studies, the training datasets for hemodynamics applications should include the data of several thousand subjects. However, such big data are not usually available for CFD studies. Developing such databases with appropriate labels for training could attract more interest to develop DL models for biomedical flow applications. In addition, data augmentation techniques can be employed to increase the size of datasets [66,70]. For instance, some studies used statistical shape models to create large synthetic databases [75,76]. Similar methods may be used to mitigate the issue of small training datasets.
In many recent DL-based CFD fluid mechanics investigations, reduced-order models, such as 1D [66,67] and 2D flow fields [91,92,93,94,95], were employed. DL has also been used for automatic parameter estimation in reduced-order models [31,34,96]. Whereas these approximations can reduce the computational cost, they are unable to provide detailed information about the local and complex flow parameters, which might be needed in some clinical applications. In addition, some DL models that are based on 3D flow studies are developed for ideal or simplified geometries with an insufficient sample resolution to predict complex flow field structures [61,97]. Although these reduced-order and simplified models decrease the computational time, they cannot estimate complex flow patterns, such as recirculation, vorticity, and wall shear stress, which are important to understand patient hemodynamics. Furthermore, the simplified assumptions of these models are associated with uncertainty in the estimated hemodynamics parameters. Future efforts should focus on developing DL models for 3D blood flow fields to handle high-resolution samples.
Most of the current DL models were designed to predict the flow behavior of simpler conditions, such as Newtonian behavior of blood flow. Whereas blood can be assumed to be a Newtonian fluid in large vessels (especially in most arteries), its viscosity varies with flow rate in smaller arteries and capillaries [98]. For medical conditions such as stenosis, a non-Newtonian model may be preferred over a Newtonian model [39]. Future efforts should consider including more complex physics in DL models to account for realistic conditions, such as non-Newtonian blood behavior in smaller arteries and viscoelastic properties of the arterial wall.
PINNs can be specifically developed for hemodynamics estimation upon availability of information on a clinical passive scalar. For example, in some procedures, such as treatment planning for liver cancer radioembolization, several angiography tests with contrast material are usually performed to identify the anatomy of the patient arterial tree, locate abnormalities, and identify ideal injection locations for the real treatment [99]. Patient-specific data obtained from these tests can be used to train PINNs in future studies. Similarly, blood velocity data estimated from other imaging modalities, such as Doppler ultrasound and 4D flow MRI, can be used to generate the concentration field required to train PINNs. These DL models can then be used to predict fluid dynamics parameters under complex conditions, such as blood flow through heart valves. Despite CFD simulations that need these data at the boundaries of the computational domain (e.g., as the inlet or outlet boundary condition), PINNs are flexible about where this clinical information (passive scalar) is measured from, as long as it is within the computational domain [46]. Utilizing patient-specific data in PINNs is a strength for this method, but it can also become a bottleneck or issue. Angiography and 4D flow MRI scans can be noisy, especially in smaller vessels. This noisy data may contradict the underlying fluid mechanics laws, which represent another central component of PINNs [34]. This issue should be addressed in by future PINN developments.
Finally, to perform a patient-specific CFD simulation, tedious procedures should be completed. From image segmentation, model preprocessing, mesh generation, and mesh quality control to boundary condition calibration, simulation parameter calculation, and postprocessing of the simulation results, each step is time-consuming and requires expertise. Current studies have investigated the potential of DL to perform each of these tasks. The focus of future studies should be on developing DL pipelines that integrate all the steps needed for a CFD simulation, from preprocessing to postprocessing of the data.

6. Conclusions

Recent advances in image-based, patient-specific CFD modeling have made this method an attractive tool to develop personalized treatments and diagnostic methods. However, bottlenecks such as the expensive computational cost of numerical models represent a major obstacle in translating them into real-time clinical tools. This review suggests that the current efforts and advances in integrating CFD with DL have a high potential to define a new, non-invasive computational paradigm for medical diagnosis, pretreatment planning, and personalized treatment.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Reid, L. An Introduction to Biomedical Computational Fluid Dynamics. In Biomedical Visualisation; Springer: Cham, Switzerland, 2021; pp. 205–222. [Google Scholar]
  2. Can, A.; Du, R. Association of Hemodynamic Factors With Intracranial Aneurysm Formation and Rupture. Neurosurgery 2016, 78, 510–520. [Google Scholar] [CrossRef] [PubMed]
  3. Ameenuddin, M.; Anand, M. A Mixture Theory Model for Blood Combined With Low-Density Lipoprotein Transport to Predict Early Atherosclerosis Regions in Idealized and Patient-Derived Abdominal Aorta. J. Biomech. Eng. 2020, 142, 101008. [Google Scholar] [CrossRef] [PubMed]
  4. Shadden, S.C.; Arzani, A. Lagrangian Postprocessing of Computational Hemodynamics. Ann. Biomed. Eng. 2015, 43, 41–58. [Google Scholar] [CrossRef] [PubMed]
  5. Khalili, F.; Gamage, P.T.; Taebi, A.; Johnson, M.E.; Roberts, R.B.; Mitchell, J. Spectral Decomposition of the Flow and Characterization of the Sound Signals through Stenoses with Different Levels of Severity. Bioengineering 2021, 8, 41. [Google Scholar] [CrossRef] [PubMed]
  6. Khalili, F.; Gamage, P.T.; Taebi, A.; Johnson, M.E.; Roberts, R.B.; Mitchel, J. Spectral Decomposition and Sound Source Localization of Highly Disturbed Flow through a Severe Arterial Stenosis. Bioengineering 2021, 8, 34. [Google Scholar] [CrossRef]
  7. Gamage, P.P.T.; Khalili, F.; Azad, K.; Mansy, H.A. Modeling Inspiratory Flow in a Porcine Lung Airway. J. Biomech. Eng. 2018, 140, 061003. [Google Scholar] [CrossRef]
  8. Nowak, N.; Kakade, P.P.; Annapragada, A.V. Computational Fluid Dynamics Simulation of Airflow and Aerosol Deposition in Human Lungs. Ann. Biomed. Eng. 2003, 31, 374–390. [Google Scholar] [CrossRef]
  9. Xi, J.; April Si, X.; Dong, H.; Zhong, H. Effects of Glottis Motion on Airflow and Energy Expenditure in a Human Upper Airway Model. Eur. J. Mech. B/Fluids 2018, 72, 23–37. [Google Scholar] [CrossRef]
  10. Tully, B.; Ventikos, Y. Coupling Poroelasticity and CFD for Cerebrospinal Fluid Hydrodynamics. IEEE Trans. Biomed. Eng. 2009, 56, 1644–1651. [Google Scholar] [CrossRef]
  11. Heidari Pahlavian, S.; Bunck, A.C.; Loth, F.; Shane Tubbs, R.; Yiallourou, T.; Robert Kroeger, J.; Heindel, W.; Martin, B.A. Characterization of the Discrepancies Between Four-Dimensional Phase-Contrast Magnetic Resonance Imaging and In-Silico Simulations of Cerebrospinal Fluid Dynamics. J. Biomech. Eng. 2015, 137, 051002. [Google Scholar] [CrossRef]
  12. Kelly, W.J.; Muske, K.R. Optimal Operation of High-Pressure Homogenization for Intracellular Product Recovery. Bioprocess Biosyst. Eng. 2004, 27, 25–37. [Google Scholar] [CrossRef] [PubMed]
  13. Yarmush, G.; Santos, L.; Yarmush, J.; Koundinyan, S.; Saleem, M.; Nativ, N.I.; Yarmush, M.L.; Berthiaume, F.; Maguire, T.J.; Guaghan, C. CFD Assessment of the Effect of Convective Mass Transport on the Intracellular Clearance of Intracellular Triglycerides in Macrosteatotic Hepatocytes. Biomech. Model. Mechanobiol. 2017, 16, 1095–1102. [Google Scholar] [CrossRef] [PubMed]
  14. Taebi, A.; Khalili, F. Advances in Noninvasive Diagnosis Based on Body Sounds and Vibrations—A Review. In Biomedical and Biotechnology; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 5. [Google Scholar] [CrossRef]
  15. Khalili, F.; Taebi, A. Advances in Computational Fluid Dynamics Modeling of Cardiac Sounds as a Non-Invasive Diagnosis Method. In Biomedical and Biotechnology; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 5. [Google Scholar] [CrossRef]
  16. Cook, J.; Umar, M.; Khalili, F.; Taebi, A. Body Acoustics for the Non-Invasive Diagnosis of Medical Conditions. Bioengineering 2022, 9, 149. [Google Scholar] [CrossRef] [PubMed]
  17. Taebi, A.; Solar, B.; Bomar, A.; Sandler, R.; Mansy, H. Recent Advances in Seismocardiography. Vibration 2019, 2, 64–86. [Google Scholar] [CrossRef] [Green Version]
  18. Meschi, S.S.; Farghadan, A.; Arzani, A. Flow Topology and Targeted Drug Delivery in Cardiovascular Disease. J. Biomech. 2021, 119, 110307. [Google Scholar] [CrossRef]
  19. Li, B.; Feng, Y. In Silico Study to Enhance Delivery Efficiency of Charged Nanoscale Nasal Spray Aerosols to the Olfactory Region Using External Magnetic Fields. Bioengineering 2022, 9, 40. [Google Scholar] [CrossRef]
  20. Taebi, A.; Vu, C.T.; Roncali, E. Multiscale Computational Fluid Dynamics Modeling for Personalized Liver Cancer Radioembolization Dosimetry. J. Biomech. Eng. 2021, 143, 011002. [Google Scholar] [CrossRef]
  21. Roncali, E.; Taebi, A.; Foster, C.; Vu, C.T. Personalized Dosimetry for Liver Cancer Y-90 Radioembolization Using Computational Fluid Dynamics and Monte Carlo Simulation. Ann. Biomed. Eng. 2020, 48, 1499–1510. [Google Scholar] [CrossRef]
  22. Ghosh, R.P.; Marom, G.; Rotman, O.M.; Slepian, M.J.; Prabhakar, S.; Horner, M.; Bluestein, D. Comparative Fluid–Structure Interaction Analysis of Polymeric Transcatheter and Surgical Aortic Valves’ Hemodynamics and Structural Mechanics. J. Biomech. Eng. 2018, 140, 121002. [Google Scholar] [CrossRef]
  23. Uchiyama, Y.; Fujimura, S.; Takao, H.; Suzuki, T.; Hayakawa, M.; Ishibashi, T.; Karagiozov, K.; Fukudome, K.; Murayama, Y.; Yamamoto, M. Hemodynamic Investigation of the Effectiveness of a Two Overlapping Flow Diverter Configuration for Cerebral Aneurysm Treatment. Bioengineering 2021, 8, 143. [Google Scholar] [CrossRef]
  24. Khalili, F. Fluid Dynamics Modeling and Sound Analysis of a Bileaflet Mechanical Heart Valve. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2018. [Google Scholar]
  25. Caballero, A.; Mao, W.; McKay, R.; Sun, W. The Impact of Balloon-Expandable Transcatheter Aortic Valve Replacement on Concomitant Mitral Regurgitation: A Comprehensive Computational Analysis. J. R. Soc. Interface 2019, 16, 20190355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. Gamage, P.T.; Dong, P.; Lee, J.; Gharaibeh, Y.; Zimin, V.N.; Dallan, L.A.P.; Bezerra, H.G.; Wilson, D.L.; Gu, L. Hemodynamic Alternations Following Stent Deployment and Post-Dilation in a Heavily Calcified Coronary Artery: In Silico and Ex-Vivo Approaches. Comput. Biol. Med. 2021, 139, 104962. [Google Scholar] [CrossRef] [PubMed]
  27. Ge, L.; Leo, H.-L.; Sotiropoulos, F.; Yoganathan, A.P. Flow in a Mechanical Bileaflet Heart Valve at Laminar and Near-Peak Systole Flow Rates: CFD Simulations and Experiments. J. Biomech. Eng. 2005, 127, 782–797. [Google Scholar] [CrossRef] [PubMed]
  28. Taylor, C.A.; Steinman, D.A. Image-Based Modeling of Blood Flow and Vessel Wall Dynamics: Applications, Methods and Future Directions. Ann. Biomed. Eng. 2010, 38, 1188–1203. [Google Scholar] [CrossRef] [PubMed]
  29. Lan, H.; Updegrove, A.; Wilson, N.M.; Maher, G.D.; Shadden, S.C.; Marsden, A.L. A Re-Engineered Software Interface and Workflow for the Open-Source SimVascular Cardiovascular Modeling Package. J. Biomech. Eng. 2018, 140, 024501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  30. Feiger, B.; Gounley, J.; Adler, D.; Leopold, J.A.; Draeger, E.W.; Chaudhury, R.; Ryan, J.; Pathangey, G.; Winarta, K.; Frakes, D.; et al. Accelerating Massively Parallel Hemodynamic Models of Coarctation of the Aorta Using Neural Networks. Sci. Rep. 2020, 10, 9508. [Google Scholar] [CrossRef]
  31. Pfaller, M.R.; Pham, J.; Verma, A.; Wilson, N.M.; Parker, D.W.; Yang, W.; Marsden, A.L. Automated Generation of 0D and 1D Reduced-Order Models of Patient-Specific Blood Flow. arXiv 2021, arXiv:2111.04878. [Google Scholar]
  32. Westerhof, N.; Lankhaar, J.W.; Westerhof, B.E. The Arterial Windkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef] [Green Version]
  33. Arzani, A.; Wang, J.-X.; D’Souza, R.M. Uncovering Near-Wall Blood Flow from Sparse Data with Physics-Informed Neural Networks. Phys. Fluids 2021, 33, 071905. [Google Scholar] [CrossRef]
  34. Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine Learning in Cardiovascular Flows Modeling: Predicting Arterial Blood Pressure from Non-Invasive 4D Flow MRI Data Using Physics-Informed Neural Networks. Comput. Methods Appl. Mech. Eng. 2020, 358, 112623. [Google Scholar] [CrossRef]
  35. Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef] [Green Version]
  36. Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine Learning–Accelerated Computational Fluid Dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef] [PubMed]
  37. Taira, K.; Brunton, S.L.; Dawson, S.T.M.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal Analysis of Fluid Flows: An Overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef] [Green Version]
  38. Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016. [Google Scholar]
  39. Carvalho, V.; Pinho, D.; Lima, R.A.; Teixeira, J.C.; Teixeira, S. Blood Flow Modeling in Coronary Arteries: A Review. Fluids 2021, 6, 53. [Google Scholar] [CrossRef]
  40. Kutz, J.N. Deep Learning in Fluid Dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef] [Green Version]
  41. Milano, M.; Koumoutsakos, P. Neural Network Modeling for Near Wall Turbulent Flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef] [Green Version]
  42. Fukami, K.; Fukagata, K.; Taira, K. Super-Resolution Reconstruction of Turbulent Flows with Machine Learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef] [Green Version]
  43. Xie, Y.; Franz, E.; Chu, M.; Thuerey, N. TempoGAN: A Temporally Coherent, Volumetric GAN for Super-Resolution Fluid Flow. ACM Trans. Graph. 2018, 37, 1–15. [Google Scholar] [CrossRef]
  44. Wang, R.; Kashinath, K.; Mustafa, M.; Albert, A.; Yu, R. Towards Physics-Informed Deep Learning for Turbulent Flow Prediction. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, ACM, New York, NY, USA, 6–10 June 2020; pp. 1457–1466. [Google Scholar]
  45. Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes Flow Nets): Physics-Informed Neural Networks for the Incompressible Navier-Stokes Equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
  46. Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden Fluid Mechanics: Learning Velocity and Pressure Fields from Flow Visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
  47. Yin, M.; Zheng, X.; Humphrey, J.D.; Karniadakis, G.E. Non-Invasive Inference of Thrombus Material Properties with Physics-Informed Neural Networks. Comput. Methods Appl. Mech. Eng. 2021, 375, 113603. [Google Scholar] [CrossRef] [PubMed]
  48. Mao, Z.; Jagtap, A.D.; Karniadakis, G.E. Physics-Informed Neural Networks for High-Speed Flows. Comput. Methods Appl. Mech. Eng. 2020, 360, 112789. [Google Scholar] [CrossRef]
  49. Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-Informed Neural Networks (PINNs) for Fluid Mechanics: A Review. Acta Mech. Sin. 2022, 37, 1727–1738. [Google Scholar] [CrossRef]
  50. Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A Survey on Deep Learning in Medical Image Analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  51. Liang, L.; Kong, F.; Martin, C.; Pham, T.; Wang, Q.; Duncan, J.; Sun, W. Machine Learning-Based 3-D Geometry Reconstruction and Modeling of Aortic Valve Deformation Using 3-D Computed Tomography Images. Int. J. Numer. Method. Biomed. Eng. 2017, 33, e2827. [Google Scholar] [CrossRef] [Green Version]
  52. Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
  53. Pouch, A.M.; Wang, H.; Takabe, M.; Jackson, B.M.; Gorman, J.H.; Gorman, R.C.; Yushkevich, P.A.; Sehgal, C.M. Fully Automatic Segmentation of the Mitral Leaflets in 3D Transesophageal Echocardiographic Images Using Multi-Atlas Joint Label Fusion and Deformable Medial Modeling. Med. Image Anal. 2014, 18, 118–129. [Google Scholar] [CrossRef] [Green Version]
  54. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
  55. Taebi, A.; Roudsari, B.; Vu, C.; Cherry, S.; Roncali, E. Hepatic Arterial Tree Segmentation: Towards Patient-Specific Dosimetry for Liver Cancer Radioembolization. J. Nucl. Med. 2019, 60 (Suppl. 1), 122. [Google Scholar]
  56. Huang, K.; Krügener, M.; Brown, A.; Menhorn, F.; Bungartz, H.-J.; Hartmann, D. Machine Learning-Based Optimal Mesh Generation in Computational Fluid Dynamics. arXiv 2021, arXiv:2102.12923. [Google Scholar]
  57. Zhang, Z.; Jimack, P.K.; Wang, H. MeshingNet3D: Efficient Generation of Adapted Tetrahedral Meshes for Computational Mechanics. Adv. Eng. Softw. 2021, 157–158, 103021. [Google Scholar] [CrossRef]
  58. Chen, X.; Liu, J.; Gong, C.; Li, S.; Pang, Y.; Chen, B. MVE-Net: An Automatic 3-D Structured Mesh Validity Evaluation Framework Using Deep Neural Networks. Comput. Des. 2021, 141, 103104. [Google Scholar] [CrossRef]
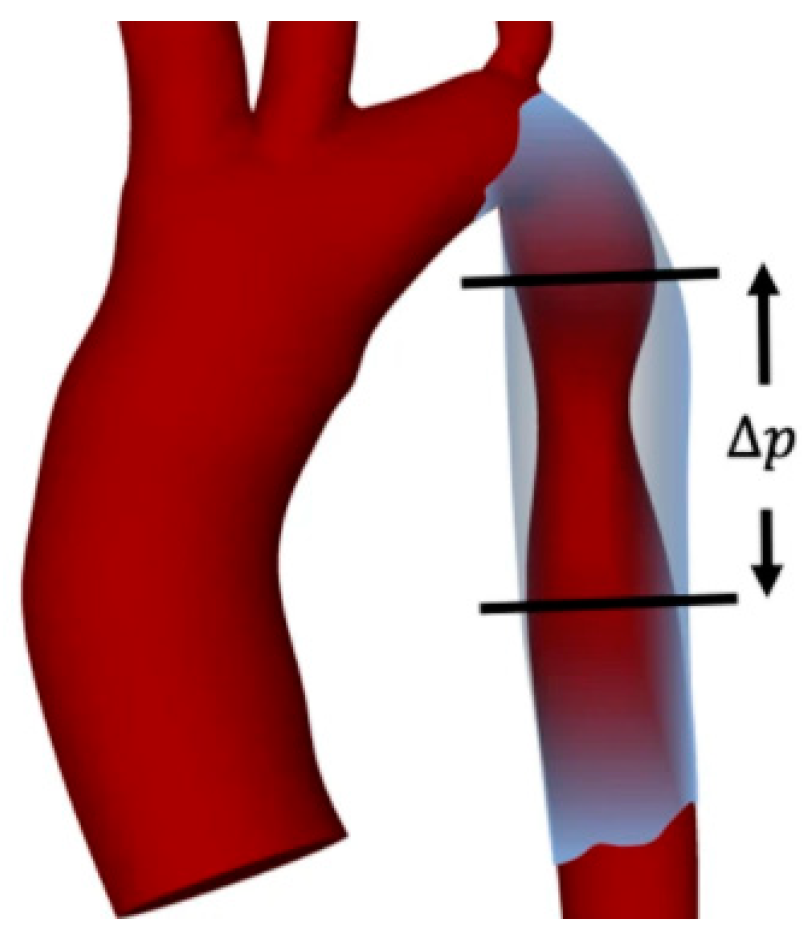
  59. Xu, Z.; Chen, X.; Chi, L.; Liu, J.; Gong, C. A Mesh Quality Discrimination Method Based on Convolutional Neural Network. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications, Dalian, China, 27–29 June 2020; pp. 481–486. [Google Scholar]
  60. Chen, X.; Liu, J.; Pang, Y.; Chen, J.; Chi, L.; Gong, C. Developing a New Mesh Quality Evaluation Method Based on Convolutional Neural Network. Eng. Appl. Comput. Fluid Mech. 2020, 14, 391–400. [Google Scholar] [CrossRef]
  61. Liang, L.; Mao, W.; Sun, W. A Feasibility Study of Deep Learning for Predicting Hemodynamics of Human Thoracic Aorta. J. Biomech. 2020, 99, 109544. [Google Scholar] [CrossRef] [PubMed]
  62. Liu, M.; Liang, L.; Sun, W. Estimation of in Vivo Constitutive Parameters of the Aortic Wall Using a Machine Learning Approach. Comput. Methods Appl. Mech. Eng. 2019, 347, 201–217. [Google Scholar] [CrossRef] [PubMed]
  63. Cilla, M.; Pérez-Rey, I.; Martínez, M.A.; Peña, E.; Martínez, J. On the Use of Machine Learning Techniques for the Mechanical Characterization of Soft Biological Tissues. Int. J. Numer. Method. Biomed. Eng. 2018, 34, e3121. [Google Scholar] [CrossRef] [Green Version]
  64. Luo, Y.; Fan, Z.; Baek, S.; Lu, J. Machine Learning-Aided Exploration of Relationship between Strength and Elastic Properties in Ascending Thoracic Aneurysm. Int. J. Numer. Method. Biomed. Eng. 2018, 34, e2977. [Google Scholar] [CrossRef]
  65. Liang, L.; Liu, M.; Martin, C.; Sun, W. A Deep Learning Approach to Estimate Stress Distribution: A Fast and Accurate Surrogate of Finite-Element Analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef] [Green Version]
  66. Itu, L.; Rapaka, S.; Passerini, T.; Georgescu, B.; Schwemmer, C.; Schoebinger, M.; Flohr, T.; Sharma, P.; Comaniciu, D. A Machine-Learning Approach for Computation of Fractional Flow Reserve from Coronary Computed Tomography. J. Appl. Physiol. 2016, 121, 42–52. [Google Scholar] [CrossRef] [Green Version]
  67. Sklet, V. Exploring the Capabilities of Machine Learning (ML) for 1D Blood Flow: Application to Coronary Flow. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
  68. Sarabian, M.; Babaee, H.; Laksari, K. Physics-Informed Neural Networks for Improving Cerebral Hemodynamics Predictions. arXiv 2021, arXiv:2108.11498. [Google Scholar]
  69. Tran, D.M.; Nguyen, M.T.; Lee, S.-W. Machine Learning Based Evaluation of Functional Index for Coronary Lesion Severity. In Proceedings of the 2nd International Conference on Machine Learning and Soft Computing, Phu Quoc Island, Vietnam, 2–4 February 2018; ACM Press: New York, NY, USA, 2018; pp. 1–4. [Google Scholar]
  70. Li, G.; Song, X.; Wang, H.; Liu, S.; Ji, J.; Guo, Y.; Qiao, A.; Liu, Y.; Wang, X. Prediction of Cerebral Aneurysm Hemodynamics With Porous-Medium Models of Flow-Diverting Stents via Deep Learning. Front. Physiol. 2021, 12, 1513. [Google Scholar] [CrossRef]
  71. Gharleghi, R.; Samarasinghe, G.; Sowmya, A.; Beier, S. Deep Learning for Time Averaged Wall Shear Stress Prediction in Left Main Coronary Bifurcations. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 1–4. [Google Scholar]
  72. Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
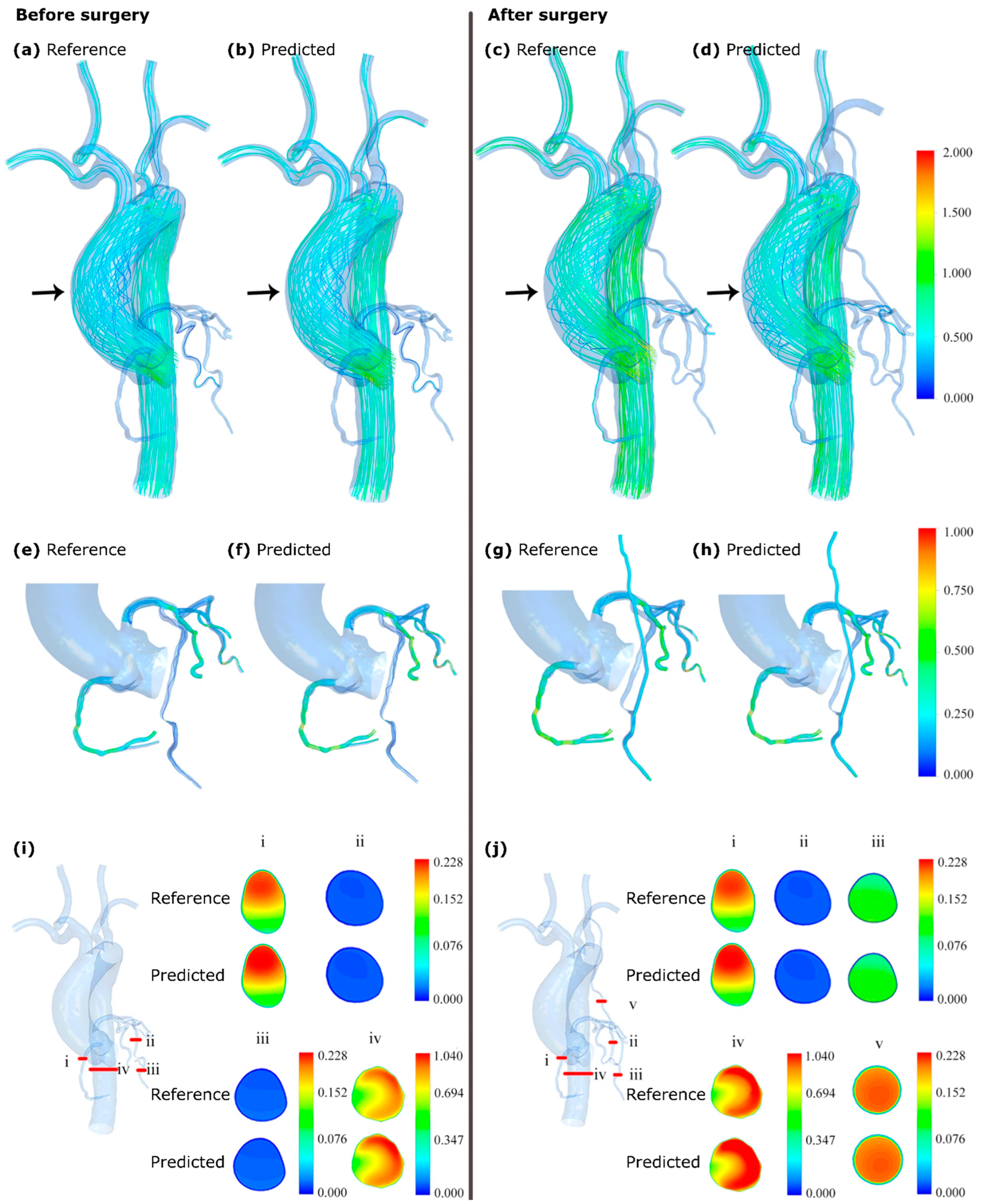
  73. Li, G.; Wang, H.; Zhang, M.; Tupin, S.; Qiao, A.; Liu, Y.; Ohta, M.; Anzai, H. Prediction of 3D Cardiovascular Hemodynamics before and after Coronary Artery Bypass Surgery via Deep Learning. Commun. Biol. 2021, 4, 99. [Google Scholar] [CrossRef]
  74. Randles, A.P.; Kale, V.; Hammond, J.; Gropp, W.; Kaxiras, E. Performance Analysis of the Lattice Boltzmann Model Beyond Navier-Stokes. In Proceedings of the IEEE 27th International Symposium on Parallel and Distributed Processing, Cambridge, MA, USA, 20–24 May 2013; pp. 1063–1074. [Google Scholar]
  75. Yevtushenko, P.; Goubergrits, L.; Gundelwein, L.; Setio, A.; Heimann, T.; Ramm, H.; Lamecker, H.; Kuehne, T.; Meyer, A.; Schafstedde, M. Deep Learning Based Centerline-Aggregated Aortic Hemodynamics: An Efficient Alternative to Numerical Modelling of Hemodynamics. IEEE J. Biomed. Heal. Inform. 2021, 26, 1815–1825. [Google Scholar] [CrossRef] [PubMed]
  76. Morales, X.; Mill, J.; Juhl, K.A.; Olivares, A.; Jimenez-Perez, G.; Paulsen, R.R.; Camara, O. Deep Learning Surrogate of Computational Fluid Dynamics for Thrombus Formation Risk in the Left Atrial Appendage. In International Workshop on Statistical Atlases and Computational Models of the Heart; Springer: Cham, Switzerland, 2020; pp. 157–166. [Google Scholar]
  77. Taebi, A.; Vu, C.T.; Roncali, E. Estimation of Yttrium-90 Distribution in Liver Radioembolization Using Computational Fluid Dynamics and Deep Neural Networks. In Proceedings of the 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 4974–4977. [Google Scholar]
  78. Taebi, A.; Vu, C.T.; Roncali, E. Prediction of Blood Flow Distribution in Liver Radioembolization Using Convolutional Neural Networks. In Biomedical and Biotechnology; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 5. [Google Scholar] [CrossRef]
  79. Logg, A.; Mardal, K.-A.; Wells, G. (Eds.) Automated Solution of Differential Equations by the Finite Element Method; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
  80. Rutkowski, D.R.; Roldán-Alzate, A.; Johnson, K.M. Enhancement of Cerebrovascular 4D Flow MRI Velocity Fields Using Machine Learning and Computational Fluid Dynamics Simulation Data. Sci. Rep. 2021, 11, 10240. [Google Scholar] [CrossRef] [PubMed]
  81. Liang, L.; Liu, M.; Martin, C.; Elefteriades, J.A.; Sun, W. A Machine Learning Approach to Investigate the Relationship between Shape Features and Numerically Predicted Risk of Ascending Aortic Aneurysm. Biomech. Model. Mechanobiol. 2017, 16, 1519–1533. [Google Scholar] [CrossRef] [PubMed]
  82. Yu, Y.; Zhang, S.; Huang, J.; Metaxas, D.; Axel, L. Sparse Deformable Models with Application to Cardiac Motion Analysis. In International Conference on Information Processing in Medical Imaging; Springer: Berlin/Heidelberg, Germany, 2013; pp. 208–219. [Google Scholar]
  83. Love, B.A.; Fischer, G.W.; Stelzer, P.; Fuster, V. Aortic Coarctation in the Adult. In Pediatric and Congenital Cardiology, Cardiac Surgery and Intensive Care; Springer: London, UK, 2014; pp. 2521–2549. [Google Scholar]
  84. Warnes, C.A.; Williams, R.G.; Bashore, T.M.; Child, J.S.; Connolly, H.M.; Dearani, J.A.; del Nido, P.; Fasules, J.W.; Graham, T.P.; Hijazi, Z.M.; et al. ACC/AHA 2008 Guidelines for the Management of Adults With Congenital Heart Disease. J. Am. Coll. Cardiol. 2008, 52, e143–e263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  85. Markl, M.; Brendecke, S.M.; Simon, J.; Barker, A.J.; Weiller, C.; Harloff, A. Co-Registration of the Distribution of Wall Shear Stress and 140 Complex Plaques of the Aorta. Magn. Reson. Imaging 2013, 31, 1156–1162. [Google Scholar] [CrossRef] [PubMed]
  86. Zhu, H.; Zhang, J.; Shih, J.; Lopez-Bertoni, F.; Hagaman, J.R.; Maeda, N.; Friedman, M.H. Differences in Aortic Arch Geometry, Hemodynamics, and Plaque Patterns Between C57BL/6 and 129/SvEv Mice. J. Biomech. Eng. 2009, 131, 121005. [Google Scholar] [CrossRef]
  87. Miles, K.A.; Lee, T.-Y.; Goh, V.; Klotz, E.; Cuenod, C.; Bisdas, S.; Groves, A.M.; Hayball, M.P.; Alonzi, R.; Brunner, T. Current Status and Guidelines for the Assessment of Tumour Vascular Support with Dynamic Contrast-Enhanced Computed Tomography. Eur. Radiol. 2012, 22, 1430–1441. [Google Scholar] [CrossRef]
  88. Markl, M.; Frydrychowicz, A.; Kozerke, S.; Hope, M.; Wieben, O. 4D Flow MRI. J. Magn. Reson. Imaging 2012, 36, 1015–1036. [Google Scholar] [CrossRef]
  89. Plein, S.; Bloomer, T.N.; Ridgway, J.P.; Jones, T.R.; Bainbridge, G.J.; Sivananthan, M.U. Steady-State Free Precession Magnetic Resonance Imaging of the Heart: Comparison with Segmented k-Space Gradient-Echo Imaging. J. Magn. Reson. Imaging 2001, 14, 230–236. [Google Scholar] [CrossRef]
  90. Ferdian, E.; Suinesiaputra, A.; Dubowitz, D.J.; Zhao, D.; Wang, A.; Cowan, B.; Young, A.A. 4DFlowNet: Super-Resolution 4D Flow MRI Using Deep Learning and Computational Fluid Dynamics. Front. Phys. 2020, 8, 138. [Google Scholar] [CrossRef]
  91. Miyanawala, T.P.; Jaiman, R.K. An Efficient Deep Learning Technique for the Navier-Stokes Equations: Application to Unsteady Wake Flow Dynamics. arXiv 2017, arXiv:1710.09099. [Google Scholar]
  92. Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model Identification of Reduced Order Fluid Dynamics Systems Using Deep Learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef] [Green Version]
  93. Lye, K.O.; Mishra, S.; Ray, D. Deep Learning Observables in Computational Fluid Dynamics. J. Comput. Phys. 2020, 410, 109339. [Google Scholar] [CrossRef] [Green Version]
  94. Lee, S.; You, D. Prediction of Laminar Vortex Shedding over a Cylinder Using Deep Learning. arXiv 2017, arXiv:1712.07854. [Google Scholar]
  95. Lee, S.; You, D. Data-Driven Prediction of Unsteady Flow over a Circular Cylinder Using Deep Learning. J. Fluid Mech. 2019, 879, 217–254. [Google Scholar] [CrossRef] [Green Version]
  96. Zhou, Y.; He, Y.; Wu, J.; Cui, C.; Chen, M.; Sun, B. A Method of Parameter Estimation for Cardiovascular Hemodynamics Based on Deep Learning and Its Application to Personalize a Reduced-order Model. Int. J. Numer. Method. Biomed. Eng. 2022, 38, e3533. [Google Scholar] [CrossRef]
  97. Guo, X.; Li, W.; Iorio, F. Convolutional Neural Networks for Steady Flow Approximation. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM Press: New York, NY, USA, 2016; pp. 481–490. [Google Scholar]
  98. Ku, D.N. Blood Flow in Arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
  99. Taebi, A.; Janibek, N.; Goldman, R.; Pillai, R.; Vu, C.T.; Roncali, E. On the Impact of Injection Distance to Bifurcations on Yttrium-90 Distribution in Liver Cancer Radioembolization. J. Vasc. Interv. Radiol. 2022, 33, 668–677.e1. [Google Scholar] [CrossRef]
Fluids 07 00197 g001 550
Figure 1. Deep learning models assist in segmenting the computational domain from medical images, generating mesh and controlling its quality, estimating parameters needed for numerical simulations, and predicting the simulation results.
Figure 1. Deep learning models assist in segmenting the computational domain from medical images, generating mesh and controlling its quality, estimating parameters needed for numerical simulations, and predicting the simulation results.
Fluids 07 00197 g001
Fluids 07 00197 g002 550
Figure 2. (a–h) Flow streamlines before and after coronary artery bypass surgery estimated by the CFD and DL models. (i,j) Velocity distribution at four cross sections before and after the surgery estimated by CFD and DL. Color bars show velocity in m/s. Adapted from ref. [73].
Figure 2. (a–h) Flow streamlines before and after coronary artery bypass surgery estimated by the CFD and DL models. (i,j) Velocity distribution at four cross sections before and after the surgery estimated by CFD and DL. Color bars show velocity in m/s. Adapted from ref. [73].
Fluids 07 00197 g002
Fluids 07 00197 g003 550
Figure 3. Aortic coarctation creates a pressure gradient across the stenosed location, which can be characterized using non-invasive numerical models. Reprinted from ref. [30].
Figure 3. Aortic coarctation creates a pressure gradient across the stenosed location, which can be characterized using non-invasive numerical models. Reprinted from ref. [30].
Fluids 07 00197 g003
Fluids 07 00197 g004 550
Figure 4. Estimation of hemodynamics in an intracranial aneurysm using PINNs. (a) Computational domain; (b) training domain with two perpendicular planes that were used for results visualization; (c) architecture of the DL model; (d) distribution of predicted and reference concentration (c), velocity, and pressure (p) fields at a time instant; (e) flow streamlines calculated from the predicted and reference velocity distributions. Adapted with permission from ref. [46]. Copyright 2020, Science.
Figure 4. Estimation of hemodynamics in an intracranial aneurysm using PINNs. (a) Computational domain; (b) training domain with two perpendicular planes that were used for results visualization; (c) architecture of the DL model; (d) distribution of predicted and reference concentration (c), velocity, and pressure (p) fields at a time instant; (e) flow streamlines calculated from the predicted and reference velocity distributions. Adapted with permission from ref. [46]. Copyright 2020, Science.
Fluids 07 00197 g004
Fluids 07 00197 g005 550
Figure 5. DL models have been used to enhance the velocity field obtained by 4D flow MRI by (a) improving near-wall velocity gradients, (b) smoothing velocity gradient transitions, (c) removing unrealistic velocity fluctuations, and (d) better characterizing near-wall velocity vectors in tortuous structures. Arrows show the main areas of image improvement. Adapted from ref. [80].
Figure 5. DL models have been used to enhance the velocity field obtained by 4D flow MRI by (a) improving near-wall velocity gradients, (b) smoothing velocity gradient transitions, (c) removing unrealistic velocity fluctuations, and (d) better characterizing near-wall velocity vectors in tortuous structures. Arrows show the main areas of image improvement. Adapted from ref. [80].
Fluids 07 00197 g005
Table
Table 1. Sample applications of deep learning for hemodynamics prediction. NN: neural network; DNN: deep NN; CNN: convolutional NN; LSTM RNN: long–short-term memory recurrent NN; PINN: physics-informed NN; 1D: one-dimensional CFD simulation; 3D: three-dimensional CFD simulation; SS: steady-state; US: unsteady; AF: axisymmetric flow; RW: rigid vessel wall; EW: elastic vessel wall; N: Newtonian flow; n-N: non-Newtonian; IC: incompressible flow; BC: CFD boundary conditions; Q: blood flow; v: velocity; P: pressure; WSS: wall shear stress; MRI: magnetic resonance imaging.
Table 1. Sample applications of deep learning for hemodynamics prediction. NN: neural network; DNN: deep NN; CNN: convolutional NN; LSTM RNN: long–short-term memory recurrent NN; PINN: physics-informed NN; 1D: one-dimensional CFD simulation; 3D: three-dimensional CFD simulation; SS: steady-state; US: unsteady; AF: axisymmetric flow; RW: rigid vessel wall; EW: elastic vessel wall; N: Newtonian flow; n-N: non-Newtonian; IC: incompressible flow; BC: CFD boundary conditions; Q: blood flow; v: velocity; P: pressure; WSS: wall shear stress; MRI: magnetic resonance imaging.
ApplicationDL ModelCFD Assumptions
(Solver)		DL InputDL OutputReference
Coronary artery lesionDNN1D, US, AF, EW, N, ICQ & P at each centerline node + Q & P of the upstream and downstream nodesFractional flow reserve along the vessel centerline[66]
Coronary blood flowDNN regressor1D, SS, RW, N, IC
(custom-built solver)		Geometry, SS P dropP drop[67]
Coronary bifurcations2D CNN3D, US, n-N
(ANSYS)		Geometric features (e.g., vessel radii, bifurcation angles, etc.), shear stress for SS flow in a constant-radius straight tubeTime-averaged WSS[71]
Aortic aneurysmDNN3D, SS, RW, N, IC
(STAR-CCM+)		3D geometry, CFD resultsv & P distributions, v magnitude[61]
Coronary stenosis
(coronary bypass surgery)		PointNet
(based on [72])		3D, SS, N, IC
(ANSYS)		3D geometry, CFD resultsv & P distributions[73]
Aortic coarctationNN3D, US, RW, N, IC
(HARVEY [74])		3D geometry, CFD resultsP, WSS[30]
Aortic coarctationDNN
(LSTM RNN + DenseNet)		SS, IC
(STAR-CCM+)		Vessel centerline, BCP, time-averaged WSS, secondary flow degree, kinetic energy (averaged at the centerline)[75]
Thrombus formation
(in left arterial appendage)		DNN3D, US, RW, N, IC
(ANSYS)		3D geometry, CFD resultsEndothelial cell activation potential[76]
Hepatic artery
(liver cancer radioembolization)		CNN3D, RW, N, IC
(SimVascular [29])		CFD results, outlet BCOutlet flow rate[77,78]
Intracranial aneurysm
(right internal carotid artery)		PINN3D, US, ICConcentration of the passive scalar, 3D geometryv & P distributions, WSS[46]
Near-wall blood flow
(in aneurysm and stenosis models)		PINN1D-3D, SS, N, IC
(FEniCS [79])		Geometry, CFD resultsv & P distributions[33]
Cerebral vasospasmPINN1D, US, EW, N, IC
(SimVascular)		3D angiography, 4D flow MRI, or ultrasound measurementsv & P distributions, vessel cross-sectional area[68]
Cerebral aneurysm
(before and after flow-diverting stent)		DNN3D, SS, N, IC, stent modeled by porous media
(ANSYS)		3D geometry, CFD resultsv & P distributions[70]
Aorta/carotid bifurcationPINN1D, US, EW, N, ICReduced-order pulsatile flow results, 4D flow MRI at some cross sectionsP wave propagation[34]
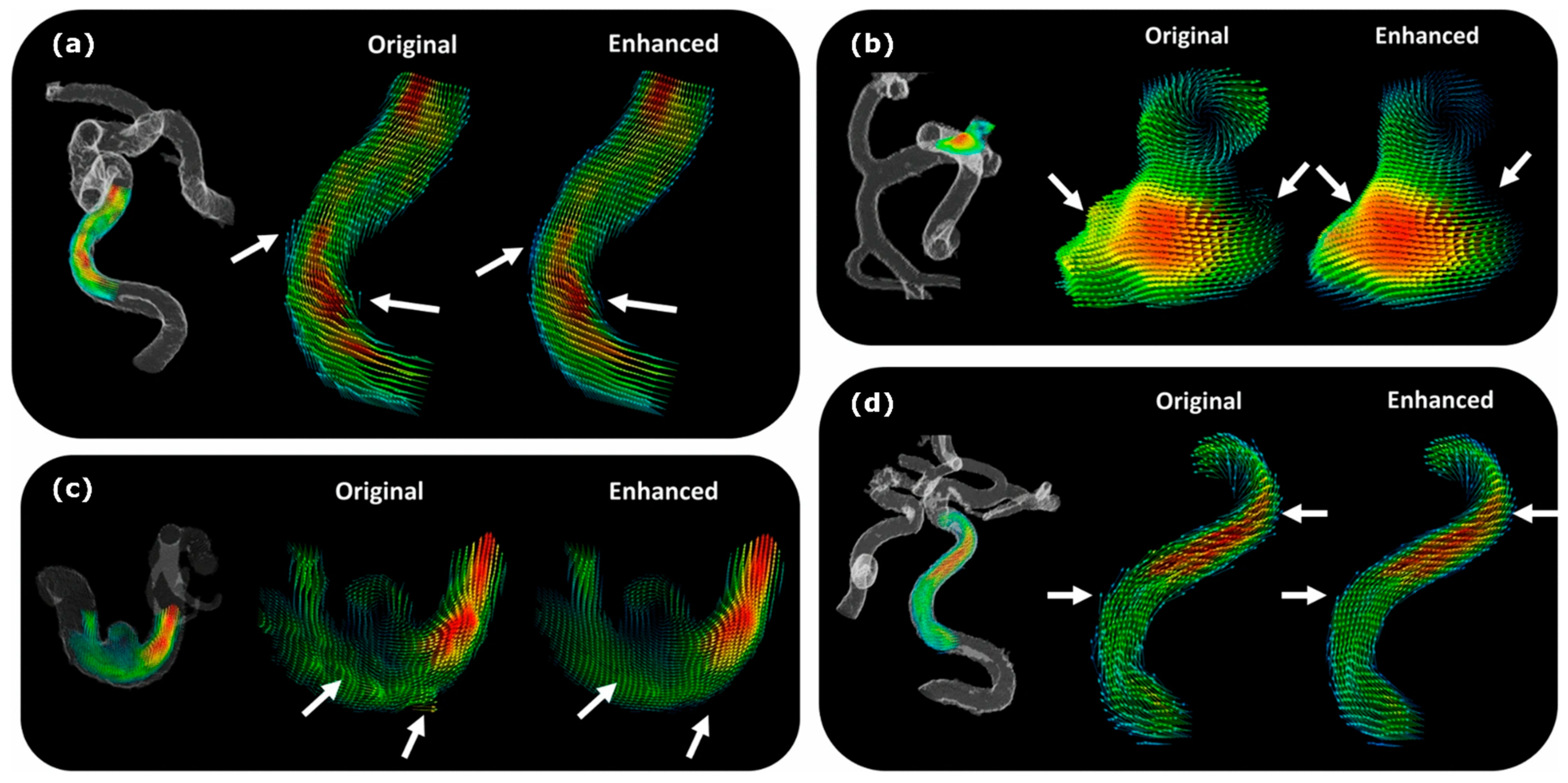
Cerebral aneurysmCNN3D, US, RW, N, IC
(CONVERGE)		3D geometry, CFD results, 4D flow MRIEnhanced 4D flow MRI[80]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Taebi, A. Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances. Fluids 2022, 7, 197. https://doi.org/10.3390/fluids7060197

AMA Style

Taebi A. Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances. Fluids. 2022; 7(6):197. https://doi.org/10.3390/fluids7060197

Chicago/Turabian Style

Taebi, Amirtahà. 2022. "Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances" Fluids 7, no. 6: 197. https://doi.org/10.3390/fluids7060197

APA Style

Taebi, A. (2022). Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances. Fluids, 7(6), 197. https://doi.org/10.3390/fluids7060197

Article Metrics

Back to TopTop