Phase Convergence and Crest Enhancement of Modulated Wave Trains
Abstract
:1. Introduction
2. Facility and Methods
2.1. Numerical Simulations
2.2. Tank Experiment
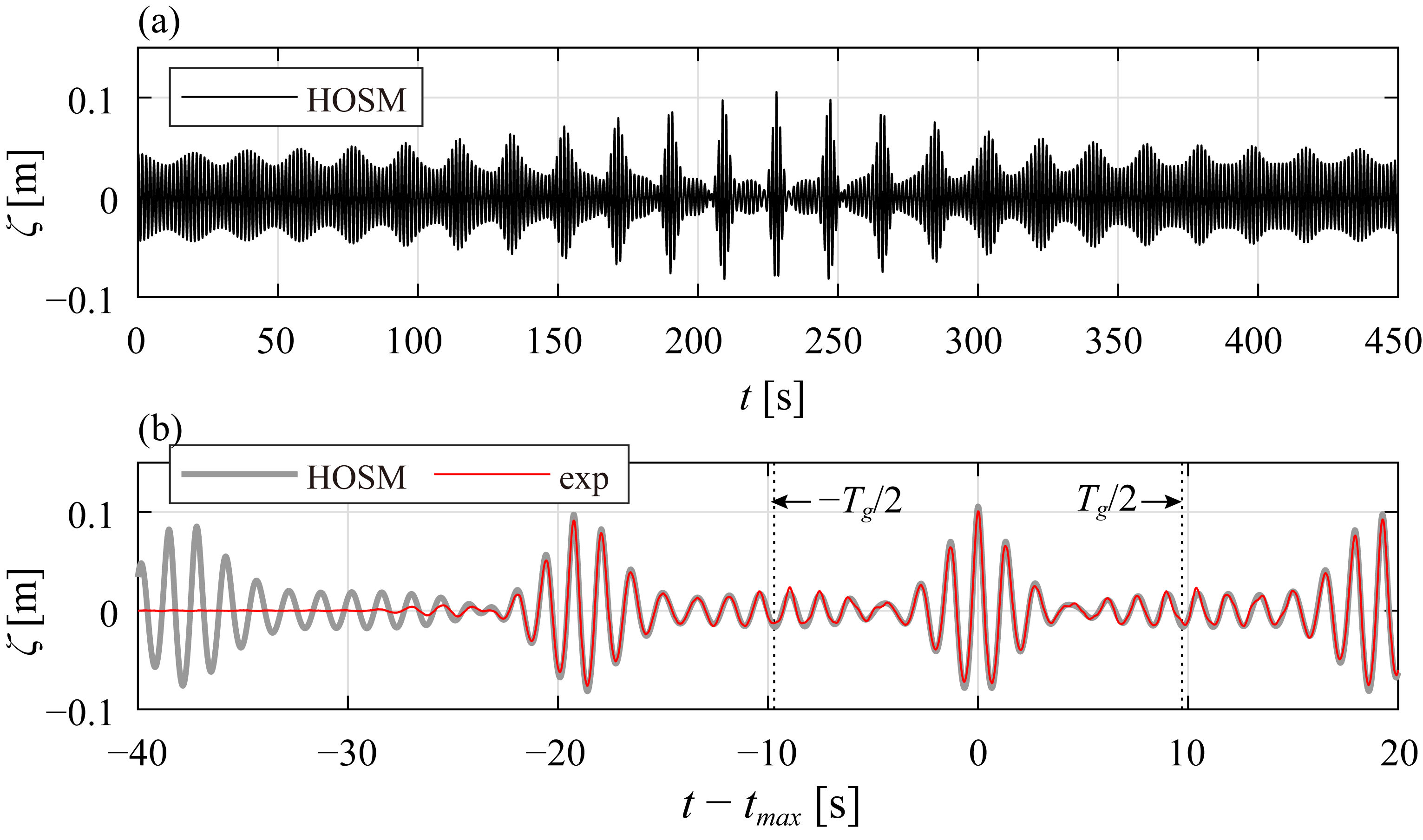
3. Results of Numerical Simulations and Experiments
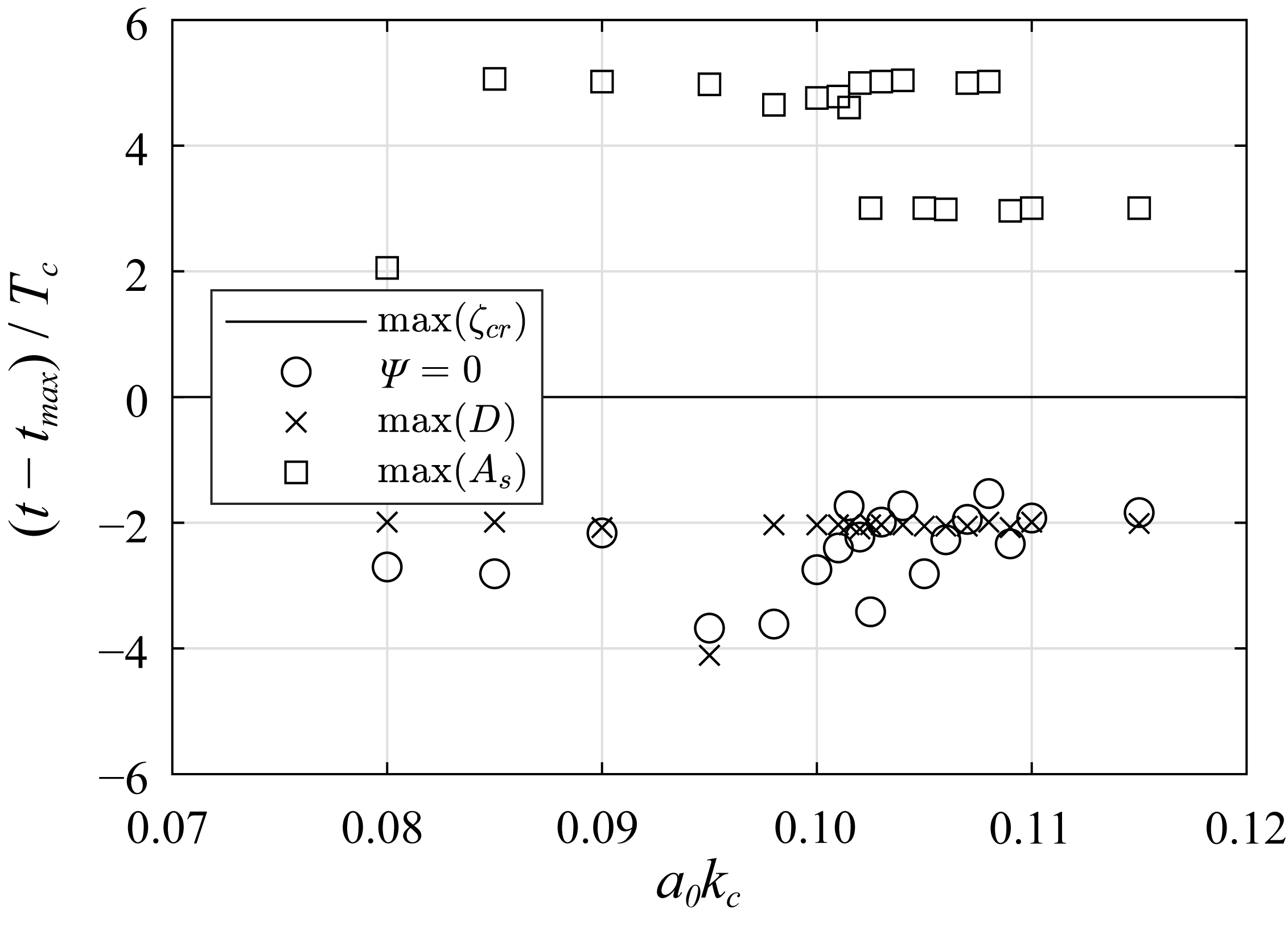
4. Discussion
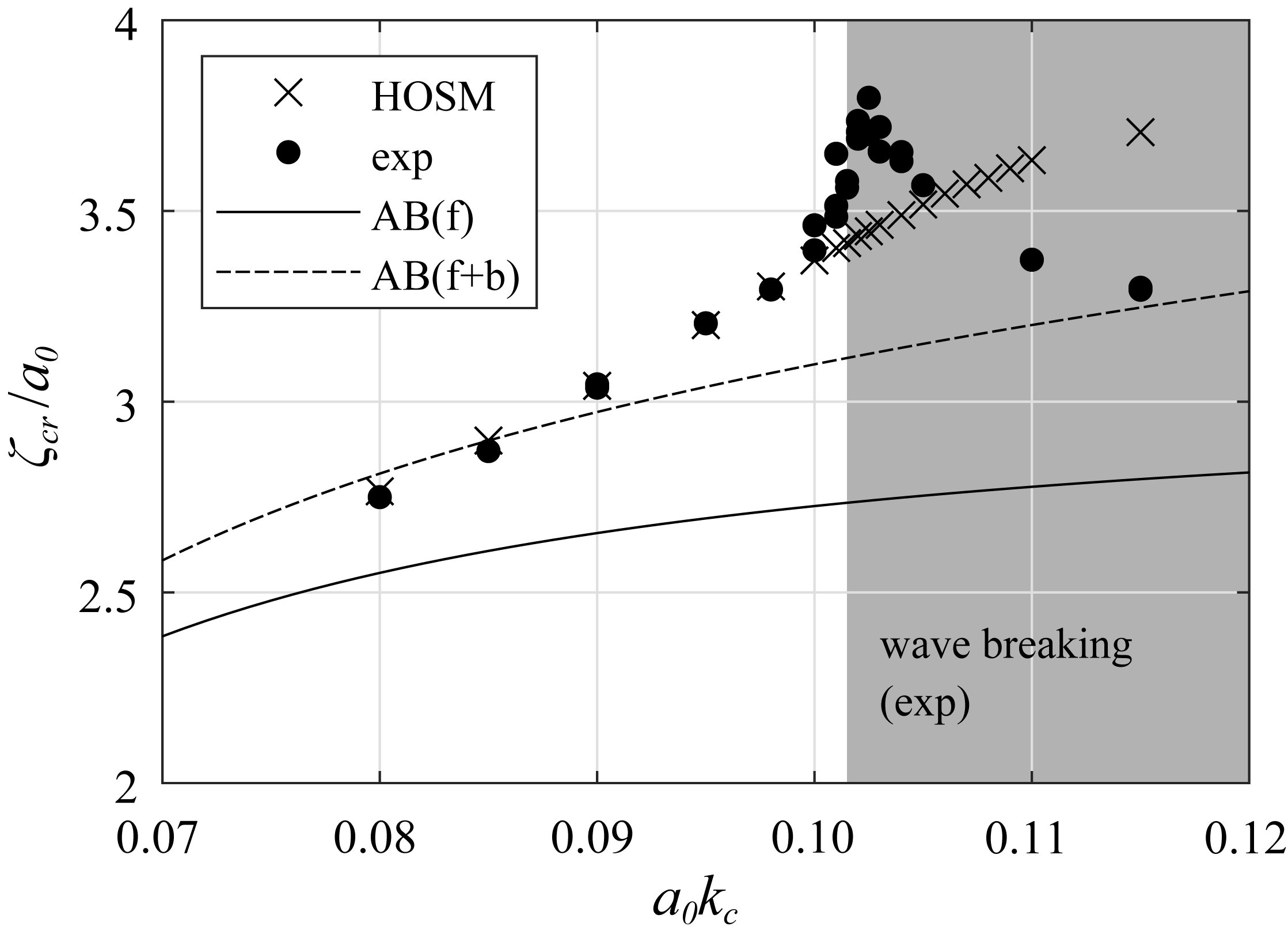
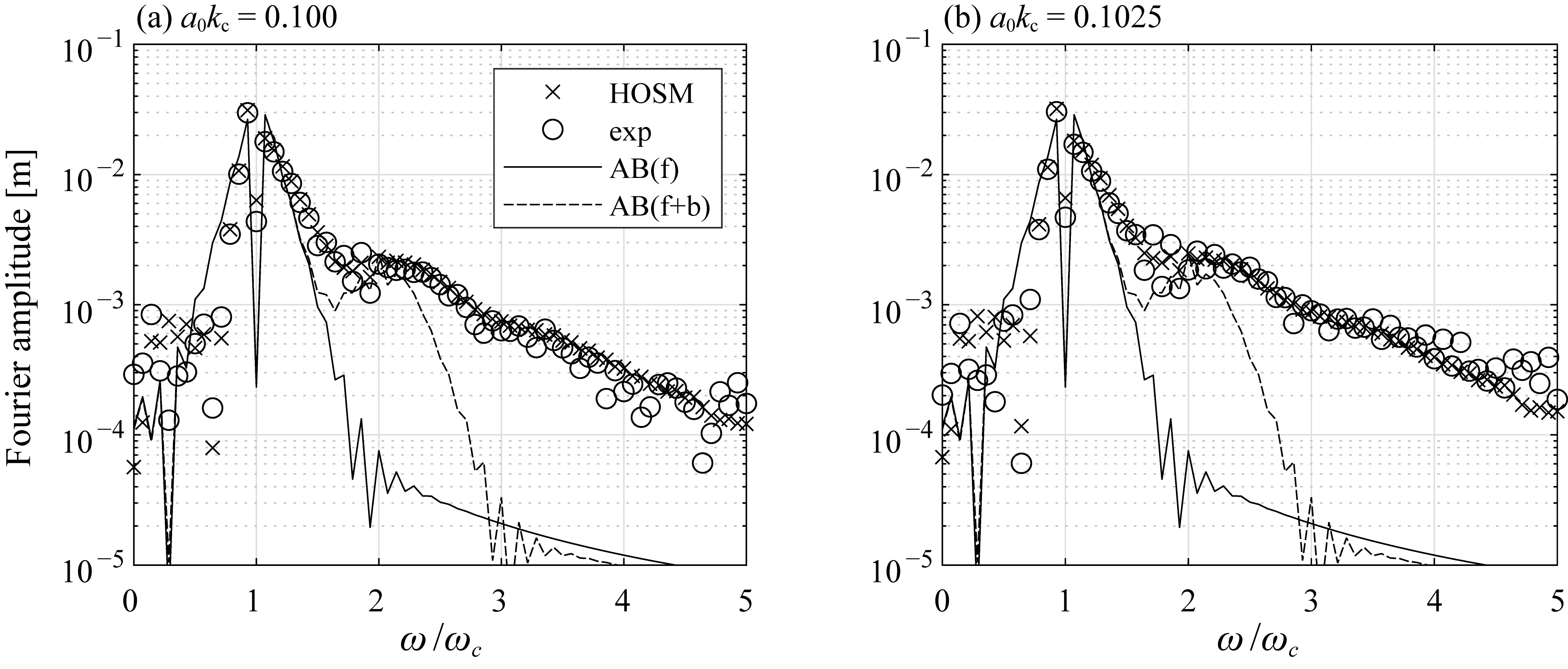
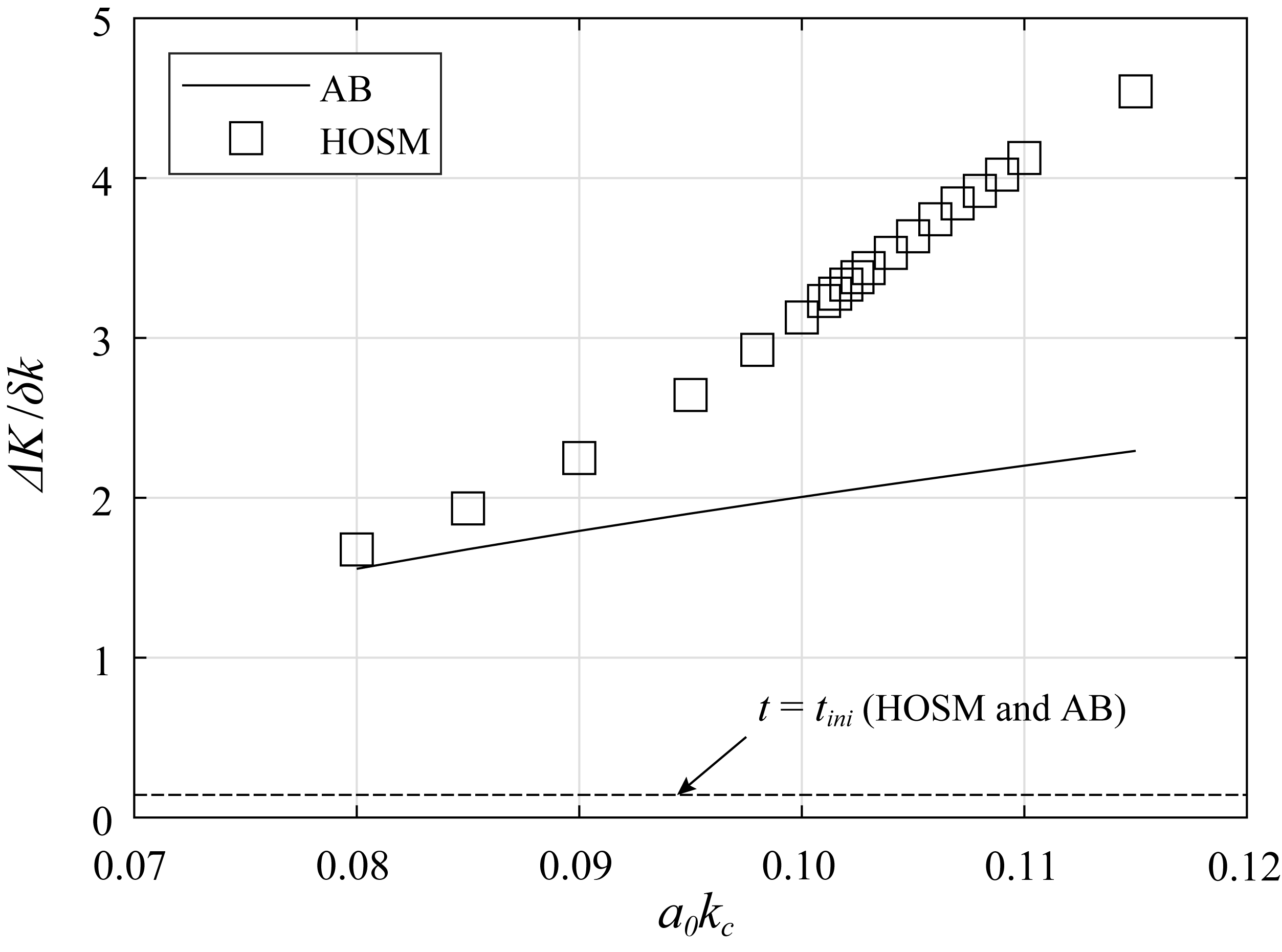
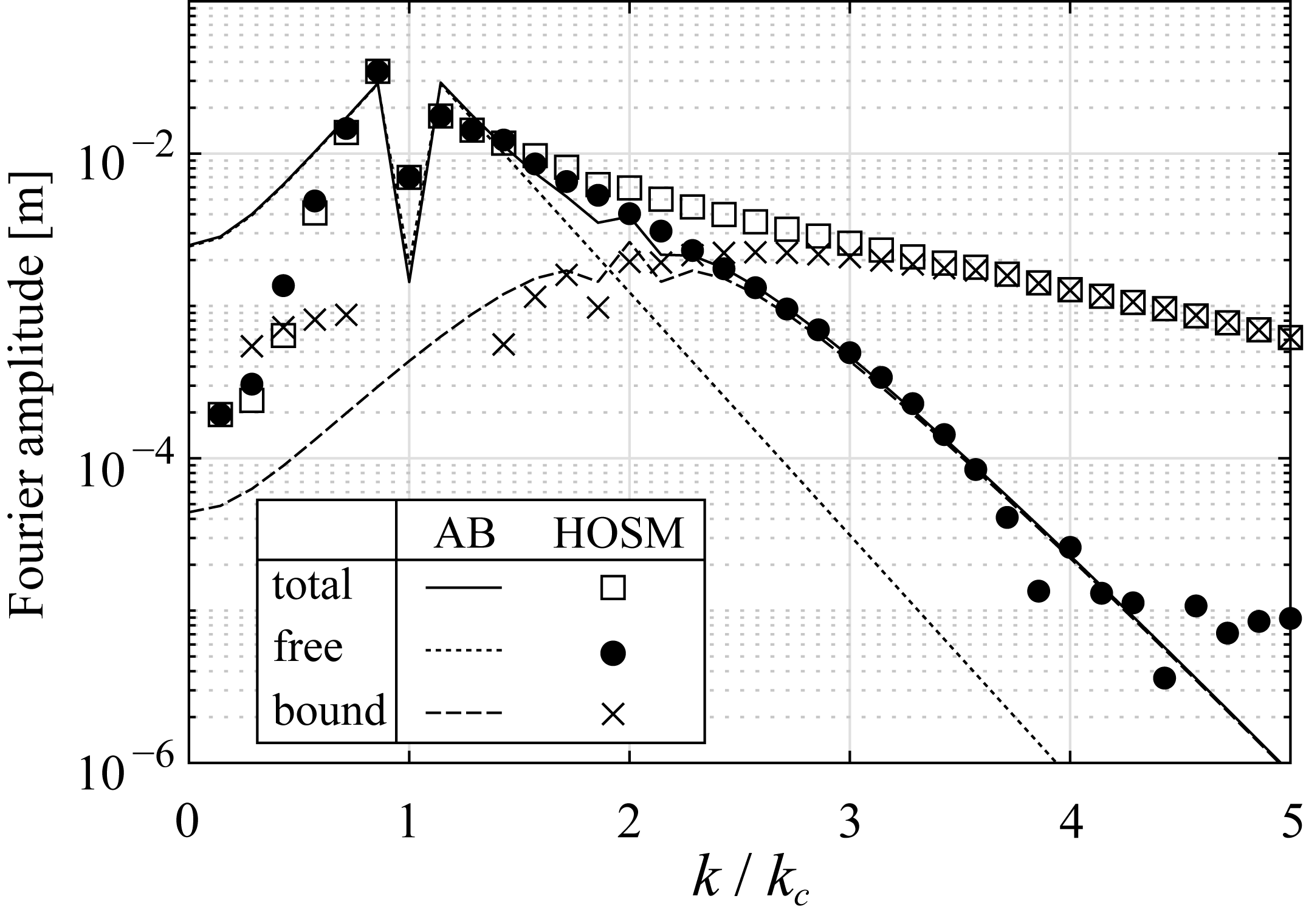
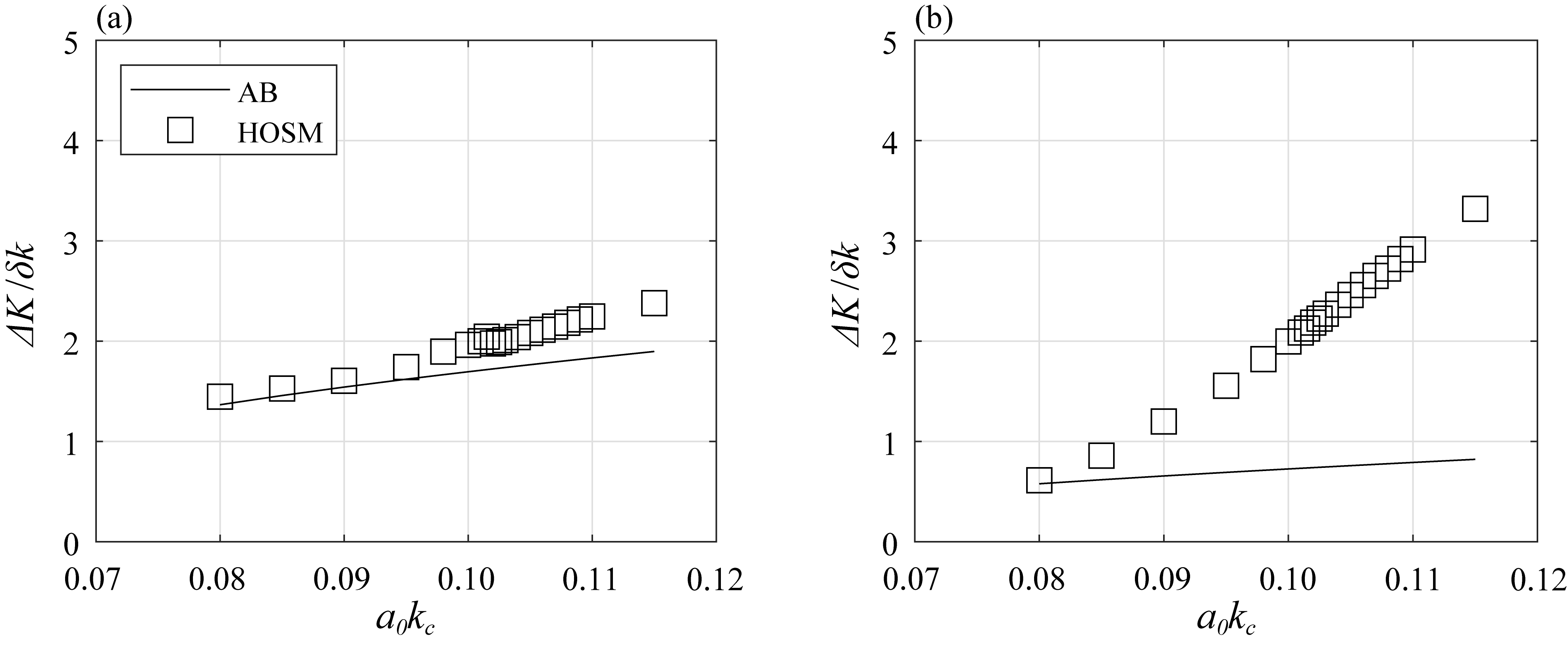
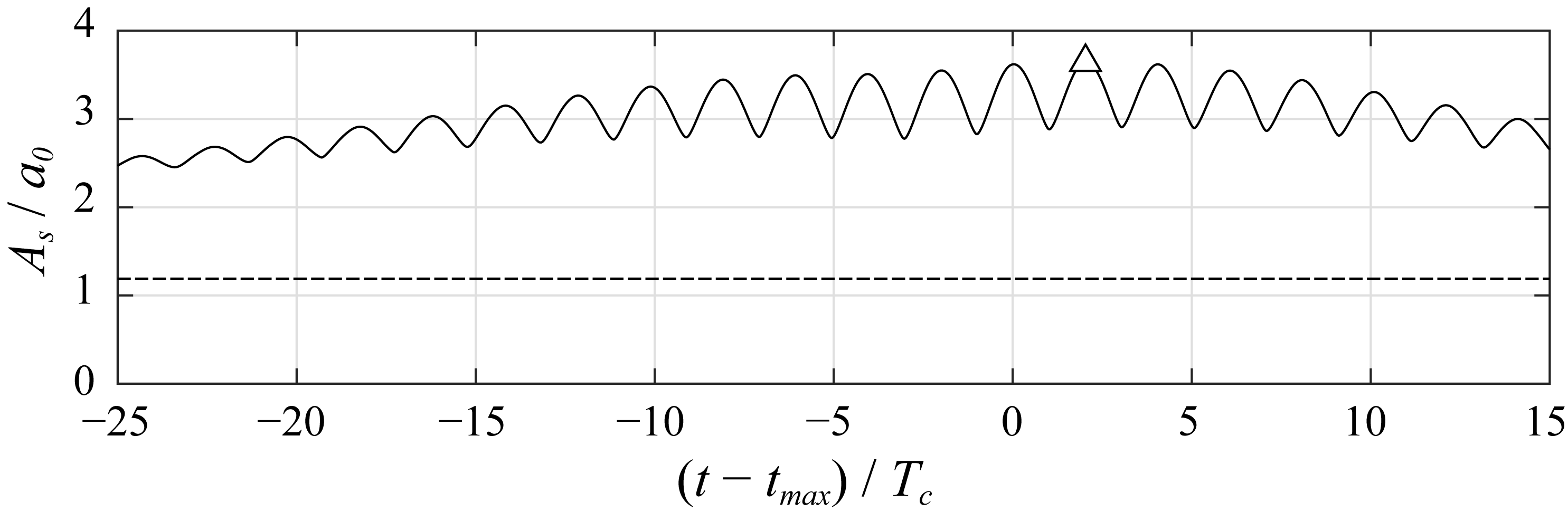
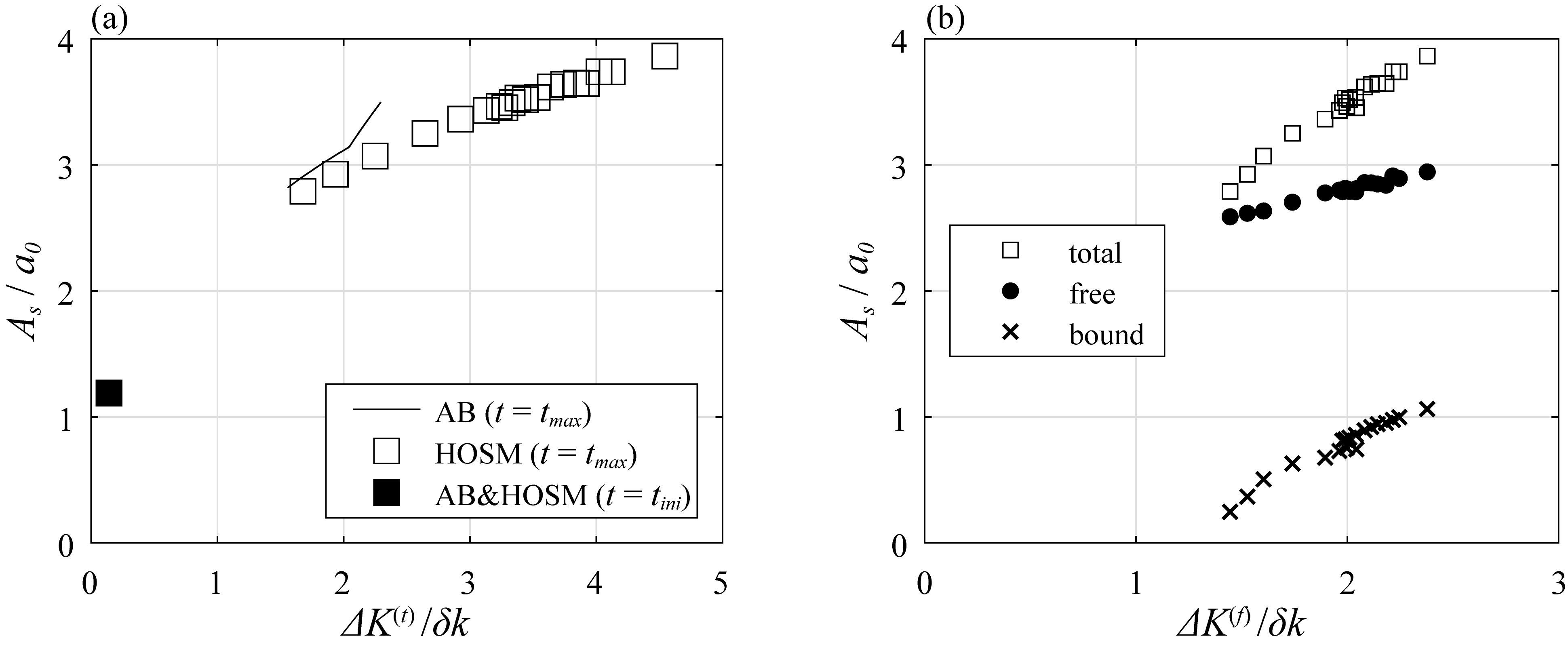
4.1. Spectral Broadening and Its Influence on Maximum Crest Height
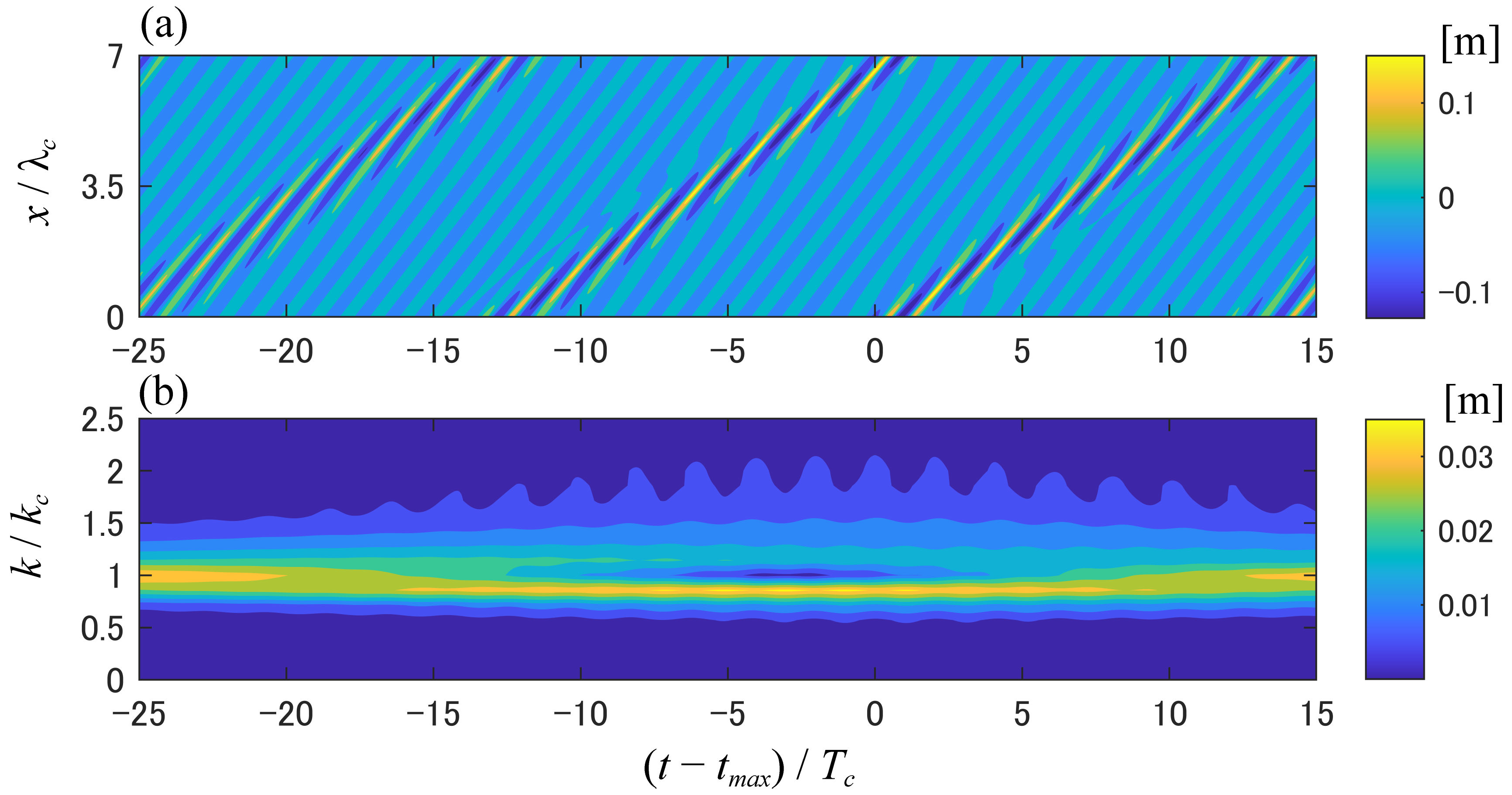
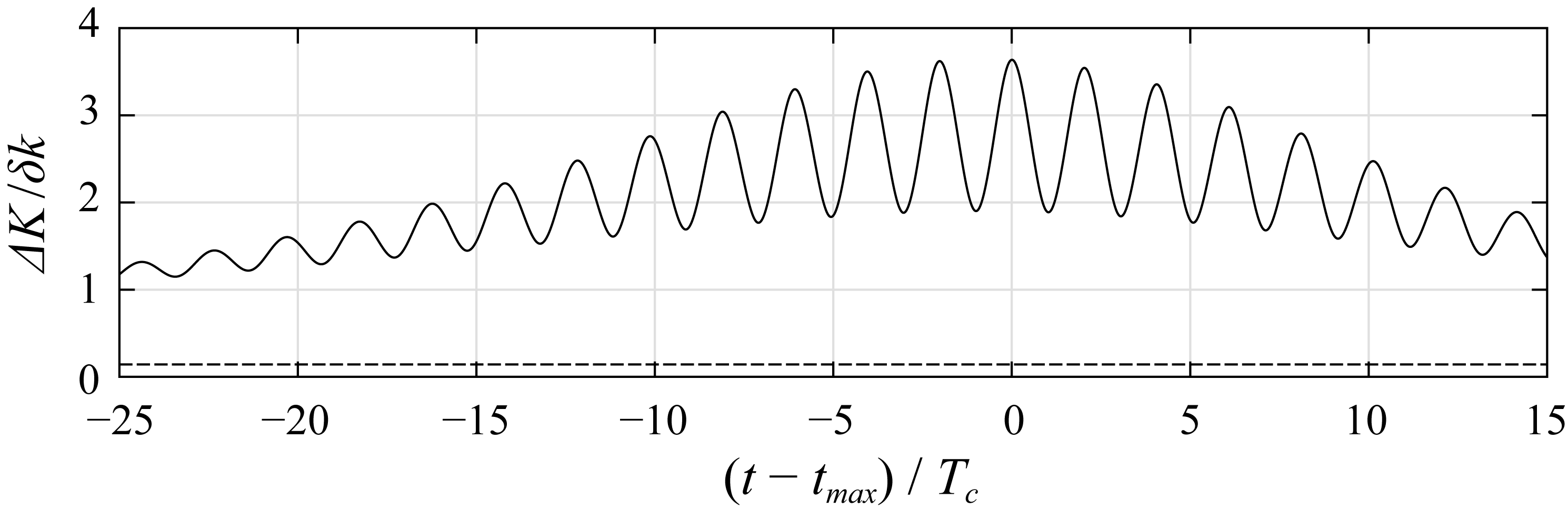
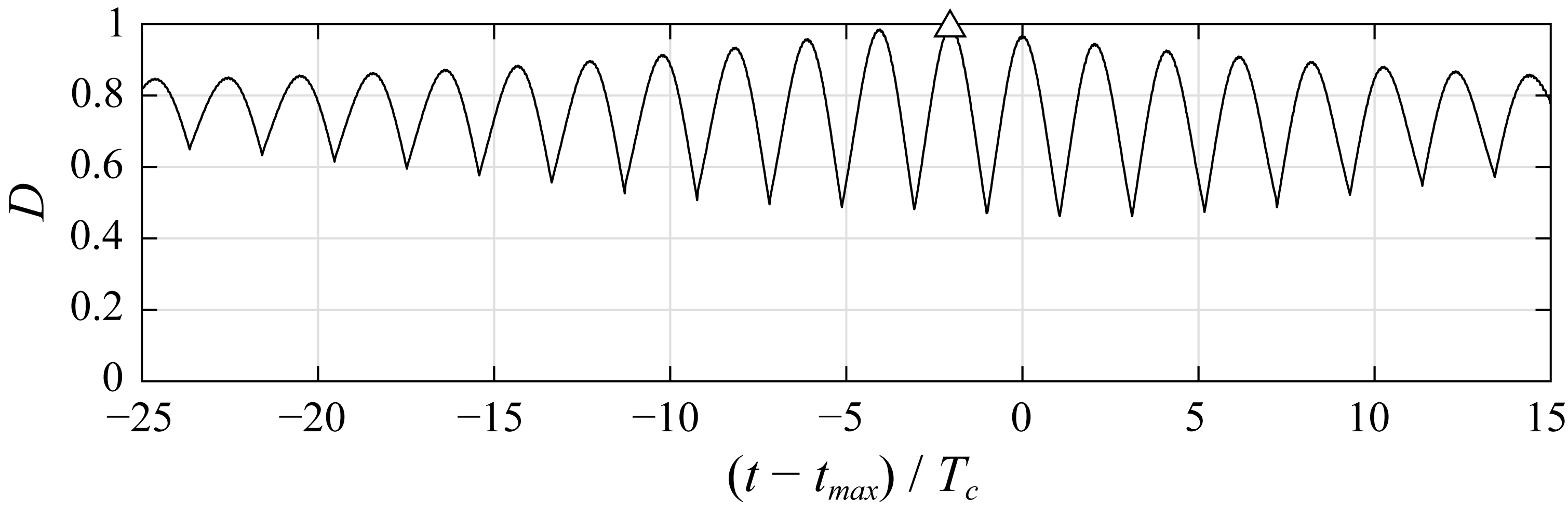
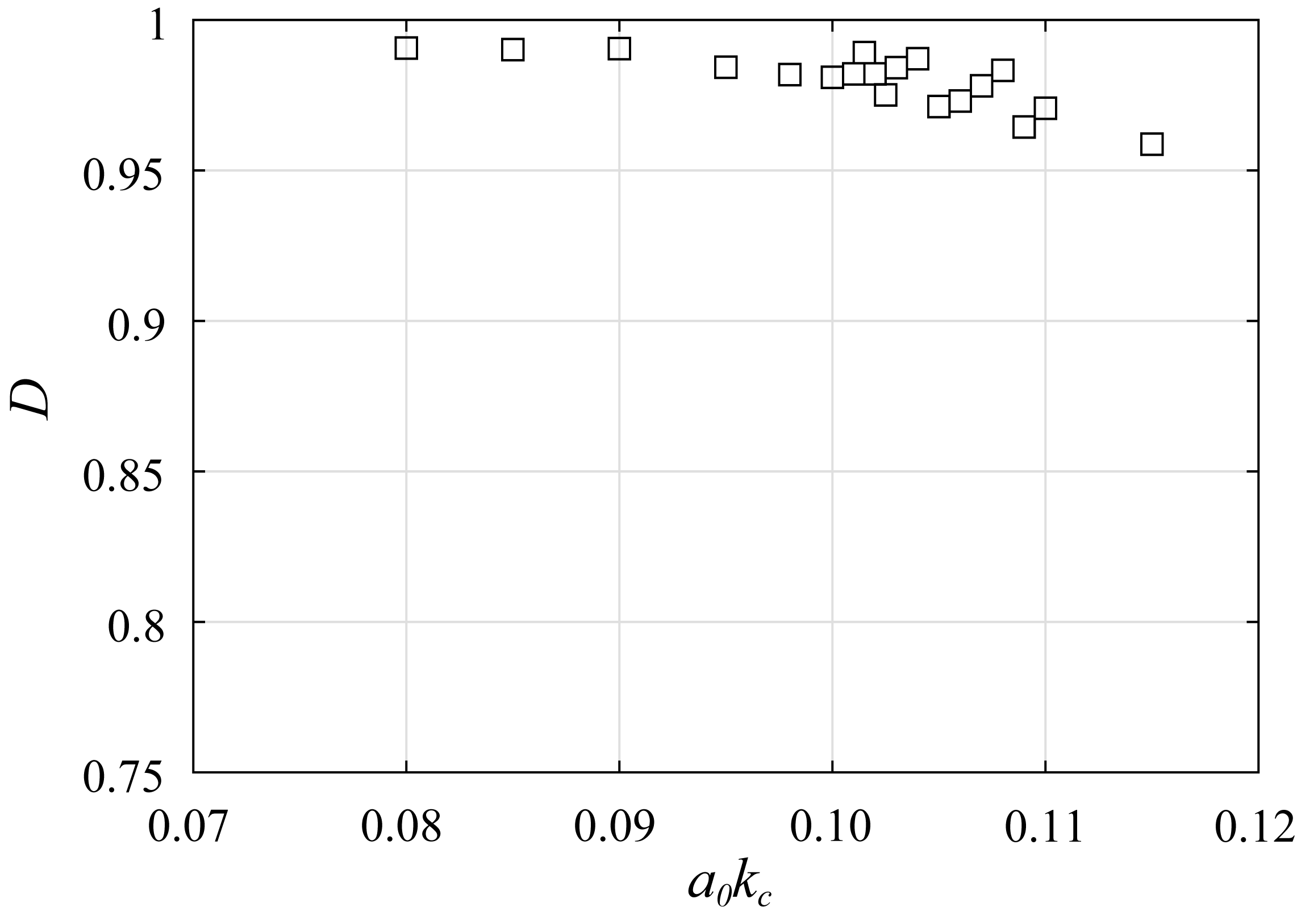
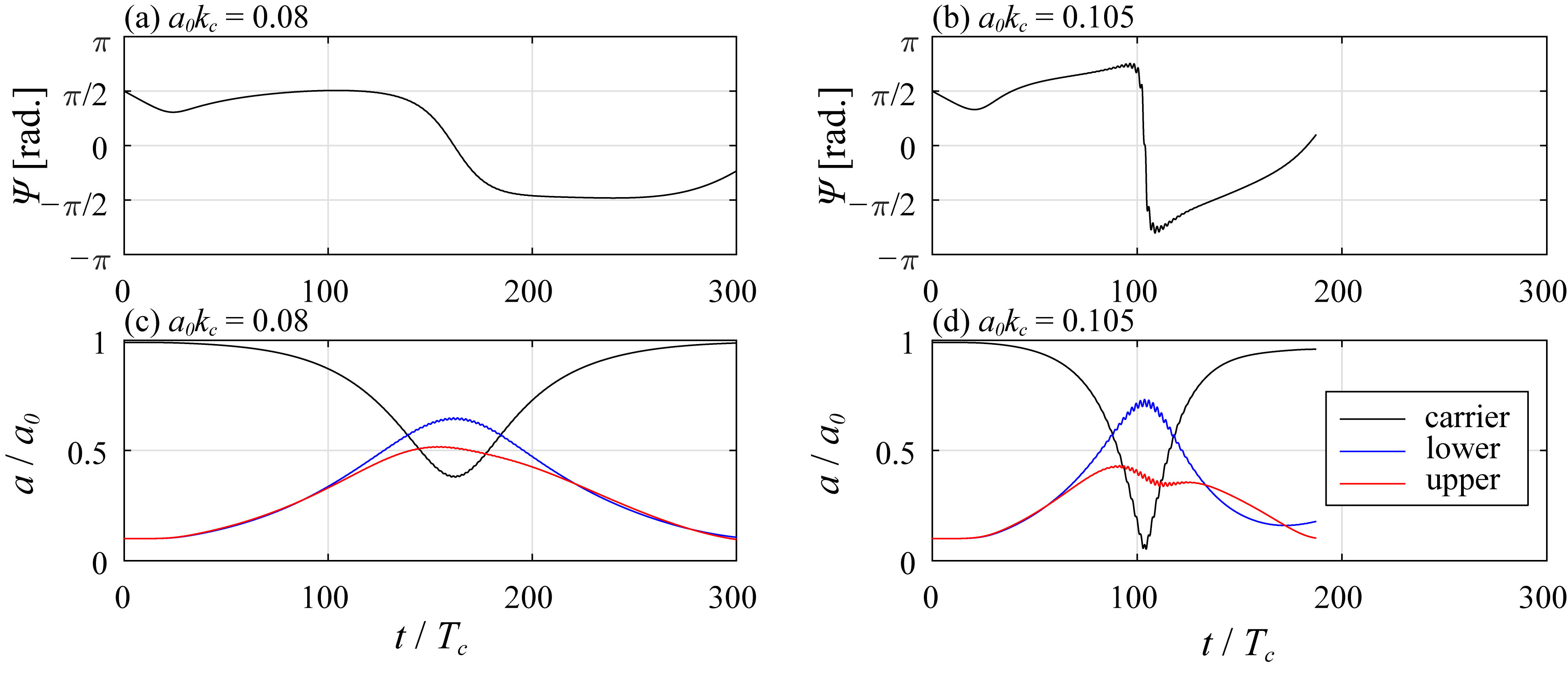
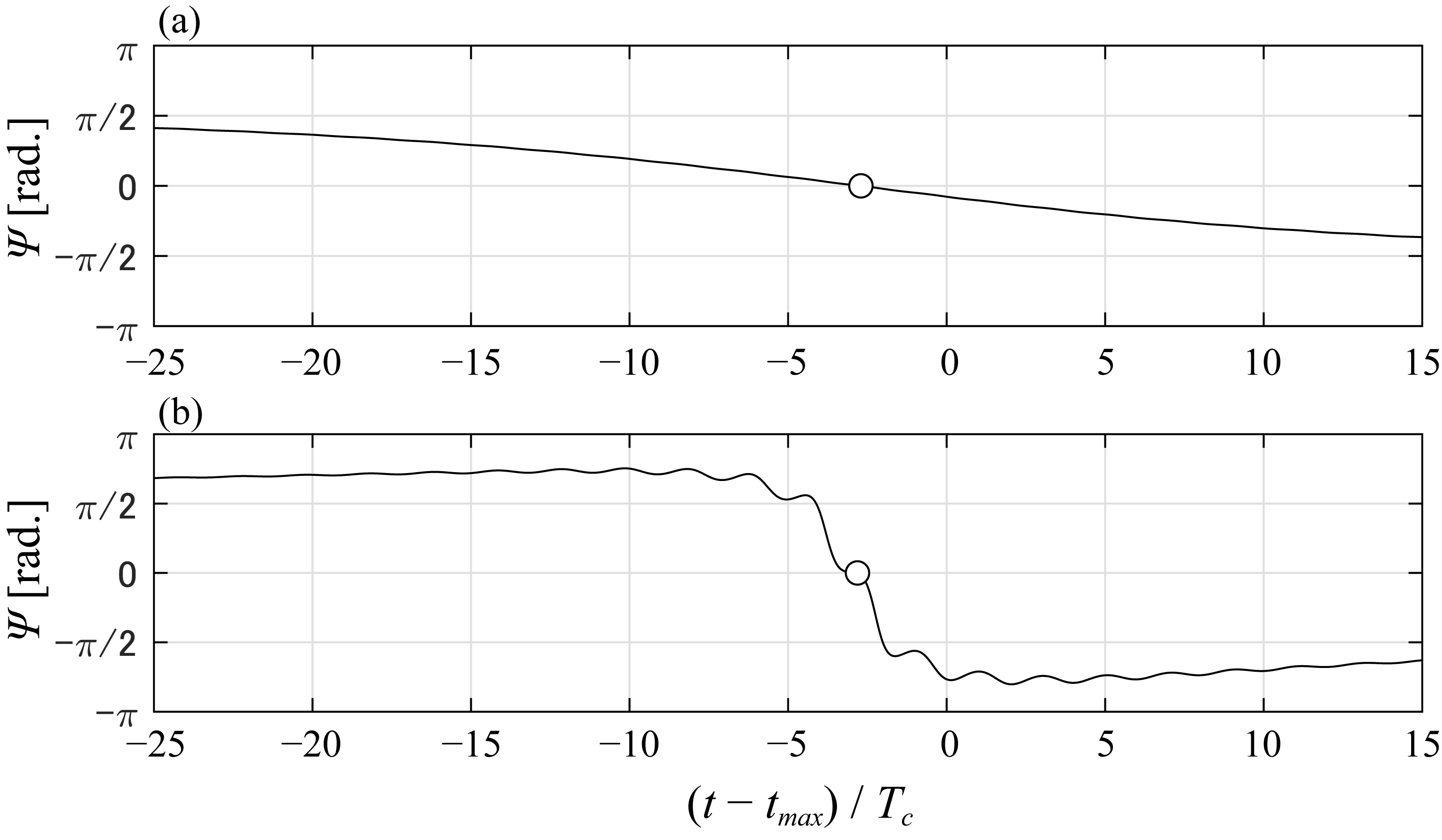
4.2. Phase Convergence during Nonlinear Evolution of a Modulated Wave Train
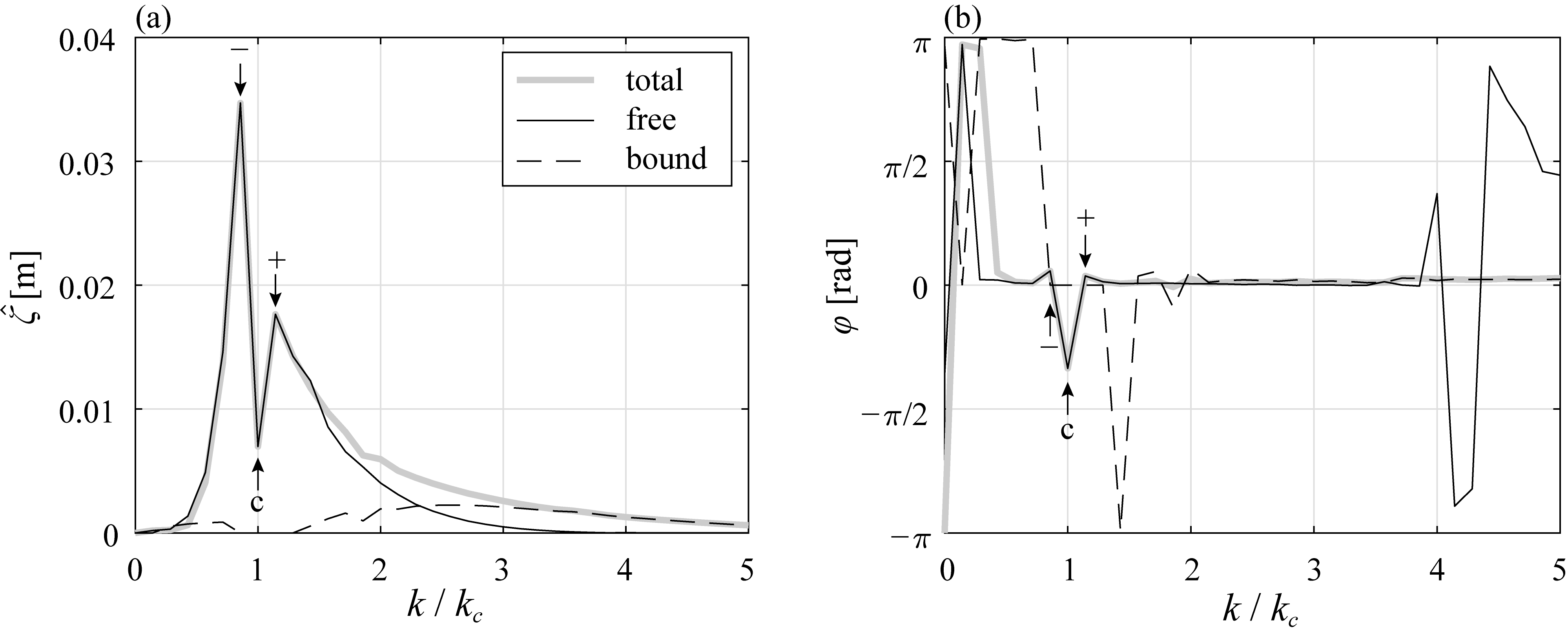
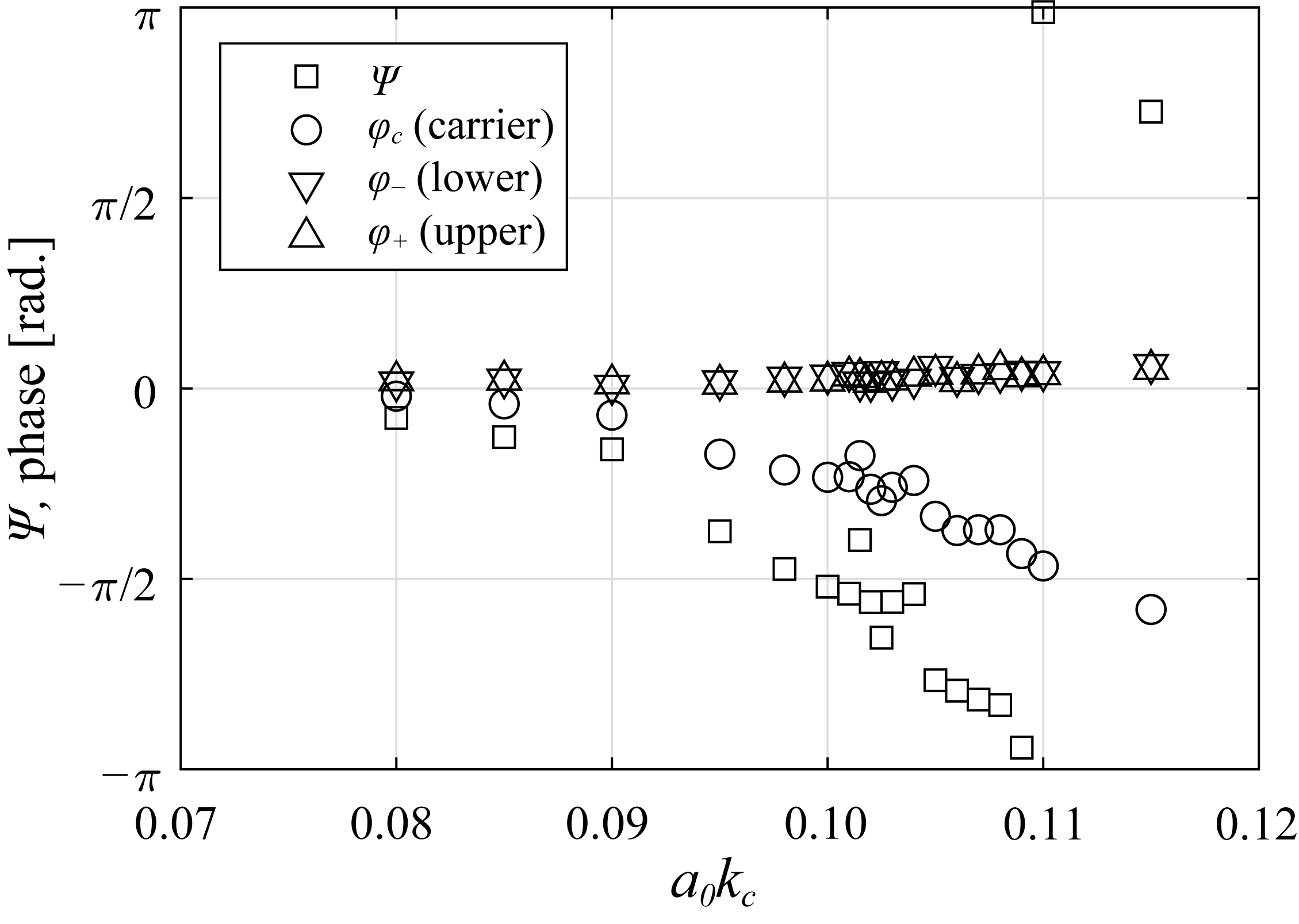
4.3. Temporal Evolution of Phase Relation among the Carrier and Sideband Waves
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Akhmediev Breather Solution
Appendix B. Phase of Second-Order Superharmonic and Subharmonic Waves
References
- Welch, S.; Levi, C.; Fontaine, E.; Tulin, M.P. Experimental loads on a flexibly mounted vertical cylinder in breaking wave groups. In Proceedings of the Eighth International Offshore and Polar Engineering Conference, Montreal, QC, Canada, 24–29 May 1998; OnePetro: Richardson, TX, USA, 1998. [Google Scholar]
- Onorato, M.; Proment, D.; Clauss, G.; Klein, M. Rogue waves: From nonlinear Schrödinger breather solutions to sea-keeping test. PLoS ONE 2013, 8, e54629. [Google Scholar] [CrossRef]
- Klein, M.; Clauss, G.F.; Rajendran, S.; Soares, C.G.; Onorato, M. Peregrine breathers as design waves for wave-structure interaction. Ocean. Eng. 2016, 128, 199–212. [Google Scholar] [CrossRef]
- Houtani, H.; Waseda, T.; Tanizawa, K.; Sawada, H. Temporal variation of modulated-wave-train geometries and their influence on vertical bending moments of a container ship. Appl. Ocean. Res. 2019, 86, 128–140. [Google Scholar] [CrossRef]
- Shahroozi, Z.; Göteman, M.; Engström, J. Experimental investigation of a point-absorber wave energy converter response in different wave-type representations of extreme sea states. Ocean. Eng. 2022, 248, 110693. [Google Scholar] [CrossRef]
- Bitner-Gregersen, E.M.; Toffoli, A. On the probability of occurrence of rogue waves. Nat. Hazards Earth Syst. Sci. 2012, 12, 751–762. [Google Scholar] [CrossRef]
- Bitner-Gregersen, E.M.; Gramstad, O. Rogue waves impact on ships and offshore structures. In Det Norske Veritas Germanischer Lloyd Strategic Research and Innovation Position Paper; DNV: Bærum, Norway, 2015. [Google Scholar]
- Forristall, G.Z. Maximum wave heights over an area and the air gap problem, OMAE2006-92022 paper. In Proceedings of the ASME 25th International Conference on Ocean Offshore, and Arctic Engineering, Hamburg, Germany, 4–9 June 2006. [Google Scholar]
- Magnusson, A.K.; Donelan, M.A. The Andrea wave characteristics of a measured North Sea rogue wave. J. Offshore Mech. Arct. Eng. 2013, 135, 31108. [Google Scholar] [CrossRef]
- Janssen, P.A. Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 2003, 33, 863–884. [Google Scholar] [CrossRef]
- Onorato, M.; Waseda, T.; Toffoli, A.; Cavaleri, L.; Gramstad, O.; Janssen, P.A.E.M.; Kinoshita, T.; Monbaliu, J.; Mori, N.; Osborne, A.R.; et al. Statistical properties of directional ocean waves: The role of the modulational instability in the formation of extreme events. Phys. Rev. Lett. 2009, 102, 114502. [Google Scholar] [CrossRef]
- Waseda, T.; Kinoshita, T.; Tamura, H. Evolution of a random directional wave and freak wave occurrence. J. Phys. Oceanogr. 2009, 39, 621–639. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Feir, J.E. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Benjamin, T.B. Instability of periodic wavetrains in nonlinear dispersive systems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 299, 59–76. [Google Scholar]
- Tulin, M.P.; Waseda, T. Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 1999, 378, 197–232. [Google Scholar] [CrossRef]
- Stiassnie, M.; Kroszynski, U.I. Long-time evolution of an unstable water-wave train. J. Fluid Mech. 1982, 116, 207–225. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Eleonskii, V.M.; Kulagin, N.E. Exact first-order solutions of the nonlinear Schrödinger equation. Theor. Math. Phys. 1987, 72, 809–818. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.R.; Serio, M. Nonlinear Dynamics of Rogue Waves. In Proceedings of the International Workshop on Wave Hindcasting and Forecasting, Monterey, CA, USA, 6–10 November 2000; pp. 470–479. [Google Scholar]
- Onorato, M.; Osborne, A.R.; Serio, M.; Damiani, T. Occurrence of freak waves from envelope equations in random ocean wave simulations. In Proceedings of the Rogue Wave 2000, Brest, France, 29–30 November 2000; pp. 181–191. [Google Scholar]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F.T. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Mori, N.; Janssen, P.A. On kurtosis and occurrence probability of freak waves. J. Phys. Oceanogr. 2006, 36, 1471–1483. [Google Scholar] [CrossRef]
- Su, M.Y.; Green, A.W. Coupled two-and three-dimensional instabilities of surface gravity waves. Phys. Fluids 1984, 27, 2595–2597. [Google Scholar] [CrossRef]
- Waseda, T. Experimental investigation and applications of the modulational wave train. In Proceedings of the Workshop on Rogue Waves, Honolulu, HI, USA, 25–28 January 2005; pp. 12–15. [Google Scholar]
- Tanaka, M. Maximum amplitude of modulated wavetrain. Wave Motion 1990, 12, 559–568. [Google Scholar] [CrossRef]
- Slunyaev, A.V.; Shrira, V.I. On the highest non-breaking wave in a group: Fully nonlinear water wave breathers versus weakly nonlinear theory. J. Fluid Mech. 2013, 735, 203–248. [Google Scholar] [CrossRef]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Dold, J.W.; Peregrine, D.H. An efficient boundary-integral method for steep unsteady water waves. Numer. Methods Fluid Dyn. II 1986, 671, 679. [Google Scholar]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A Math. Phys. Sci. 1979, 369, 105–114. [Google Scholar]
- Chabchoub, A.; Kibler, B.; Dudley, J.M.; Akhmediev, N. Hydrodynamics of periodic breathers. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20140005. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E.; Dyachenko, A.I.; Vasilyev, O.A. New method for numerical simulation of a nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. B Fluids 2002, 21, 283–291. [Google Scholar] [CrossRef]
- Chaplin, J.R. On frequency-focusing unidirectional waves. Int. J. Offshore Polar Eng. 1996, 6, 131–137. [Google Scholar]
- West, B.J.; Brueckner, K.A.; Janda, R.S.; Milder, D.M.; Milton, R.L. A new numerical method for surface hydrodynamics. J. Geophys. Res. Ocean. 1987, 92, 11803–11824. [Google Scholar] [CrossRef]
- Dommermuth, D.G.; Yue, D.K. A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 1987, 184, 267–288. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillatory waves. Trans. Camb. Philos. Soc. 1847, 8, 441–455. [Google Scholar]
- Houtani, H.; Waseda, T.; Tanizawa, K. Experimental and numerical investigations of temporally and spatially periodic modulated wave trains. Phys. Fluids 2018, 30, 34101. [Google Scholar] [CrossRef]
- Houtani, H.; Waseda, T.; Fujimoto, W.; Kiyomatsu, K.; Tanizawa, K. Generation of a spatially periodic directional wave field in a rectangular wave basin based on higher-order spectral simulation. Ocean. Eng. 2018, 169, 428–441. [Google Scholar] [CrossRef]
- Kirezci, C.; Babanin, A.V.; Chalikov, D.V. Modelling rogue waves in 1D wave trains with the JONSWAP spectrum, by means of the High Order Spectral Method and a fully nonlinear numerical model. Ocean. Eng. 2021, 231, 108715. [Google Scholar] [CrossRef]
- Tanaka, M. A method of studying nonlinear random field of surface gravity waves by direct numerical simulation. Fluid Dyn. Res. 2001, 28, 41. [Google Scholar] [CrossRef]
- Tian, Z.; Perlin, M.; Choi, W. Evaluation of a deep-water wave breaking criterion. Phys. Fluids 2008, 20, 66604. [Google Scholar] [CrossRef]
- Dommermuth, D. The initialization of nonlinear waves using an adjustment scheme. Wave Motion 2000, 32, 307–317. [Google Scholar] [CrossRef]
- Houtani, H.; Waseda, T.; Tanizawa, K. Measurement of spatial wave profiles and particle velocities on a wave surface by stereo imaging–validation with unidirectional regular waves. J. Jpn. Soc. Nav. Archit. Ocean. Eng. 2017, 25, 93–102. (In Japanese) [Google Scholar]
- Houtani, H.; Waseda, T.; Fujimoto, W.; Kiyomatsu, K.; Tanizawa, K. Freak wave generation in a wave basin with HOSM-WG method. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56550, p. V007T06A085. [Google Scholar]
- Thyagaraja, A. Recurrent motions in certain continuum dynamical systems. Phys. Fluids 1979, 22, 2093–2096. [Google Scholar] [CrossRef]
- Martin, D.U.; Yuen, H.C. Spreading of energy in solutions of the nonlinear Schrödinger equation. Phys. Fluids 1980, 23, 1269–1271. [Google Scholar] [CrossRef]
- Gibson, R.S.; Swan, C. The evolution of large ocean waves: The role of local and rapid spectral changes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 21–48. [Google Scholar] [CrossRef]
- Rapp, R.J.; Melville, W.K. Laboratory measurements of deep-water breaking waves. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1990, 331, 735–800. [Google Scholar]
- Waseda, T. Laboratory Study of Wind-and Mechanically-Generated Water Waves. Ph.D. Thesis, University of California, Santa Barbara, CA, USA, 1997. [Google Scholar]
- Waseda, T.; Tulin, M.P. Experimental study of the stability of deep-water wave trains including wind effects. J. Fluid Mech. 1999, 401, 55–84. [Google Scholar] [CrossRef]
- Liu, S.; Waseda, T.; Zhang, X. Phase Locking Phenomenon in the Modulational Instability of Surface Gravity Waves. In Proceedings of the 36th International Workshop on Water Waves and Floating Bodies (IWWWFB), Seoul, Korea, 25–28 April 2021; pp. 117–120. [Google Scholar]
- Gemmrich, J.; Cicon, L. Generation mechanism and prediction of an observed extreme rogue wave. Sci. Rep. 2022, 12, 1718. [Google Scholar] [CrossRef] [PubMed]
- Slunyaev, A.V. A high-order nonlinear envelope equation for gravity waves in finite-depth water. J. Exp. Theor. Phys. 2005, 101, 926–941. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Akhmediev, N. Super rogue waves: Observation of a higher-order breather in water waves. Phys. Rev. X 2012, 2, 11015. [Google Scholar] [CrossRef]
- Dalzell, J.F. A note on finite depth second-order wave-wave interactions. Appl. Ocean. Res. 1999, 21, 105–111. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| 3 m | |
| 1/7 | |
| 0.1 | |
| 0.08–0.115 | |
| 0.62–0.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Houtani, H.; Sawada, H.; Waseda, T. Phase Convergence and Crest Enhancement of Modulated Wave Trains. Fluids 2022, 7, 275. https://doi.org/10.3390/fluids7080275
Houtani H, Sawada H, Waseda T. Phase Convergence and Crest Enhancement of Modulated Wave Trains. Fluids. 2022; 7(8):275. https://doi.org/10.3390/fluids7080275
Chicago/Turabian StyleHoutani, Hidetaka, Hiroshi Sawada, and Takuji Waseda. 2022. "Phase Convergence and Crest Enhancement of Modulated Wave Trains" Fluids 7, no. 8: 275. https://doi.org/10.3390/fluids7080275
APA StyleHoutani, H., Sawada, H., & Waseda, T. (2022). Phase Convergence and Crest Enhancement of Modulated Wave Trains. Fluids, 7(8), 275. https://doi.org/10.3390/fluids7080275







