Abstract
In past investigations of elastic instabilities and elastic turbulence, almost no attention has been devoted to the effects and influences of inertial phenomena. Within the present investigation, Nusselt number data are provided to illustrate the relative influences of inertia and polymeric viscoelastic phenomena within a rotating Couette flow (RCF) environment. Data are provided from experimental measurements of local surface heat transfer characteristics for different flow passage heights, one radial position, and different values of disk rotational speed for polyacrylamide polymer concentrations ρ of 0 ppm, 100 ppm, 150 ppm, and 300 ppm. With this approach, data for a wide range of shear rate values, Weissenberg numbers, and first normal stress difference values are provided. Nusselt number data are provided as dependent upon a newly developed parameter, equal to , which collapse into a single distribution over the range of values considered which range from 0 to about 182. Such characteristics indicate that the parameter provides an appropriate means to simultaneously account for the relative influences of inertia and polymeric viscoelastic effects. The use of such a power law dependence for additionally gives values which are dominated by values when the Weissenberg number Wi is greater than the elastic instability transition onset value. The experimental conditions associated with this value correspond to the change from inertia domination (with buoyance influences) to polymeric viscoelastic domination which occurs for shear rates in the vicinity of 11 to 12 s−1. For Weissenberg numbers greater than the onset value, Nusselt numbers associated with H = 5 mm are generally the highest values measured, with magnitudes that steadily increase with . Associated Nusselt numbers become as high as about 3.0, whereas zero-shear rate values (obtained with zero rotation) are in the vicinity of 1.0. At lower Weissenberg number magnitudes (below the transition onset value), Nusselt numbers cover a wide range of values as experimental conditions and configuration are varied, as a consequence of the complicated and simultaneous influences of inertia, buoyancy, and dilute polymer presence.
1. Introduction
The present investigation considers Nusselt number data, which illustrate the relative influences of inertia and polymeric viscoelastic phenomena within a rotating Couette flow (RCF) environment. This combination of effects is considered within polyacrylamide polymer solution flows because the resulting elastic instability development is often present simultaneously in combination with inertia influences. To illustrate this development, the present data are provided for different flow passage heights, one radial position, and different values of disk rotational speed for polyacrylamide polymer concentrations ρ of 0 ppm, 100 ppm, 150 ppm, and 300 ppm. With this approach, data for a diversity of experimental conditions are provided over a wide range of shear rate values, Weissenberg numbers, and first normal stress difference values.
Larson [1] and Pathak et al. [2] provide fundamental information on the development and nature of elastic instabilities within non-Newtonian viscoelastic fluids. The associated local flow instabilities develop at very low Reynolds numbers and include the formation and growth of local secondary flows, and increased local mixing. Such effects are initiated by local stretching, convolutions, and twisting of long-chain flexible polymers, which are distributed throughout the viscoelastic fluid. According to Arratia et al. [3], Pan et al. [4], and Zhang et al. [5], the presence of local flow strain is a key ingredient in the initiation of elastic instabilities. Such strain can be imposed from the presence of velocity gradients normal to flow streamlines, which can be induced by flow through a curved passage, by confined rotational flow, or by flow around obstructions or protrusions of different types. Other investigators [2,6,7,8,9] indicate that, for some situations, associated elastic instabilities lead to elastic turbulence, which is a chaotic flow that shows increased flow resistance with characteristics that are similar statistical properties to Newtonian turbulence. A chaotic state is the result, which is highly nonlinear, and can be present for Reynolds numbers that are very low, with values that are less than 1.
Only a handful of investigations consider convective heat transfer associated with elastic instabilities and elastic turbulence [10,11,12,13,14]. Of these, Whalley et al. [10] employ a serpentine channel. Traore et al. [11] investigate elastic turbulence phenomena within von Karman flows. Abed et al. [12] use a millimeter-scale serpentine duct to address the development of a variety of thermal and flow phenomena. These investigators provide ratios of polymer solution Nusselt number and Newtonian flow Nusselt number, which increase substantially as the Weissenberg number increases from 0 to values as high as 210. Li et al. [13] utilize a serpentine micro-channel with a square flow cross-section and observe surface Nusselt number values that are as high as 11. Ligrani et al. [14] give results from another recent investigation. From measurements within a viscous disk pump, surface heat transfer enhancements as large as 240 percent are reported, relative to Newtonian conditions. Data with and without elastic instabilities are compared at the same shear rate, rotation speed, passage height, and flow temperature.
The present investigation considers Nusselt number behavior within a rotating Couette flow environment with polyacrylamide polymer solution flows wherein elastic instabilities develop as significant inertia flow phenomena are also present. No previous investigation is known that systematically considers the simultaneous presence of these phenomena with heat transfer. Provided are Nusselt number data for rotating Couette flow passage height H values of 5 mm and 7 mm, a radial position of 2/31, polyacrylamide polymer concentrations ρ of 0 ppm, 100 ppm, 150 ppm, and 300 ppm, and different values of disk rotational speed ω. As such, the present investigation provides new insight into associated convective heat transfer variations, within an environment and with flow conditions and significant temperature gradients, which have never before been investigated.
2. Experimental Apparatus and Procedures
2.1. Rotating Couette Flow (RCF) Experimental Apparatus
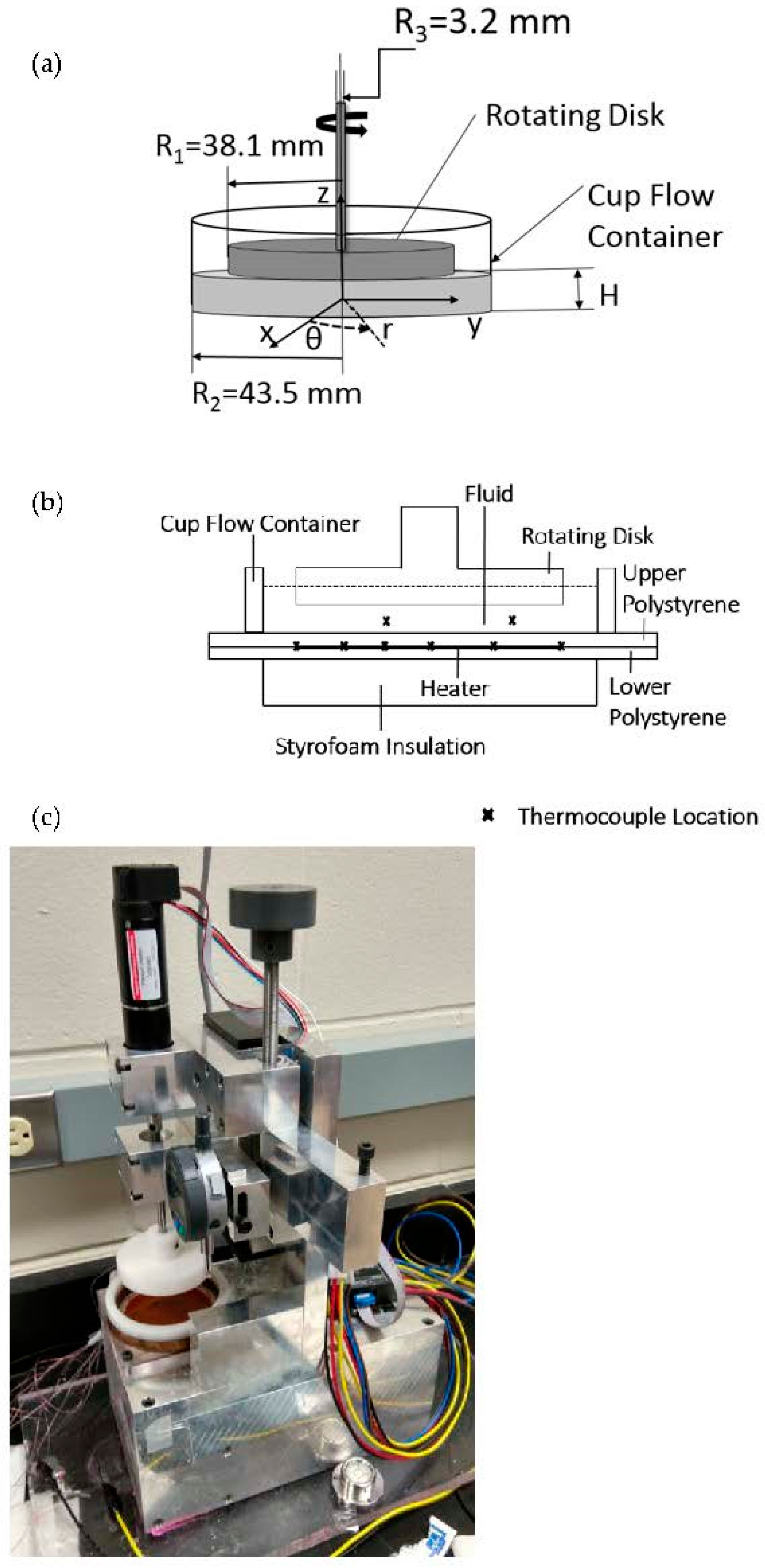
The rotating Couette flow arrangement used within the present investigation is shown schematically in Figure 1a,b. The associated cylindrical coordinate system is then presented in Figure 1a. A photograph of the experimental facility, including a number of instrumentation items, is shown in Figure 1c. Here, the z coordinate is directed in a normal direction from the bottom surface of the cup flow container, and the r coordinate is directed from the center of rotation. A detailed description of the rotating Couette flow facility is provided by Ligrani et al. [15]. Within the present investigation, the depth of the rotating Couette flow passage H is set either to 5.0 mm or 7.0 mm in order to provide a larger range of shear rates , Weissenberg numbers Wi, and elastic instability Reynolds numbers , relative to previous investigations [14,15,16].
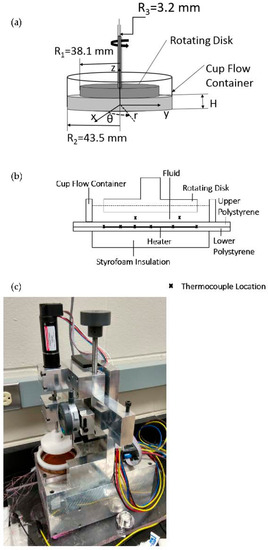
Figure 1.
(a) Rotating Couette flow device. (b) Heat transfer measurement apparatus. Note that thermocouples are located both above and below the heater at each surface location. (c) Photograph of experimental apparatus employed for heat transfer measurements and analysis.
2.2. Polymer Solution Preparation
Four different solutions are utilized each with a different polymer concentration: 0 ppm, 100 ppm, 150 ppm, and 300 ppm, where ppm refers to parts per million. As such, the 0 ppm arrangement is utilized with a 65 percent sucrose solution (without added polymers) as a solvent solution. Each viscoelastic solution is then prepared by adding the appropriate amount of polyacrylamide powder into the sucrose solution in order to achieve the desired polymer concentration. The procedure for mixing different polymer solutions is adopted from Abed et al. [12]. Additional discussion of polymer solution preparation is provided within Ref. [15].
Table 1 gives physical properties of the different working fluids from Ref. [15]. Uncertainty magnitudes of polymer relaxation times, given within this table, are from 5 to 7 percent. The data given in Table 1 show that absolute viscosity values at zero-shear rates are slightly larger than values associated with higher, non-zero-shear rates. This is because of mild shear-thinning behavior, as zero-shear rate is approached, for the present polymer solutions. Note that absolute viscosity is approximately constant with shear rate for shear rate values which are slightly greater than zero.

Table 1.
Physical properties of working fluids [15].
Because of the challenges in preparing and characterizing polymer solutions that result in elastic instabilities, only one type of solution (involving the use of combinations of polyacrylamide and sucrose) is considered within the present investigation.
2.3. Heat Transfer and Nusselt Number Measurement Apparatus and Procedures
Within the present study, the RCF configuration is employed for measurement of heat transfer coefficients and Nusselt numbers over portions of the flow passage surface area. Details of this facility, along with surface heat transfer measurement apparatus and procedures, are provided within Ref. [15], along with procedures to determine local Nusselt numbers. Local Nusselt numbers are given by , where is the thermal conductivity for the solvent or polymer solution that is employed.
2.4. Experimental Uncertainty Magnitudes
Experimental uncertainty magnitudes associated with experimentally measured temperatures and Nusselt numbers are discussed within Ref. [15]. Uncertainty values are presented in Table 2 and are determined using procedures which are described by Moffat [17].

Table 2.
Uncertainty values of experimental quantities [15].
3. Characterization of Inertial and Polymeric Viscoelastic Influences
Of interest is the characterization of the relative influences of inertial and polymeric viscoelastic phenomena. Inertial effects are quantified, relative to viscosity, using the Reynolds number, as given by:
where ωR quantifies the flow speed at the surface of the rotating disk V, such that R is determined at the radius of interest, which is equal to 2/3R1. Note that Qin et al. [9] suggest a similar inertia Reynolds number. Within Equation (1), density ρ0 and absolute viscosity η0 are overall solution values, where the solution is comprised of a solvent component and a polymeric viscoelastic component, such that:
Within Equation (2), is then the polymeric viscoelastic contribution to the viscosity and is the solvent contribution to the viscosity.
A characteristic Reynolds number to quantify polymeric viscoelastic influences is expressed using an equation of the form:
Here, is the tensile stress value or first normal stress difference. This quantity is estimated using the Oldroyd-B model for relatively low shear rate values, using the equation which is given by:
According to Pan et al. [4], is a measure of the elastic stresses present within the polymeric solution. Within this equation, the shear rate is defined using the equation which is expressed using:
As such, the elastic instability Reynolds number is also given as:
which is the same as the square of the Weissenberg number Wi, which is expressed by the equation:
Note that the critical Weissenberg number Wi at the onset of elastic instability is based upon the flow condition wherein the polymer stretch rate exceeds the inverse polymer relation time. From experimental measurements, this condition is quantified by Ligrani et al. [15] using Wi = 30 for the same type of environment as used in the present investigation. According to Larson [1], Pathak et al. [2], De Gennes [18], and others, non-inertial viscoelastic instabilities develop within a variety of configurations with dilute polymer solutions, provided appropriate magnitudes of shear rate and flow strain are present. Within such pure shear flows, the major non-linear elastic effect is in the form of negative normal stress along the flow direction. The result is purely elastic instabilities when inertial effects are either minimal or non-existent. A consequence is augmented local mixing from distortion, convolutions, and interactions of long polymer chain molecules, which results in distributions of enhanced secondary flows. Such an arrangement is present with finite values of and , as given by Equations (3) and (4), respectively, but also with near zero or very small values of , as given by Equation (1).
The present investigation considers rotating Couette flow environments wherein both inertial and polymeric viscoelastic influences are present. With this arrangement, , , , and are all non-zero and finite, with relative values that change with the experimental condition. To quantify the relative influences of these two types of phenomena, the parameter is then employed, as expressed in terms of the ratio of the two types of Reynolds numbers.
The result within Equation (8) is also expressed using equations of the form:
To consider different magnitudes of elastic instability influence, relative to inertial effects, an extensive range of shear rates is considered within the present investigation. These are provided using different rotating Couette flow passage heights H of either 5.0 mm or 7.0 mm, a radial position of 2/31, and different disk rotational speeds ω. The resulting data are provided for different polymer relaxation times of 0 s, 1.42 s, 1.89 s, and 2.82 s, which are provided by respective polymer concentrations ρ of 0 ppm, 100 ppm, 150 ppm, and 300 ppm. With these arrangements, a wide range of parameter values is provided.
4. Experimental Results and Discussion
Nusselt number data are provided to illustrate the relative influences of inertia and polymeric viscoelastic phenomena. These data are given for flow passage height H values of 5 mm and 7 mm, a radial position R of 2/3R1, and different values of disk rotational speed ω. By varying these parameters, data for a wide range of shear rate values are provided, as polyacrylamide polymer concentrations ρ of 0 ppm, 100 ppm, 150 ppm, and 300 ppm are utilized. Note that inlet passage flow temperature is maintained constant as all of these experimental parameters are varied.
Within the present study, two different methods are used to determine shear rates using Equation (5). With the first, the R radial location of 2/3R1 is employed because this value is representative of the Couette flow passage and because this is the location used for the surface Nusselt number measurements. Shear rates determined with this approach are denoted 1. Weissenberg numbers determined with this approach are denoted Wi1.
With the second approach, the R radial location of R3 is employed. This value is associated with the minimum radius of the rotating Couette flow, and as such, is the radial location associated with the onset of elastic instabilities. According to Hietsch et al. [16], onset occurs in the vicinity of the minimum shear rate, such that the relatively small value of R3 is associated with minimum values of spatially varying parameters at the onset of elastic instability. Shear rates determined with this approach are denoted 3, and Weissenberg numbers determined with this approach are denoted Wi3.
4.1. Nusselt Number Variations with Shear Rate
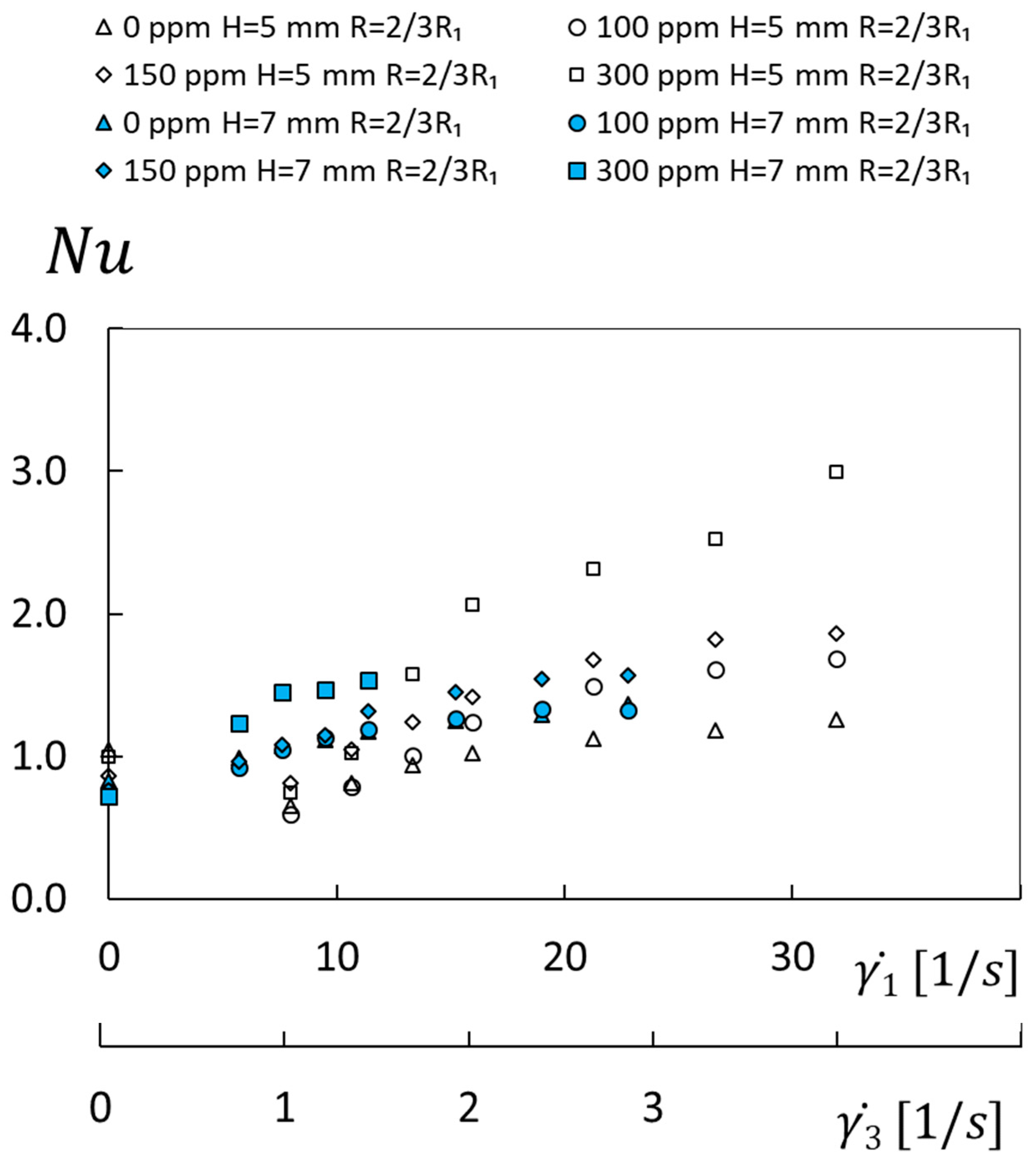
Figure 2 shows Nusselt number variations with shear rate 1 for different polymer concentrations, different flow passage heights, and one radial location. Eight different sets of data are included within this figure, where shear rate variations for each data set are induced using different disk rotational speeds. Here, the lowest Nusselt numbers are generally associated with the sucrose solvent flows where ρ = 0 ppm. The highest Nusselt numbers are associated with the highest polymer concentration ρ of 300 ppm, the smallest gap height H of 5 mm, and a radial position R of 2/3R1. Here, the highest Nusselt number value is 2.99, which is associated with a shear rate of 31.9 s−1. Nusselt numbers for a zero-shear rate and the same values of R, H, and ρ are approximately equal to 1.0. Associated Nusselt number enhancement ratios are then as high as 2.4, relative to conditions associated with 0 ppm sucrose solution flows, when compared are the same shear rate.
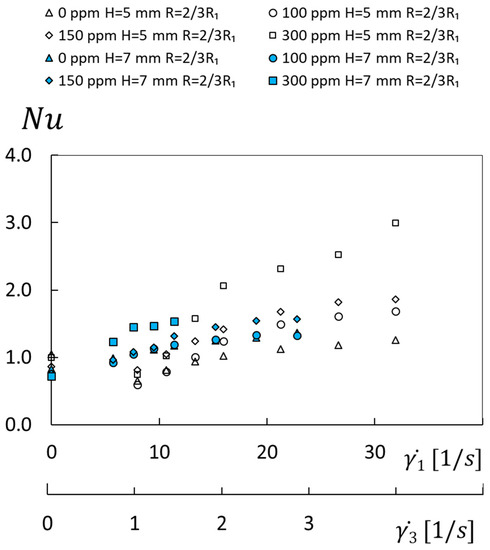
Figure 2.
Nusselt number variations with shear rate and with shear rate for different polymer concentrations, different flow passage heights, and a radial position of R = 2/3R1.
With the exception of data presented for shear rates 1 less than about 12 s−1, Figure 2 also indicates that Nusselt number values for each data set for particular values of passage height H, radial location R, and polymer concentration ρ generally increase as the shear rate 1 becomes larger. When compared at particular values of shear rate 1, passage height H, and radial location R, Nusselt numbers generally increase with polymer concentration ρ, especially for shear rates greater than 11 to 12 s−1, since higher concentrations are associated with longer polymer relaxation times. As such, Nusselt number dependence upon shear rate changes as polymer concentration varies. Such characteristics are a consequence of the convolution and interactions of long-chain polymers as flow shear rate and negative normal stress along the flow direction increase, resulting in the development of local secondary flows and small-scale mixing. Such events occur as the polymer solutions proceed toward the development and initiation of elastic instabilities.
Such elastic instability characteristics are consistent with the results of Larson [1] and Pathak et al. [2]. In particular, the presently observed Nusselt number variations with shear rate and polymer concentration are a consequence of locally increased flow mixing and disturbances, which are associated with the local stretching, convolutions, and twisting of long-chain flexible polymers as they are distributed throughout the viscoelastic fluid. The flow strain within the present rotating Couette flow (RCF) environment, discussed by Arratia et al. [3], Pan et al. [4], Zhang et al. [5], and others, is induced by the curvature of streamlines from flow rotation. The magnitude of flow strain is quantified by shear rate, which varies with flow passage height H and speed of rotation .
According to Ligrani et al. [15], as polymer concentration ρ, passage height H, and shear rate 1 are constant, Nusselt numbers for R = 1/3R1 are generally lower than values associated with R = 2/3R1. Comparisons of data within Figure 2 indicate that, as polymer concentration ρ, radial location R, and shear rate 1 are constant, Nusselt numbers for passage height H of 7 mm are often generally lower than values associated with a passage height H of 5 mm. The most important exceptions to these trends are present for lower values of shear rate 1 less than 11 to 13 s−1, when flow and thermal transport are generally dominated mostly by inertial influences.
The data within Figure 2 are also given as they vary with the 3 shear rate. Here, 3 shear rates are about eight times smaller than 1 shear rates.
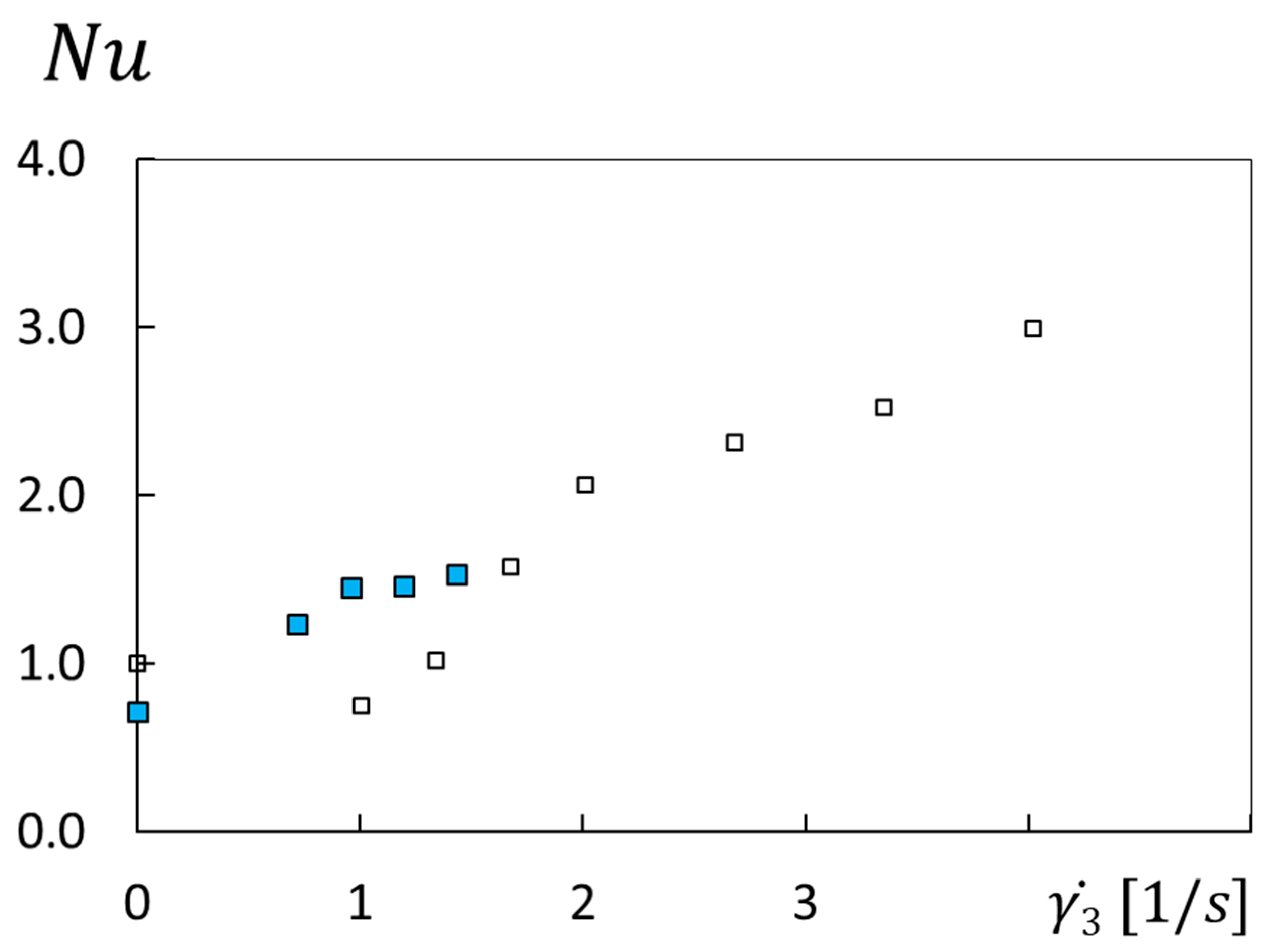
Additional insight into the effects of inertia and polymeric viscoelastic phenomena is provided by the data from Figure 2, which are also presented in Figure 3. Here, clarification of Nusselt number variations with shear rate 3 is provided for a polymer concentration ρ of 300 ppm which are associated with H values of 5 mm and 7 mm and with an R value of 2/3R1. For 3 shear rates greater than 1.5 s−1 to 1.6 s−1, Nusselt numbers associated with H = 5 mm are the highest values measured, with magnitudes that steadily increase with 3. At lower shear rates, Nusselt number characteristics are generally dominated by inertial phenomena. Here, H = 5 mm Nusselt numbers are lower than values associated with H = 7 mm, when compared at the same shear rate 3. Such characteristics provide evidence of initial suppression of local flow thermal transport by the presence of dilute polymers within certain physical environments until sufficient shear and flow strain are present to induce polymer motions and interactions which lead to the development of elastic instabilities. Such suppression is likely also encouraged by local mixed convection buoyancy influences which not only oppose forced flow transport mechanisms but are also more significant within the rotating Couette flow passage with a smaller height of 5 mm. Rayleigh numbers, which characterize mixed convection effects, are as low as 0.027 for the highest rotational disk speed employed, which evidences negligible buoyancy influences. Mixed convection buoyancy then begins to affect local flow behavior in an observable fashion as Raleigh numbers approach and exceed 0.5, which occurs for smaller values of shear rate and disk rotational speed. The data within Figure 2 and Figure 3 indicate that the change from inertia domination (with buoyance influences) to polymeric viscoelastic domination occurs for 1 shear rates in the vicinity of 11 to 12 s−1, and for 3 shear rates in the vicinity of 1.4 to 1.5 s−1, which correspond to a critical Weissenberg number Wi3c of about 3.8 [16].
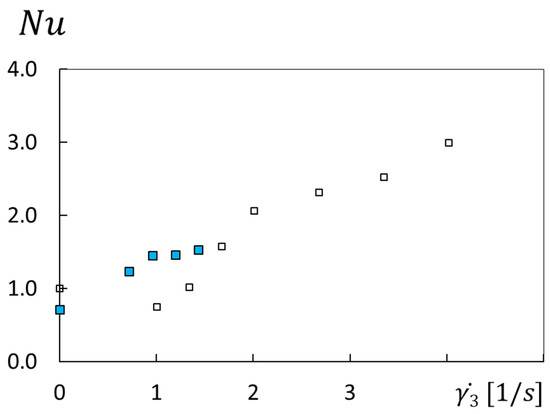
Figure 3.
Nusselt number variations with shear rate for different flow passage heights and a radial position of R = 2/3R1 for a polymer concentration of 300 ppm. Symbols are defined within Figure 2.
Figure 2 also shows that, with no elastic instabilities present, Nusselt numbers for 1 shear rates less than approximately 12 s−1 are about the same as, or slightly lower than, values associated with zero-shear rate. Note that the zero-shear rate condition is produced with the disk stationary, without rotation. Resulting zero-shear rate Nusselt number variations are then a result only of diffusion-related phenomena. When 1 shear rates then become greater than 0 s−1 because of disk rotation (but continue to be less than 12 s−1), Nusselt numbers are then a result of both advection and diffusion-related effects. With these experimental conditions, intricate interactions are thus present between polymers and the surrounding, adjacent flows, which are affected in a significant manner by inertia including buoyancy effects.
4.2. Nusselt Number Variations with Shear Rate and Reynolds Number When Dominated by Inertial Influences
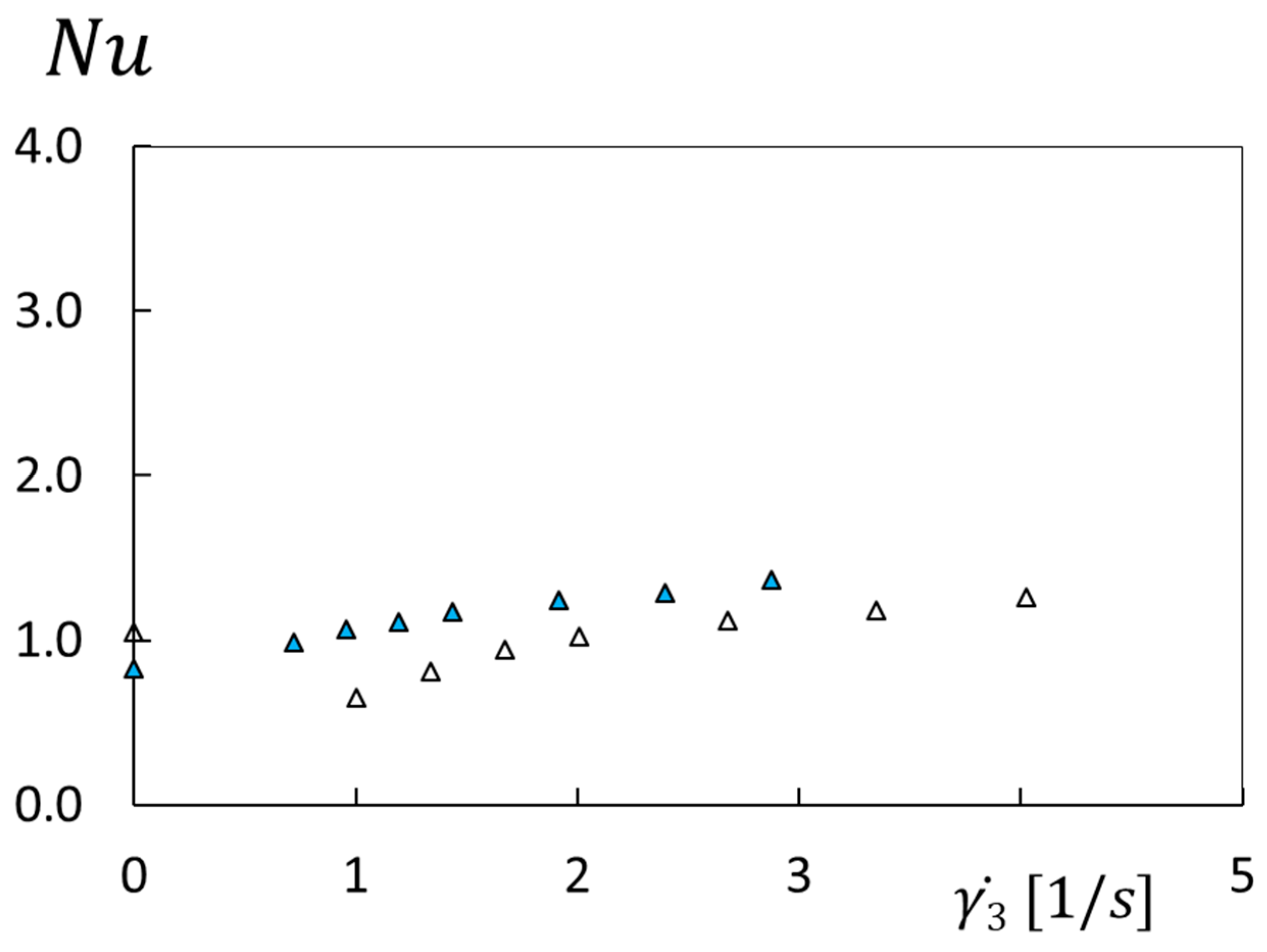
Figure 4 shows Nusselt number data variations with shear rate 3 for 0 ppm, with no polymers present within the flow. As a consequence, all of the data in this figure evidence the effects of inertial flow influences. H values are 5 mm and 7 mm, and the R value is 2/3R1 for these data. Note that data distributions within Figure 4 generally collect along two different paths, one for the H = 5 mm data and one for the H = 7 mm data. Here, Nusselt numbers associated with H = 5 mm are consistently lower than values associated with H = 7 mm, when compared at the same value of shear rate 3.
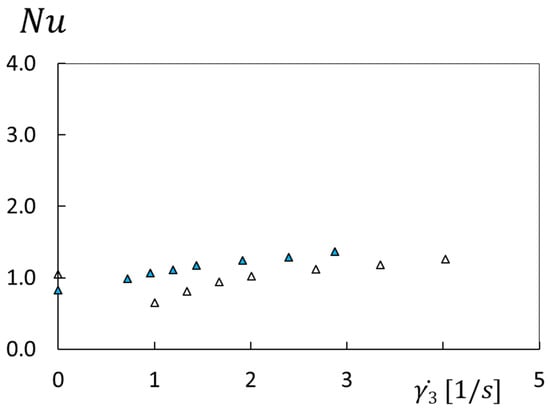
Figure 4.
Nusselt number variations with shear rate for different flow passage heights and a radial position of R = 2/3R1 for a polymer concentration of 0 ppm. Symbols are defined within Figure 2.
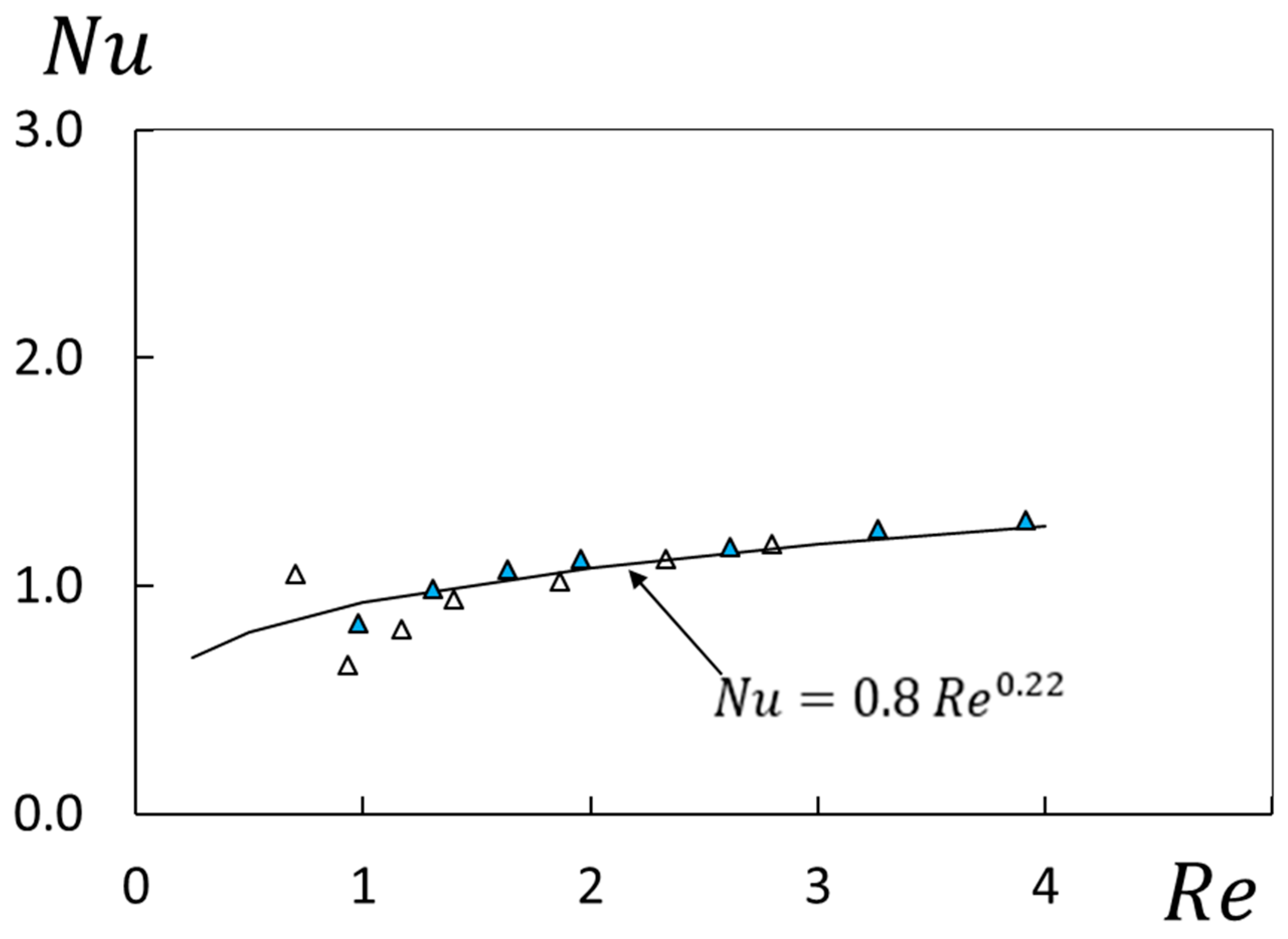
All of the data within Figure 4 are again presented in Figure 5 as they vary with Reynolds number Re, as determined using Equation (1). Note that the R radial location of 2/3R1 is used for velocity determination in regard the Re values presented within this figure. With this arrangement, all of these data collect into one distribution, which is well represented by the equation which is given by:
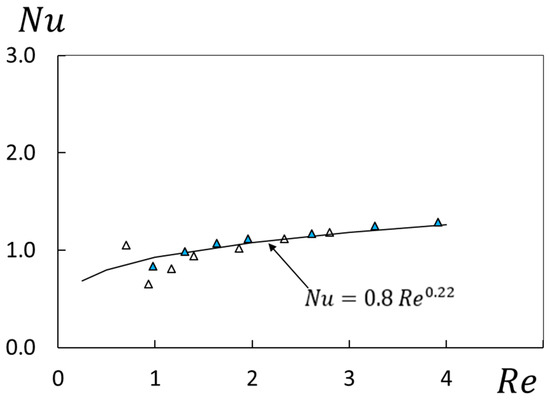
Figure 5.
Nusselt number variations with Reynolds number for different flow passage heights and a radial position of R = 2/3R1 for a polymer concentration of 0 ppm. Symbols are defined within Figure 2.
Such characteristics provide evidence of the dominating influences of inertia, including the presence of mixed convection buoyancy effects on the Nusselt number variations, which are shown in Figure 5.
4.3. Nusselt Number Variations with Reynolds Number
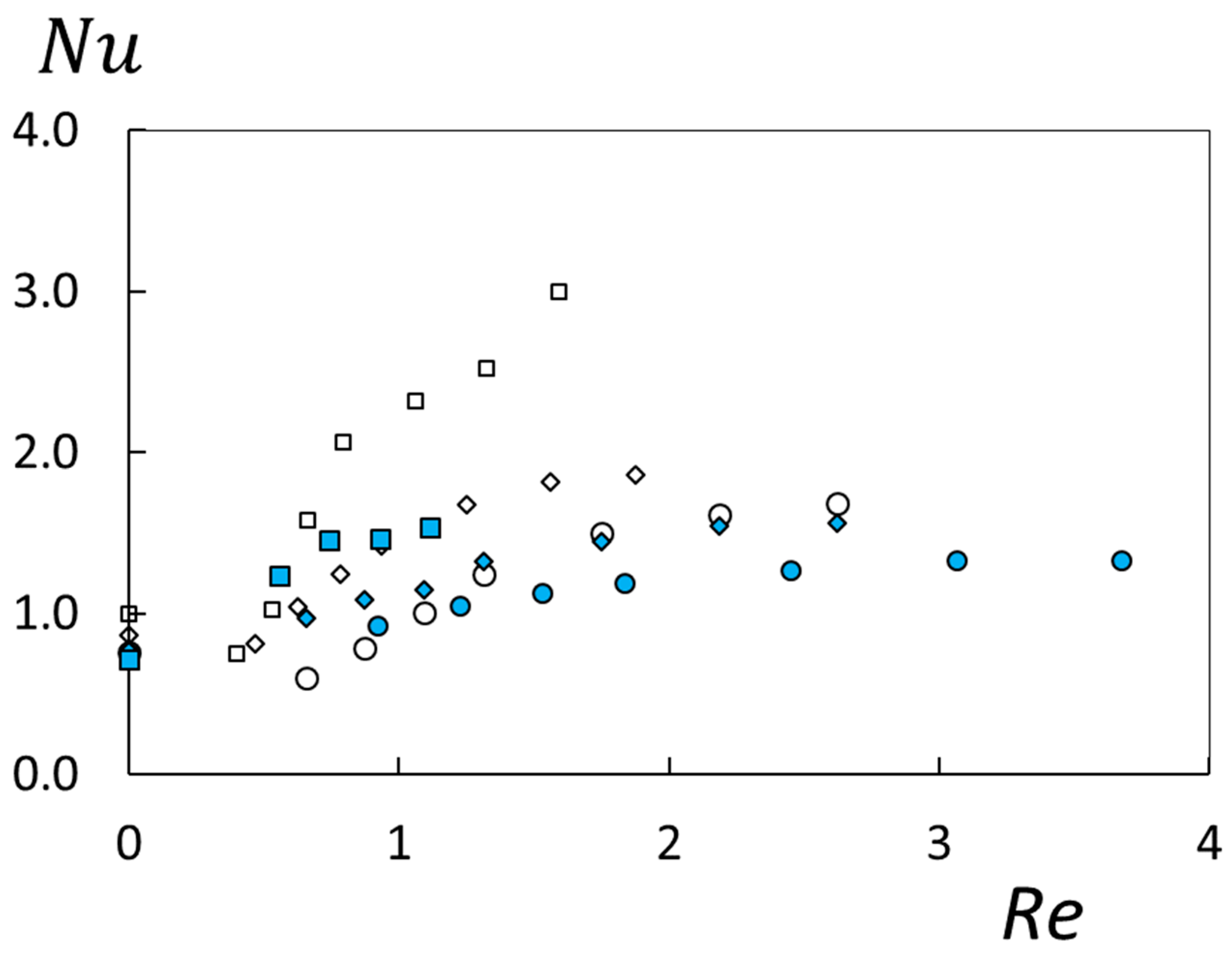
Figure 6 shows Nusselt number variations with Reynolds number Re for polymer concentrations ρ of 100 ppm, 150 ppm, and 300 ppm, H values of 5 mm and 7 mm, and an R value of 2/3R1. Within this figure, values are widely distributed relative to data within Figure 5, which are represented by Equation (10) and are only affected by inertial effects. Associated deviations within Figure 6, especially for higher shear rates , are mostly due to polymeric viscoelastic phenomena. Here, Nusselt numbers consistently increase with polymer concentration ρ for a particular Re Reynolds number value, provided flow passage height H and radial location R are constant. Thus, from these data, it is evident that the onset and development of elastic instability transition occurs at significantly different Reynolds number values as polymer concentration varies. At lower shear rates, quantitative data variations are also affected by buoyancy effects, as well as by the suppression of thermal transport by polymer presence prior to the initial development of elastic instabilities, as mentioned previously.
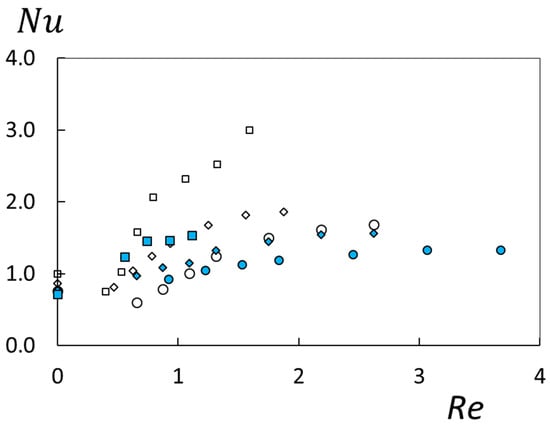
Figure 6.
Nusselt number variations with Reynolds number for different polymer concentrations, different flow passage heights, and a radial position of R = 2/3R1. Symbols are defined within Figure 2.
4.4. Nusselt Number Variations with Weissenberg Number
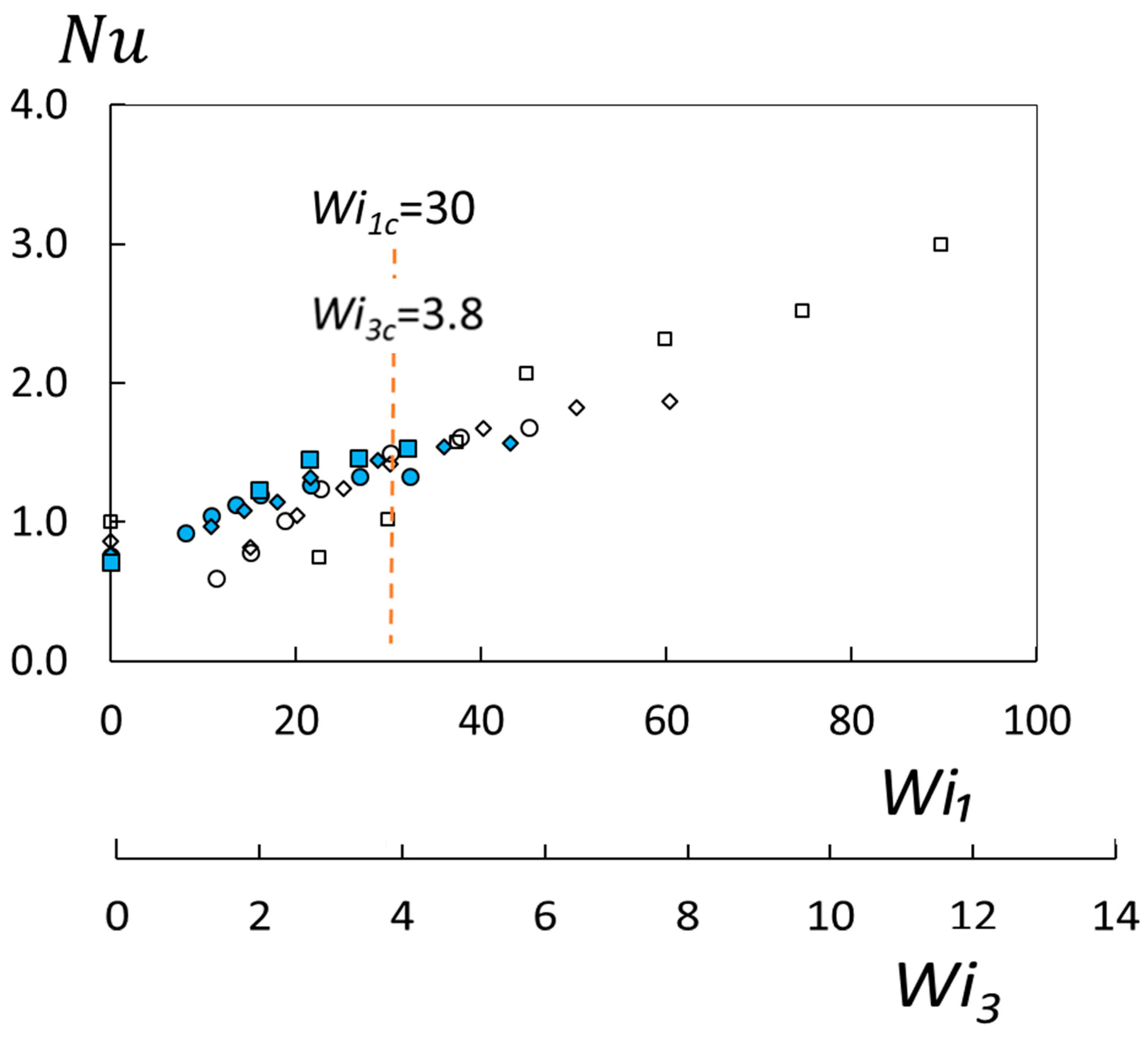
Nusselt numbers for one radial location R = 2/3R1, H values of 5 mm and 7 mm, and ρ values of 100 ppm, 150 ppm, and 300 ppm are again presented in Figure 7, but as a function of Weissenberg number Wi1. According to Ligrani et al. [15], elastic instability transition onset is well represented by the Wi1c = 30 experimental conditions when associated shear rates 1 are determined using R = 2/3R1. Note that the Wi1c = 30 value is indicated within Figure 7. Associated transition onset Nusselt numbers within this figure range from 1.02 to 1.52. For Weissenberg numbers greater than the transition onset value, Nusselt numbers associated with H = 5 mm are generally the highest values measured, with magnitudes that steadily increase with 1 and Wi1. At lower Weissenberg number magnitudes, Nusselt numbers cover a wide range of values as R, H, and ρ are varied, as a consequence of the complicated and simultaneous influences of inertia, buoyancy, and dilute polymer presence. When the Weissenberg number is less than 30, Nusselt numbers for H = 7 mm are consistently higher than values for H = 5 mm, when compared at the same value of the Weissenberg number. Complicated interactions of multiple phenomena mentioned previously are responsible for these variations. For higher values of the Weissenberg number, Nusselt numbers for both H values approximately collect into one distribution wherein Nusselt numbers increase steadily and continually as the Weissenberg number increases. Such behavior is of course due to the dominating influences of polymeric viscoelastic phenomena in the form of elastic instabilities.
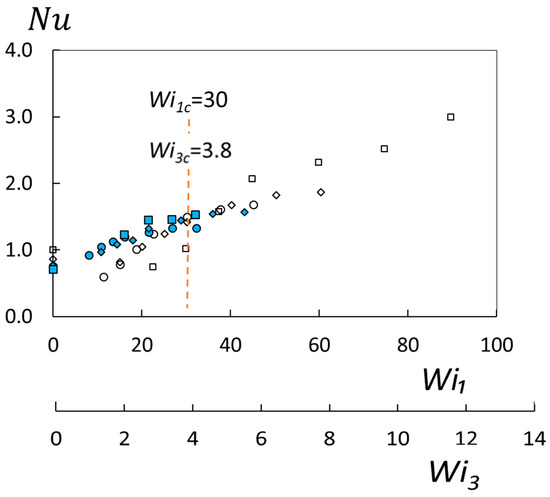
Figure 7.
Nusselt number variations with Weissenberg number Wi1 and with Weissenberg number Wi3 for different polymer concentrations, different flow passage heights, and a radial position of R = 2/3R1. Symbols are defined within Figure 2.
The data within Figure 7 are also given as they vary with the Wi3 Weissenberg number. Here, Wi3 Weissenberg number values within this figure are about eight times smaller than Wi1 Weissenberg number values. Within Figure 7, the transition onset Weissenberg number, based upon results from Hietsch et al. [16], is equal to 3.8 and is denoted Wi3c.
4.5. Nusselt Number Variations with a Modified P Parameter
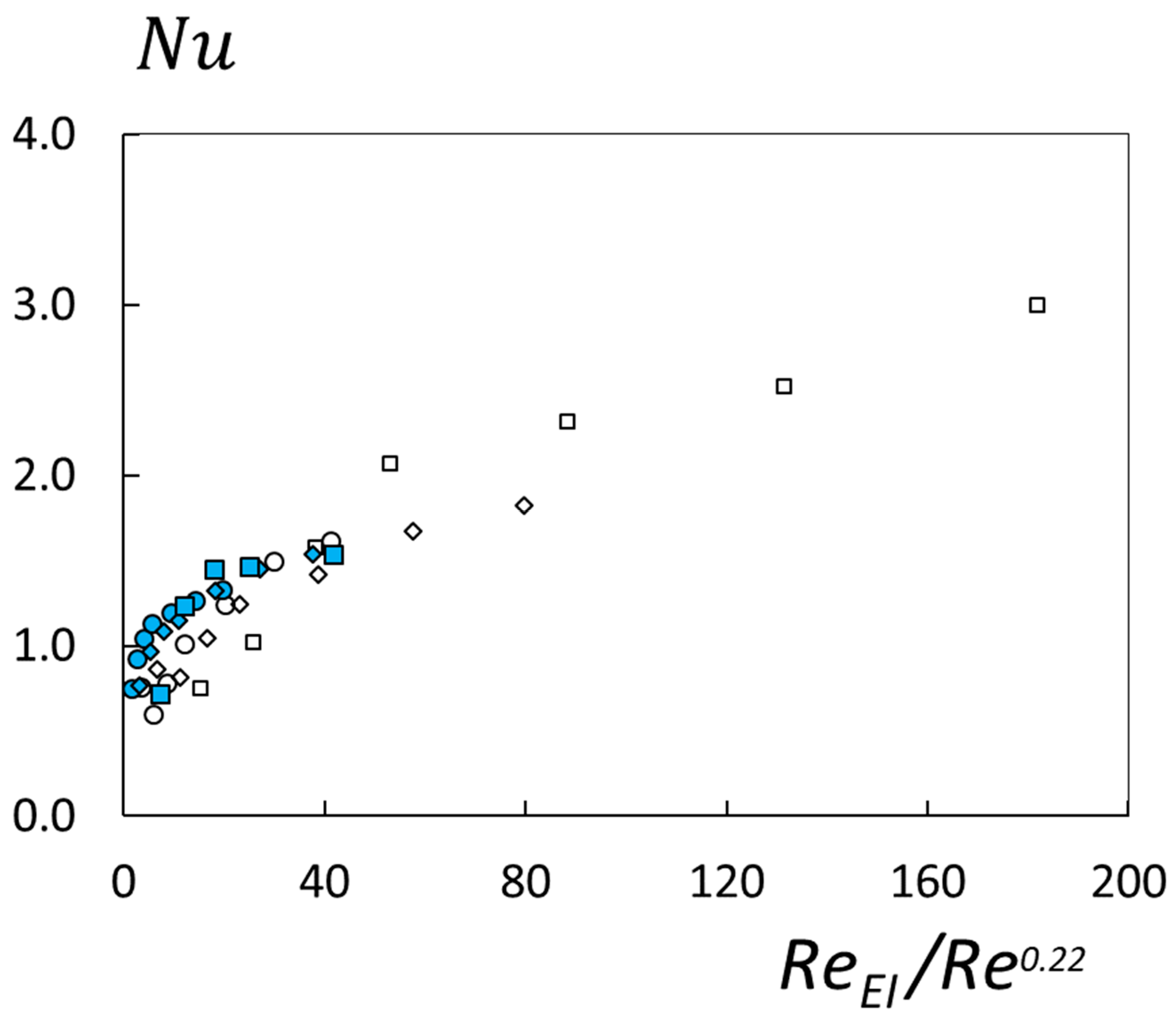
All of the data that are shown in Figure 2 are again presented in Figure 8, but as dependent upon a modified version of the parameter, which is given by the equation, which is of the form:
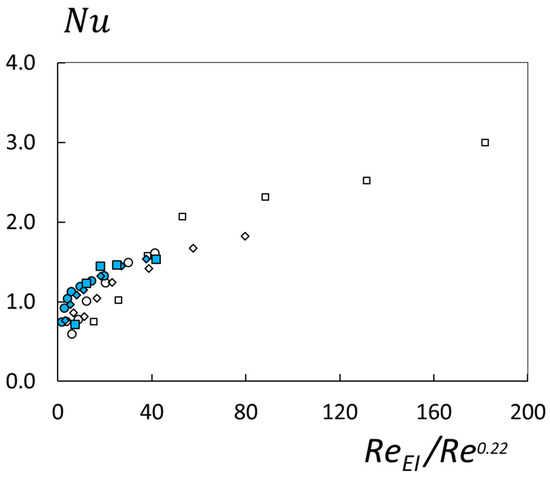
Figure 8.
Nusselt number variations with parameter for different polymer concentrations, different flow passage heights, and a radial position of R = 2/3R1. Symbols are defined within Figure 2.
Note that the dependence on Reynolds number within this equation is the same as included within Equation (10) for Nusselt number variations within an inertial Newtonian flow without any polymers present and ρ = 0 ppm. For the data within Figure 8, values are determined with Equation (6) using shear rate 3 and Weissenberg number Wi3. Re values are determined with Equation (1).
Data within Figure 8 are provided for R = 2/3R1, H values of 5 mm and 7 mm, and polymer concentrations ρ of 100 ppm, 150 ppm, and 300 ppm. Here, the parameter simultaneously accounts for the relative influences of inertia and polymeric viscoelastic phenomena. The dependence of Reynolds number on a power law exponent that is less than 1 reflects inertial influences that are altered by the presence of mixed convection buoyancy. The use of such a power law dependence for gives values using Equation (11), which are dominated by values when the Weissenberg number Wi3 is greater than about 3.8. Nusselt number data shown in Figure 8 dependent upon the parameter generally collapse into a single distribution over the range of values considered, which range from 0 to about 182.
Such characteristics provide evidence that the parameter provides an appropriate means to simultaneously account for the relative influences of inertia and polymeric viscoelastic phenomena. Such an arrangement is consistent with Dubief et al. [19] who indicate that a high-dimensional parameter space offers several pathways to elasto-inertial turbulence.
5. Summary and Conclusions
Nusselt number data are provided to illustrate the relative influences of inertia and polymeric viscoelastic phenomena within a rotating Couette flow (RCF) environment. Surface heat transfer rates for the determination of local Nusselt numbers are based upon a constant surface heat flux thermal boundary condition. These data are given for rotating Couette flow passage height H values of 5 mm and 7 mm, a radial position R of 2/3R1, polyacrylamide polymer concentrations ρ of 0 ppm, 100 ppm, 150 ppm, and 300 ppm, and different values of disk rotational speed ω. With this approach, data for a wide range of shear rate values, Weissenberg numbers, and first normal stress difference values are provided.
When Nusselt number data are provided as dependent upon a newly developed parameter, equal to , associated data collapse into single distribution over the range of values considered, which range from 0 to about 182. Such characteristics indicate that the parameter provides an appropriate means to simultaneously account for the relative influences of inertia and polymeric viscoelastic phenomena. Within the parameter expression, the overall dependence of the Reynolds number on a power law exponent that is less than 1 then reflects inertial influences that are altered by the presence of mixed convection buoyancy. The use of such a power law dependence for Re additionally gives values that are dominated by values when the Weissenberg number Wi3 is greater than about 3.8. The present data provide evidence that the change from inertia domination (with buoyance influences) to polymeric viscoelastic domination occurs for 3 shear rates in the vicinity of 1.4 to 1.5 s−1, which corresponds to a Weissenberg number Wi3c transition onset value of about 3.8.
For Weissenberg numbers greater than the transition onset value, Nusselt numbers associated with H = 5 mm are generally the highest values measured, with magnitudes that steadily increase with 3. With such experimental conditions, Nusselt numbers are as high as about 3.0 at the 2/3R1 location for the highest polymer concentration and highest shear rate considered, whereas zero-shear rate Nusselt number values (obtained with zero rotation) are in the vicinity of 1.0. At lower Weissenberg number magnitudes (below the transition onset value), Nusselt numbers cover a wide range of values as R, H, and ρ are varied, as a consequence of the complicated and simultaneous influences of inertia, buoyancy, and dilute polymer presence. The present data indicate that initial suppression of local flow thermal transport by the presence of dilute polymers occurs within certain physical environments until sufficient shear and flow strain are present to induce polymer motions and interactions, which lead to the development of elastic instabilities.
Author Contributions
Conceptualization, P.L.; methodology, P.L.; software, M.S.; validation, M.S. and V.H.; formal analysis, M.S. and V.H.; investigation, P.L., M.S. and V.H.; resources, P.L.; data curation, P.L.; writing—original draft preparation, P.L., M.S. and V.H.; writing—review and editing, P.L., M.S. and V.H.; heat transfer measurements, M.S. and V.H.; supervision, P.L.; project administration, P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
The research described in this paper is supported by the U.S. National Science Foundation, Grant No. CBET-1501587.
Data Availability Statement
Data from the present research effort are available upon request.
Acknowledgments
The Anton Paar Corporation is acknowledged for their guidance and support in regard to our use of a commercial Anton Paar Rheometer MCR 302 during the present investigation.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Cp | Specific heat (kJ/kg K) |
| h | Heat transfer coefficient (kW/m2K) |
| H | Flow passage height (m) |
| Kf | Thermal conductivity of the fluid (kW/mK) |
| Nu | Nusselt number |
| Nus | Nusselt number associated with sucrose solvent flow |
| r | Radial coordinate (m) |
| R | Radial location (m) |
| R1 | Outer radius of disk, and thermo-foil heater radius (m) |
| R2 | Inner radius of cup flow container (m) |
| R3 | Outer radius of rotating shaft (m) |
| Reynolds number | |
| Elastic instability Reynolds number | |
| Wi | Weissenberg number |
| x | First lateral coordinate (m) |
| y | Second lateral coordinate (m) |
| z | Normal coordinate (m) |
| Greek Symbols | |
| θ | Circumferential coordinate (m) |
| λ | Polymer relaxation time (s) |
| η | Absolute viscosity (kg/m s) |
| ηoo | Absolute viscosity at zero-shear rate (kg/m s) |
| η∞ | Absolute viscosity at infinite shear rate (kg/m s) |
| ηo | Absolute viscosity associated with solvent and polymer mixture flow (kg/m s) |
| ηs | Absolute viscosity associated with solvent flow (kg/m s) |
| ηp | Absolute viscosity associated with polymer flow (kg/m s) |
| ρ | Polymer concentration (ppm) |
| ρo | Fluid static density associated with solvent and polymer mixture flow (kg/m3) |
| σ11 | First normal stress difference in the direction of the flow (Pa) |
| Local fluid shear rate (1/s) | |
| ω | Angular rotation speed of disk (rad/s) |
References
- Larson, R.G. Instabilities in viscoelastic flows. Rheol. Acta 1992, 31, 213–263. [Google Scholar] [CrossRef]
- Pathak, J.A.; Ross, D.; Migler, K.B. Elastic flow instability, curved streamlines, and mixing in microfluidic flows. Phys. Fluids 2004, 16, 4028–4034. [Google Scholar] [CrossRef]
- Arratia, P.E.; Thomas, C.C.; Diorio, J.; Gollub, J.P. Elastic instabilities of polymer solutions in cross-channel flow. Phys. Rev. Lett. 2006, 96, 144502. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Morozov, A.; Wagner, C.; Arratia, P.E. Nonlinear elastic instability in channel flows at low Reynolds numbers. Phys. Rev. Lett. 2013, 110, 174502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-N.; Li, F.-C.; Cao, Y.; Kunugi, T.; Yu, B. Direct numerical simulation of elastic turbulence and its mixing-enhancement effect in a straight channel. Chin. Phys. B 2013, 22, 024703. [Google Scholar] [CrossRef]
- Burghelea, T.; Segre, E.; Bar-Joseph, I.; Groisman, A.; Steinberg, V. Chaotic flow and efficient mixing in a microchannel with a polymer solution. Phys. Rev. E 2004, 69, 066305. [Google Scholar] [CrossRef] [PubMed]
- Groisman, A.; Steinberg, V. Elastic turbulence in a polymer solution flow. Nature 2000, 405, 53–55. [Google Scholar] [CrossRef] [PubMed]
- Groisman, A.; Steinberg, V. Efficient mixing at low Reynolds numbers using polymer additives. Nature 2001, 410, 905–908. [Google Scholar] [CrossRef] [PubMed]
- Qin, B.; Salipante, P.F.; Hudson, S.D.; Arratia, P.E. Flow resistance and structures in viscoelastic channel flows at low Re. Phys. Rev. Lett. 2019, 123, 194501. [Google Scholar] [CrossRef] [PubMed]
- Whalley, R.D.; Abed, W.M.; Dennis, D.J.C.; Poole, R.J. Enhancing heat transfer at the micro-scale using elastic turbulence. Theor. Appl. Mech. Lett. 2015, 5, 103–106. [Google Scholar] [CrossRef]
- Traore, B.; Castelain, C.; Burghelea, T. Efficient heat transfer in a regime of elastic turbulence. J. Non-Newton. Fluid Mech. 2015, 223, 62–76. [Google Scholar] [CrossRef]
- Abed, W.M.; Whalley, R.D.; Dennis, D.J.C.; Poole, R.J. Experimental investigation of the impact of elastic turbulence on heat transfer in a serpentine channel. J. Non-Newton. Fluid Mech. 2016, 231, 68–78. [Google Scholar] [CrossRef]
- Li, D.-Y.; Li, X.-B.; Zhang, H.-N.; Li, F.-C.; Qian, S.; Joo, S.W. Efficient heat transfer enhancement by elastic turbulence with polymer solution in a curved microchannel. Microfluid. Nanofluidics 2017, 21, 1846. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Copeland, D.; Ren, C.; Su, M.; Suzuki, M. Heat transfer enhancements from elastic turbulence using sucrose-based polymer solutions. AIAA J. Thermophys. Heat Transf. 2018, 32, 51–60. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Su, M.; Pippert, A.; Handler, R.A. Thermal transport of viscoelastic fluids within rotating Couette flows. AIAA J. Thermophys. Heat Transf. 2020, 34, 121–133. [Google Scholar] [CrossRef]
- Hietsch, V.; Ligrani, P.M.; Su, M. Characterization of effective diffusion within viscoelastic fluids with elastic instabilities. Fluids 2022, 7, 33. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- De Gennes, P.G. Coil-stretch transition of dilute flexible polymers under ultrahigh velocity gradients. J. Chem. Phys. 1974, 60, 5030. [Google Scholar] [CrossRef]
- Dubief, Y.; Terrapon, V.E.; Hof, B. Elasto-inertial turbulence. Annu. Rev. Fluid Mech. 2023, 55, 675–705. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).