A Comparison of Newtonian and Non-Newtonian Models for Simulating Stenosis Development at the Bifurcation of the Carotid Artery
Abstract
:1. Introduction
2. Numerical Model
2.1. The Lattice Boltzmann Method
2.2. Non-Newtonian Simulations
2.3. Boundary Conditions
- The LBM simulation is run until it reaches equilibrium using the healthy artery model.
- A single period of the flow is simulated.
- The haemodynamic parameter (TAWSS or O:WS) is monitored over the period at all wall-adjacent fluid sites.
- The site where TAWSS has a minimum value (or O:WS a maximum) is selected.
- The artery wall is moved into the fluid at the selected site by a distance of 0.3 of the grid length (this may move it beyond the fluid site, which will then become a wall site).
- Steps 1–5 are repeated.
3. Model Parameters
4. Results and Discussion
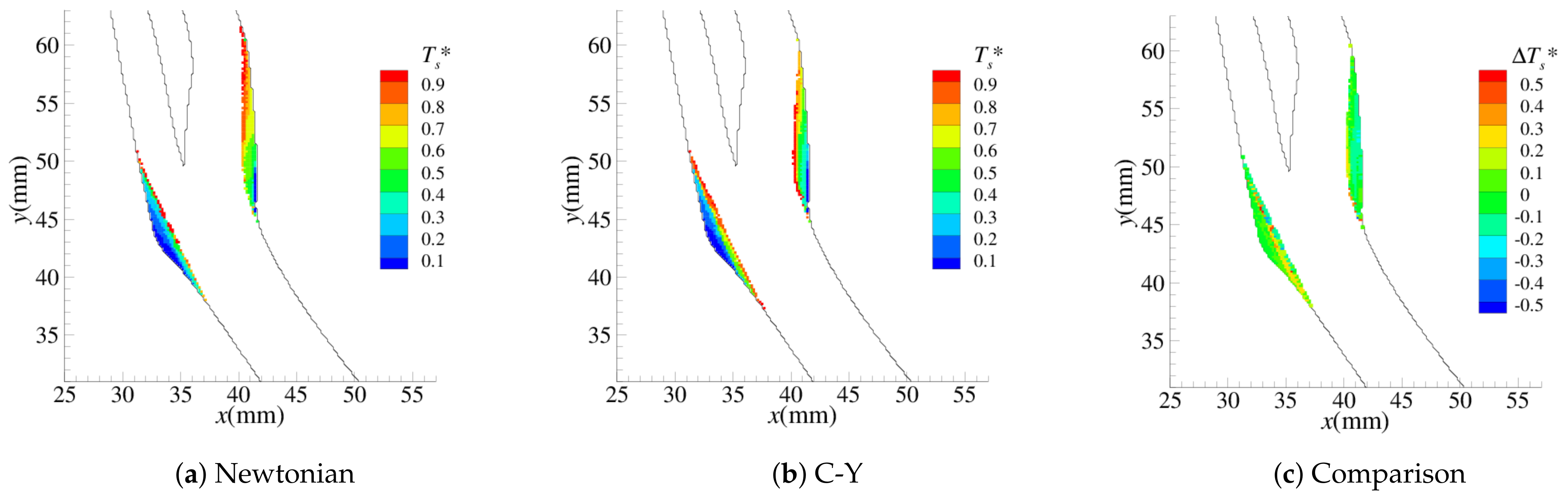
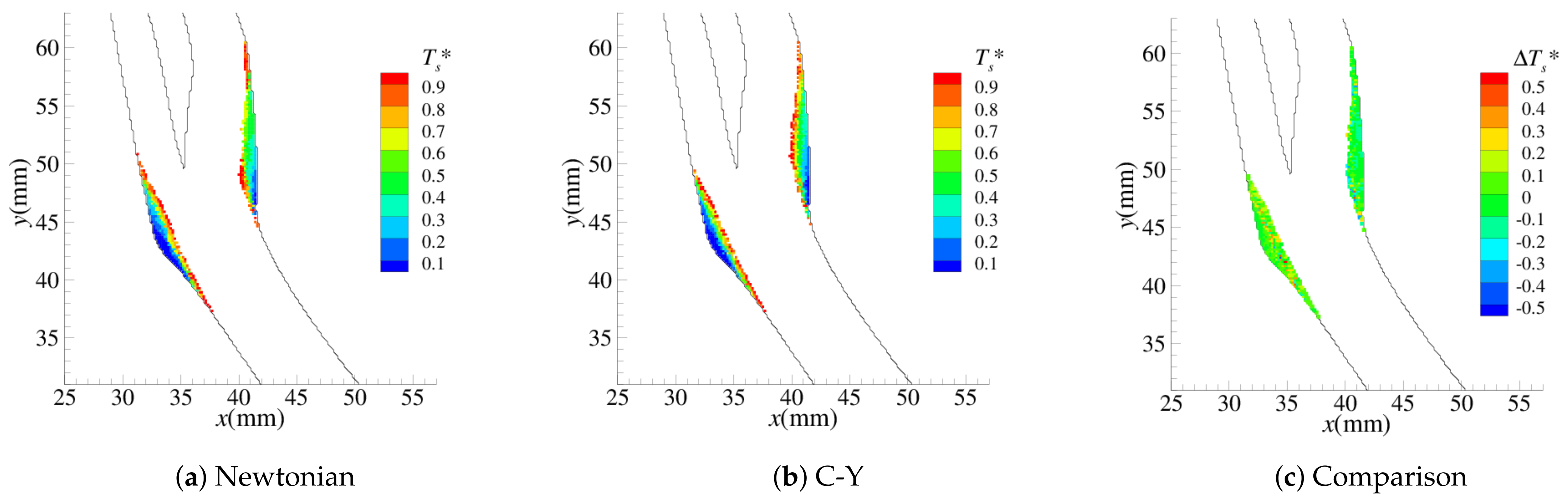
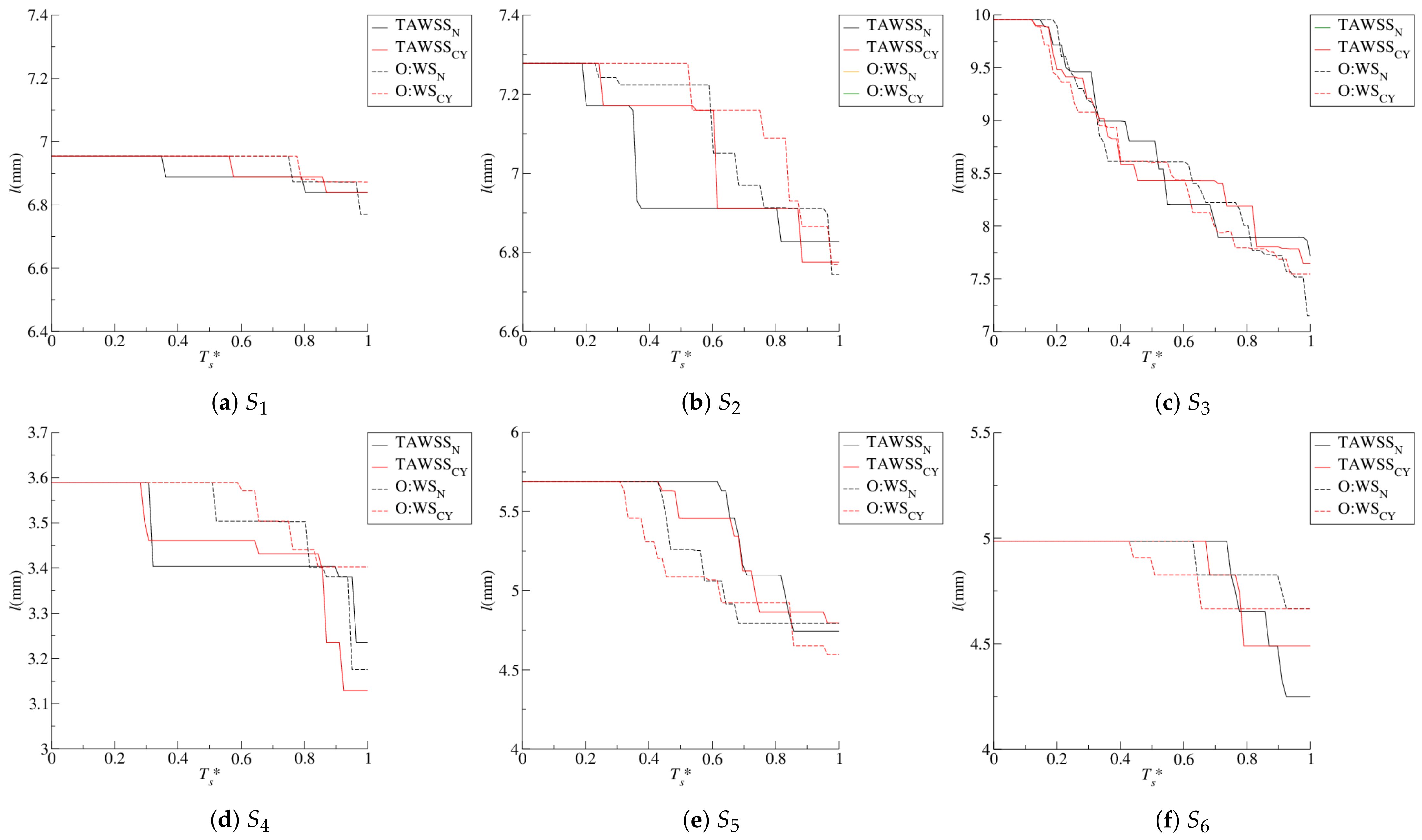
4.1. Stenosis Development
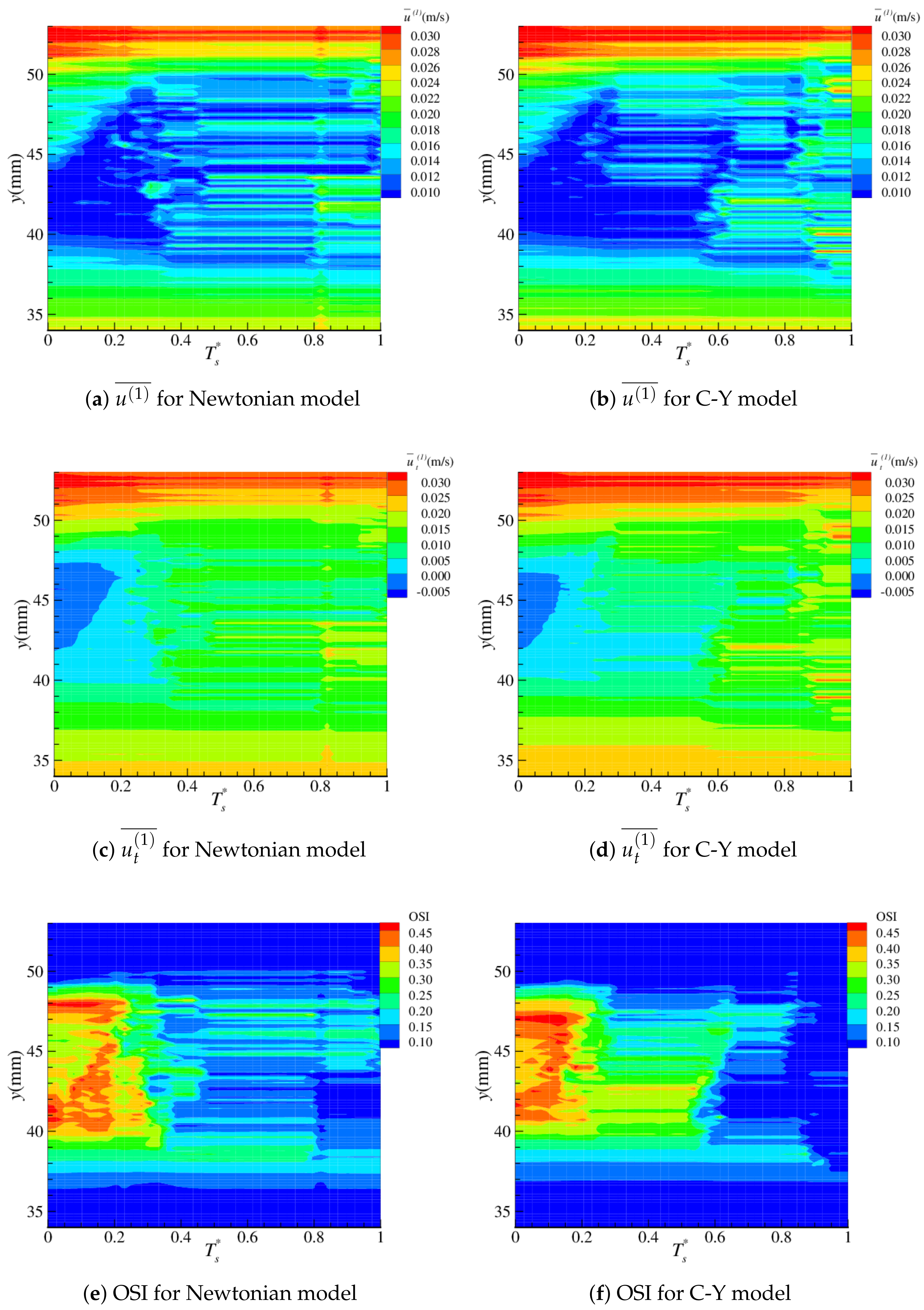
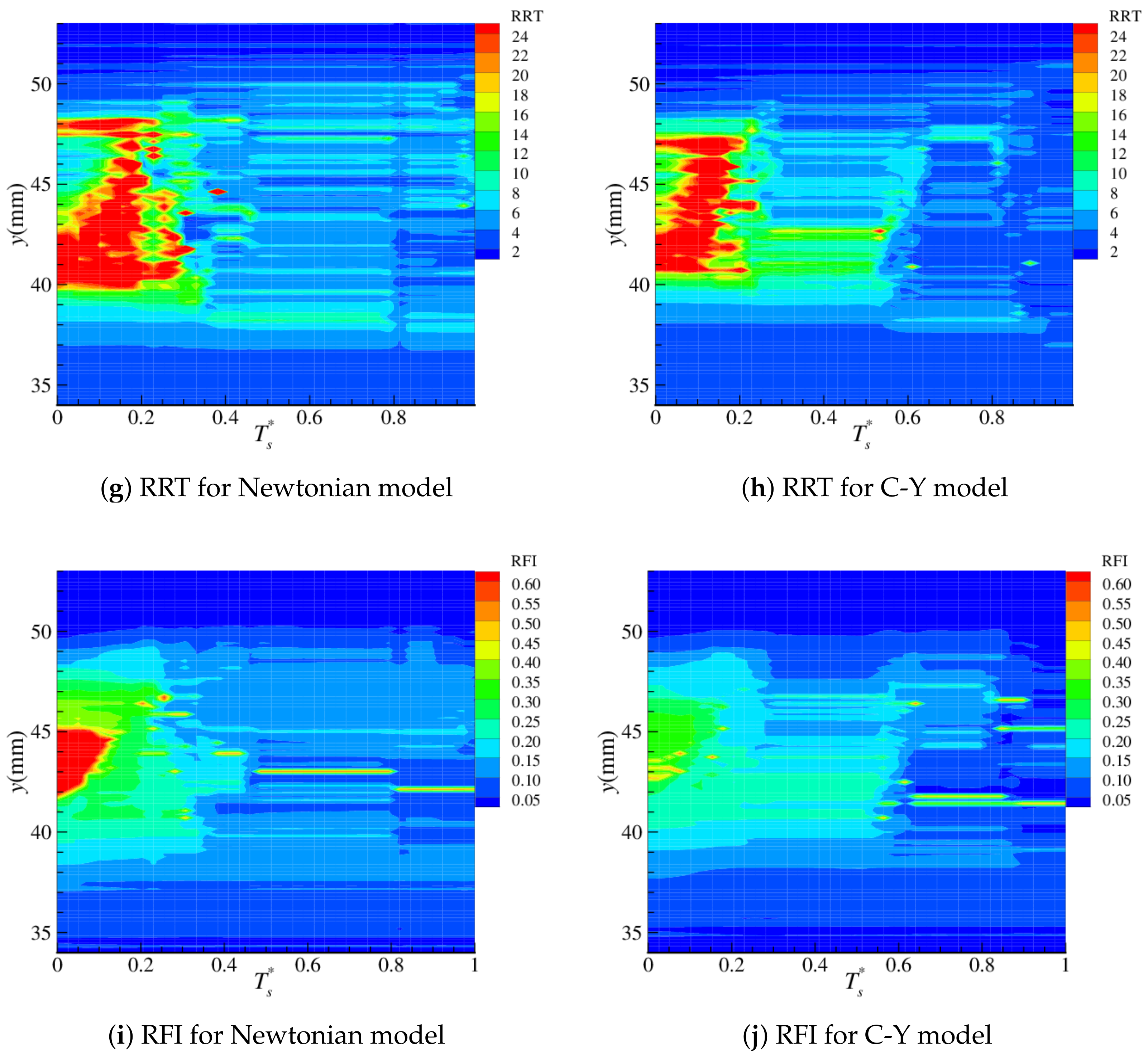
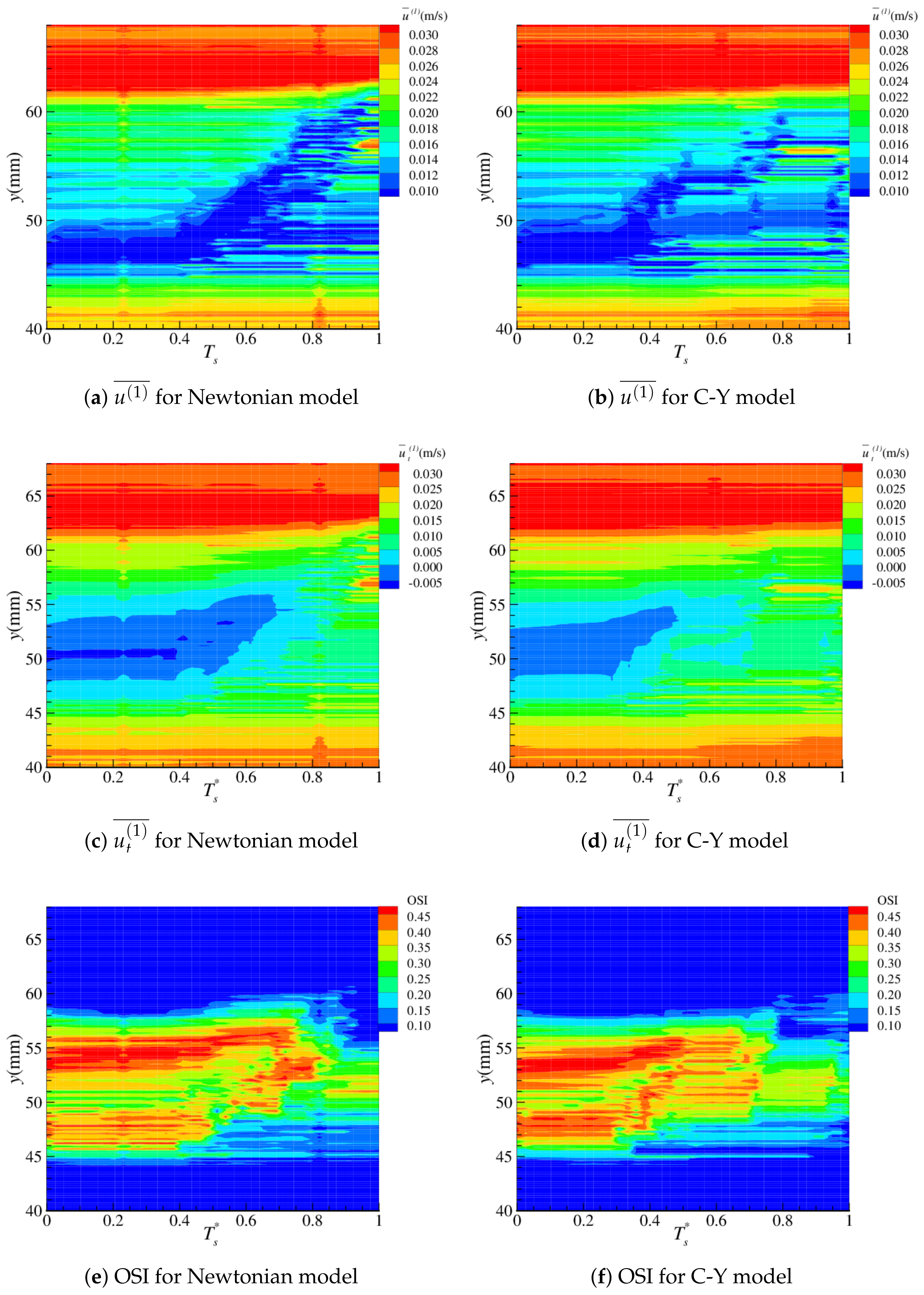
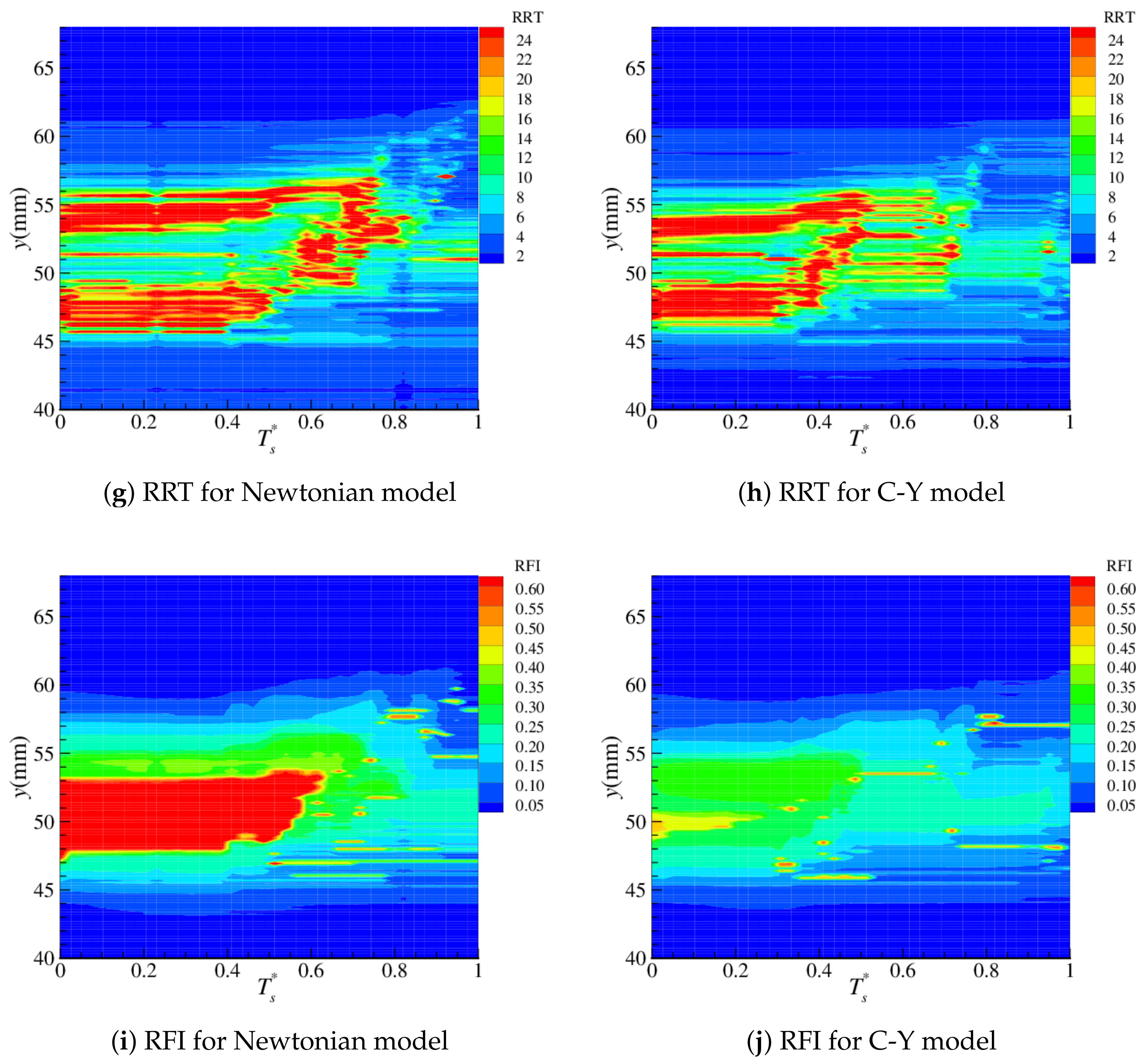
4.2. Near-Wall Haemodynamics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BGK | Bhatnagar–Gross–Krook |
| CCA | Common Carotid Artery |
| C-Y | Carreau–Yasuda |
| ECA | External Carotid Artery |
| ICA | Internal Carotid Artery |
| LBM | Lattice Boltzmann Method |
| OSI | Oscillatory Shear Index |
| O:WS | OSI/TAWSS |
| RFI | Reverse Flow Index |
| RRT | Relative Residency Time |
| TA | Time-Averaged |
| TAWSS | Time-Averaged Wall Shear Stress |
| WSS | Wall Shear Stress |
References
- Chien, S.; Usami, S.; Dellenback, R.J.; Gregersen, M.I. Shear-dependent deformation of erythrocytes in rheology of human blood. Am. J. Physiol. Leg. Content 1970, 219, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Chien, S. Biophysical behavior of red cells in suspensions. Red Blood Cell 1975, 2, 1031–1133. [Google Scholar]
- Pries, A.; Secomb, T.W.; Gaehtgens, P. Biophysical aspects of blood flow in the microvasculature. Cardiovasc. Res. 1996, 32, 654–667. [Google Scholar] [CrossRef] [PubMed]
- Mejia, J.; Mongrain, R.; Bertrand, O.F. Accurate prediction of wall shear stress in a stented artery: Newtonian versus non-Newtonian models. J. Biomech. Eng. 2011, 133, 074501. [Google Scholar] [CrossRef] [PubMed]
- Gijsen, F.; van de Vosse, F.; Janssen, J. The influence of the non-Newtonian properties of blood on the flow in large arteries: Steady flow in a carotid bifurcation model. J. Biomech. 1999, 32, 601–608. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Khader, S.M.A.; Pai, R.B.; Kyriacou, P.A. Effect of Newtonian and non-Newtonian flow in subject specific carotid artery. J. Eng. Sci. Technol. 2020, 15, 2764–2780. [Google Scholar]
- Weddell, J.C.; Kwack, J.; Imoukhuede, P.I.; Masud, A. Hemodynamic Analysis in an Idealized Artery Tree: Differences in Wall Shear Stress between Newtonian and Non-Newtonian Blood Models. PLoS ONE 2015, 10, e0124575. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Bernsdorf, J. Lattice Boltzmann simulation of steady non-Newtonian blood flow in a 3D generic stenosis case. Comput. Math. Appl. 2009, 58, 1030–1034. [Google Scholar] [CrossRef]
- Rabby, M.G.; Razzak, A.; Molla, M.M. Pulsatile non-Newtonian blood flow through a model of arterial stenosis. Procedia Eng. 2013, 56, 225–231. [Google Scholar] [CrossRef]
- Baaijens, J.; Van Steenhoven, A.; Janssen, J. Numerical analysis of steady generalized Newtonian blood flow in a 2D model of the carotid artery bifurcation. Biorheology 1993, 30, 63–74. [Google Scholar]
- Boyd, J.; Buick, J.M. Comparison of Newtonian and non-Newtonian flows in a two-dimensional carotid artery model using the Lattice Boltzmann method. Phys. Med. Biol. 2007, 52, 6215–6228. [Google Scholar] [CrossRef] [PubMed]
- Morbiducci, U.; Gallo, D.; Massai, D.; Ponzini, R.; Deriu, M.A.; Antiga, L.; Redaelli, A.; Montevecchi, F.M. On the importance of blood rheology for bulk flow in hemodynamic models of the carotid bifurcation. J. Biomech. 2011, 44, 2427–2438. [Google Scholar] [CrossRef] [PubMed]
- Perktold, K.; Peter, R.O.; Resch, M.; Langs, G. Pulsatile non-Newtonian blood flow in three-dimensional carotid bifurcation models: A numerical study of flow phenomena under different bifurcation angles. J. Biomed. Eng. 1991, 13, 507–515. [Google Scholar] [CrossRef] [PubMed]
- Abugattas, C.; Aguirre, A.; Castillo, E.; Cruchaga, M. Numerical study of bifurcation blood flows using three different non-Newtonian constitutive models. Appl. Math. Model. 2020, 88, 529–549. [Google Scholar] [CrossRef]
- Gijsen, F.; Katagiri, Y.; Barlis, P.; Bourantas, C.; Collet, C.; Coskun, U.; Daemen, J.; Dijkstra, J.; Edelman, E.; Evans, P.; et al. Expert recommendations on the assessment of wall shear stress in human coronary arteries: Existing methodologies, technical considerations, and clinical applications. Eur. Heart J. 2019, 40, 3421–3433. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Steinman, D.A. On the relative importance of rheology for image-based CFD models of the carotid bifurcation. J. Biomech. Eng. 2007, 129, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Gharahi, H.; Zambrano, B.A.; Zhu, D.C.; DeMarco, J.K.; Baek, S. Computational fluid dynamic simulation of human carotid artery bifurcation based on anatomy and volumetric blood flow rate measured with magnetic resonance imaging. J. Eng. Sci. Technol. 2016, 8, 46–60. [Google Scholar] [CrossRef] [PubMed]
- Fatahian, E.; Kordani, N.; Fatahian, H. The Application of Computational Fluid Dynamics CFD Method and Several Rheological Models of Blood Flow: A Review. Gazi Univ. J. Sci. 2018, 31, 1213–1227. [Google Scholar]
- Karimi, S.; Dabagh, M.; Vasava, P.; Dadvar, M.; Dabir, B.; Jalali, P. Effect of rheological models on the hemodynamics within human aorta: CFD study on CT image-based geometry. J. Non-Newton. Fluid Mech. 2014, 207, 42–52. [Google Scholar] [CrossRef]
- Tamagawa, M.; Matsuo, S. Predictions of thrombus formation using Lattice Boltzmann Method (modeling of adhesion force for particles to wall). JSME Int. J. Ser. C 2004, 47, 1027–1034. [Google Scholar] [CrossRef]
- Tamagawa, M.; Kaneda, H.; Hiramoto, M.; Nagahama, S. Simulation of thrombus formation in shear flows using Lattice Boltzmann Method. Artif. Organs 2009, 33, 604–610. [Google Scholar] [CrossRef] [PubMed]
- Harrison, S.; Smith, S.; Bernsdorf, J.; Hose, D.; Lawford, P. Application and validation of the Lattice Boltzmann Method for modelling flow-related clotting. J. Biomech. 2007, 40, 3023–3028. [Google Scholar] [CrossRef] [PubMed]
- Bernsdorf, J.; Harrison, S.E.; Smith, S.M.; Lawford, P.V.; Hose, D.R. Applying the Lattice Boltzmann technique to biofluids: A novel approach to simulate blood coagulation. Comput. Math. Appl. 2008, 55, 1408–1414. [Google Scholar] [CrossRef]
- Moiseyev, G.; Bar-Yoseph, P.Z. No need for particle tracing: From accumulating fluid properties to novel blood coagulation model in the lattice Boltzmann method. J. Biomech. 2010, 43, 864–870. [Google Scholar] [CrossRef] [PubMed]
- Karimpour, H.; Javdan, E. Simulation of stenosis growth in the carotid artery by Lattice Boltzmann Method. J. Mech. Med. Biol. 2014, 14, 1450016. [Google Scholar] [CrossRef]
- Stamou, A.C.; Buick, J.M. An LBM based model for initial stenosis development in the carotid artery. J. Phys. A Math. Theor. 2016, 49, 195602. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid. Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Li, H.; Fang, H.; Lin, Z.; Xu, S.; Chen, S. Lattice Boltzmann simulation on particle suspensions in a two-dimensional symmetric stenotic artery. Phys. Rev. E 2004, 69, 031919. [Google Scholar] [CrossRef]
- Boyd, J.; Buick, J.M. Three-dimensional modelling of the human carotid artery using the lattice Boltzmann method: I. Model and velocity analysis. Phys. Med. Biol. 2008, 53, 5767–5779. [Google Scholar] [CrossRef]
- Zhang, J.; Johnson, P.C.; Popel, A.S. Red blood cell aggregation and dissociation in shear flows simulated by lattice Boltzmann method. J. Biomech. 2008, 41, 47–55. [Google Scholar] [CrossRef]
- Dupin, M.; Halliday, I.; Care, C.; Munn, L. Lattice Boltzmann modelling of blood cell dynamics. Int. J. Comput. Fluid Dyn. 2008, 22, 481–492. [Google Scholar] [CrossRef]
- Yun, B.M.; Dasi, L.; Aidun, C.; Yoganathan, A. Computational modelling of flow through prosthetic heart valves using the entropic lattice-Boltzmann method. J. Fluid Mech. 2014, 743, 170–201. [Google Scholar] [CrossRef]
- Yi, H. Numerical Simulation of Particle Deposition in Arterial Bifurcation via Lattice Boltzmann Method. J. Funct. Spaces 2022, 2022, 3873484. [Google Scholar] [CrossRef]
- Wang, L.; Dong, D.; Tian, F.B. Fast prediction of blood flow in stenosed arteries using machine learning and immersed boundary lattice Boltzmann method. Front. Physiol. 2022, 13, 953702. [Google Scholar] [CrossRef] [PubMed]
- Lobovský, L.; Bublík, O.; Heidler, V.; Vimmr, J. Numerical and experimental prediction of free surface flow of shear-thinning fluids. Comput. Fluids 2021, 225, 104969. [Google Scholar] [CrossRef]
- Xia, Y.; Lin, J.; Ku, X. Flow-induced rotation of circular cylinder in Poiseuille flow of power-law fluids. J. Non-Newton. Fluid Mech. 2018, 260, 120–132. [Google Scholar] [CrossRef]
- Ohta, M.; Nakamura, T.; Yoshida, Y.; Matsukuma, Y. Lattice Boltzmann simulations of viscoplastic fluid flows through complex flow channels. J. Non-Newton. Fluid Mech. 2011, 166, 404–412. [Google Scholar] [CrossRef]
- Bisht, M.; Patil, D.V. Power-law fluid flow in driven enclosures with undulation using MRT-lattice Boltzmann method. Comput. Math. Appl. 2020, 79, 100–110. [Google Scholar] [CrossRef]
- Kefayati, G.; Tang, H.; Chan, A.; Wang, X. A lattice Boltzmann model for thermal non-Newtonian fluid flows throug porous media. Comput. Fluids 2018, 176, 226–244. [Google Scholar] [CrossRef]
- Osaki, S.; Hayashi, K.; Kimura, H.; Seta, T.; Kohmura, E.; Tomiyama, A. Numerical simulations of flows in cerebral aneurysms using the lattice Boltzmann method with single- and multiple-relaxation time collision models. Comput. Math. Appl. 2019, 78, 2746–2760. [Google Scholar] [CrossRef]
- Ashrafizaadeh, M.; Bakhshaei, H. A comparison of non-Newtonian models for lattice Boltzmann blood flow simulations. Comput. Math. Appl. 2009, 58, 1045–1054. [Google Scholar] [CrossRef]
- De Rosis, A. Harmonic oscillations of laminae in non-Newtonian fluids: A lattice Boltzmann-Immersed Boundary approach. Adv. Water Resour. 2014, 73, 97–107. [Google Scholar] [CrossRef]
- Zhang, J.; Kwok, D.Y. Lattice Boltzmann Method (LBM). In Encyclopedia of Microfluidics and Nanofluidics; Li, D., Ed.; Springer: Boston, MA, USA, 2008; pp. 981–985. [Google Scholar] [CrossRef]
- Yu, D.; Mei, R.; Luo, L.S.; Shyy, W. Viscous flow computations with the method of lattice Boltzmann equation. Prog. Aerosp. Sci. 2003, 39, 329–367. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I: Small amplitude processes in charged and neutral one-component system. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Boyd, J.; Buick, J.; Green, S. A second order accurate lattice Boltzmann non-Newtonian flow model. J. Phys. A Math. Gen. 2006, 39, 14241–14247. [Google Scholar] [CrossRef]
- Frisch, U.; d’ Humières, D.; Hasslacher, B.; Lallemand, P.; Pomeau, Y.; Rivet, J.P. Lattice Gas Hydrodynamics in Two and Three Dimensions. Complex Syst. 1987, 1, 649–707. [Google Scholar]
- Artoli, A. Mesoscopic Computational Haemodynamics; Technical Report; University of Amsterdam: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Wang, C.H.; Ho, J.R. A lattice Boltzmann approach for the non-Newtonian effect in the blood flow. Comput. Math. Appl. 2011, 62, 75–86. [Google Scholar] [CrossRef]
- Aharonov, E.; Rothman, D. Non-Newtonian flow (through porous media): A lattice-Boltzmann method. Geophys. Res. Lett. 1993, 20, 679–682. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Yasuda, K.; Armstrong, R.; Cohen, R. Shear flow properties of concentrated solutions of linear and star branched polystyrenes. Rheol. Acta 1981, 20, 163–178. [Google Scholar] [CrossRef]
- Yasuda, K. A multi-mode viscosity model and its applicability to non-Newtonian fluids. J. Text. Eng. 2006, 52, 171–173. [Google Scholar] [CrossRef]
- Holdsworth, D.; Norley, C.; Frayne, R.; Steinman, D.; Rutt, B. Characterisation of common carotid artery blood-flow waveforms in normal human subjects. J. Physiol. Meas. 1999, 20, 219–240. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, C.M.; Malek, A.M. Computational fluid dynamic characterization of carotid bifurcation stenosis in patient-based geometries. Brain Behav. 2012, 2, 42–52. [Google Scholar] [CrossRef] [PubMed]
- Wild, N.C.; Bulusu, K.V.; Plesniak, M.W. Vortical Structures Promote Atheroprotective Wall Shear Stress Distributions in a Carotid Artery Bifurcation Model. Bioengineering 2023, 10, 1036. [Google Scholar] [CrossRef] [PubMed]
- Zalud, N.C.; Bulusu, K.V.; Plesniak, M.W. Shear stress metrics associated with pro-atherogenic high-risk anatomical features in a carotid artery bifurcation model. Clin. Biomech. 2023, 105, 105956. [Google Scholar] [CrossRef]
- Cox, C.; Plesniak, M.W. The effect of entrance flow development on vortex formation and wall shear stress in a curved artery model. Phys. Fluids 2021, 33, 101908. [Google Scholar] [CrossRef]
- Lee, U.Y.; Kim, C.I.; Chung, G.H.; Jung, J.; Kwak, H.S. Hemodynamic Changes in the Carotid Artery after Infusion of Normal Saline Using Computational Fluid Dynamics. Diagnostics 2020, 10, 473. [Google Scholar] [CrossRef]
- Neal, M. A Study of the Brass Instrument Lip Reed Mechanism using Artificial Lips and Lattice Boltzmann Flow Simulations. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2002. [Google Scholar]
- Guo, Z.; Zheng, C.; Shi, B. An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 2002, 14, 2007–2010. [Google Scholar] [CrossRef]
- Stamou, A.; Radulovic, J.; Buick, J. Effect of stenosis growth on blood flow at the bifurcation of the carotid artery. J. Comput. Sci. 2021, 54, 101435. [Google Scholar] [CrossRef]
- Stamou, A.C.; Radulovic, J.; Buick, J.M. Investigation of hemodynamic markers for stenosis development. Eng. Rep. 2021, 3, e12389. [Google Scholar] [CrossRef]
- Boyd, J.; Buick, J.; Cosgrove, J.; Stansell, P. Application of the lattice Boltzmann method to arterial flow simulation: Investigation of boundary conditions for complex arterial geometries. Australas. Phys. Eng. Sci. Med. 2004, 27, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Abraham, F.; Behr, M.; Heinkenschloss, M. Shape Optimisation in Steady Blood Flow: A Numerical Study of Non–Newtonian Effects. Comput. Methods Biomech. Biomed. Eng. 2005, 8, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Antiga, L.; Steinman, D.A. Correlations Among Indicators of Disturbed Flow at the Normal Carotid Bifurcation. J. Biomech. Eng. 2009, 131, 061013. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Antiga, L.; Spence, J.D.; Steinman, D.A. Geometry of the Carotid Bifurcation Predicts Its Exposure to Disturbed Flow. Stroke 2008, 39, 2341–2347. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, J.; Rai, S.; Ghafghazi, S.; Berson, R.E. Blood residence time to assess significance of coronary artery stenosis. Sci. Rep. 2020, 10, 11658. [Google Scholar] [CrossRef] [PubMed]
- Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol. Heart Circ. Physiol. 2004, 286, H1916–H1922. [Google Scholar] [CrossRef]
- Lou, Z.; Yang, W.J. A computer simulation of the non-Newtonian blood flow at the aortic bifurcation. J. Biomech. 1993, 26, 37–49. [Google Scholar] [CrossRef]
- Nakamura, M.; Sawada, T. Numerical Study on the Unsteady Flow of Non–Newtonian Fluid. J. Biomech. Eng. 1990, 112, 100–103. [Google Scholar] [CrossRef]
- Gallo, D.; Steinman, D.A.; Bijari, P.B.; Morbiducci, U. Helical flow in carotid bifurcation as surrogate marker of exposure to disturbed shear. J. Biomech. 2012, 45, 2398–2404. [Google Scholar] [CrossRef]
- Harloff, A.; Albrecht, F.; Spreer, J.; Stalder, A.; Bock, J.; Frydrychowicz, A.; Schöllhorn, J.; Hetzel, A.; Schumacher, M.; Hennig, J.; et al. 3D blood flow characteristics in the carotid artery bifurcation assessed by flow-sensitive 4D MRI at 3T. Magn. Reson. Med. 2009, 61, 65–74. [Google Scholar] [CrossRef]
- Boyd, J.; Buick, J.M. Three-dimensional modelling of the human carotid artery using the lattice Boltzmann method: II. Shear analysis. Phys. Med. Biol. 2008, 53, 5781–5795. [Google Scholar] [CrossRef]
- Björkegren, J.L.; Lusis, A.J. Atherosclerosis: Recent developments. Cell 2022, 185, 1630–1645. [Google Scholar] [CrossRef]
- Michal, K.; Cudnoch-Jedrzejewska, A. Pathophysiology of Atherosclerotic Plaque Development-Contemporary Experience and New Directions in Research. Int. J. Mol. Sci. 2021, 22, 3513. [Google Scholar]


| Parameter | Artery | Boltzmann (lu) |
|---|---|---|
| D | 36 | |
| Pa · s | ||
| T | 66,987 | |
| 307 | 307 |
| Parameter | SI | Boltzmann (lu) |
|---|---|---|
| Pa · s | ||
| Pa · s | ||
| 603,619 | ||
| a | ||
| n |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamou, A.C.; Radulovic, J.; Buick, J.M. A Comparison of Newtonian and Non-Newtonian Models for Simulating Stenosis Development at the Bifurcation of the Carotid Artery. Fluids 2023, 8, 282. https://doi.org/10.3390/fluids8100282
Stamou AC, Radulovic J, Buick JM. A Comparison of Newtonian and Non-Newtonian Models for Simulating Stenosis Development at the Bifurcation of the Carotid Artery. Fluids. 2023; 8(10):282. https://doi.org/10.3390/fluids8100282
Chicago/Turabian StyleStamou, Aikaterini C., Jovana Radulovic, and James M. Buick. 2023. "A Comparison of Newtonian and Non-Newtonian Models for Simulating Stenosis Development at the Bifurcation of the Carotid Artery" Fluids 8, no. 10: 282. https://doi.org/10.3390/fluids8100282
APA StyleStamou, A. C., Radulovic, J., & Buick, J. M. (2023). A Comparison of Newtonian and Non-Newtonian Models for Simulating Stenosis Development at the Bifurcation of the Carotid Artery. Fluids, 8(10), 282. https://doi.org/10.3390/fluids8100282









