Research Progress on Active Secondary Jet Technology in Supersonic Flow Field of Aerospace Propulsion Systems
Abstract
:1. Introduction
2. Advancements in Secondary Jet Research
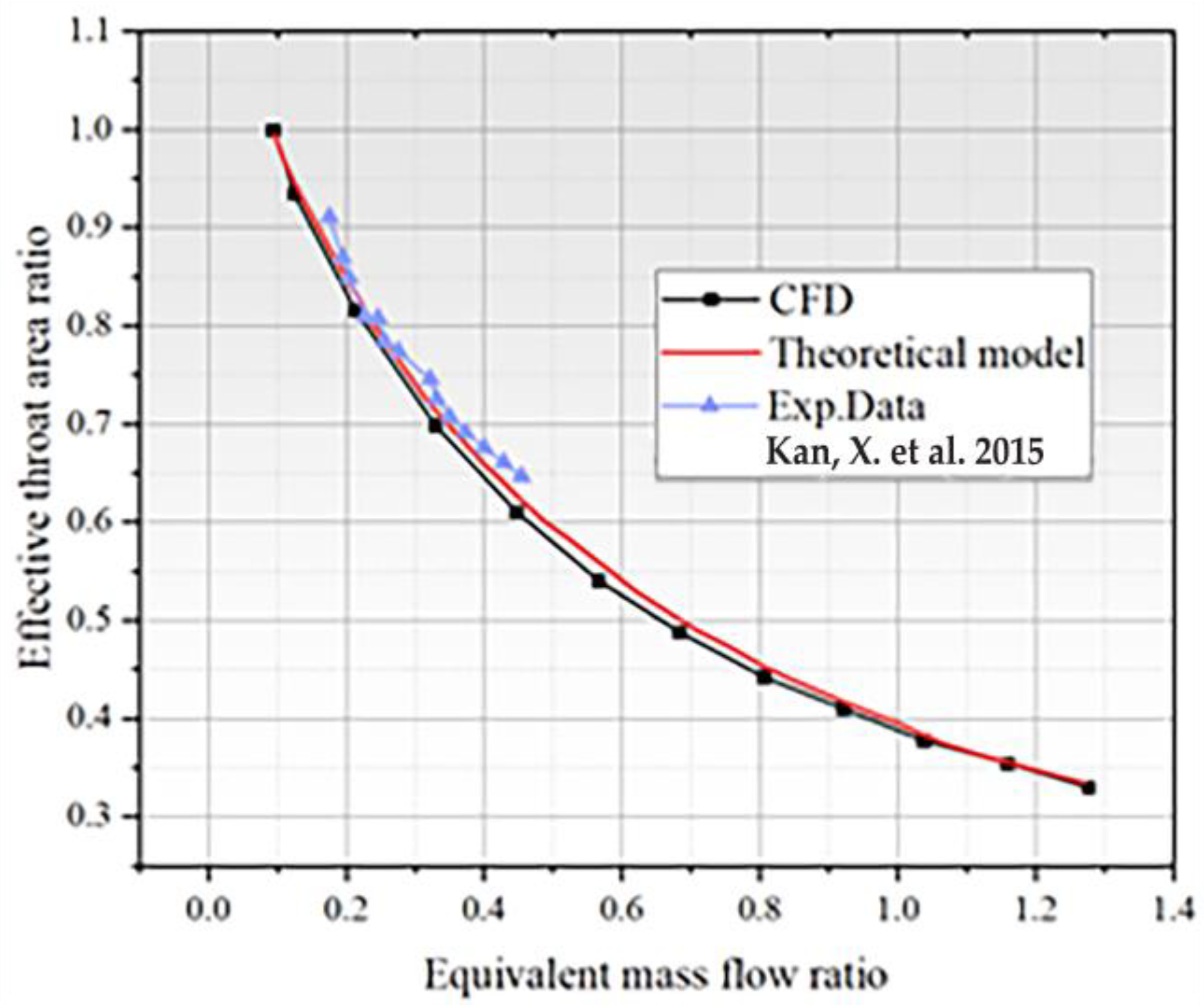
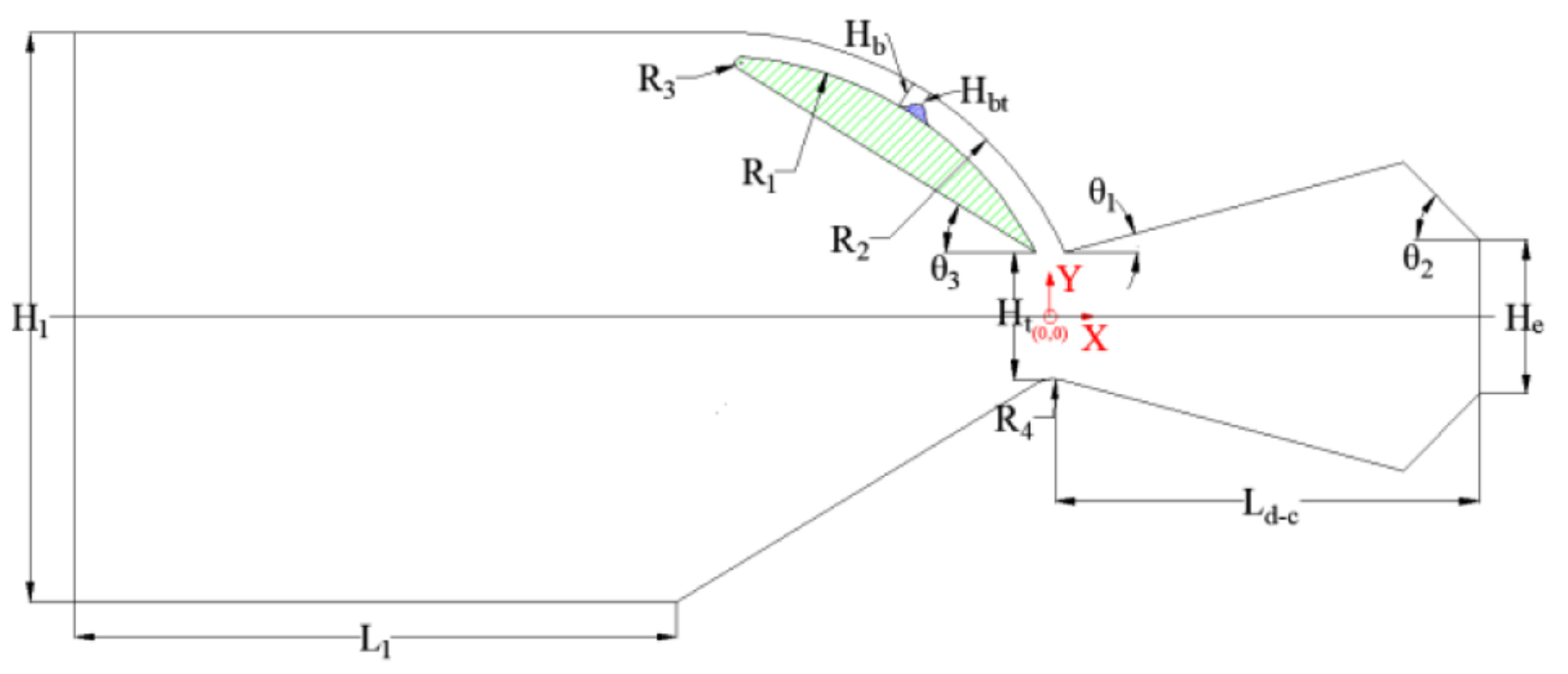
3. Thrust Adjustment by Fluid Throat
- (1)
- The efficiency improvement of dual nozzles is not significant;
- (2)
- The larger the reverse injection angle, the greater the range of variation in the effective throat area;
- (3)
- The closer the nozzle is to the throat, the higher the fluid throat performance is;
- (4)
- A small curvature of the throat results in high FNT performance. However, beyond a certain value, increasing the curvature does not yield significant improvements;
- (5)
- A small nozzle convergence angle can improve the FNT performance, but there will be a peak value;
- (6)
- Increasing the mass flow ratio or total temperature ratio significantly improves FNT choke performance;
- (7)
- The small expansion ratio nozzle may have greater choke performance.
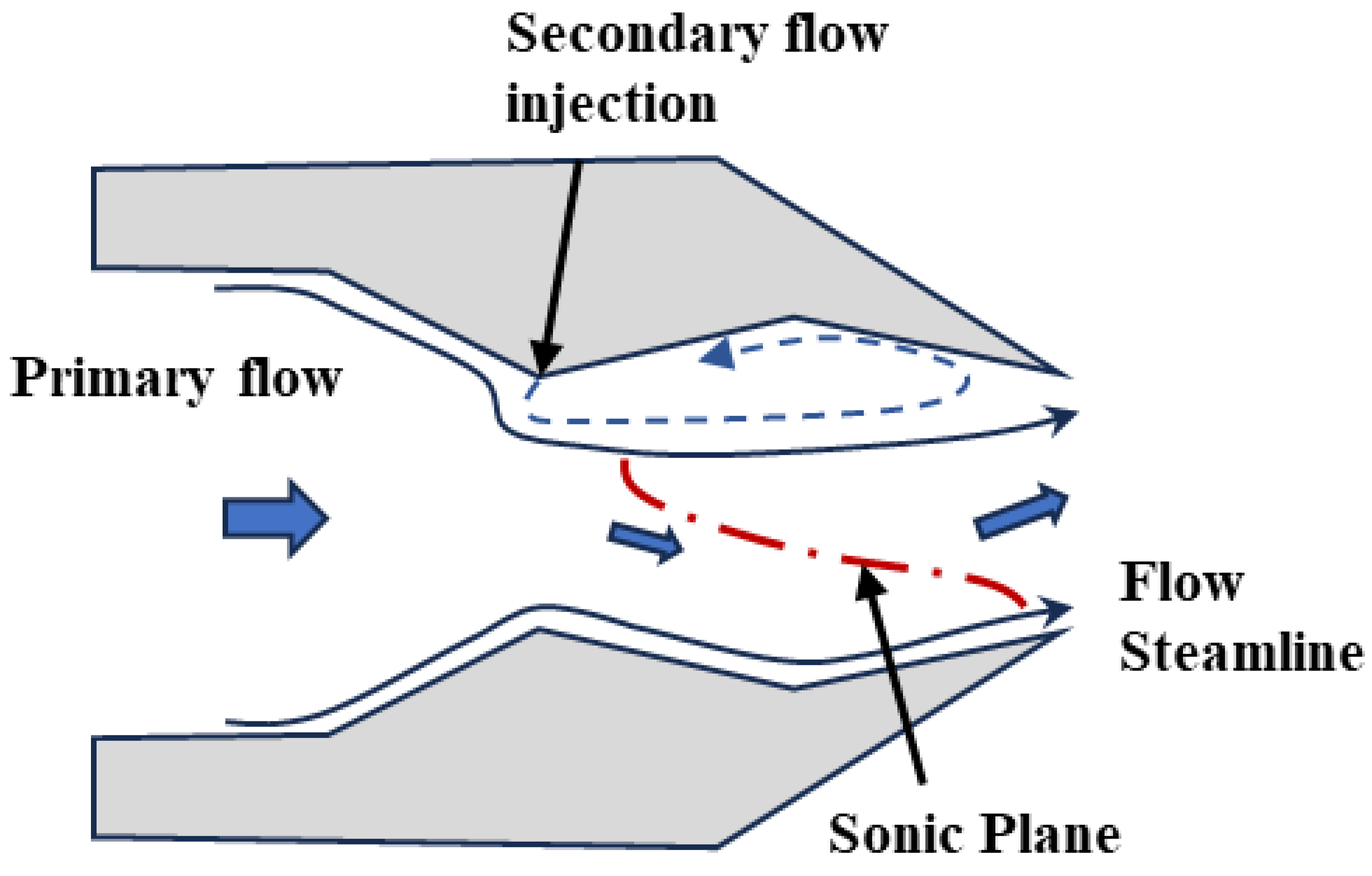
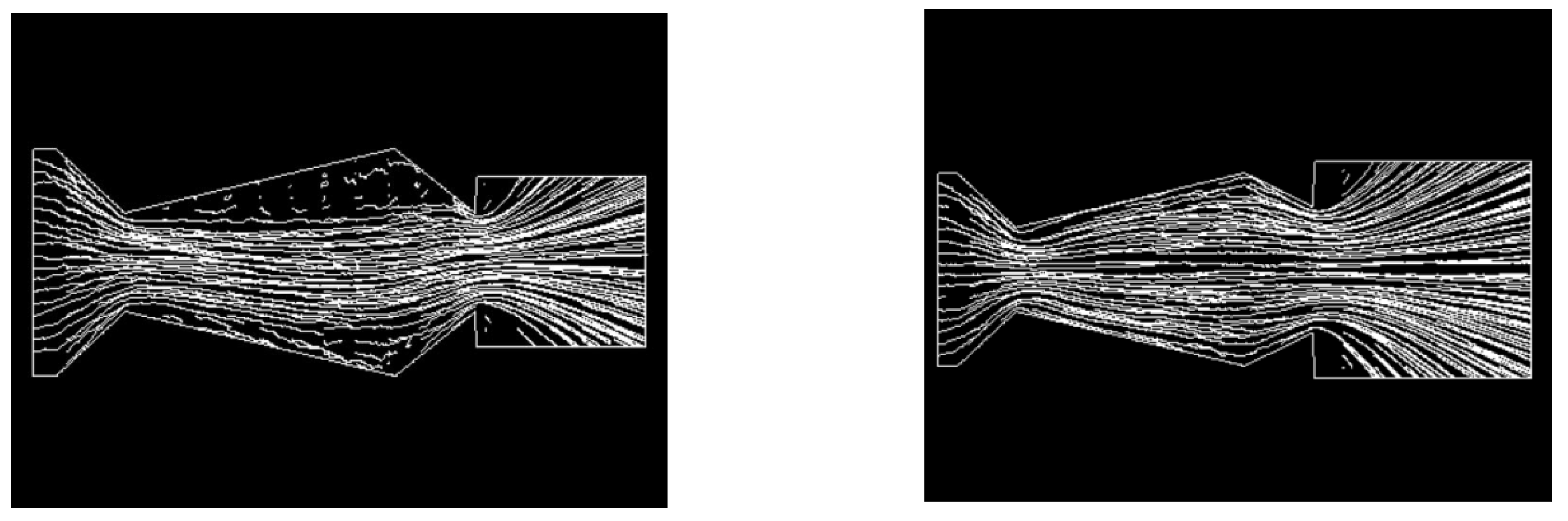
4. Thrust Vectoring
- (1)
- Controlling the flow separation in the reentrant is the key to improving the vector deflection angle;
- (2)
- The expansion angle of the reentrant should not exceed 10°;
- (3)
- Increasing the angle of the secondary flow and the angle of convergence of the reentrant can improve the vector angle;
- (4)
- Reducing the length of the reentrant can increase the thrust coefficient and thrust vectoring efficiency.
5. Fuel Mixing in a Scramjet Engine
6. Jet Noise Control
7. Other Application
8. Conclusions
- (1)
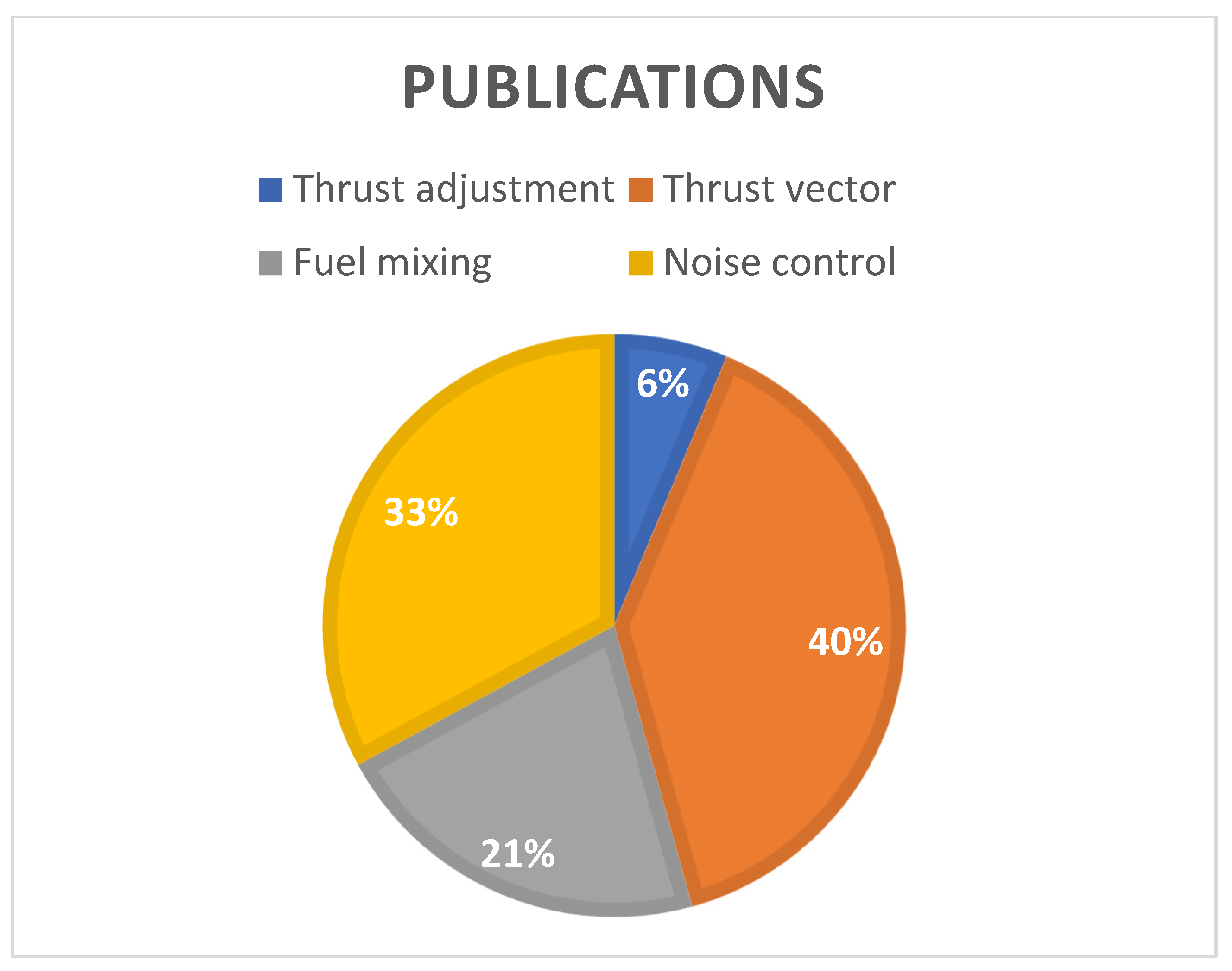
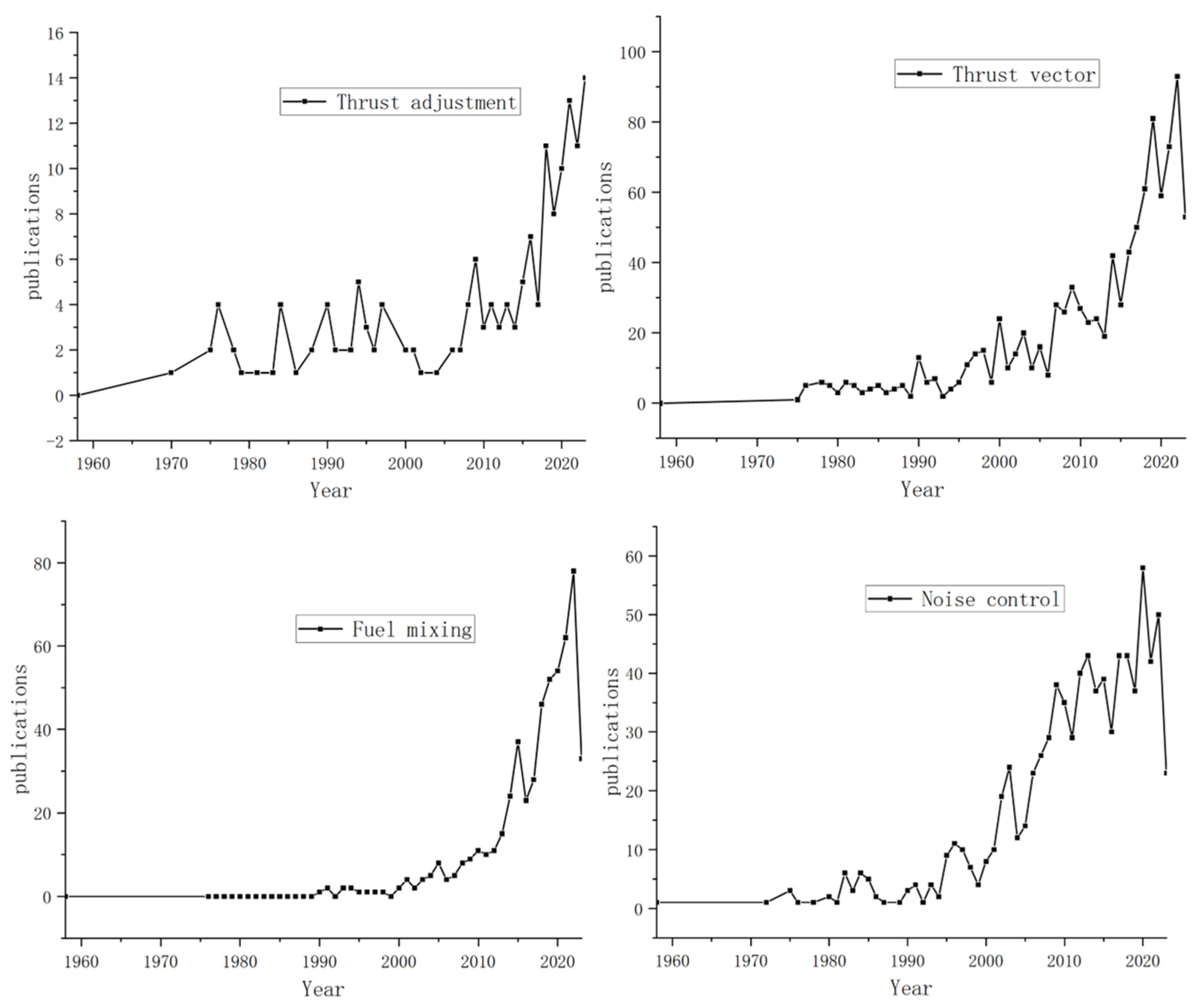
- The use of active secondary injection for thrust regulation offers advantages such as simple structure, lightweight, and absence of component erosion compared to mechanical adjustment methods. This makes it particularly suitable for rocket engines, especially solid rocket engines. However, the range of thrust adjustment with secondary jet is still limited by the large flow rate of the secondary jet. Therefore, research on the regulation of thrust magnitude in throat-jet is relatively limited, accounting for approximately 6% of the total publication quantity for the four typical applications. However, the combination of a pintle structure and secondary jet may lead to further development of this technology. It not only enables effective thrust adjustment, but also ensures longer operation because of protection of the secondary jet on the pintle surface. However, the mechanical structure resulting from this combination will be a challenge that needs to be optimized in the next step.
- (2)
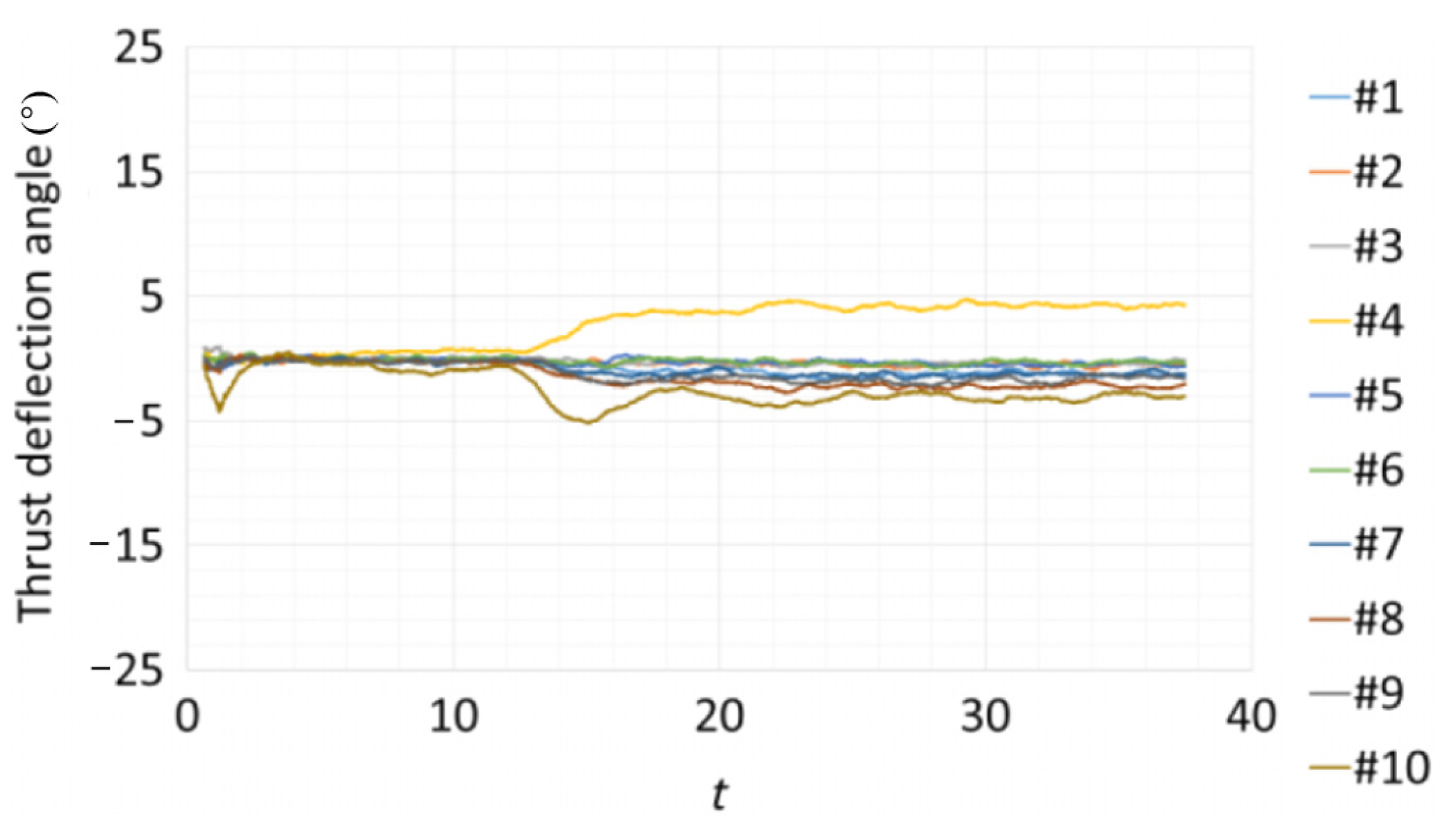
- Thrust vectoring is currently the most prominent application of active secondary injection in the aerospace propulsion field. Especially after the introduction of the dual-throat nozzle in 2003, the number of relevant publications has rapidly increased. The introduction of a passive bypass jet scheme further simplifies the system structures of the secondary flow and achieves a thrust vector angle above 24°, which is far surpassing other thrust vectoring technologies (around 15°). However, some studies have indicated that the dual-throat nozzle may experience uncontrolled small vector angles in certain cases, which may be caused by fluctuations in the engine flow field. This issue can be effectively addressed by increasing the area of the second throat, but the impact on the thrust vectoring capability after expanding the second throat is not yet clear.
- (3)
- For fuel mixing, the use of multi-portholes injection can effectively improve the mixing efficiency of fuel and air, and some studies indicate that if parts of the multi-portholes are used to inject air, the air and fuel can mix with each other in the strong turbulence structure downstream of the jet, which achieves an efficiency improvement of 116%. However, additional air sources will inevitably cause redundancy in the system structure. Meanwhile, bypass structures similar to those used in thrust vectoring studies have been shown to enhance the mixing efficiency of individual fuel injection porthole, which means the application of this approach in multi-porthole jets is also promising, especially when applied to multi-portholes, as it may further enhance mixing efficiency while simplifying the structure. On the other hand, pulsed fuel jets can also significantly enhance the mixing efficiency, but further research is needed to characterize the features and related mechanisms affecting fuel mixing in pulsed jet flow fields. In fact, many technologies that promote fuel mixing are not mutually exclusive. Therefore, in the future, it can be explored to combine multiple techniques in jet research to further uncover the potential of jets in fuel mixing.
- (4)
- Normally, engines generate large noise during operation, which can pose a threat to personnel and the delicate components. Current research indicates that noise can be effectively suppressed by utilizing secondary jets on the nozzle wall. However, in fact, the publication quantity indicates that before the emergence of micro-jet noise reduction technology in 2002, traditional jet noise reduction techniques required a jet flow rate near 100% of the primary flow, making it difficult to have practical engineering significance. The development of micro-jet noise reduction technology greatly promoted the advancement of aerospace propulsion system noise reduction techniques. The fluidic embedded nozzle technology proposed in 2013 has attracted wide attention from scholars due to its lower flow consumption and better noise reduction effect, which can obtain a reduction of 5 dB with a jet flow rate ratio of 4%. Currently, the structural optimization of fluidic embedded nozzle technology and related mechanism analysis still require further research.
- (5)
- In recent years, there have been numerous attempts to explore other applications of secondary jets, but it is worth noting is that in many applications, the injection positions of the secondary jets in the engine are actually highly overlapped. For instance, in applications such as conical nozzle thrust vectoring and noise suppression, the jet positions mainly concentrate in the expansion section of the nozzle. For applications such as thrust vectoring in dual-throat nozzles, thrust adjustment, and infrared radiation suppression, the jet positions primarily focus on the throat section of the nozzle. It is indicated that secondary jets at a specific position may bring multiple benefits, but there has been little research systematically considering the comprehensive effects of jet parameters on different applications. Instead, the optimization has been limited to a single application. In the future, it may be worthwhile to analyze and optimize jet parameters for multiple applications, which could further reveal the potential of active secondary jets in engine applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deere, K. Summary of fluidic thrust vectoring research at NASA Langley Research Center. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3800. [Google Scholar]
- Lian, Y. Fluidic thrust vectoring techniques research. Aircr. Des. 2008, 28, 19–24. [Google Scholar]
- Ali, A.; Rodriguez, C.; Neely, A.; Young, J. Combination of fluidic thrust modulation and vectoring in a 2D nozzle. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012; p. 3780. [Google Scholar]
- Guo, C.; Wei, Z.; Xie, K.; Wang, N. Thrust control by fluidic injection in solid rocket motors. J. Propul. Power 2017, 33, 815–829. [Google Scholar] [CrossRef]
- Das, A.K.; Acharyya, K.; Mankodi, T.K.; Saha, U.K. Fluidic Thrust Vector Control of Aerospace Vehicles: State-of-the-Art Review and Future Prospects. J. Fluids Eng. 2023, 145, 080801. [Google Scholar] [CrossRef]
- Choubey, G.; Yuvarajan, D.; Huang, W.; Shafee, A.; Pandey, K. Recent research progress on transverse injection technique for scramjet applications-a brief review. Int. J. Hydrogen Energy 2020, 45, 27806–27827. [Google Scholar] [CrossRef]
- Salehian, S.; Mankbadi, R.R. A review of aeroacoustics of supersonic jets interacting with solid surfaces. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0006. [Google Scholar]
- Chang-Lu, H. Aufrollung eines zylindrischen Strahles durch Querwind. In The Roll-Up of a Cylindrical Jet in a Cross Flow; USAF-AFRL 73-0131; Nagaraja, K.S., Schrade, H.O., Eds. and Translators; University of Göttingen: Göttingen, Germany, 1973. [Google Scholar]
- Ehrich, F.F. Penetration and deflection of jets oblique to a general stream. J. Aeronaut. Sci. 1953, 20, 99–104. [Google Scholar] [CrossRef]
- Broadwell, J.E. Analysis of the fluid mechanics of secondary injection for thrust vector control. AIAA J. 1963, 1, 1067–1075. [Google Scholar] [CrossRef]
- Zukoski, E.E.; Spaid, F.W. Secondary injection of gases into a supersonic flow. AIAA J. 1964, 2, 1689–1696. [Google Scholar] [CrossRef]
- Schetz, J.A.; Billig, F.S. Penetration of gaseous jets injected into a supersonic stream. J. Spacecr. Rocket. 1966, 3, 1658–1665. [Google Scholar] [CrossRef]
- Blllig, F.; Orth, R.; Lasky, M. A unified analysis of gaseous jet penetration. AIAA J. 1971, 9, 1048–1058. [Google Scholar] [CrossRef]
- Santiago, J.G.; Dutton, J.C. Velocity measurements of a jet injected into a supersonic crossflow. J. Propul. Power 1997, 13, 264–273. [Google Scholar] [CrossRef]
- Kumar, A.; Rudy, D.; Drummond, J.; Harris, J. Experiences with explicit finite-difference schemes for complex fluid dynamics problems on STAR-100 and CYBER-203 computers. NASA STI/Recon Tech. Rep. A 1982, 82, 43251. [Google Scholar]
- MacCormack, R.W. A numerical method for solving the equations of compressible viscous flow. AIAA J. 1982, 20, 1275–1281. [Google Scholar] [CrossRef]
- Kumar, A. Three-Dimensional Inviscid Analysis of the Scramjet Inlet Flowfield. J. Aircr. 1982, 19, 892–893. [Google Scholar] [CrossRef]
- Smith, R.E. Two-Boundary Grid Generation for the Solution of the Three Dimensional Compressible Navier-Stokes Equations; NASA: Hampton, VA, USA, 1981.
- Peyret, R.; Viviand, H.; Smolderen, J. Computation of viscous compressible flows based on the Navier-Stokes equations. NASA STI/Recon Tech. Rep. N 1975, 76, 11380. [Google Scholar]
- Pulliam, T.H.; Steger, J.L. Implicit finite-difference simulations of three-dimensional compressible flow. AIAA J. 1980, 18, 159–167. [Google Scholar] [CrossRef]
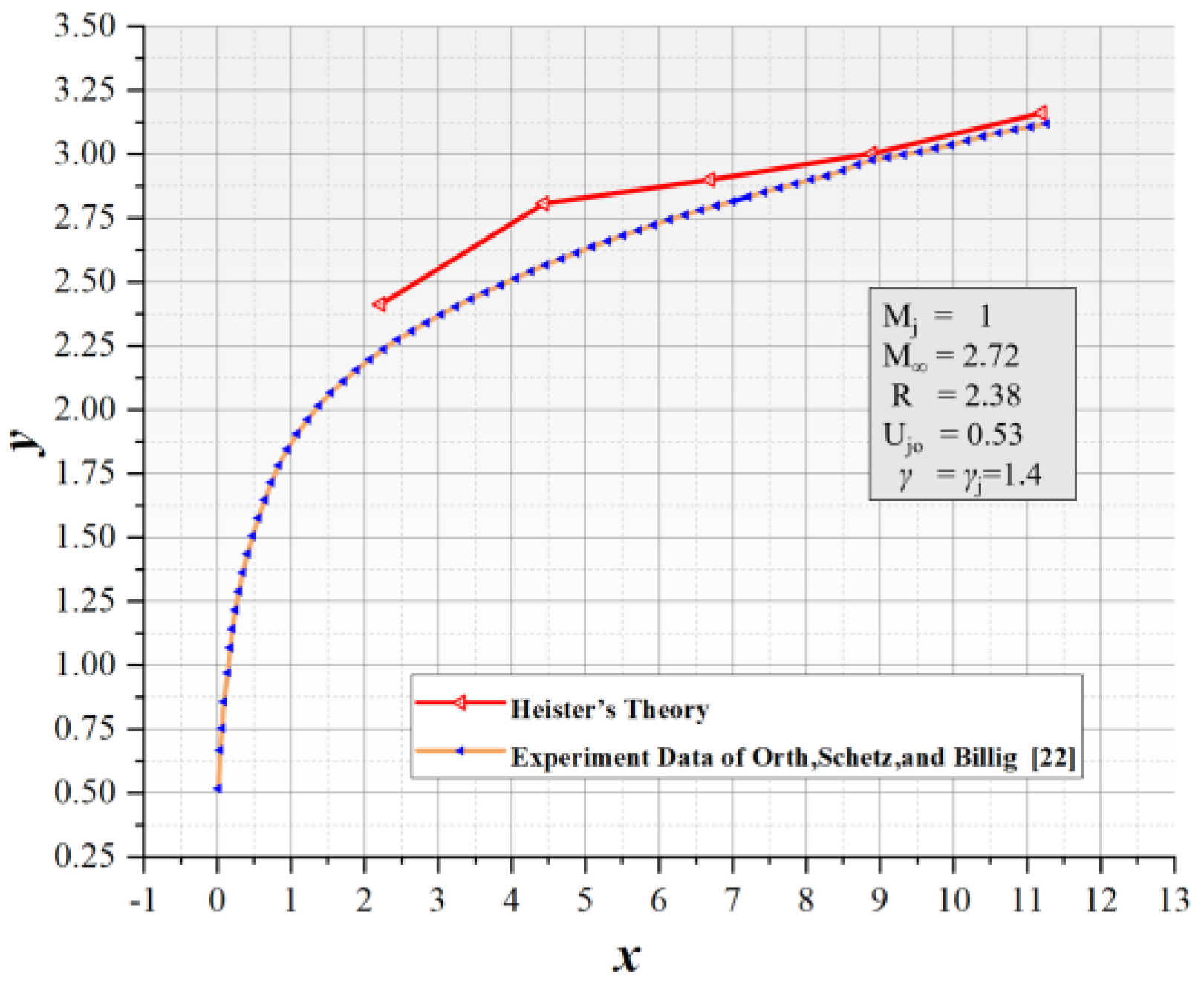
- Heister, S.; Karagozian, A. Gaseous jet in supersonic crossflow. AIAA J. 1990, 28, 819–827. [Google Scholar] [CrossRef]
- Billig, F.S.; Orth, R.; Schetz, J. The Interaction and Penetration of Gaseous Jets in Supersonic Flow; NASA: Silver Spring, MD, USA, 1969.
- Wilcox, D.C. Comparison of two-equation turbulence models for boundary layers with pressure gradient. AIAA J. 1993, 31, 1414–1421. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Tam, C.-J.; Baurle, R.; Gruber, M. Numerical study of jet injection into a supersonic crossflow. In Proceedings of the 35th Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999; p. 2254. [Google Scholar]
- Viti, V.; Schetz, J.; Neel, R. Comparison of first and second order turbulence models for a jet/3D ramp combination in supersonic flow. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 1100. [Google Scholar]
- Viti, V.; Neel, R.; Schetz, J.A. Detailed flow physics of the supersonic jet interaction flow field. Phys. Fluids 2009, 21, 046101. [Google Scholar] [CrossRef]
- Peterson, D.M.; Candler, G.V. Hybrid Reynolds-averaged and large-eddy simulation of normal injection into a supersonic crossflow. J. Propul. Power 2010, 26, 533–544. [Google Scholar] [CrossRef]
- Won, S.-H.; Jeung, I.-S.; Parent, B.; Choi, J.-Y. Numerical investigation of transverse hydrogen jet into supersonic crossflow using detached-eddy simulation. AIAA J. 2010, 48, 1047–1058. [Google Scholar] [CrossRef]
- Kawai, S.; Lele, S.K. Large-eddy simulation of jet mixing in supersonic crossflows. AIAA J. 2010, 48, 2063–2083. [Google Scholar] [CrossRef]
- Bender, E.; Miller, D.; Smith, B.; Yagle, P.; Vermeulen, P.; Walker, S. Simulation of pulsed injection in a cross flow using 3-D unsteady CFD. In Proceedings of the Fluids 2000 Conference and Exhibit, Denver, CO, USA, 19–22 June 2000; p. 2318. [Google Scholar]
- Linden, P.; Turner, J. The formation of ‘optimal’ vortex rings, and the efficiency of propulsion devices. J. Fluid Mech. 2001, 427, 61–72. [Google Scholar] [CrossRef]
- McManus, K.; Magill, J. Separation control in incompressible and compressible flows using pulsed jets. In Proceedings of the Fluid Dynamics Conference, New Orleans, LA, USA, 17–20 June 1996; p. 1948. [Google Scholar]
- Campolo, M.; Salvetti, M.V.; Soldati, A. Mechanisms for microparticle dispersion in a jet in crossflow. AIChE J. 2005, 51, 28–43. [Google Scholar] [CrossRef]
- Agati, G.; Borello, D.; Camerlengo, G.; Rispoli, F.; Sesterhenn, J. DNS of an oblique jet in a particle-laden crossflow: Study of solid phase preferential concentration and particle-wall interaction. Flow Turbul. Combust. 2020, 105, 517–535. [Google Scholar] [CrossRef]
- Park, J.; Park, H. Particle dispersion induced by vortical interactions in a particle-laden upward jet with a partial crossflow. J. Fluid Mech. 2021, 915, A5. [Google Scholar] [CrossRef]
- Schetz, J.; Kush, E., Jr.; Joshi, P. Wave phenomena in liquid jet breakup in a supersonic crossflow. AIAA J. 1980, 18, 774–778. [Google Scholar] [CrossRef]
- Im, K.-S.; Lin, K.-C.; Lai, M.-C. Spray atomization of liquid jet in supersonic cross flows. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 732. [Google Scholar]
- Im, K.-S.; Lin, K.-C.; Lai, M.-C.; Chon, M. Breakup modeling of a liquid jet in cross flow. Int. J. Automot. Technol. 2011, 12, 489–496. [Google Scholar] [CrossRef]
- Feng, L.; Fuguo, L.; Weidong, L.; Kai, Z.; Changsheng, W.; Yiwei, X. Breakup characteristics of liquid jet in supersonic cross flow. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 2356–2362. (In Chinese) [Google Scholar]
- Napior, J.; Garmy, V. Controllable solid propulsion for launch vehicle and spacecraft application. In Proceedings of the 57th International Astronautical Congress, Valencia, Spain, 2–6 October 2006; p. C4.2.04. [Google Scholar]
- Casiano, M.J.; Hulka, J.R.; Yang, V. Liquid-propellant rocket engine throttling: A comprehensive review. J. Propul. Power 2010, 26, 897–923. [Google Scholar] [CrossRef]
- Ostrander, M.; Bergmans, J.; Thomas, M.; Burroughs, S. Pintle motor challenges for tactical missiles. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2000; p. 3310. [Google Scholar]
- Burroughs, S. Status of army pintle technology for controllable thrust propulsion. In Proceedings of the 37th Joint Propulsion Conference and Exhibit, Salt Lake City, UT, USA, 8–11 July 2001; p. 3598. [Google Scholar]
- Heo, J.; Jeong, K.; Sung, H.-G. Numerical study of the dynamic characteristics of pintle nozzles for variable thrust. J. Propul. Power 2015, 31, 230–237. [Google Scholar] [CrossRef]
- Martin, A. The aerodynamic variable nozzle. J. Aeronaut. Sci. 1957, 24, 357–362. [Google Scholar] [CrossRef]
- Gunter, F.L.; Fahrenholz, F. Final report on a study of rocket thrust control by gas injection. Mass. Inst. Technol. Nav. Supersonic Lab. Tech. Rep. 1961, 448. [Google Scholar]
- Zumwalt, G.; Jackomis, W.N. Aerodynamic throat nozzle for thrust magnitude control of solid fuel rockets. Am. Rocket Soc. J. 1962, 32, 1934–1936. [Google Scholar]
- Betts, E.; Frederick, R. A historical systems study of liquid rocket engine throttling capabilities. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010; pp. 2010–6541. [Google Scholar]
- Dressler, G. Summary of deep throttling rocket engines with emphasis on Apollo LMDE. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006; pp. 2006–5220. [Google Scholar]
- Miller, D.; Catt, J. Conceptual development of fixed-geometry nozzles using fluidic injection for throat area control. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995; p. 2603. [Google Scholar]
- Walker, S.; Walker, S. Lessons learned in the development of a national cooperative program. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997; pp. 1997–3348. [Google Scholar]
- Weber, Y.; Bowers, D. Advancements in exhaust system technology for the 21st century. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; p. 3100. [Google Scholar]
- Catt, J.; Miller, D.; Giuliano, V. A static investigation of fixed-geometry nozzles using fluidic injection for throat area control. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995; pp. 1995–2604. [Google Scholar]
- Randolph, H.; Chew, L.; Johari, H. Pulsed jets in supersonic crossflow. J. Propul. Power 1994, 10, 746–748. [Google Scholar] [CrossRef]
- Abramovich, G.N. The Theory of Turbulent Jets; MassachusettsInst. of Technology Press: Cambridge, MA, USA, 1963; Chapter 12, Section 4. [Google Scholar]
- Baruzzini, D.; Domel, N.; Miller, D. Pulsed injection flow control for throttling in supersonic nozzles—A computational fluid dynamics design study. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007; p. 4215. [Google Scholar]
- Domel, N.; Baruzzini, D.; Miller, D. Pulsed Injection Flow Control for Throttling in Supersonic Nozzles—A Computational Fluid Dynamics Based Performance Correlation. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007; p. 4214. [Google Scholar]
- Kan, X.; Yu, L.; Bai, W.Y. Investigation of ring aerodynamic throat for solid rocket motor. J. Aerosp. Power 2009, 24, 2631–2636. (In Chinese) [Google Scholar]
- Kan, X.; Bai, W.Y.; Yu, L. Simulation for the two-phase flow aerodynamic throat of solid rocket motors. J. Propuls. Technol. 2010, 31, 56–60. (In Chinese) [Google Scholar]
- Kan, X.; Bo, L.; Chao, G.C.; Fei, W.N. Thrust Control Features for Aerodynamic Throat for Solid Rocket Motor. J. Propuls. Technol. 2015, 36, 194–199. (In Chinese) [Google Scholar]
- Minghui, Y. Research on Thrust Characteristics of Solid Rocket Motor Based on the Catalytic &Oxidative Secondary Flow Injection. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Chao, G.C. Research on Dynamic Characteristics of Fluidic Nozzle Throat in Solid Rocket Motor. Ph.D Thesis, Beijing Institute of Technology, Beijing, China, 2018. [Google Scholar]
- Yan, D.; Wei, Z.; Xie, K.; Wang, N. Simulation of thrust control by fluidic injection and pintle in a solid rocket motor. Aerosp. Sci. Technol. 2020, 99, 105711. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, K.; Li, X.; Yan, D.; Li, J.; Wang, N. The Effect of Fluidic Pintle Nozzle on the Ablative Features. In Liutex and Third Generation of Vortex Identification: Workshop from Aerospace and Aeronautics World Forum 2021; Springer Nature: Singapore, Singapore, 2023; pp. 327–344. [Google Scholar]
- Hsia, H.T.-S.; Karamcheti, K.; Seifert, H.S. Shocks induced by secondary fluid injection. J. Spacecr. Rocket. 1965, 2, 67–72. [Google Scholar] [CrossRef]
- Martin, C.L.; Powers, L. Feasibility Study of LITVC for Shuttle SRB; National Aeronautics and Space Administration, Marshall Space Flight Center: Huntsville, AL, USA, 1981.
- Deere, K. PAB3D simulations of a nozzle with fluidic injection for yaw thruseronautics and Space Admint-vector control. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; pp. 1998–3254. [Google Scholar]
- Balu, R.; Marathe, A.; Paul, P.; Mukunda, H. Analysis of performance of a hot gas injection thrust vector controlsystem. J. Propuls. Power 1991, 7, 580–585. [Google Scholar] [CrossRef]
- Azevedo, D. Measured thrust losses associated with secondary air injection through nozzle walls. J. Propuls. Power 1993, 9, 43–50. [Google Scholar] [CrossRef]
- Yagle, P.; Miller, D.; Ginn, K.; Hamstra, J. Demonstration of fluidic throat skewing for thrust vectoring in structurally fixed nozzles. J. Eng. Gas Turbines Power 2001, 123, 502–507. [Google Scholar] [CrossRef]
- Deere, K.; Berrier, B.; Flamm, J.; Johnson, S. A Computational Study of a Dual Throat Fluidic Thrust Vectoring Nozzle Concept. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005; p. 3502. [Google Scholar]
- Flamm, J.; Deere, K.; Berrier, B.; Johnson, S.; Mason, M. Experimental study of a dual-throat fluidic thrust-vectoring nozzle concept. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005; pp. 2005–3503. [Google Scholar]
- Shin, C.S.; Kim, H.D.; Setoguchi, T.; Matsuo, S. A computational study of thrust vectoring control using dual throat nozzle. J. Therm. Sci. 2010, 19, 486–490. [Google Scholar] [CrossRef]
- Ferlauto, M.; Marsilio, R. Numerical investigation of the dynamic characteristics of a dual-throat-nozzle for fluidic thrust-vectoring. AIAA J. 2017, 55, 86–98. [Google Scholar] [CrossRef]
- Gu, R.; Xu, J. Effects of cavity on the performance of dual throat nozzle during the thrust-vectoring starting transient process. J. Eng. Gas Turbines Power 2014, 136, 014502. [Google Scholar] [CrossRef]
- Ming, L. Characterization of a Dual-Throat Aerodynamic Vector Nozzle. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Chen, L.Y.; Lei, X.J.; Xing, H.J.; Shuai, H.; Sheng, W.Y. Flight test of a fluidic thrust vectoring flying wing without rudder. J. Aerosp. Power 2019, 34, 7. (In Chinese) [Google Scholar]
- Jing, J.J. Research on Bypass Dual Throat Nozzle with Parallelogram Cross-section and the Transition Section. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Wu, K.; Kim, H. A fluidic thrust vector control using the bypass flow in a dual throat nozzle. J. Mech. Sci. Technol. 2021, 35, 3435–3443. [Google Scholar] [CrossRef]
- Maruyama, Y.; Sakata, M.; Takahashi, Y. Performance analyses of fluidic thrust vector control system using dual throat nozzle. AIAA J. 2022, 60, 1730–1744. [Google Scholar] [CrossRef]
- Afridi, S.; Khan, T.A.; Shah, S.I.A.; Shams, T.A.; Mehmood, K.; Li, W.; Kukulka, D. Numerical Investigation on the Thrust Vectoring Performance of Bypass Dual Throat Nozzle. Energies 2023, 16, 594. [Google Scholar] [CrossRef]
- Ohlhorst, C.W.; Glass, D.E.; Bruce III, W.E.; Lindell, M.C.; Vaughn, W.L.; Dirling, R., Jr.; Hogenson, P.; Nichols, J.; Risner, N.; Thompson, D. Development of X-43A mach 10 leading edges. In Proceedings of the 56th International Astronautical Congress 2005, Fukuoka, Japan, 17–21 October 2005. [Google Scholar] [CrossRef]
- Waltrup, P.; White, M.; Zarlingo, F.; Gravlin, E. History of US Navy ramjet, scramjet, and mixed-cycle propulsion development. J. Propul. Power 2002, 18, 14–27. [Google Scholar] [CrossRef]
- Sancho, M.; Colin, Y. The French hypersonic research program-Progress review. Int. Aerosp. Planes Hypersonics Technol. 1995, 6004. [Google Scholar] [CrossRef]
- Novelli, P. European efforts towards mastering hypersonic propulsion. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayto, OH, USA, 14–17 July 2003; p. 2604. [Google Scholar]
- Seiner, J.M.; Dash, S.; Kenzakowski, D. Historical survey on enhanced mixing in scramjet engines. J. Propul. Power 2001, 17, 1273–1286. [Google Scholar] [CrossRef]
- Rogers, R.C. Mixing of Hydrogen Injected from Multiple Injectors Normal to a Supersonic Airstream; TN D-6476; National Aeronautics and Space Administration: Hampton, VA, USA, 1971.
- Arai, T.; Schetz, J. Penetration and mixing of bubbling liquid jets from multiple injectors normal to a supersonic air stream. In Proceedings of the AlAA 4th International Aerospace Planes Conference, Orlando, FL, USA, 1–4 December 1992; p. 5060. [Google Scholar]
- Gerdroodbary, M.B.; Ganji, D.; Amini, Y. Numerical study of shock wave interaction on transverse jets through multiport injector arrays in supersonic crossflow. Acta Astronaut. 2015, 115, 422–433. [Google Scholar] [CrossRef]
- Gerdroodbary, M.B.; Mokhtari, M.; Fallah, K.; Pourmirzaagha, H. The influence of micro air jets on mixing augmentation of transverse hydrogen jet in supersonic flow. Int. J. Hydrogen Energy 2016, 41, 22497–22508. [Google Scholar] [CrossRef]
- Gerdroodbary, M.B.; Fallah, K.; Pourmirzaagha, H. Characteristics of transverse hydrogen jet in presence of multi air jets within scramjet combustor. Acta Astronaut. 2017, 132, 25–32. [Google Scholar] [CrossRef]
- Sharma, V.; Eswaran, V.; Chakraborty, D. Determination of optimal spacing between transverse jets in a SCRAMJET engine. Aerosp. Sci. Technol. 2020, 96, 105520. [Google Scholar] [CrossRef]
- Dong, M.-z.; Liao, J.; Choubey, G.; Huang, W. Influence of the secondary flow control on the transverse gaseous injection flow field properties in a supersonic flow. Acta Astronaut. 2019, 165, 150–157. [Google Scholar] [CrossRef]
- Abdollahi, S.A.; Rajabikhorasani, G.; Alizadeh, A.a. Influence of extruded injector nozzle on fuel mixing and mass diffusion of multi fuel jets in the supersonic cross flow: Computational study. Sci. Rep. 2023, 13, 12095. [Google Scholar] [CrossRef]
- Sekar, A.; Vaidyanathan, A. Mixing enhancement of ethylene secondary jet injected into supersonic cross-flow using curved pylon. Acta Astronaut. 2023, 210, 253–267. [Google Scholar] [CrossRef]
- Kouchi, T.; Sakuranaka, N.; Izumikawa, M.; Tomioka, S. Pulsed transverse injection applied to a supersonic flow. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007; p. 5405. [Google Scholar]
- Cutler, A.; Harding, G.; Diskin, G. High frequency pulsed injection into a supersonic duct flow. AIAA J. 2013, 51, 809–818. [Google Scholar] [CrossRef]
- Shi, H.; Wang, G.; Luo, X.; Yang, J.; Lu, X.-Y. Large-eddy simulation of a pulsed jet into a supersonic crossflow. Comput. Fluids 2016, 140, 320–333. [Google Scholar] [CrossRef]
- Zhao, M.; Li, Q.; Ye, T. Investigation of an optimal pulsed jet mixing and combustion in supersonic crossflow. Combust. Flame 2021, 227, 186–201. [Google Scholar] [CrossRef]
- Narayanan, S.; Barooah, P.; Cohen, J. Dynamics and control of an isolated jet in crossflow. AIAA J. 2003, 41, 2316–2330. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, D. RANS investigation of the effect of pulsed fuel injection on scramjet HyShot II engine. Aerosp. Sci. Technol. 2019, 84, 182–192. [Google Scholar] [CrossRef]
- Ding, H.; Zhuo, C.; Chen, X.; Deng, H.; Li, M.; Sun, B.; Li, C. Numerical study on the transverse jet flow and mixing characteristics of hydrogen/metal powder fuel in powder fuel scramjet. Fuel 2022, 326, 125088. [Google Scholar] [CrossRef]
- Zhao, K.; Xia, Z.; Ma, L.; Duan, Y.; Zhang, J.; Feng, Y.; Cheng, B.; Yang, P. Large-eddy simulation of gas-particle two-phase jet into a supersonic crossflow. Phys. Fluids 2023, 35, 023310. [Google Scholar] [CrossRef]
- Jordan, P.; Colonius, T. Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 2013, 45, 173–195. [Google Scholar] [CrossRef]
- Henderson, B.; Bridges, J. An MDOE investigation of chevrons for supersonic jet noise reduction. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010; p. 3926. [Google Scholar]
- Kuo, C.-W.; Veltin, J.; McLaughlin, D.K. Acoustic assessment of small-scale military-style nozzles with chevrons. Noise Control Eng. J. 2012, 60, 559–576. [Google Scholar] [CrossRef]
- Seiner, J.; Ukeiley, L.; Jansen, B. Aero-performance efficient noise reduction for the F404-400 engine. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 3048. [Google Scholar]
- Seiner, J.; Ukeiley, L.; Jansen, B.; Kannepalli, C.; Dash, S. Noise reduction technology for F/A-18 E/F aircraft. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004; p. 2972. [Google Scholar]
- Powell, A. The influence of the exit velocity profile on the noise of a jet. Aeronaut. Q. 1954, 4, 341–360. [Google Scholar] [CrossRef]
- Manson, L.; Burge, H. Jet-Noise Reduction through Liquid-Base Foam Injection. J. Acoust. Soc. Am. 1971, 50, 1067–1074. [Google Scholar] [CrossRef]
- Burge, H.; Lieberman, S.; Manson, L. A Study of the Use of Liquid Base Foams for Jet Noise Reduction; NASA: Washington, DC, USA, 1971.
- Norum, T. Reductions in multi-component jet noise by water injection. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004; p. 2976. [Google Scholar]
- Krothapalli, A.; Soderman, P.; Allen, C.; Hayes, J.; Jaeger, S. Flight effects on the far-field noise of a heated supersonic jet. AIAA J. 1997, 35, 952–957. [Google Scholar] [CrossRef]
- Tanna, H.; Dean, P.; Fisher, M. The influence of temperature on shock-free supersonic jet noise. J. Sound Vib. 1975, 39, 429–460. [Google Scholar] [CrossRef]
- Tanna, H. An experimental study of jet noise Part I: Turbulent mixing noise. J. Sound Vib. 1977, 50, 405–428. [Google Scholar] [CrossRef]
- Krothapalli, A.; Arakeri, A.; Greska, B.; Joseph, T. High speed jet noise reduction using microjets. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference & Exhibit, Breckenridge, CO, USA, 17–19 June 2002; p. 2450. [Google Scholar]
- Greska, B.; Krothapalli, A. Jet noise reduction using aqueous microjet injection. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004; p. 2971. [Google Scholar]
- Callender, B.; Gutmark, E.; Martens, S. A comprehensive study of fluidic injection technology for jet noise reduction. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; p. 3608. [Google Scholar]
- Camussi, R.; Guj, G.; Tomassi, F.; Yao, P.; Pieroni, A.; Sisto, R. Air injection through microjets in low Mach number turbulent jet flows. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; p. 3644. [Google Scholar]
- Zaman, K. Subsonic jet noise reduction by microjets with various injection port geometry. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; p. 3643. [Google Scholar]
- Castelain, T.; Sunyach, M.; Juve, D.; Bera, J.C. Effect of microjets on a high-subsonic jet. Parametric study of far-field noise reduction. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. [Google Scholar]
- Castelain, T.; Sunyach, M.; Juvé, D.; Béra, J.-C. Jet-noise reduction by impinging microjets: An acoustic investigation testing microjet parameters. AIAA J. 2008, 46, 1081–1087. [Google Scholar] [CrossRef]
- Greska, B.; Krothapalli, A.; Seiner, J.; Jansen, B.; Ukeiley, L. The effects of microjet injection on an F404 jet engine. In Proceedings of the 11th AIAA/CEAS aeroacoustics conference, Monterey, CA, USA, 23–25 May 2005; p. 3047. [Google Scholar]
- Kandula, M. Numerical simulation of noise from a supersonic jet passing through a rigid duct. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004; p. 2935. [Google Scholar]
- Xu, Y.; Zhou, X.; Zhang, Z.C.; Chen, Y.; Liu, L.H. Reduction of rocket engine jet noise by water injection. J. Aerosp. Power 2010, 25, 816–820. (In Chinese) [Google Scholar]
- Powers, R.W.; Kuo, C.-W.; McLaughlin, D.K. Experimental comparison of supersonic jets exhausting from military style nozzles with interior corrugations and fluidic inserts. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2186. [Google Scholar]
- Powers, R.W.; Kuo, C.-W.; McLaughlin, D.K.; Morris, P.J. Supersonic jet noise reduction by nozzle fluidic inserts with simulated forward flight. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2474. [Google Scholar]
- Morris, P.J.; McLaughlin, D.K.; Powers, R.W.; Kapusta, M.J. Prediction, experiments and optimization of high-speed jet noise reduction using fluidic inserts. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, 29–30 July 2014; p. 3737. [Google Scholar]
- Powers, R.W.; Hromisin, S.; McLaughlin, D.K.; Morris, P.J. Mean velocity and turbulence measurements of supersonic jets with fluidic inserts. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 0001. [Google Scholar]
- Morgan, J.; McLaughlin, D.K.; Morris, P.J. Experimental results for supersonic jet noise reduction using nozzle fluidic inserts. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. 3518. [Google Scholar]
- Sikarwar, N.; Morris, P.J. Optimization of blowing in a convergent-divergent nozzle for noise reduction. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2473. [Google Scholar]
- Sikarwar, N.; Morris, P.J. The use of an adjoint method for optimization of blowing in a convergent-divergent nozzle. Int. J. Aeroacoustics 2015, 14, 327–351. [Google Scholar] [CrossRef]
- Kapusta, M.; Powers, R.W.; Morris, P.J.; McLaughlin, D.K. Numerical simulations for supersonic jet noise reduction using fluidic inserts. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 0758. [Google Scholar]
- Morgan, J.; Morris, P.J.; McLaughlin, D.K.; Prasad, C. Further development of supersonic jet noise reduction using nozzle fluidic inserts. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0683. [Google Scholar]
- Coderoni, M.; Lyrintzis, A.S.; Blaisdell, G.A. Noise reduction analysis of supersonic unheated jets with fluidic injection using large eddy simulations. Int. J. Aeroacoustics 2018, 17, 467–501. [Google Scholar] [CrossRef]
- Coderoni, M.; Lyrintzis, A.S.; Blaisdell, G.A. Large-eddy simulations analysis of supersonic heated jets with fluid injection for noise reduction. AIAA J. 2019, 57, 3442–3455. [Google Scholar] [CrossRef]
- Prasad, C.; Morris, P.J. A study of noise reduction mechanisms of jets with fluid inserts. J. Sound Vib. 2020, 476, 115331. [Google Scholar] [CrossRef]
- Prasad, C.; Hromisin, S.; Morris, P.J. Leveraging large eddy simulations to assess noise source imaging of a controlled supersonic jet. Int. J. Aeroacoustics 2022, 21, 438–456. [Google Scholar] [CrossRef]
- Smith, T.D.; Cain, A.B.; Chenault, C.F. Numerical simulation of enhanced mixing in jet plumes using pulsed blowing. J. Aircr. 2001, 38, 458–463. [Google Scholar] [CrossRef]
- Thakre, P.; Yang, V. Mitigation of graphite nozzle erosion by boundary-layer control in solid propellant rocket motors. J. Propul. Power 2009, 25, 1079–1085. [Google Scholar] [CrossRef]
- Lei, Z.H.; Hua, Q.; Cha, X.; Xi, Z.L. Propulsive Performance of Pulse Detonation Engine with Fluidically Augmented Nozzle. J. Propul. Power 2014, 35, 1002–1008. (In Chinese) [Google Scholar]
- Cai, G.; Cao, B.; Zhu, H.; Tian, H.; Ma, X. Parametric investigation of secondary injection in post-chamber on combustion performance for hybrid rocket motor. Acta Astronaut. 2017, 140, 427–438. [Google Scholar] [CrossRef]
- Lv, Z.; Xu, J.; Mo, J. Numerical investigation of improving the performance of a single expansion ramp nozzle at off-design conditions by secondary injection. Acta Astronaut. 2017, 133, 233–243. [Google Scholar] [CrossRef]
- Luo, Z.X. Study on Aerodynamic Performance and Infrared Radiation Characteristics of Single Expansion Ramp Nozzle with Secondary Flow. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]

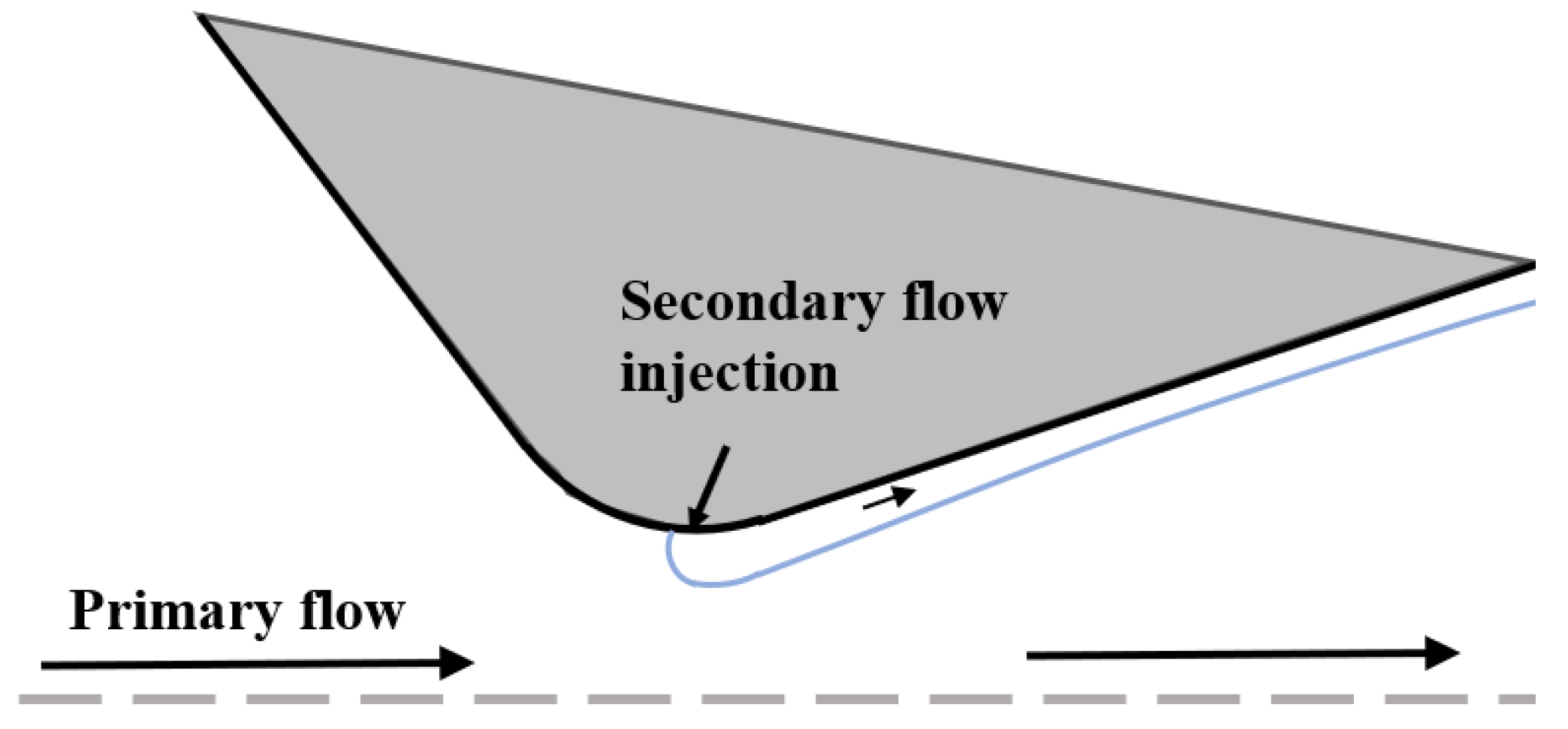
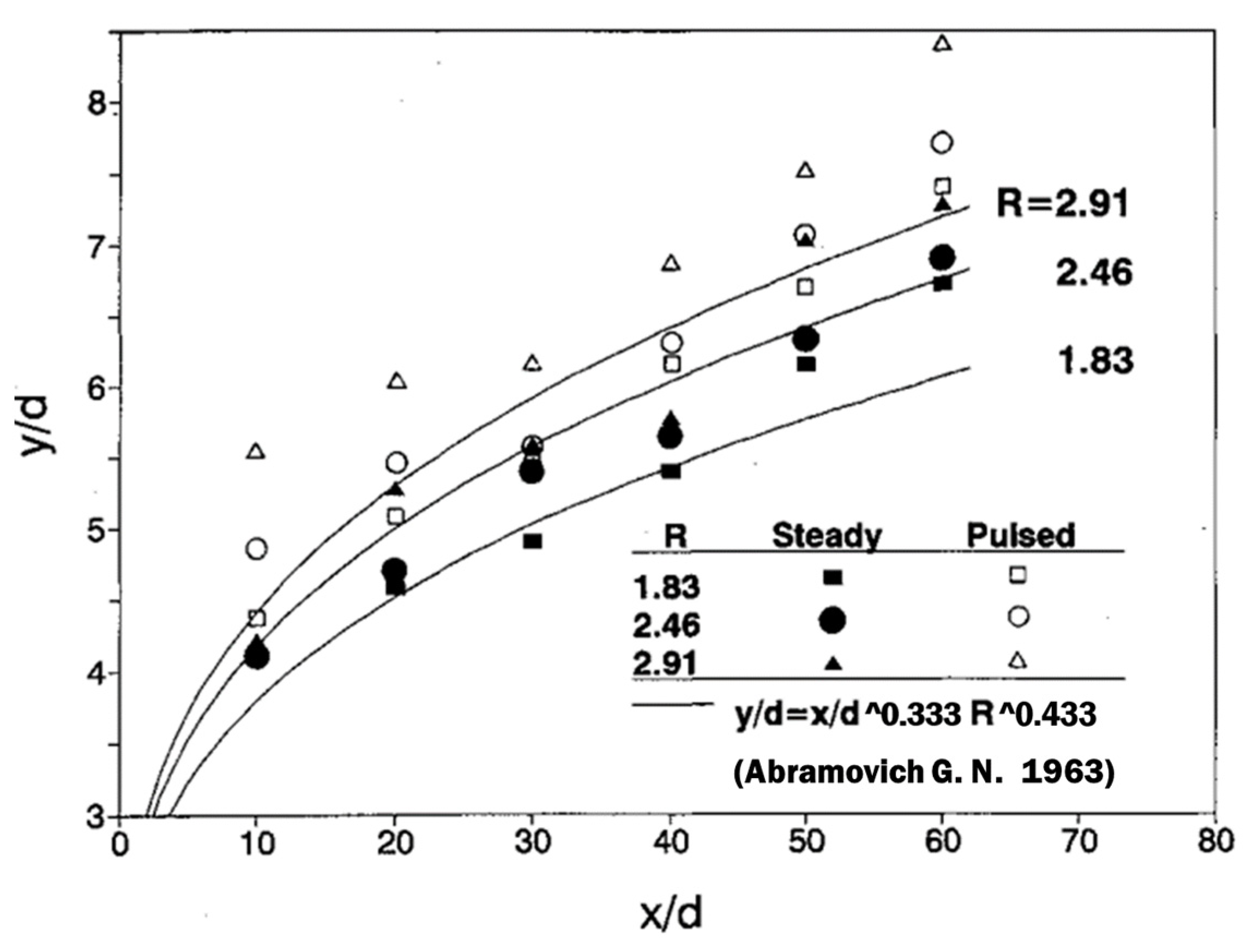

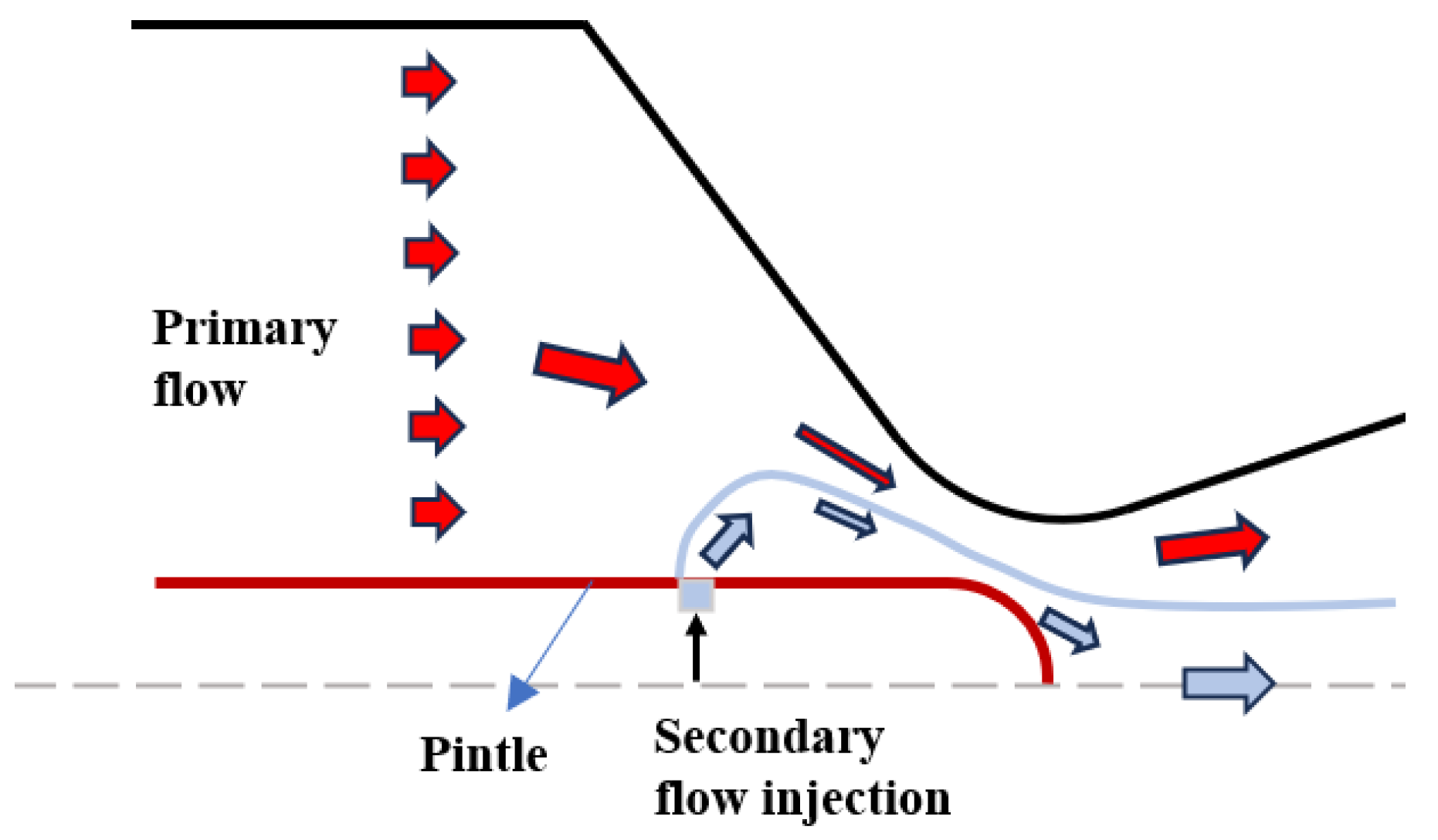
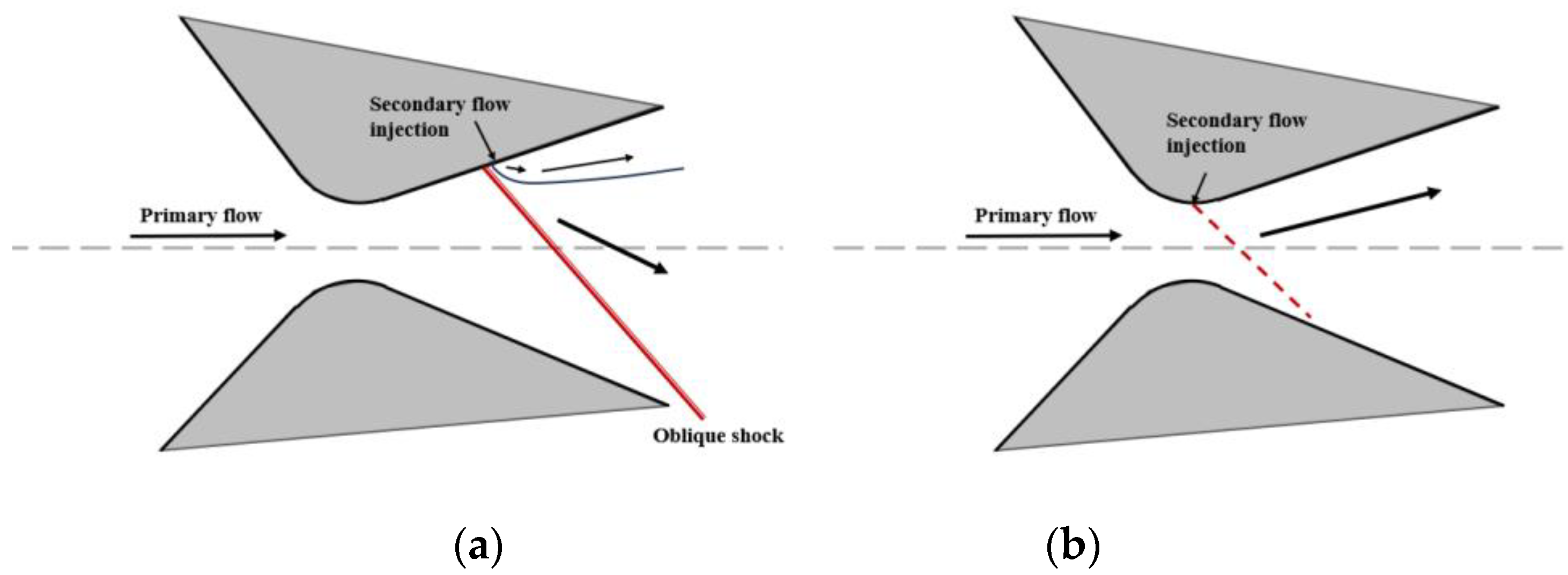

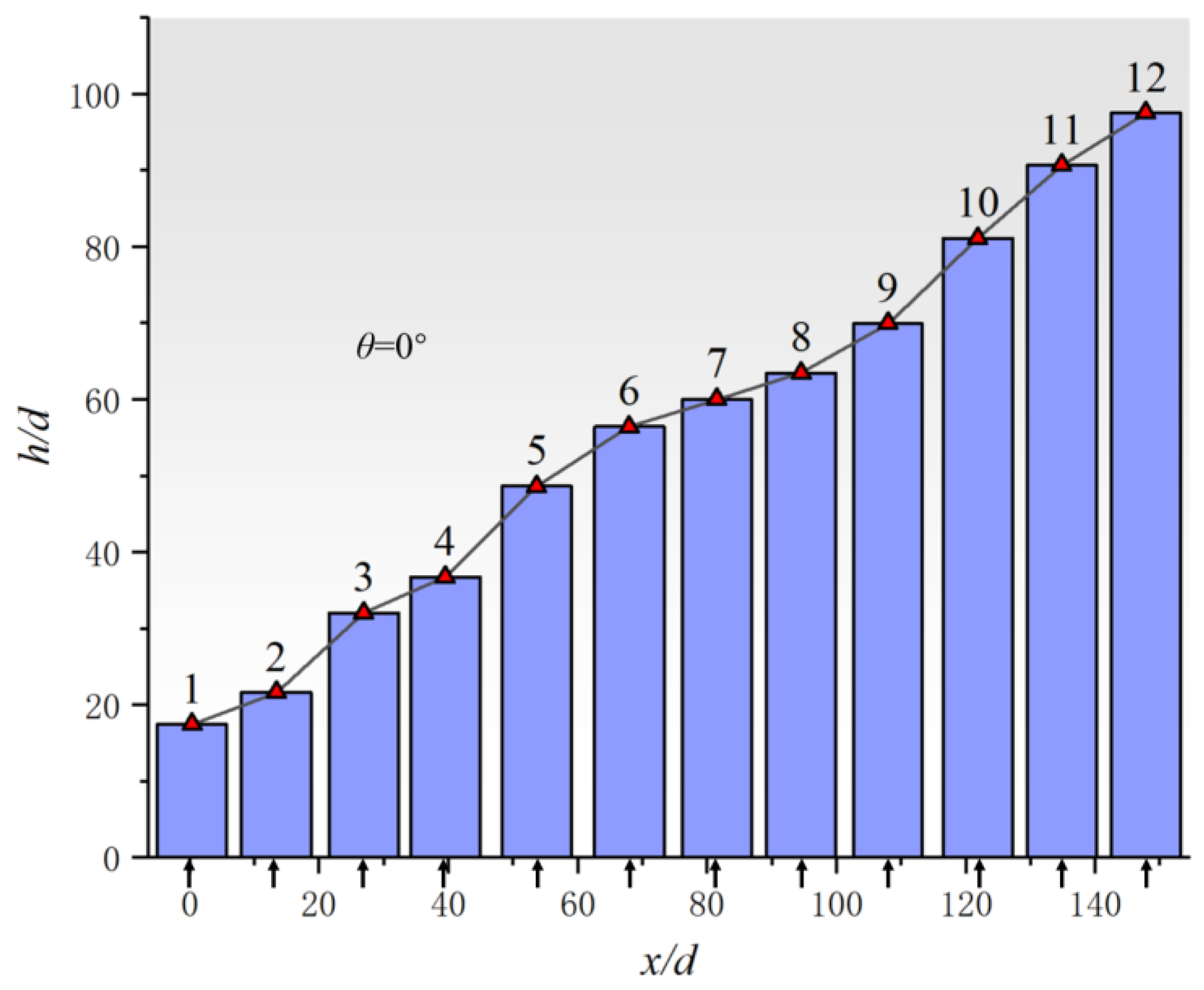

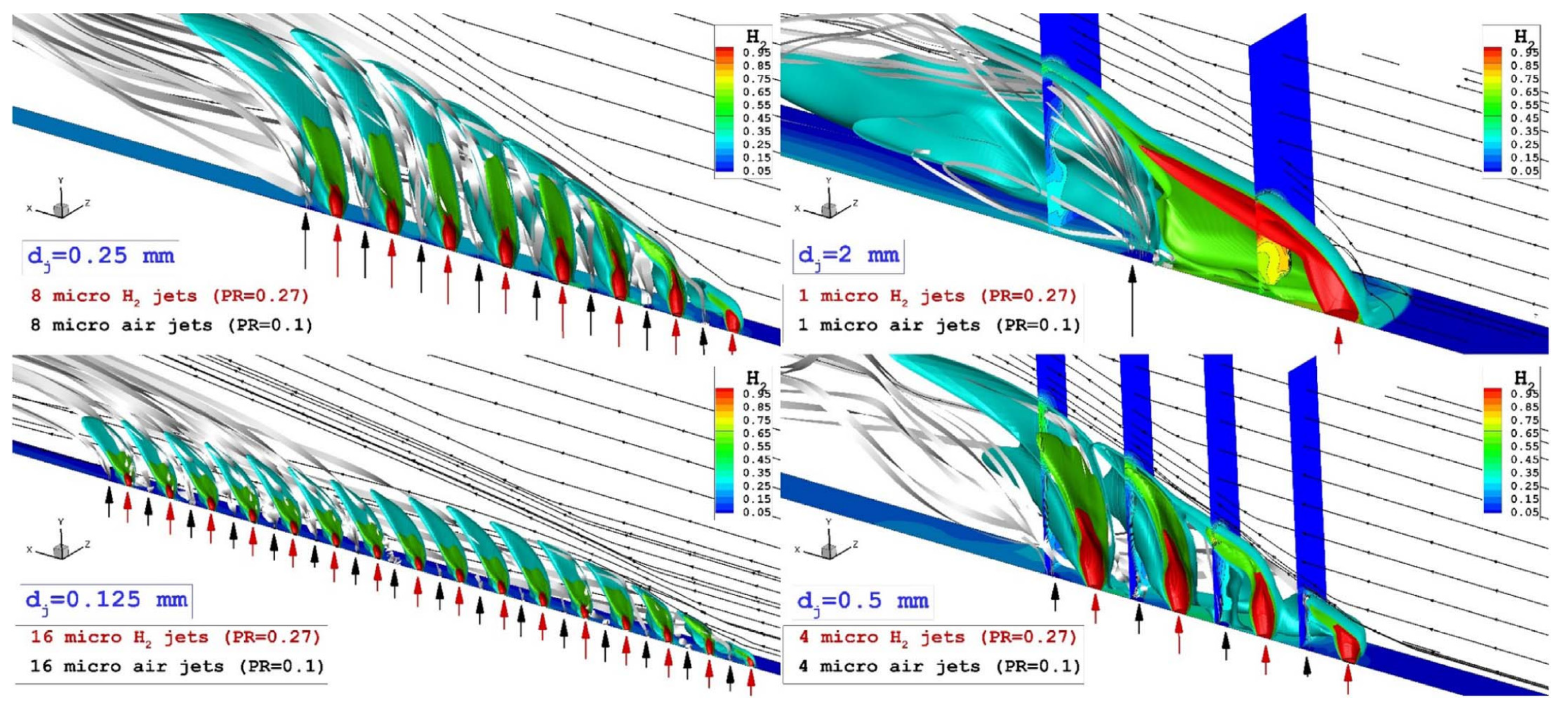
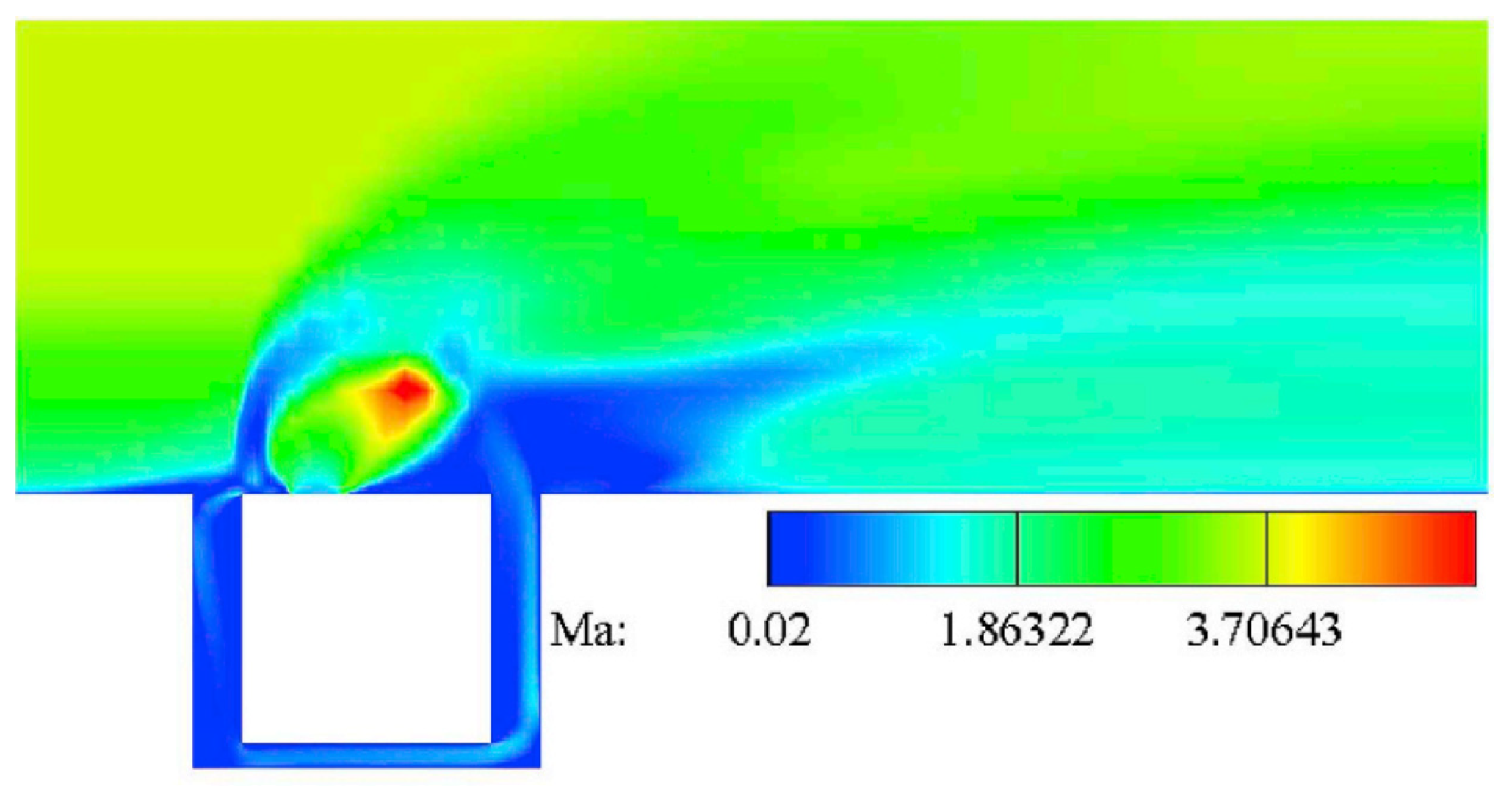
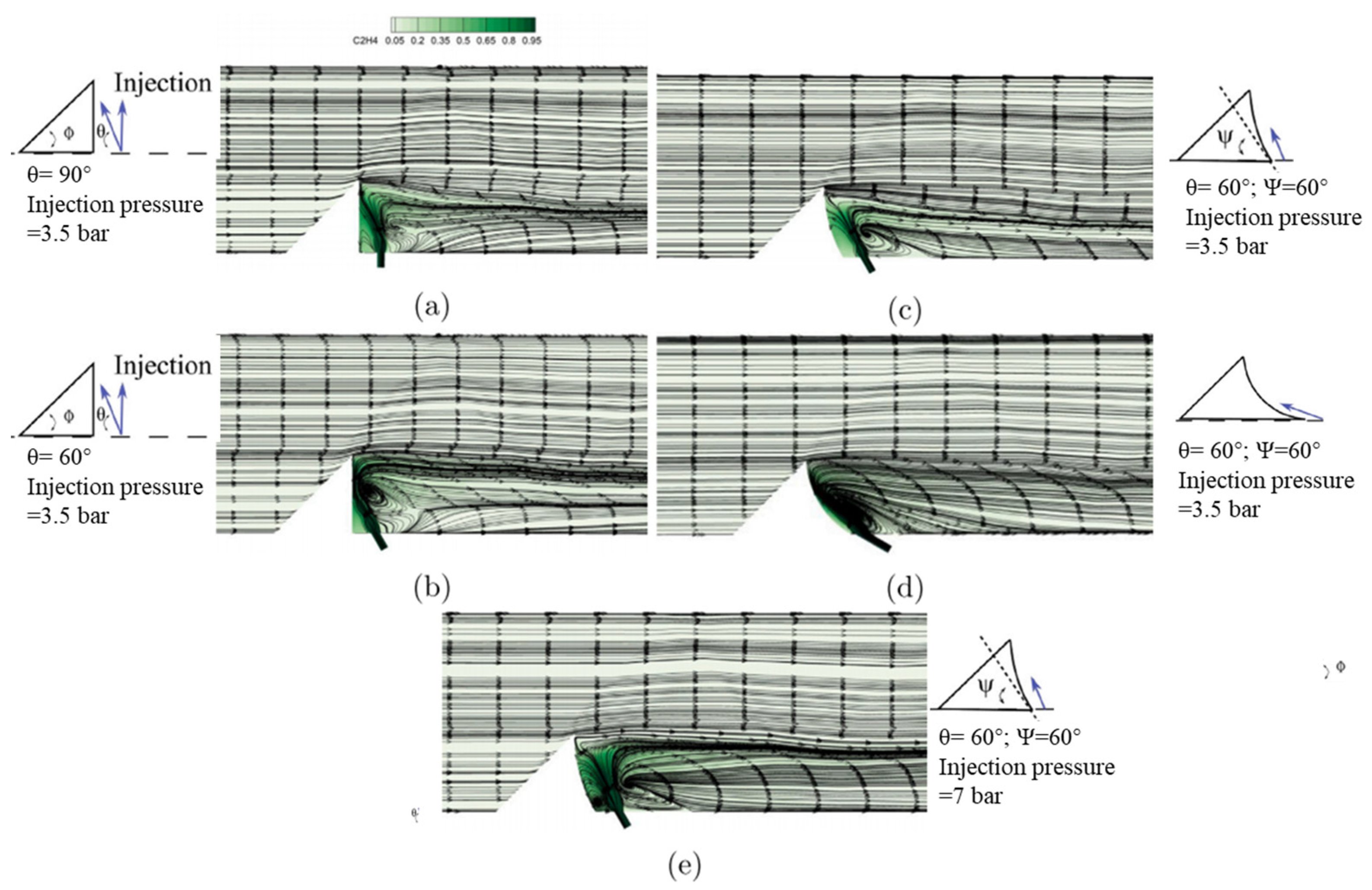


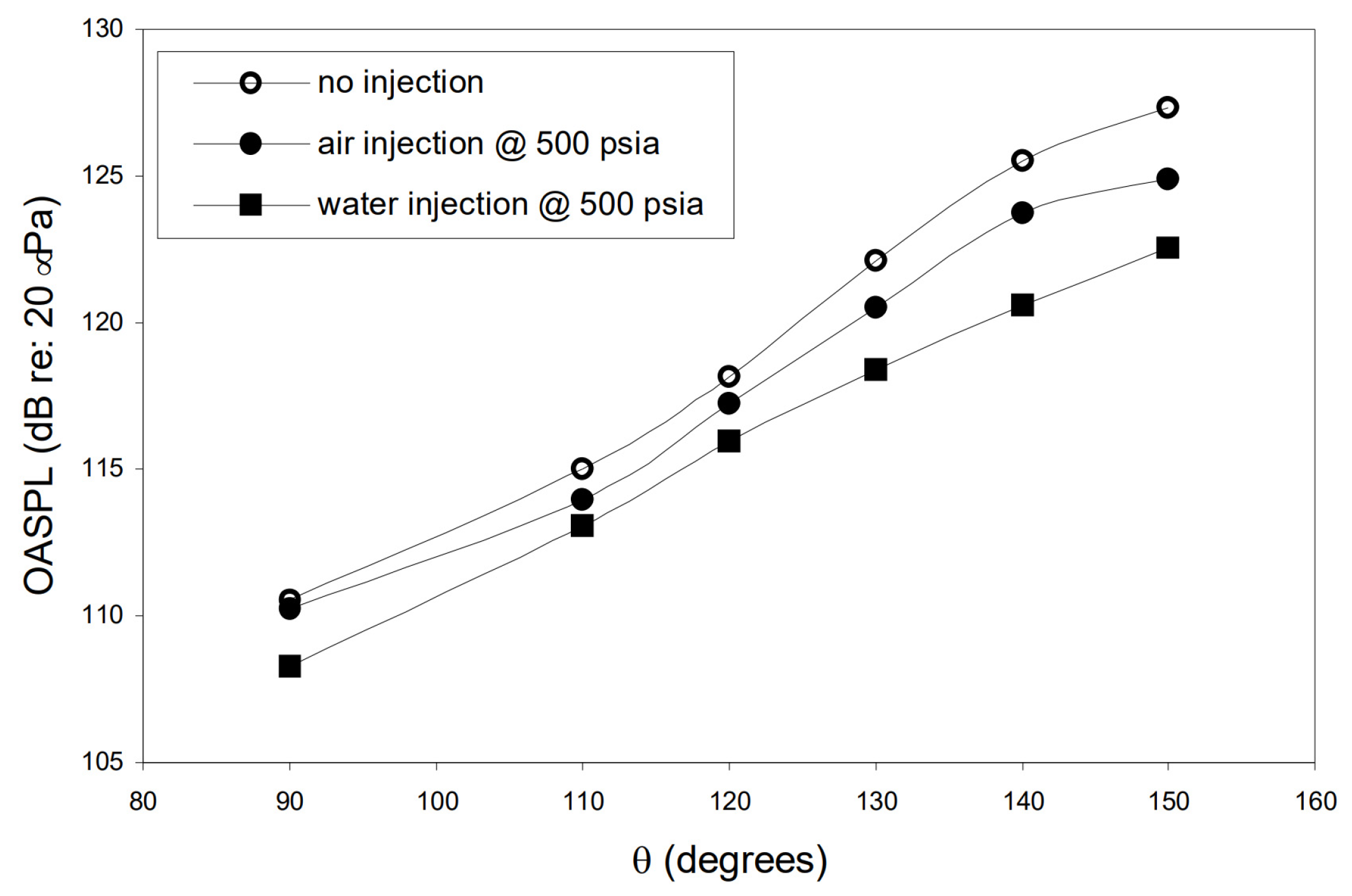
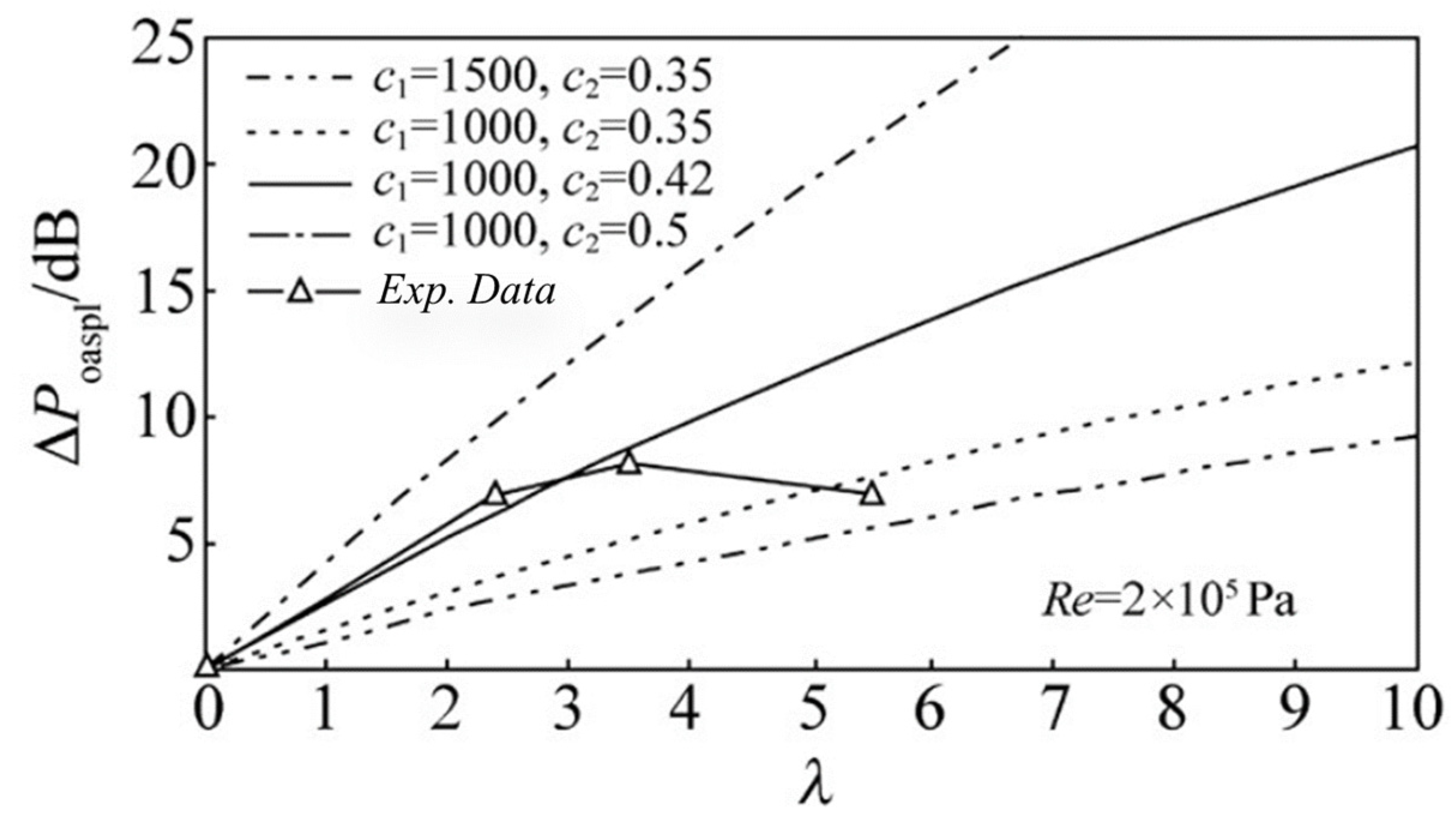
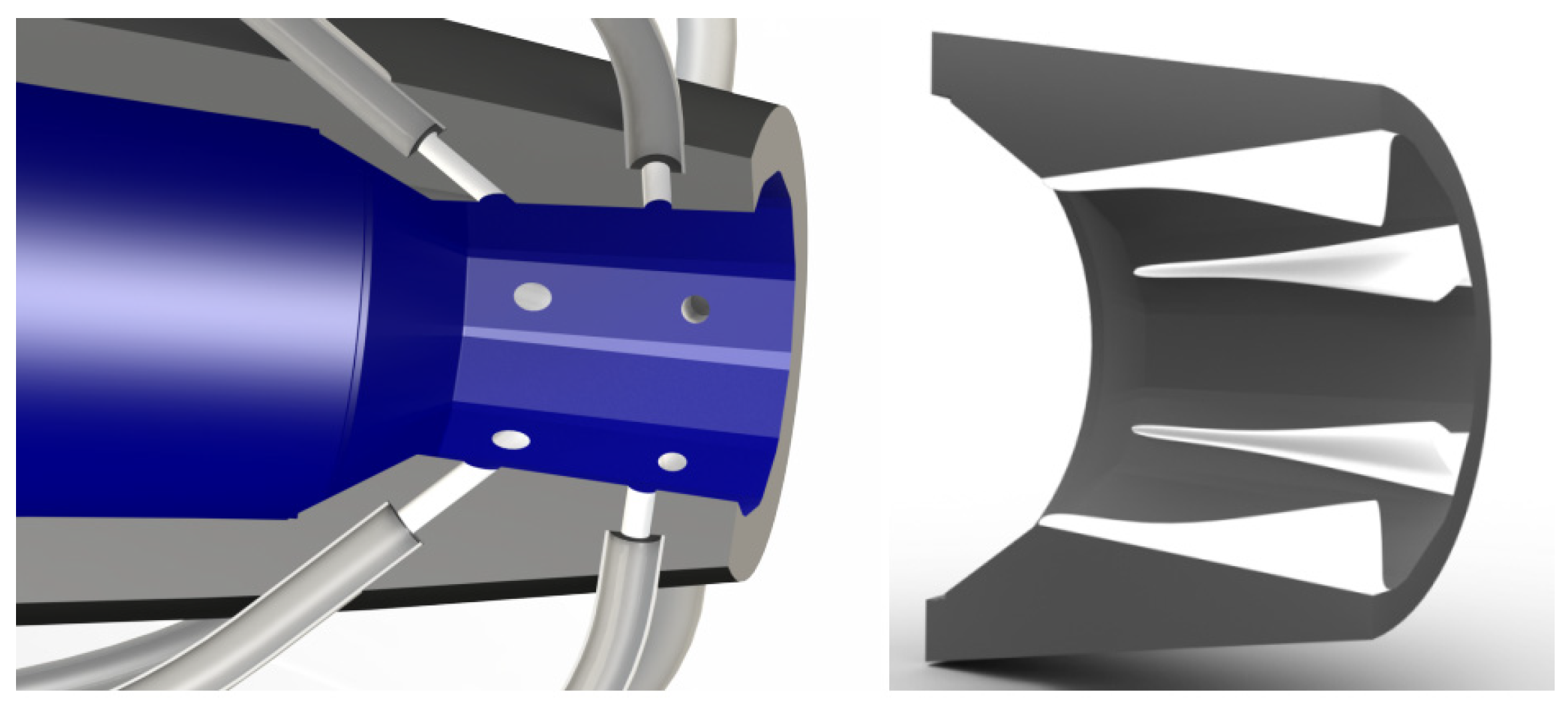
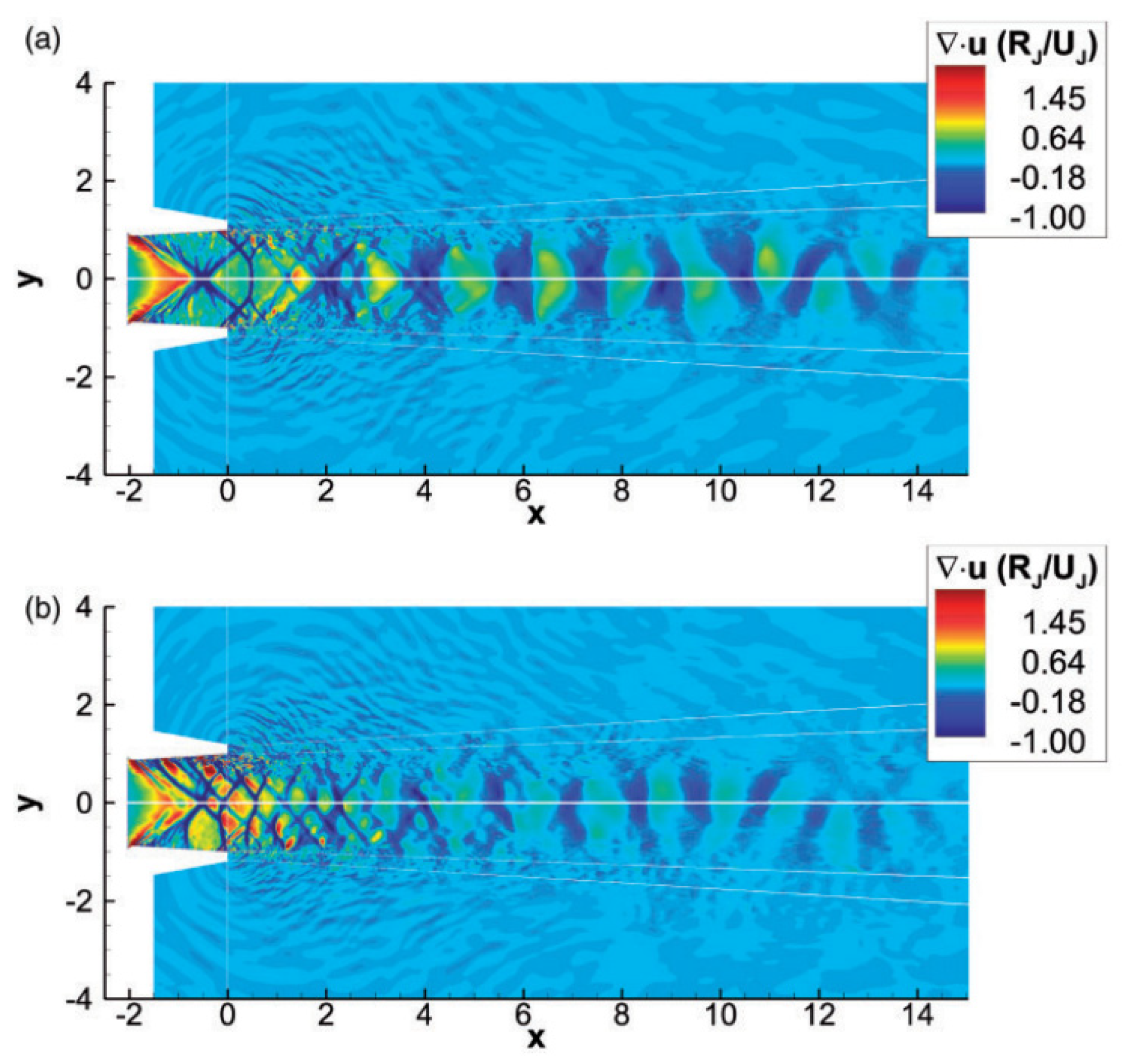


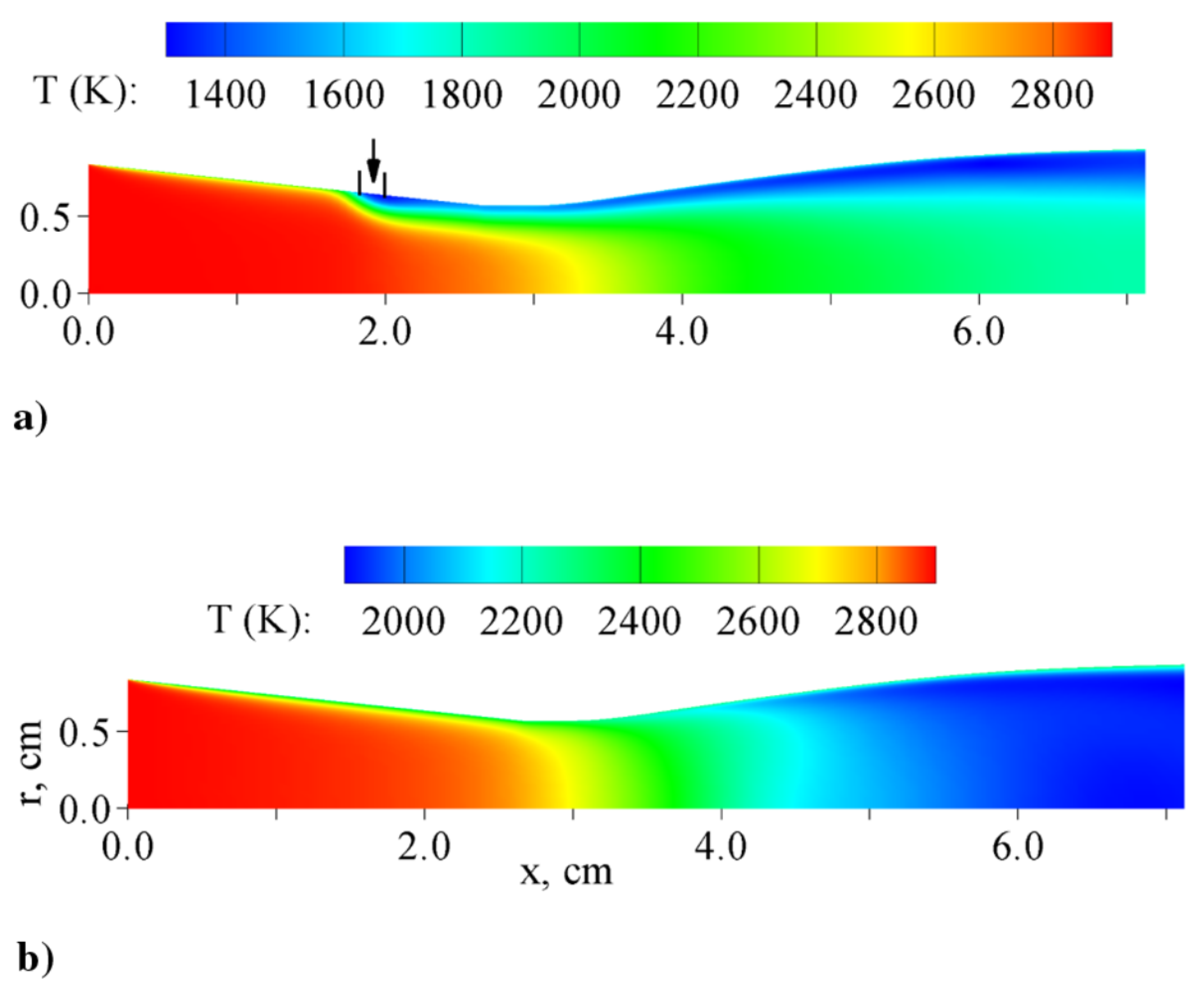


| Application | Technology | Applicable Scenarios | Specificities | Prominent Study | Ref. |
|---|---|---|---|---|---|
| Thrust adjustment | Throat injection | Liquid rocket motor | Compared to mechanical mechanisms, it is simpler, lighter, and free from erosion issues; however, achieving a wide range of thrust adjustments requires a large mass flow rate. | First proposed concept. | [46] |
| Improved theoretical models and researched detailed parameter. | [47] | ||||
| Low benefits in engineering applications were found. | [52] | ||||
| Throat injection | Solid rocket motor | It enables solid rocket engines to have thrust adjustment capability, but the achievable range of thrust conditions is not wide. | Attempted application in solid rocket engines. | [48] | |
| Identify the impact laws of multiple parameters on thrust modulation. | [51] | ||||
| Introduction of the theoretical formula for vertical jetting. | [4] | ||||
| Pulse jets | Rocket motor | Compared to steady jet, it has better thrust adjustment characteristics at the same mass flow rate, but the variation is not significant. However, the structural weight required to generate pulses may offset the benefits of pulse jet propulsion. | First application and research. | [56] | |
| Clarify the influence of each parameter. | [57] | ||||
| Based on quantitative analysis, it was found that the benefits of pulse jetting are relatively small. | [58] | ||||
| Throat injection + pintle | Solid rocket motor | It is easier to achieve throat area control and thrust modulation, while the erosion problem of the structure is not severe. However, it can lead to a more complex engine configuration. | First proposed concept. | [64] | |
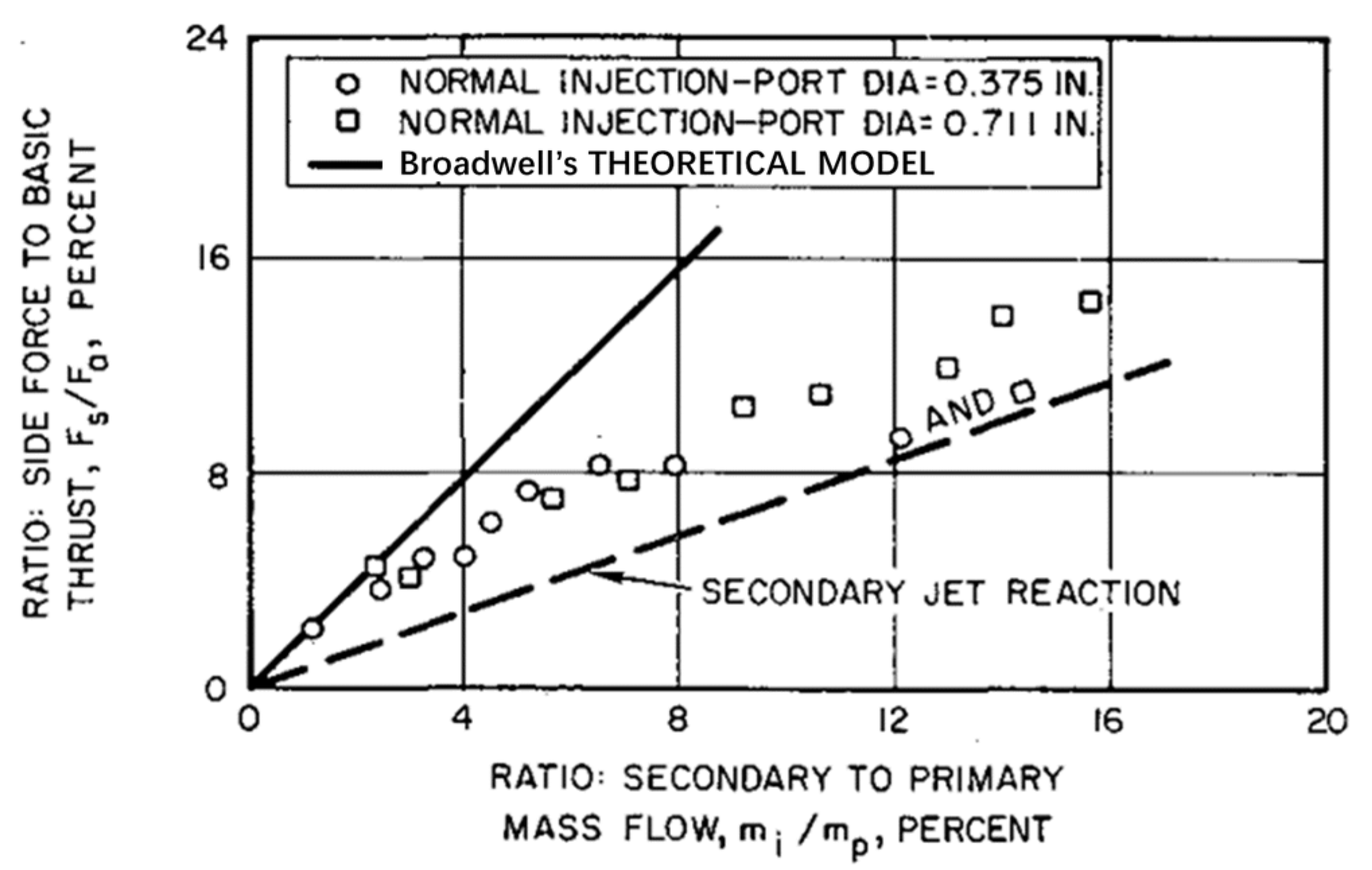
| Thrust vector | Shock vector control | Aeroengines/rocket motors | Compared to mechanical thrust vectoring schemes, it has a simpler structure and lighter weight, but it is difficult to achieve large vector angles. | Proposed calculation formula for lateral force caused by secondary flow. | [11] |
| Applied to solid rocket booster systems and found that the actual performance is unsatisfactory. | [67] | ||||
| Single throat. fluidic throat skewing | Aeroengines/rocket motors | It can achieve larger thrust vector angles than the SVC method but requires an additional set of injection points, making the structure slightly more complex. | First conducted related research. | [68] | |
| Verified the technical feasibility. | [71] | ||||
| Dual throat. fluidic throat skewing | Aeroengines | By changing the nozzle configuration, it is possible to achieve larger vector angles with a smaller secondary flow rate. However, this type of nozzle structure is not suitable for rocket engines. | First proposed the design scheme. | [72] | |
| Successfully completed experimental validation with excellent results. | [73] | ||||
| Bypass dual throat. fluidic throat skewing | Aeroengines | Based on DTN technology, it has achieved passive secondary injection without the need for additional gas sources. This results in a lighter structural weight, and the maximum thrust vector angle can exceed other methods (up to 24°). | First proposed concept. | [76] | |
| BDTN technology in actual aircraft flight tests. | [78] | ||||
| Fuel mixing in a scramjet engine | Multi-portholes fuel injection | Scramjet | It has a simple structure and significantly improves the mixing efficiency compared to single-hole injection. | Introduction of the theoretical model for single-hole injection. | [10] |
| Study on longitudinal row strategy of multi-portholes. | [89] | ||||
| Allocating some injection holes for air and implementing fuel-air staged injection. | [92] | ||||
| Pulse jets | Scramjet | It can achieve better mixing efficiency when the injection hole layout is the same. However, the related mechanisms are still under investigation. | Discovered the significant impact of pulse jetting on penetration depth. | [55] | |
| Detailed analysis of the flow field of pulse jetting. | [99] | ||||
| Determination of the optimal pulse frequency. | [100] | ||||
| Powder fuel jet | Solid rocket scramjet | Key technology for solid rocket ramjet engines, the flow field structure is extremely complex, and the current simulation and computational research is still not fully developed. | Described the distribution of different-sized particles in the jet vortices. | [104] | |
| Jet noise control | Jet at nozzle exit | Aeroengines/rocket motors | Compared to methods such as modifying nozzle structure, it has higher nozzle efficiency, but achieving the desired noise reduction effect typically requires a larger flow rate. | First proposed concept. | [110] |
| Low mass flow rate jet noise reduction. | [117] | ||||
| Experimental testing of microjet noise reduction on the F404-GE-402 jet engine. | [124] | ||||
| Fluid insert nozzle | Aeroengines/rocket motors | It is possible to achieve good noise reduction effects with a lower flow rate. However, the related flow field mechanisms are still not clear. | First proposed concept. | [127] | |
| Flow field analysis of noise reduction using a fluid insert nozzle. | [136] | ||||
| Research on noise reduction mechanisms based on LES method. | [137] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Guo, H.; Sun, J.; Tian, H.; Cai, G. Research Progress on Active Secondary Jet Technology in Supersonic Flow Field of Aerospace Propulsion Systems. Fluids 2023, 8, 313. https://doi.org/10.3390/fluids8120313
Zhu H, Guo H, Sun J, Tian H, Cai G. Research Progress on Active Secondary Jet Technology in Supersonic Flow Field of Aerospace Propulsion Systems. Fluids. 2023; 8(12):313. https://doi.org/10.3390/fluids8120313
Chicago/Turabian StyleZhu, Hao, Haizhou Guo, Junjie Sun, Hui Tian, and Guobiao Cai. 2023. "Research Progress on Active Secondary Jet Technology in Supersonic Flow Field of Aerospace Propulsion Systems" Fluids 8, no. 12: 313. https://doi.org/10.3390/fluids8120313
APA StyleZhu, H., Guo, H., Sun, J., Tian, H., & Cai, G. (2023). Research Progress on Active Secondary Jet Technology in Supersonic Flow Field of Aerospace Propulsion Systems. Fluids, 8(12), 313. https://doi.org/10.3390/fluids8120313