Numerical Analysis of Multi-Particulate Flow Behaviour in CFB Riser Coupled with a Kinetic Theory
Abstract
:1. Introduction
2. Mathematical Model
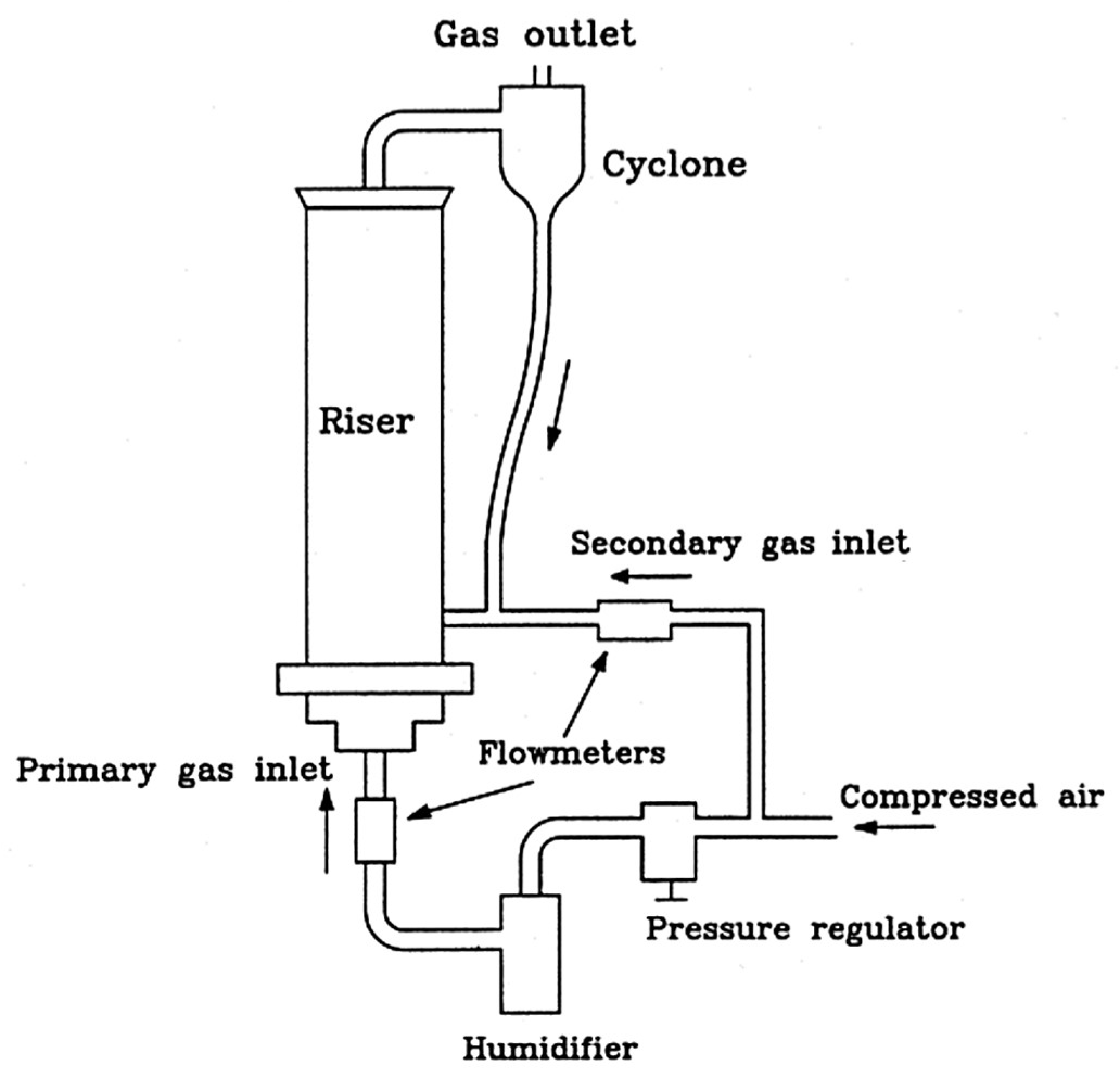
3. The CFB System
4. Grid and Physical Domain
5. Boundary and Initial Conditions
6. Results and Discussion
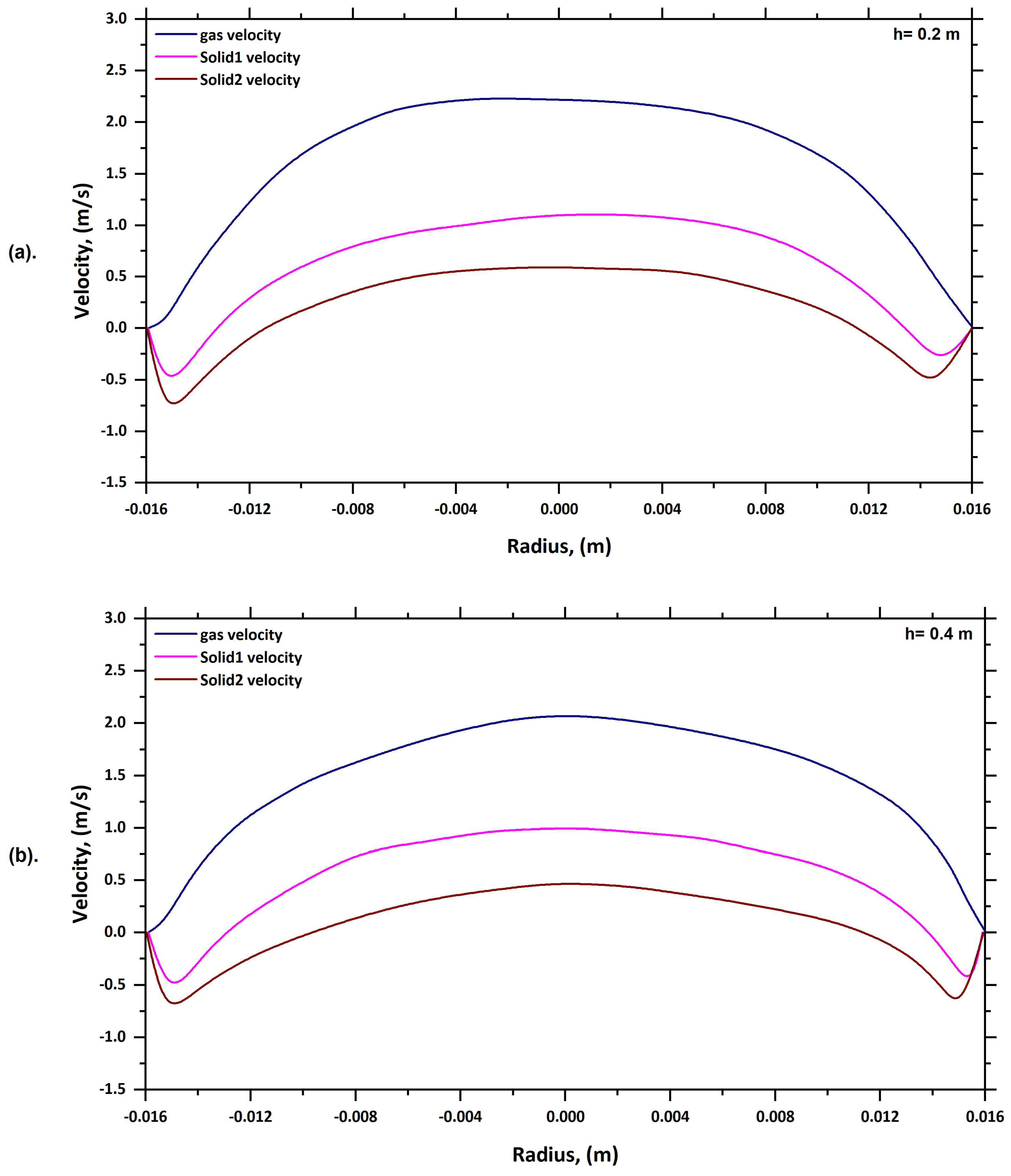
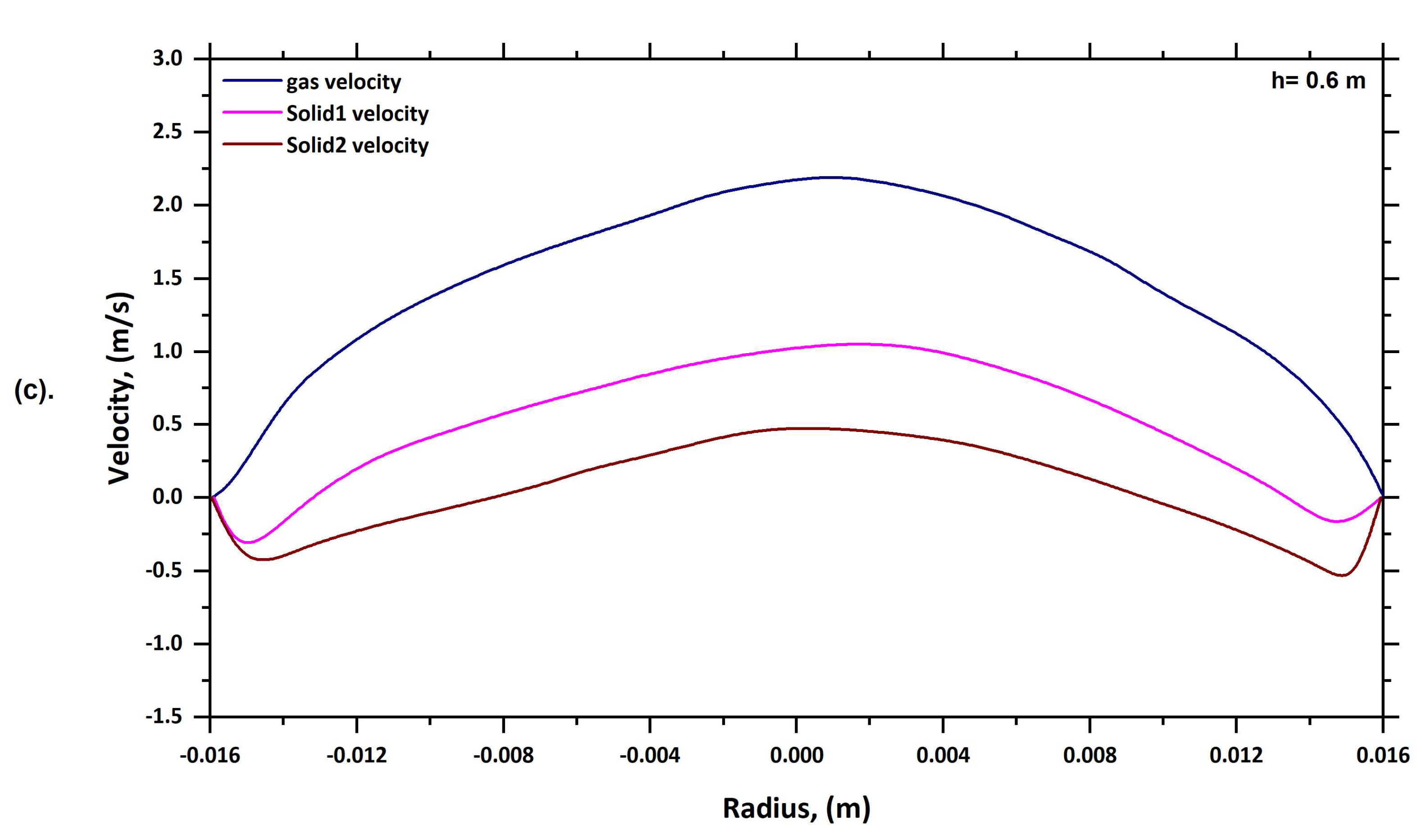
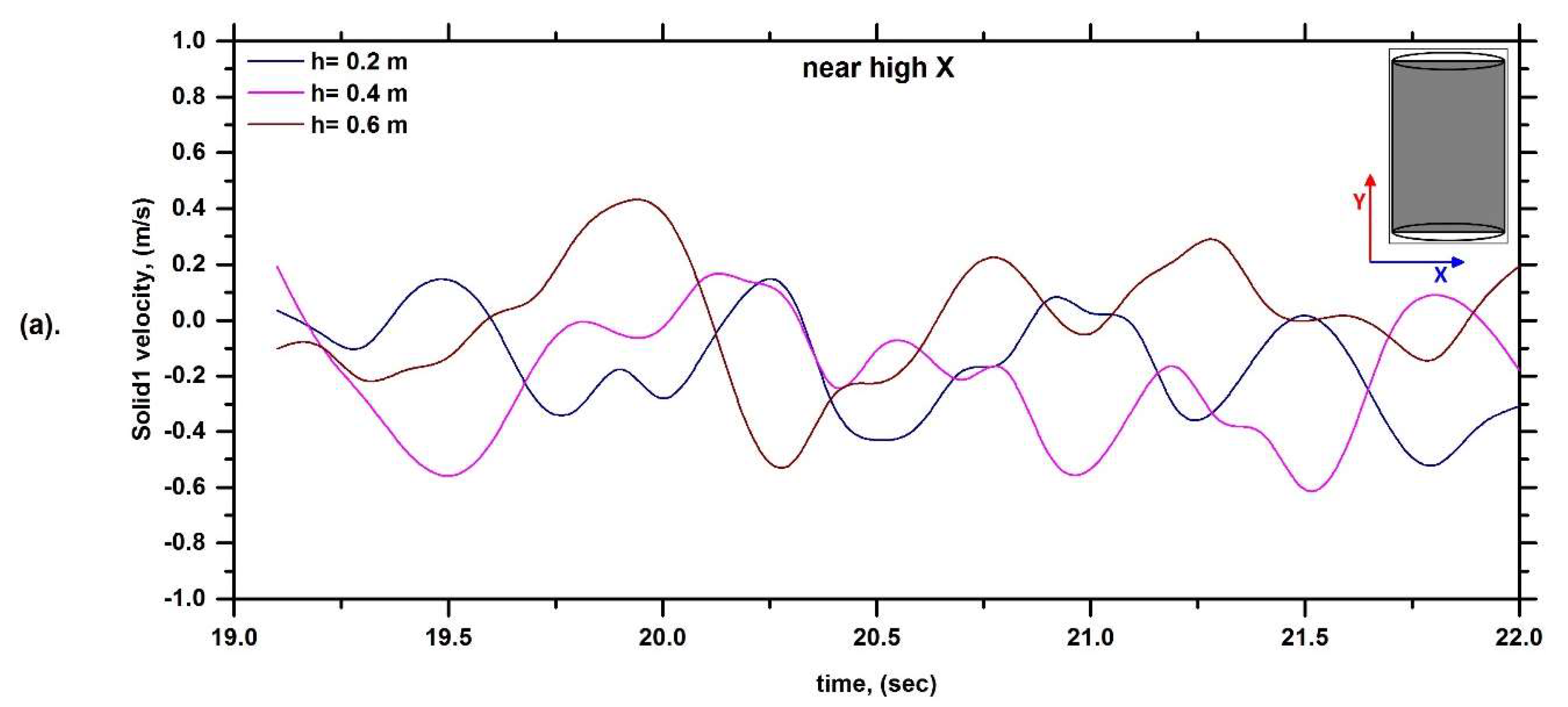
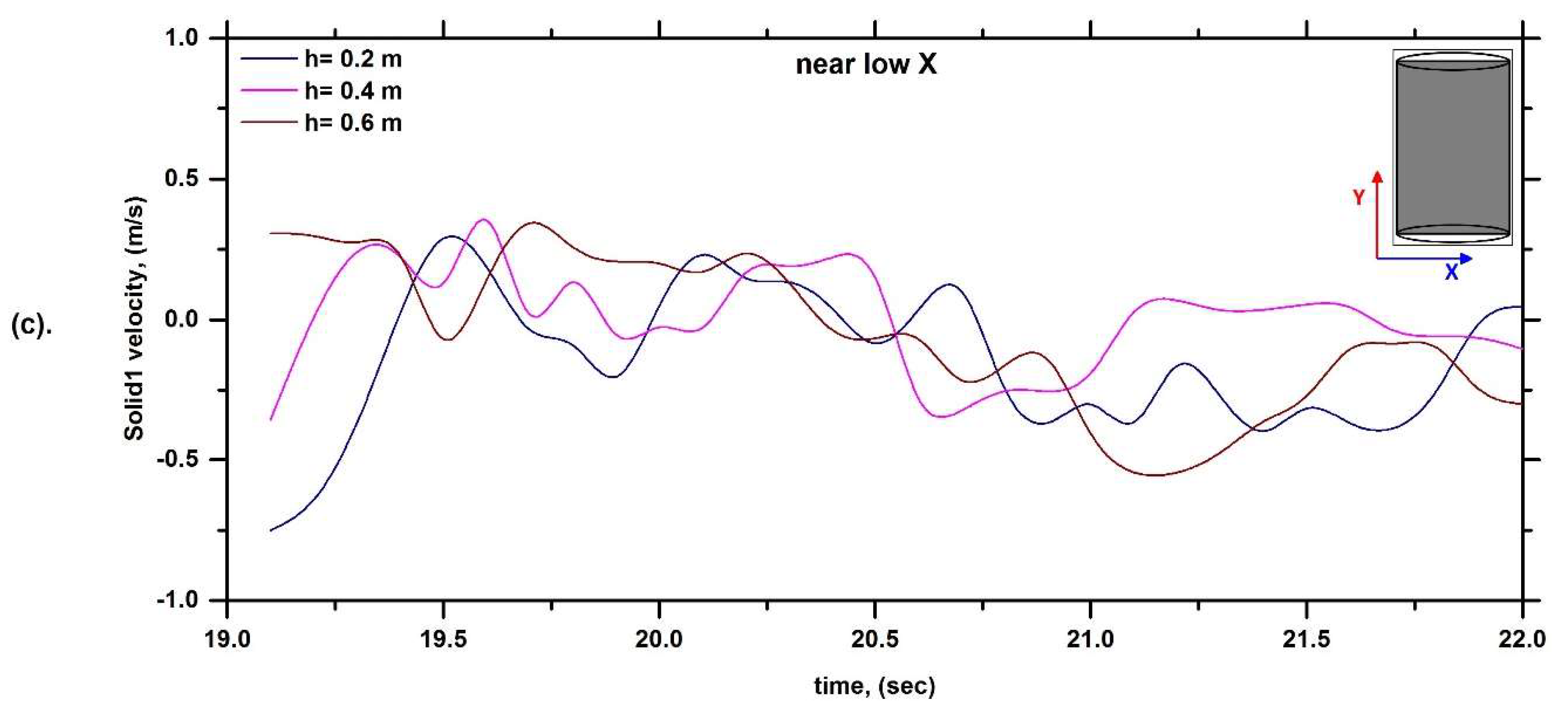
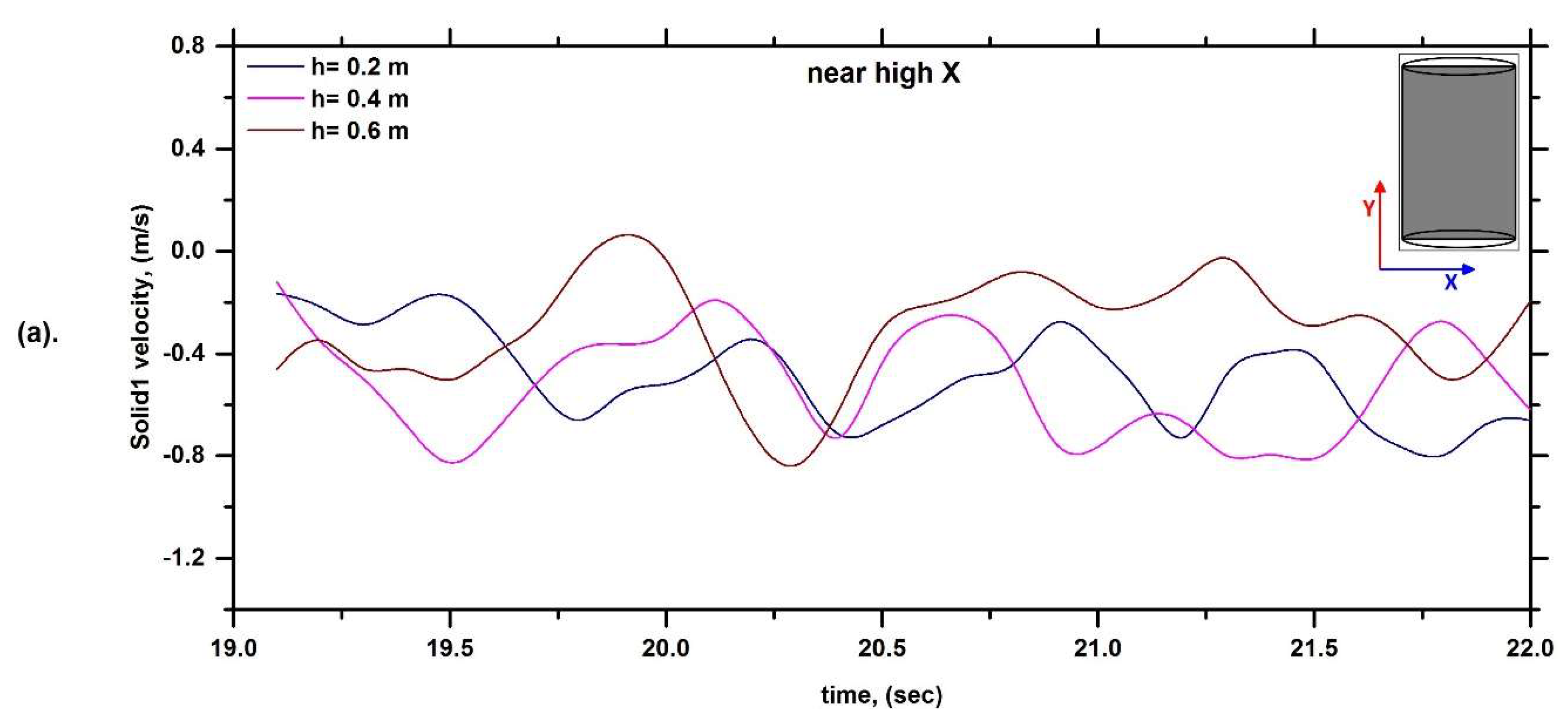
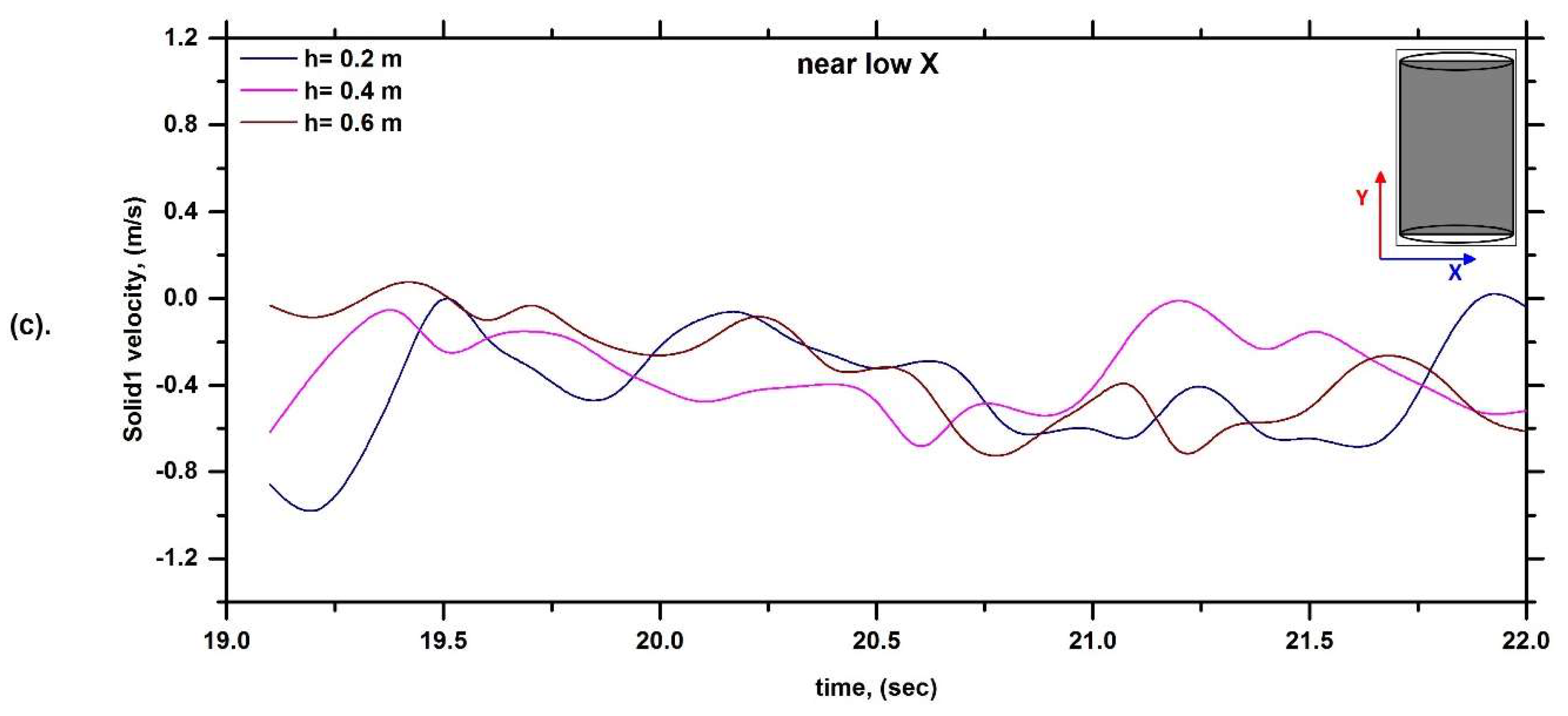
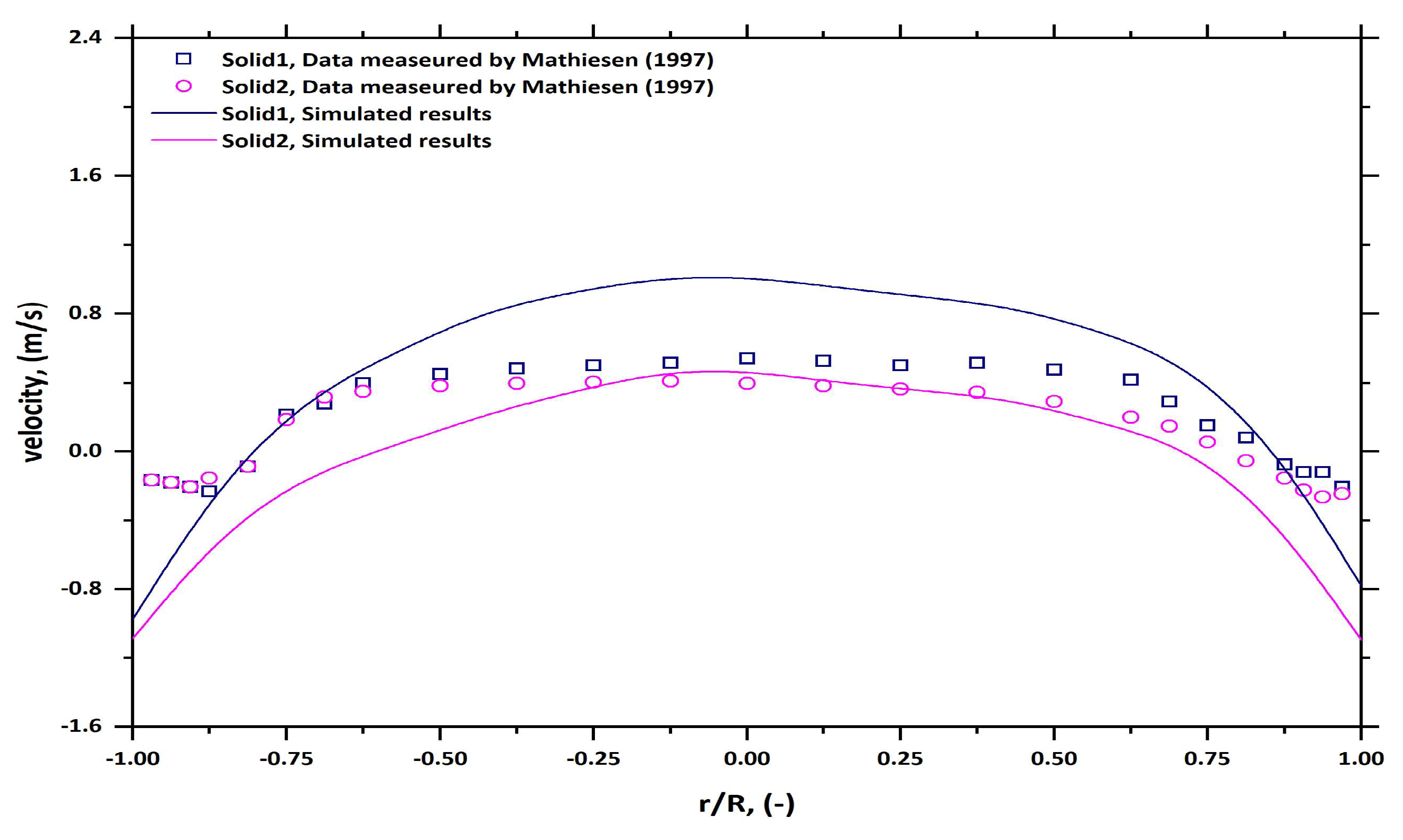
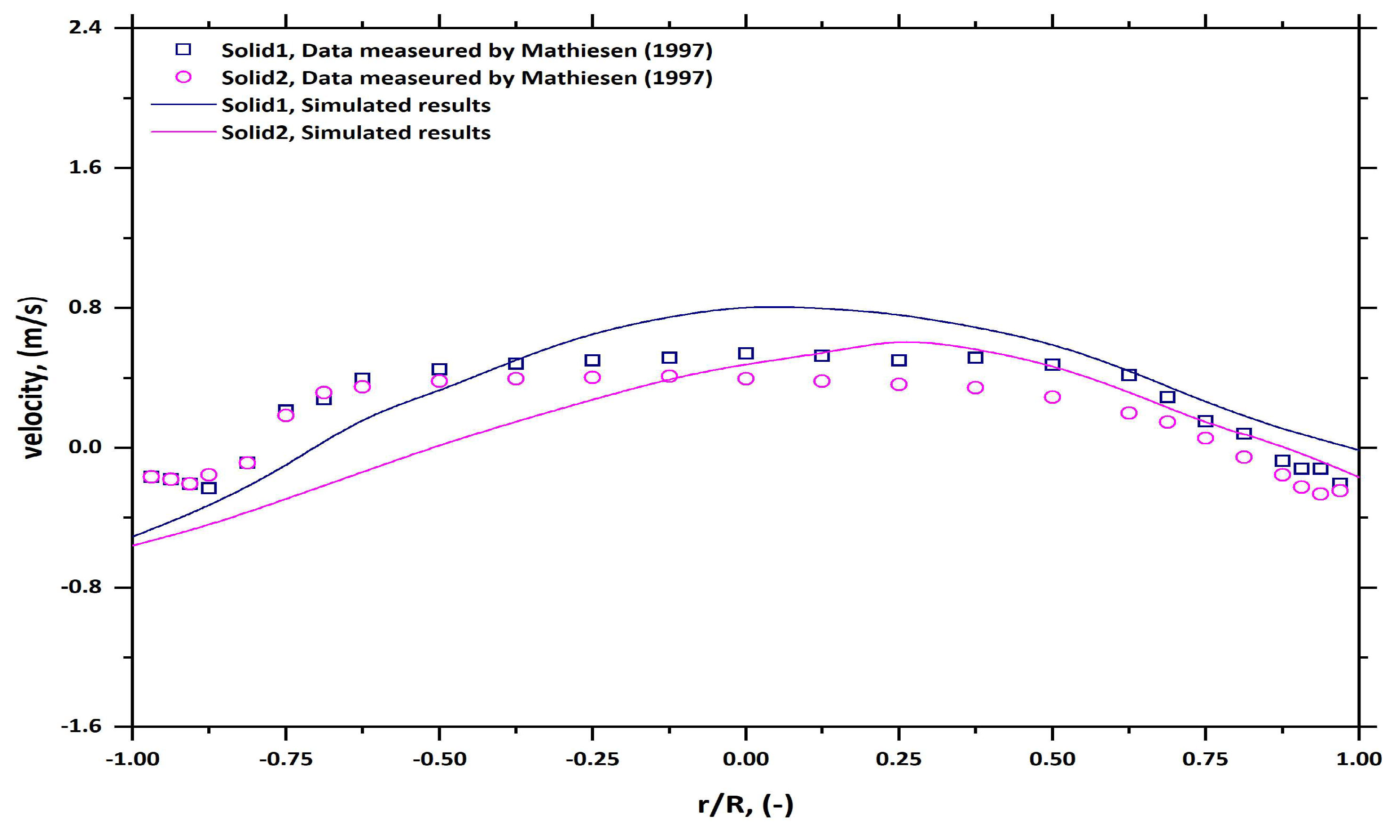
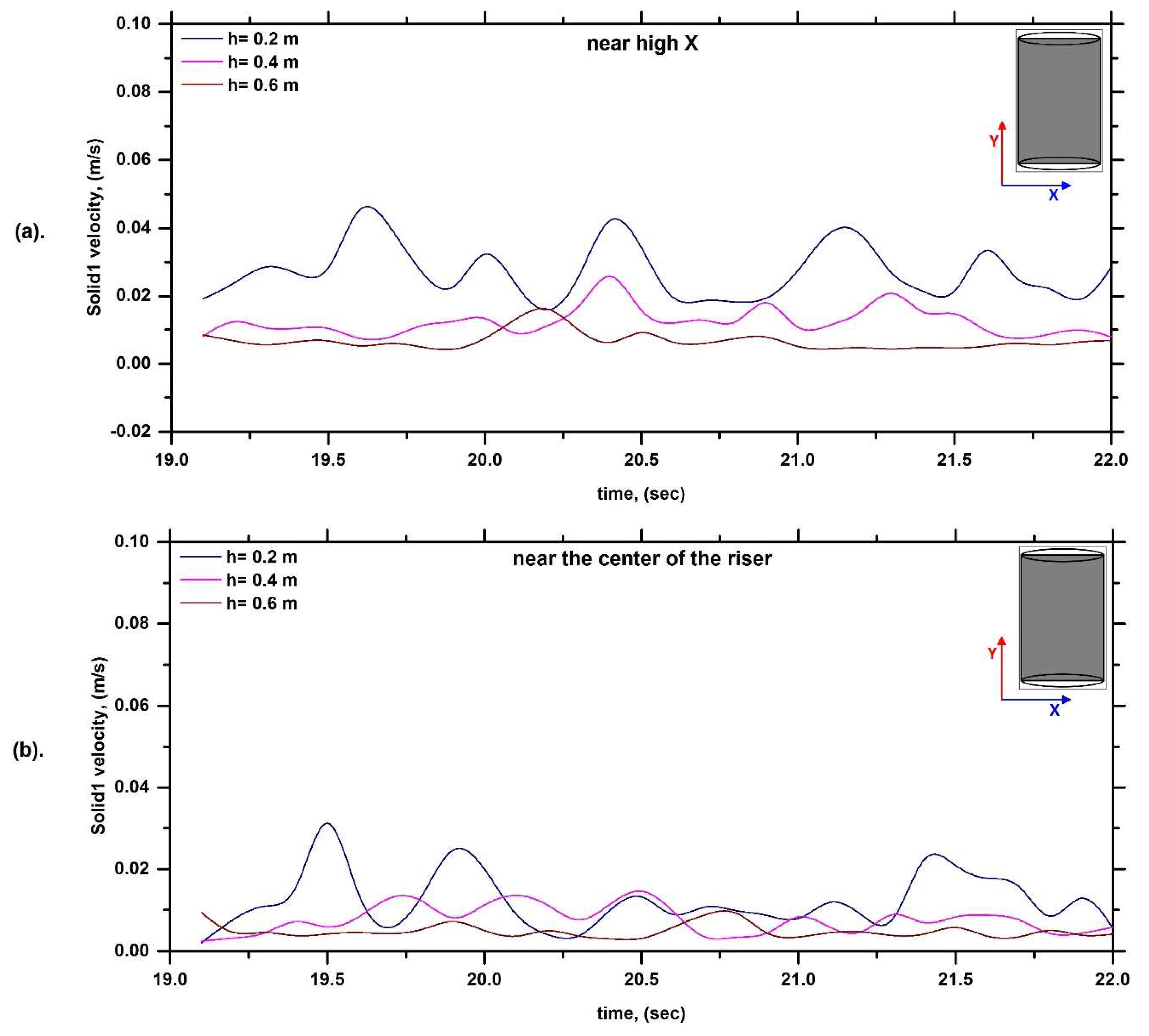
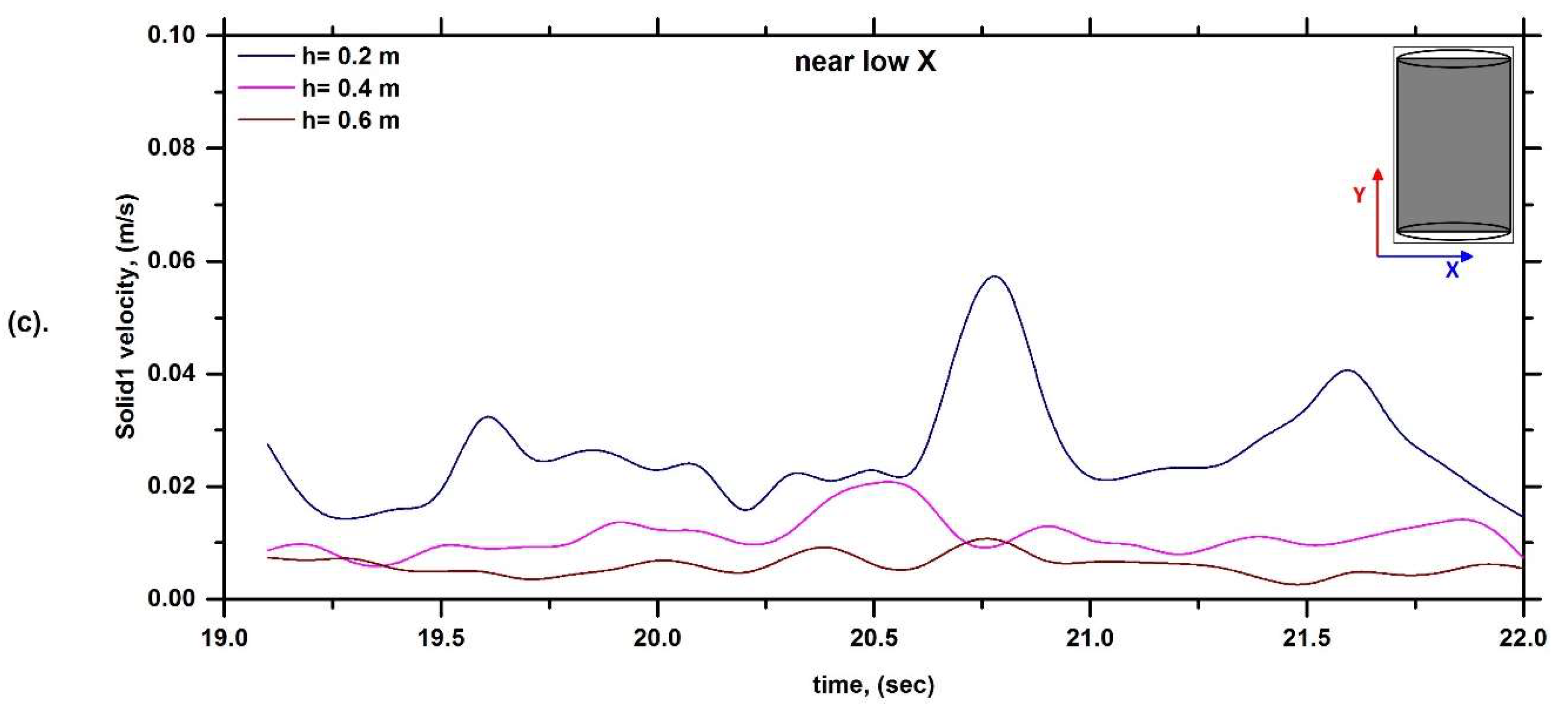
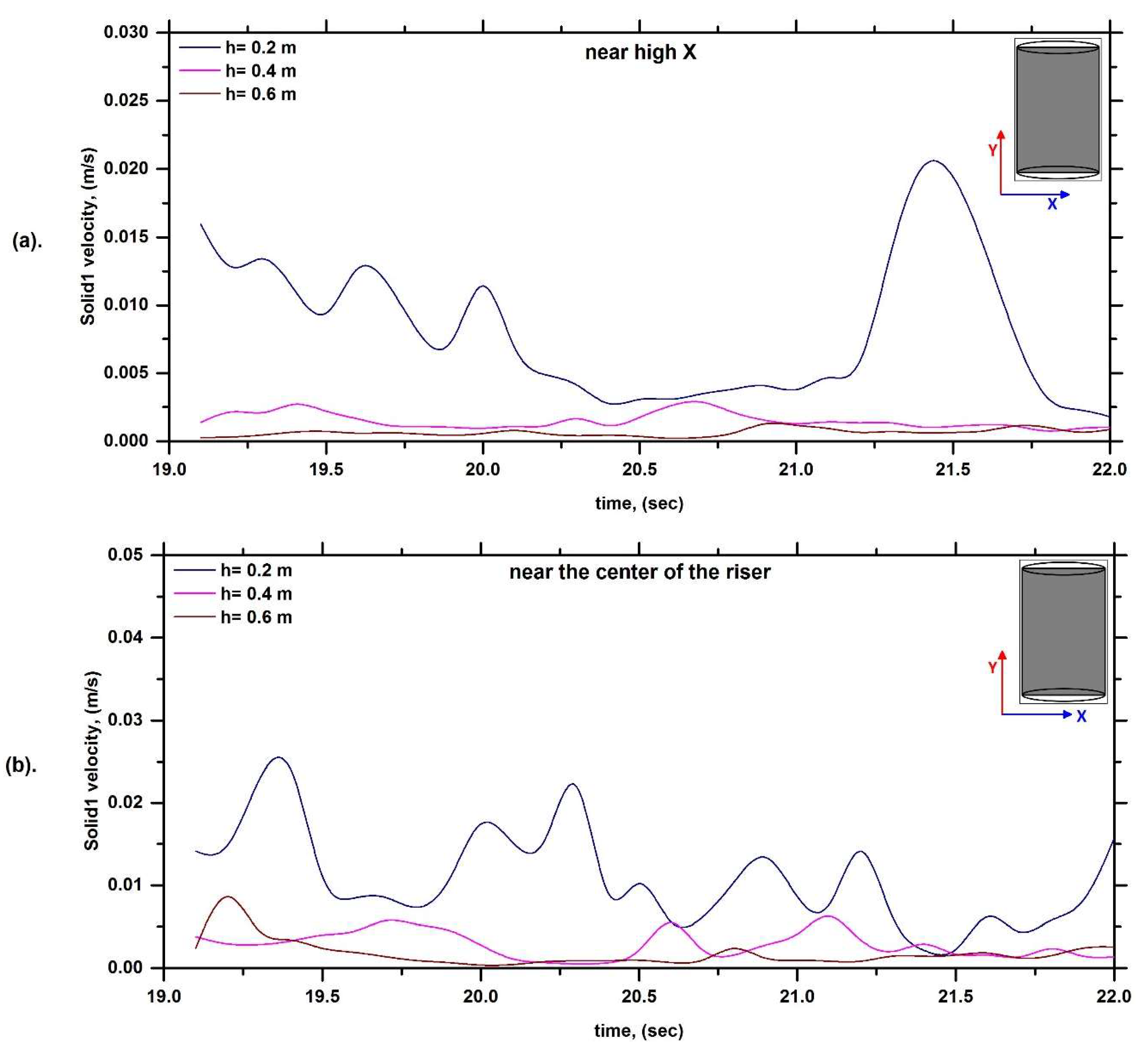
6.1. Solid Velocity Profile
6.2. Validation of the Numerical Results
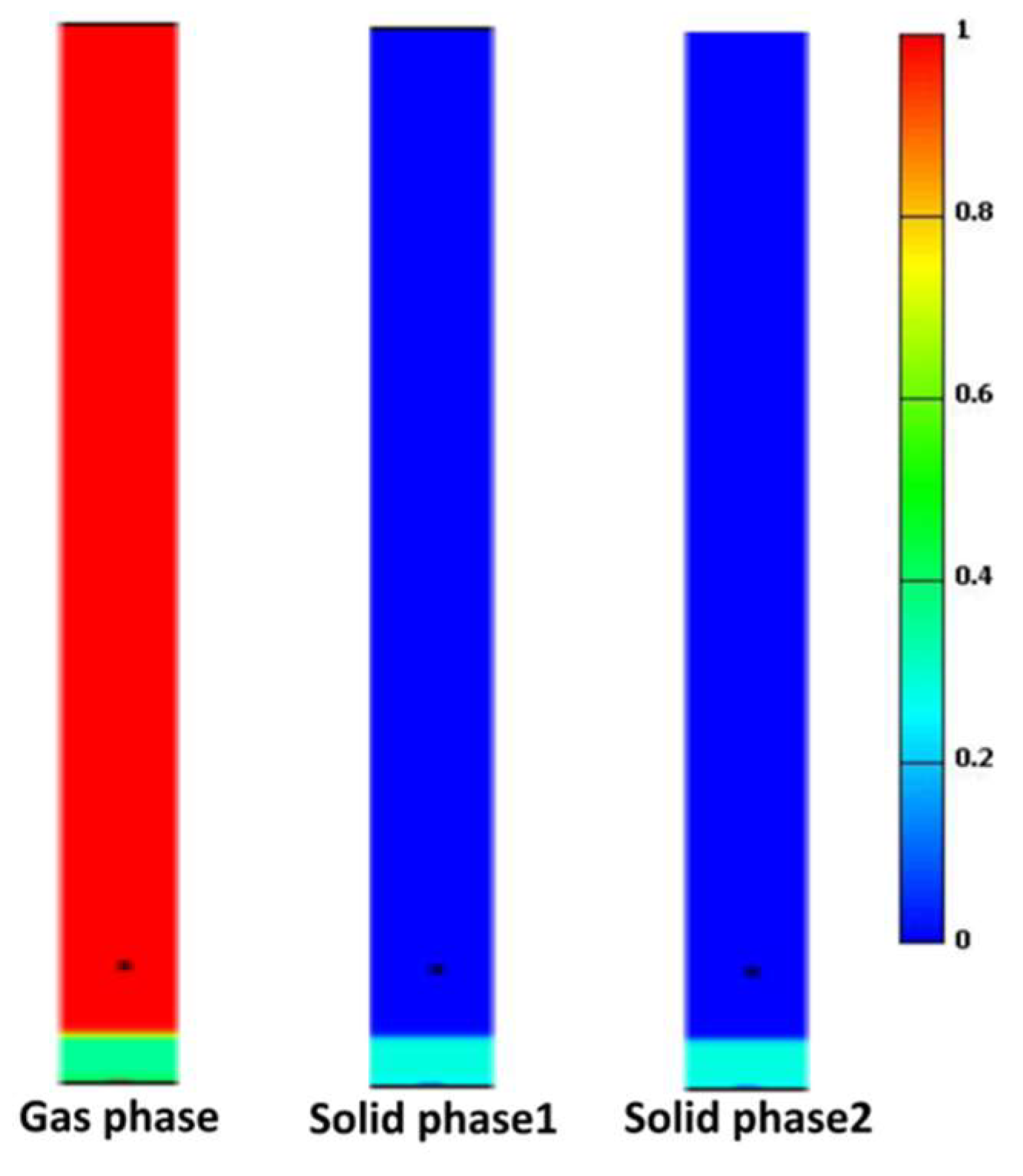
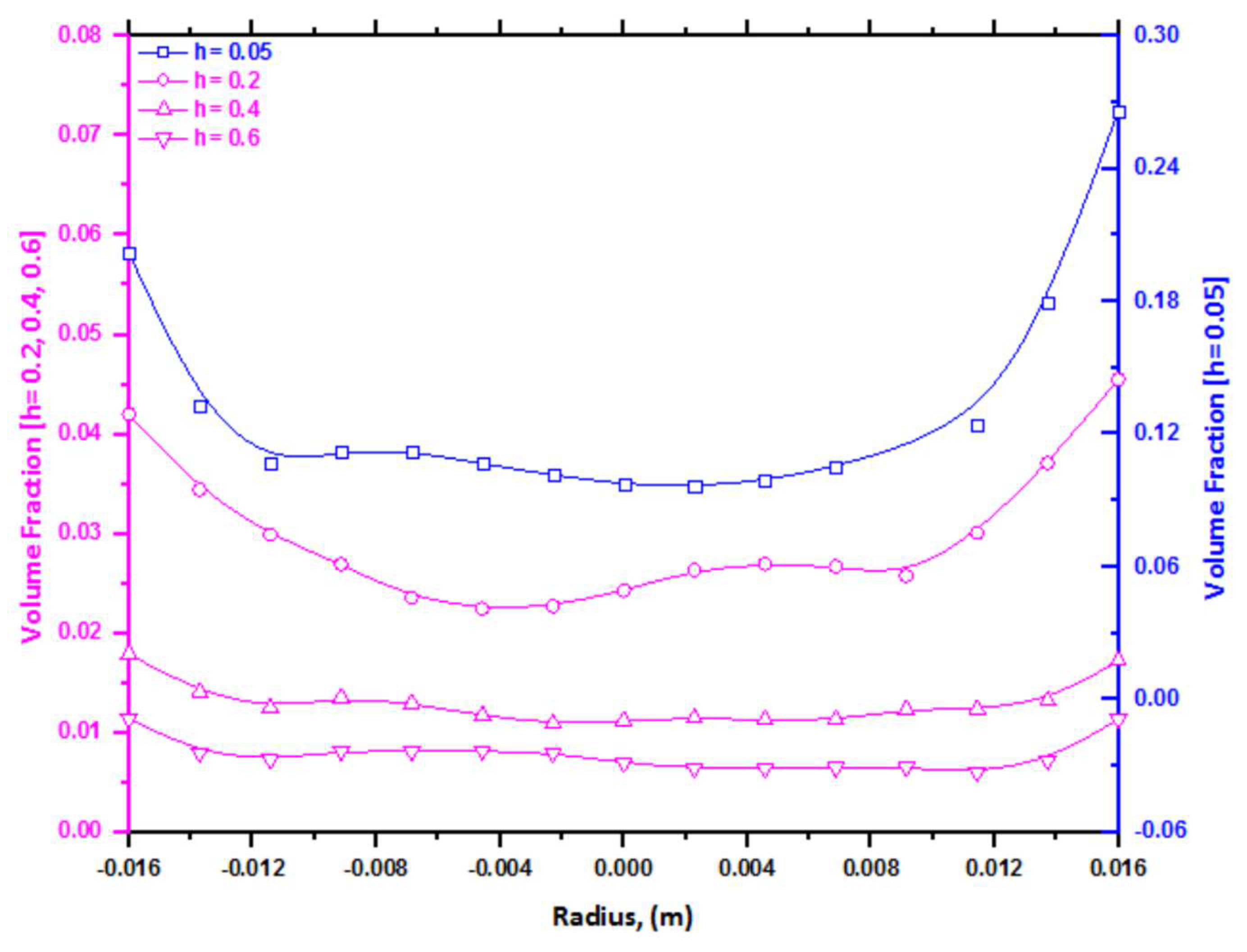
6.3. Volume Fraction Profile
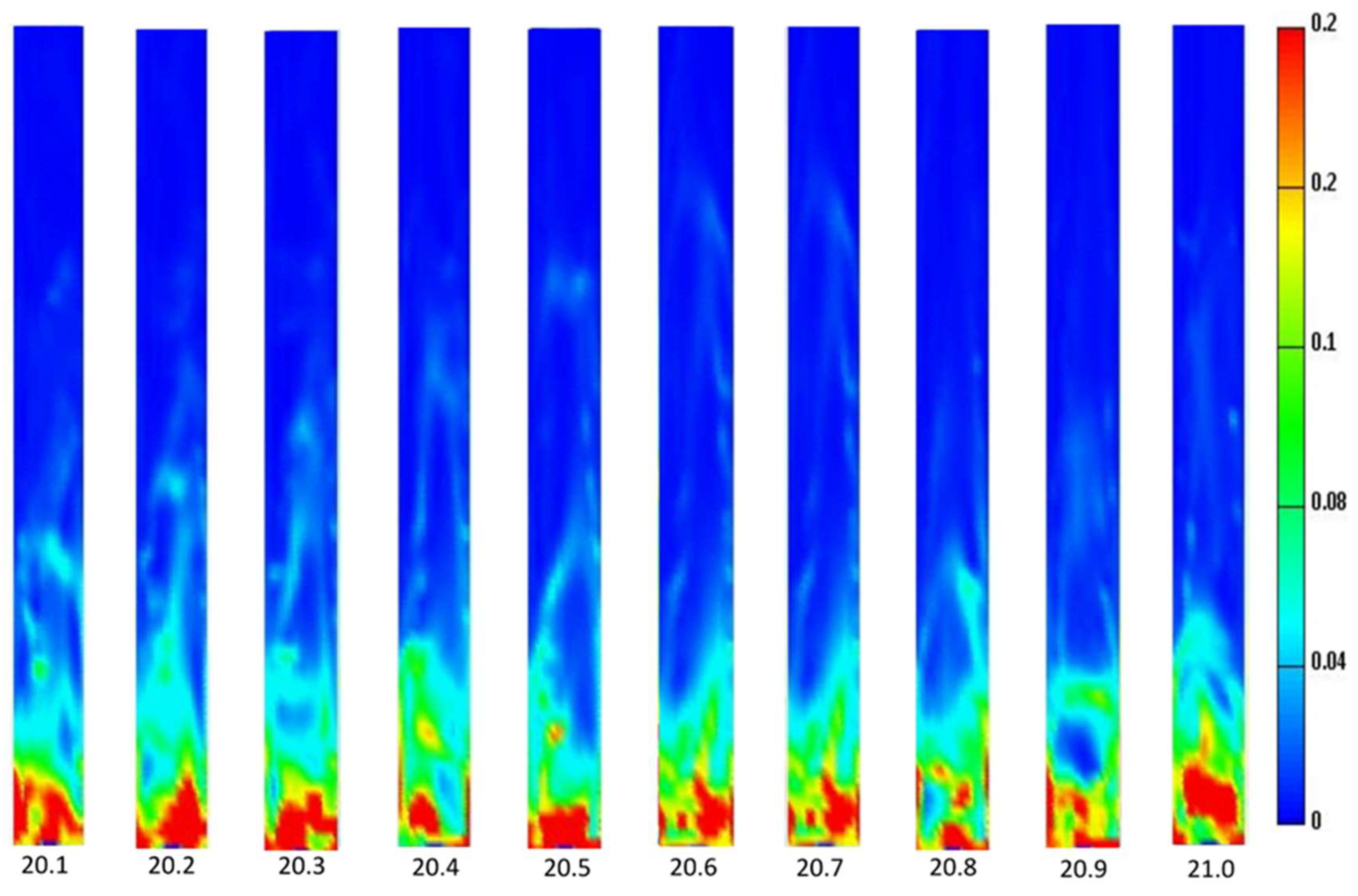
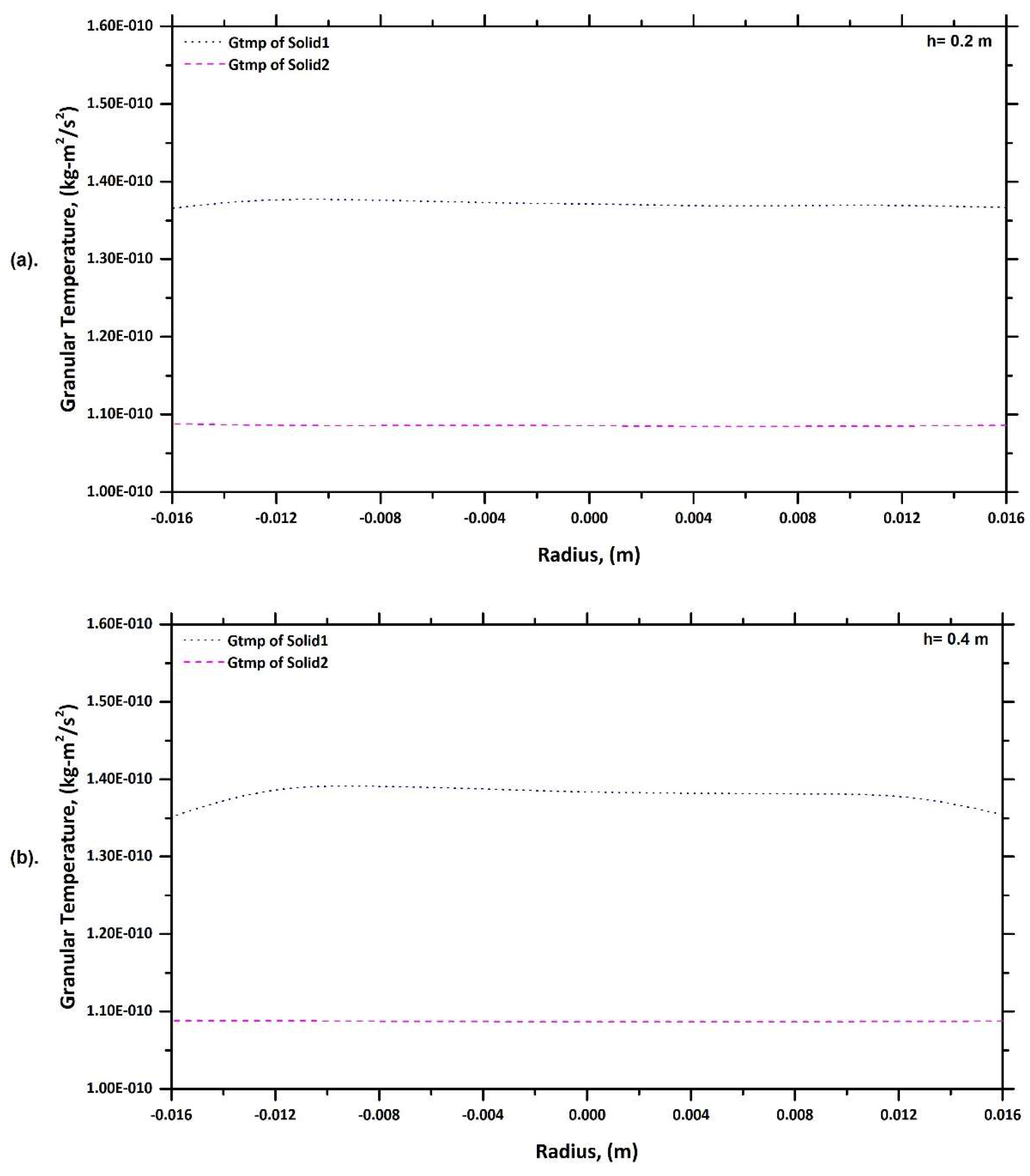
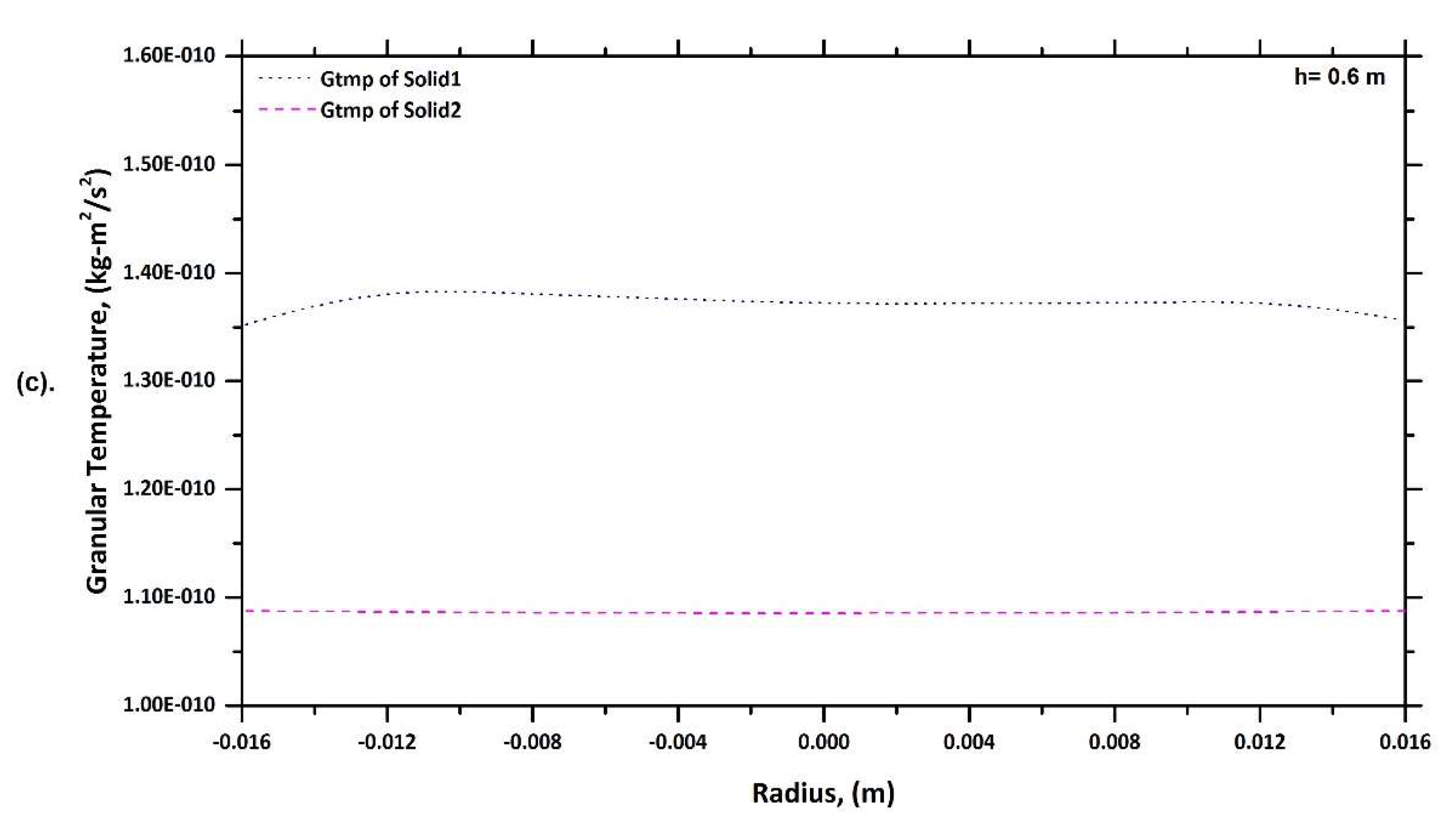
6.4. Granular Temperature Profile
7. Conclusions
- Core–annular flow in the riser,
- Particle carryover,
- Cluster formation,
- Downward particle flow near the riser wall,
- Relative velocity between particles of different sizes,
- Different granular temperatures for particles of different sizes,
- A turbulent bed of large diameter particles in the base of the riser and transport of the smaller particles well in the top section of the riser,
- A higher concentration of solids in the wall region compared to the centre.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Particle projected area |
| Cd | Drag coefficient |
| Cg | Fluctuating velocity of gas |
| ci | Instantaneous velocity of particle i |
| cij | Relative velocity |
| cj | Instantaneous velocity of particle j |
| Cp | Fluctuating velocity of particles |
| d | Diameter of particle |
| Dw | West diffusion coefficient |
| e | Restitution coefficient |
| F | Total external force |
| fi | Velocity distribution of phase i |
| fj | Velocity distribution of phase j |
| Fp | Particle drag force |
| G | Combined velocity during collision |
| g | Radial distributive function |
| hw | Distance between west and central nodes |
| I | Unit tensor |
| mi | mass of particle i |
| mj | mass of particle j |
| mk | mass of particle k |
| n | Cell face normal vector |
| N | Number of phases |
| ni | Number of particles in i phase |
| Nij | Number of collisions between i and j particles |
| n | Number of particles |
| P | Particle stress or pressure tensor |
| P | Pressure |
| Pc | Collisional stress tensor |
| Pk | Kinetic stress tensor |
| Pk,i | Kinetic stress tensor of phase i |
| qc | Collisional heat flux |
| qk | Kinetic heat flux |
| r | Position vector |
| Re | Reynolds number |
| ri | Radius of particle i |
| Rij | Summation of the radius (ri + rj) |
| rj | Radius of particle j |
| S | Source term |
| t | Time |
| vi | Hydrodynamic mean velocity of i phase |
| vj | Hydrodynamic mean velocity of j phase |
| Vp | Volume of particle |
| xi | Arbitrary position of particle i. |
| xj | Arbitrary position of particle j. |
| Greek Symbols | |
| η | Kolmogorov length scale |
| θ | Granular temperature (old definition) |
| μs | Solid viscosity |
| μcol,s | Collisional part of solid viscosity |
| μkin,s | Kinetic part of solid viscosity |
| μdil,s | Dilute viscosity |
| ε | Volume fraction |
| ρ | Density |
| τs | Shear stress |
| βgs | Drag coefficient between gas and solid |
| Γ | Diffusion coefficient |
| ω | Angular velocity |
| ζi | Bulk viscosity of phase I |
References
- Zhao, G.J.; Shi, X.G.; Wu, Y.Y.; Wang, M.; Zhang, M.X.; Gao, J.S.; Lan, X.Y. 3D CFD simulation of gas-solids hydrodynamics and bubbles behaviors in empty and packed bubbling fluidized beds. Powder Technol. 2019, 351, 1–15. [Google Scholar] [CrossRef]
- Luo, Z.; Zhao, Y.; Lv, B.; Fu, Y.; Xu, X.; Chen, C. Dry coal beneficiation technique in the gas–solid fluidized bed: A review. Int. J. Coal Prep. Util. 2019, 42, 1–29. [Google Scholar] [CrossRef]
- Rahaman, M.F.; Naser, J.; Witt, P.J. An unequal granular temperature kinetic theory: Description of granular flow with multiple particle classes. Powder Technol. 2003, 138, 82–92. [Google Scholar] [CrossRef]
- Lv, B.; Luo, Z.; Fu, Y.; Zhang, B.; Qin, X.; Zhu, X. Particle mixing behavior of fine coal in density control of gas–solid separation fluidized bed. Particuology 2019, 50, 76–87. [Google Scholar] [CrossRef]
- Fu, Z.; Zhu, J.; Barghi, S.; Zhao, Y.; Luo, Z.; Duan, C. The distribution of bed density in an air dense medium fluidized bed with single and binary mixtures of Geldart B and/or D particles. Miner. Eng. 2019, 142, 105926. [Google Scholar] [CrossRef]
- Ostermeier, P.; Vandersickel, A.; Gleis, S.; Spliethoff, H. Numerical Approaches for Modeling Gas–Solid Fluidized Bed Reactors: Comparison of Models and Application to Different Technical Problems. J. Energy Resour. Technol. 2019, 141, 070707. [Google Scholar] [CrossRef]
- Gidaspow, D.; Lu, H.L. Collisional viscosity of FCC particles in a CFB. Aiche J. 1996, 42, 2503–2510. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A Bubbling Fluidization Model Using Kinetic-Theory of Granular Flow. Aiche J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Arastoopour, H.; Pakdel, P.; Adewumi, M. Hydrodynamic analysis of dilute gas—Solids flow in a vertical pipe. Powder Technol. 1990, 62, 163–170. [Google Scholar] [CrossRef]
- Peng, L.; Wu, Y.; Wang, C.; Gao, J.; Lan, X. 2.5D CFD simulations of gas–solids flow in cylindrical CFB risers. Powder Technol. 2016, 291, 229–243. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, J. CFD study of mixing and segregation in CFB risers: Extension of EMMS drag model to binary gas–solid flow. Chem. Eng. Sci. 2015, 122, 637–651. [Google Scholar] [CrossRef]
- Wang, S.; Liu, G.D.; Lu, H.L.; Sun, L.Y.; Xu, P.F. CFD simulation of bubbling fluidized beds using kinetic theory of rough sphere. Chem. Eng. Sci. 2012, 71, 185–201. [Google Scholar] [CrossRef]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Jenkins, J.T.; Savage, S.B. A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 1983, 130, 187–202. [Google Scholar] [CrossRef]
- Yang, L.; Padding, J.T.; Kuipers, J.A.M. Modification of kinetic theory of granular flow for frictional spheres, Part I: Two-fluid model derivation and numerical implementation. Chem. Eng. Sci. 2016, 152, 767–782. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Manger, E. Modelling and Simulation of Gas/Solids Flow in Curvilinear Co ordinates. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1996. [Google Scholar]
- Bell, R.A. Numerical Modelling of Multi-Particle Flows in Bubbling Gas-Solid Fluidized Beds; Swinburne University of Technology: Melbourne City, Australia, 2000. [Google Scholar]
- Huilin, L.; Wenti, L.; Rushan, B.; Lidan, Y.; Gidaspow, D. Kinetic theory of fluidized binary granular mixtures with unequal granular temperature. Phys. A Stat. Mech. Its Appl. 2000, 284, 265–276. [Google Scholar] [CrossRef]
- Mathiesen, V.; Solberg, T.; Hjertager, B.H. An experimental and computational study of multiphase flow behavior in a circulating fluidized bed. Int. J. Multiph. Flow 2000, 26, 387–419. [Google Scholar] [CrossRef]
- Dodds, D.; Sarhan, A.R.; Naser, J. CFD Investigation into the Effects of Surrounding Particle Location on the Drag Coefficient. Fluids 2022, 7, 331. [Google Scholar] [CrossRef]
- Weaver, D.S.; Mišković, S. An Analysis of CFD-DEM with Coarse Graining for Turbulent Particle-Laden Jet Flows. Fluids 2023, 8, 215. [Google Scholar] [CrossRef]
- Wang, S.; Luo, K.; Hu, C.S.; Sun, L.Y.; Fan, J.R. Effect of superficial gas velocity on solid behaviors in a full-loop CFB. Powder Technol. 2018, 333, 91–105. [Google Scholar] [CrossRef]
- Zhang, W.; You, C.F. Numerical simulation of particulate flows in CFB riser with drag corrections based on particle distribution characterization. Chem. Eng. J. 2016, 303, 145–155. [Google Scholar] [CrossRef]
- Wang, Q.; Niemi, T.; Peltola, J.; Kallio, S.; Yang, H.; Lu, J.; Wei, L. Particle size distribution in CPFD modeling of gas–solid flows in a CFB riser. Particuology 2015, 21, 107–117. [Google Scholar] [CrossRef]
- Rossbach, V.; Utzig, J.; Decker, R.K.; Noriler, D.; Meier, H.F. Numerical gas-solid flow analysis of ring-baffled risers. Powder Technol. 2016, 297, 320–329. [Google Scholar] [CrossRef]
- Wu, J.; Binbo, J.; Chen, J.; Yang, Y. Multi-scale study of particle flow in silos. Adv. Powder Technol. 2009, 20, 62–73. [Google Scholar] [CrossRef]
- Miin, C.S.; Sulaiman, S.A.; Raghavan, V.R.; Heikal, M.R.; Naz, M.Y. Hydrodynamics of multi-sized particles in stable regime of a swirling bed. Korean J. Chem. Eng. 2015, 32, 2361–2367. [Google Scholar] [CrossRef]
- Zheng, N.; Liu, H.; Fang, J.; Wei, J. Numerical investigation of bed-to-tube heat transfer in a shallow fluidized bed containing mixed-size particles. Int. J. Heat Mass Transf. 2023, 211, 124252. [Google Scholar] [CrossRef]
- Mathiesen, V. An Experimental and computational Study of Multiphase Flow Behavior in Circulating Fluidized Beds; Telemark Institute of Technology: Notodden, Norway, 1997. [Google Scholar]
- Rahaman, M.F.; Sarhan, A.R.; Naser, J. Kinetic theory for multi-particulate flow: Description of granular flow with rotary movement of particles. Powder Technol. 2020, 360, 780–788. [Google Scholar] [CrossRef]
- Abramov, R.V. Turbulence via Intermolecular Potential: Viscosity and Transition Range of the Reynolds Number. Fluids 2023, 8, 101. [Google Scholar] [CrossRef]
- Witt, P.J.; Perry, J.H.; Schwarz, M.P. A numerical model for predicting bubble formation in a 3D fluidized bed. Appl. Math. Model. 1998, 22, 1071–1080. [Google Scholar] [CrossRef]
- Van Wachem, B.G.M.; Schouten, J.C.; van den Bleek, C.M.; Krishna, R.; Sinclair, J.L. Comparative analysis of CFD models of dense gas–solid systems. Aiche J. 2001, 47, 1035–1051. [Google Scholar] [CrossRef]
- Tsuo, Y.P.; Gidaspow, D. Computation of Flow Patterns in Circulating Fluidized-Beds. Aiche J. 1990, 36, 885–896. [Google Scholar] [CrossRef]
- Sobieski, W. Drag Coefficient in Solid–Fluid System Modeling with the Eulerian Multiphase Model. Dry. Technol. 2011, 29, 111–125. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Arastoopour, H. Dilute Fluidized Cracking Catalyst Particles—Gas-Flow Behavior in the Riser of a Circulating Fluidized-Bed. Powder Technol. 1995, 84, 221–229. [Google Scholar] [CrossRef]
- Miller, A.; Gidaspow, D. Dense, Vertical Gas-Solid Flow in a Pipe. Aiche J. 1992, 38, 1801–1815. [Google Scholar] [CrossRef]
- Farrell, M.; Lun, C.K.K.; Savage, S.B. A simple kinetic theory for granular flow of binary mixtures of smooth, inelastic, spherical particles. Acta Mech. 1986, 63, 45–60. [Google Scholar] [CrossRef]
- Jenkins, J.T.; Mancini, F. Balance Laws and Constitutive Relations for Plane Flows of a Dense, Binary Mixture of Smooth, Nearly Elastic, Circular Disks. J. Appl. Mech. T ASME 1987, 54, 27–34. [Google Scholar] [CrossRef]






| 1. The number of binary collisions |
| were coefficients A, B, D: |
| 2. The conservation equations |
| Collisional stress contribution: |
| Conservation of mass for species i: |
| Volume fraction of species i: |
| Conservation of momentum of species i: |
| Conservation equation for the fluctuating translational energy for species i: |
| 3. Constitutive relations |
| Pressure tensor |
| Solid phase pressure |
| Solid shear viscosity |
| Dilute viscosity |
| Energy dissipation |
| Riser Dimensions-Cylindrical | Diameter | 0.032 m |
| Height | 1.0 m | |
| Operating conditions | Gas phase | ρg = 1.2 kg m−3, μg = 0.00001 Pa s |
| Solid Phase I | ρsI = 2400 kg m−3, dI = 120 μm | |
| Solid Phase II | ρsII = 2400 kg m−3, dII = 185 μm | |
| Initial bed height | 0.04 m | |
| Pressure | Atmospheric pressure | |
| Inlet gas velocity | Jg = 1.2 m s−1 | |
| Fraction of solids | 0.63 |
| Property | Minimum | Maximum | Average |
|---|---|---|---|
| Volume | 1.878 × 10−8 | 5.565 × 10−8 | 3.499 × 10−8 |
| Skew | 0.9 | 1.0 | 0.9752 |
| Twist | 1.0 | 1.0 | 1.0 |
| Taper | 0.7588 | 1.0 | 0.8597 |
| Stretch | 0.6362 | 1.0 | 0.8585 |
| Block | NI | NJ | NK | NCell |
|---|---|---|---|---|
| 1 | 6 | 4 | 200 | 4800 |
| 2 | 6 | 4 | 200 | 4800 |
| 3 | 6 | 4 | 200 | 4800 |
| 4 | 4 | 4 | 200 | 3200 |
| 5 | 6 | 4 | 200 | 4800 |
| Total number of grid cells | 22,400 | |||
| Commercial Software | CFX | |
|---|---|---|
| General | Linear solver type | GSTB |
| Pressure formulation | SIMPLE | |
| Run mode | Unsteady, ∆t = 0.001 s | |
| Total time | 32.5 h | |
| Gravitational body force | Full body force–Y direction | |
| Convergence criteria | 0.0001 | |
| Mesh type | 22,400 grids, symmetric grid | |
| Models | The Eulerian–Eulerian flow approach using Reynold’s Averaged Navier Stocks (RANS) and continuity Equations | |
| Drag model | Schiller–Neumann Equation for particles [36]. | |
| Turbulence model | Viscous-standard k–ε, dispersed | |
| Control | Number of phases = 2 | |
| Continuous phase = solid | ||
| Secondary phase = gas | ||
| Minimum volume fraction | 1 × 10−6 | |
| Boundary conditions | Inlet condition | Normal velocity, 10% mean kinetic energy for k. |
| Outlet condition | Static pressure, 100,000 Pa, zero gradient for k-ε. | |
| Wall condition | No slip conditions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahaman, F.; Sarhan, A.A.R.; Naser, J. Numerical Analysis of Multi-Particulate Flow Behaviour in CFB Riser Coupled with a Kinetic Theory. Fluids 2023, 8, 257. https://doi.org/10.3390/fluids8090257
Rahaman F, Sarhan AAR, Naser J. Numerical Analysis of Multi-Particulate Flow Behaviour in CFB Riser Coupled with a Kinetic Theory. Fluids. 2023; 8(9):257. https://doi.org/10.3390/fluids8090257
Chicago/Turabian StyleRahaman, Fardausur, Abd Alhamid Rafea Sarhan, and Jamal Naser. 2023. "Numerical Analysis of Multi-Particulate Flow Behaviour in CFB Riser Coupled with a Kinetic Theory" Fluids 8, no. 9: 257. https://doi.org/10.3390/fluids8090257
APA StyleRahaman, F., Sarhan, A. A. R., & Naser, J. (2023). Numerical Analysis of Multi-Particulate Flow Behaviour in CFB Riser Coupled with a Kinetic Theory. Fluids, 8(9), 257. https://doi.org/10.3390/fluids8090257







