Engine Mass Flow Estimation through Neural Network Modeling in Semi-Transient Conditions: A New Calibration Approach
Abstract
1. Introduction
1.1. Engine Calibration
1.2. Artificial Neural Networks (ANNs)
1.3. Tree Ensemble Models
1.4. The Present Study
2. Materials and Methods
- Gradient-Boosted Decision Tree Regressor [28]: This is a popular machine learning model consisting of an ensemble of decision trees trained sequentially. A decision tree is a non-parametric model that learns simple binary decision rules over the inputs—structured hierarchically in a tree—to approximate the target. The tree is constructed using the inputs and targets of the training data. To make a prediction for a test datapoint, the datapoint is “carried” along a branch of the tree according to how the inputs behave under the learned binary rules. Then, once a leaf is reached, the prediction is made using the average target values of the training datapoints that belong to that leaf. Decision trees are known to be prone to overfitting, and to be unable to learn very flexible decision boundaries: however, this can be significantly improved by “ensembling” multiple trees together. In particular, gradient-boosting is a technique whereby decision trees are sequentially fitted to the residual error (aka the “gradient”) of the previous tree.
- Artificial Neural Network [35]: This class of models provides the highest level of flexibility in terms of the input-target relationships that can be learned. In particular, we focus on Feed-Forward Fully Connected Neural Networks. The fundamental building block of these is the perceptron, which takes as input a set of features, linearly combines them into a single value using learned weights and biases, and finally transforms said value with a simple nonlinear “activation” function. Multiple perceptrons can be combined in parallel, forming a layer, and layers are stacked, with the outputs of perceptrons in one layer being fed as inputs to the perceptrons in the next layer. Neural networks are trained using the backpropagation algorithm, whereby a loss function between the network’s output and the target is determined—in our case the Mean Squared Error loss—and the gradient of the loss value is backpropagated through the network using automatic differentiation; finally, the network parameters—weights and biases of the linear layers—are updated by taking a step in the direction of the gradient, using a predetermined learning rate.
3. Results
3.1. ECU Strategies and Calibrations
- is the air flow rate expressed in
- λ is the lambda of the mixture
- is the stoichiometric air-fuel ratio, 14.65 in this case since the fuel is gasoline
- is the injection time expressed in
- is the fuel density expressed in , in this case, it is 750
- is the injector gain, which is the quantity corresponding to the fuel flow rate deliverable by the model being used, expressed in , in this case, it is 280
- Combustion Delay:
- Transmission delay:
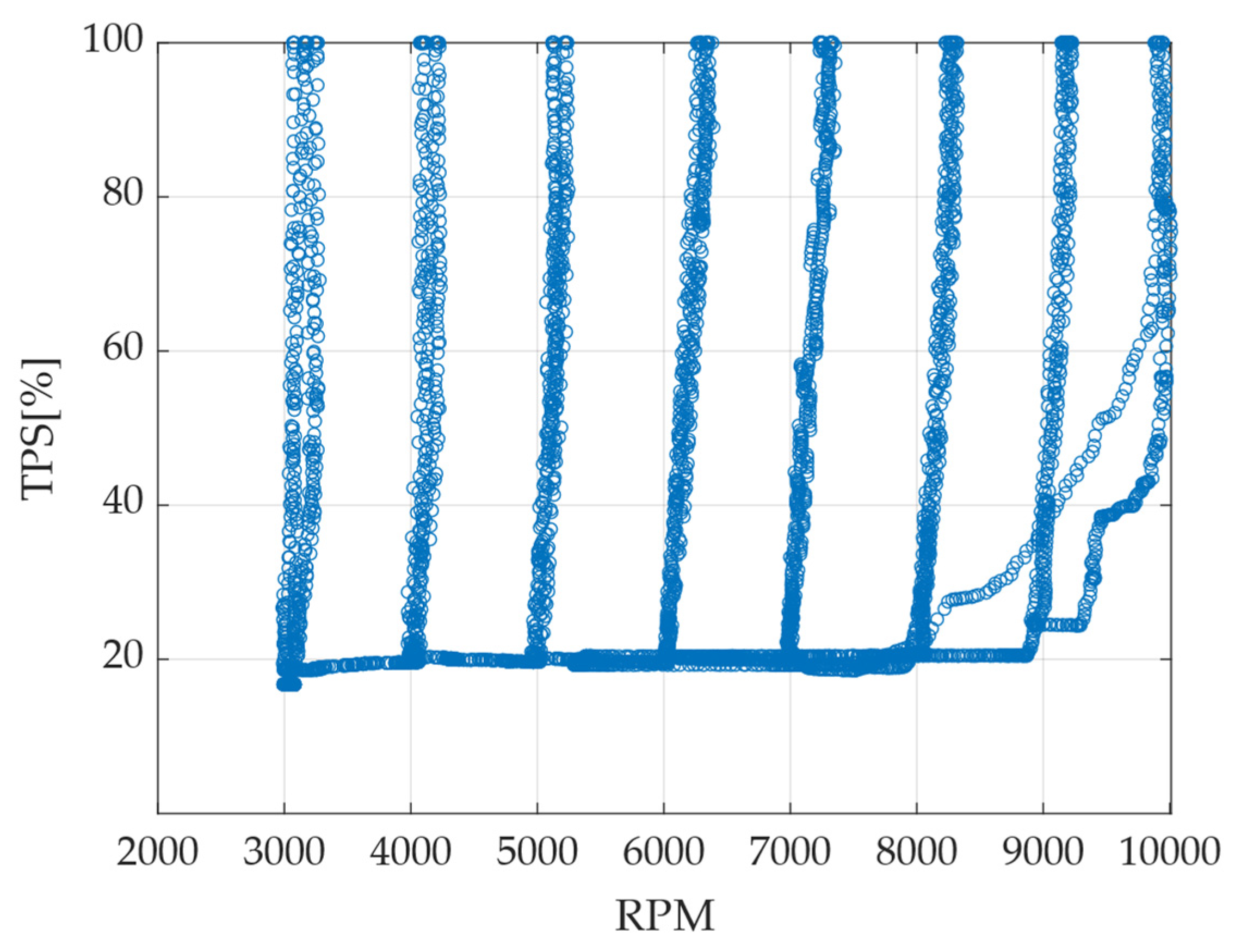
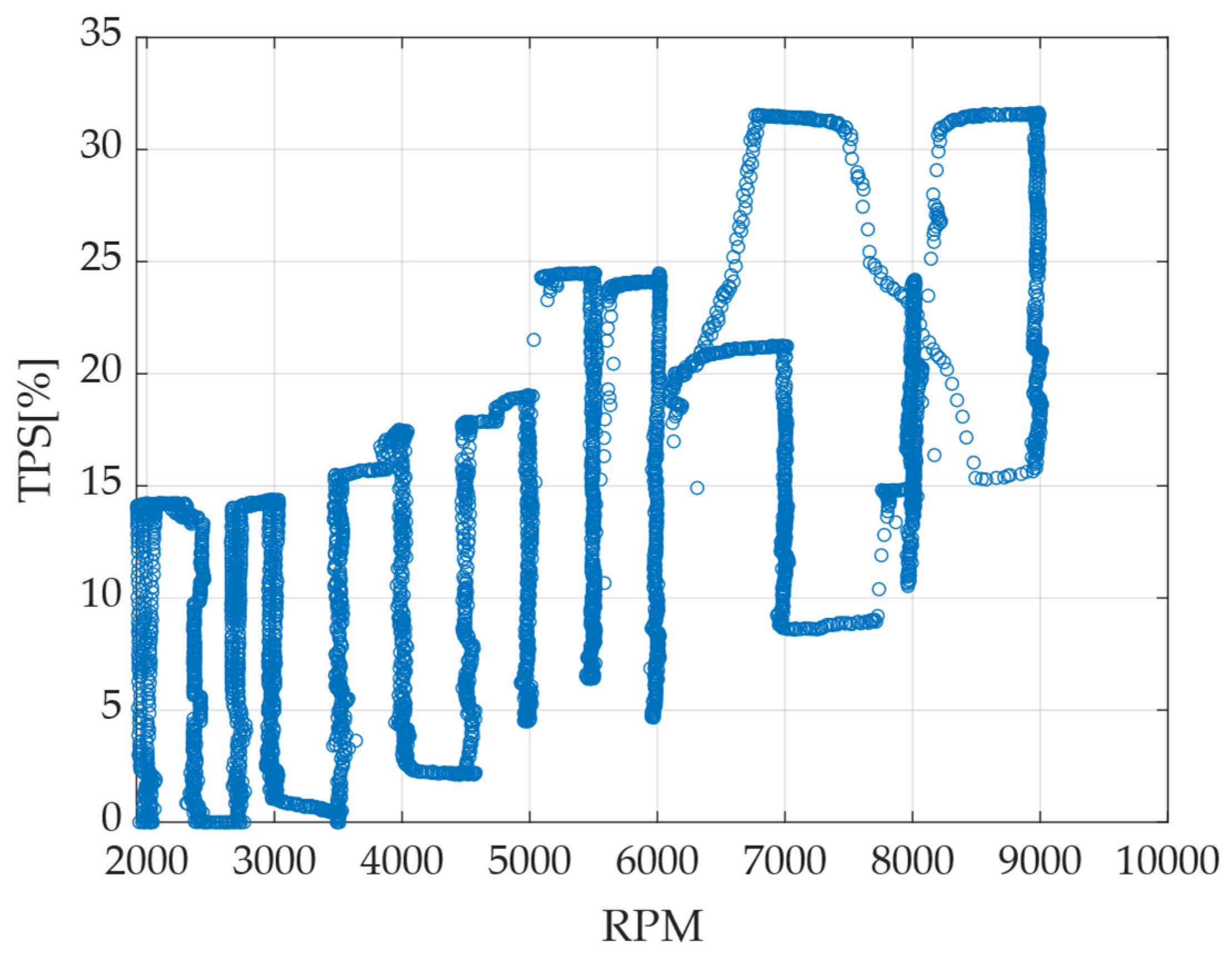
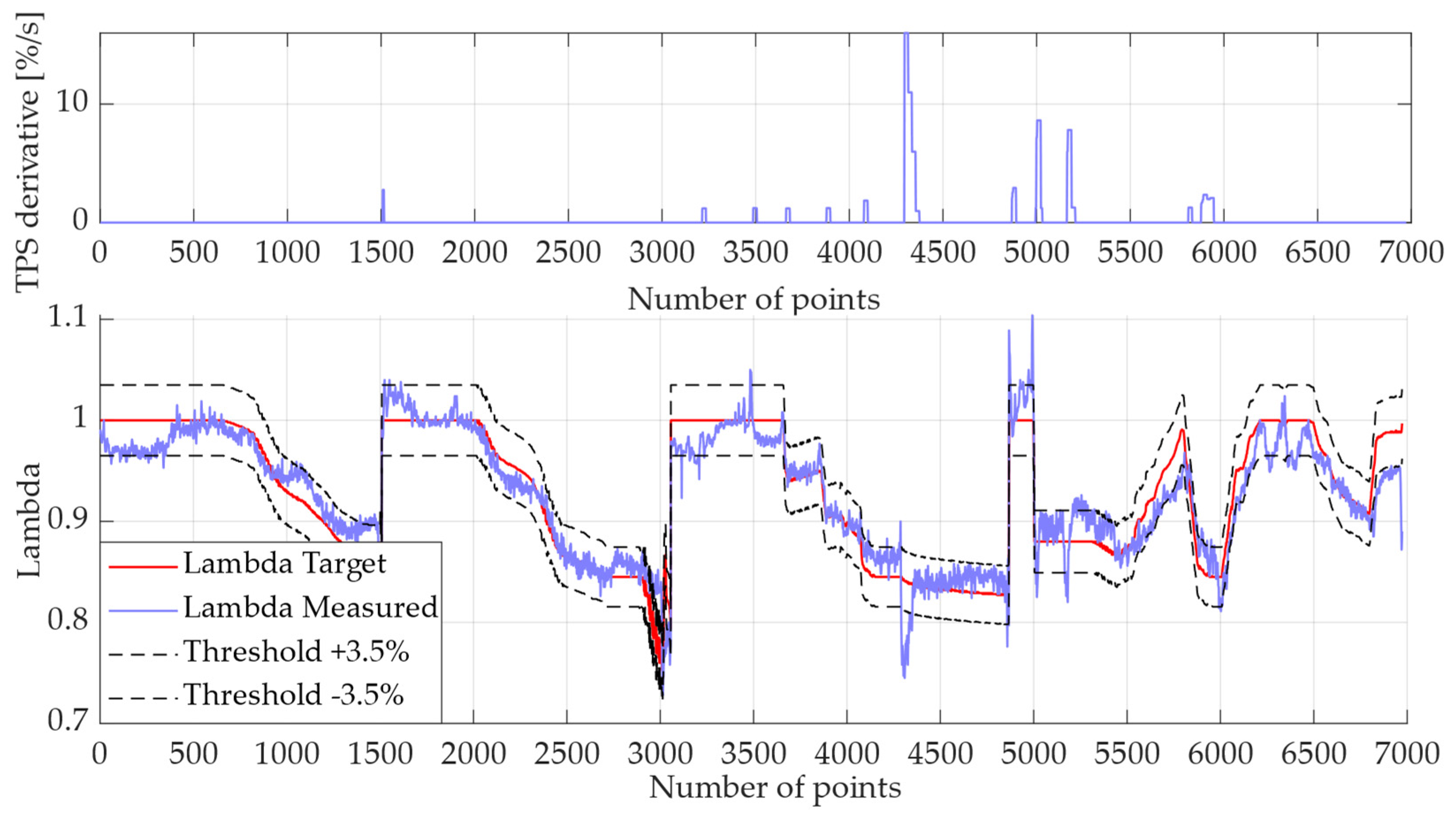
3.2. Data Training Acquisition and Creation of Models
4. Discussion
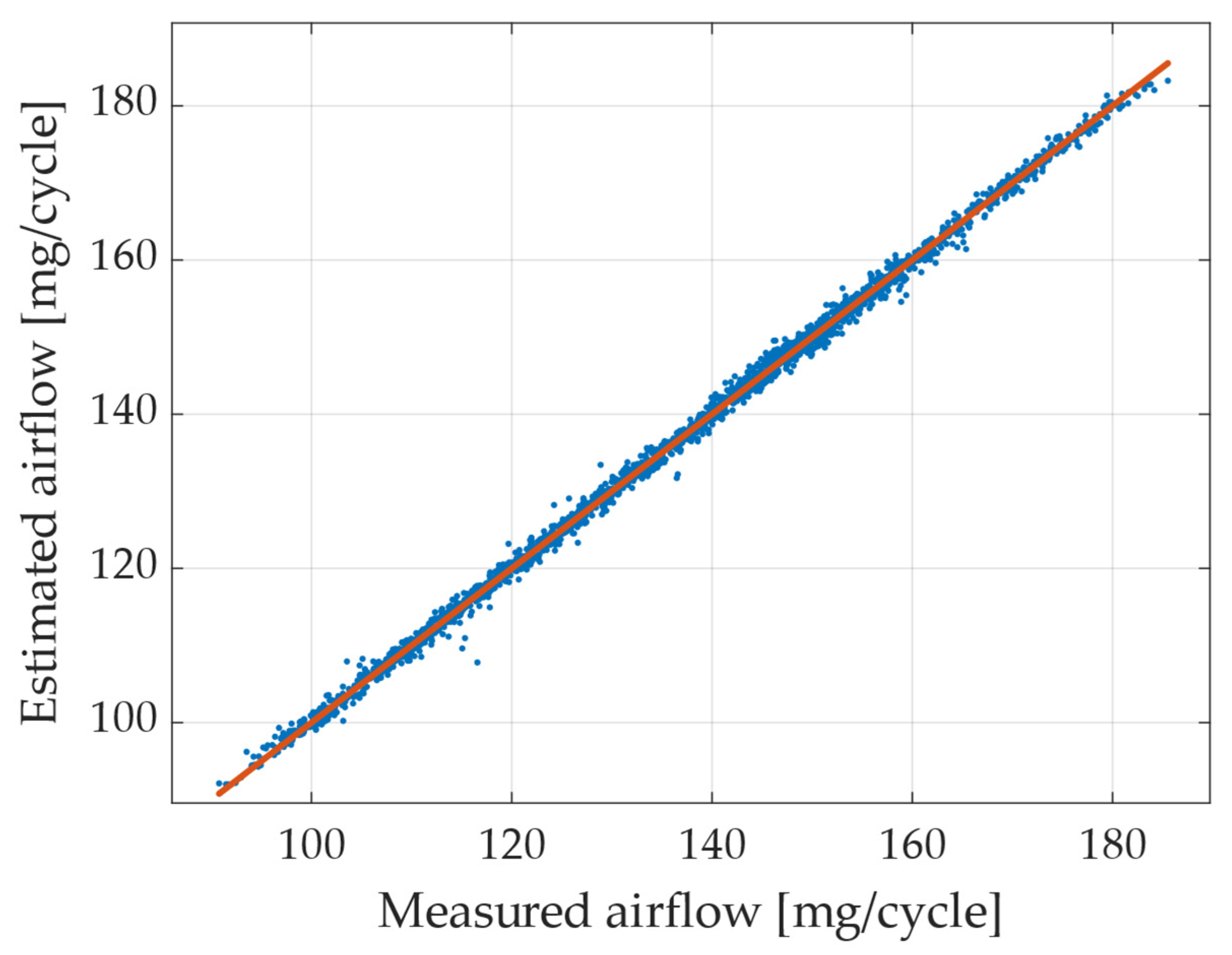
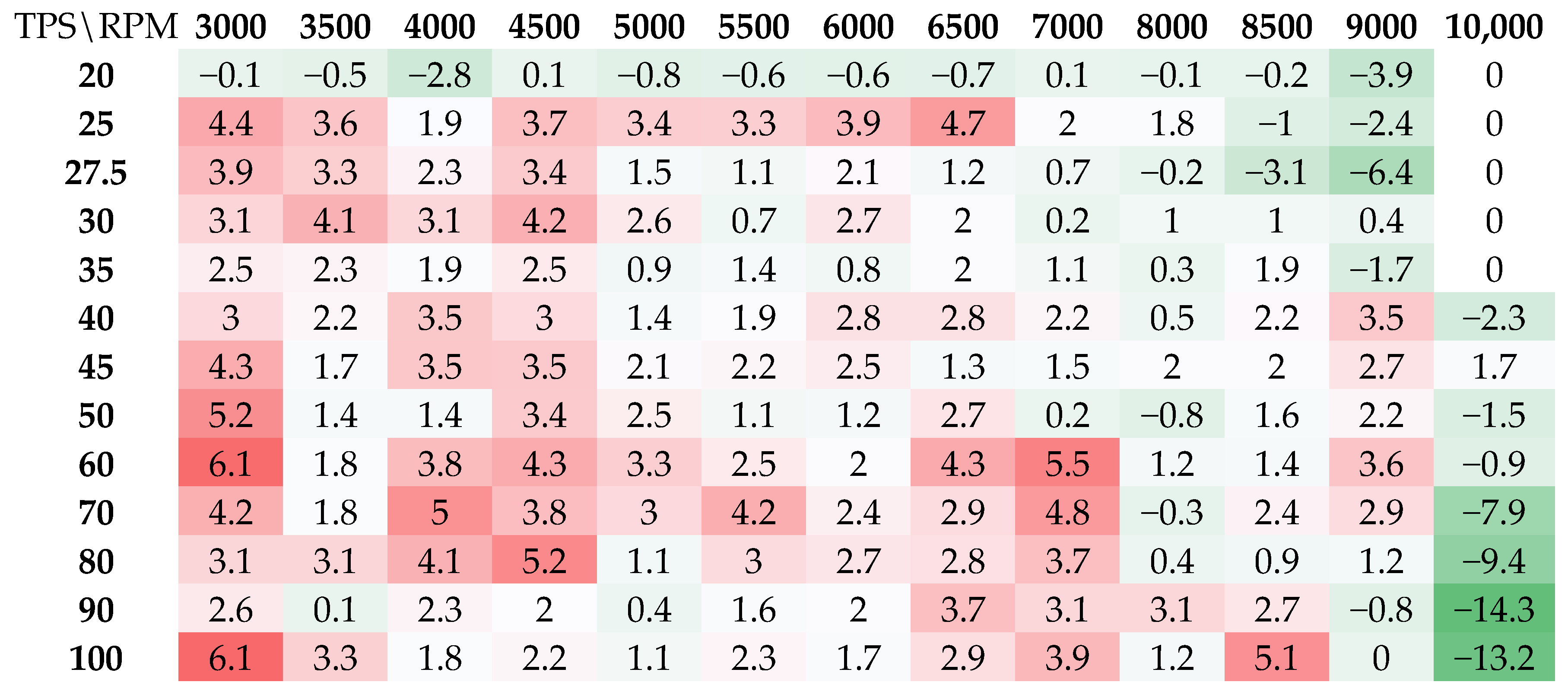
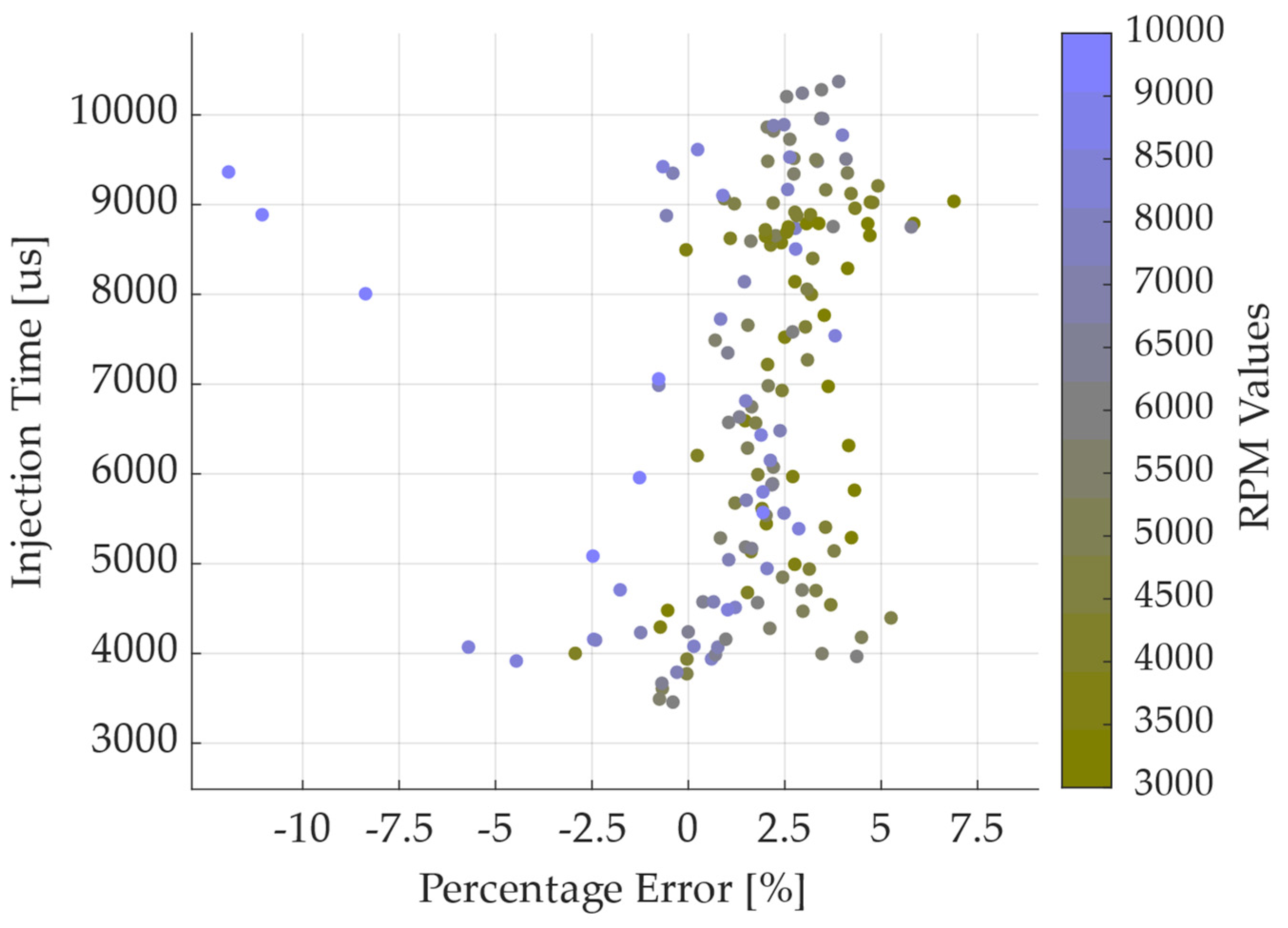
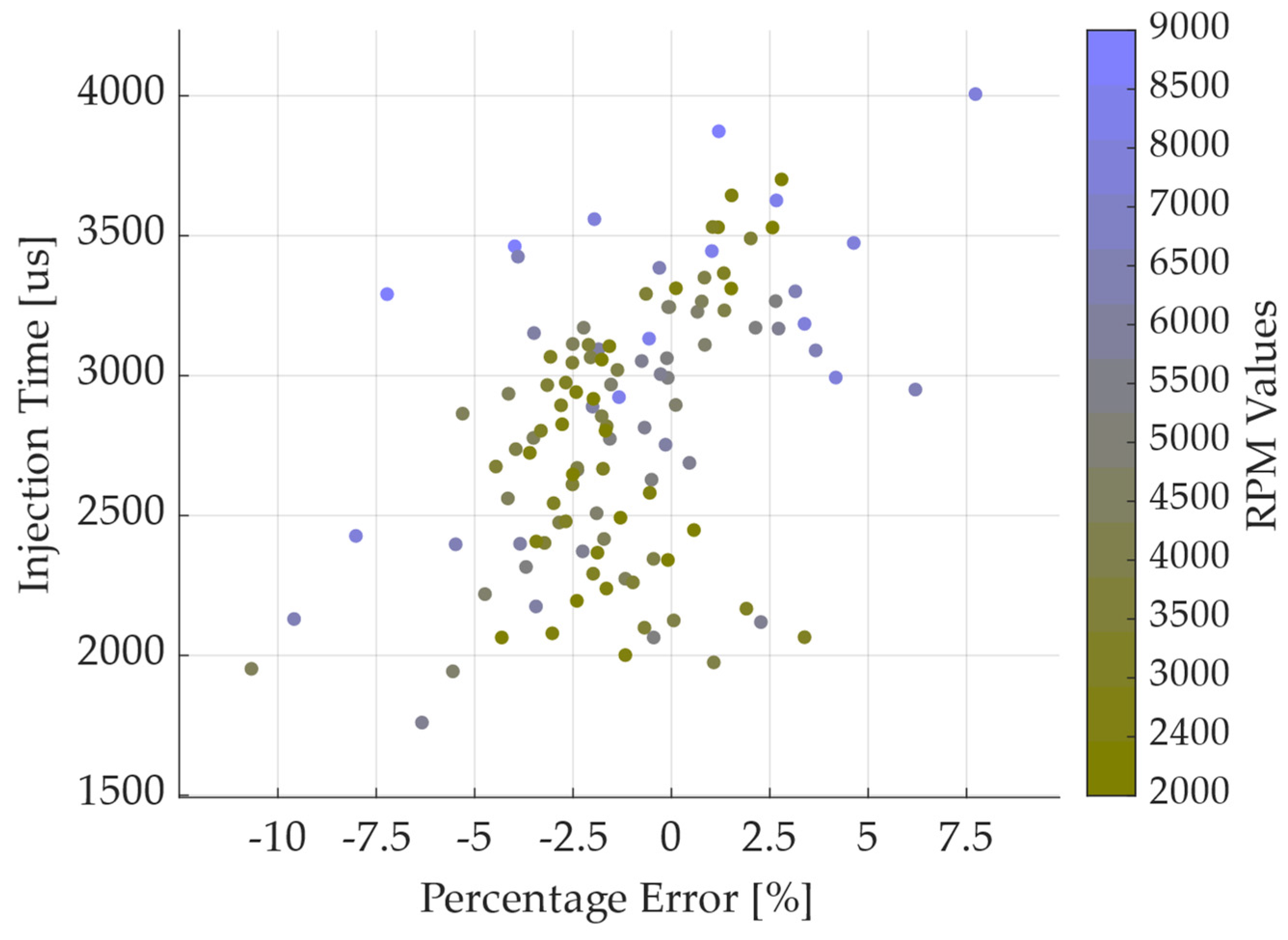
4.1. Model Perfomance Evalutation
4.2. Motorcycle Calibration Validation
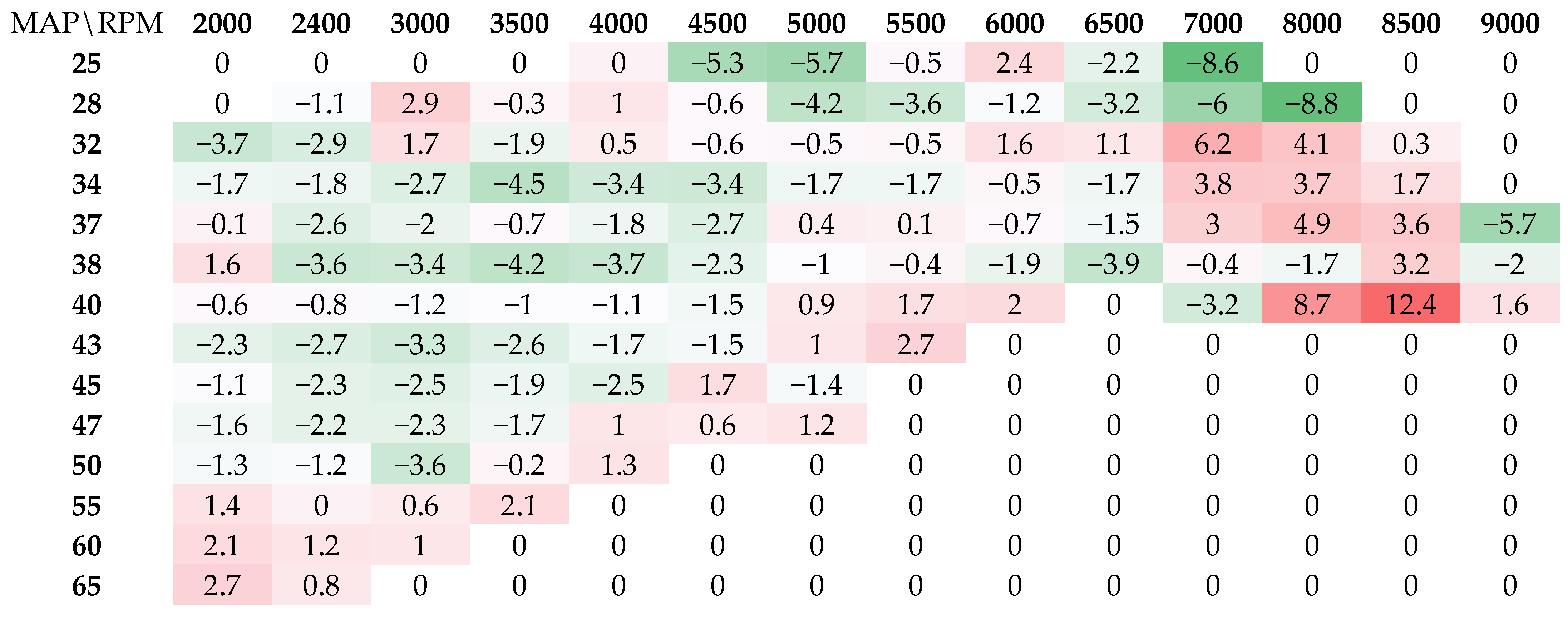
4.3. DOE Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ECU | Engine Control Unit |
| CAN | Controlled Area Network |
| TPS | Throttle Position Sensor |
| ALR | Auto Load Regulation |
| ASR | Auto Speed Regulation |
| UEGO | Universal Exhaust Gas Oxygen sensor |
| MAP | Manifold Absolute Pressure |
| CL | Closed Loop |
| SD | Speed Density |
| AS | Alfa Speed |
| DOE | Design Of Experiment |
| RLC | Road Load Control |
References
- Martyr, A.J.; Plint, M.A. Engine Testing: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-08-052472-6. [Google Scholar]
- Johnson, T.; Joshi, A. Review of Vehicle Engine Efficiency and Emissions. SAE Int. J. Engines 2018, 11, 1307–1330. [Google Scholar] [CrossRef]
- Ashok, B.; Ashok, S.D.; Kumar, C.R. A review on control system architecture of a SI engine management system. Annu. Rev. Control. 2016, 41, 94–118. [Google Scholar] [CrossRef]
- Castagné, M.; Bentolila, Y.; Chaudoye, F.; Hallé, A.; Nicolas, F.; Sinoquet, D. Comparison of Engine Calibration Methods Based on Design of Experiments (DoE). Oil Gas Sci. Technol. Rev. d’IFP Energies Nouv. 2008, 63, 563–582. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J.P.; De Moor, B.L. Artificial Neural Networks for Modelling and Control of Non-Linear Systems; Springer International Publishing: Cham, Switzerland, 2012; ISBN 978-1-4757-2493-6. [Google Scholar]
- Samadani, E.; Shamekhi, A.H.; Behrouzi, M.; Chini, R. A method for pre-calibration of DI diesel engine emissions and performance using neural network and multi-objective genetic algorithm. SID 2009, 28, 61–70. [Google Scholar]
- Turkson, R.F.; Yan, F.; Ali, M.K.A.; Hu, J. Artificial neural network applications in the calibration of spark-ignition engines: An overview. Eng. Sci. Technol. Int. J. 2016, 19, 1346–1359. [Google Scholar] [CrossRef]
- De Simio, L.; Iannaccone, S.; Iazzetta, A.; Auriemma, M. Artificial neural networks for speeding-up the experimental calibration of propulsion systems. Fuel 2023, 345, 128194. [Google Scholar] [CrossRef]
- Boccardo, G.; Piano, A.; Zanelli, A.; Babbi, M.; Cambriglia, L.; Mosca, S.; Millo, F. Development of a virtual methodology based on physical and data-driven models to optimize engine calibration. Transp. Eng. 2022, 10, 100143. [Google Scholar] [CrossRef]
- Yang, R.; Yan, Y.; Sun, X.; Wang, Q.; Zhang, Y.; Fu, J.; Liu, Z. An Artificial Neural Network Model to Predict Efficiency and Emissions of a Gasoline Engine. Processes 2022, 10, 204. [Google Scholar] [CrossRef]
- Jaliliantabar, F.; Ghobadian, B.; Najafi, G.; Yusaf, T. Artificial Neural Network Modeling and Sensitivity Analysis of Performance and Emissions in a Compression Ignition Engine Using Biodiesel Fuel. Energies 2018, 11, 2410. [Google Scholar] [CrossRef]
- Ziółkowski, J.; Oszczypała, M.; Małachowski, J.; Szkutnik-Rogoż, J. Use of Artificial Neural Networks to Predict Fuel Consumption on the Basis of Technical Parameters of Vehicles. Energies 2021, 14, 2639. [Google Scholar] [CrossRef]
- Brahma, I.; Sharp, M.C.; Richter, I.B.; Frazier, T.R. Development of the nearest neighbour multivariate localized regression modelling technique for steady state engine calibration and comparison with neural networks and global regression. Int. J. Engine Res. 2008, 9, 297–323. [Google Scholar] [CrossRef]
- Meli, M.; Wang, Z.; Bailly, P.; Pischinger, S. Neural Network Modeling of Black Box Controls for Internal Combustion Engine Calibration; SAE Technical Paper 2024-01–2995; SAE International: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- de Nola, F.; Giardiello, G.; Gimelli, A.; Molteni, A.; Muccillo, M.; Picariello, R. Volumetric efficiency estimation based on neural networks to reduce the experimental effort in engine base calibration. Fuel 2019, 244, 31–39. [Google Scholar] [CrossRef]
- Zhou, H.; Li, X.; Lee, C.-F.F. Investigation on soot emissions from diesel-CNG dual-fuel. Int. J. Hydrogen Energy 2019, 44, 9438–9449. [Google Scholar] [CrossRef]
- Pan, T.; Cai, Y.; Chen, S. Development of an Engine Calibration Model Using Gaussian Process Regression. Int. J. Automot. Technol. 2021, 22, 327–334. [Google Scholar] [CrossRef]
- Jacob, A.; Ashok, B. An interdisciplinary review on calibration strategies of engine management system for diverse alternative fuels in IC engine applications. Fuel 2020, 278, 118236. [Google Scholar] [CrossRef]
- Rahimi-Gorji, M.; Ghajar, M.; Kakaee, A.-H.; Ganji, D.D. Modeling of the air conditions effects on the power and fuel consumption of the SI engine using neural networks and regression. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 375–384. [Google Scholar] [CrossRef]
- Garg, A.B.; Diwan, P.; Saxena, M. Artificial neural networks based methodologies for optimization of engine operations. Int. J. Sci. Eng. Res. 2012, 3, 1–5. [Google Scholar]
- Shayler, P.; Goodman, M.; Ma, T. The exploitation of neural networks in automotive engine management systems. Eng. Appl. Artif. Intell. 2000, 13, 147–157. [Google Scholar] [CrossRef]
- Schoeggl, P.; Ramschak, E. Vehicle Driveability Assessment Using Neural Networks for Development, Calibration and Quality Tests; SAE Technical Paper 2000-01–0702; SAE International: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Atkinson, C.; Mott, G. Dynamic Model-Based Calibration Optimization: An Introduction and Application to Diesel Engines; SAE Technical Paper 2005-01–0026; SAE International: Warrendale, PA, USA, 2005. [Google Scholar] [CrossRef]
- Lowe, D.; Zapart, C. Point-Wise Confidence Interval Estimation by Neural Networks: A Comparative Study based on Automotive Engine Calibration. Neural Comput. Appl. 1999, 8, 77–85. [Google Scholar] [CrossRef]
- Friedrich, C.; Auer, M.; Stiesch, G. Model Based Calibration Techniques for Medium Speed Engine Optimization: In-vestigations on Common Modeling Approaches for Modeling of Selected Steady State Engine Outputs. SAE Int. J. Engines 2016, 9, 1989–1998. [Google Scholar] [CrossRef]
- Vinoth, B.; Uma, G.; Umapathy, M. Recurrent Neural Network based Soft Sensor for flow estimation in Liquid Rocket Engine Injector calibration. Flow Meas. Instrum. 2022, 83, 102105. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why do tree-based models still outperform deep learning on typical tabular data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Random Forest Machine Learning Model for Predicting Combustion Feedback Information of a Natural Gas Spark Ignition Engine. J. Energy Resour. Technol. 2020, 143, 012301. [Google Scholar] [CrossRef]
- Kefalas, A.; Ofner, A.B.; Pirker, G.; Posch, S.; Geiger, B.C.; Wimmer, A. Estimation of Combustion Parameters from Engine Vibrations Based on Discrete Wavelet Transform and Gradient Boosting. Sensors 2022, 22, 4235. [Google Scholar] [CrossRef]
- Ono Sokki Official Website. Available online: https://www.onosokki.net/ (accessed on 7 October 2024).
- Preda, I.; Covaciu, D.; Ciolan, G. Coast Down Test—Theoretical and Experimental Approach; Transilvania University Press: Brașov, Romania, 2010. [Google Scholar]
- INCA Base Product. ETAS Group. Available online: https://www.etas.com (accessed on 7 October 2024).
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Espinoza-Jurado, J.; Dávila, E.; Rivera, J.; Raygoza-Panduro, J.J.; Ortega, S. Robust Control of the Air to Fuel Ratio in Spark Ignition Engines with Delayed Measurements from a UEGO Sensor. Math. Probl. Eng. 2015, 2015, 989674. [Google Scholar] [CrossRef]
- Meng, L.; Wang, X.; Zeng, C.; Luo, J. Adaptive Air-Fuel Ratio Regulation for Port-Injected Spark-Ignited Engines Based on a Generalized Predictive Control Method. Energies 2019, 12, 173. [Google Scholar] [CrossRef]
- Zhai, Y.-J.; Yu, D.-L. A Neural Network Model Based MPC of Engine AFR with Single-Dimensional Optimization. In Advances in Neural Networks—ISNN 2007; Liu, D., Fei, S., Hou, Z.-G., Zhang, H., Sun, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 339–348. ISBN 978-3-540-72383-7. [Google Scholar] [CrossRef]
- Uzun, A. Air mass flow estimation of diesel engines using neural network. Fuel 2014, 117, 833–838. [Google Scholar] [CrossRef]
- Pontes, F.J.; Amorim, G.F.; Balestrassi, P.P.; Paiva, A.P.; Ferreira, J.R. Design of experiments and focused grid search for neural network parameter optimization. Neurocomputing 2016, 186, 22–34. [Google Scholar] [CrossRef]




| Injection Strategy | Alpha Speed | Speed Density |
|---|---|---|
| Model type | Neural network | Gradient boosted trees |
| Model features |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savioli, T.; Pampanini, M.; Visani, G.; Esposito, L.; Rinaldini, C.A. Engine Mass Flow Estimation through Neural Network Modeling in Semi-Transient Conditions: A New Calibration Approach. Fluids 2024, 9, 239. https://doi.org/10.3390/fluids9100239
Savioli T, Pampanini M, Visani G, Esposito L, Rinaldini CA. Engine Mass Flow Estimation through Neural Network Modeling in Semi-Transient Conditions: A New Calibration Approach. Fluids. 2024; 9(10):239. https://doi.org/10.3390/fluids9100239
Chicago/Turabian StyleSavioli, T., M. Pampanini, G. Visani, L. Esposito, and C. A. Rinaldini. 2024. "Engine Mass Flow Estimation through Neural Network Modeling in Semi-Transient Conditions: A New Calibration Approach" Fluids 9, no. 10: 239. https://doi.org/10.3390/fluids9100239
APA StyleSavioli, T., Pampanini, M., Visani, G., Esposito, L., & Rinaldini, C. A. (2024). Engine Mass Flow Estimation through Neural Network Modeling in Semi-Transient Conditions: A New Calibration Approach. Fluids, 9(10), 239. https://doi.org/10.3390/fluids9100239







