Prediction of Scour Depth for Diverse Pier Shapes Utilizing Two-Dimensional Hydraulic Engineering Center’s River Analysis System Sediment Model

Abstract

Examining scouring around bridge piers is crucial for ensuring water-related infrastructure’s long-term safety and stability. Accurate forecasting models are essential for addressing scour, especially in complex water systems where traditional methods fall short. This study investigates the application of the HEC-RAS 2D sedimentation model, which has recently become available for detailed sediment analysis, to evaluate its effectiveness in predicting scoring around various pier shapes and under different water conditions. This study offers a comprehensive assessment of the model’s predictive capabilities by focusing on variables such as water velocity, shear stress, and riverbed changes. Particular attention was paid to the influence of factors like floating debris and different pier geometries on scour predictions. The results demonstrate that while the HEC-RAS 2D model generally provides accurate predictions for simpler pier shapes—achieving up to 85% precision—it shows varied performance for more complex designs and debris-influenced scenarios. Specifically, the model overpredicted scouring depths by approximately 20% for diamond-shaped piers and underpredicted by 15% for square piers in debris conditions. Elliptical piers, in contrast, experienced significantly less erosion, with scour depths up to 30% shallower compared to other shapes. This study highlights the novel application of the HEC-RAS 2D model in this context and underscores its strengths and limitations. Identified issues include difficulties in modeling water flow and debris-induced bottlenecks. This research points to the improved calibration of sediment movement parameters and the development of advanced computational techniques to enhance scour prediction accuracy in complex environments. This work contributes valuable insights for future research and practical applications in civil engineering, especially where traditional scour mitigation methods, such as apron coverings, are not feasible.

1. Introduction

Local scour around bridge piers is a critical issue in hydraulic engineering, posing significant risks to the structural integrity of bridges. While the fundamental concepts of local scour are well established, recent research has increasingly focused on the impact of floating debris on scour processes. This growing body of work provides insights into the mechanisms of scour and the effectiveness of various mitigation strategies. Recent studies have utilized computational fluid dynamics (CFDs) to analyze the effects of different pier shapes and the addition of debris on bridge scour. For instance, ref. [1] conducted a CFDs analysis, comparing various pier shapes and the inclusion of a debris fin, demonstrating significant variations in scour patterns and depths depending on the pier configuration and debris presence. Another important aspect is the performance of collars in mitigating scour at bridge piers with debris accumulation. Ref. [2] investigated the effectiveness of collars in reducing scour depths under conditions of debris accumulation, finding that collars can significantly mitigate scour, but their performance is influenced by the amount and type of debris. The evolution of scour in the presence of debris, particularly at bridge piers located near riverbanks, has also been studied. Ref. [3] examined how debris accumulation affects scour evolution, highlighting that debris increases shear stress and turbulence, thereby enhancing scour depth. Experimental studies have further explored the impact of debris on scour around slotted bridge piers. Ref. [4] conducted experiments to assess the effectiveness of slots in reducing scour in the presence of debris, finding that while slots can be effective, their efficiency varies with debris shape and positioning. Significant instances of bridge collapses caused by scour in Europe include the Sava bridge disaster in Zagreb and the detonation of the Malahide viaduct in Ireland [5]. Also, the collapse of the Hinza Ribeiro bridge in portages was due to two leading causes: the sand dredging in the last 25 years and sediment transport due to five severe floods between 2000 and 2001 [6]. In the United States, it has been estimated that the mean flood damage per bridge is approximately USD 1.4 million because of the hundreds of instances of bridge collapses between 1989 and 2000 [7,8,9]. Furthermore, due to fluctuations in rainfall patterns and an increased occurrence of storms, the risks of scouring are anticipated to be exacerbated by climate change. Over 20% of Europe’s bridges will face an increased danger of scouring. The countries most affected by this threat are likely to be Italy, Portugal, Spain, and Austria [10].

The Hydraulic Engineering Center’s River Analysis System (HEC-RAS) is a vital computational tool that permits complex fluid dynamics and sediment transport modeling and offers crucial data on scouring patterns close to hydraulic facilities [11,12]. Moreover, recent advancements in HEC-RAS have expanded its capabilities to include sediment transport modeling in 2D, enabling researchers to analyze sediment transport patterns around different shapes of bridge piers [13]. For instance, ref. [14] developed a 2D sediment transport model to simulate the bed level change, especially around the Kelanisiri bridge pier. The researchers found the sediment model able to accurately calculate the depth of holes around the piers and changes in the riverbed level. One-dimensional modeling assumes that water forces primarily act in one direction, while two-dimensional models consider forces in two directions. Two-dimensional models offer advantages such as faster mesh development and ease of visualization, striking a balance between computational time and cost. Although 3D models provide the most detailed analysis, they require significant resources and expertise. In many cases, 2D models offer a practical and efficient alternative to 3D models and provide better hydraulic representation than 1D models [15].

This study investigates the impact of debris presence and pier shape variations on local scour using the HEC-RAS 2D sediment model. The novelty of this research lies in its comprehensive examination of how different pier shapes and varying debris configurations affect scour depth, leveraging the advanced capabilities of the HEC-RAS 2D model. Pier shape significantly influences scour patterns at bridge foundations, with aerodynamic shapes generally reducing scour compared to blunt ones [16,17,18,19]. Despite this, the presence of debris during floods complicates scour predictions by altering flow patterns and exacerbating localized scour, which can threaten bridge stability and safety [20,21,22,23,24,25]. Furthermore, this research builds on foundational theories by incorporating recent computational advancements from the HEC-RAS 2D model, which allows for detailed sediment transport simulations that have not been extensively applied in this context. Using experimental data from ref. [26], this study rigorously assesses the model’s ability to replicate sediment movement and bed changes around various pier shapes. It evaluates the impact of grid size, calibrates parameters based on model accuracy, and employs statistical measures to identify and address limitations. This study enhances scour predictions by applying Melville’s effective pier width (De) and Lagasse’s equivalent pier width (a) methods, incorporating adjustments for debris-induced flow resistance.

This research also provides a novel comparison of simulated results against traditional empirical equations (e.g., CSU 2001 [27], Melville 1988 [28]) and experimental data [26], highlighting the strengths and limitations of the HEC-RAS 2D model in diverse scenarios. By simulating various debris types and thickness-to-width ratios, this study contributes valuable insights into improving scour predictions and model sensitivity, advancing the field of hydraulic and sediment transport modeling.

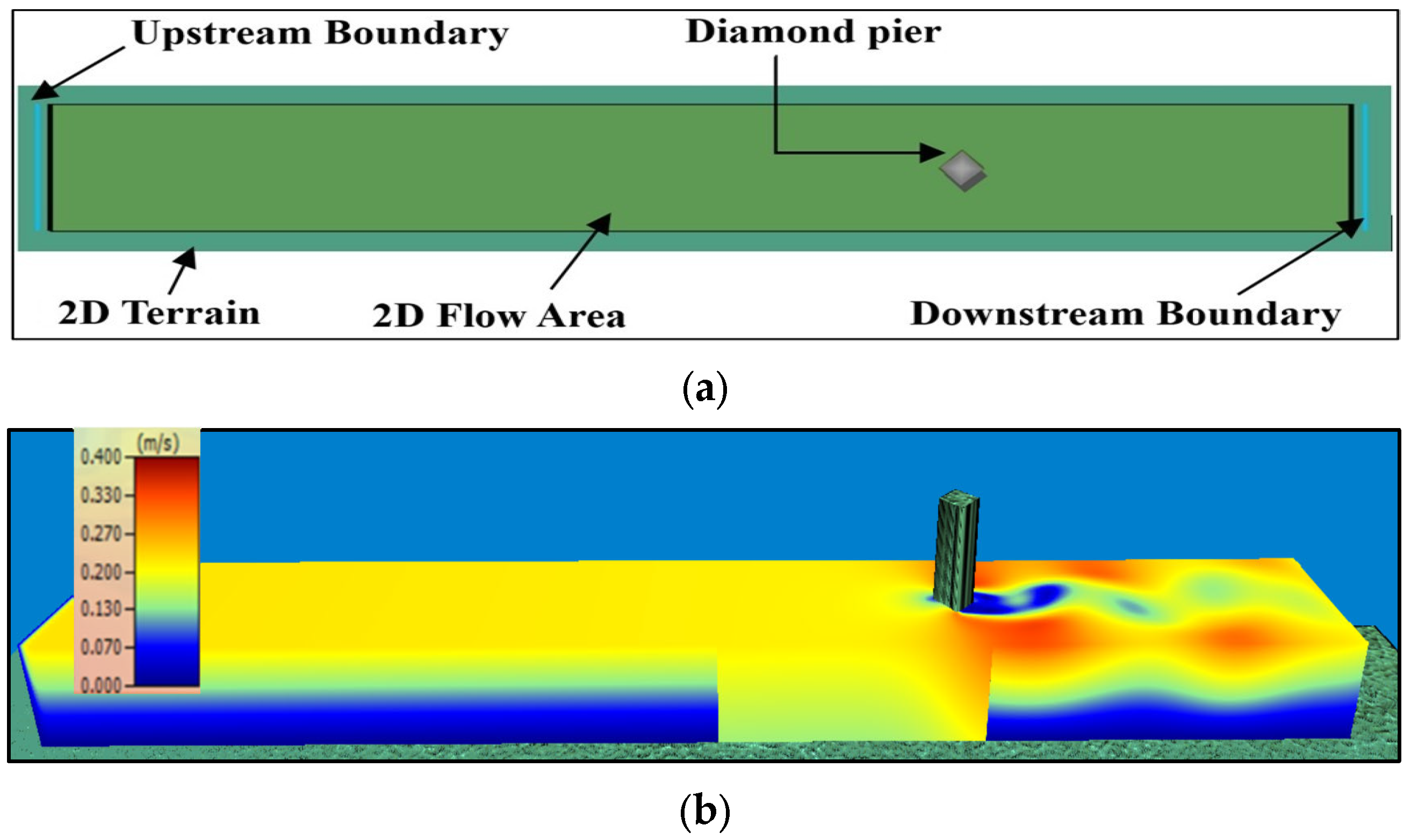
2. Two-Dimensional Model of HEC-RAS

According to its most recent edition, 2D sediment transport modeling is now a part of this software’s capabilities. Data administration and model visualization are significantly improved by adding an easy-to-use graphical user interface, which is part of this upgrade. When solving grid-scale flow dynamics, HEC-RAS employs three sets of equations. As stated in reference [11], the acronyms SWE-ELM and SWE-EM stand for “Shallow Water Equations using the Eulerian Method” and “Diffusion Wave Equation”, respectively. Complex streams, silt, and scour are explained in this difficult lecture using two-dimensional flow modeling and HEC-RAS. This model improves the accuracy of scour predictions and makes it easier to devise effective countermeasures to scour-related dangers. Studies have shown that HEC-RAS 2D may potentially forecast scour as well. According to studies by [13], two-dimensional models may represent sediment movement and flow in artificial channels more accurately. A collection of mathematical formulae aimed at clarifying the behavior of a fluid layer that maintains hydrostatic equilibrium is known as shallow water equations (SWEs). While representing fundamental physical processes rather accurately, these equations simplify the study of three-dimensional fluid dynamics. An essential presumption of SWEs is the significant disparity between horizontal and vertical length scales. Additionally, SWEs assume that fluid flow is incompressible, fluid density is uniform, and hydrostatic pressure is present [11]. One way to describe the continuity equation for incompressible flow is as follows:

$${\displaystyle \frac{\partial h}{\partial t}}+{\displaystyle \frac{\partial hu}{\partial x}}+{\displaystyle \frac{\partial hv}{\partial y}}=q$$

Here, ‘$t$’ represents time, ‘$h$’ corresponds to water depth, ‘$u$’ and ‘$v$’ denote velocity sections in the x and y directions, and ‘$q$’ signifies the rate. Notably, a subgrid bathymetry approach can enhance computational efficiency, mainly when dealing with terrain data on a coarse grid [12]. For the calculation of the bottom friction coefficient, Manning’s formula is applied, as demonstrated in the following equation:

$$C_f={\displaystyle \frac{n^{2}V\left|V\right|}{R^{4/3}}}$$

Within this equation, ‘$n$’ represents Manning’s roughness coefficient [s/m^{^(1/3)})], ‘$R$’ signifies hydraulic radius [m], and ‘$V$’ stands for current velocity [m/s] [12].

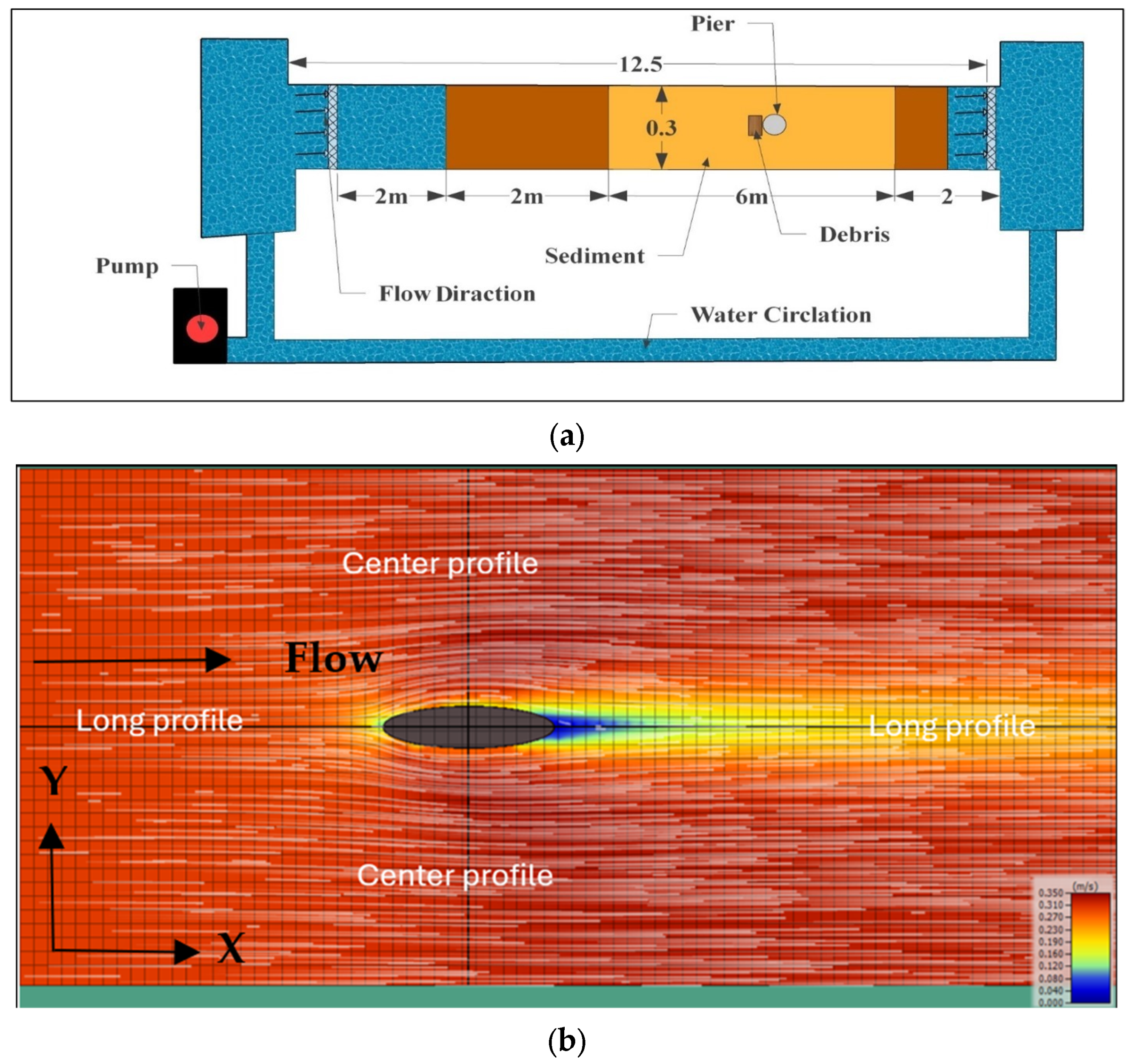
3. Input Data

This study adopted the experimental setup outlined in reference [26], which became the foundation for gathering data. Laboratory tests were carried out on a specially built flume, measuring 12.50 m in length, 0.30 m in width, and 0.50 m in height. Flow measurements were precisely taken using a volumetric flow meter with an accuracy of 1% and an electronic gauge in the flume’s discharge system, achieving an impressive accuracy of 0.05%. The experiments were conducted at a flow velocity of 0.29 m/s and a water depth of 0.12 m, lasting six hours each. Figure 1a shows the design and top view of the flume. A 15 cm thick layer of sand formed the base, which was smoothed before each experiment. Analysis of the sediment showed a median diameter (D₅₀) of 0.93 mm and a gradation coefficient (σ) of 1.27. This research examined seven different shapes of the pier: cylindrical (C), square (S), rectangular (Re), diamond (D), oval (OV), ogival (OG), and elliptical (E), each with a consistent width of 2.5 cm, except for the cylindrical, square, and diamond shapes. The elliptical, oval, rectangular, and ogival shapes had a length of 10 cm. Figure 1b delineates the positioning of two profile lines for evaluating bed changes: the Center and Long profile. These lines were strategically drawn in alignment with the locations of the piers. The directional arrows within the figure denote the flow orientation, illustrating the alignment of cross-section lines from the left to the right. Figure 2a,b illustrate the rectangular flume with a Dimond pier in a two-dimensional state, serving as an actual representation of the terrain model utilized in the study and 3D-Ras viewer tools.

4. Hydraulic Model’s Performance

4.1. Setup Hydraulic Model

For accurate sediment and hydraulics modeling, it is crucial to establish a precise terrain model. A 2D terrain file was created using RAS Mapper in the physical model. It is essential to highlight that this terrain file was derived from a 1D rectangular flume, but it was developed using a spatially scaled reference frame to depict the topographical features accurately. The pier was added to the terrain, precisely aligning it with its position in the physical model. The upstream boundary condition was specified as the external flow hydrograph, incremented every minute, with a constant flow rate of 0.011 m³/s applied to the 2D flow area. The boundary condition method of Normal Depth was utilized to facilitate the flow out from the 2D flow area. To compute flow depth according to Manning’s Equation, specifying a frictional slope for the flume is essential. Figure 2 provides a visual representation of the rectangular flume with a diamond pier, which serves as a concrete example of the terrain model used in this study. The careful methodology employed in terrain modeling dramatically enhances the reliability of the sediment and hydraulics model. Figure 3 shows the procedure of the approach methodology used for 2D HEC-RAS models.

4.2. Sediment Transport Modeling

The Hydrologic Engineering Center River Analysis System (HEC-RAS) has reached a new milestone with the introduction of version 6.0, showcasing advanced capabilities in modeling dynamic and unstable two-dimensional (2D) sediment movement and bed changes. This version employs a non-equilibrium total-load approach, integrating Integral Finite-Volume techniques for precise particle movement calculations on a uniform unstructured mesh. Noteworthy inclusions incorporate sediment movement at every phase of the flow simulation and explicit consideration of subgrid terrain changes within the framework, facilitating the utilization of coarser meshes and reducing computational times for implemented 2D flow algorithms [29]. The computational framework governing two-dimensional sediment transport revolves around the resolution of a bed-material load transport equation. This equation distinctly segregates the bed-material load into bedload and suspended loads, employing the following empirical formulas [30]:

$${\displaystyle \frac{\partial }{\partial t}}\left({\displaystyle \frac{h{C}_{tk}}{{\beta }_{tk}}}\right)+\nabla .\left(hU{C}_{tk}\right)=\nabla .({\epsilon }_{tk}h\nabla C_{tk})+E_{tk}^{HF}-D_{tk}^{HF}+S_{tk}$$

where $C_{tk}$ represents the total-load sediment concentration, ${\beta }_{tk}$ is the total-load correction factor, $U$is the depth-averaged current velocity, $h$ is the water depth, ${\epsilon }_{tk}$ is the total-load diffusion (mixing) coefficient, $E$ is the total-load erosion rate in hydraulic flow, $D$ is the total-load deposition rate in hydraulic flow, and $S$ is the total-load source/sink. The computational model integrates eleven distinct sediment transport functions, including Ackers–White, Englund–Hansen, Laursen, Meyer Peter Muller (MPM), Tofaletti, Yang, MPM–Toffaleti, Wilcock and Crowe, Soulsby–van Rijn, van Rijn, and Wu et al. The accurate representation of the model hinges on carefully selecting functions pertinent to the simulation. Calibration involves the utilization of actual bed changes, with [12] providing a comprehensive list of functions and their development conditions. Function selection is critical, considering particle diameters and water temperature factors. Sediment transport functions mimic non-linear transport processes, resulting in distinct outcomes. The model’s accuracy is intricately tied to the chosen function, and different functions yield diverse results for non-linear transport processes. Function selection significantly influences model outcomes, requiring scrutiny of the hypotheses, hydrodynamic circumstances, and sediment particle sizes for each approach. Two specific sediment transport functions, Wu et al. [31] and the van Rijn formulae [32,33], are considered for their relevance. Wu et al.’s equation is expressed as follows:

$$q_{bk}=\left\{\begin{array}{c}0.0053\sqrt{R_{k}g{d}_k^3}{\left({\displaystyle \frac{{\tau }_b^{\iota }}{{\tau }_{crk}}}-1\right)}^{2.2}for {\tau }_b^{\iota }>{\tau }_{crk} \\ 0 otherwise\end{array}\right.$$

where $q_{bk}$ is the fractional bedload sediment transport potential, $R_k$ is the submerged specific gravity of a particle, $d$ is the sediment diameter, ${\tau }_b^{\iota }$is the skin bed shear stress, and ${\tau }_{crk}$is the critical shear stress. The van Rijn formulae initially suggested uniformly distributed sediments, but they have been adapted for nonuniform materials. The sediment transportation equation from refs. [32,33] is expressed as follows:

$$q_{bk}=0.015Uh{\left({\displaystyle \frac{U-U_{crk}}{\sqrt{R_{k}g{d}_k}}}\right)}^{1.5}{\left({\displaystyle \frac{d_k}{h}}\right)}^{1.2}$$

where $U$ is the effective depth-averaged current velocity [m/s], $U_{crk}$is the critical depth-average velocity for incipient motion [m/s], and $h$is the flow depth.

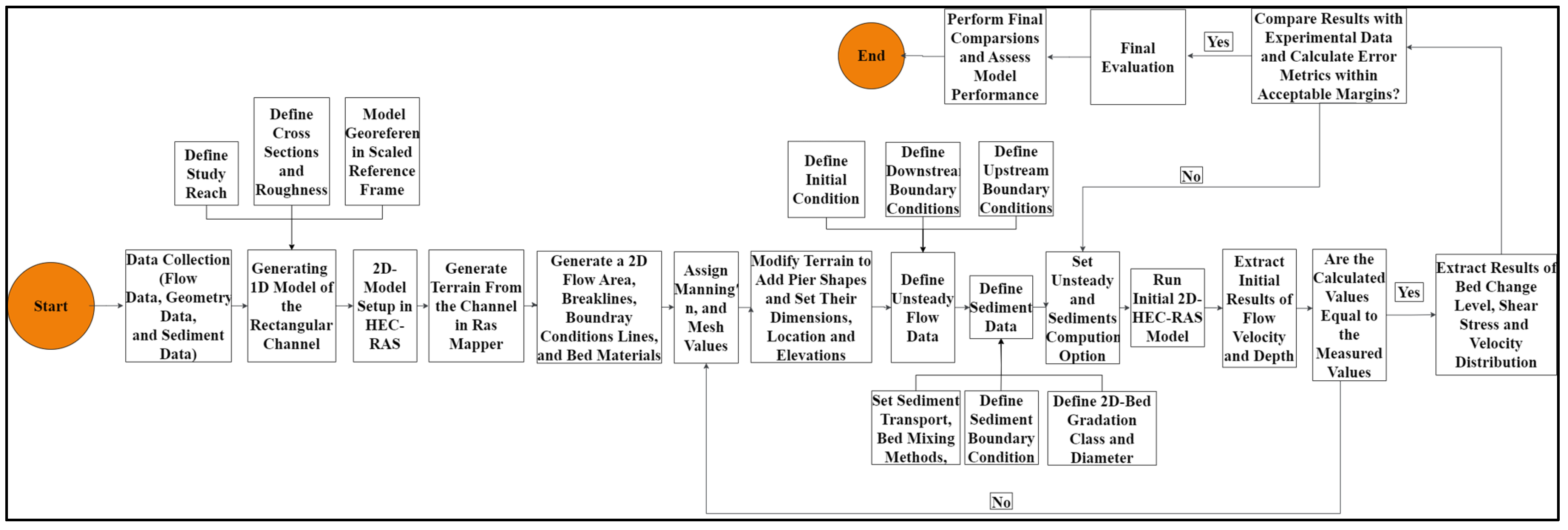
5. Model Calibration and Validation

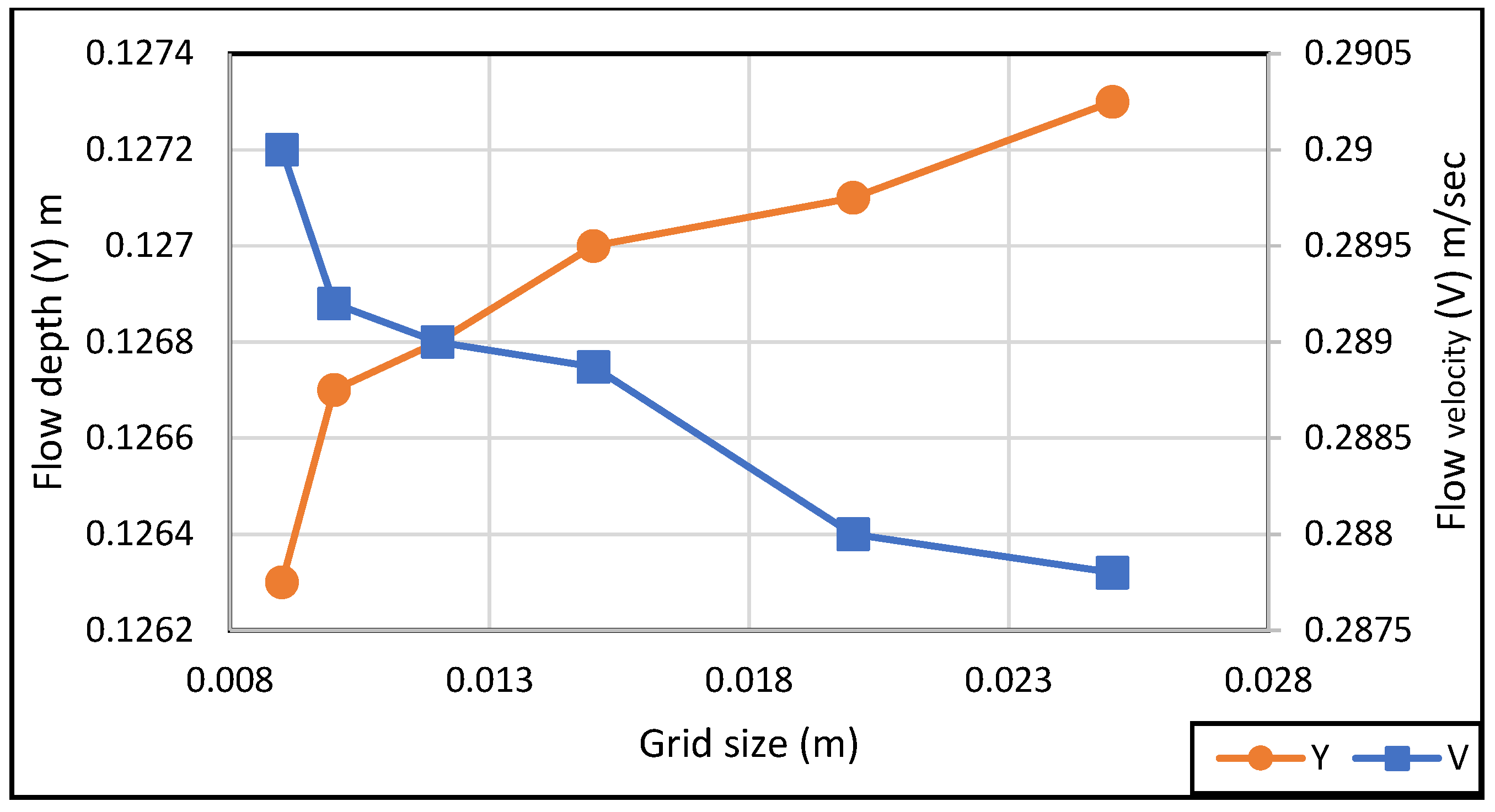
5.1. Grid Size

Grid construction plays a pivotal role in numerical modeling endeavors. The model integrates a structured grid, extending the complete length of the test channel, with some exceptions at the boundaries. Notably, a central break line aligns the grid with the flow direction, while break lines along the edges differentiate the channel bed level from the channel banks. Experimental runs were executed using non-aligned grids, wherein hydraulic and sediment models operated without stability concerns or errors. However, a notable enhancement of the model’s performance was observed when utilizing grids aligned with the flow direction. Aligning cells with the flow mitigates numerical diffusion issues, resulting in superior outcomes, as elucidated by [29]. The selection of a 2 cm grid produced satisfactory computational results; nevertheless, simulation outcomes indicated that this grid size was comparatively large. To thoroughly address flow turbulence around the piers, careful consideration was given to refining the mesh size. A reduction to a smaller mesh size of approximately 8 mm was recommended, acknowledging the complexities of fluid dynamics near the piers where localized turbulence and vortices play a pivotal role in shaping scour patterns and hydraulic characteristics.

Consequently, multiple simulations were conducted with varying grid sizes to assess the impact of decreasing grid size on the outcomes. Reducing the grid size from 2 cm to 8 mm resulted in nearly negligible changes in flow velocity (V) and flow depth (Y), as illustrated in Figure 4. This analysis underscores the significance of grid size in influencing model precision, especially concerning flow turbulence around the piers.

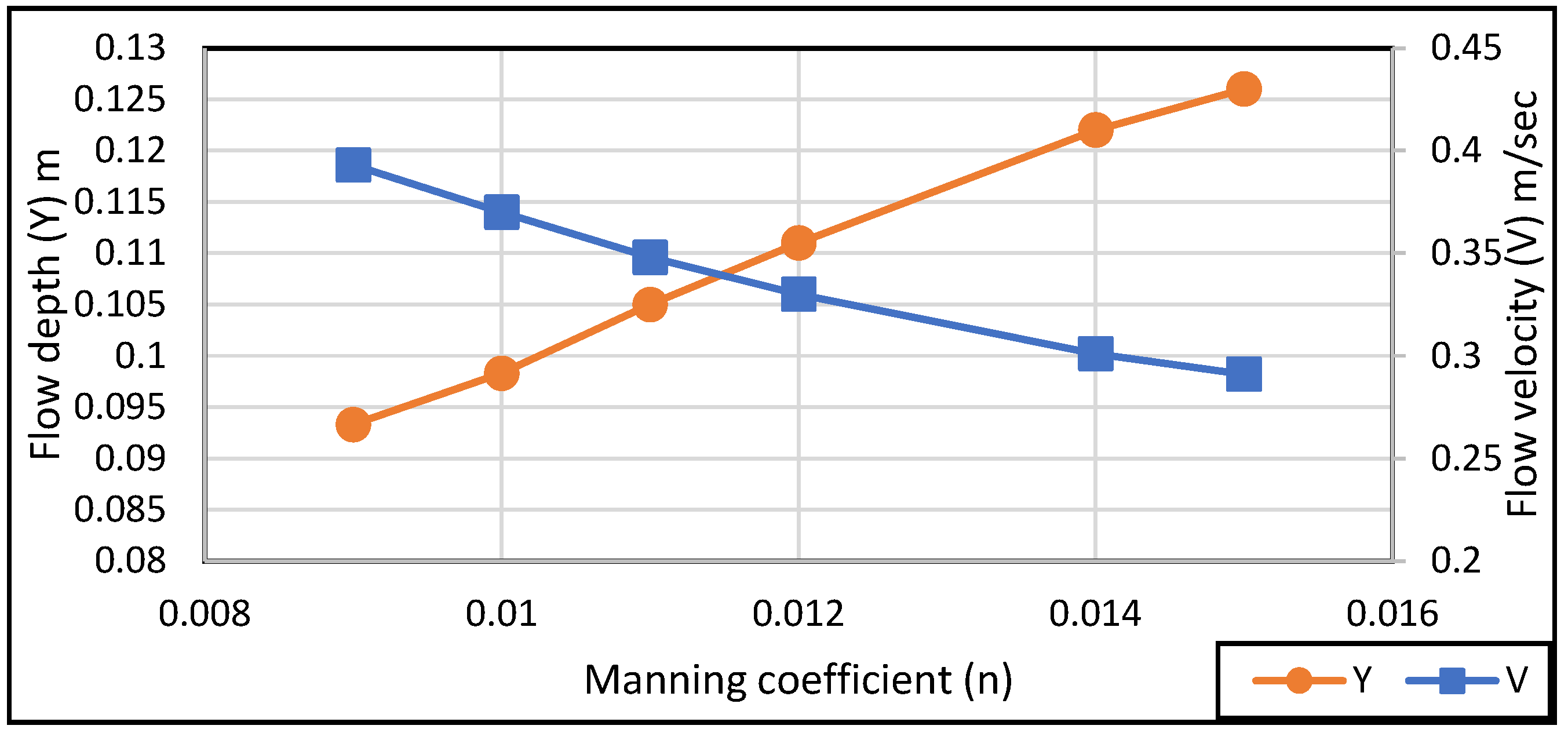
5.2. Manning Coefficient

Once the optimal grid size for computation was determined, the model underwent further calibration by incorporating the Manning number. The model was calibrated using water surface elevations and flow velocity at different time steps with a constant mesh size of 1 cm. The range of Manning’s number used for calibrating the initial plain bed is typically between 0.009 and 0.015, as shown in Figure 5. The final results showed that the optimal Manning coefficient value equals 0.014, which gives a flow depth and velocity, equal to the physical model, of 0.12 m and 0.3 m/s, respectively.

5.3. Time Step

When establishing a robust computational grid for a two-dimensional flow model, selecting an appropriate calculation time step is crucial. This step must align with the grid dimensions and the modeled conditions. The choice of time step can be either fixed or variable, with the latter being defined by the Courant number. The variable time step is particularly important in areas with rapid changes in flow, such as around structures like piers, where fast surface and velocity changes occur. In these regions, the mean grid size (ΔX) is essential for determining the optimal time step. Initially, an estimate of the highest expected speed is made before running the model. This estimate is then refined by mapping maximum velocities around different pier designs, as shown in Figure 6. The goal is to ensure that the Courant number © is set to the recommended value, ideally 1, for the shallow water equations. This method improves both the computational efficiency and the accuracy of the two-dimensional flow simulation model.

6. Results and Discussion

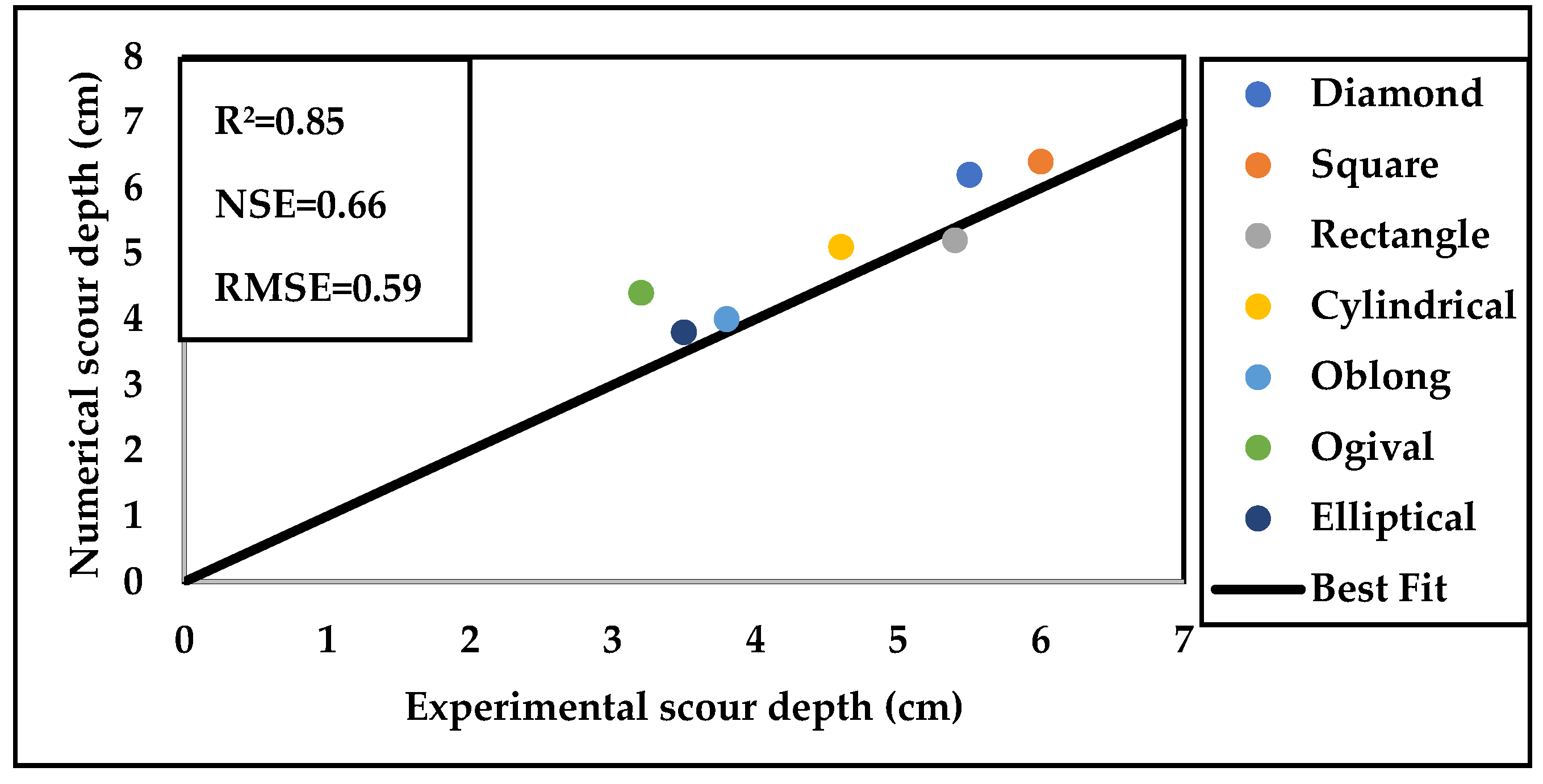
6.1. The Model’s Performance

Accurate shear stress prediction is crucial for evaluating the erosive forces on the riverbed brought about by various pier configurations. Figure 7a,b visually depict the water flow velocity, depth, and bed shear stress for diamond and elliptical pier designs, respectively. An in-depth analysis of simulated water surface velocity levels and patterns yields intriguing information. For instance, in the case of a diamond-shaped pier, maximum velocity is observed at both edges, registering around 0.4 m/s, with a water depth of 0.125 m and shear stress of 0.82 pascal. Contrastingly, the elliptical pier shape exhibits an even velocity distribution across the longer sides, mitigating the impact of downflow by dispersing the force along the extended area. Consequently, this distribution reduces the scouring depth, with a velocity of 3.3 m/s, depth of 12.4 m, and shear stress of 0.68 pascal.

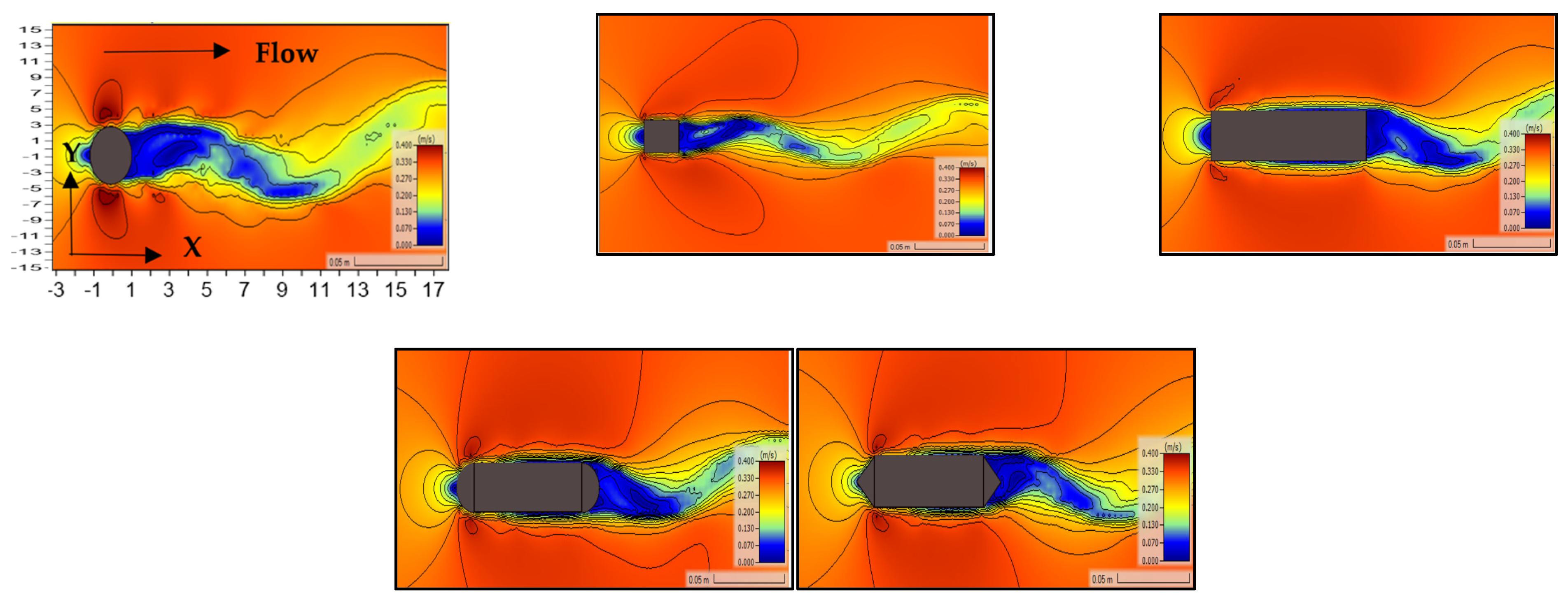
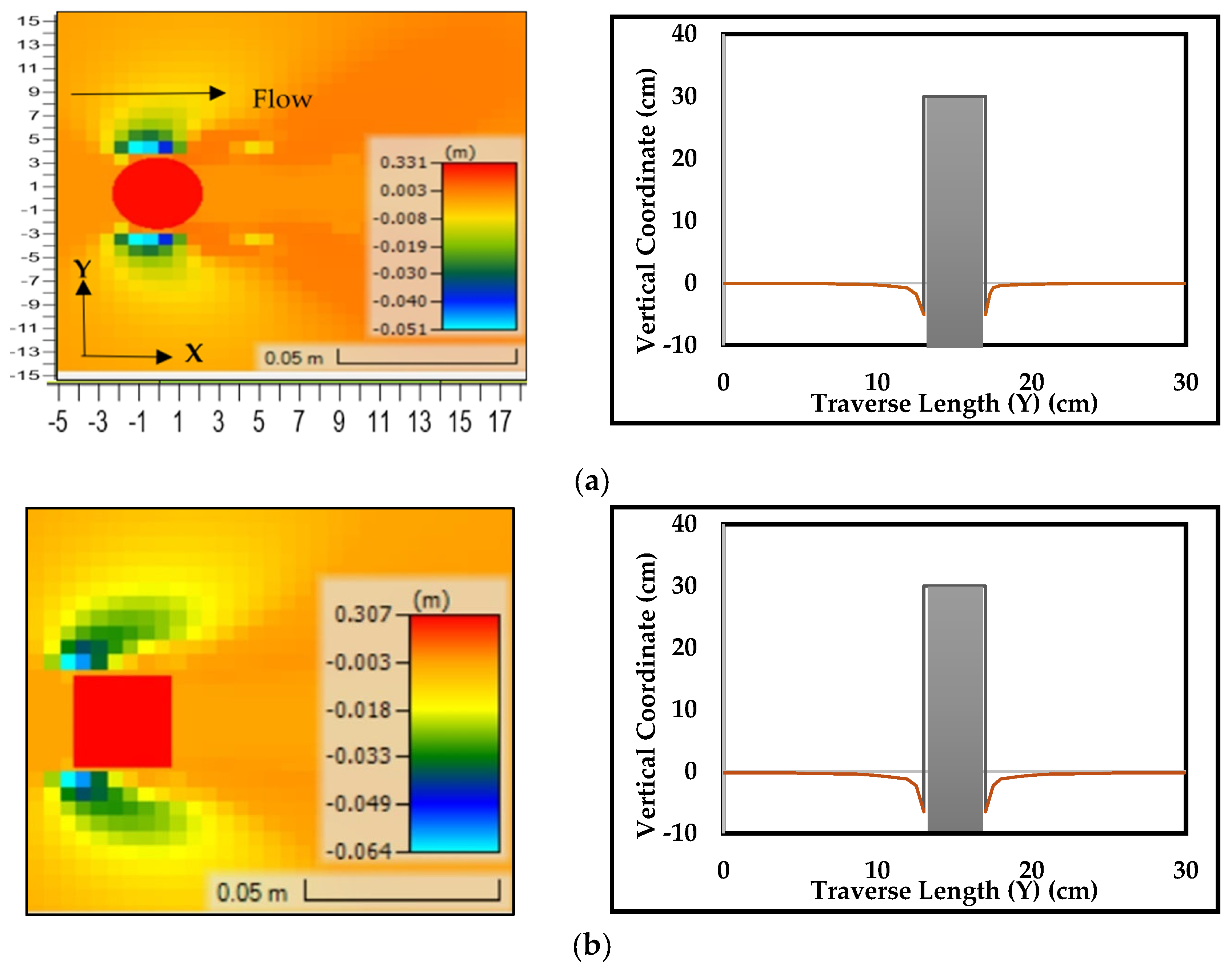
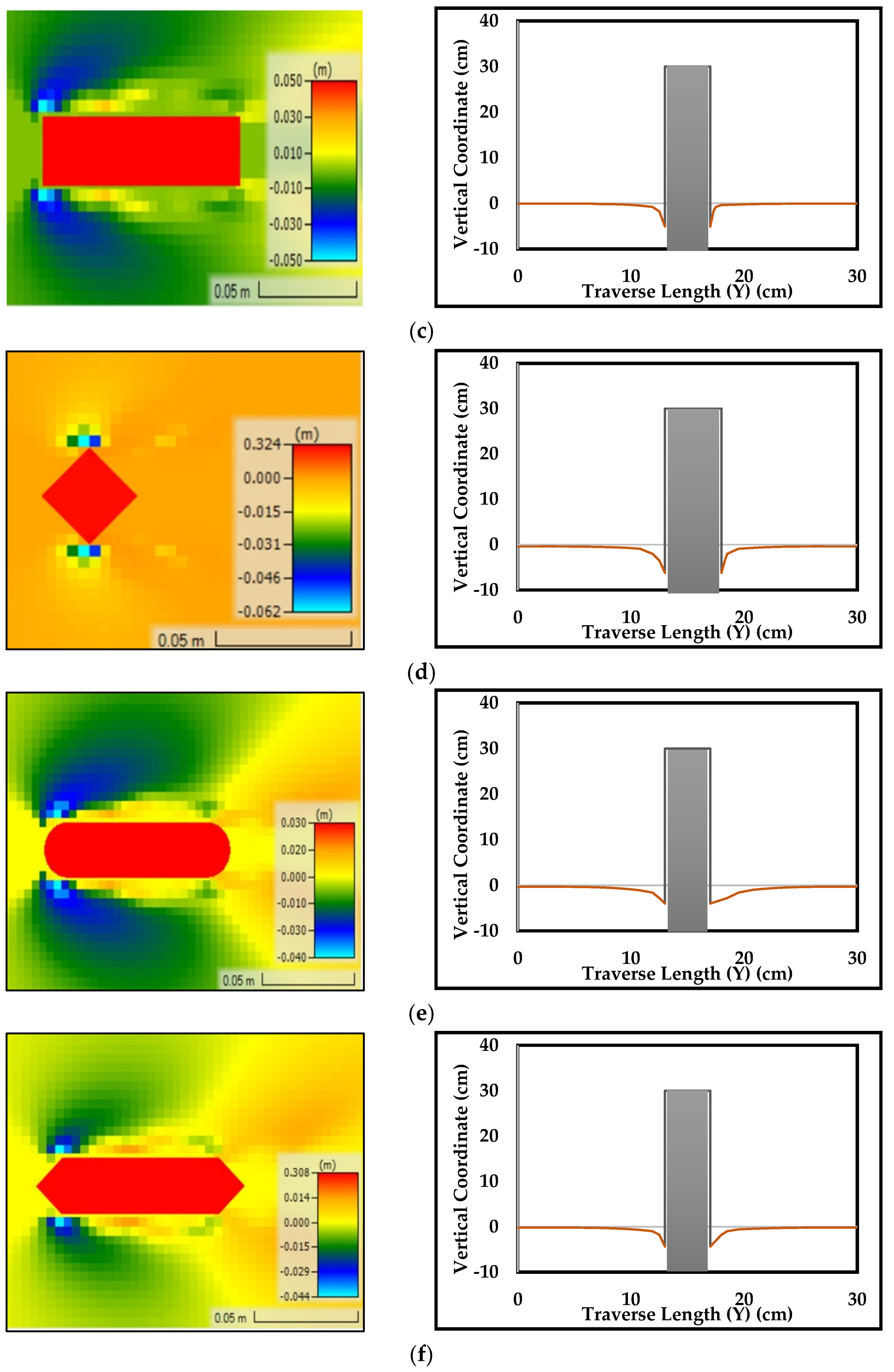
6.2. Bed Level Change

The investigation establishes a simple situation where a solitary pier is situated, preserving the hydraulic environment’s original nature. Figure 8a–g present a comprehensive depiction of the morphologies in both the longitudinal and transverse directions, carefully examining the degraded regions surrounding the bridge piers, which illustrates seven distinct pier shapes—cylindrical, square, oblong, ogival, elliptical, rectangular, and diamond—where each preserves comparable dimensions and is exposed to identical discharge rates and existing hydrodynamic conditions. These illustrations depict the calculated depth of the scour hole formed by multiple testing circumstances. The varied layouts of the bridge piers substantially alter the principal scour zones downstream and the general shape of the impacted area. The square-shaped pier exhibits the deepest erosion, with a maximum depth of 6.4 cm at its upstream edge. In contrast, the elliptical-shaped piers, measuring 3.8 cm, demonstrate the least erosion, with a maximum depth of scouring, primarily concentrated at the diverging intersection of its sides. The diamond-shaped piers show a maximum erosion depth of 6.2 cm, with the scour evenly distributed along both edges. Cylindrical and rectangular piers, both with an erosion depth of 5.2 cm, exhibit their deepest scour at the upstream face. Similarly, the ogival shape has an erosion depth of 4.4 cm, while the oblong shape displays 4 cm of scouring. This suggests that square and cylindrical shapes are more vulnerable to erosion upstream, while the elliptical and diamond shapes show more complex erosion patterns.

The alignment between experimental findings and model predictions was assessed through various statistical metrics: Nash–Sutcliffe Efficiency (NSE), Root Mean Square Error (RMSE), Coefficient of Determination (R²), and Mean Absolute Percentage Error (MAPE). From experimental and computational studies, Figure 9 compares scouring depth around different pier shapes. The RMSE value, near 0.59, suggests a reliable accuracy in estimating scour depths. With an NSE of around 0.66, the model shows strong agreement between measured and simulated data, whereas the MAPE of 11% indicates an acceptable margin of prediction error. The R² value of 0.85 further highlights a strong correlation between predicted and actual scour depths, suggesting the model’s effectiveness in capturing variations across different pier designs.

Nonetheless, model precision does show variation with pier shape. For example, lower squared and mean squared errors indicate high accuracy for the elliptical pier, with an error margin of roughly 8.6%, and for the rectangular pier, with an error margin of around 3.7%. On the other hand, higher errors are noted for shapes like the ogival and diamond piers, with percentage errors of about 37.5% and 12.7%, respectively, indicating that these are harder to predict accurately. This underlines the significance of accounting for shape-specific differences in modeling accuracy. Angled piers such as diamond and ogival shapes, with edges on either side, exhibit higher scour due to intensified turbulence and flow separation at the edges, leading to increased localized shear stresses and sediment transport.

Conversely, rounded shapes like cylindrical and oblong piers and straight-edged shapes like rectangular and square piers tend to generate more uniform flow patterns around them, contributing to less scour depths. While the HEC-RAS 2D model is effective at making general predictions, its performance can be improved by accounting for site-specific factors and the geometric complexities of different pier designs. The variations in forecasting scour depths around different pier shapes stem from difficulties encountered during the simulation using HEC-RAS 2D V6.4.1 software. A significant challenge is the lack of symmetry in velocity and bed level around the pier. Although attempts have been made to improve model accuracy by reducing grid size to less than 4 mm and refining terrain precision to a raster size of 1 mm, these issues persist. Discrepancies between actual and predicted outcomes are partly due to data from only one side of the pier, assuming symmetry on the other side. This simplification leads to inaccuracies.

The shallow water (SW) and Diffusion Wave Approximation (DSW) equations used in HEC-RAS 2D modeling can introduce inaccuracies in scour predictions due to several limitations. One significant limitation is the assumption that vertical velocities are negligible compared to horizontal velocities, leading to inaccuracies in complex flow conditions where vertical motion is essential [12]. Additionally, these models often ignore unsteady and viscous terms, potentially missing key aspects of flow dynamics. While efficient, the coarse computational grid may not capture fine-scale topographic details, leading to errors in regions with significant small-scale features. Turbulence is modeled using eddy viscosity, which may not fully represent complex turbulent interactions, particularly in high-shear environments. Furthermore, relying on Manning’s roughness coefficient for bottom friction can introduce errors if not accurately specified [11,12].

Moreover, the HEC-RAS 2D sediment model has inherent drawbacks related to sediment transport parameters and settings that can further affect model accuracy. The model’s extensive feature set, which provides flexibility and calibration options, can be overwhelming and confusing. Due to the dispersed nature of these settings across various menus in HEC-RAS, users may struggle to identify and adjust the most critical parameters effectively. For example, the interaction between particle sizes, controlled by the hiding and exposure parameters, can significantly influence sediment transport predictions. If not correctly calibrated, this parameter can either overestimate or underestimate sediment transport, affecting overall model stability.

Similarly, the adaptation length parameter, which dictates the rate of erosion and deposition, needs careful tuning. An inappropriate adaptation length can either smooth out sediment dynamics too much or lead to unrealistic fluctuations in erosion and deposition rates. Another challenge is choosing a sediment matrix solver. The default Paradiso solver is highly accurate but also computationally intensive. Faster solvers like FGMRES-SOR may improve runtime but could compromise precision, impacting the reliability of sediment transport predictions [29]. The trade-off between accuracy and computational efficiency must be managed carefully. The numerical methods used in the model also present limitations. For instance, the reliance on diffusion wave equations rather than full shallow water equations may not accurately capture complex flow dynamics, leading to discrepancies in sediment transport predictions.

Additionally, the model’s turbulence settings, which influence momentum transfer between cells, may not fully account for real-world flow asymmetries and interactions, affecting sediment transport accuracy. The model’s sensitivity to parameters such as the sediment computation multiplier and morphological acceleration factor further complicates accurate predictions, as described in

Table 1. Summary of key parameters used in 2D sediment modeling, including descriptions of their function and impact on model performance.

Parameter	Description
Shallow Water Flow Equations	Uses the full shallow water flow equations for accurate 2D sediment transport modeling.
Hydraulic Warmup	Fills the 2D model with water before sediment transport to prevent instability and poor initial conditions.
Adaptation Length	Controls the speed of erosion and deposition; longer lengths slow changes, whereas shorter lengths accelerate them.
Sediment Matrix Solver	Numerical method for solving sediment transport equations; Paradiso is accurate but slower, and FGMRESSOR is faster.
Sediment Computation Multiplier	Adjust the balance between water and sediment travel times; higher values reduce runtime but may affect stability.
Morphological Acceleration	Scales bed changes to shorten simulation time; recommended factors below 25 for balance between speed and accuracy.

[29].

Continuously refining the sediment transport parameters and settings is crucial to improve the model’s performance [29]. Enhancing the model’s ability to capture asymmetric flow patterns and bed levels around piers, fine-tuning grid size and terrain data resolution, and conducting thorough field validation will help address these challenges. Careful calibration of sediment transport parameters and consideration of specific sediment settings are essential to enhance the HEC-RAS 2D model’s accuracy and reliability in predicting pier scour.

6.3. Effect of Floating Debris

Traditional hydraulic modeling tools, such as HEC-RAS 2D, face notable challenges in accurately predicting scouring around bridge piers when floating debris is present. Two methodologies are employed to modify the representation of piers in hydraulic models to account for debris impacts. The first approach, the effective pier width method proposed by Melville [22], adjusts the pier’s effective width to incorporate the additional debris-induced flow resistance. This adjustment aims to enhance the model’s accuracy in predicting scour depths by more realistically simulating the blockage effects of debris. The authors in [22] introduced an approach to account for the obstruction caused by debris through an effective pier width (De). This method modifies the pier width to reflect the additional blockage created by the debris, ensuring that the hydraulic model accurately considers the increased flow resistance. The equation for the effective pier width is as follows:

$$De={\displaystyle \frac{T^{\mathrm{*}}W+\left(Y-T^{\mathrm{*}}\right)D}{Y}}$$

where $T^{\mathrm{*}}=0$.52* T, T, and W are the debris submerged thickness and width, Y is the flow depth, and D is the pier width. Similarly, expanding on the foundation set by [22], Lagasse [19] introduced a pioneering equation designed to address the effects of rectangular and triangular debris accumulation against square piers, specifically for calculating the equivalent pier width (a). This equation, shown below, emphasizes the significant impact of debris thickness (T) and length (L) on the downflow intensity experienced at the pier.

$$\mathrm{a}={\displaystyle \frac{Kd1\ast TW\ast {\left(\frac{L}{Y}\right)}^{Kd2}+\left(Y-Kd1\ast T\right)D}{Y}}$$

where $Kd1$ = 0.39 and 0.14 are the rectangular and triangular debris shape factors. $Kd2$ = −0.79 and −0.17 are the plunging flow intensity factor for the rectangular and triangular debris. This study applies these methods within the HEC-RAS 2D framework to evaluate their effectiveness in practical scenarios. The primary objectives are to assess the reliability of these adjusted pier dimensions in improving scour depth predictions compared to traditional empirical equations and to analyze the sensitivity of HEC-RAS 2D to variations in pier dimensions and their impact on scour depth calculations. This study examines cylindrical pier geometry. It evaluates different types of debris, such as rectangular and triangular shapes, with thickness-to-width ratios of 0.25 and 0.5. The results from HEC-RAS 2D simulations are compared with empirical scour depth predictions and semi-empirical equations from sources such as CSU (2001) [27] and Melville (1988) [28], as well as with experimental data obtained from physical experiments of this study. The equations of CSU (2001) [27] and Melville (1989) [28] are expressed as follows:

$${\displaystyle \frac{ds}{D}}=\left\{\begin{array}{c}1.872{\left({\displaystyle \frac{Y}{D}}\right)}^{0.255} (Y/D<2.6)\\ 2.4 (Y/D\ge 2.6) \end{array}\right.$$

$$Y_s=2K_1{K}_2{K}_3{K}_4{D}^{0.65}{Y}^{0.35}{Fr}^{0.43}$$

where $ds$ and $Y_s$are the pier scour depth, the pier width is denoted by $D$, the flow depth is represented by $Y$, and the Froud number of upstream flows is denoted by $Fr$. $K_{1,}{K}_2,K_3{,and K}_4$ represented the correction factors for pier shape, direction of flow, bed situation, and armored pier condition. This comparative analysis aims to determine whether incorporating the effects of floating debris using the effective (De) and equivalent (a) pier width methods improves the accuracy of scour depth predictions and illuminate how these modifications influence the model’s performance. The evaluation primarily centered on situations where debris was submerged beneath the free surface with relative thicknesses (T/Y = 0.25 and 0.5), explicitly encompassing rectangular (RB) and triangle yield (TY) debris configurations.

Figure 10a–g and

Table 2. Comparison of scour depth measurements for various debris configurations between experimental values, the HEC-RAS model, Melville (1988) [28], and CSU (2001) [27], with percentage errors and performance relative to experimental values.

Debris Configuration	Experimental (cm)	HEC-RAS (cm)	Melville (1988) [28] (cm)	CSU (2001) [27] (cm)	% Error HEC-RAS	% Error Melville (1988) [28]	% Error CSU (2001) [27]	Performance Relative to Experimental Values
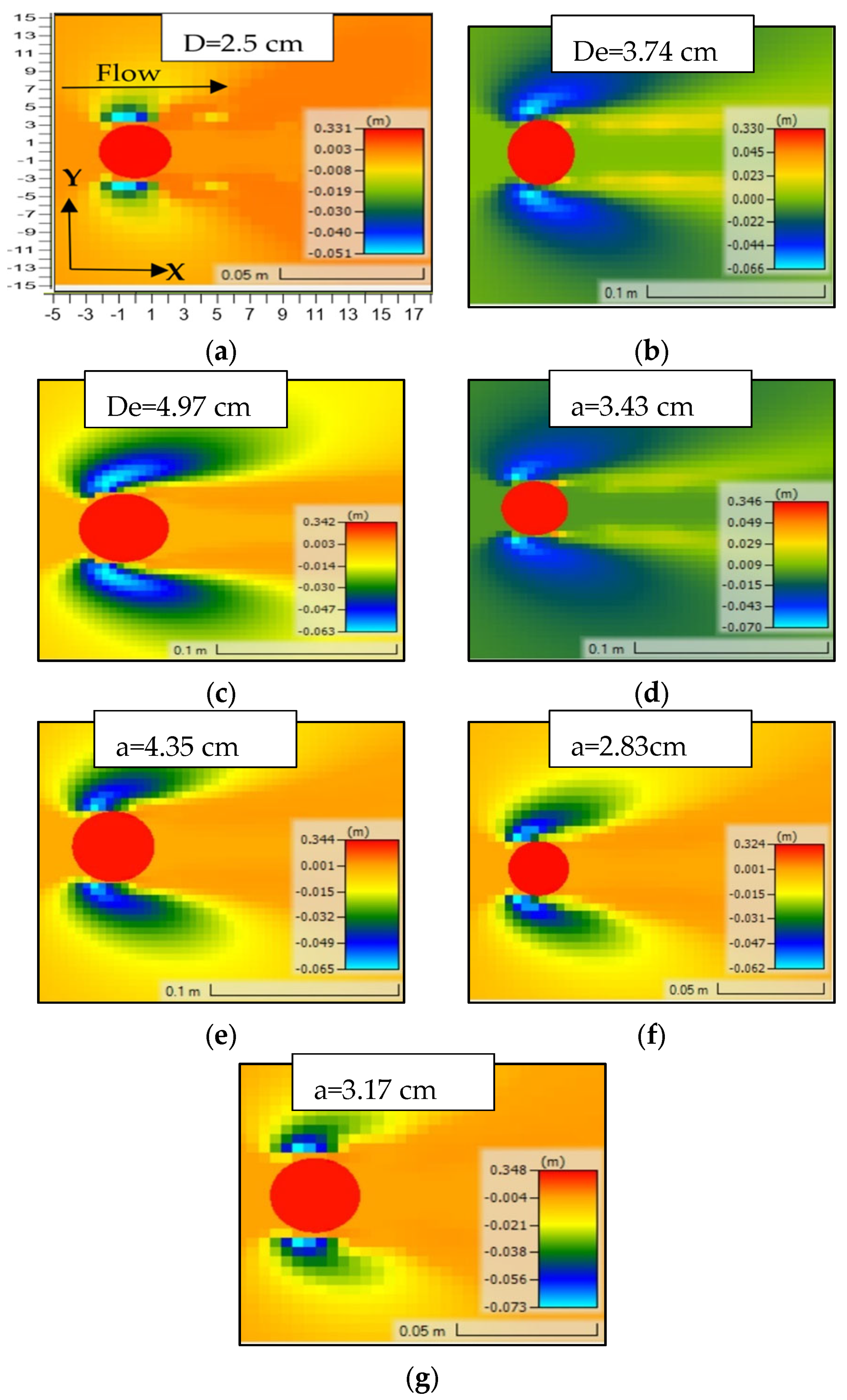
No Debris D = 2.5 cm	4.6	5.1	6	4.84	10.87%	30.43%	5.22%	HEC-RAS: Underestimates; CSU (2001) [27] is closer to the experimental value.
Rectangle Debris-T/Y = 0.25-De = 3.74 cm	7.1	6.6	8.964	6.28	7.04%	26.25%	11.55%	HEC-RAS: Closest to experimental value; best performance among all methods.
Rectangle Debris-T/Y = 0.5-De = 4.97 cm	9.7	6.3	11.648	7.56	35.05%	20.08%	22.06%	HEC-RAS: Largest error compared to experimental values; all methods show high error.
Triangle Debris-T/Y = 0.25-De = 3.74 cm	6	6.6	8.964	6.28	10.00%	49.40%	4.67%	HEC-RAS: Slight overestimation; CSU (2001) [27] has the lowest error.
Triangle Debris-T/Y = 0.5-De = 4.97 cm	8.8	6.3	11.648	7.56	28.41%	32.36%	14.09%	HEC-RAS: Underestimates; CSU (2001) [27] provides a closer approximation to experimental values.
Rectangle Debris-T/Y = 0.25-a = 3.43 cm	7.1	7	8.223	5.94	1.41%	15.82%	16.34%	HEC-RAS: Closest to experimental value; best performance among all methods.
Rectangle Debris-T/Y = 0.5-a = 4.35 cm	9.7	6.5	10.446	6.93	32.99%	7.69%	28.56%	HEC-RAS: Larger error than experimental values; Melville (1988) [28] performs better.
Triangle Debris-T/Y = 0.25-a = 2.83 cm	6	6.2	6.798	5.24	3.33%	13.30%	12.67%	HEC-RAS: Slightly overestimates; close to experimental values; best among methods.
Triangle Debris-T/Y = 0.5-a = 3.17 cm	8.8	7.3	7.596	5.64	17.05%	13.68%	35.91%	HEC-RAS: Underestimates; Melville (1988) [28] is closer to experimental values.

illustrate the comparison of scour depth results for various debris configurations and relative thicknesses (T/Y) using different methods, such as the HEC-RAS, Melville (1988) [28], and CSU (2001) [27] methods, with the experimental results of this study. To visually distinguish between the performance of the different methods, a color system can be applied to the percentage error values in the table. Green bars can represent lower errors, indicating better performance in approximating the experimental values, while red bars can represent higher errors, indicating poorer performance. Each method’s performance varies depending on the specific debris scenario. This investigation particularly emphasizes the percentage of errors evident in the HEC-RAS forecasts. Key observations show that in scenarios with no debris, with pier diameters of 2.5 cm, HEC-RAS registers a 10.87% discrepancy, indicating moderate inaccuracies in simpler setups. Error rates associated with HEC-RAS exhibit significant variability for rectangular and triangle debris conditions, ranging from 7.04% in De = 3.74 cm to 35% in broader pier effective width (De). This variance highlights the difficulties in accurately capturing complex hydraulic phenomena with HEC-RAS. The error rates reduce dramatically for rectangular and triangle debris conditions with the equivalent pier width (a) method, ranging from 1.4% in a = 3.43 cm to 33% in wider (a). Among the models examined, CSU (2001) [27] consistently yielded results most aligned with the experimental data, particularly in clear-water conditions and several debris scenarios, thereby suggesting its superior accuracy under specific circumstances. However, all models reviewed display challenges in accurately predicting outcomes for certain conditions, such as those involving triangular debris, underscoring the absence of a universally optimal model across all configurations assessed.

A detailed sensitivity analysis of HEC-RAS, focusing on the impact of changes in pier diameter, revealed notable inaccuracies, especially in scenarios characterized by increased complexity. These findings point to a critical threshold beyond which HEC-RAS’s prediction accuracy significantly diverges from actual observations, emphasizing the importance of selecting models based on specific hydraulic scenario characteristics. In conclusion, while HEC-RAS demonstrates variable precision dependent upon the scenario in question, it performs better in less complex situations. The analysis highlights the urgent need for more advanced modeling techniques capable of more efficiently addressing complex debris setups and accommodating larger pier diameters, identifying gaps within the current methodologies and suggesting avenues for future enhancements.

7. Conclusions

This study evaluates the ability of the HEC-RAS 2D sediment model to predict scour depths around various pier designs under different debris conditions. One of the key findings is the impact of pier shape on scour depth. The model effectively captures variations, with the square pier experiencing the deepest scour (6.4 cm) and the elliptical pier the shallowest (3.8 cm). Other pier shapes exhibit scour depths within this range, highlighting the importance of pier geometry in influencing scour behavior. In terms of model accuracy, the overall performance is solid, with a Nash–Sutcliffe Efficiency (NSE) of 0.66, a Root Mean Square Error (RMSE) of 0.59, and an R² of 0.85. However, accuracy varies across different pier shapes. The elliptical and rectangular piers show lower error margins of 8.6% and 3.7%, respectively, indicating strong predictive performance. In contrast, the ogival and diamond piers have higher error margins, at 37.5% and 12.7%, suggesting that the model struggles to capture the scour patterns for these shapes accurately.

This study also identifies limitations, particularly the inaccuracies arising from shallow water (SW), as well as the model’s sensitivity to various parameters and numerical methods. Despite efforts to refine these factors, some discrepancies remain, indicating areas where the model could be improved. The effects of debris further complicate the accuracy of the scour predictions. While incorporating debris into the model using the practical and equivalent pier width methods enhances accuracy, the HEC-RAS model still shows errors ranging from 7.04% to 35.05%. Comparatively, the CSU (2001) [27] method consistently offers better accuracy in predicting scour under debris conditions. Future recommendations include refining the model to better represent complex flows and debris effects, as well as improving the representation of sediment transport parameters to enhance the overall predictive accuracy.