Computational Analysis of Blood Flow in Healthy Pulmonary Arteries in Comparison to Repaired Tetralogy of Fallot Results: A Small Cohort Study
Abstract
:1. Introduction
2. Materials and Methods
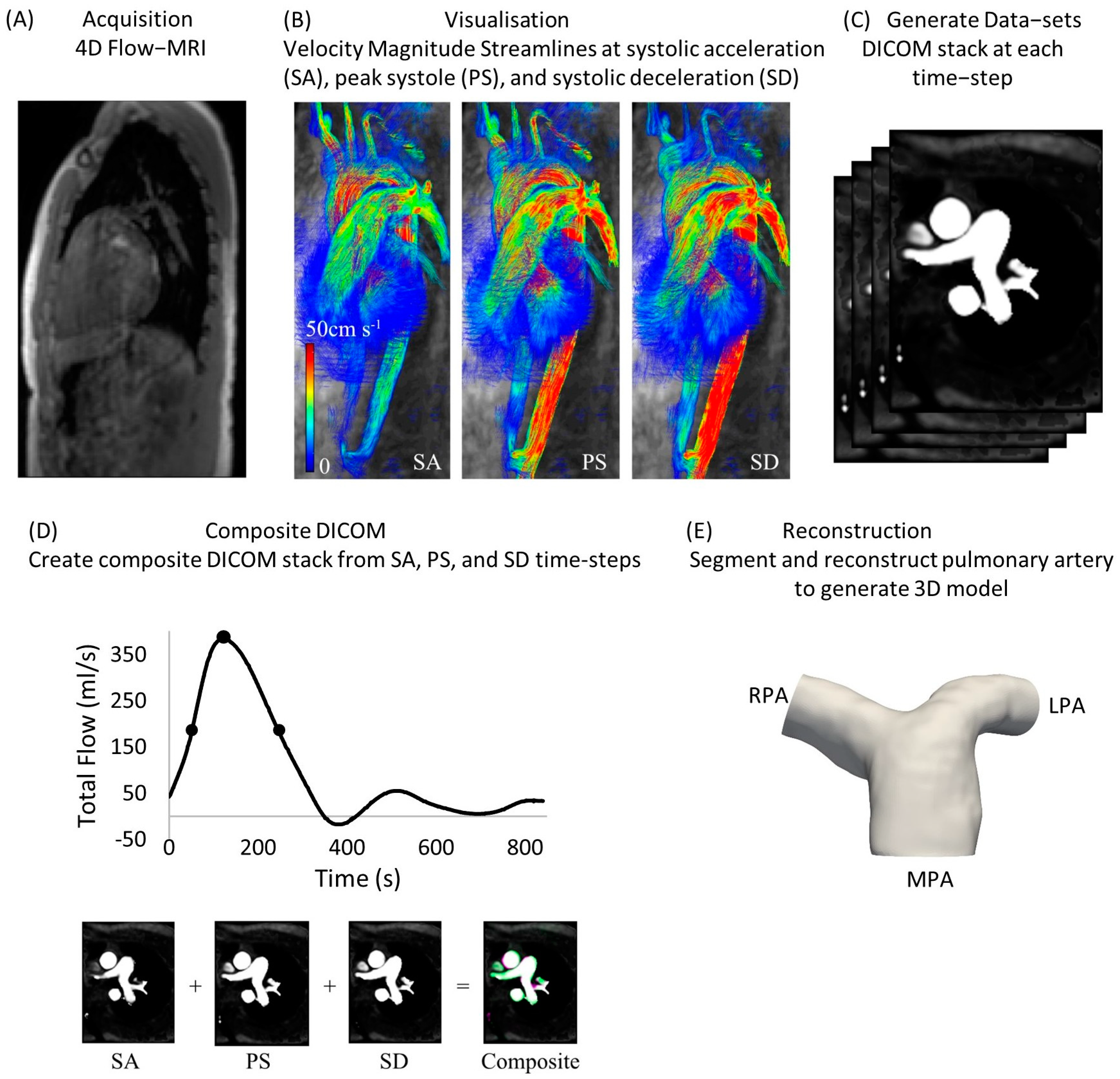
2.1. Cohorts and Extraction of DICOM Stacks
| Healthy Subject | Sex | Age at Scan | Flow Split (QRPA:QLPA) |
|---|---|---|---|
| 1 | Female | 47 years | 56.2:43.8 |
| 2 | Male | 59 years | 53.2:46.8 |
| 3 | Male | 33 years | 52.2:47.8 |
| 4 | Male | 57 years | 54.1:45.9 |
| 5 | Male | 27 years | 44.0:56.0 |
| Mean value | - | 44.6 ± 14.2 years | 52.0:48.0 |
2.2. Flow Information
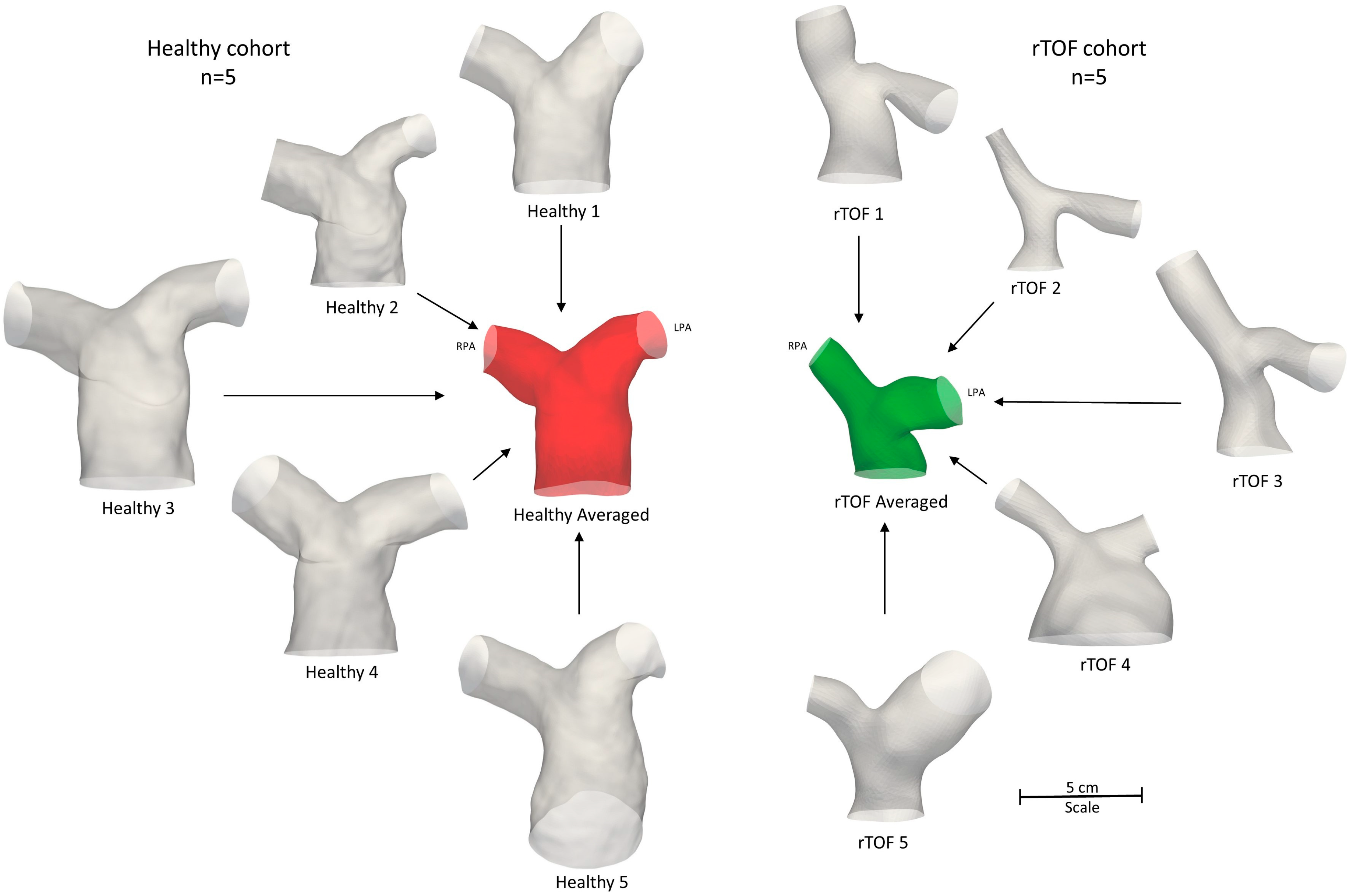
2.3. Subject-Specific and Anatomical Averaged Models
2.4. Morphological Analysis
2.5. Computational Methods
3. Results
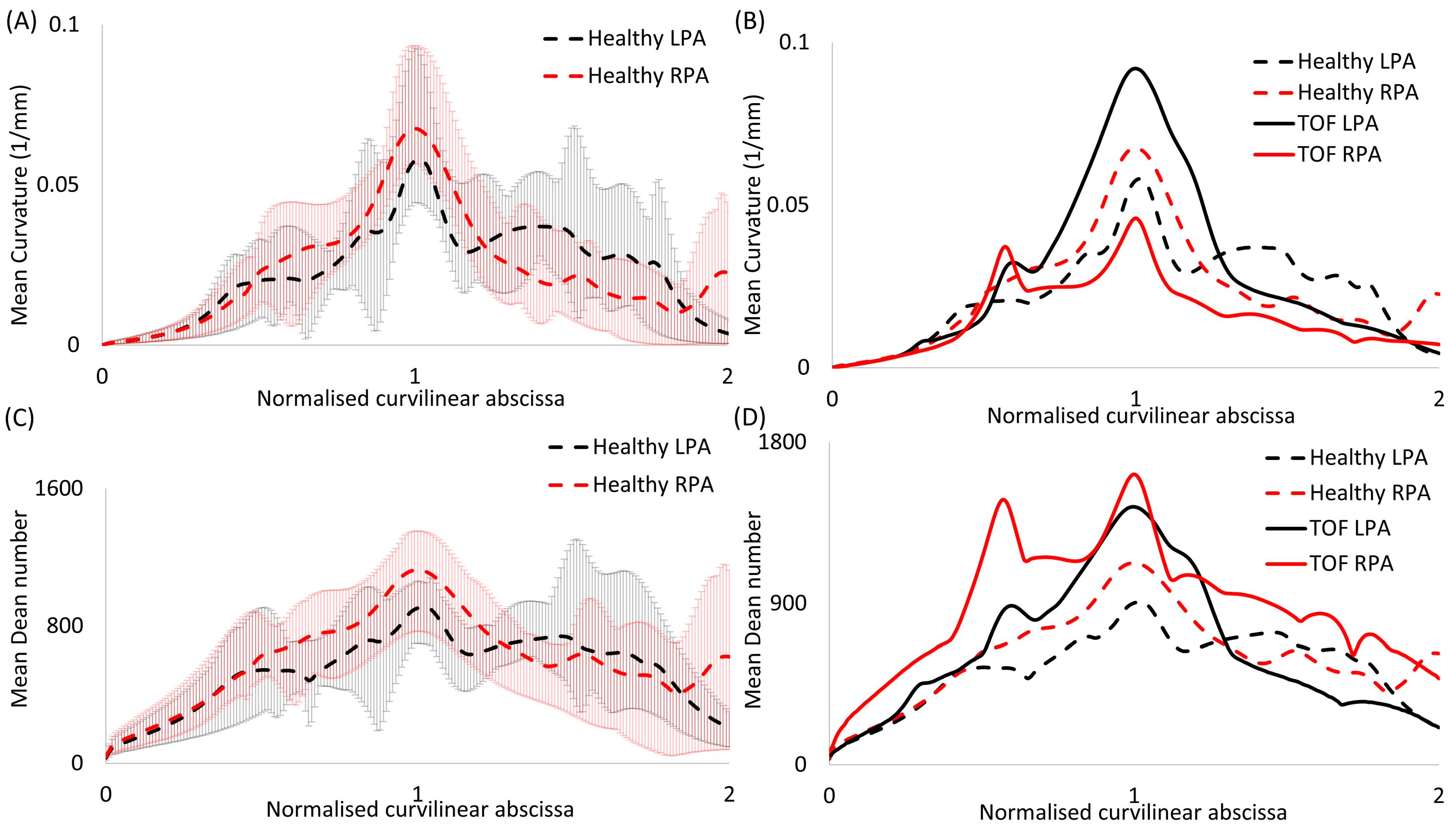
3.1. Morphological Analysis
3.2. Dimensionless Numbers
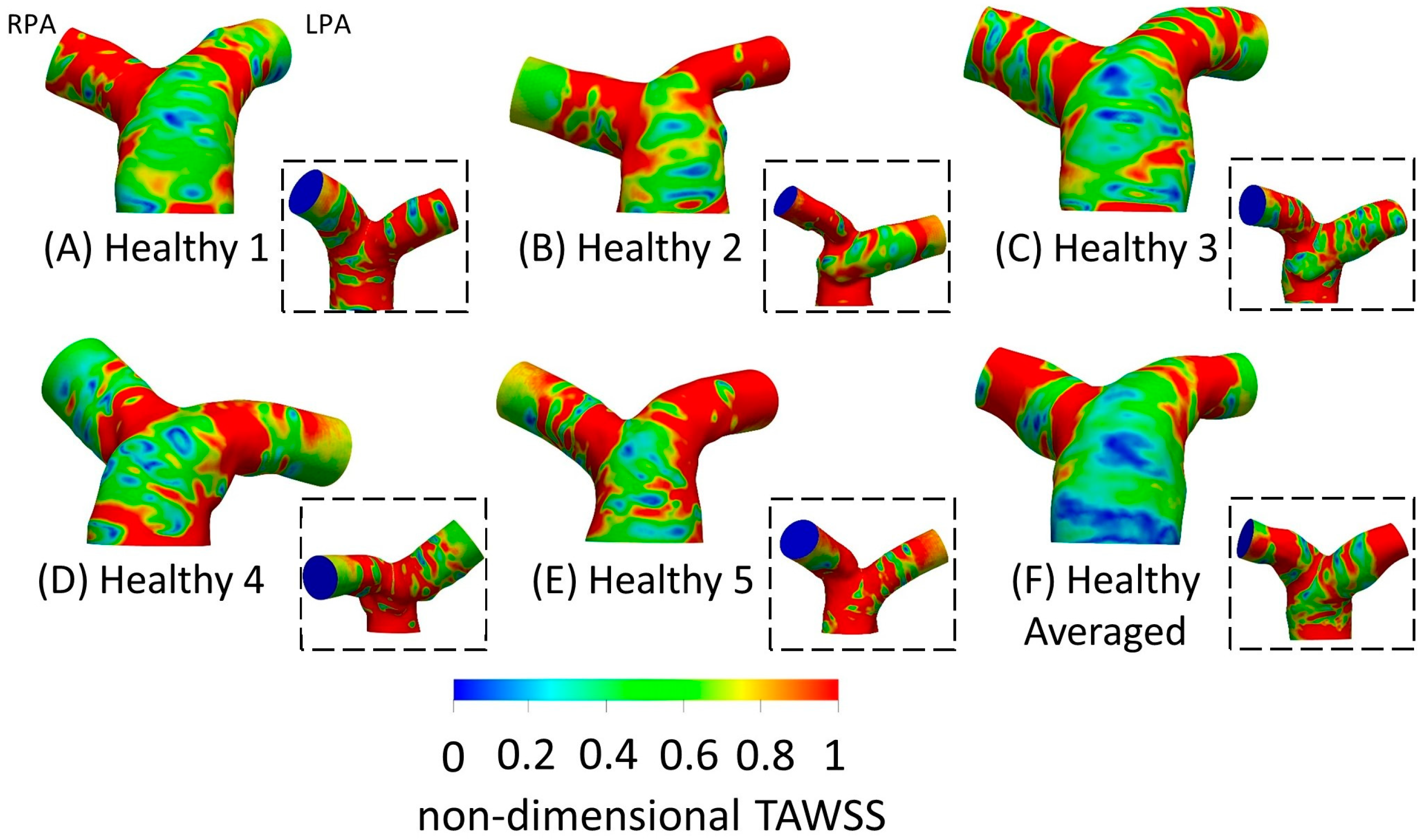
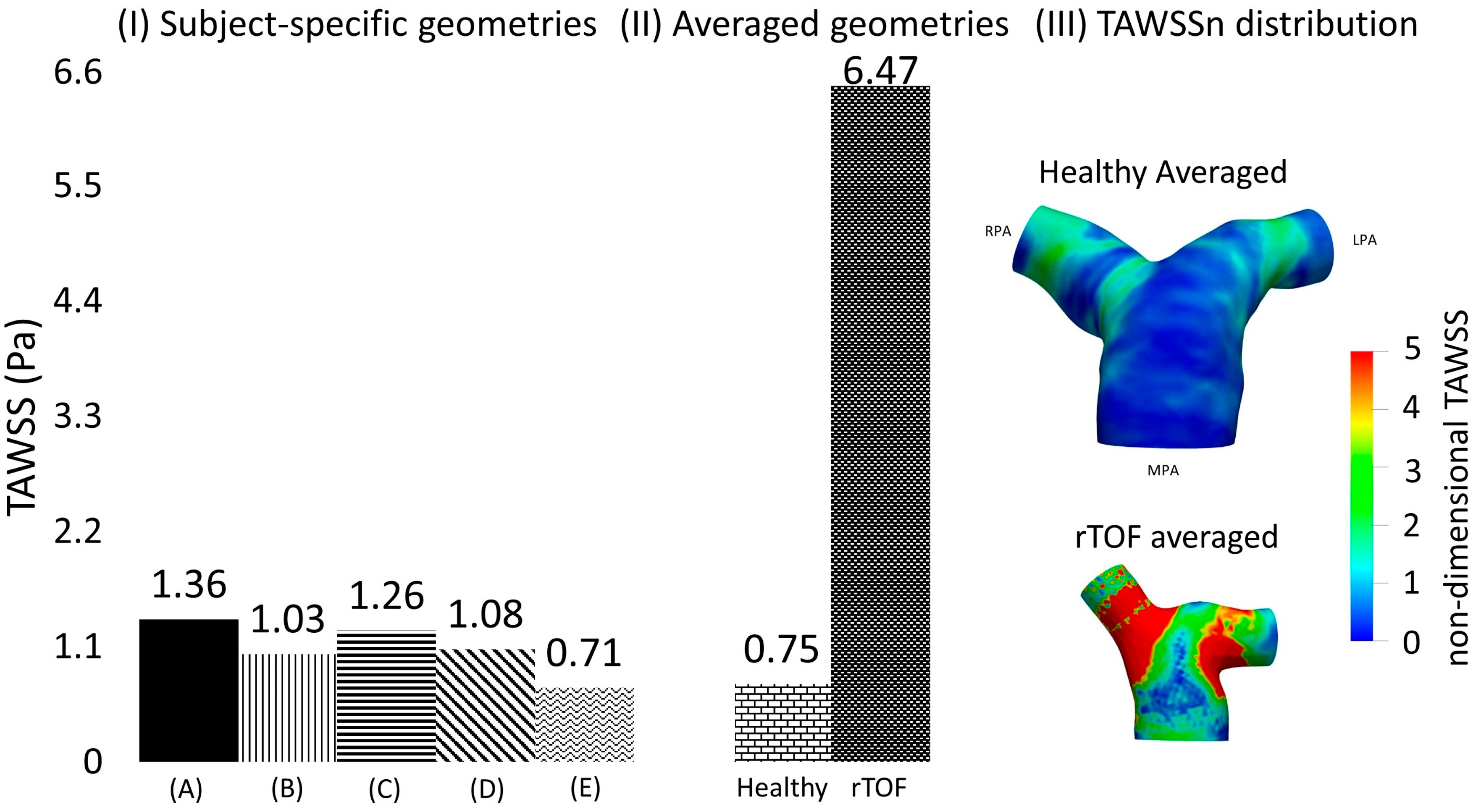
3.3. Time-Averaged Wall Shear Stress
3.4. Averaged Healthy vs. Averaged rTOF Geometries
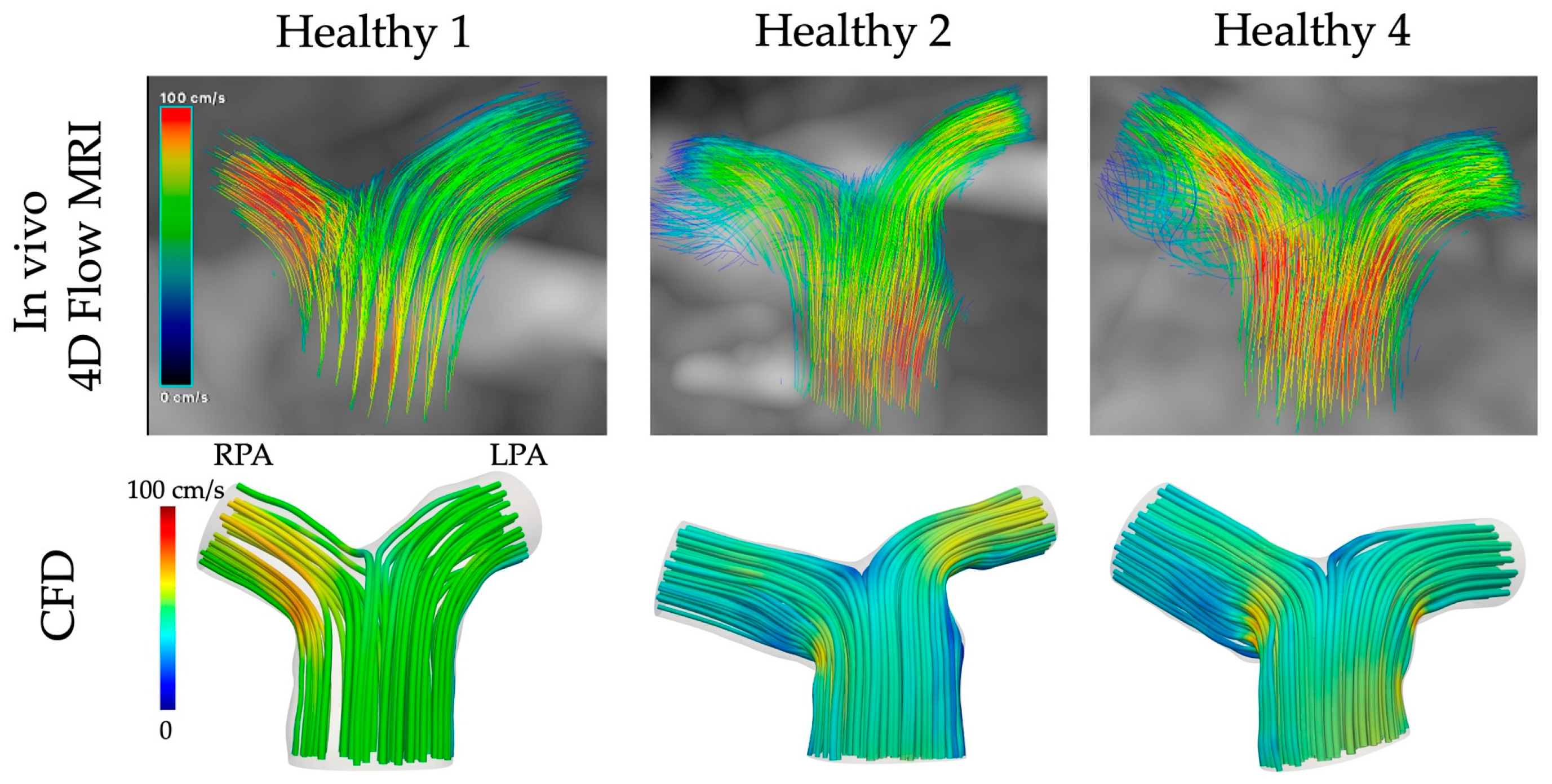
3.5. CFD vs. In Vivo 4D Flow MRI
4. Discussion
Limitations
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ASO | Arterial switch operation |
| CFD | Computational fluid dynamics |
| De | Dean number |
| DICOM | Digital Imaging and Communications in Medicine |
| LPA | Left pulmonary artery |
| MPA | Main pulmonary artery |
| MRI | Magnetic resonance imaging |
| PAH | Pulmonary arterial hypertension |
| PS | Peak systole |
| Re | Reynolds number |
| RPA | Right pulmonary artery |
| rTOF | repaired Tetralogy of Fallot |
| SA | Systolic acceleration |
| SD | Systolic deceleration |
| TAG | Transposition of great arteries |
| TAWSS | Time averaged wall shear stress |
| TOF | Tetralogy of Fallot |
| VENC | Velocity encoding |
| Wo | Womersley number |
References
- Tan, W.; Madhavan, K.; Hinter, K.S.; Park, D.; Stenmark, K.R. Vascular stiffening in pulmonary hypertension: Cause or consequence? (2013 Grover Conference series). Pulm. Circc. 2014, 4, 560–580. [Google Scholar] [CrossRef] [PubMed]
- Galié, N.; Torbicki, A.; Barst, R.; Dartevelle, P.; Haworth, S.; Higenbottan, T.; Dartevelle, P.; Haworth, S.; Higenbottam, T.; Olschewski, H.; et al. Guidelines on diagnosis and treatment of pulmonary arterial hypertension: The task force on diagnosis and treatment of pulmonary arterial hypertension of the European Society of Cardiology. Eur. Heart J. 2004, 25, 2243–2278. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J. Mechanisms of arterial remodeling in hypertension: Coupled roles of wall shear and intramural stress. Hypertension 2008, 52, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Hanna, B.D. Blood flow in normal and diseased pulmonary arteries. In Ventricular Function and Blood Flow in Congenital Heart Disease; Wiley-Blackwell: Hoboken, NJ, USA, 2005; pp. 275–285. [Google Scholar] [CrossRef]
- Caro, C.; Pedley, T.; Schroter, R.; Seed, W.; Parker, K. The pulmonary circulation. In The Mechanics of the Circulation; Cambridge University Press: Cambridge, UK, 2011; pp. 467–506. [Google Scholar] [CrossRef]
- Shaher, R.M. Complete and inverted transposition of the great vessels. Br. Heart J. 1964, 26, 51–66. [Google Scholar] [CrossRef] [PubMed]
- Villafañe, J.; Lantin-Hermoso, M.R.; Bhatt, A.B.; Tweddell, J.S.; Geva, T.; Nathan, M.; Elliott, M.J.; Vetter, V.L.; Paridon, S.M.; Kochilas, L.; et al. D-transposition of the great arteries: The current era of the arterial switch operation. J. Am. Coll. Cardiol. 2014, 64, 498–511. [Google Scholar] [CrossRef] [PubMed]
- Capuano, F.; Loke, Y.-H.; Balaras, E. Blood Flow Dynamics at the Pulmonary Bifurcation. Fluids 2019, 4, 190. [Google Scholar] [CrossRef]
- Louvelle, L.; Doyle, M.; Van Arsdell, G.; Amon, C. The Effect of Geometric and Hemodynamic Parameters on Blood Flow Efficiency in Repaired Tetralogy of Fallot Patients. Ann. Biomed. Eng. 2021, 49, 2297–2310. [Google Scholar] [CrossRef] [PubMed]
- Ntsinjana, H.N.; Capelli, C.; Biglino, G.; Cook, A.C.; Tann, O.; Derrick, G.; Taylor, A.M.; Schievano, S. 3D Morphometric Analysis of the Arterial Switch Operation Using In Vivo MRI Data. Clin. Anat. 2014, 27, 1212–1222. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.T.; Fonte, T.A.; Chan, F.R.; Tsao, P.S.; Feinstein, J.A.; Taylor, C.A. Three-dimensional hemodynamics in the human pulmonary arteries under resting and exercise conditions. Ann. Biomed. Eng. 2011, 39, 347–358. [Google Scholar] [CrossRef]
- Bächler, P.; Pinochet, N.; Sotelo, J.; Crelier, G.; Irarrazaval, P.; Tejos, C.; Uribe, S. Assessment of normal flow patterns in the pulmonary circulation by using 4D magnetic resonance mapping. Magn. Reson. Imaging 2013, 31, 178–188. [Google Scholar] [CrossRef]
- Hu, L.; Ouyang, R.; Sun, A.; Wang, Q.; Guo, C.; Peng, Y.; Qin, Y.; Zhang, Y.; Xiang, Y.; Zhong, Y. Pulmonary artery hemodynamic assessment of blood characteristics in repaired tetralogy of Fallot patients versus healthy child volunteers. Quant. Imaging Med. Surg. 2020, 10, 921–933. [Google Scholar] [CrossRef] [PubMed]
- Bailliard, F.; Anderson, R.H. Tetralogy of Fallot. Orphanet. J. Rare Dis. 2009, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Rao, B.N.S.; Anderson, R.C.; Edwards, J.E. Anatomic variations in the tetralogy of Fallot. Am. Heart J. 1971, 81, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Geva, T. Repaired tetralogy of Fallot: The roles of cardiovascular magnetic resonance in 728 evaluating pathophysiology and for pulmonary valve replacement decision support. J. Cardiovasc. Magn. Reson. 2011, 13, 24. [Google Scholar] [CrossRef] [PubMed]
- Kordybach Prokopiuk, M.; Kowalski, M.; Spiewak, M.; Piotrowicz, E.; Hoffman, P. What can 731 pulmonary regurgitation indices reflect in patients after tetralogy of Fallot repair? Kardiol. Pol. 2015, 73, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Babu-Narayan, S.V.; Gatzoulis, M.A. Management of Adults with Operated Tetralogy of Fallot. Curr. Treat. Options Cardiovasc. Med. 2003, 5, 389–398. [Google Scholar] [CrossRef]
- Boumpouli, M.; Sauvage, E.L.; Capelli, C.; Schievano, S.; Kazakidi, A. Characterization of flow dynamics in the pulmonary bifurcation of patients with repaired Tetralogy of Fallot: A computational approach. Front. Cardiovasc. Med. 2021, 8, 703717. [Google Scholar] [CrossRef]
- Black, S.M.; Maclean, C.; Hall Barrientos, P.; Ritos, K.; Kazakidi, A. Reconstruction and Validation of Arterial Geometries for Computational Fluid Dynamics Using Multiple Temporal Frames of 4D Flow-MRI Magnitude Images. Cardiovasc. Eng. Technol. 2023, 14, 655–676. [Google Scholar] [CrossRef] [PubMed]
- Yushkevich, P.A.; Piven, J.; Hazlett, H.C.; Smith, R.G.; Ho, S.; Gee, J.C.; Gerig, G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. NeuroImage 2006, 31, 1116–1128. [Google Scholar] [CrossRef]
- Bone, A.; Colliot, O.; Durrleman, S. Learning Distributions of Shape Trajectories from Longitudinal Datasets: A Hierachical model on a manifold of diffeomorphisms. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9271–9280. [Google Scholar] [CrossRef]
- Suinesiaputra, A.; Ablin, P.; Albà, X.; Alessandrini, M.; Allen, J.; Bai, W.; Çimen, S.; Claes, P.; Cowan, B.R.; D’hooge, J.; et al. Statistical shape modeling of the left ventricle: Myocardial infarct classification challenge. IEEE J. Biomed. Health Inform. 2018, 22, 503–515. [Google Scholar] [CrossRef]
- Biglino, G.; Capelli, C.; Bruse, J.L.; Bosi, G.M.; Taylor, A.M.; Schievano, S. Computational modelling for congenital heart disease: How far are we from clinical translation? Heart 2016, 103, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Bruse, J.L.; McLeod, K.; Biglino, G.; Ntsinjana, H.N.; Capelli, C.; Hsia, T.-Y.; Sermesant, M.; Pennec, X.; Taylor, A.M.; Schievano, S. A statistical shape modelling framework to extract 3D shape biomarkers from medical imaging data: Assessing arch morphology of repaired coarctation of the aorta. BMC Med. Imaging 2016, 16, 40. [Google Scholar] [CrossRef] [PubMed]
- Piccinelli, M.; Veneziani, A.; Steinman, D.A.; Remuzzi, A.; Antiga, L. A framework for geometric analysis of vascular structures: Application to cerebral aneurysms. IEEE Trans. Med. Imaging 1987, 28, 1141–1155. [Google Scholar] [CrossRef] [PubMed]
- Antiga, L.; Piccinelli, M.; Botti, L.; Ene-Iordache, B.; Remuzzi, A.; Steinman, D.A. An image-based modeling framework for patient-specific computational hemodynamics. Med. Biol. Eng. Comput. 2008, 46, 1097–1112. [Google Scholar] [CrossRef] [PubMed]
- Doyle, M.G.; Crawford, S.A.; Osman, E.; Eisenberg, N.; Tse, L.; Amon, C.H.; Forbes, T.L. Analysis of Iliac Artery Geometric Properties in Fenestrated Aortic Stent Graft Rotation. Vasc. Endovasc. Surg. 2018, 52, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.B.; Antiga, L.; Che, S.L.; Milner, J.S.; Steinman, D.A.H.; Spence, J.D.; Rutt, B.K.; Steinman, D.A. Variation in the carotid bifurcation geometry of young versus older adults. Implications for geometric risk of atherosclerosis. Stroke 2005, 36, 2450–2456. [Google Scholar] [CrossRef]
- Boumpouli, M.; Danton, M.H.D.; Gourlay, T.; Kazakidi, A. Blood flow simulations in the pulmonary bifurcation in relation to adult patients with repaired tetralogy of Fallot. Med. Eng. Phys. 2020, 85, 123–138. [Google Scholar] [CrossRef] [PubMed]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbulence, Heat and Mass Transfer 4. In Proceedings of the Fourth International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003; pp. 625–632. [Google Scholar]
- Liu, M.; Martino, S.; Salerno, M.; Quadrio, M. On the Turbulence Modeling of the Blood Flow in a Stenotic Vessel. J. Biomed. Eng. 2020, 142, 011009. [Google Scholar] [CrossRef]
- Boumpouli, M. Blood Flow Dynamics in Surviving Patients with Repaired Tetralogy of Fallot. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2021. [Google Scholar]
- Johnston, L.; Allen, R.; Hall-Barrientos, P.; Mason, A.; Kazakidi, A. Hemodynamic Abnormalities in the Aorta of Turner Syndrome Girls. Front. Cardiovasc. Med. 2021, 8, 670841. [Google Scholar] [CrossRef]
- Hyde-Linaker, G.; Barientos, P.H.; Stoumpos, S.; Kingsmore, D.B.; Kazakidi, A. Patient specific computational haemodynamics associated with surgical creation of an arteriovenous fistula. Med. Eng. Phys. 2022, 105, 103814. [Google Scholar] [CrossRef]
- Kazakidi, A.; Sherwin, S.J.; Weinberg, P.D. Effect of Reynolds number and flow division on patterns of haemodynamic wall shear stress near branch points in the descending thoracic aorta. J. R. Soc. Interface 2009, 6, 539–548. [Google Scholar] [CrossRef]
- Kazakidi, A.; Plata, A.M.; Sherwin, S.J.; Weinberg, P.D. Effect of reverse flow on the pattern of wall shear stress near arterial branches. J. R. Soc. Interface 2011, 8, 1594–1603. [Google Scholar] [CrossRef] [PubMed]
- Evergen, P.; Fuchs, L.; Revstedt, J. On the secondary flow through bifurcating pipes. Phys. Fluids 2010, 22, 103601. [Google Scholar] [CrossRef]
- Yoon, K.; Jung, H.W.; Chun, M.-S. Secondary Dean flow characteristics of inelastic Bird-Carreau fluid in curved microchannels. Korea-Aust. Rheol. J. 2020, 32, 61–70. [Google Scholar] [CrossRef]
- Zhao, Q.; Yuan, D.; Zhang, J.; Li, W. A Review of Secondary Flow in Inertial Microfluidics. Micromachines 2020, 11, 461. [Google Scholar] [CrossRef]
- Chassagne, F.; Barbour, M.C.; Chivukula, V.K.; Machicoane, N.; Kim, L.J.; Levitt, M.R.; Aliseda, A. The effect of Dean, Reynolds and Womersley numbers on the flow in a spherical cavity on a curved round pipe. Part 1. Fluid mechanics in the cavity as a canonical flow representing intracranial aneurysms. J. Fluid Mech. 2021, 915, A123. [Google Scholar] [CrossRef]
- Migliavacca, F.; de Level, M.R.; Dubini, G.; Pietrabissa, R.; Fumero, R. Computational fluid dynamic simulations of cavopulmonary connections with an extracardiac lateral conduit. Med. Eng. Phys. 1999, 21, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Migliavacca, F.; Kilner, P.J.; Pennati, G.; Dubini, G.; Pietrabissa, R.; Fumero, R.; de Leval, M.R. Computational fluid dynamics and magnetic resonance analyses of flow distribution between the lungs after total cavopulmonary connection. IEEE Trans. Biomed. Eng. 1999, 46, 393–399. [Google Scholar] [CrossRef]
- Migliavacca, F.; Dubini, G.; Bove, E.L.; de Leval, M.R. Computational fluid dynamics simulations in realistic 3-D geometries of the total cavopulmonary anastomosis: The influence of the inferior caval anastomosis. J. Biomech. Eng. 2003, 125, 805–813. [Google Scholar] [CrossRef]
- Ensley, A.E.; Ramuzat, A.; Healy, T.M.; Chatzimavroudis, G.P.; Lucas, C.; Sharma, S.; Pettigrew, R.; Yoganathan, A.P. Fluid mechanic assessment of the total cavopulmonary connection using magnetic resonance phase velocity mapping and digital particle image velocimetry. Ann. Biomed. Eng. 2000, 28, 1172–1183. [Google Scholar] [CrossRef]
- Marsden, A.L.; Vignon-Clementel, I.E.; Chan, F.P.; Feinstein, J.A.; Taylor, C.A. Effects of Exercise and Respiration on Hemodynamic Efficiency in CFD Simulations of the Total Cavopulmonary Connection. Ann. Biomed. Eng. 2007, 35, 250–263. [Google Scholar] [CrossRef]
- De Leval, M.R.; Kilner, P.; Gewillig, M.; Bull, C.; McGoon, D.C. Total cavopulmonary connection: A logical alternative to atriopulmonary connection for complex Fontan operations: Experimental studies and early clinical experience. J. Thorac. Cardiovasc. Surg. 1988, 96, 682–695. [Google Scholar] [CrossRef]
- Dubini, G.; de Leval, M.R.; Pietrabissa, R.; Montevecchi, F.M.; Fumero, R. A numerical fluid mechanical study of repaired congenital heart defects. Appl. Total Cavopulmonary Connect. J. Biomech. 1996, 29, 111–121. [Google Scholar] [CrossRef]
- Spazzapan, M.; Sastry, P.; Dunning, J.; Nordsletten, D.; de Vecchi, A. The use of Biophysical Flow Models in the Surgical Management of Patients Affected by Chronic Thromboembolic Pulmonary Hypertension. Front. Physiol. 2018, 9, 341819. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, J.; Yan, Q.; Liu, J.; Hong, H.; Mao, L. Computational haemodynamic analysis of left pulmonary artery angulation effects on pulmonary blood flow. Interact. Cardiovasc. Thorac. Surg. 2016, 23, 519–525. [Google Scholar] [CrossRef] [PubMed]
- Chern, M.J.; Wu, M.T.; Wang, H.L. Numerical investigation of regurgitation phenomena in pulmonary arteries of Tetralogy of Fallot patients after repair. J. Biomech. 2008, 41, 3002–3009. [Google Scholar] [CrossRef]
- Chern, M.J.; Wu, M.T.; Wei-Her, S. Numerical Study for Blood Flow in Pulmonary Arteries after Repair of Tetralogy of Fallot. Comput. Math. Methods Med. 2012, 2012, 198108. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.T.; Pickard, S.S.; Chan, F.P.; Tsao, P.S.; Taylor, C.A.; Feinstein, J.A. Wall shear stress is decreased in the pulmonary arteries of patients with pulmonary arterial hypertension: An image-based, computational fluid dynamics study. Pulm. Circ. 2012, 2, 470–476. [Google Scholar] [CrossRef]
- Gimbrone, M.A. Vascular Endothelium: An Integrator of Pathophysiologic Stimuli in Atherosclerosis. Am. J. Cardiol. 1995, 75, 67B–70B. [Google Scholar] [CrossRef]
- Sabri, M.R.; Daryoushi, H.; Gharipour, M. Endothelial function state following repair of cyanotic congenital heart disease. Cardiol. Young 2015, 25, 222–227. [Google Scholar] [CrossRef]
- Capuano, F.; Loke, Y.H.; Cronin, I.; Olivieri, L.J.; Balaras, E. Computational Study of Pulmonary Flow Patterns after Repair of Transposition of Great Arteries. J. Biomech. Eng. 2019, 141, 051008. [Google Scholar] [CrossRef] [PubMed]
- Bordones, A.D.; Leroux, M.; Kheyfets, V.O.; Wu, Y.-A.; Chen, C.-Y.; Final, E.A. Computational Fluid Dynamics Modeling of the Human Pulmonary Arteries with Experimental Validation. Ann. Biomed. Eng. 2018, 46, 1309–1324. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.D.; Rose, M.J.; Joh, M.; Jarvis, K.; Schnell, S.; Barker, A.J.; Rigsby, C.K.; Markl, M. 4-D flow magnetic-resonance-imaging-derived energetic biomarkers are abnormal in children with repaired tetralogy of Fallot and associated with disease severity. Pediatr. Radiol. 2019, 49, 308–317. [Google Scholar] [CrossRef] [PubMed]
- Fanni, B.M.; Gasparotti, E.; Vignali, E.; Capelli, C.; Positano, V.; Celi, S. An integrated in-vitro and in-silico workflow to study the pulmonary bifurcation hemodynamics. Comput. Fluids 2023, 260, 105912. [Google Scholar] [CrossRef]
- Loke, Y.-H.; Capuano, F.; Mandell, J.; Cross, R.R.; Cronin, I.; Mass, P.; Balaras, E.; Olivieri, L.J. Abnormal Pulmonary Artery Bending Correlates With Increased Right Ventricular Afterload Following the Arterial Switch Operation. World J. Pediatr. Congenit. Heart Surg. 2019, 10, 572–581. [Google Scholar] [CrossRef] [PubMed]
- Sloth, E.; Houlind, K.C.; Oyre, S.; Kim, W.Y.; Pedersen, E.M.; Jørgensen, H.S.; Hasenkam, J.M. Three-dimensional visualization of velocity profiles in the human main pulmonary artery with magnetic resonance phase-velocity mapping. Am. Heart J. 1994, 128, 1130–1138. [Google Scholar] [CrossRef]
- Johnston, L.; Boumpouli, M.; Kazakidi, A. Hemodynamics in the Aorta and Pulmonary Arteries of Congenital Heart Disease Patients: A Mini Review. J. Cardiol. Cardiovasc. Sci. 2021, 5, 1–5. [Google Scholar] [CrossRef]
- Misaki, K.; Futami, K.; Uno, T.; Nambu, I.; Yoshikawa, A.; Kamide, T.; Nakada, M. Inflow hemodynamics of intracranial aneurysms: A comparison of computational fluid dynamics and 4D flow magnetic resonance imaging. J. Stroke Cerebrovasc. Dis. 2021, 30, 105685. [Google Scholar] [CrossRef]
- Shahid, L.; Rice, J.; Berhane, H.; Rigsby, C.; Robinson, J.; Griffin, L.; Markl, M.; Roldán-Alzate, A. Enhanced 4D flow MRI-based CFD with adaptive mesh refinement for flow dynamics assessment in coarctation of the aorta. Ann. Biomed. Eng. 2022, 50, 1001–1016. [Google Scholar] [CrossRef]
- Black, S.M.; Maclean, C.; Barrientos, P.H.; Ritos, K.; McQueen, A.; Kazakidi, A. Calibration of patient-specific boundary conditions for coupled CFD models of the aorta derived from 4D Flow-MRI. Front. Bioeng. Biotechnol. 2023, 11, 1178483. [Google Scholar] [CrossRef]
- Stokes, C.; Bonfanti, M.; Li, Z.; Xiong, J.; Chen, D.; Balabani, S.; Díaz-Zuccarini, V. A novel MRI-based data fusion methodology for efficient, personalised, compliant simulations of aortic haemodynamics. J. Biomech. 2021, 129, 110793. [Google Scholar] [CrossRef]
- Szajer, J.; Ho-Shon, K. A comparison of 4D flow MRI-derived wall shear stress with computational fluid dynamics methods for intracranial aneurysms and carotid bifurcations—A review. Magn. Reson. Imaging 2018, 48, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Johnston, L.; Allen, R.; Mason, A.; Kazakidi, A. Morphological characterisation of pediatric Turner syndrome aortae: Insights from a small cohort study. Med. Eng. Phys. 2023, 120, 104045. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Oshinski, J.; Giddens, D.P. Effects of Wall Motion and Compliance on Flow Patterns in the Ascending Aorta. J. Biomech. Eng. 2003, 125, 347–354. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Benson, D.J.; Sankaran, S.; Marsden, A.L. Computational fluid structure interaction: Methods and application to a total cavopulmonary connection. Comput. Mech. 2009, 45, 77–89. [Google Scholar] [CrossRef]
- Cowley, J.; Luo, X.; Stewart, G.D.; Shu, W.; Kazakidi, A. A mathematical model of blood loss during renal resection. Fluids 2023, 8, 316. [Google Scholar] [CrossRef]
- Van Doormaal, M.A.; Kazakidi, A.; Wylezinska, M.; Hunt, A.; Tremoleda, J.L.; Prottis, A.; Bohraus, Y.; Gsell, W.; Weinberg, P.D.; Ethier, C.R. Haemodynamics in the mouse aortic arch computed from MRI-derived velocities at the aortic root. J. R. Soc. Interface 2012, 9, 2834–2844. [Google Scholar] [CrossRef]
- Armour, C.H.; Guo, B.; Pirola, S.; Saitta, S.; Liu, Y.; Dong, Z.; Xu, X.Y. The influence of inlet velocity profile on predicted flow in type B aortic dissection. Biomech. Model. Mechanobiol. 2021, 20, 481–490. [Google Scholar] [CrossRef]

| Mean Healthy | ±SD Healthy | Mean rTOF | ±SD rTOF | |
|---|---|---|---|---|
| DMPA (m) | 0.029 | 0.002 | 0.029 | 0.012 |
| DRPA (m) | 0.021 | 0.002 | 0.016 | 0.004 |
| DLPA (m) | 0.020 | 0.001 | 0.020 | 0.005 |
| Qmean (mL/s) | 86.300 | 12.069 | 85.280 | 24.298 |
| UmeanMPA (m/s) | 0.131 | 0.024 | 0.111 | 0.049 |
| UmeanRPA (m/s) | 0.136 | 0.046 | 0.298 | 0.254 |
| UmeanLPA (m/s) | 0.134 | 0.019 | 0.190 | 0.274 |
| UmaxMPA (m/s) | 0.463 | 0.067 | 0.758 | 0.362 |
| UmaxRPA (m/s) | 0.473 | 0.116 | 1.832 | 0.879 |
| UmaxLPA (m/s) | 0.476 | 0.059 | 0.865 | 0.650 |
| Mean Value Healthy | ±SD Healthy | Mean Value rTOF | ±SD rTOF | |
|---|---|---|---|---|
| Curvature RPA (mm−1) (mean/max) | 0.018/0.068 | 0.001/0.014 | 0.016/0.051 | 0.002/0.022 |
| Curvature LPA (mm−1) (mean/max) | 0.016/0.064 | 0.002/0.018 | 0.027/0.091 | 0.013/0.029 |
| Tortuosity (RPA/LPA) | 0.083/0.115 | 0.020/0.028 | 0.035/0.153 | 0.041/0.068 |
| Min Sphere Radius (mm) (RPA/LPA) | 9.062/7.984 | 0.778/1.282 | 5.840/6.300 | 1.396/2.664 |
| In-Plane Angles (RPA/LPA) | 138.4°/138.7° | 3.482°/15.054° | 145.3°/136.7° | 16.598°/52.860° |
| Out-of-Plane Angles (RPA/LPA) | 2.02°/−7.6° | 6.181°/16.181° | −16.4°/22.9° | 15.908°/23.747° |
| Subjects | 1 | 2 | 3 | 4 | 5 | Averaged | Mean |
|---|---|---|---|---|---|---|---|
| Volume Healthy (mm3) | 5259.3 | 5873.5 | 10069.2 | 8130.9 | 8205.6 | 6577.6 | 7352.7 |
| Volume rTOF (mm3) | 5658.6 | 3097.2 | 5866.7 | 6774.6 | 6730.4 | 4491.2 | 5436.5 |
| Remean_MPA (Remax_MPA) | Remean_RPA (Remax_RPA) | Remean_LPA (Remax_LPA) | Demax_RPA | Demax_LPA | Wo | |
|---|---|---|---|---|---|---|
| Mean Healthy | 1006 (3571) | 737 (2594) | 705 (2513) | 1231 | 1240 | 20.8 |
| ±SD Healthy | 157.17 (526.07) | 188.22 (488.39) | 88.76 (390.52) | 264.10 | 331.61 | 0.66 |
| Mean rTOF | 852 (5011) | 1180 (6807) | 844 (4031) | 1945 | 1594 | 21.2 |
| ±SD rTOF | 554.09 (1083.90) | 1031.84 (1150.61) | 1031.38 (2321.43) | 802.80 | 388.52 | 10.81 |
| Healthy | rTOF | |||
|---|---|---|---|---|
| Anatomical Averaged TAWSS (Pa) | Geometries 1–5 Mean TAWSS ± SD (Pa) | Anatomical Averaged TAWSS (Pa) | Geometries 1–5 Mean TAWSS ± SD (Pa) | |
| RPA—Cross-section (α) | 0.743 | 0.822 ± 0.263 | 8.7 | 13.3 ± 6.6 |
| LPA—Cross-section (γ) | 0.748 | 1.35 ± 0.333 | 4.2 | 10.9 ± 7.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boumpouli, M.; Black, S.M.; Kazakidi, A. Computational Analysis of Blood Flow in Healthy Pulmonary Arteries in Comparison to Repaired Tetralogy of Fallot Results: A Small Cohort Study. Fluids 2024, 9, 85. https://doi.org/10.3390/fluids9040085
Boumpouli M, Black SM, Kazakidi A. Computational Analysis of Blood Flow in Healthy Pulmonary Arteries in Comparison to Repaired Tetralogy of Fallot Results: A Small Cohort Study. Fluids. 2024; 9(4):85. https://doi.org/10.3390/fluids9040085
Chicago/Turabian StyleBoumpouli, Maria, Scott MacDonald Black, and Asimina Kazakidi. 2024. "Computational Analysis of Blood Flow in Healthy Pulmonary Arteries in Comparison to Repaired Tetralogy of Fallot Results: A Small Cohort Study" Fluids 9, no. 4: 85. https://doi.org/10.3390/fluids9040085
APA StyleBoumpouli, M., Black, S. M., & Kazakidi, A. (2024). Computational Analysis of Blood Flow in Healthy Pulmonary Arteries in Comparison to Repaired Tetralogy of Fallot Results: A Small Cohort Study. Fluids, 9(4), 85. https://doi.org/10.3390/fluids9040085








