Characterization of the Three-Dimensional Flowfield over a Truncated Linear Aerospike
Abstract
:1. Introduction
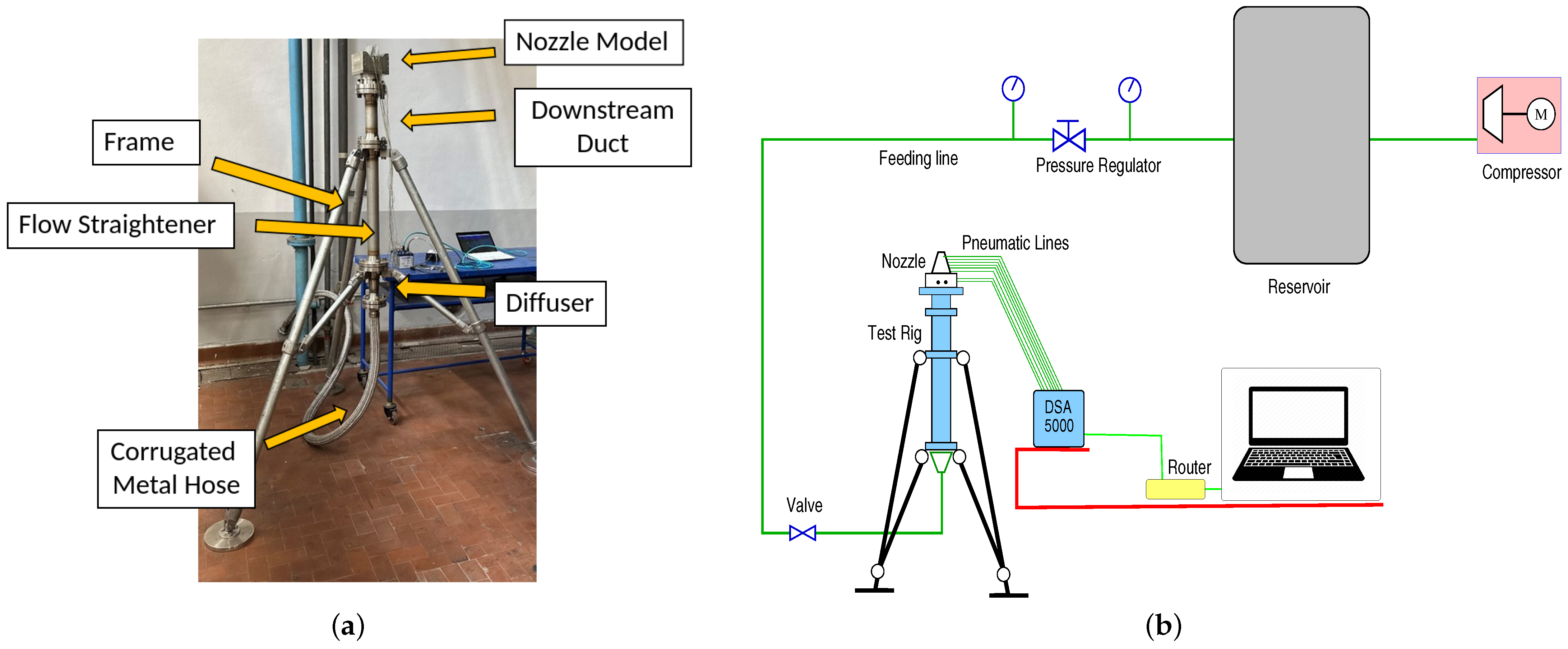
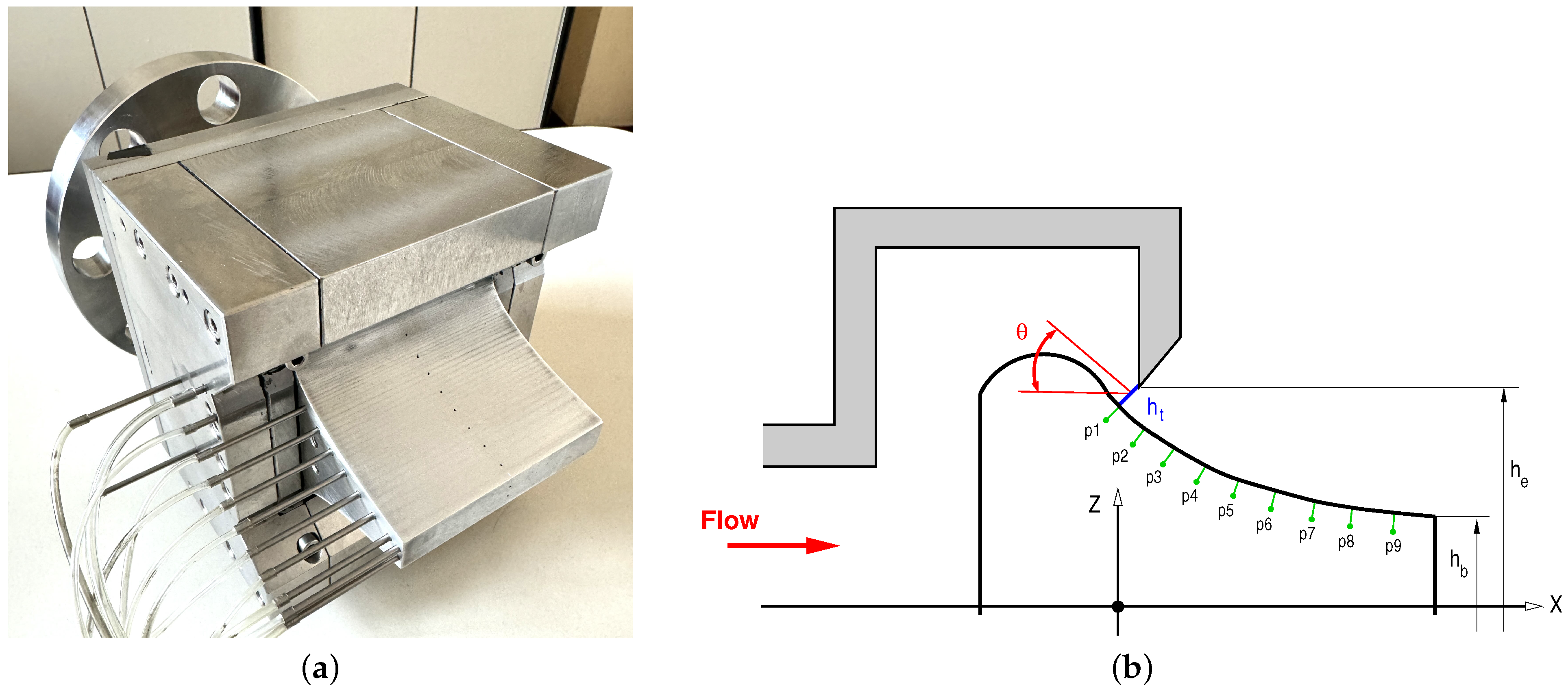
2. Nozzle Geometry and Experimental Setup
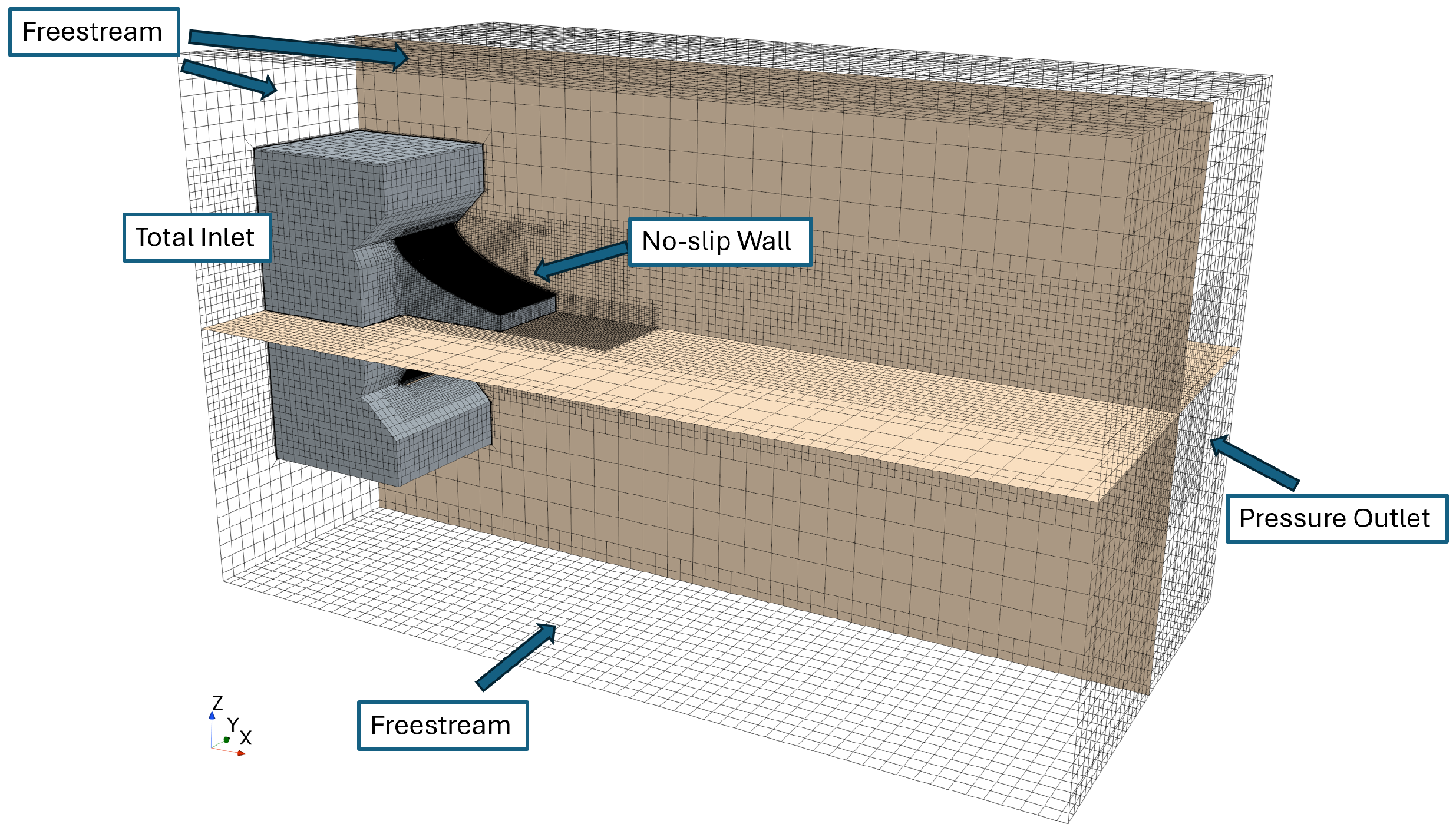
3. Mathematical Model and Numerical Method
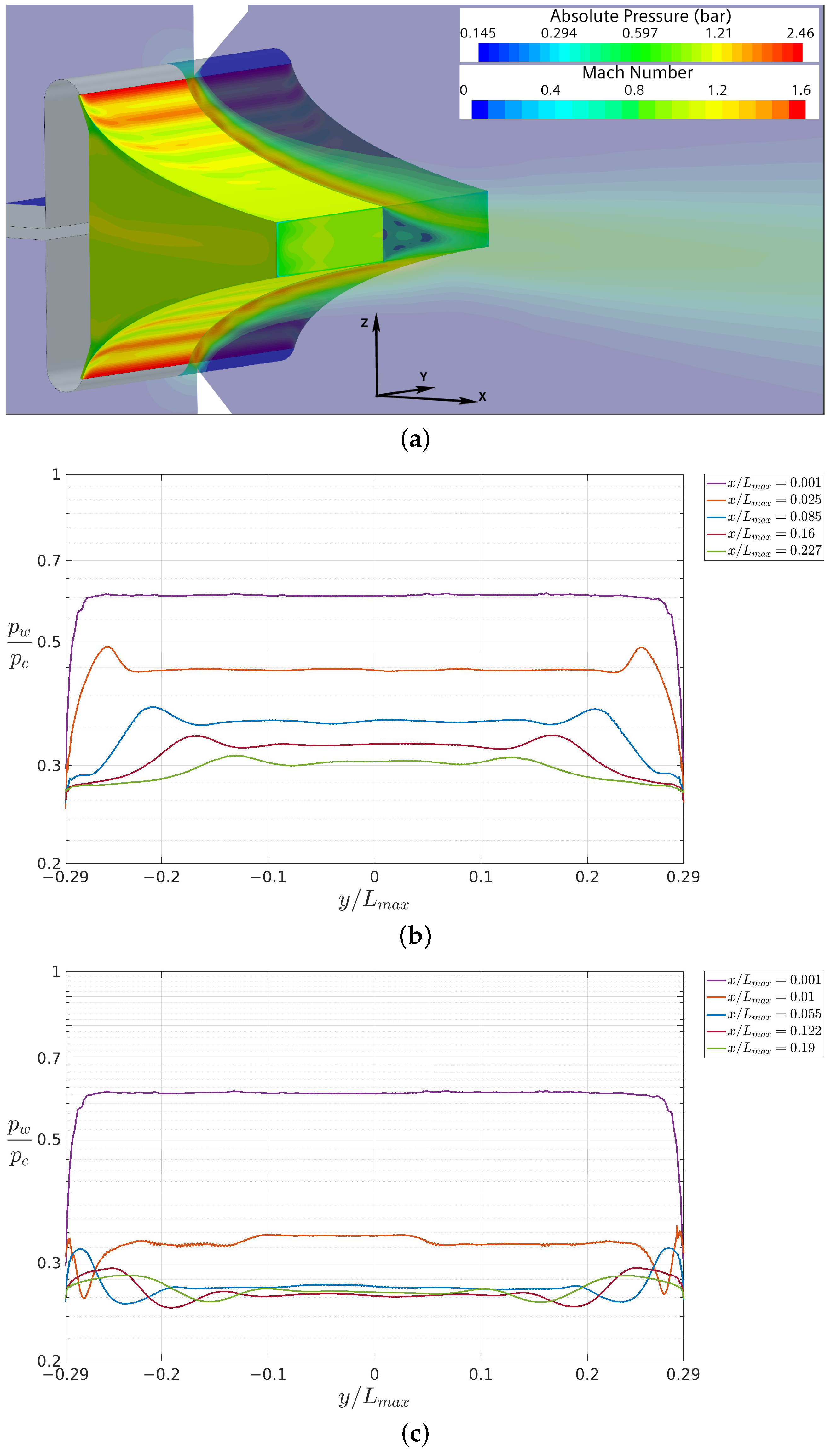
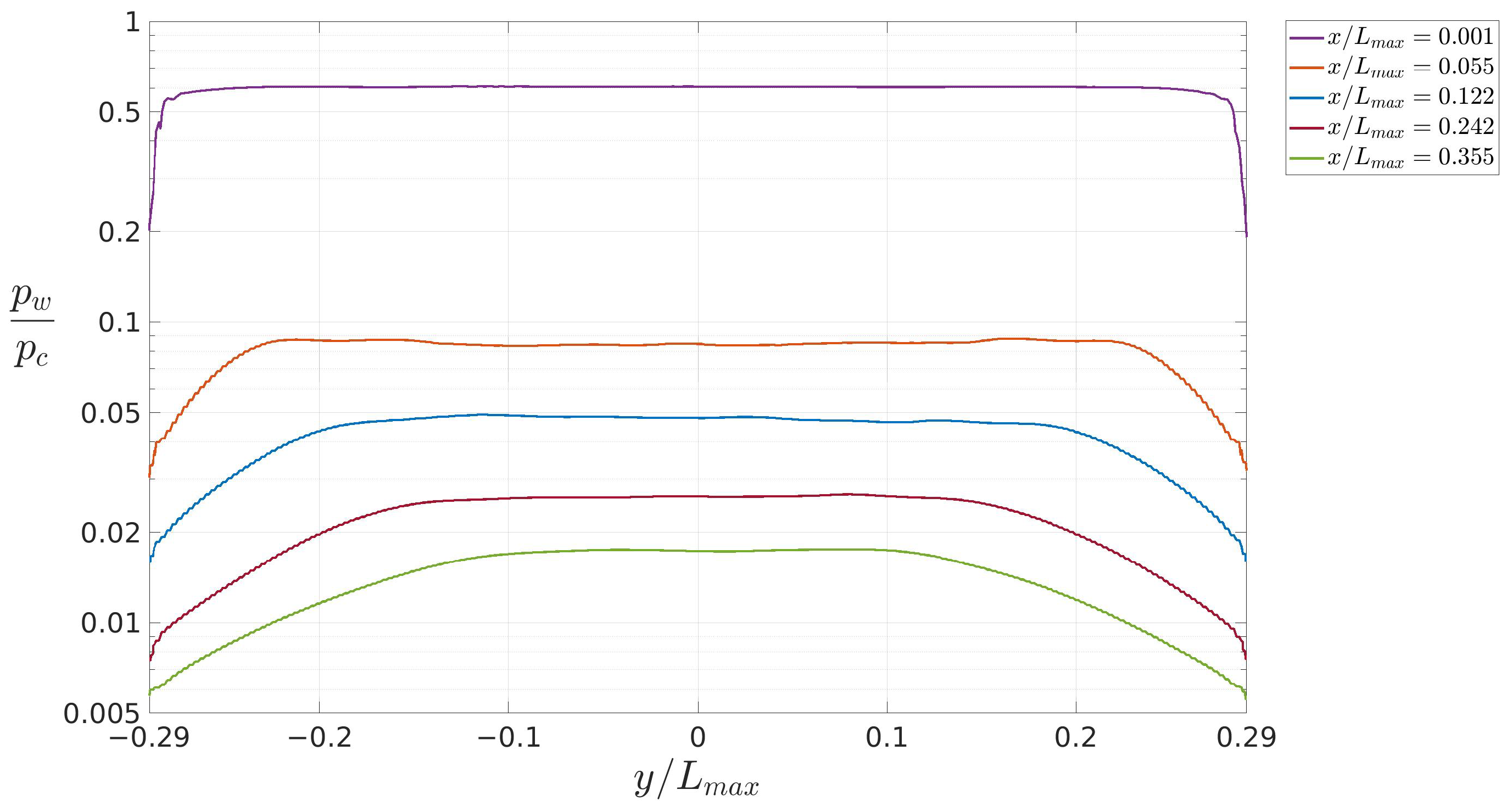
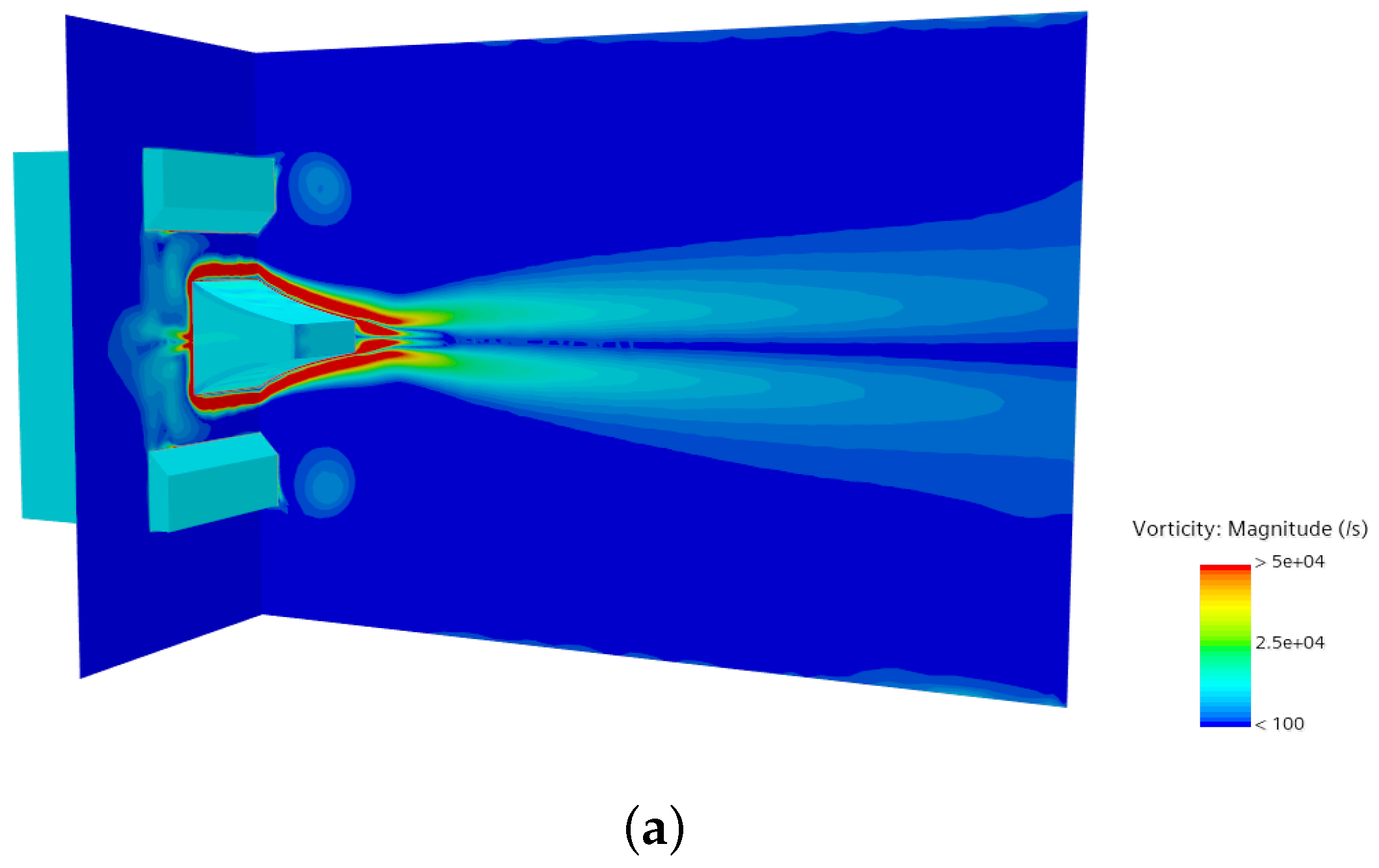
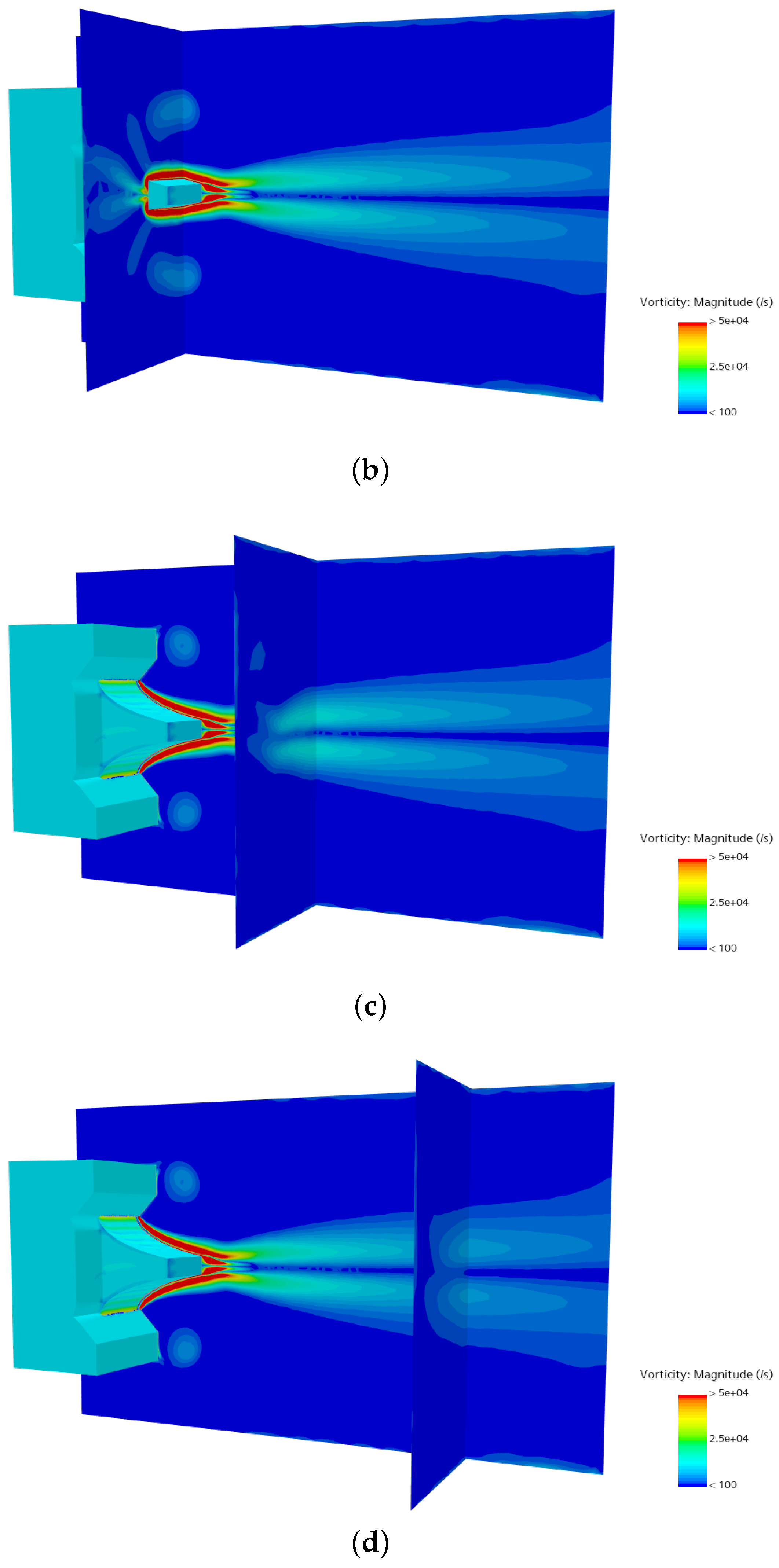
4. Numerical and Experimental Results
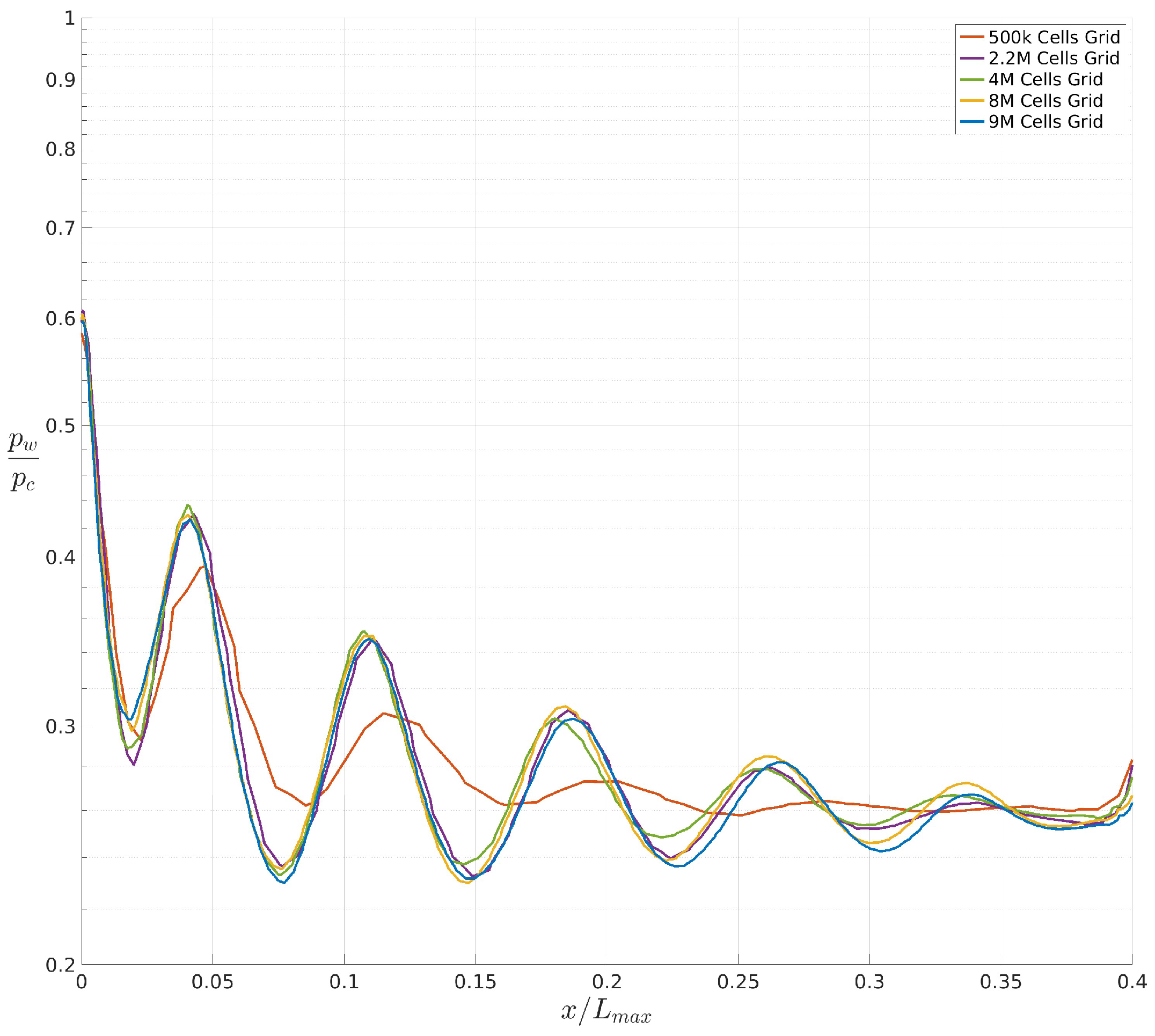
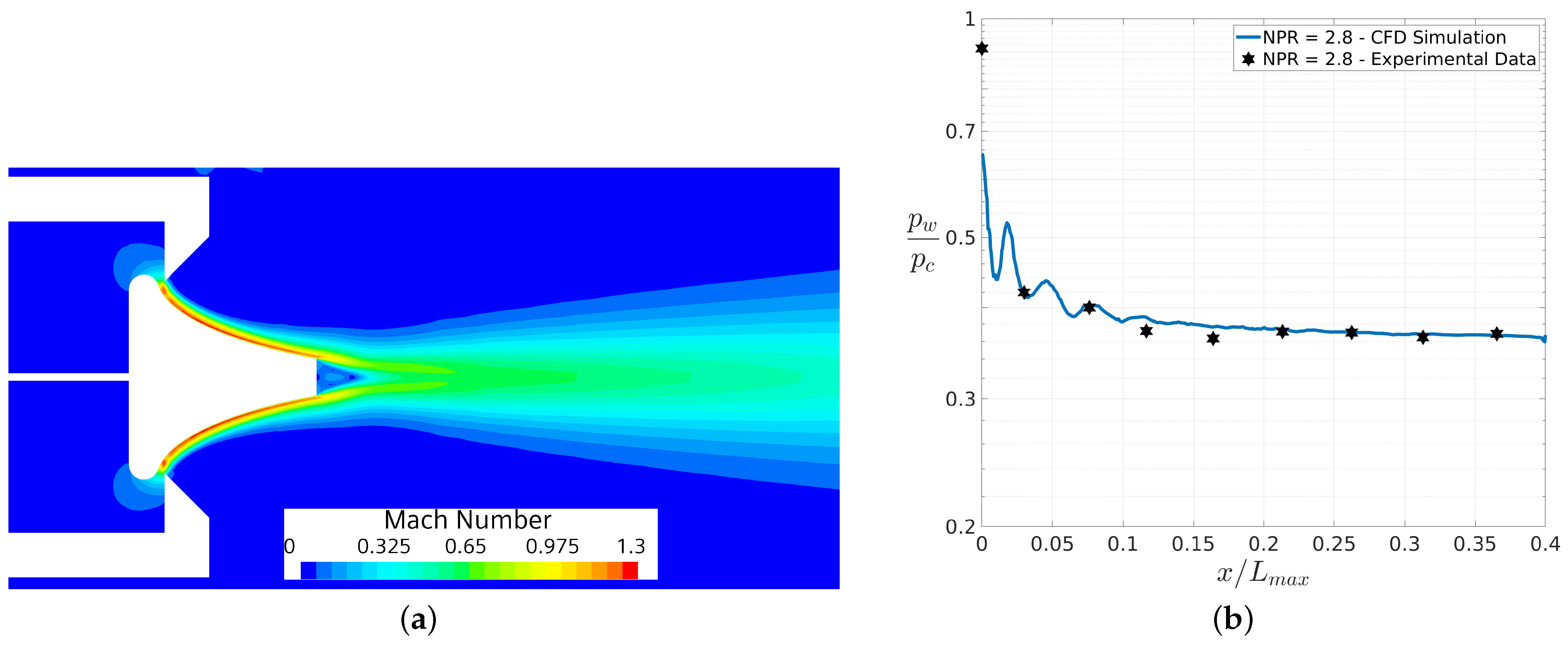
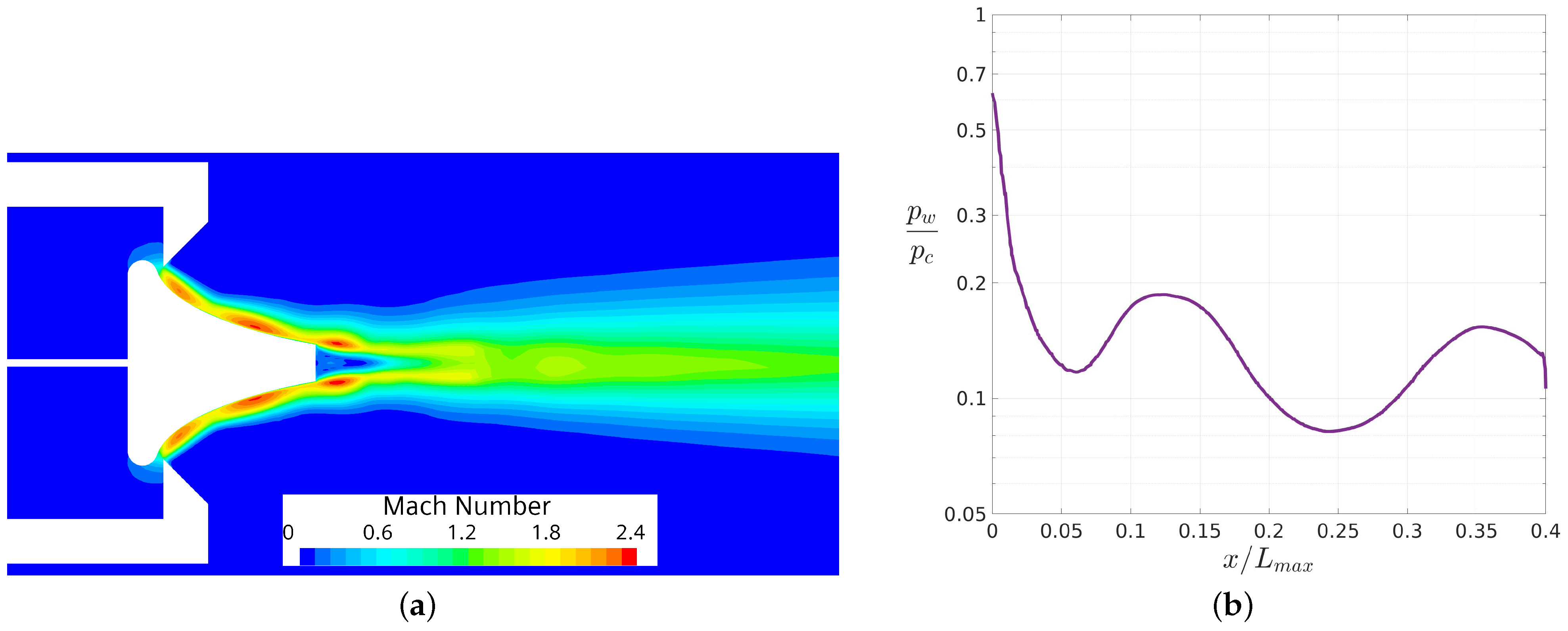
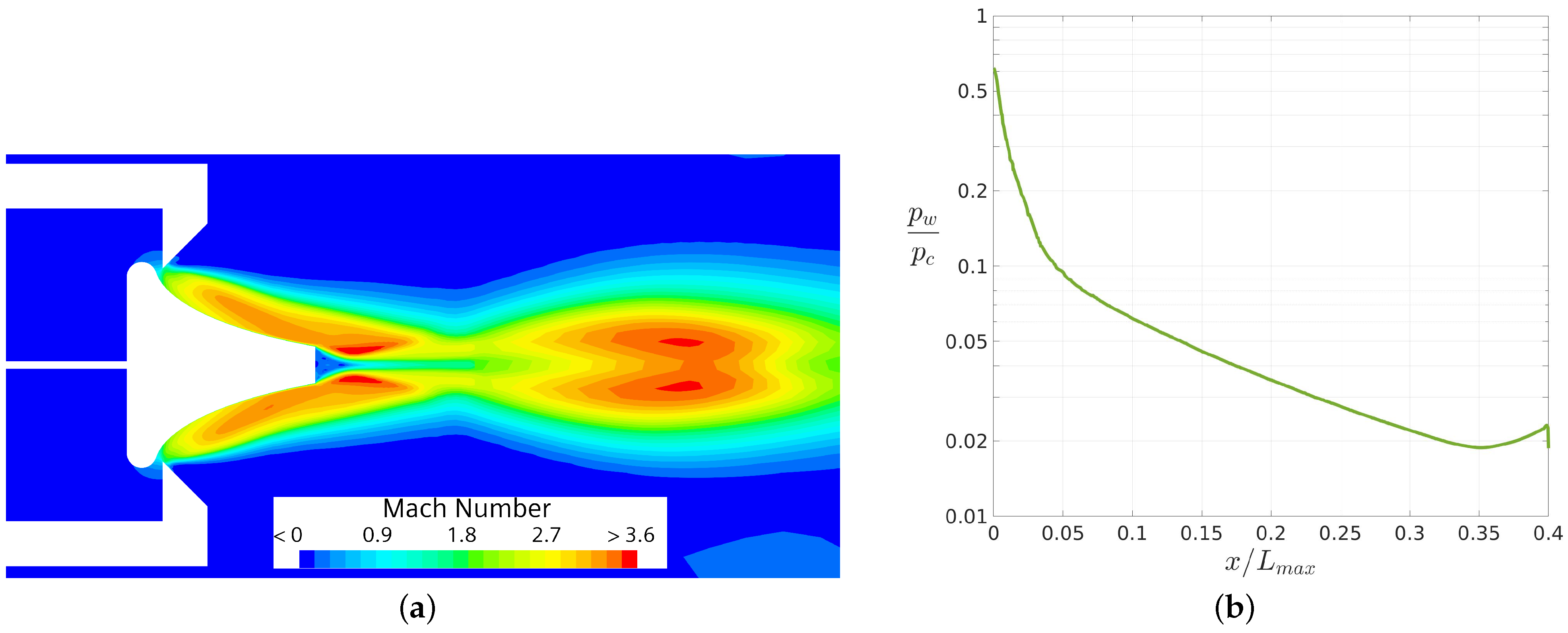
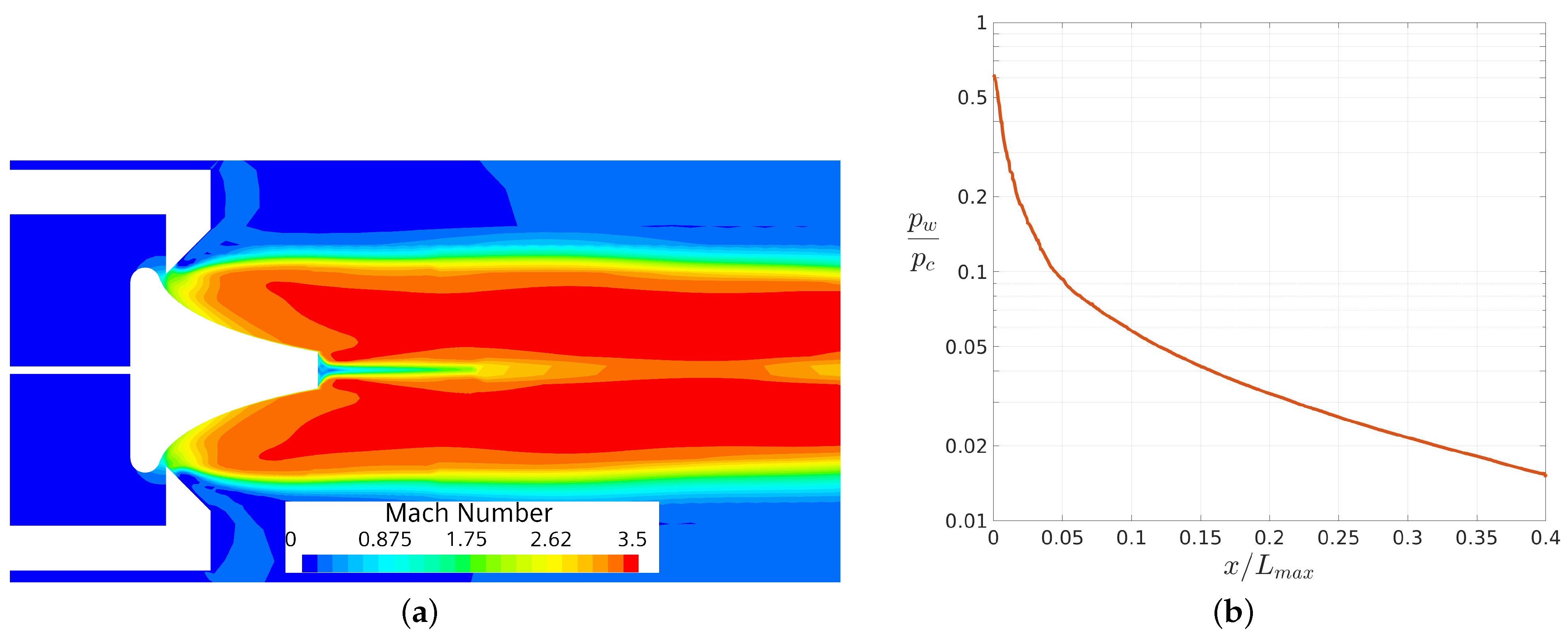
4.1. CFD and Experimental Data Comparison
4.2. Analysis of the Flowfield Side Effects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| = Exit section area | |
| = Throat section area | |
| b | = Plug width |
| = Plug base height | |
| = Exit section height | |
| = Throat height | |
| = Ideal aerospike length | |
| = Ambient pressure | |
| = Static chamber pressure | |
| = Total chamber pressure | |
| = Static wall pressure | |
| = Throat tilt angle | |
| = Dynamic viscosity | |
| = Thermal conductivity | |
| NPR | = Nozzle pressure ratio, |
| NPRd | = Design nozzle pressure ratio, |
References
- Guo, C.; Wei, Z.; Xie, K.; Wang, N. Thrust Control by Fluidic Injection in Solid Rocket Motors. J. Propuls. Power 2017, 33, 815–829. [Google Scholar] [CrossRef]
- Hagemann, G.; Immich, H.; Van Nguyen, T.; Dumnov, G. Advanced rocket nozzles. J. Propuls. Power 1998, 14, 620–634. [Google Scholar] [CrossRef]
- Manski, D. Clustered Plug Nozzles for Future European Reusable Rocket Launchers; German Aerospace Research Establishment, Lampoldshausen: Baden-Württemberg, Germany, 1981; pp. 643–681. [Google Scholar]
- Dumnov, G.; Nikulin, G.; Ponomaryov, N. Investigation of advanced nozzles for rocket engines. Space Rocket Eng. Power Plants 1993, 4, 10–12. [Google Scholar]
- Reijasse, P.; Gorbel, B. Experimental analysis of the supersonic flow confluence past a jet-on axisymmetric afterbody. In Proceedings of the 14th Applied Aerodynamics Conference, New Orleans, LA, USA, 17–20 June 1996; p. 2449. [Google Scholar]
- Tomita, T.; Tamura, H.; Takahashi, M. An experimental evaluation of plug nozzle flowfield. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996; p. 2632. [Google Scholar]
- Takahashi, H.; Tomioka, S.; Sakuranaka, N.; Tomita, T.; Kuwamori, K.; Masuya, G. Experimental Study on the Aerodynamic Performance of Clustered Linear Aerospike Nozzles. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012; p. 5933. [Google Scholar]
- Hao, Z.; Tian, H.; Guo, Z.; Hedong, L.; Li, C. Numerical and experimental investigation of throttleable hybrid rocket motor with aerospike nozzle. Aerosp. Sci. Technol. 2020, 106, 105983. [Google Scholar]
- Besnard, E.; Chen, H.H.; Mueller, T.; Garvey, J. Design, manufacturing and test of a plug nozzle rocket engine. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, Indiana, 7–10 July 2002; p. 4038. [Google Scholar]
- The Linear Aerospike Engine. 1998; From X-33 Prog OFC 8055725801, NASA. Available online: https://ntrs.nasa.gov/api/citations/19990004339/downloads/19990004339.pdf (accessed on 28 June 2024).
- Bach, C.; Schongarth, S.; Bust, B.; Propst, M.; Sieder-Katzmann, J.; Tajmar, M. How to steer an aerospike. In Proceedings of the 69th International Astronautical Congress (IAC), Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Saadia, A.; Tariq, A.K. Techniques of Fluidic Thrust Vectoring in Jet Engine Nozzles: A Review. Energies 2023, 16, 5721. [Google Scholar] [CrossRef]
- Warsop, C.; Crowther, W. Fluidic Flow Control Effectors for Flight Control. AIAA J. 2018, 56, 3808–3824. [Google Scholar] [CrossRef]
- Deng, R.; Setoguchi, T.; Dong Kim, H. Large eddy simulation of shock vector control using bypass flow passage. Int. J. Heat Fluid Flow 2016, 62, 474–481. [Google Scholar] [CrossRef]
- Waithe, K.; Deere, K. An Experimental and Computational Investigation of Multiple Injection Ports in a Convergent-Divergent Nozzle for Fluidic Thrust Vectoring. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003. AIAA Paper 2003-3802. [Google Scholar]
- Forghany, F.; Taeibe-Rahni, M.; Asadollahi-Ghohieh, A.; Banazdeh, A. Numerical investigation of injection angle effects on shock vector control performance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 233, 405–417. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Huang, S.; Lin, Y.; Jiang, J. Computationl study of axisymmetric divergent bypass dual throat nozzle. Aerosp. Sci. Technol. 2019, 86, 177–190. [Google Scholar] [CrossRef]
- Kexin Wu, K.; Kim, H.; Jin, Y. Fluidic thrust vector control based on counter-flow concept. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1412–1422. [Google Scholar]
- Banazadeh, A.; Saghafi, F. An investigation of empirical formulation and design optimisation of co-flow fluidic thrust vectoring nozzles. Aeronaut. J. 2016, 121, 213–236. [Google Scholar] [CrossRef]
- Deere, K.; Flamm, J.; Berrier, B.; Johnson, S. Computational Study of an Axisymmetric Dual Throat Fluidic Thrust Vectoring Nozzle for a Supersonic Aircraft Application. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. AIAA paper 2007-5085. [Google Scholar]
- Flamm, J.; Deere, K.; Mason, M.; Berrier, B.; Johnson, S. Experimental Study of an Axisymmetric Dual Throat Fluidic Thrust Vectoring Nozzle for a Supersonic Aircraft Application. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. AIAA paper 2007-5084. [Google Scholar]
- Ferlauto, M.; Ferrero, A.; Marsicovetere, M.; Marsilio, R. Differential Throttling and Fluidic Thrust Vectoring in a Linear Aerospike. Int. J. Turbomach. Propuls. Power 2021, 6, 8. [Google Scholar] [CrossRef]
- Resta, E.; Marsilio, R.; Ferlauto, M. Thrust vectoring of a fixed axisymmetric supersonic nozzle using the Shock-Vector Control method. Fluids 2021, 6, 441. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Huang, S.; Jiang, J.; Pan, R. Design and Preliminary Analysis of the Variable Axisymmetric Divergent Bypass Dual Throat Nozzle. J. Fluids Eng. 2020, 142, 061204. [Google Scholar] [CrossRef]
- Páscoa, J.; Dumas, A.; Trancossi, M.; Stewart, P.; Vucinic, D. A review of thrust-vectoring in support of a V/STOL non-moving mechanical propulsion system. Open Eng. 2013, 3, 374–388. [Google Scholar] [CrossRef]
- Zmijanovic, V.; Leger, L.; Sellam, M.; Chpoun, A. Assessment of transition regimes in a dual-bell nozzle and possibility of active fluidic control. Aerosp. Sci. Technol. 2018, 82, 1–8. [Google Scholar] [CrossRef]
- Di Cicca, G.M.; Hassan, J.; Resta, E.; Marsilio, R.; Ferlauto, M. Experimental Characterization of a Linear Aerospike Nozzle Flow. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Milan, Italy, 19–22 June 2023. [Google Scholar]
- Bonnet, V.; Ortone, F.; Di Cicca, G.M.; Marsilio, R.; Ferlauto, M. Cold Gas Measurement System for Linear Aerospike Nozzles. In Proceedings of the 2022 IEEE 9th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 27–29 June 2022. [Google Scholar]
- Angelino, G. Approximate method for plug nozzle design. AIAA J. 1964, 2, 1834–1835. [Google Scholar] [CrossRef]
- Ferlauto, M.; Ferrero, A.; Marsilio, R. Shock Vector Control Technique for Aerospike Nozzles. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Tian, C.; Lu, Y. Turbulence Models of Separated Flow in Shock Wave Thrust Vector Nozzle. Eng. Appl. Comput. Fluid Mech. 2013, 7, 182–192. [Google Scholar] [CrossRef]
- Liou, M.S. A sequel to ausm: Ausm+. J. Comput. Phys. 1996, 129, 364–382. [Google Scholar] [CrossRef]
- Poinsot, T.; Lele, S. Boundary conditions for direct simulations of compressible viscous reacting flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]


| Quantity | Value | |
|---|---|---|
| Throat height | mm | |
| Throat width | b | mm |
| Width/height throat ratio | 30.41 | |
| Exit section height | mm | |
| Plug base height | mm | |
| Throat section area | mm2 | |
| Exit section area | mm2 | |
| Area ratio | 12.65 | |
| Ideal aerospike length | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marsilio, R.; Di Cicca, G.M.; Resta, E.; Ferlauto, M. Characterization of the Three-Dimensional Flowfield over a Truncated Linear Aerospike. Fluids 2024, 9, 179. https://doi.org/10.3390/fluids9080179
Marsilio R, Di Cicca GM, Resta E, Ferlauto M. Characterization of the Three-Dimensional Flowfield over a Truncated Linear Aerospike. Fluids. 2024; 9(8):179. https://doi.org/10.3390/fluids9080179
Chicago/Turabian StyleMarsilio, Roberto, Gaetano Maria Di Cicca, Emanuele Resta, and Michele Ferlauto. 2024. "Characterization of the Three-Dimensional Flowfield over a Truncated Linear Aerospike" Fluids 9, no. 8: 179. https://doi.org/10.3390/fluids9080179
APA StyleMarsilio, R., Di Cicca, G. M., Resta, E., & Ferlauto, M. (2024). Characterization of the Three-Dimensional Flowfield over a Truncated Linear Aerospike. Fluids, 9(8), 179. https://doi.org/10.3390/fluids9080179






