Abstract
Using the potential function method, a theoretical model of the interaction was presented, and the interaction force between atoms/ions and (doped) graphene was obtained. Based on the interaction force, the dynamical control equation of atom/ion migration was derived. The dynamical behavior of atom/ion migrating on finite-size graphene surfaces along a specific direction and the regulation of boron nitride (BN) doping on the migration behavior were studied. The results show that the atoms/ions exhibit different migration mechanical behaviors due to different lateral forces inside and at the edges of the graphene surface. In addition, near the normal equilibrium height, atoms/ions are mainly affected by the lateral force, and their migration behavior is also influenced by the initial position, initial height, initial lateral velocity, etc. Furthermore, BN doping can affect the energy barrier of atom/ion migration on the graphene surface and effectively regulate the migration behavior of atoms/ions at the edge of the graphene surface. The research results can provide a theoretical reference for graphene surface localization modification and graphene-based atom/ion screening and detection.
1. Introduction
As a typical two-dimensional material, graphene shows excellent mechanical properties [1,2,3] and adsorption properties [4,5,6] due to its unique atomic structure and large specific surface area, and it has broad application prospects in sewage treatment, gas sensing, ion battery electrodes, atom/ion screening, and other fields [7,8,9,10]. For example, graphene, as an adsorbent, can effectively remove some organic molecules and heavy metal ions from sewage [11,12]. By analyzing the carrier velocity of different gas molecules adsorbed, graphene can be used for the detection of CO, NO2, and H2O [13]. As the anode material of a sodium ion battery, graphene has a good diffusion rate and cycle performance [14]. Based on the difference in the mechanical behaviors of different atoms/ions on the graphene surface, the screening of atoms/ions can be realized [15], etc. In these applications, the mechanical behavior of the adsorption and migration of microscopic particles on the surface of graphene is the key scientific issue. At present, a great deal of research work has been carried out to study the adsorption properties of graphene, but the research on the dynamical behavior of microscopic particles, especially atoms/ions, migrating on the surface of graphene is still insufficient.
The experimental studies on the migration and diffusion of microscopic particles and atoms/ions on the surface of graphene mainly focus on metal atoms/ions. Gan [16] et al. observed the migration behavior of single gold and platinum atoms in the graphene layer through high-resolution transmission electron microscopy (TEM). The experiment proved that metal atoms interact strongly with carbon atoms in graphene, and at 600~700 °C, the metal atoms have different diffusion behaviors within the layer and at the edge: two-dimensional diffusion occurs in the layer, while one-dimensional diffusion occurs at the edge. In addition, the experiment also found that the diffusion of metal atoms in the curved graphene nanotube layers was slightly faster than that in the planar graphene layer. These results are also helpful for improving the catalytic growth model of graphene and other nanostructures [17]. Yao [18] et al. studied the migration behavior of lithium ions on the surface of graphene using two graphene samples prepared by chemical vapor deposition (CVD). The experimental studies found that defects could promote the migration behavior of lithium ions in the direction perpendicular to graphene but limit their diffusion behavior parallel to graphene.
In addition, the theoretical models based on the potential function method [19,20], density functional theory [21,22,23], first principles [24,25], and molecular dynamics simulation [26,27] were also widely used to study the diffusion and migration behaviors of atoms/ions on the graphene surface. Most of the research work focuses on the energy barrier of atom/ion migration on the surface of graphene. Yu [19] et al. studied the adsorption and migration behaviors of lithium ions on the finite-size graphene surface using a theoretical model based on the potential function method. The calculation showed that the lithium ions preferentially migrate within graphene, and the energy barrier of the lithium-ion migration exhibits an edge effect. Li [20] et al. used a theoretical model based on the same potential function method to find that the wavelength and amplitude of graphene sinusoidal wrinkle will change the energy barrier of lithium-ion migration on the graphene surface. Using the density functional theory (DFT), Leggesse [21] et al. also found the adsorption and diffusion behaviors of lithium ions on graphite and graphene. It was found that the lithium-ion binding energy at all adsorption sites in the edge-modified one-dimensional graphene was higher, and lithium ions were easier to diffuse. Xian [22] et al. revealed that silicon atoms and carbon atoms have different energy barriers on the surface of graphene and between layers through DFT calculations. Silicon atoms can move almost freely on the surface of graphene and between layers, while carbon atoms are difficult to migrate due to a larger migration barrier. This also explained the phenomenon and application of epitaxial graphene growth on SiC surfaces from the perspective of energy [28,29]. Using the same method, Zhang [23] et al. showed that gold atoms are easier to move towards the edge of graphene, and the energy barrier along the edge is only 1.4 eV. Using the first principle, Tang [24] et al. studied the trapping position and energy barrier of metal atoms (Pt, Pd, Sn, and Au) in a single-vacancy (SV) graphene system. It was discovered that metal atoms have different capture regions and diffusion barriers in the SV graphene system. Pt and Pd atoms have larger capture regions than Au and Sn atoms, and Pt and Au atoms have the largest and smallest diffusion potential barriers on SV graphene surfaces, respectively. Based on the difference between the capture zone and the diffusion barrier, metal atoms can be adsorbed to a specified site on the graphene surface. Zhang [25] et al. used first-principles calculation to show that chloride ions can penetrate the defective graphene due to the reduced migration potential of chloride ions at the defect site. Tachikawa [26] et al. found by molecular dynamics simulations that Na+ could diffuse freely on the graphene surface, but there was a high energy potential barrier in the edge region, and Na+ could not migrate towards the edge region. Using the same approach, they also found F-atom confinement when lithium ions migrated on the surface of F- and H-atom edge-modified graphene. Due to the repulsive effect of the positive charge of C-F carbon atoms, lithium ions cannot approach the F-edge region of FH graphene, while lithium ions can preferentially enter and exit the C-H edge sites because of the attractive effect of the negative charge of the carbon atoms in C-F [27].
Doping can change the adsorption properties and migration behaviors of graphene surfaces and can affect the band gap of graphene. A variety of doped graphene-based nanomaterials have been widely used [30,31,32,33,34,35]. Boron and nitrogen, as non-metallic elements, have small changes in lattice structure and formation energy of graphene caused by doping due to their similar sizes to carbon atoms, resulting in relatively stable doped graphene structures, which are typically used to improve the adsorption and migration properties of adsorbed substances on graphene-based materials [36,37,38]. Gao [39] et al. found that boron doping could increase the diffusion barrier of lithium atoms on the graphene surface, and the proportion of boron doping was a key factor affecting the migration barrier of lithium atoms. Lee [40] et al. found that the migration barrier of sodium at the edge of nitrogen-doped graphene nanoribbons (GNRs) was lower than that of pristine graphene. Therefore, nitrogen doping at the edges of GNRs could facilitate the adsorption and diffusion of sodium on GNRs. In addition, the transverse heterostructure formed by boron nitride (it is an even harder material than diamond structure) composed of boron and nitrogen elements doped with graphene can also improve the adsorption and migration behaviors of atoms/ions [41]. However, there is no corresponding theoretical model to quantitatively characterize the dynamical behavior of atom/ion migration on the surface of finite-size graphene and its doped heterostructure. Li [15] et al. combined the interaction between atoms/ions and infinite graphene with the dynamical equation and found that atoms/ions can be captured at specific positions on the graphene surface by changing the velocity of atoms/ions. However, they did not study the effect of graphene size and edge on the mechanical behavior of atom/ion migration, nor did they consider the effect of doping on the dynamical behavior of atom/ion migration on the graphene surface.
To address the above issues using the potential function method, the interaction force between atoms/ions and finite-sized pristine/BN-doped graphene was calculated. Based on the interaction force, the dynamical equations of atom/ion migration on the graphene surface were established, and the dynamical behavior of atom/ion migration was studied. The effects of the initial height, initial position, and initial velocity of atoms/ions on the migration dynamical behavior were analyzed. In addition, the regulation mechanism of BN doping on the dynamical behavior of atom/ion migration on graphene surfaces was also studied.
2. Theoretical Model and Method
Figure 1 is a schematic diagram of an atom/ion migrating on the surface of (doped) graphene, where the atom/ion is located directly above the smooth rectangular (doped) graphene. The atom/ion cannot migrate through the graphene due to the huge energy barrier but can migrate on the graphene surface [19]. In order to study the influence of the size and edge on the migration of atoms/ions on the surface of graphene, the coordinate system as shown in Figure 1 is established with a rectangular graphene plane of finite size as the xoy plane. The zigzag and armchair edges of graphene are along the y and x axes, respectively. The spatial position of the atom/ion can be represented by the coordinates (x, y, z), and the coordinates of the carbon atom in graphene can be represented by (X, Y, Z). Since the atomic structure of graphene is periodic, a representative unit consisting of four carbon atoms in different locations can be found in graphene, as shown in Figure 1. Graphene can be viewed as being obtained by translating and replicating this representative unit along the x and y directions. Therefore, the position coordinates of carbon atoms in graphene (X, Y, Z) can be expressed by four carbon atoms in the representative unit.
where l (l = 0.142 nm) is the carbon–carbon (C-C) bond length. The values of j and k denote the positions of different carbon atoms in rectangular graphene, so the graphene size can be calculated by defining the maximum values m and n for j and k, i.e., 1 ≤ j ≤ m, and 1 ≤ k ≤ n (j, k, m, and n are all positive integers). Therefore, the length and width of graphene can be determined by L = (3m − 1)l and W = nl, respectively.
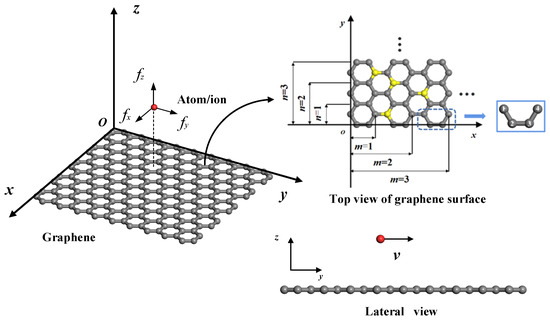
Figure 1.
Schematic diagram of atom/ion migrating on the surface of (doped) graphene; the size and representative unit of graphene consists of four carbon atoms in different locations. (In the figure, the gray balls are carbon atoms, the yellow balls are doped atoms, and the red ball is a migrating atom/ion.)
The potential function method is a common mathematical method to describe the interaction between molecules or atoms and can be widely used to calculate the potential energy and potential energy distribution between molecules or atoms [42]. In this study, the 6–12 form of the Lennard–Jones (L-J) potential, which contains an attractive and a repulsive component, is used to describe the interaction between an adsorbing atom/ion and each atom in graphene. It has the following form:
where σ and ε denote the equilibrium distance and potential energy at the equilibrium distance, respectively. Their values are dependent on the atomic type, and r is the distance between atoms. According to the atomic position coordinates defined above, the distance ri between atoms in the graphene and an atom/ion can be expressed as
where Xi, Yi, and Zi are the coordinates of the atoms at four different positions in the representative unit. Based on the Lennard–Jones potential, the interaction potential of an adsorbing atom/ion and graphene can be expressed as the sum of the L-J potential between the atom/ion and all atoms in the graphene, i.e.,
where subscripts a and b represent the adsorbing atom/ion and atoms in the graphene, respectively.
In addition, in order to study the migration behavior of atoms/ions on the graphene surface, it is necessary to give the force of atoms/ions on the graphene surface. According to F = −∇E, the x- and y-directional lateral forces and z-directional normal force acting on atoms/ions on the graphene surface can be expressed as
As can be seen in Equations (8)−(10), the interaction forces between atoms/ions and graphene depend on the type of atoms/ions, the distance ri between them and graphene, and the graphene size.
When an atom/ion migrates on the surface of graphene, it will be mainly affected by the lateral forces fx, fy in the Equations (8) and (9) and the normal force fz in Equation (10). Taking lithium-ion (Li-ion) as an example, when it is located somewhere at the edge of graphene, the changes of the forces in three directions with height are shown in Figure 2a. Obviously, the normal force fz is more sensitive to the change in height than the lateral forces fx and fy. Generally, the normal force is greater than the lateral force. Moreover, it can be seen in the figure that there is a height where the normal force of Li-ion is zero on the surface of graphene, and this height is defined as the normal equilibrium height (NEH). The Li-ion has an NEH at each horizontal position on the graphene surface. Therefore, there is an NEH surface on which the normal force acting on Li-ion is zero. Due to the periodicity of graphene, the NEH surface is a periodically changing surface, except for the edge (as shown in Figure 2b). For other atoms/ions, there are similar NEH surfaces on the graphene surface. Within the NEH surface, the lateral forces fx and fy play a dominant role in the migration behavior of atoms/ions on the graphene surface, mainly changing the horizontal positions of the atoms/ions. When atoms/ions are not on the NEH surface, the normal force will play a major role, mainly changing the heights of the atoms/ions. The final migration positions of the atoms/ions will also stop on the NEH surface.
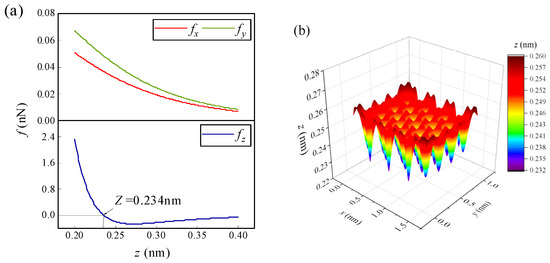
Figure 2.
(a) The variations of the triaxial force of the Li-ion at a certain position on the edge of graphene with height, (b) NEH surface of the Li-ion on the m = 4 and n = 4 size of the graphene surface.
Based on the lateral and normal forces given in Equations (8)−(10), the dynamical equations for the migration of atoms/ions on a finite-size graphene surface can be established. As shown in Figure 1, an atom/ion with a specified initial velocity migrates on a finite-size graphene surface, where the atom/ion is only acted on by the graphene. The energy dissipation, which results from the electronic shells of all atoms, is treated as a velocity-dependent damping term. At this moment, the atom/ion can be regarded as a mass point [43]. Thus, the dynamical equations can be expressed as
where m is the mass of the atom/ion, γ is the damping factor in three directions, and the lateral forces fx, fy and the normal force fz are the forces acting on the atom/ion by the finite-size graphene. By solving Equations (8)−(13) numerically, the velocity, position, and migration path of an atom/ion as it migrates on the graphene surface can be obtained. In addition, the dynamical behavior of the atom/ion migration on the graphene surface is also influenced by the initial height, initial position, initial velocity of the atom/ion, etc.
3. Results and Discussion
3.1. Migration of Atoms/Ions along Specific Paths Inside a Finite-Size Graphene Surface
The adsorption energy of atoms/ions at the Hollow (H-) site on the infinite pristine graphene (PG) surface is the lowest and the adsorption is the most stable, followed by the Bridge (B-) site and Top (T-) site (as shown in Figure 3a). When an atom/ion migrates from one stable adsorption site to another, it needs to cross one or several energy barriers. The energy barrier to overcome along the H-B-H path (y-direction) is lower than that of the H-T-B-T-H path (x-direction), and the migration is also more regular and stable [21,44], so this work focuses on the dynamical behavior of atoms/ions migrating along the H-B-H path (y-direction) on the graphene surface. In order to avoid edge effects, a sufficiently large m = 9 and n = 7 size graphene is selected when atoms/ions migrate along a specific path inside a finite-size graphene surface (as shown in Figure 3a). Taking Li-ion as an example, when it migrates along the y1 and y2 paths on the graphene surface, the x-directional lateral force is almost zero compared to the y-directional lateral force and the z-directional normal force due to being far from the edge (as shown in Figure 3b,c). Therefore, when migrating along these two paths, the Li-ion is only affected by the lateral force fy and the normal force fz. At this point, the migration of the Li-ion will not show a displacement in the x-direction, and its migration path will behave as a two-dimensional movement parallel to the yoz plane.
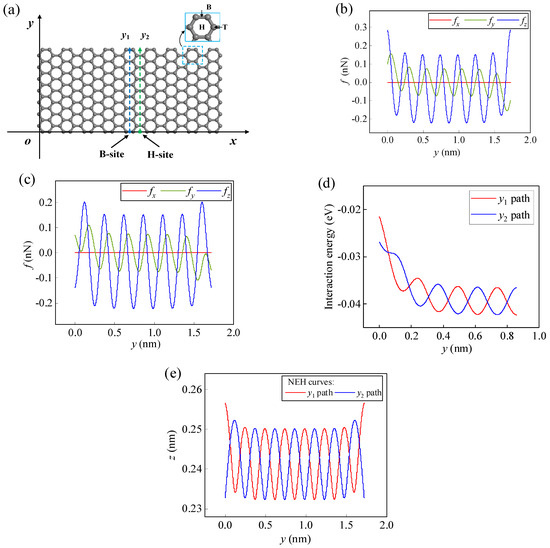
Figure 3.
(a) Schematic diagram of the migration paths of a Li-ion on the m = 9 and n = 7 graphene surface. At z = 0.245 nm, the lateral forces fx, fy and the normal force fz of the Li-ion along (b) the y1 path and (c) the y2 path. (d) The interaction energy curves of the Li-ion along the y1 and y2 paths for z = 0.233 nm. (e) NEH curves of the Li-ion on the y1 and y2 paths.
As the Li-ion migrates along the y1 and y2 paths, the NEH surface becomes two curves (Figure 3e). These two NEH curves are the boundary lines of the normal force state of the Li-ion on the graphene surface. When the Li-ion is below this line, it is repulsed by graphene; when it is over this line, it is attracted by graphene. Combining Figure 2b with Figure 3e, it can be seen that the NEH curve is related to the size of graphene, the type of atoms/ions, and the migration path. When atoms/ions are just on the NEH curve, the lateral force fy plays a dominant role in the migration behavior of the atoms/ions on the graphene surface; when the atoms/ions are not on the curve, the normal force will play a major effect. Moreover, the final migration positions of atoms/ions will also be on the curve. The NEH surface gives the range of heights where atoms/ions reach equilibrium on the graphene surface, which can be determined by Equation (10). The range of equilibrium heights for a Li-ion on the y1 and y2 paths given by the NEH curves is 0.233–0.257 nm. The lateral and normal forces along the y1 and y2 paths for the Li-ion at an initial height of 0.245 nm are given in Figure 3b,c, respectively. In addition, the initial height, initial position, and initial velocity factors of the Li-ion all affect its migration behavior on the graphene surface. Given the initial conditions and the relevant parameter values (m = 1.153 × 10−26 kg, σ = 0.2473 nm, ε = 4.330 meV, γy = γz = 1 nN·ps/nm), the migration process of the Li-ion on the graphene surface can be obtained by solving Equations (12) and (13), and the parameter values of other atoms/ions are shown in Table S1.
3.1.1. Effect of Initial Height on the Spontaneous Migration of Atoms/Ions
As can be seen from the previous analysis, at different heights on the graphene surface, the Li-ion has different interaction forces with graphene. Therefore, the initial height of the Li-ion will have an impact on the migration path. Figure 4 shows the effect of the initial height on the lateral force fy, the normal force fz, and the migration path at the two initial sites when a Li-ion migrates from the initial B-site and H-site along the specific y1 and y2 paths inside the graphene. As shown in Figure 4a–c, there are lateral force fy and normal force fz in the initial position of the Li-ion so that the Li-ion can migrate spontaneously, even if the initial velocity is zero. Since there is no initial velocity, the direction of spontaneous Li-ion migration is determined by the lateral force fy and the normal force fz. The lateral force fy of Li-ion at the initial position changes from negative to positive with the increase in initial height (Figure 4a,b), while the normal force fz goes from positive to negative (Figure 4c). Thus, the initial height affects the initial force direction of the Li-ion and its path of spontaneous migration.
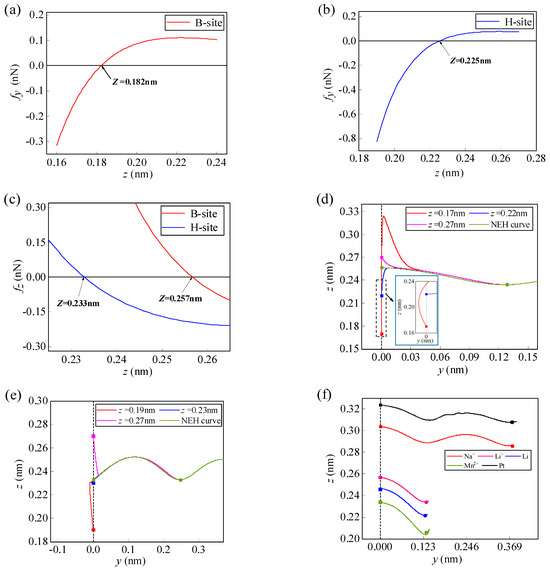
Figure 4.
Variations of the lateral force fy with initial height for the Li-ion at the initial (a) B-site (b) and H-site. (c) Variations of the normal force fz with initial height for the Li-ion at the initial B-site and H-site. Spontaneous migration paths and NEH curves for the Li-ion at the initial (d) B-site and (e) H-site with different heights. (f) Spontaneous migration paths for several types of atoms/ions at NEHs along the y1 direction. (In the figure, the solid square dots represent the initial migration sites and the solid round dots represent the final migration sites).
When a Li-ion migrates along the y1 path, the initial position is at the B-site. The heights where the lateral force fy and the normal force fz are equal to zero are 0.182 nm and 0.257 nm, respectively (Figure 4a,c). There are three different migration behaviors of the Li-ions in the three areas separated by these two heights (Figure 4d). When the initial height is lower than 0.182 nm, the spontaneous migration path of the Li-ion increases horizontally away from the graphene and then decreases close to the graphene; when the initial height is higher than 0.182 nm and lower than 0.257 nm, the migration path shows horizontal migration towards the center of the graphene and the height increases and then decreases; and when the initial height is higher than 0.257 nm, the migration path shows horizontal migration towards the center of the graphene and the height keeps decreasing. However, regardless of the initial height, the Li-ion eventually moves back onto the NEH curve. When the Li-ion migrates along the y2 path, its initial position is at the H-site. The heights where the lateral force fy and the normal force fz are equal to zero are 0.225 nm and 0.233 nm, respectively (Figure 4b,c). The Li-ion in the three areas separated by these two heights similarly shows three migration behaviors (as shown in Figure 4e). When the initial height of the Li-ion is equal to the NEH at the B-site and H-site (0.257 nm and 0.233 nm, respectively), the normal force fz is zero, the lateral force fy dominates the migration direction, and the Li-ion migrates spontaneously along the NEH curves. At this moment, the migration efficiency of the Li-ion is highest in the horizontal direction on the graphene surface. Furthermore, it is shown in Figure 4d,e that the variations of initial height will not affect the final migration position of Li-ion, which will eventually return to the NEH curves. The final position of spontaneous migration is the H-site of the first complete carbon ring adjacent to the initial position in the y-direction. However, different atoms/ions have different NEHs at the initial B-site and H-site at the edge of the graphene (as shown in Table 1). Therefore, their final positions of spontaneous migration are not necessarily the same. For example, the spontaneous migration position of Li-ion, lithium-atom, and manganese-ion is the H-site of the first completed carbon ring adjacent to the initial position in the y-direction, while that of sodium-ion and platinum-atom is the H-site of the second completed carbon ring (Figure 4f).

Table 1.
NEHs of different atoms/ions at the B-site and H-site on the edge of the graphene.
3.1.2. Effect of Initial Velocity on Atom/Ion Migration
A previous study [15] has shown that when a Li-ion migrates from the most stable H-site on the surface of infinite graphene, along a specific path with a certain initial velocity, there are three migration modes. First, the initial velocity is very small and the Li-ion hardly migrates at the H-site; second, the Li-ion migrates from the H-site in the carbon ring, and because the kinetic energy cannot overcome the energy barrier, it does not continue to migrate but moves in the opposite direction and stops at the original H-site; and third, the kinetic energy of the Li-ion is powerful enough to cross one or more energy barriers and then stops at the H-site of the other carbon ring. During the migration process, the Li-ion is only subject to lateral force from graphene along the migration path. In fact, the Li-ion must be affected by normal force in addition to the lateral force as it migrates along a given path, unless it always resides on the NEH curve. Therefore, there is also a normal displacement when the Li-ion migrates, which has not been considered in previous theoretical research [15].
In the above section, the spontaneous migration behavior of the Li-ion with an initial velocity of zero has been investigated. In this section, the migration behavior of the Li-ion will be studied when it has a certain initial velocity. The migration paths are still along the y1 and y2 directions (Figure 3a) and the corresponding initial positions are at the B-site and H-site, respectively. The initial heights are the NEHs of the Li-ion at the B-site and H-site. Due to the symmetry of the interaction energy curves of graphene along the y1 and y2 paths, the migration zone is chosen to be half of the graphene size along the migration path direction.
It is assumed that a Li-ion has an initial velocity vy in the y-direction. In the initial position, it is only subjected to the lateral force fy, but once it leaves the initial position, it will be subjected to both the lateral force fy and the normal force fz since it is no longer on the NEH curve. By solving Equations (12) and (13), the path, final position, and critical velocity of the Li-ion can be obtained as it migrates along the y1 and y2 paths on the graphene surface (Figure 5). As can be seen in Figure 5a,b, when the initial velocity of the Li-ion is low, it migrates to the same final position at the H-site of the first carbon ring adjacent to the initial position. The horizontal migration path of the Li-ion to the position can be divided into two modes. First, in the horizontal direction, the Li-ion migrates all the way to the final position; second, the Li-ion crosses the final position and then moves backward and returns to the final position, which is consistent with the migration patterns of the one-dimensional path in the literature [15]. In contrast, the vertical migration behaviors all show a movement from the initial position towards the NEH curve. As the initial velocity of the Li-ion increases, it is possible for it to gain enough energy to cross more energy barriers to reach the H-site of the second or even further carbon ring. The arrival of Li-ion at the H-site of each carbon ring corresponds to a minimum initial lateral velocity, which is defined as the critical initial lateral (CIL) velocity. Figure 5c,d show the CIL velocities and the paths of the Li-ion as it reaches the H-site of several adjacent carbon rings. Based on the energy barrier along the two migration paths (Figure 3d), it can be found that the two adjacent CIL velocities form a velocity interval corresponding to a final migration position. For example, along path y1, when the initial velocity of the Li-ion is between 0 and 20.3 nm/ps, the Li-ion will stop at the first H-site; when the initial velocity is between 20.3 and 42.6 nm/ps, the Li-ion will stop at the second H-site, and so on (Figure 5c). And, as can be seen in Figure 5e, the CIL velocity is approximately linear with the final position as the Li-ion migrates along the y1 and y2 path.
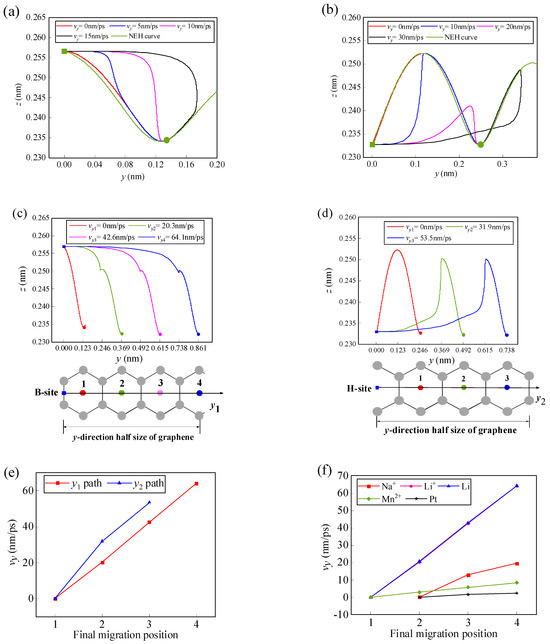
Figure 5.
Trajectories of the Li-ion at different initial lateral velocities along the (a) y1 path and (b) y2 path to the H-site of the first adjacent carbon ring on the m = 9 and n = 7 size graphene surface. CIL velocities and trajectories of the Li-ion along the (c) y1 path and (d) y2 path to the H-sites of different carbon rings. (e) The relationship between the CIL velocity and the final migration position. (f) The relationship curves between the CIL velocity and the final migration position when several kinds of atoms/ions migrate along the y1 path.
The mechanical behavior of other atoms/ions on the graphene surface is similar to that of Li-ion. Figure 5f gives the relation curves between the CIL velocity and the final position for five different types of atoms/ions migrating along the y1 path. In the figure, it can be seen that the CIL velocity of each atom/ion also shows an approximately linear relationship with the final migration position. However, the CIL velocities required to reach the same position are different for different atoms/ions. The CIL velocity of lithium-atom and the Li-ion is the greatest, while that of platinum-atom is the smallest. When the initial lateral velocities are the same, different atoms/ions may reach different final stable positions. For example, when the initial lateral velocity is 2 nm/ps, lithium-atom, Li-ion, and manganese-ion finally stabilize in the first H-site, sodium-ion in the second H-site, and platinum-atom in the third H-site. Therefore, atom/ion screening can be achieved based on this.
If Li-ion has not only initial lateral velocity vy in the y-direction but also initial normal velocity vz in the z-direction at the initial position, then the initial normal velocity vz will affect the migration behavior of the Li-ion. It is assumed that the Li-ion migrates along the y1 path from the B-site at the edge of graphene. Figure 6a shows the variations of the CIL velocity to each final site with different initial normal velocities. It can be seen in the figure that the existence of the initial normal velocity affects the CIL velocity of the Li-ion to the final migration site and exhibits an obvious edge effect. As the Li-ion migrates along the y1 path, except for the first H-site where the CIL velocity is zero (vy0 = 0), the CIL velocities of the Li-ion to reach other H-sites decrease with increasing initial normal velocity. Moreover, the effect of the initial normal velocity on the CIL velocity becomes smaller as the migration destination gradually moves away from the graphene edge. It can be seen in Figure 6a that the influence of the initial normal velocity on the CIL velocity (vy3) of the Li-ion reaching the fourth H-site is negligible.
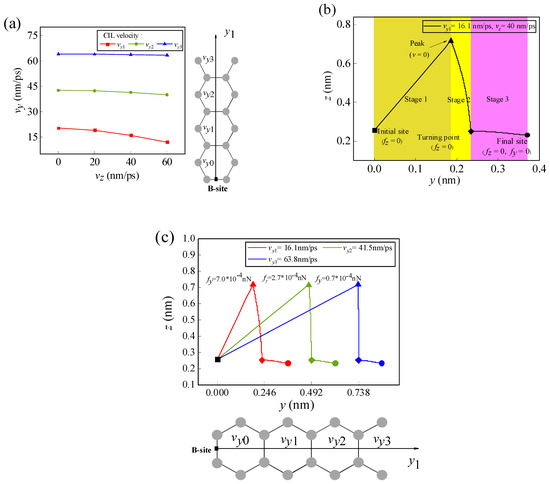
Figure 6.
(a) The variations of the CIL velocity of the Li-ion as it migrates from the B-site along the y1 path with different normal velocities vz. (b) Schematic diagram of the movement trajectory of the Li-ion when the initial normal velocity is 40 nm/ps and the CIL velocity is 16.1 nm/ps. (c) Trajectories of the Li-ions at different CIL velocities when the initial normal velocity is 40 nm/ps. (In the figure, the solid square dots represent the initial migration sites and the solid round dots represent the final migration sites).
Figure 6b shows the trajectory of the Li-ion as it migrates along the y1 path at the initial normal velocity of 40 nm/ps and the CIL velocity of 16.1 nm/ps. In the figure, it can be seen that the trajectory of the Li-ion is divided into three stages. In the first stage, the Li-ion migrates to the highest point, and the initial normal velocity gradually decreases to 0; in the second stage, the Li-ion falls from the peak to the NEH curve; and in the third stage, the Li-ion migrates to its final position along the NEH curve. In the first stage, the initial normal and lateral velocities of the Li-ion play a dominant role, and the initial normal velocity determines the highest point of the Li-ion trajectory. In the second stage, the normal force plays a leading role, resulting in the Li-ion moving back to the NEH curve. In the third stage, the lateral force plays a dominant role, causing the Li-ion to move to the final stable position. The trajectory of the Li-ion at different CIL velocities when the initial normal velocity is 40 nm/ps is shown in Figure 6c. It can be seen that as the CIL velocity increases, the final position of Li-ion migration moves farther away from the edge, and the lateral offset of the second stage motion trajectory gradually decreases. The analysis of the lateral forces at the highest points reveals that the closer to the edge of the graphene, the higher the lateral force. When the normal velocity is in existence at the highest point of the migration trajectory and since the lateral force near the starting edge is more effective than that inside graphene, the initial lateral velocity required to reach the equilibrium position near the edge becomes smaller. As the final migration position of the Li-ion moves away from the edge, the lateral force at the highest position decreases and has a negligible effect on the initial lateral velocity. This explains the reason why the effect of the initial normal velocity on the CIL velocity has an edge effect.
3.2. Migration of the Li-Ion along the Specific Path at the Edge of the Graphene Surface
There are edge effects on energy barriers and forces of atoms/ions on the surface of the graphene with a finite size. Li-ions, for example, experience different forces on the edges of the graphene than they do on the inside, so they behave differently on the edges of the graphene than they do on the inside. From the previous analyses, the initial height and initial velocity can affect the dynamical behaviors of atoms/ions migrating along specific paths inside the graphene. Moreover, around the NEH, the lateral force and the lateral velocity are the main factors affecting the final position of the atoms/ions, and there is a linear relationship between the CIL and the final migration position of the atoms/ions. If the atoms/ions migrate along a path at the edge of the graphene, edge effects will have an impact on their migration behaviors.
Similarly, using the Li-ion as an example, its migration path is assumed to be in the y3 direction (Figure 7a). By examining the forces on the y3 path (Figure 7b), the Li-ion is subjected to the lateral forces fx, fy and the normal force fz, and the x-directional lateral force fx is no longer approximately zero. Therefore, as the Li-ion migrates along the y3 path from the B-site, it is possible to generate the x-directional displacement due to the x-directional lateral force. Thus, the trajectory of the Li-ion is no longer confined to the plane parallel to the yoz plane but will generate displacement in three directions. By solving Equations (8)−(10), the force of the Li-ion in the three directions can be obtained, and then by solving three equations in Equations (11)−(13), the migration process of the Li-ion along the y3 path can be obtained. In numerical calculations, the parameters are set as before. In addition, the initial height and velocity can affect the migration behavior of the Li-ion.
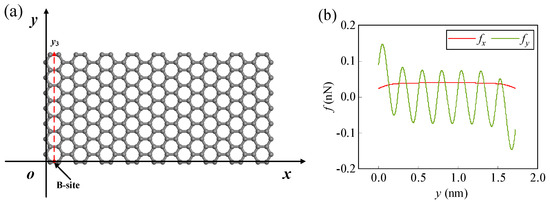
Figure 7.
(a) Schematic diagram of the migration path of the Li-ion at the edge of the m = 9 and n = 7 graphene, (b) lateral forces fx and fy on the Li-ion along the y3 path for z = 0.245 nm.
3.2.1. Effect of Initial Height on the Spontaneous Migration of Li-Ions
From the previous analysis, it can be seen that the NEH surface is the equilibrium surface of normal force, where the lateral forces play major roles in the spontaneous migration of atoms/ions. Outside the NEH surface, the normal force plays an important role in the migration of atoms/ions. Figure 8 shows the trajectories of the Li-ion and its projections for different initial heights as it migrates along the y3 direction from the B-site on the graphene surface. It is not difficult to find that the initial height has a significant effect on the final equilibrium position of the Li-ion’s spontaneous migration. Near the NEH, the final position of Li-ion migration is at the first H-site, which is consistent with the result of migration along the y1 path in the interior of graphene. However, when the initial height is far away from the NEH, the effect of the normal force is enhanced. Under the combined action of normal force and x- and y-directional lateral forces, the Li-ion will cross the energy barrier of the adjacent carbon ring and migrate to the H-sites of other carbon rings (Figure 8).
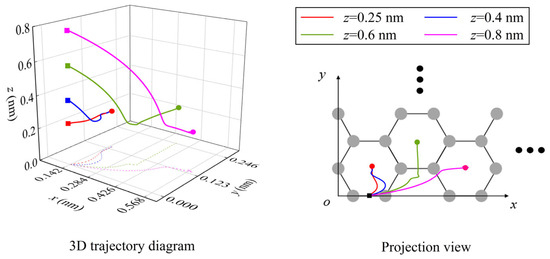
Figure 8.
The trajectories of the Li-ion and its projections on the graphene surface when it migrates in the y3 direction with different initial heights. (In the figure, the solid square dots represent initial positions and the solid round dots represent final migration positions).
3.2.2. Effect of Initial Velocity on the Migration of the Li-Ion
The initial lateral velocity enables Li-ions to cross more energy barriers and migrate to further equilibrium sites. At the edge, the initial lateral velocity of Li-ions, the lateral forces in two directions, and the normal force all influence their migration along the y3 direction on the graphene surface (Figure 9). As before, the initial height of the Li-ion is assumed to be the NEH, and the migration region is taken to be half the width of the graphene size in the direction of the migration path.
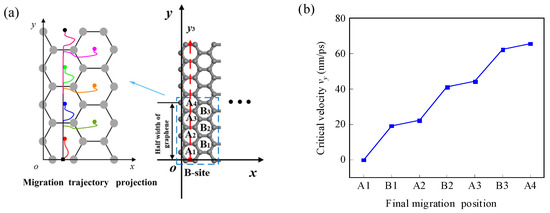
Figure 9.
(a) The projections of migration trajectories and the final positions of the Li-ion for different CIL velocities as it migrates along the y3 direction from the edge B-site. (b) The relationship between the CIL velocity and the final position.
3.3. Regulation of BN Doping on Li-Ion Migration Behavior
BN doping can change the potential energy curve of the graphene surface, reduce the adsorption energy at the doping position, and improve the adsorption stability of atoms/ions. In addition, the migration behavior of atoms/ions can be regulated by a reasonable design of the BN doping [36]. When a Li-ion migrates on the BN-doped graphene surface, the interaction energy and interaction force between the Li-ion and BN-doped graphene can be calculated by Equations (7)−(10) and parameters in the literature [36]. The lateral and normal forces and the energy barrier are all changed at the doping position, so the migration path, CIL velocity, and final migration position of the Li-ion are also affected.
3.3.1. Effect of BN Doping on the Migration Behavior of the Li-Ion along a Specific Internal Path
It is assumed that a Li-ion still migrates from the B-site along the y1 path on the surface of the graphene. Along the y1 path direction, the graphene has been partially doped with BN at three different positions (Figure 10a). The changes in the CIL velocities of Li-ions along the y1 path to the three adjacent equilibrium sites are given in Figure 10b. As can be seen in the figure, compared with the pristine graphene, the CIL velocities of Li-ions migrating into the BN-doped positions are smaller, that is, Li-ions are more likely to migrate to the doping site from the undoped graphene site. However, the CIL velocities of the Li-ion crossing the BN-doped positions increase, which means that it is more difficult for the Li-ion to migrate away from the BN-doped site. Figure 10c shows the interaction energy when the initial height of the Li-ion migration is the NEH, and it migrates along the y1 path on the surface of the pristine graphene BNG-1, BNG-2, and BNG-3 structures. It can be seen in the figure that the Li-ion has a lower adsorption energy and more stable adsorption at the BN-doped site. Thus, compared with the pristine graphene, the Li-ion is more likely to reach the BN-doped site and requires a smaller CIL velocity. However, at the next stable adsorption site adjacent to the BN-doped site, although the adsorption energy also decreases compared to the pristine graphene, the required CIL velocity increases due to the higher energy barrier needed to overcome to cross the doping site. Therefore, the CIL velocity of Li-ion migration can be regulated by local doping so as to control its final migration position.
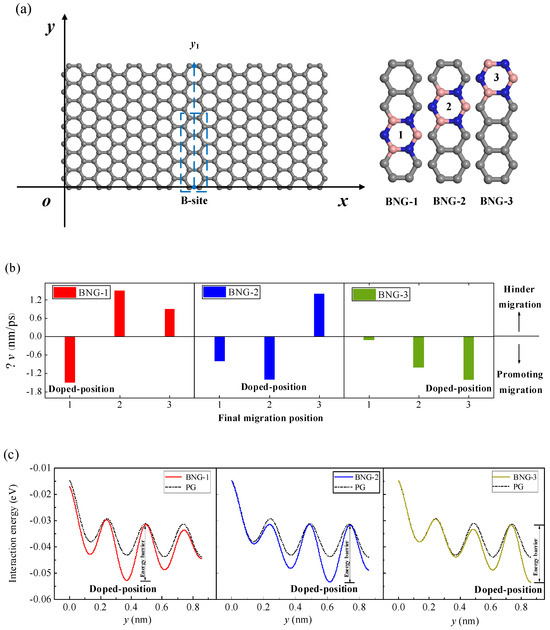
Figure 10.
(a) Three types of BN doping along the y1 path direction of the graphene (the dotted box shows the position of the three types of BN-doped graphene), (b) compared with the pristine graphene, the change Δv of the CIL velocity when the Li-ion migrates on the surface of three BN-doped graphenes, (c) the interaction energy of the Li-ion as it migrates along the y1 path on the surfaces of BNG-1, BNG-2, and BNG-3 at z = 0.233 nm.
3.3.2. Regulation of BN Doping on Li-ion Migration Behavior along a Specific Path at the Edge
According to the analyses in Section 4, as Li-ions migrate along the y3 path at the edge of the pristine graphene, there is x-directional displacement due to the existence of x-directional lateral force, causing the final migration position to be not all along the expected y3 path, and the relationship between the CIL velocity and the final position is no longer linear. The migration of Li-ions is actually a process in which it crosses one energy barrier after another with the help of the initial kinetic energy and the lateral force. If the energy barrier in the x-direction is increased, it is possible to control the Li-ion from producing displacement in the x-direction. As shown in Figure 11a, the edge of the graphene is doped with BN. As shown in Figure 11b, the energy curve changes significantly before and after doping, and the energy barrier of Li-ion migrating along the x-direction becomes larger after doping, thus limiting the movement of the Li-ion in the x-direction. As a result, the final position of the Li-ion can be restricted to the y3 path (Figure 11a). Moreover, the CIL velocity of Li-ion migration shows a linear relationship with the final migration position again (Figure 11c).
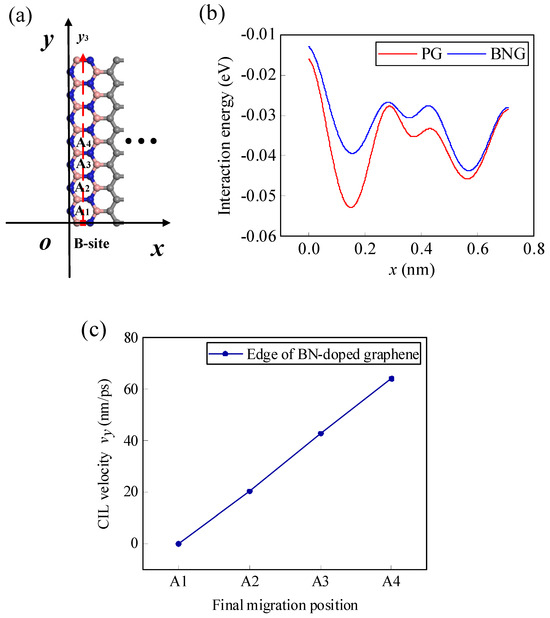
Figure 11.
(a) Schematic diagram of the zigzag edge of the BN line-doped graphene and the final migration positions of the Li-ion, (b) interaction energy curves along the x-direction before and after BN doping, and (c) the relationship between the CIL velocity and the final position.
4. Conclusions
In the research, the expressions of the interaction forces between an atom/ion and pristine/doped graphene were obtained using the potential function method. The migration mechanical behavior of atoms/ions on the surface of single-layer pristine/doped graphene was investigated using improved dynamical equations. The atoms/ions on the graphene surface are acted on by lateral forces in the x- and y-directions and normal forces in the z-direction. On the NEH surface, the normal force is zero, and the lateral force plays a dominant role in atom/ion migration. Outside the NEH surface, atoms/ions migrate under the action of both normal and lateral forces.
Taking the Li-ion as an example, as it migrates along specific paths within the graphene, it can migrate spontaneously at an initial velocity of zero with the combined action of normal and lateral forces. The final position of Li-ion migration is determined by the initial lateral velocity, and the CIL velocity is approximately linearly related to the final migration position. The initial normal velocity will affect the CIL velocity of the Li-ion near the starting position of the boundary. The CIL velocity required for different atoms/ions to migrate to the same position along a specific path on the graphene surface is different. Conversely, when the initial lateral velocity is the same, different atoms/ions will reach different final stable positions based on which atom/ion screening can be achieved.
When migrating along a specific path on the edge, the Li-ion will be displaced in the x-direction due to the existence of x-directional lateral force, and the final migration position will no longer be exactly on the specific path but will be offset in the x-direction. In this case, the CIL velocity is no longer linear to the final position. BN doping at the edge can change the energy barrier at the edge, thus preventing the deviation of the final migration position caused by the x-directional force. At the same time, BN doping in specific internal paths can change the CIL velocity at the doping position and then regulate the migration behavior of atoms/ions.
This research can provide theoretical reference for the application of graphene-based highly sensitive sensors, atom/ion screening devices, atom storage, etc. However, in this research, the thermal noise caused by Brownian motions and the influence of external electric fields were not taken into consideration, and they will be discussed in our future work.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/c10030059/s1, Table S1: The parameters of the dynamical equation [15].
Author Contributions
T.-K.Z.: methodology, investigation, software, data curation, visualization, validation, writing—original draft, and writing—review and editing. L.-J.Z.: investigation, validation, and writing—review and editing. J.-G.G.: supervision, methodology, validation, writing—original draft, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was founded by the National Natural Science Foundation of China (Grant No. 12372115, 12172250) and the Innovative Group Project of the National Natural Science Foundation of China (Grant No. 12021002).
Data Availability Statement
Data will be made available upon request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Liu, Y.L.; Xie, B.; Zhang, Z.; Zheng, Q.S.; Xu, Z.P. Mechanical properties of graphene papers. J. Mech. Phys. Solids 2012, 60, 591–605. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, K.; Dixit, A.R. A review of the mechanical and thermal properties of graphene and its hybrid polymer nanocomposites for structural applications. J. Mater. Sci. 2019, 54, 5992–6026. [Google Scholar] [CrossRef]
- Young, R.J.; Kinloch, I.A.; Gong, L.; Novoselov, K.S. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 2012, 72, 1459–1476. [Google Scholar] [CrossRef]
- Wang, J.; Chen, B.L. Adsorption and coadsorption of organic pollutants and a heavy metal by graphene oxide and reduced graphene materials. Chem. Eng. J. 2015, 281, 379–388. [Google Scholar] [CrossRef]
- Liu, X.; Sun, J.; Xu, X.T.; Alsaedi, A.; Hayat, T.; Li, J.X. Adsorption and desorption of U (VI) on different-size graphene oxide. Chem. Eng. J. 2019, 360, 941–950. [Google Scholar] [CrossRef]
- Bu, J.Q.; Yuan, L.; Zhang, N.; Liu, D.; Meng, Y.; Peng, X. High-efficiency adsorption of methylene blue dye from wastewater by a thiosemicarbazide functionalized graphene oxide composite. Diam. Relat. Mater. 2020, 101, 107604. [Google Scholar] [CrossRef]
- Suarez-Iglesias, O.; Collado, S.; Oulego, P.; Diaz, M. Graphene-family nanomaterials in wastewater treatment plants. Chem. Eng. J. 2017, 313, 121–135. [Google Scholar] [CrossRef]
- Chatterjee, S.G.; Chatterjee, S.; Ray, A.K.; Chakraborty, A.K. Graphene-metal oxide nanohybrids for toxic gas sensor: A review. Sens. Actuator B Chem. 2015, 221, 1170–1181. [Google Scholar] [CrossRef]
- Ye, M.H.; Zhang, Z.P.; Zhao, Y.; Qu, L.T. Graphene platforms for smart energy generation and storage. Joule 2018, 2, 245–268. [Google Scholar] [CrossRef]
- Wong, D.; Corsetti, F.; Wang, Y.; Brar, V.W.; Tsai, H.Z.; Wu, Q.; Kawakami, R.K.; Zettl, A.; Mostofi, A.A.; Lischner, J.; et al. Spatially resolving density-dependent screening around a single charged atom in graphene. Phys. Rev. B 2017, 95, 205419. [Google Scholar] [CrossRef]
- Ersan, G.; Apul, O.G.; Perreault, F.; Karanfil, T. Adsorption of organic contaminants by graphene nanosheets: A review. Water Res. 2017, 126, 385–398. [Google Scholar] [CrossRef] [PubMed]
- Velusamy, S.; Roy, A.; Sundaram, S.; Mallick, T.K. A review on heavy metal ions and containing dyes removal through graphene oxide-based adsorption strategies for textile wastewater treatment. Chem. Rec. 2021, 21, 1570–1610. [Google Scholar] [CrossRef] [PubMed]
- Hosseingholipourasl, A.; Ariffin, S.H.S.; Al-Otaibi, Y.D.; Akbari, E.; Hamid, F.K.H.; Koloor, S.S.R.; Petrů, M. Analytical approach to study sensing properties of graphene based gas sensor. Sensors 2020, 20, 1506. [Google Scholar] [CrossRef]
- Yu, D.Y.W.; Prikhodchenko, P.V.; Mason, C.W.; Batabyal, S.K.; Gun, J.; Sladkevich, S.; Medvedev, A.G.; Lev, O. High-capacity antimony sulphide nanoparticle-decorated graphene composite as anode for sodium-ion batteries. Nat. Commun. 2013, 4, 2922. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Guo, J.G. Theoretical characterization and application of mechanical behavior of atoms/ions migrating on graphene surface. Mater. Chem. Phys. 2021, 260, 124138. [Google Scholar] [CrossRef]
- Gan, Y.J.; Sun, L.T.; Banhart, F. One- and two-dimensional diffusion of metal atoms in graphene. Small 2008, 4, 587–591. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xiong, W.; Zhou, Y.S.; Lu, Y.F.; Zeng, X.C. An ab initio study of the nickel- catalyzed transformation of amorphous carbon into graphene in rapid thermal processing. Nanoscale 2016, 8, 9746–9755. [Google Scholar] [CrossRef]
- Yao, F.; Günes, F.; Ta, H.Q.; Lee, S.M.; Chae, S.J.; Sheem, K.Y.; Cojocaru, C.S.; Xie, S.S.; Lee, Y.H. Diffusion mechanism of lithium ion through basal plane of layered graphene. J. Am. Chem. Soc. 2012, 134, 8646–8654. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.Z.; Guo, J.G.; Zhou, L.J. Theoretical investigation on the adsorption and diffusion of lithium-ion on and between graphene layers with size and defect effects. Adsorpt. Sci. Technol. 2016, 34, 212. [Google Scholar] [CrossRef]
- Li, M.; Guo, J.G. Theoretical study for adsorption and migration behavior of atoms/ions on sinusoidal corrugated graphene surface. Mater. Chem. Phys. 2020, 254, 123527. [Google Scholar] [CrossRef]
- Leggesse, E.G.; Chen, C.L.; Jiang, J.C. Lithium diffusion in graphene and graphite: Effect of edge morphology. Carbon 2016, 103, 209–216. [Google Scholar] [CrossRef]
- Xian, L.; Chou, M.Y. Diffusion of Si and C atoms on and between graphene layers. J. Phys. D Appl. Phys. 2012, 45, 455309. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, L.T.; Xu, Z.J.; Krasheninnikov, A.V.; Huai, P.; Zhu, Z.Y.; Banhart, F. Migration of gold atoms in graphene ribbons: Role of the edges. Phys. Rev. B 2010, 81, 125425. [Google Scholar] [CrossRef]
- Tang, Y.N.; Yang, Z.X.; Dai, X.Q. Trapping of metal atoms in the defects on graphene. J. Chem. Phys. 2011, 135, 224704. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.H.; Zhao, J. The effect of carbon defects on Cl anion diffusion in graphene based on first principles calculations. Mater. Res. Express 2017, 4, 075604. [Google Scholar] [CrossRef]
- Tachikawa, H.; Kawabata, H. DFT and direct MD study of the diffusion of sodium ion on graphenes. Thin Solid Films 2009, 518, 873–876. [Google Scholar] [CrossRef]
- Tachikawa, H.; Iyama, T.; Kawabata, H. Effects of fluorine atom substitution of graphene edge site on the diffusion of lithium ion. Jpn. J. Appl. Phys. 2010, 49, 01AH02. [Google Scholar] [CrossRef]
- Han, D.; Wang, X.; Zhao, Y.B.; Chen, Y.; Tang, M.X.; Zhao, Z.Q. High-quality graphene synthesis on amorphous SiC through a rapid thermal treatment. Carbon 2017, 124, 105–110. [Google Scholar] [CrossRef]
- Mishra, N.; Boeckl, J.; Motta, N.; Iacopi, F. Graphene growth on silicon carbide: A review. Phys. Status Solidi A 2016, 213, 2277–2289. [Google Scholar] [CrossRef]
- Chen, K.; Sun, Z.H.; Fang, R.P.; Shi, Y.; Cheng, H.M.; Li, F. Metal-organic frameworks (MOFs)-derived nitrogen-doped porous carbon anchored on graphene with multifunctional effects for lithium-sulfur batteries. Adv. Funct. Mater. 2018, 28, 1707592. [Google Scholar] [CrossRef]
- Nong, W.; Liang, H.K.; Qin, S.H.; Li, Y.; Wang, C.X. Computational design of two-dimensional boron-containing compounds as efficient metal-free electrocatalysts toward nitrogen reduction independent of heteroatom doping. ACS Appl. Mater. Inter. 2020, 12, 50505–505015. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.L.; Na, N.; Mohamadi, A. Investigation the application of pristine graphdiyne (GDY) and boron-doped graphdiyne (BGDY) as an electronic sensor for detection of anticancer drug. Comput. Theor. Chem. 2020, 1190, 112996. [Google Scholar] [CrossRef]
- Li, J.; Lin, L.; Rui, D.; Li, Q.; Zhang, J.; Kang, N.; Zhang, Y.; Peng, H.; Liu, Z.; Xu, H.Q. Electron–hole symmetry breaking in charge transport in nitrogen-doped graphene. ACS Nano 2017, 11, 4641–4650. [Google Scholar] [CrossRef] [PubMed]
- Marconcini, P.; Cresti, A.; Roche, S. Effect of the channel length on the transport characteristics of transistors based on boron-doped graphene ribbons. Materials 2018, 11, 667. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Shen, Z.; Liu, A.Q.; Kuo, J.-L. Band gap opening of graphene by doping small boron nitride domains. Nanoscale 2012, 4, 2157–2165. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.K.; Guo, J.G.; Zhou, L.J. Theoretical studies on adsorption and migration of atoms/ions on the surface of boron, nitrogen and boron nitride doped graphene. Appl. Phys. A 2022, 128, 887. [Google Scholar] [CrossRef]
- Nachimuthu, S.; Lai, P.J.; Leggesse, E.G.; Jiang, J.C. A first principles study on boron-doped graphene decorated by Ni-Ti-Mg atoms for enhanced hydrogen storage performance. Sci. Rep. 2015, 5, 16797. [Google Scholar] [CrossRef]
- Das, D.; Kim, S.; Lee, K.R.; Singh, A.K. Li diffusion through doped and defected graphene. Phys. Chem. Chem. Phys. 2013, 15, 15128–15134. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.H.; Ren, Z.Y.; Wan, L.J.; Zheng, J.M.; Guo, P.; Zhou, Y.X. Density functional theory prediction for diffusion of lithium on boron-doped graphene surface. Appl. Surf. Sci. 2011, 257, 7443–7446. [Google Scholar] [CrossRef]
- Lee, H.W.; Moon, H.S.; Hur, J.; Kim, I.T.; Park, M.S.; Yun, J.M.; Kim, K.H.; Lee, S.G. Mechanism of sodium adsorption on N-doped graphene nanoribbons for sodium ion battery applications: A density functional theory approach. Carbon 2017, 119, 492–501. [Google Scholar] [CrossRef]
- Petrushenko, I.K.; Petrushenko, K.B. Adsorption of diatomic molecules on graphene, h-BN and their BNC heterostructures: DFT study. Diam. Relat. Mater. 2019, 100, 107575. [Google Scholar] [CrossRef]
- Ornstein, R.L.; Rein, R.; Breen, D.L.; Macelroy, R.D. An optimized potential function for the calculation of nucleic acid interaction energies I. Base stacking. Biopolymers 1978, 17, 2341–2360. [Google Scholar] [CrossRef] [PubMed]
- Hölscher, H.; Schwarz, U.D.; Wiesendanger, R. Modelling of the scan process in lateral force microscopy. Surf. Sci. 1997, 375, 395–402. [Google Scholar] [CrossRef]
- Zheng, J.M.; Ren, Z.Y.; Guo, P.; Fang, L.; Fan, J. Diffusion of Li+ ion on graphene: A DFT study. Appl. Surf. Sci. 2011, 258, 1651–1655. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).