Experimental Volumetric Hydrogen Uptake Determination at 77 K of Commercially Available Metal-Organic Framework Materials
Abstract
:1. Introduction
2. Materials and Methods
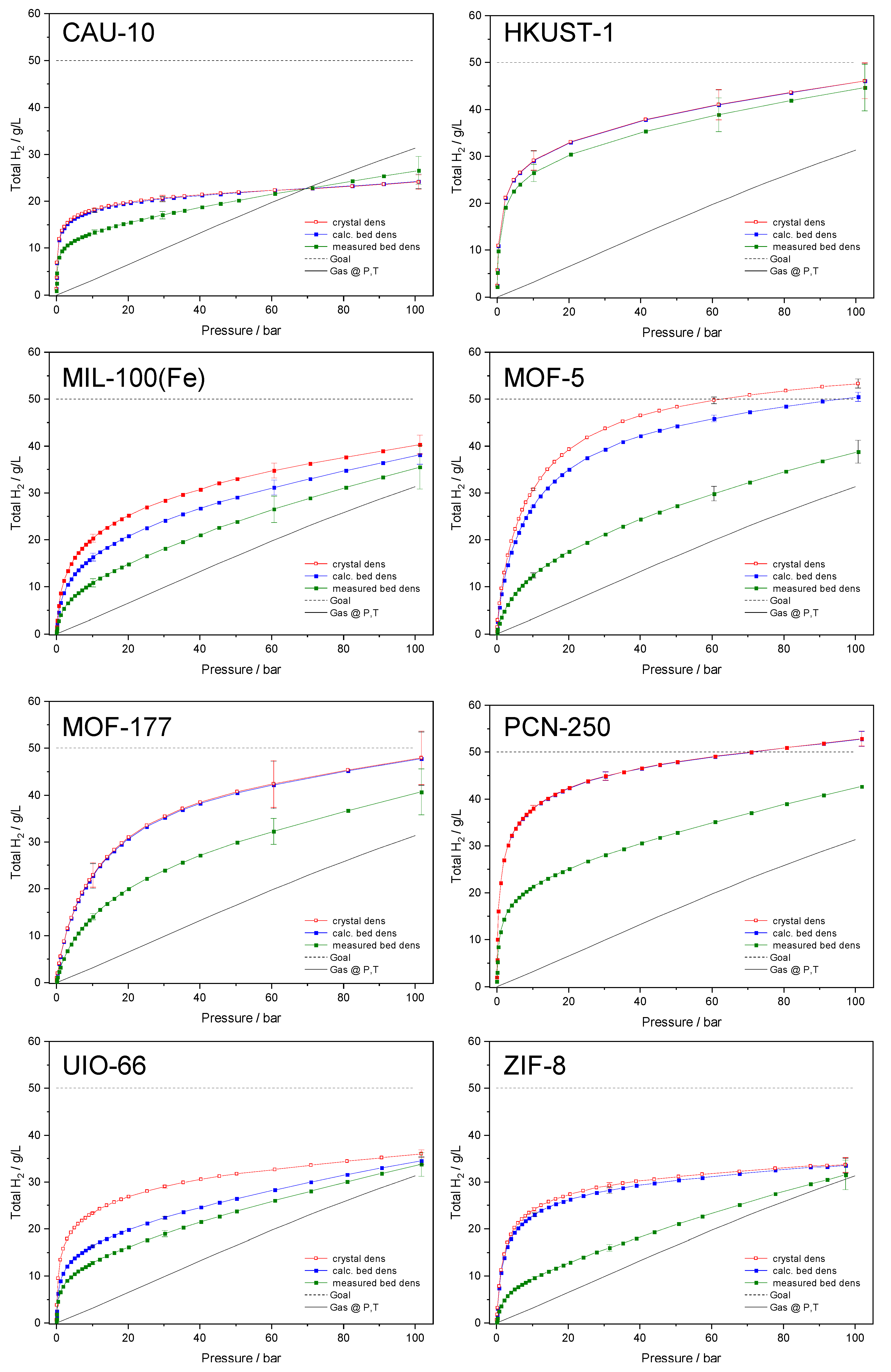
3. Results
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Andersson, J.; Gronkvist, S. Large-scale storage of hydrogen. Int. J. Hydrogen Energ. 2019, 44, 11901–11919. [Google Scholar] [CrossRef]
- Abe, J.O.; Popoola, A.P.I.; Ajenifuja, E.; Popoola, O.M. Hydrogen energy, economy and storage: Review and recommendation. Int. J. Hydrogen Energ. 2019, 44, 15072–15086. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, L.; Amer, W.A.; Yu, H.; Ji, J.; Huang, L.; Shan, J.; Tong, R. Hydrogen Storage in Metal-Organic Frameworks. J. Inorg. Organomet. Polym. Mater. 2012, 23, 270–285. [Google Scholar] [CrossRef]
- Schlichtenmayer, M.; Hirscher, M. Nanosponges for hydrogen storage. J. Mater. Chem. 2012, 22, 10134–10143. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, Y.P.; Sun, Y. Enhanced storage of hydrogen at the temperature of liquid nitrogen. Int. J. Hydrogen Energ. 2004, 29, 319–322. [Google Scholar] [CrossRef]
- Chanchetti, L.F.; Leiva, D.R.; de Faria, L.I.L.; Ishikawa, T.T. A scientometric review of research in hydrogen storage materials. Int. J. Hydrogen Energ. 2020, 45, 5356–5366. [Google Scholar] [CrossRef]
- Dalebrook, A.F.; Gan, W.; Grasemann, M.; Moret, S.; Laurenczy, G. Hydrogen storage: Beyond conventional methods. Chem. Commun. 2013, 49, 8735–8751. [Google Scholar] [CrossRef]
- Aboutalebi, S.H.; Aminorroaya-Yamini, S.; Nevirkovets, I.; Konstantinov, K.; Liu, H.K. Enhanced Hydrogen Storage in Graphene Oxide-MWCNTs Composite at Room Temperature. Adv. Energy Mater. 2012, 2, 1439–1446. [Google Scholar] [CrossRef]
- Shet, S.P.; Priya, S.S.; Sudhakar, K.; Tahir, M. A review on current trends in potential use of metal-organic framework for hydrogen storage. Int. J. Hydrogen Energ. 2021, 46, 11782–11803. [Google Scholar] [CrossRef]
- Kalidindi, S.B.; Fischer, R.A. Covalent organic frameworks and their metal nanoparticle composites: Prospects for hydrogen storage. Phys. Status Solidi B Basic Solid State Phys. 2013, 250, 1119–1127. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Yu, F.; Ma, J. Nanoconfinement engineering for enchanced adsorption of carbon materials, metal-organic frameworks, mesoporous silica, MXenes and porous organic polymers: A review. Environ. Chem. Lett. 2021. [Google Scholar] [CrossRef]
- Poirier, E.; Dailly, A. On the nature of the adsorbed hydrogen phase in microporous metal-organic frameworks at supercritical temperatures. Langmuir 2009, 25, 12169–12176. [Google Scholar] [CrossRef] [Green Version]
- Nalaparaju, A.; Babarao, R.; Zhao, X.S.; Jiang, J.W. Atomistic insight into adsorption, mobility, and vibration of water in ion-exchanged zeolite-like metal-organic frameworks. ACS Nano 2009, 3, 2563–2572. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, Q.; Zhang, L.; Liu, Y.C.; Kang, Y. Adsorption sites of hydrogen in zeolitic imidazolate frameworks. J. Phys. Chem. B 2009, 113, 11049–11053. [Google Scholar] [CrossRef] [PubMed]
- Gygi, D.; Bloch, E.D.; Mason, J.A.; Hudson, M.R.; Gonzalez, M.I.; Siegelman, R.L.; Darwish, T.A.; Queen, W.L.; Brown, C.M.; Long, J.R. Hydrogen storage in the expanded pore metal-organic frameworks M2 (dobpdc) (M = Mg, Mn, Fe, Co, Ni, Zn). Chem. Mater. 2016, 28, 1128–1138. [Google Scholar] [CrossRef]
- Furukawa, H.; Ko, N.; Go, Y.B.; Aratani, N.; Choi, S.B.; Choi, E.; Yazaydin, A.O.; Snurr, R.Q.; O’Keeffe, M.; Kim, J.; et al. Ultrahigh porosity in metal-organic frameworks. Science 2010, 329, 424–428. [Google Scholar] [CrossRef] [Green Version]
- Balderas-Xicohténcatl, R.; Schlichtenmayer, M.; Hirscher, M. Volumetric Hydrogen Storage Capacity in Metal-Organic Frameworks. Energy Technol. 2018, 6, 578–582. [Google Scholar] [CrossRef] [Green Version]
- Suresh, K.; Aulakh, D.; Purewal, J.; Siegel, D.J.; Veenstra, M.; Matzger, A.J. Optimizing Hydrogen Storage in MOFs through Engineering of Crystal Morphology and Control of Crystal Size. J. Am. Chem. Soc. 2021, 143, 10727–10734. [Google Scholar] [CrossRef]
- Wang, T.C.; Wright, A.M.; Hoover, W.J.; Stoffel, K.J.; Richardson, R.K.; Rodriguez, S.; Flores, R.C.; Siegfried, J.P.; Vermeulen, N.A.; Fuller, P.E.; et al. Surviving Under Pressure: The Role of Solvent, Crystal Size, and Morphology During Pelletization of Metal-Organic Frameworks. ACS Appl. Mater. Interfaces 2021, 13, 52106–52112. [Google Scholar] [CrossRef] [PubMed]
- Severino, M.I.; Gkaniatsou, E.; Nouar, F.; Pinto, M.L.; Serre, C. MOFs industrialization: A complete assessment of production costs. Faraday Discuss. 2021, 231, 326–341. [Google Scholar] [CrossRef]
- Broom, D.P.; Hirscher, M. Improving Reproducibility in Hydrogen Storage Material Research. ChemPhysChem 2021, 22, 2141–2157. [Google Scholar] [CrossRef]
- Tranchemontagne, D.J.; Hunt, J.R.; Yaghi, O.M. Room temperature synthesis of metal-organic frameworks: MOF-5, MOF-74, MOF-177, MOF-199, and IRMOF-0. Tetrahedron 2008, 64, 8553–8557. [Google Scholar] [CrossRef]
- Saha, D.; Deng, S.G. Structural Stability of Metal Organic Framework MOF-177. J. Phys. Chem. Lett. 2010, 1, 73–78. [Google Scholar] [CrossRef]
- Ming, Y.; Purewal, J.; Yang, J.; Xu, C.C.; Veenstra, M.; Gaab, M.; Muller, U.; Siegel, D.J. Stability of MOF-5 in a hydrogen gas environment containing fueling station impurities. Int. J. Hydrogen Energ. 2016, 41, 9374–9382. [Google Scholar] [CrossRef] [Green Version]
- Bae, J.; Choi, J.S.; Hwang, S.; Yun, W.S.; Song, D.; Lee, J.; Jeong, N.C. Multiple Coordination Exchanges for Room-Temperature Activation of Open-Metal Sites in Metal-Organic Frameworks. ACS Appl. Mater. Interfaces 2017, 9, 24743–24752. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Leachman, J.W.; Jacobsen, R.T.; Penoncello, S.G.; Lemmon, E.W. Fundamental Equations of State for Parahydrogen, Normal Hydrogen, and Orthohydrogen. J. Phys. Chem. Ref. Data 2009, 38, 721–748. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 6 March 2020).
- Blach, T.P.; Gray, E.M. Sieverts apparatus and methodology for accurate determination of hydrogen uptake by light-atom hosts. J. Alloy. Compd. 2007, 446, 692–697. [Google Scholar] [CrossRef]
- Purewal, J.; Veenstra, M.; Tamburello, D.; Ahmed, A.; Matzger, A.J.; Wong-Foy, A.G.; Seth, S.; Liu, Y.Y.; Siegel, D.J. Estimation of system-level hydrogen storage for metal-organic frameworks with high volumetric storage density. Int. J. Hydrog. Energy 2019, 44, 15135–15145. [Google Scholar] [CrossRef]
- Chavan, S.; Vitillo, J.G.; Gianolio, D.; Zavorotynska, O.; Civalleri, B.; Jakobsen, S.; Nilsen, M.H.; Valenzano, L.; Lamberti, C.; Lillerud, K.P.; et al. H2 storage in isostructural UiO-67 and UiO-66 MOFs. Phys. Chem. Chem. Phys. 2012, 14, 1614–1626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Lange, M.F.; van Velzen, B.L.; Ottevanger, C.P.; Verouden, K.J.; Lin, L.C.; Vlugt, T.J.; Gascon, J.; Kapteijn, F. Metal-Organic Frameworks in Adsorption-Driven Heat Pumps: The Potential of Alcohols as Working Fluids. Langmuir 2015, 31, 12783–12796. [Google Scholar] [CrossRef]
- Yuan, S.; Feng, L.; Wang, K.; Pang, J.; Bosch, M.; Lollar, C.; Sun, Y.; Qin, J.; Yang, X.; Zhang, P.; et al. Stable Metal-Organic Frameworks: Design, Synthesis, and Applications. Adv. Mater. 2018, 30, e1704303. [Google Scholar] [CrossRef] [Green Version]
- Villajos, J.A.; Zimathies, A.; Prinz, C. A fast procedure for the estimation of the hydrogen storage capacity by cryoadsorption of metal-organic framework materials from their available porous properties. Int. J. Hydrogen Energ. 2020, 46, 29323–29331. [Google Scholar] [CrossRef]
- Horcajada, P.; Surble, S.; Serre, C.; Hong, D.Y.; Seo, Y.K.; Chang, J.S.; Greneche, J.M.; Margiolaki, I.; Ferey, G. Synthesis and catalytic properties of MIL-100(Fe), an iron(III) carboxylate with large pores. Chem. Commun. 2007, 27, 2820–2822. [Google Scholar] [CrossRef]
- Seo, Y.K.; Yoon, J.W.; Lee, J.S.; Lee, U.H.; Hwang, Y.K.; Jun, C.H.; Horcajada, P.; Serre, C.; Chang, J.S. Large scale fluorine-free synthesis of hierarchically porous iron(III) trimesate MIL-100(Fe) with a zeolite MTN topology. Microporous Mesoporous Mater. 2012, 157, 137–145. [Google Scholar] [CrossRef]
- Winarta, J.; Shan, B.; Mcintyre, S.M.; Ye, L.; Wang, C.; Liu, J.; Mu, B. A decade of UiO-66 research: A historic review of dynamic structure, synthesis mechanisms, and characterization techniques of an archetypal metal-organic framework. Cryst. Growth Des. 2019, 20, 1347–1362. [Google Scholar] [CrossRef]
- Vo, T.K.; Le, V.N.; Yoo, K.S.; Song, M.; Kim, D.; Kim, J. Facile Synthesis of UiO-66(Zr) Using a Microwave-Assisted Continuous Tubular Reactor and Its Application for Toluene Adsorption. Cryst. Growth Des. 2019, 19, 4949–4956. [Google Scholar] [CrossRef]
- Chung, Y.G.; Camp, J.; Haranczyk, M.; Sikora, B.J.; Bury, W.; Krungleviciute, V.; Yildirim, T.; Farha, O.K.; Sholl, D.S.; Snurr, R.Q. Computation-Ready, Experimental Metal-Organic Frameworks: A Tool To Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mater. 2014, 26, 6185–6192. [Google Scholar] [CrossRef]
- Zlotea, C.; Moretto, P.; Steriotis, T. A Round Robin characterisation of the hydrogen sorption properties of a carbon based material. Int. J. Hydrogen Energ. 2009, 34, 3044–3057. [Google Scholar] [CrossRef]
- Broom, D.P.; Hirscher, M. Irreproducibility in hydrogen storage material research. Energy Environ. Sci. 2016, 9, 3368–3380. [Google Scholar] [CrossRef] [Green Version]
- Hurst, K.E.; Gennett, T.; Adams, J.; Allendorf, M.D.; Balderas-Xicohtencatl, R.; Bielewski, M.; Edwards, B.; Espinal, L.; Fultz, B.; Hirscher, M.; et al. An International Laboratory Comparison Study of Volumetric and Gravimetric Hydrogen Adsorption Measurements. ChemPhysChem 2019, 20, 1997–2009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, B.; Ockwig, N.W.; Millward, A.R.; Contreras, D.S.; Yaghi, O.M. High H2 adsorption in a microporous metal-organic framework with open metal sites. Angew. Chem. Int. Ed. 2005, 44, 4745–4749. [Google Scholar] [CrossRef]
- Zhou, H.-C.; Liu, D.-J. Final Project Report for DOE/EERE High-Capacity and Low-Cost Hydrogen-Storage Sorbents for Automotive Applications; Texas A & M Univ.: College Station, TX, USA, 2017. [Google Scholar]
- Yoon, J.W.; Seo, Y.K.; Hwang, Y.K.; Chang, J.S.; Leclerc, H.; Wuttke, S.; Bazin, P.; Vimont, A.; Daturi, M.; Bloch, E.; et al. Controlled reducibility of a metal-organic framework with coordinatively unsaturated sites for preferential gas sorption. Angew. Chem. Int. Ed. Engl. 2010, 49, 5949–5952. [Google Scholar] [CrossRef]
- Liu, Y.; Kabbour, H.; Brown, C.M.; Neumann, D.A.; Ahn, C.C. Increasing the density of adsorbed hydrogen with coordinatively unsaturated metal centers in metal-organic frameworks. Langmuir 2008, 24, 4772–4777. [Google Scholar] [CrossRef]
- Fairen-Jimenez, D.; Moggach, S.A.; Wharmby, M.T.; Wright, P.A.; Parsons, S.; Duren, T. Opening the gate: Framework flexibility in ZIF-8 explored by experiments and simulations. J. Am. Chem. Soc. 2011, 133, 8900–8902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, T.; Wharmby, M.T.; Parra, J.B.; Ania, C.O.; Fairen-Jimenez, D. Role of crystal size on swing-effect and adsorption induced structure transition of ZIF-8. Dalton Trans. 2016, 45, 6893–6900. [Google Scholar] [CrossRef] [Green Version]
- Broom, D.P.; Webb, C.J.; Fanourgakis, G.S.; Froudakis, G.E.; Trikalitis, P.N.; Hirscher, M. Concepts for improving hydrogen storage in nanoporous materials. Int. J. Hydrogen Energ. 2019, 44, 7768–7779. [Google Scholar] [CrossRef]
- Gomez-Gualdron, D.A.; Wang, T.C.; Garcia-Holley, P.; Sawelewa, R.M.; Argueta, E.; Snurr, R.Q.; Hupp, J.T.; Yildirim, T.; Farha, O.K. Understanding Volumetric and Gravimetric Hydrogen Adsorption Trade-off in Metal-Organic Frameworks. ACS Appl. Mater. Interfaces 2017, 9, 33419–33428. [Google Scholar] [CrossRef]
- Yan, Y.; da Silva, I.; Blake, A.J.; Dailly, A.; Manuel, P.; Yang, S.; Schroder, M. High Volumetric Hydrogen Adsorption in a Porous Anthracene-Decorated Metal-Organic Framework. Inorg. Chem. 2018, 57, 12050–12055. [Google Scholar] [CrossRef] [Green Version]
- Parilla, P.A.; Gross, K.; Hurst, K.; Gennett, T. Recommended volumetric capacity definitions and protocols for accurate, standardized and unambiguous metrics for hydrogen storage materials. Appl. Phys. A-Mater. 2016, 122, 201. [Google Scholar] [CrossRef]
- DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles. Available online: https://www.energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles (accessed on 30 November 2021).
- Ahmed, A.; Seth, S.; Purewal, J.; Wong-Foy, A.G.; Veenstra, M.; Matzger, A.J.; Siegel, D.J. Exceptional hydrogen storage achieved by screening nearly half a million metal-organic frameworks. Nat. Commun. 2019, 10, 1568. [Google Scholar] [CrossRef] [Green Version]
- DOE Technical Targets for Hydrogen Storage Systems for Portable Power Equipment. Available online: https://www.energy.gov/eere/fuelcells/doe-technical-targets-hydrogen-storage-systems-portable-power-equipment (accessed on 30 November 2021).
- Collings, I.E.; Goodwin, A.L. Metal-organic frameworks under pressure. J. Appl. Phys. 2019, 126, 181101. [Google Scholar] [CrossRef] [Green Version]
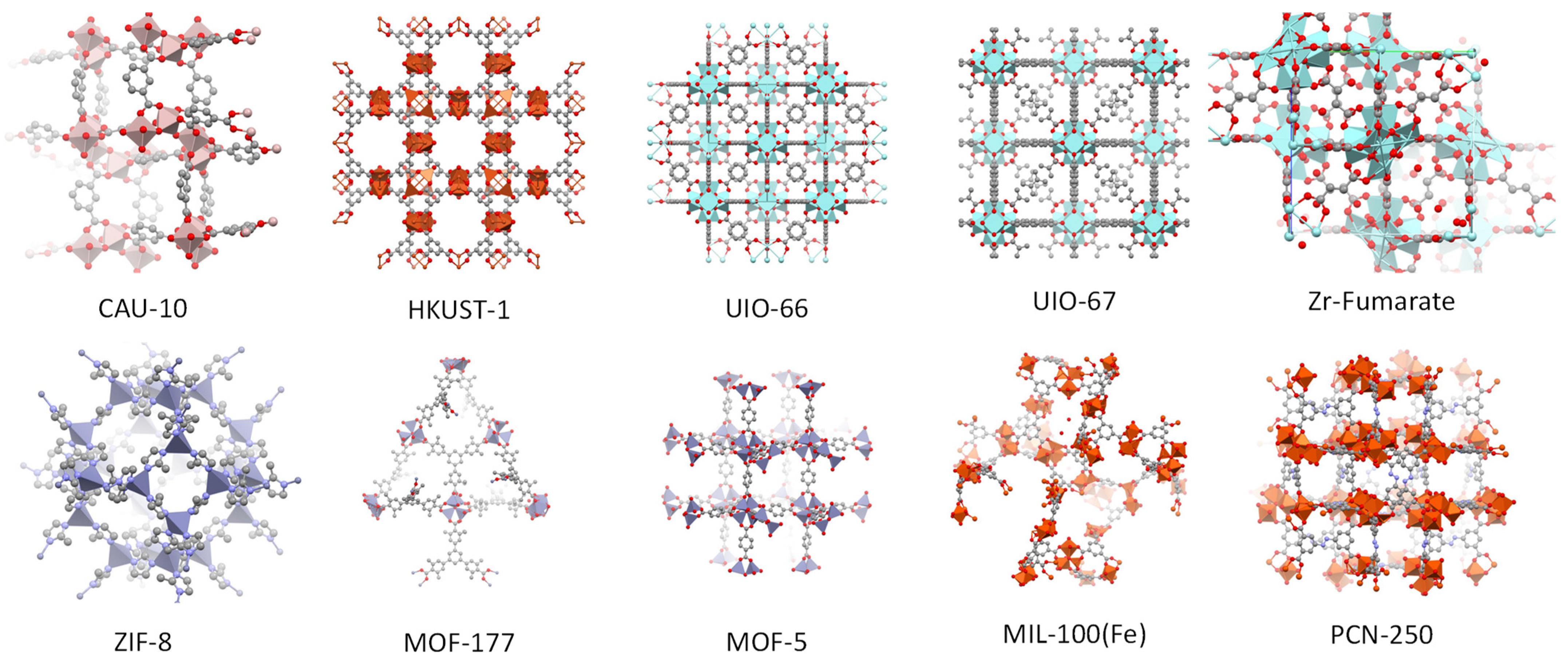
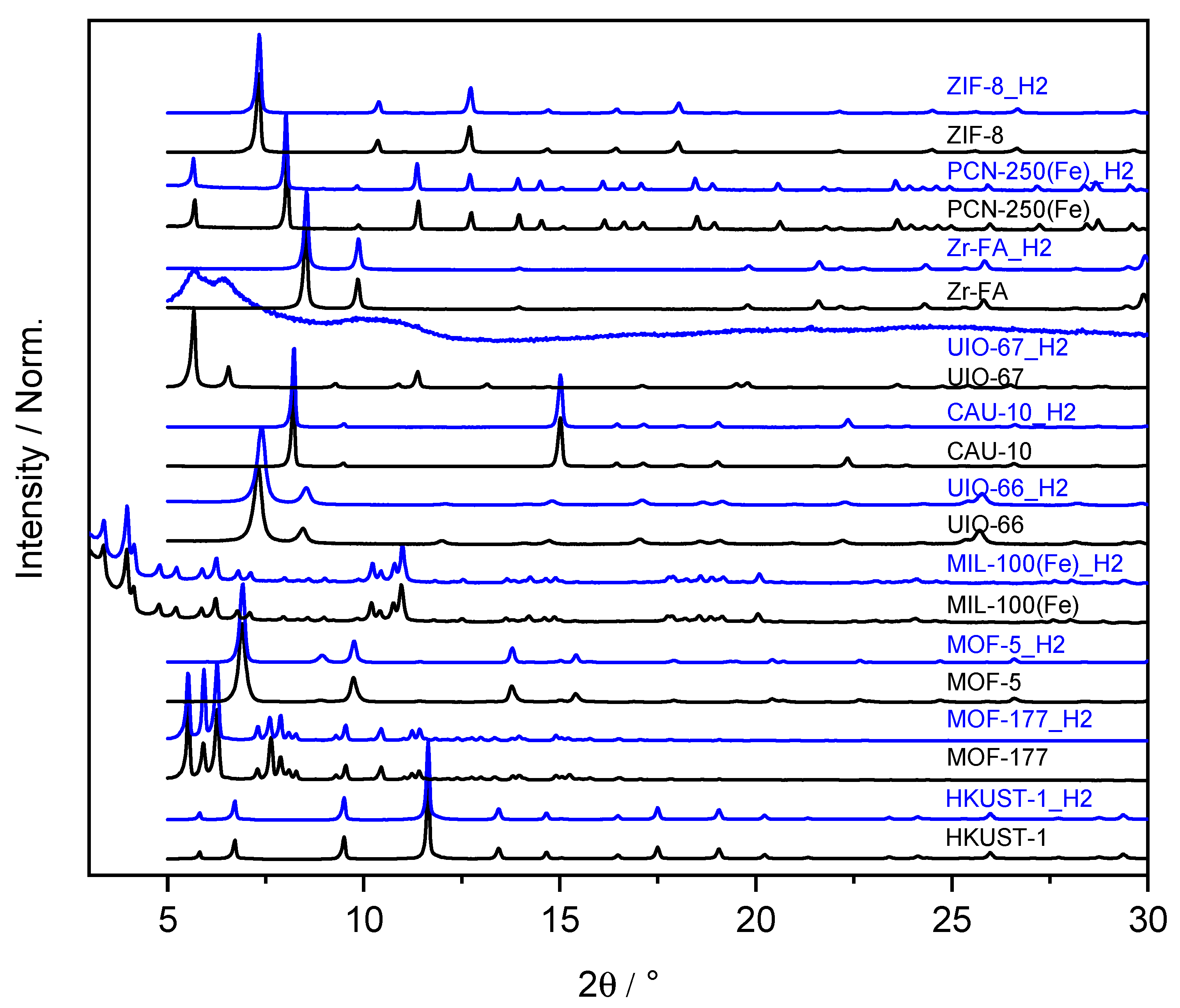
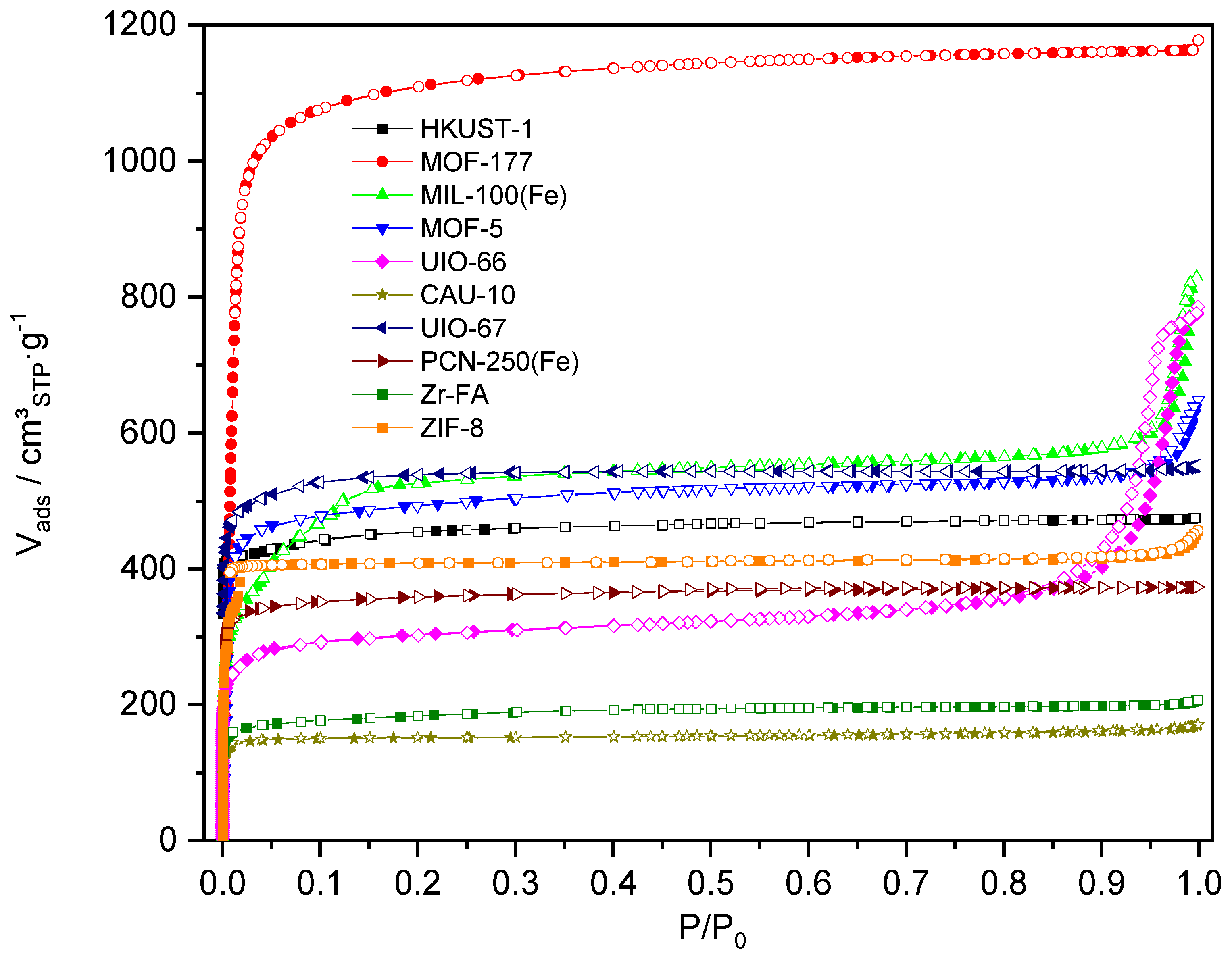
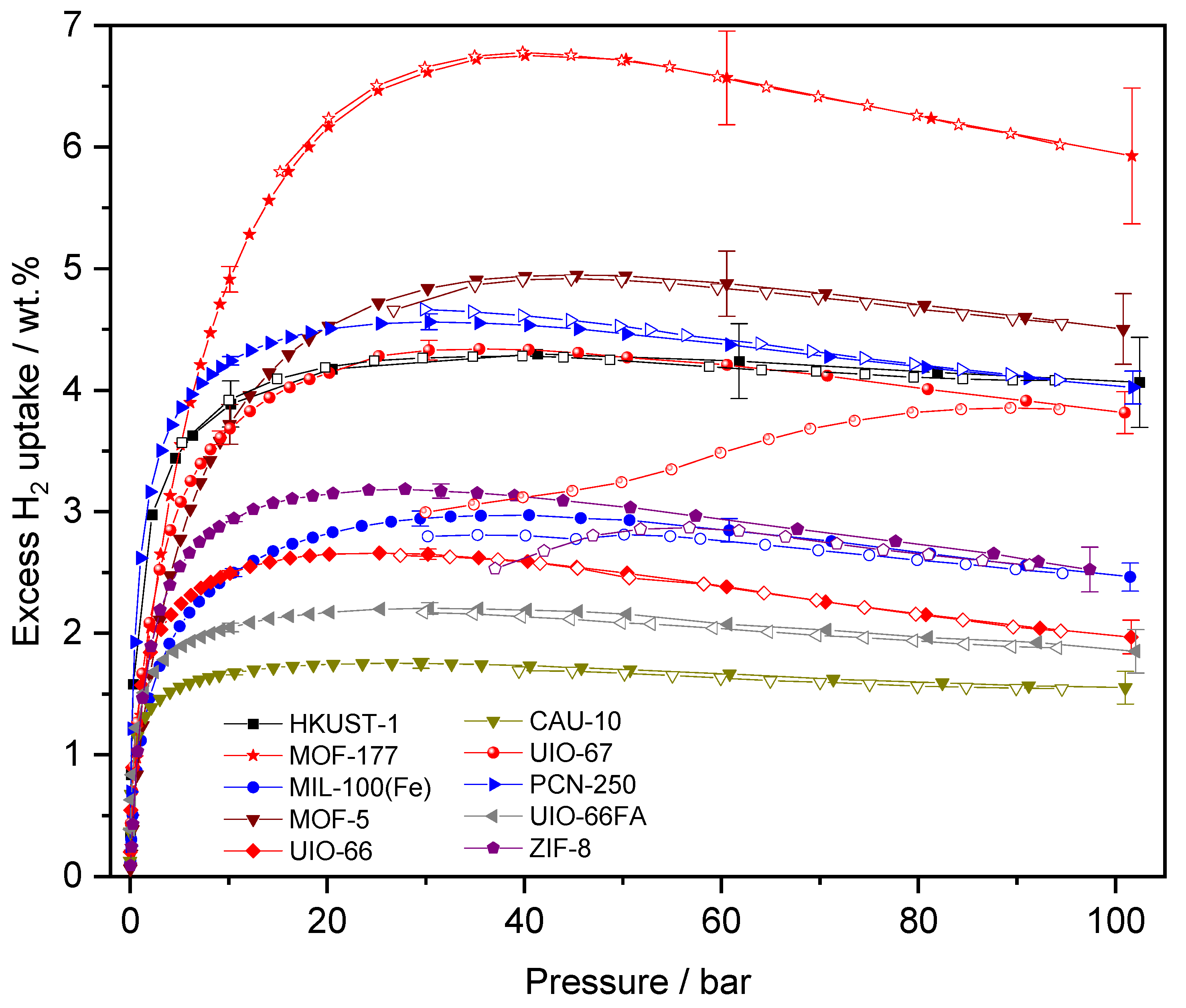

| Name | ABET (m²·g−1) | Vp 1 (cm³·g−1) | Vµp 2 (cm³·g−1) | Tactivation 3 (°C) |
|---|---|---|---|---|
| MOF-177 | 4449.29 | 1.82 ± 0.01 | 1.80 ± 0.01 | 120 |
| MOF-5 | 1976.50 | 1.00 ± 0.01 | 0.80 ± 0.01 | 120 |
| UIO-67 | 2135.00 | 0.85 ± 0.01 | 0.84 ± 0.01 | 120 |
| MIL-100(Fe) | 2015.00 | 1.28 ± 0.01 | 0.88 ± 0.01 | 150 |
| PCN-250(Fe) | 1811.30 | 0.72 ± 0.01 | 0.72 ± 0.01 | 190 |
| HKUST-1 | 1800.16 | 0.73 ± 0.01 | 0.73 ± 0.01 | 200 |
| ZIF-8 | 1734.03 | 0.71 ± 0.01 | 0.63 ± 0.01 | 200 |
| UIO-66 | 1201.54 | 1.22 ± 0.01 | 0.62 ± 0.01 | 150 |
| Zr-FA | 717.91 | 0.32 ± 0.01 | 0.31 ± 0.01 | 120 |
| CAU-10 | 629.65 | 0.26 ± 0.01 | 0.25 ± 0.01 | 100 |
| Name | ρsk 1 (g·cm−3) | ρcr 2 (g·cm−3) | ρbed,calc 3 (g·cm−3) | ρcr 4 (g·cm−3) | ρbed,meas 5 (g·cm−3) |
|---|---|---|---|---|---|
| MOF-177 | 1.46 ± 0.03 | 0.40 ± 0.01 | 0.40 ± 0.01 | 0.43 | 0.22 ± 0.01 |
| MOF-5 | 1.87 ± 0.04 | 0.75 ± 0.02 | 0.65 ± 0.02 | 0.60 | 0.25 ± 0.02 |
| UIO-67 | 1.70 ± 0.03 | 0.70 ± 0.02 | 0.69 ± 0.02 | 0.73 | n.a. |
| MIL-100(Fe) | 2.28 ± 0.05 | 0.77 ± 0.02 | 0.59 ± 0.02 | 0.68 | 0.34 ± 0.02 |
| PCN-250(Fe) | 1.98 ± 0.04 | 0.82 ± 0.03 | 0.81 ± 0.03 | 0.89 | 0.42 ± 0.03 |
| HKUST-1 | 1.69 ± 0.03 | 0.74 ± 0.02 | 0.74 ± 0.02 | 0.88 | 0.67 ± 0.04 |
| ZIF-8 | 1.41 ± 0.03 | 0.75 ± 0.03 | 0.71 ± 0.02 | 0.92 | 0.22 ± 0.01 |
| UIO-66 | 2.09 ± 0.04 | 0.92 ± 0.03 | 0.59 ± 0.02 | 1.20 | 0.43 ± 0.03 |
| Zr-FA | 2.12 ± 0.04 | 1.28 ± 0.07 | 1.26 ± 0.06 | 1.57 | n.a. |
| CAU-10 | 1.37 ± 0.03 | 1.02 ± 0.06 | 1.00 ± 0.06 | 3.20 | 0.68 ± 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villajos, J.A. Experimental Volumetric Hydrogen Uptake Determination at 77 K of Commercially Available Metal-Organic Framework Materials. C 2022, 8, 5. https://doi.org/10.3390/c8010005
Villajos JA. Experimental Volumetric Hydrogen Uptake Determination at 77 K of Commercially Available Metal-Organic Framework Materials. C. 2022; 8(1):5. https://doi.org/10.3390/c8010005
Chicago/Turabian StyleVillajos, Jose A. 2022. "Experimental Volumetric Hydrogen Uptake Determination at 77 K of Commercially Available Metal-Organic Framework Materials" C 8, no. 1: 5. https://doi.org/10.3390/c8010005
APA StyleVillajos, J. A. (2022). Experimental Volumetric Hydrogen Uptake Determination at 77 K of Commercially Available Metal-Organic Framework Materials. C, 8(1), 5. https://doi.org/10.3390/c8010005






